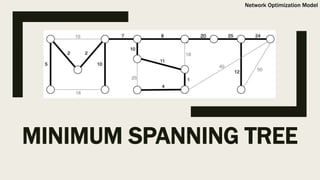
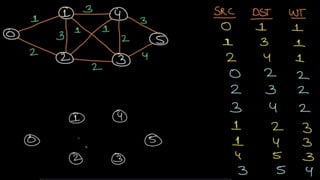
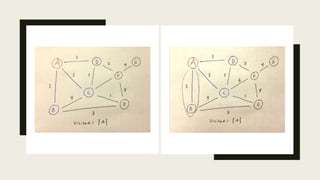
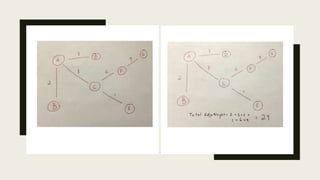
The document discusses the Travelling Salesman Problem (TSP), which involves finding the shortest route visiting each city once and returning to the start. It describes two phases of solving TSP using methods like the Hungarian method and inspection, along with examples and cost matrices. Additionally, it introduces minimum spanning trees and algorithms like Kruskal's and Prim's for optimizing network structures.

1. THE TRAVELLING
SALESMAN
PROBLEM
Reported by: Kimberley E. Ga
Network Optimization Model

2. Given a set of cities and distance
between every pair of cities, the
problem is to find the shortest
possible route that visits every city
exactly once and returns to the
starting point
WHAT
IS
TSP?
The travelling salesman problem

3. MAIN CONDITION FOR TSP
The salesman starts from his home city, he must
visit every city exactly once and returns to his
home city.

4. PHASE I PHASE II
 TSP can be first solved by
Assignment Problem (AP)
using Hungarian Method to
find the optimum solution.
 Then check the TSP
condition.
 If the condition is satisfied,
then AP solution will be the
optimum solution even for
TSP.
 If not, go to Phase II
 The solution can be adjusted
by inspection method.

5. EXAMPLE PROBLEM (PHASE I)
A travelling salesman has
planned to visit four (4)
cities. He would like to start
from a particular city, visit
each city only once and
return to the starting city.
The travelling cost is given in
the table.
Find the least cost (in Pesos)
route.
TO
FROM
CITY A B C D
A 0 25 75 45
B 35 0 150 25
C 35 40 0 15
D 65 75 130 0

6. Hungarian Method:
Row & Column Reduction
TO
FROM
CITY A B C D
A - 25 75 45
B 35 - 150 25
C 35 40 - 15
D 65 75 130 -
TO
FROM
CITY A B C D
A - 0 50 20
B 10 - 125 0
C 20 25 - 0
D 0 10 65 -
GIVEN NEW MATRIX AFTER
ROW REDUCTION

7. TO
FROM
CITY A B C D
A - 0 0 20
B 10 - 75 0
C 20 25 - 0
D 0 10 15 -
NEW MATRIX AFTER
COLUMN REDUCTION
TO
FROM
CITY A B C D
A - 0 50 20
B 10 - 125 0
C 20 25 - 0
D 0 10 65 -
NEW MATRIX AFTER
ROW REDUCTION

8. Row & Column Scanning
TO
FROM
CITY A B C D
A - 0 0 20
B 10 - 75 0
C 20 25 - 0
D 0 10 15 -

9. Row & Column Scanning
TO
FROM
CITY A B C D
A - 0 0 30
B 10 - 65 0
C 20 15 - 0
D 0 0 5 -

10. Row & Column Scanning
TO
FROM
CITY A B C D
A - 0 0 40
B 0 - 55 0
C 10 5 - 0
D 0 0 5 -

11. TO
FROM
CITY A B C D
A 0 25 75 45
B 35 0 150 25
C 35 40 0 15
D 65 75 130 0
GIVEN
OPTIMUM SOLUTION:
A – C – D – B – A

12. EXAMPLE PROBLEM (PHASE II)
A travelling salesman wants to
visit Cities A, B, C, D and E. He
does not want to visit any city
twice before completing his
tour of all the cities and wishes
to return to the point of starting
journey. Cost of going from
one city to another (in Peso) is
given in the table.
Find the least cost route.
TO
FROM
CITY A B C D E
A - 2 5 8 1
B 6 - 3 9 2
C 8 7 - 4 8
D 13 4 7 - 5
E 1 3 2 8 -

13. TO
FROM
CITY A B C D E
A - 2 5 8 1
B 6 - 3 9 2
C 8 7 - 4 8
D 13 4 7 - 5
E 1 3 2 8 -
GIVEN
Hungarian Method:
Row & Column Reduction
TO
FROM
CITY A B C D E
A - 1 4 7 0
B 4 - 1 7 0
C 4 3 - 0 4
D 9 0 3 - 1
E 0 2 1 7 -
NEW MATRIX AFTER ROW
REDUCTION

14. TO
FROM
CITY A B C D E
A - 1 4 7 0
B 4 - 1 7 0
C 4 3 - 0 4
D 9 0 3 - 1
E 0 2 1 7 -
NEW MATRIX AFTER ROW
REDUCTION
TO
FROM
CITY A B C D E
A - 1 3 7 0
B 4 - 0 7 0
C 4 3 - 0 4
D 9 0 2 - 1
E 0 2 0 7 -
NEW MATRIX AFTER
COLUMN REDUCTION

15. Row & Column Scanning
TO
FROM
CITY A B C D E
A - 1 3 7 0
B 4 - 0 7 0
C 4 3 - 0 4
D 9 0 2 - 1
E 0 2 0 7 -
Optimum Solution for
TSP:

16. TO
FROM
CITY A B C D E
A - 1 3 7 0
B 4 - 0 7 0
C 4 3 - 0 4
D 9 0 2 - 1
E 0 2 0 7 -
Row & Column Scanning

17. TO
FROM
CITY A B C D E
A - 2 5 8 1
B 6 - 3 9 2
C 8 7 - 4 8
D 13 4 7 - 5
E 1 3 2 8 -
GIVEN
OPTIMUM SOLUTION:
A – B – C – D – E - A

18. MINIMUM SPANNING TREE
Network Optimization Model

19. A tree has one path joining two
vertices.
A spanning tree of a graph is a
tree that:
 Contains all the original
graph’s vertices
 Reaches out to all
vertices
 Is acylic. In other words,
the graph doesn’t have
any nodes which loop
back to its self.

20. Minimum Spanning Tree
 A special kind of tree that minimizes the
lengths (or “weights”) of the edges of the tree
Goal:
Cover all vertices
with minimum
possible edges

21. How to find minimum spanning tree?
KRUSKAL’S ALGORITHM
Key points:
 No. of vertices = V
No. of edges in MST = V-1
 MST can be found on
connected graphs only
STEPS:
1) Sort all the edges in non-decreasing order of
their weight
2) - Pick the smallest edge
- Check if the new edge forms a cycle in
our spanning tree being formed
- If cycle is not formed, include the edge
OTHERWISE discard the edge
3) Repeat step 2 unless (v-1) edges are
included in MST

24. PRIM’S ALGORITHM
STEPS:
1) Create an empty list called “visited”
VISITED { }
2) Pick an arbitrary node

30. REFERENCES
 https://blog.routific.com/travelling-salesman-problem
 https://www.geeksforgeeks.org/travelling-salesman-problem-set-1/
 https://cameroncounts.wordpress.com/2012/07/19/the-traveling-salesman-
problem-an-optimization-model/
 https://www.youtube.com/watch?v=k3I2eThAErc
 https://www.youtube.com/watch?v=e_lWrF_RiZ8
 https://www.youtube.com/watch?v=cplfcGZmX7I
 https://www.statisticshowto.com/minimum-spanning-tree/
 https://www.youtube.com/watch?v=71UQH7Pr9kU

31. Thank you!