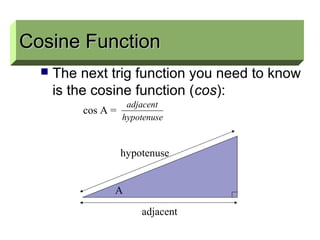
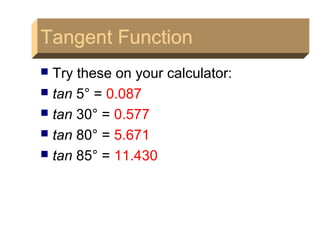
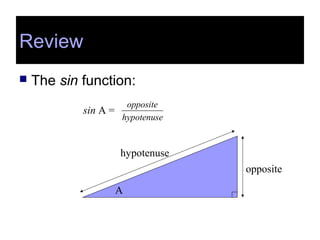
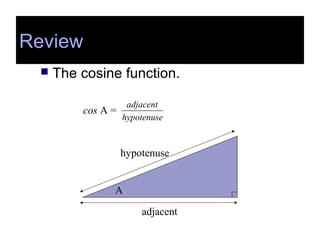
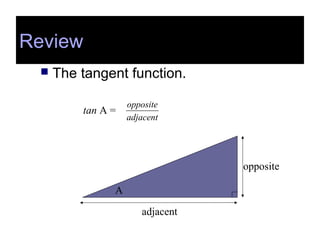
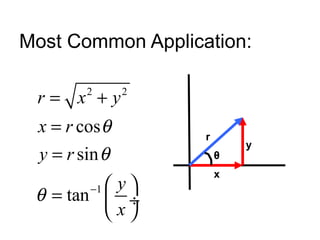
This document covers the basics of trigonometry, specifically focusing on sine, cosine, and tangent functions, and their calculations using a calculator. Each function is illustrated with examples and includes instructions for finding both the functions and their inverses. Additionally, the document discusses the law of cosines for non-right triangles and emphasizes memorization of key formulas.

1. Vidya Bharti Educational Institutions

2. Trigonometry Basics
Right Triangle Trigonometry

4. Sine FunctionSine Function
 When you talk about the sin of an angle,
that means you are working with the
opposite side, and the hypotenuse of a
right triangle.

5. Sine functionSine function
 Given a right triangle, and reference angle A:
sin A =
hypotenuse
opposite
A
opposite
hypotenuse
The sin function specifies
these two sides of the
triangle, and they must be
arranged as shown.

6. Sine FunctionSine Function
 For example to evaluate sin 40°…
 Type-in 40 on your calculator (make sure
the calculator is in degree mode), then
press the sin key.
 It should show a result of 0.642787…
 Note: If this did not work on your calculator,Note: If this did not work on your calculator,
try pressing thetry pressing the sinsin key first, then type-in 40.key first, then type-in 40.
Press the = key to get the answer.Press the = key to get the answer.

7. Sine Function
 Try each of these on your calculator:
 sin 55°
 sin 10°
 sin 87°
Sine FunctionSine Function

8. Sine Function
 Try each of these on your calculator:
 sin 55° = 0.819
 sin 10° = 0.174
 sin 87° = 0.999
Sine FunctionSine Function

9. Inverse Sine FunctionInverse Sine Function
 Using sin-1
(inverse sin):
If 0.7315 = sin θ
then sin-1
(0.7315) = θ
 Solve for θ if sin θ = 0.2419
Inverse Sine FunctionInverse Sine Function

10. Cosine function
 The next trig function you need to know
is the cosine function (cos):
cos A =
hypotenuse
adjacent
A
adjacent
hypotenuse
Cosine FunctionCosine Function

11. Cosine Function
 Use your calculator to determine cos 50°
 First, type-in 50…
 …then press the cos key.
 You should get an answer of 0.642787...
Note: If this did not work on your calculator,
try pressing the cos key first, then type-in 50.
Press the = key to get the answer.
Cosine FunctionCosine Function

12. Cosine Function
 Try these on your calculator:
 cos 25°
 cos 0°
 cos 90°
 cos 45°
Cosine FunctionCosine Function

13. Cosine Function
 Try these on your calculator:
 cos 25° = 0.906
 cos 0° = 1
 cos 90° = 0
 cos 45° = 0.707
Cosine FunctionCosine Function

14.  Using cos-1
(inverse cosine):
If 0.9272 = cos θ
then cos-1
(0.9272) = θ
 Solve for θ if cos θ = 0.5150
Inverse Cosine FunctionInverse Cosine Function

15. Tangent function
 The last trig function you need to know
is the tangent function (tan):
tan A =
adjacent
opposite
A
adjacent
opposite
Tangent FunctionTangent Function

16. Tangent FunctionTangent Function
 Use your calculator to determine tan
40°
 First, type-in 40…
 …then press the tan key.
 You should get an answer of 0.839...
Note: If this did not work on your
calculator, try pressing the tan key first,
then type-in 40. Press the = key to get the
answer.

17. Tangent Function
 Try these on your calculator:
 tan 5°
 tan 30°
 tan 80°
 tan 85°
Tangent FunctionTangent Function

18. Tangent Function
 Try these on your calculator:
 tan 5° = 0.087
 tan 30° = 0.577
 tan 80° = 5.671
 tan 85° = 11.430
Tangent FunctionTangent Function

19.  Using tan-1
(inverse tangent):
If 0.5543 = tan θ
then tan-1
(0.5543) = θ
 Solve for θ if tan θ = 28.64
Inverse Tangent FunctionInverse Tangent Function

20. Review
 These are the only trig functions you will
be using in this course.
 You need to memorize each one.
 Use the memory device: SOH CAH TOA
adj
opp
A
hyp
adj
A
hyp
opp
A
=
=
=
tan
cos
sin
Review

21. Review
 The sin function:
sin A =
hypotenuse
opposite
A
opposite
hypotenuse

22. Review
 The cosine function.
cos A =
hypotenuse
adjacent
A
adjacent
hypotenuse
Review

23. Review
 The tangent function.
tan A =
adjacent
opposite
A
adjacent
opposite
Review

24. Most Common Application:
2 2
1
cos
sin
tan
r x y
x r
y r
y
x
θ
θ
θ −
= +
=
=
 
=  ÷
 
x
y
r
θ

25. Review
 Solve for x:
x = sin 30°
x = cos 45°
x = tan 20°
Review

26. Review
 Solve for θ:
0.7987 = sin θ
0.9272 = cos θ
2.145 = tan θ
Review

27. What if it’s not a right triangle?
- Use the Law of Cosines:
The Law of Cosines
In any triangle ABC, with sides a, b, and c,
.cos2
cos2
cos2
222
222
222
Cabbac
Baccab
Abccba
−+=
−+=
−+=

28. What if it’s not a right triangle?
 Law of Cosines - The square of the magnitude
of the resultant vector is equal to the sum of the
magnitude of the squares of the two vectors, minus two
times the product of the magnitudes of the vectors,
multiplied by the cosine of the angle between them.
R2
= A2
+ B2
– 2AB cosθ
θ

29. Vidya Bharti Educational Institutions