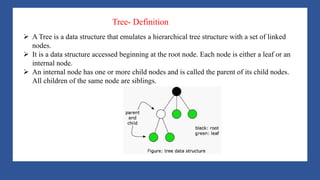
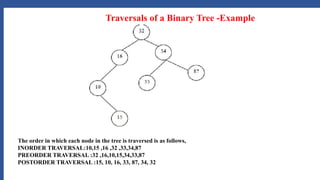
This document discusses tree data structures and tree traversal methods. It defines a tree as a hierarchical data structure with nodes connected in a parent-child relationship. Binary trees are discussed where each node has at most two children. The document covers tree terminology and properties of binary trees. Finally, it describes three tree traversal methods - preorder, inorder, and postorder - and provides an example of each on a sample binary tree.

1. Tree Traversals
Ms. Mary Jacob
Assistant Professor
Kristu Jayanti College (Autonomous),Bangalore

2. 1.Tree- Definition
2.Binary tree
3.Binary tree - Properties
4.Traversals
CONTENTS

3. A Tree is a data structure that emulates a hierarchical tree structure with a set of linked
nodes.
It is a data structure accessed beginning at the root node. Each node is either a leaf or an
internal node. An internal node has one or more child nodes and is called the parent of its
child nodes. All children of the same node are siblings. Contrary to a physical tree, the root
is usually depicted at the top of the structure, and the leaves are depicted at the bottom.
Ø A Tree is a data structure that emulates a hierarchical tree structure with a set of linked
nodes.
Ø It is a data structure accessed beginning at the root node. Each node is either a leaf or an
internal node.
Ø An internal node has one or more child nodes and is called the parent of its child nodes.
All children of the same node are siblings.
Tree- Definition

4. A Tree is a data structure that emulates a hierarchical tree
structure with a set of linked nodes.
It is a data structure accessed beginning at the root node. Each
node is either a leaf or an internal node. An internal node has
one or more child nodes and is called the parent of its child
nodes. All children of the same node are siblings. Contrary to a
physical tree, the root is usually depicted at the top of the
structure, and the leaves are depicted at the bottom.
Ø Root: node without parent (A)
Ø Internal node: node with at least one child (A, B, C, F)
Ø External node: a kind of leaf node without children (E, I, J, K, G, H, D)
Ø Ancestors of a node: parent, grandparent, grand-grandparent, etc
Ø Depth of a node: number of ancestors
Ø Height of a tree: maximum depth of any node (3)
Ø Descendant of a node: child, grandchild, grand-grandchild, etc
Ø Degree of an element: no. of children it has
Ø Sub tree: tree consisting of a node and its descendants
Ø Path: traversal from node to node along the edges that results in
a sequence
Ø Root: node at the top of the tree
Ø Parent: any node, except root has exactly one edge running upward to
another node. The node above it is called parent.
Tree Terminologies

5. A Tree is a data structure that emulates a hierarchical tree structure with a set of linked
nodes.
It is a data structure accessed beginning at the root node. Each node is either a leaf or an
internal node. An internal node has one or more child nodes and is called the parent of its
child nodes. All children of the same node are siblings. Contrary to a physical tree, the root
is usually depicted at the top of the structure, and the leaves are depicted at the bottom.
Ø Child: any node may have one or more lines running downward
to other nodes. Nodes below are children.
Ø Leaf: a node that has no children
Ø Sub tree: any node can be considered to be the root of a subtree,
which consists of its children and its children's children and so
on.
Ø Visiting: a node is visited when program control arrives at the
node, usually for processing.
Ø Traversing: to traverse a tree means to visit all the nodes in
some specified order.
Ø Levels: the level of a particular node refers to how many
generations the node is from the root. Root is assumed to be
level 0.
Tree Terminologies

6. A Tree is a data structure that emulates a hierarchical tree structure with a set of linked
nodes.
It is a data structure accessed beginning at the root node. Each node is either a leaf or an
internal node. An internal node has one or more child nodes and is called the parent of its
child nodes. All children of the same node are siblings. Contrary to a physical tree, the root
is usually depicted at the top of the structure, and the leaves are depicted at the bottom.
Ø Binary tree is a set of finite nodes which is either empty or consists of one or more nodes in
which each node has at most two disjoint binary sub trees called left sub tree or right sub tree
respectively.
Ø There may be a zero degree node or a one degree node or a two degree node.
Binary Tree

7. A Tree is a data structure that emulates a hierarchical tree structure with a set of linked
nodes.
It is a data structure accessed beginning at the root node. Each node is either a leaf or an
internal node. An internal node has one or more child nodes and is called the parent of its
child nodes. All children of the same node are siblings. Contrary to a physical tree, the root
is usually depicted at the top of the structure, and the leaves are depicted at the bottom.
Binary Tree - Properties
Ø The maximum number of nodes at a level I of binary tree is 2I where I>=0.
Ø If h = height of a binary tree,
max number of nodes possible in a binary tree of height h is 2h-1
min number of nodes possible in a binary tree of height h is h
Ø For any non empty tree, number of terminal or leaf nodes is equal to number of non
terminal nodes(internal nodes) +1.
Ø For any non empty binary tree, if ‘n’ is the number of nodes and ‘e’ is the number of
edges, then n=e+1;
Ø Total number of binary trees possible with n nodes is 1/(n+1)2ncn
Ø A binary tree with height h and 2h + 1 - 1 nodes (or 2h leaves) is called a full binary
tree

8. A Tree is a data structure that emulates a hierarchical tree structure with a set of linked
nodes.
It is a data structure accessed beginning at the root node. Each node is either a leaf or an
internal node. An internal node has one or more child nodes and is called the parent of its
child nodes. All children of the same node are siblings. Contrary to a physical tree, the root
is usually depicted at the top of the structure, and the leaves are depicted at the bottom.
Traversals of a Binary Tree
The tree can be traversed in inorder, preorder and postorder methods.
PREORDER TRAVERSAL:
Ø Process the root R.
Ø Traverse the left sub tree of R in preorder.
Ø Traverse the right sub tree of R in preorder.
INORDER TRAVERSAL:
Ø Traverse the left sub tree of R in inorder.
Ø Process the root R.
Ø Traverse the right sub tree of R in inorder.
POSTORDER TRAVERSAL :
Ø Traverse the left sub tree of R in postorder.
Ø Traverse the right sub tree of R in postorder.
Ø Process the root R.

9. The order in which each node in the tree is traversed is as follows,
INORDER TRAVERSAL:10,15 ,16 ,32 ,33,34,87
PREORDER TRAVERSAL :32 ,16,10,15,34,33,87
POSTORDER TRAVERSAL :15, 10, 16, 33, 87, 34, 32
Traversals of a Binary Tree -Example
The order in which each node in the tree is traversed is as follows,
INORDER TRAVERSAL:10,15 ,16 ,32 ,33,34,87
PREORDER TRAVERSAL :32 ,16,10,15,34,33,87
POSTORDER TRAVERSAL :15, 10, 16, 33, 87, 34, 32

10. Thank You