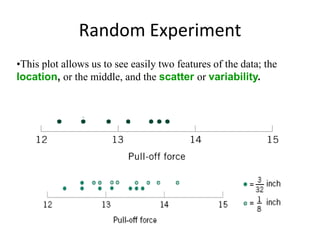
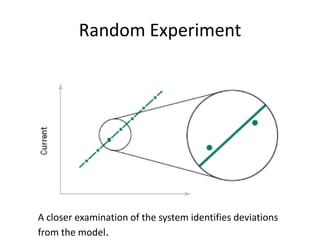
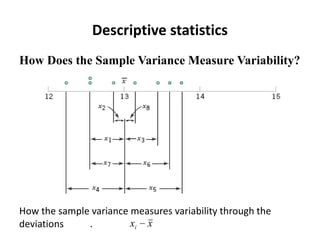
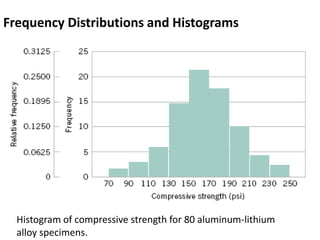
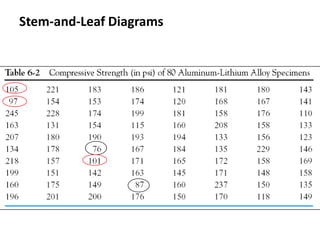
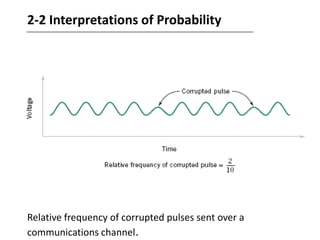
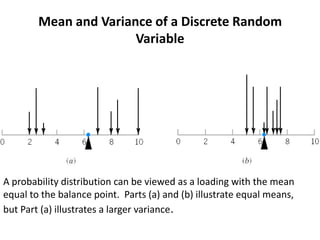
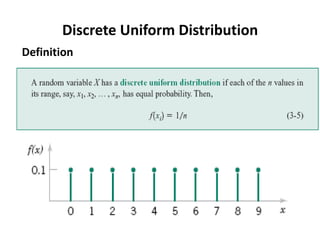
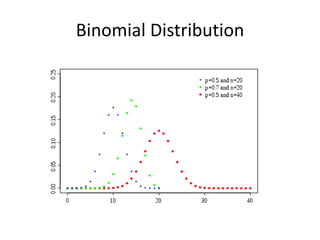
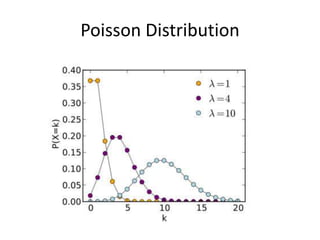
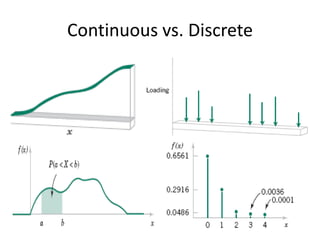
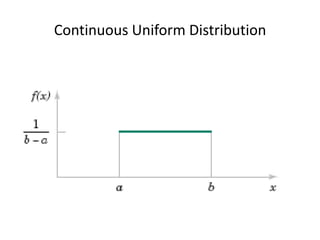
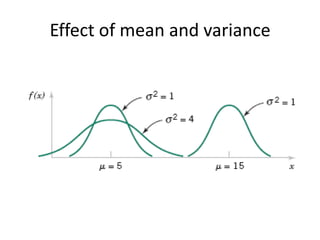
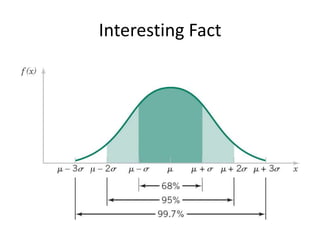
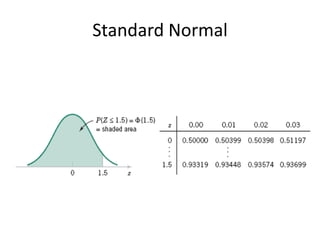
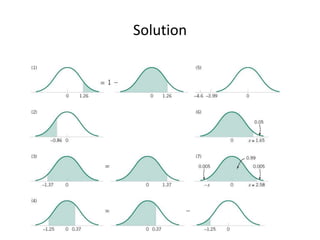
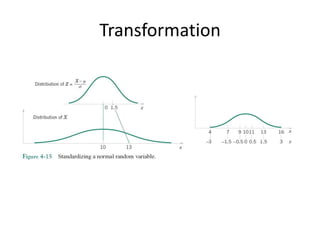
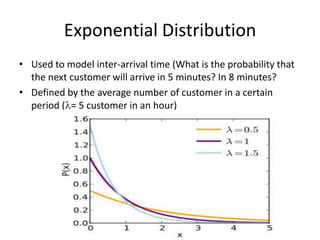
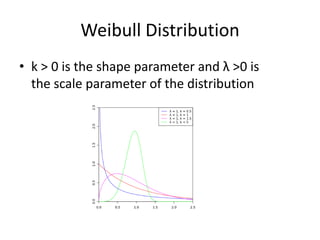
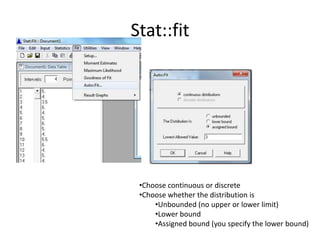
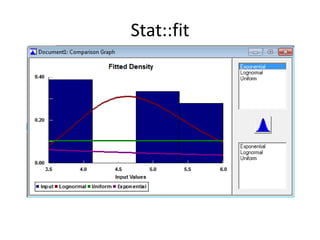
This document discusses statistical concepts like variability, random experiments, descriptive statistics, probability distributions, and statistical data analysis. It provides examples of different probability distributions like binomial, Poisson, normal, exponential, and Weibull distributions. It also discusses the four basic steps of statistical data analysis: defining the problem, collecting the data, analyzing the data, and reporting results. Methods like hypothesis testing are discussed as part of data analysis.

1. Basics of statisticsand Data collection and analysisWeeks 2,3, and 4

2. Variability Statistical techniques are useful for describing and understanding variability.

3. Variability: Successive observations of a system or phenomenon do not produce exactly the same result.

4. Statistics gives us a framework for describing this variability and for learning about potential sources of variability.Nylon connector to be used in an automotive engine application.

5. Design specification on wall thickness at 3/32 inch

6. The effect of this decision on the connector pull-off force. If the pull-off force is too low, the connector may fail when it is installed in an engine.

7. Eight prototype units are produced and their pull-off forces measured (in pounds): 12.6, 12.9, 13.4, 12.3, 13.6, 13.5, 12.6, 13.1.Random Experiment

8. This plot allows us to see easily two features of the data; the location, or the middle, and the scatter or variability.Random Experiment

9. DefinitionRandom Experiment

10. A closer examination of the system identifies deviations from the model.Random Experiment

11. Discrete Random VariablesThey are variables which have finite (countable) range.They can not be assigned other value.Examples:Let x be your grade S={A,A-,B+,B,B-,C,D}Let y be a working day in a week S={M,T,W,R,F}Let z be your weight S={40k<z<300K} this is not discrete, it is continuous, z can be 120.63k48 digital lines are observed, x indicate how many are in use, x can be any integer from 1 to 48….Note x can not be 1.5

12. Descriptive statisticsDefinition: Sample Mean

13. Definition: Sample VarianceDescriptive statistics

14. Descriptive statisticsHow Does the Sample Variance Measure Variability?How the sample variance measures variability through the deviations .

15. Descriptive statisticsDefinition

16. Stem-and-Leaf Diagrams

17. Frequency Distributions and Histograms A frequency distribution is a more compact summary of data than a stem-and-leaf diagram.

18. To construct a frequency distribution, we must divide the range of the data into intervals, which are usually called class intervals, cells, or bins.Constructing a Histogram (Equal Bin Widths):

19. Frequency Distributions and Histograms Histogram of compressive strength for 80 aluminum-lithium alloy specimens.

20. Stem-and-Leaf Diagrams

21. Stem-and-Leaf Diagrams Data FeaturesWhen an ordered set of data is divided into four equal parts, the division points are called quartiles. The firstor lower quartile, q1, is a value that has approximately one-fourth (25%) of the observations below it and approximately 75% of the observations above. The second quartile, q2, has approximately one-half (50%) of the observations below its value. The second quartile is exactly equal to the median. The thirdor upper quartile, q3, has approximately three-fourths (75%) of the observations below its value. As in the case of the median, the quartiles may not be unique.

22. Stem-and-Leaf Diagrams Data FeaturesThe interquartile range is the difference between the upper and lower quartiles, and it is sometimes used as a measure of variability.

23. In general, the 100kth percentile is a data value such that approximately 100k% of the observations are at or below this value and approximately 100(1 - k)% of them are above it.Stem-and-Leaf Diagrams Stem-and-leaf diagram for the compressive strength data

24. 2-2 Interpretations of ProbabilityRelative frequency of corrupted pulses sent over a communications channel.

25. 2-2 Interpretations of Probability2-2.2 Axioms of Probability

26. DistributionProbability distribution of variable x is the description of the probability of each outcome of x.Examples:Tossing a coin, x is getting head, s={0,1} P(x=0)=0.5, P(x=1)=0.5In an experiment of examining 2 independent items from a product line, the probability that an item passes the test is 0.8, if x is the number of products passing the inspection. What is the distribution of x?

27. Mean and Variance of a Discrete Random VariableA probability distribution can be viewed as a loading with the mean equal to the balance point. Parts (a) and (b) illustrate equal means, but Part (a) illustrates a larger variance.

28. Discrete Uniform DistributionDefinition

29. Binomial DistributionYou know the probability of the outcome of interest in a single try.

30. Flip a coin P(H)=1/2

31. Draw a card P(K)=4/52

32. In a production line P(defective)=0.10

33. You repeat the experiment (trial) n times WITH REPLACEMENT

34. Flip the coin 7 times

35. Draw 5 cards

36. (Take an item, test it, return it back) 25 times

37. You want to know the probability that you will get a certain outcome x times.

38. Probability of getting 3 heads in 7 times knowing that P(H)=0.5

39. Probability of getting 5 Kings in 5 drawn cards knowing that P(K)=4/52

40. Probability of getting 2 defectives in a sample of 25 items knowing that P(d)=0.1Binomial Distribution

41. Poisson DistributionThis distribution deals with the case that you only know THE AVERAGE NUMBER of the required outcomeExamplesFlaws in a rolls of textileCalls to a telephone exchange

42. Poisson Distribution

43. Continuous vs. Discrete

44. Continuous Uniform Distribution

45. Normal DistributionThe most widely used distributionAlso called Gaussian distributionCan be used to virtually approximate results of any experiment as we will see in later chapters.Characterized by mean and variance.Can you notice it represents weight, height, your strength?

46. Effect of mean and variance

47. Interesting Fact