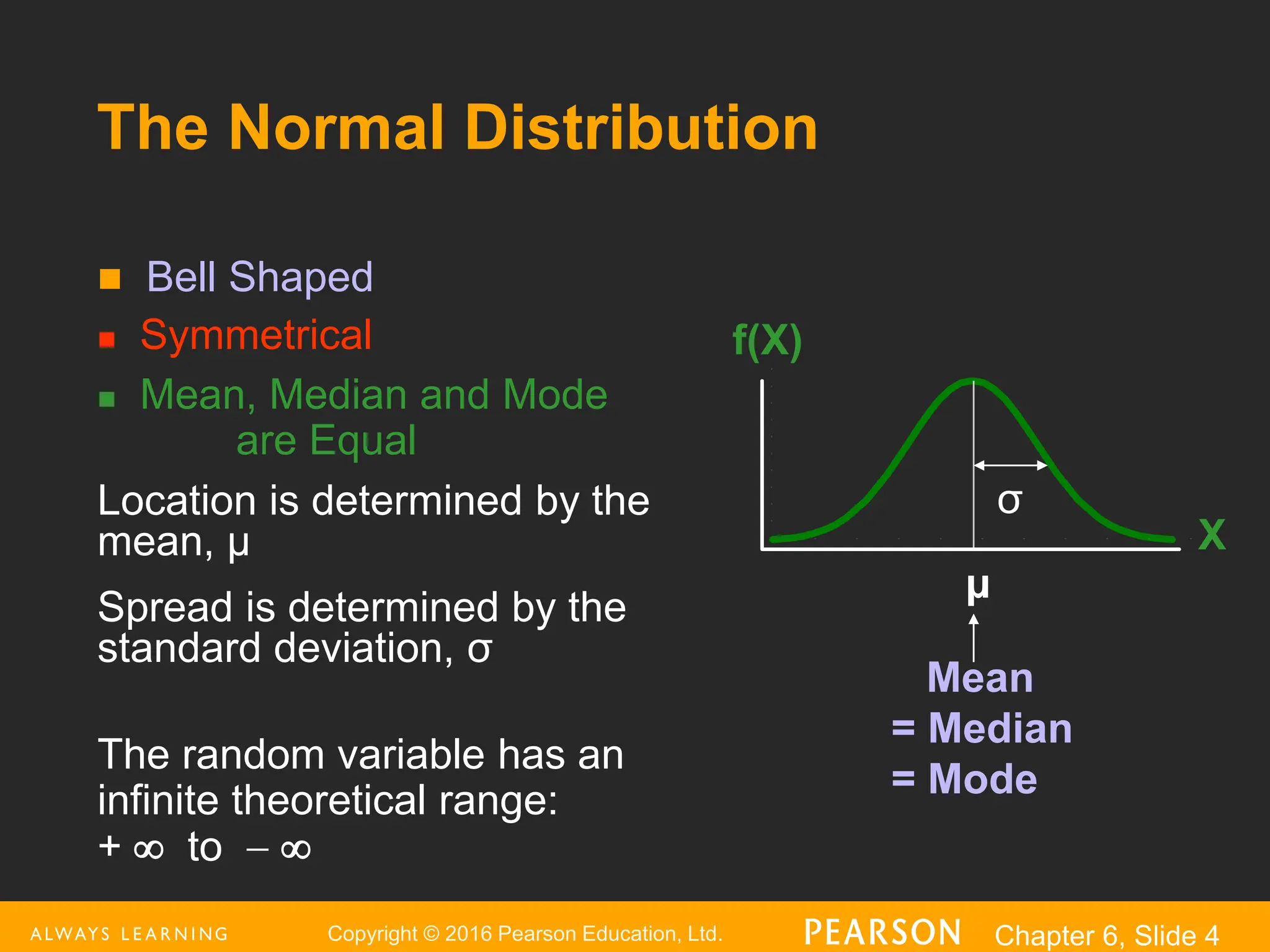
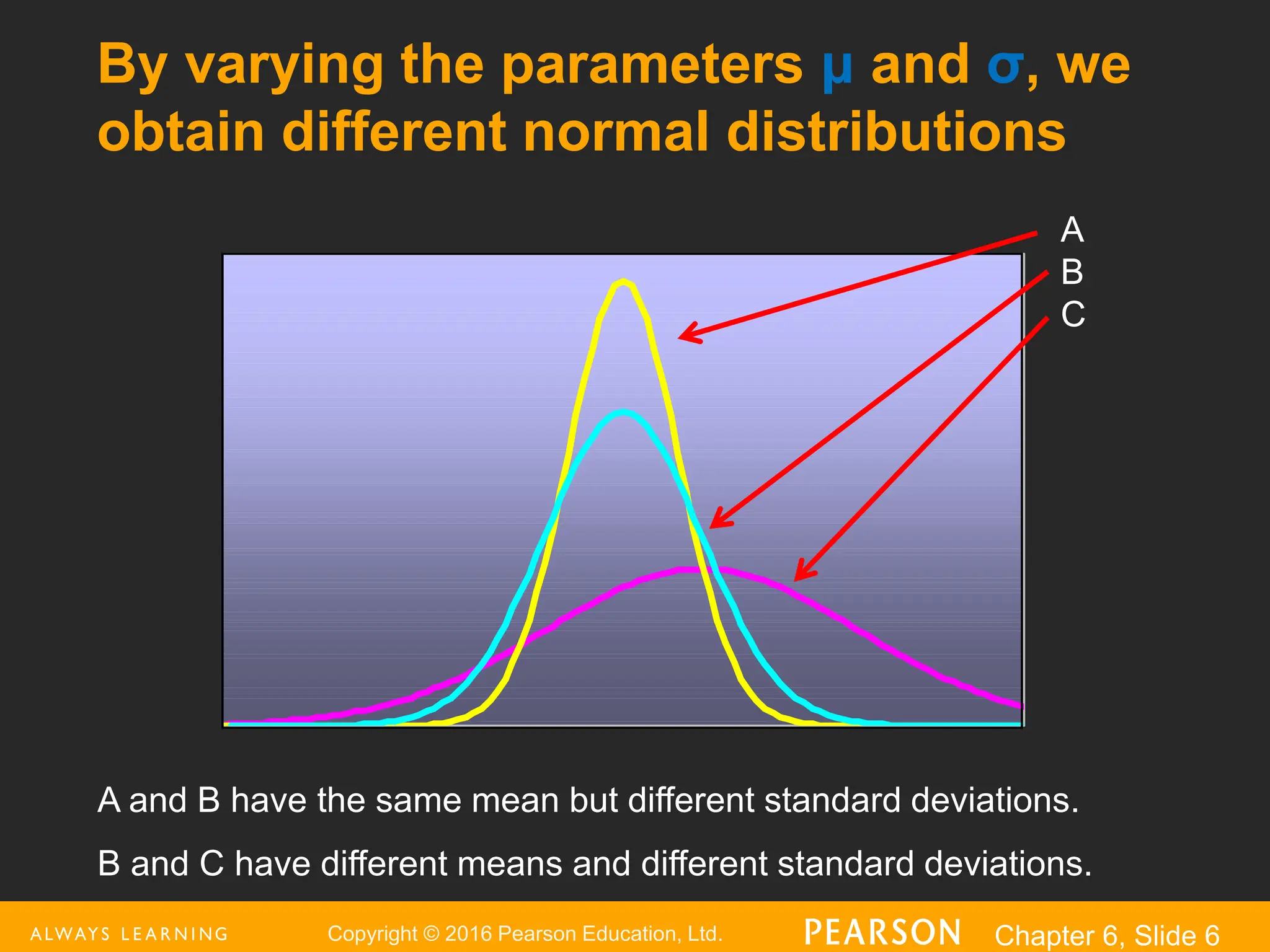
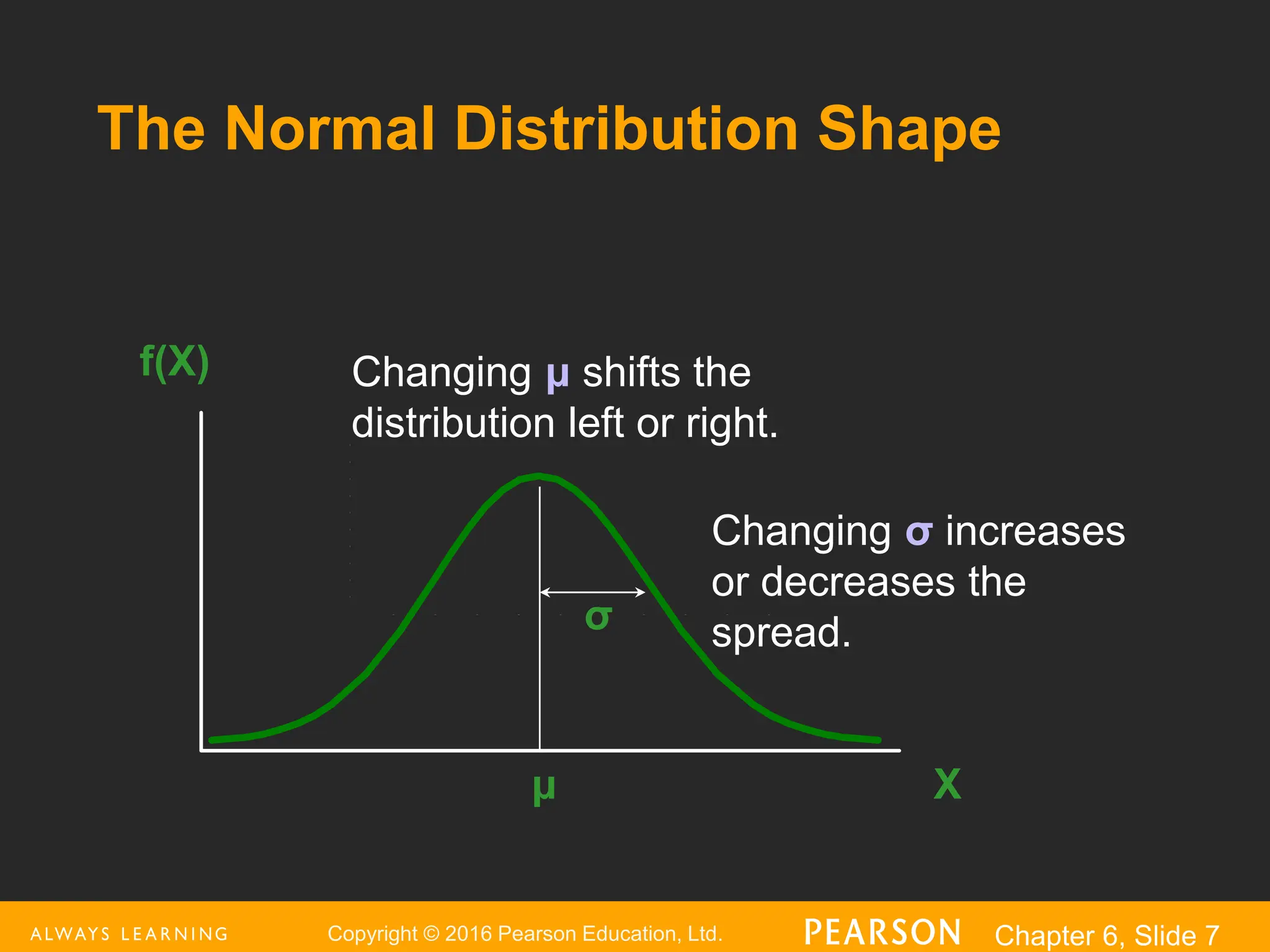
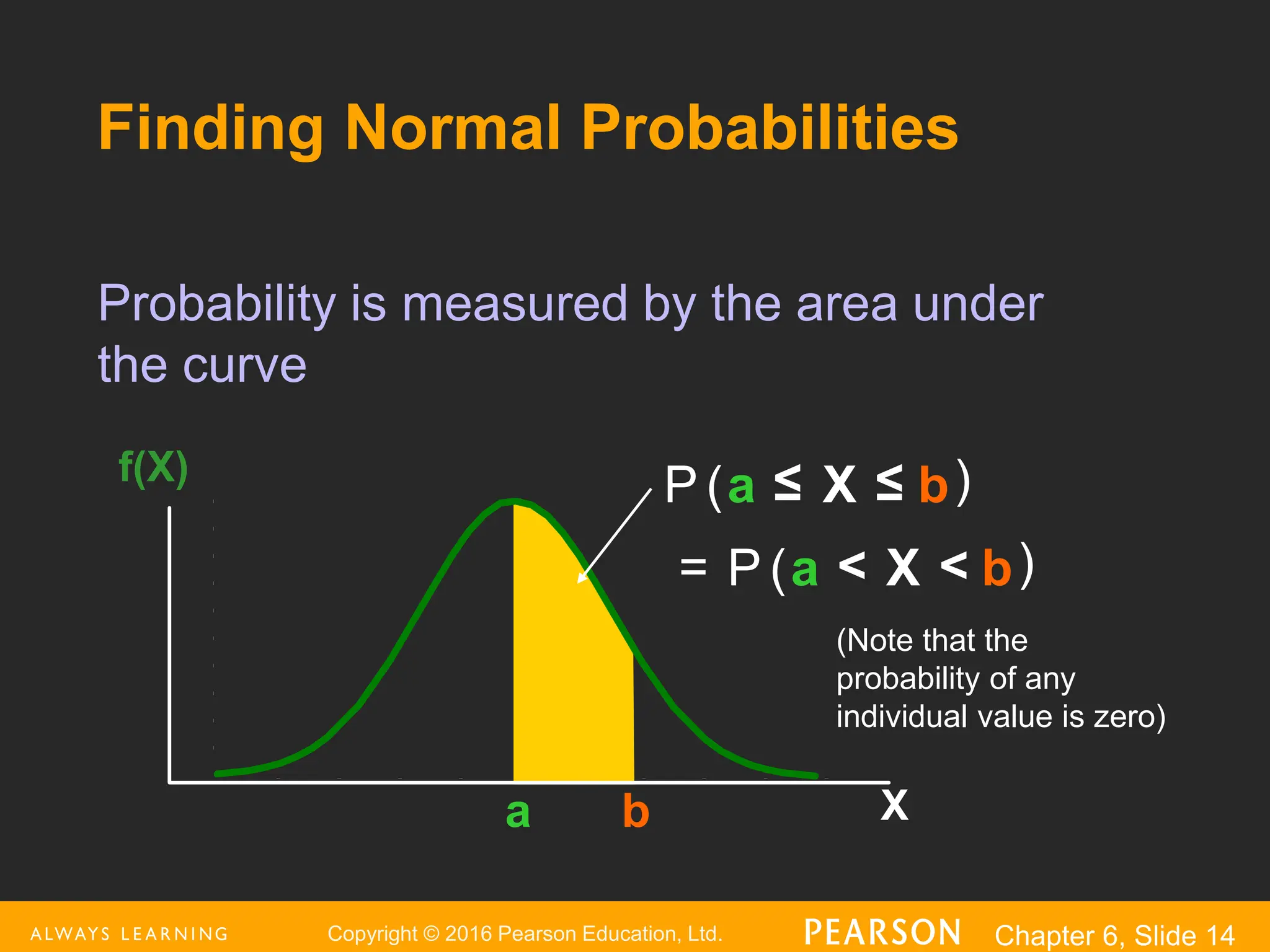
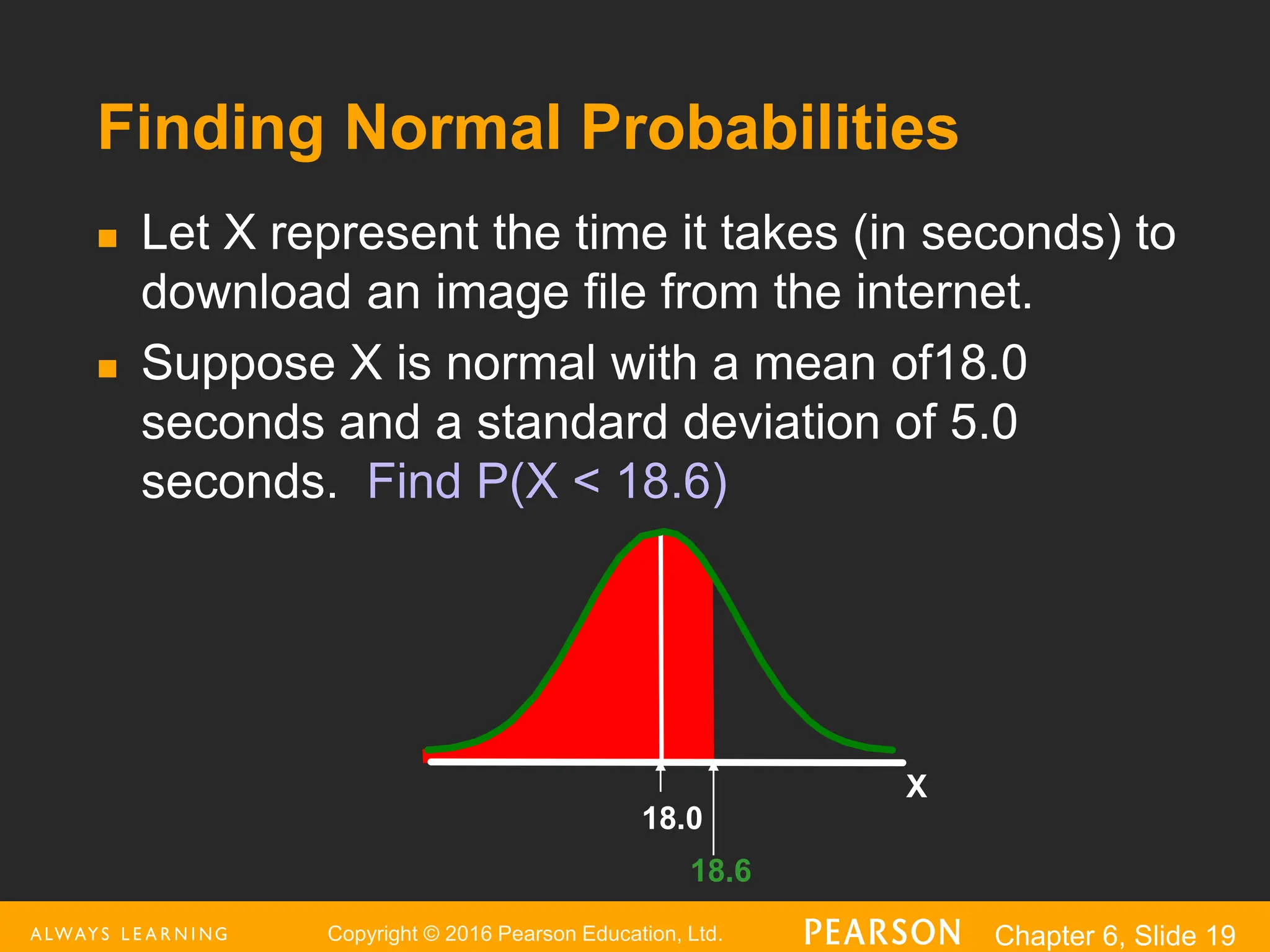
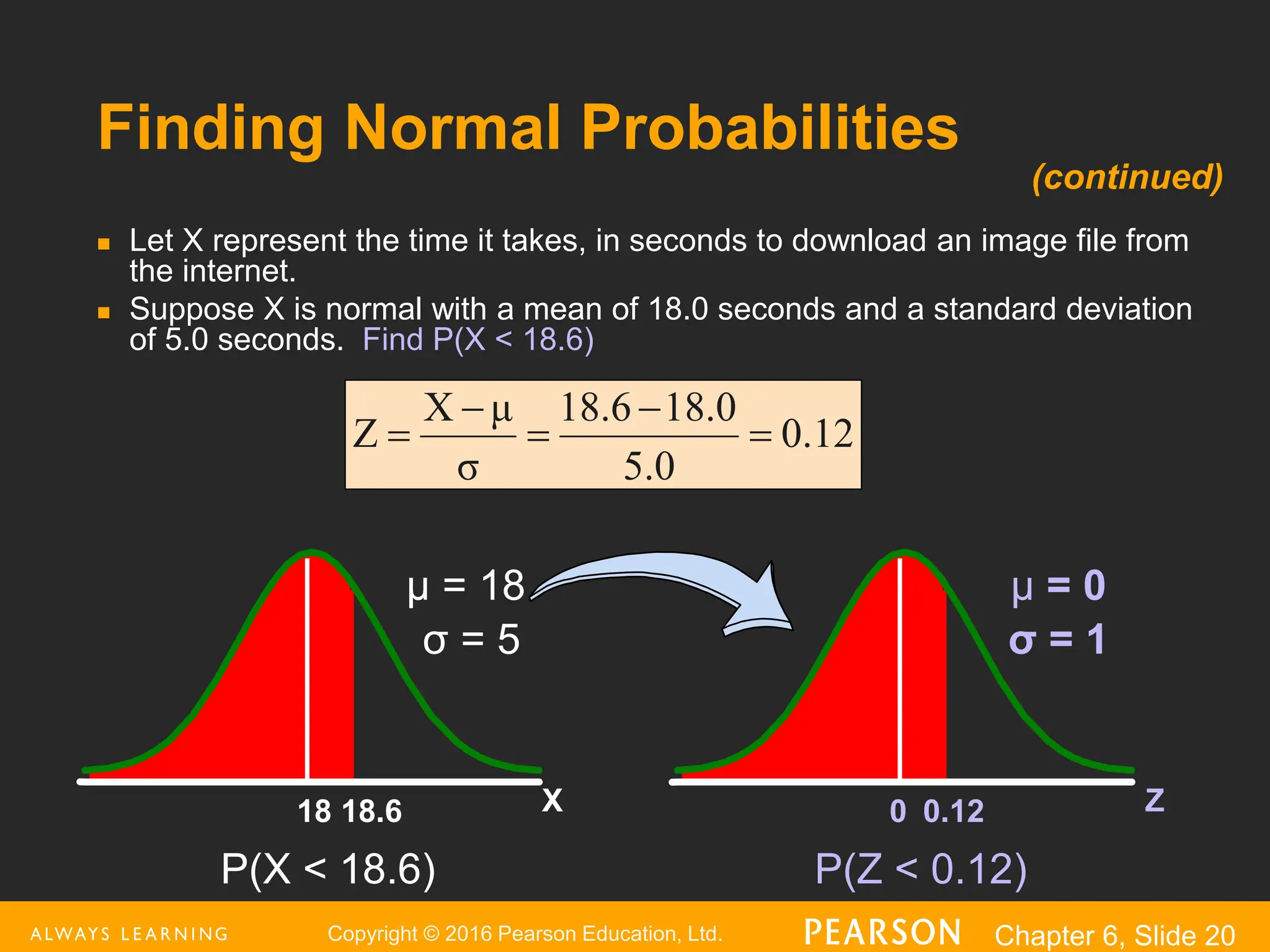
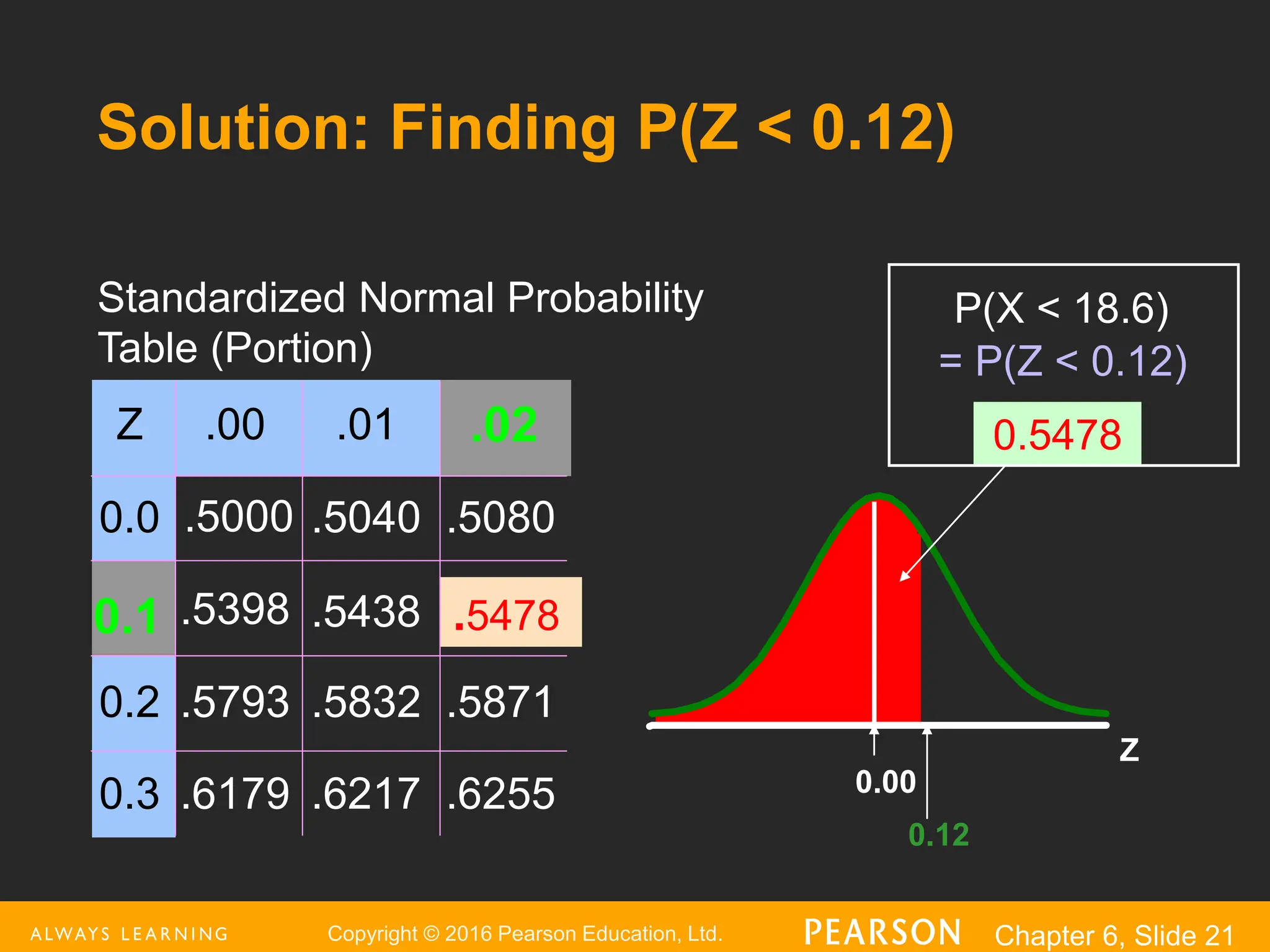
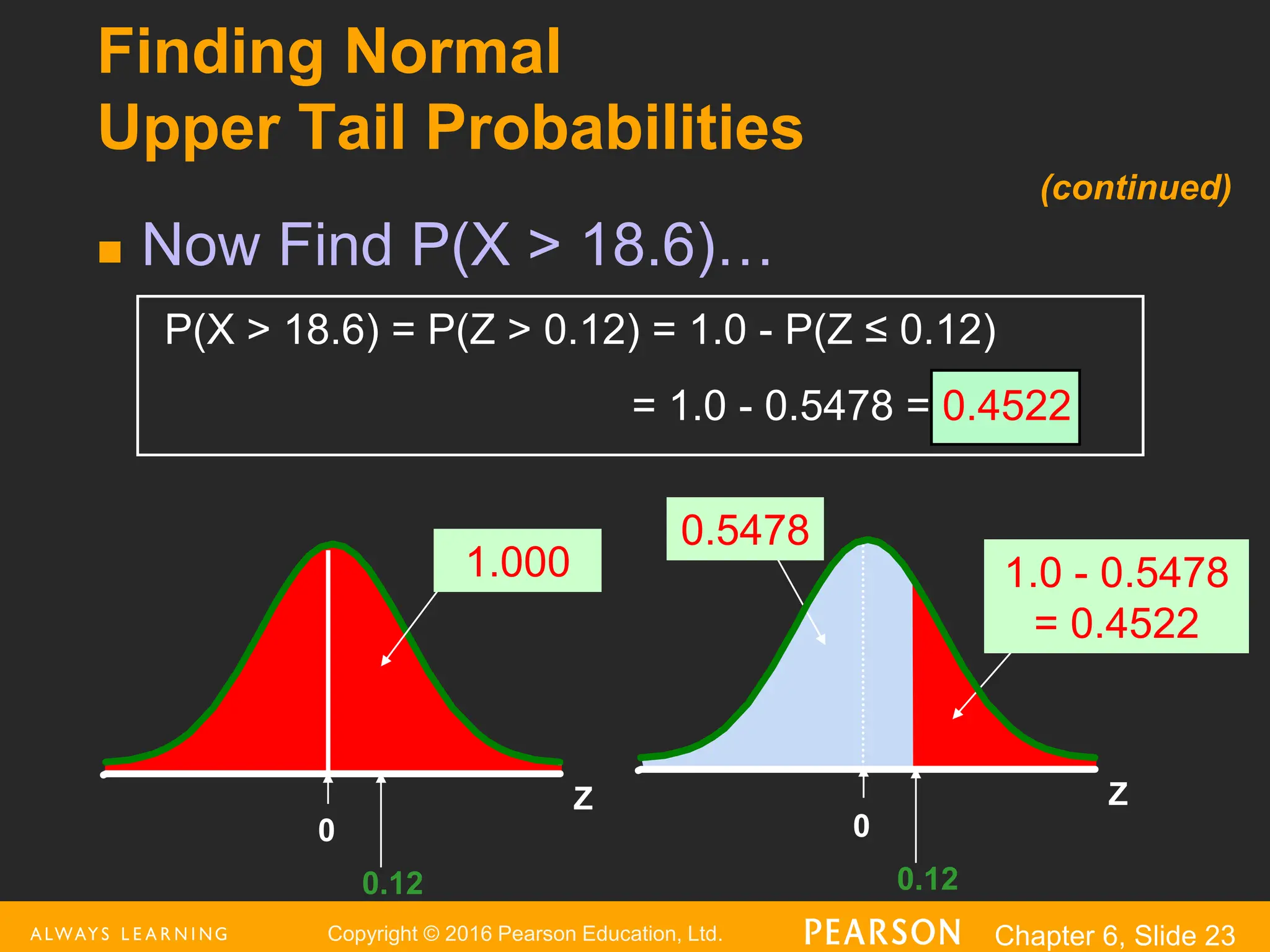
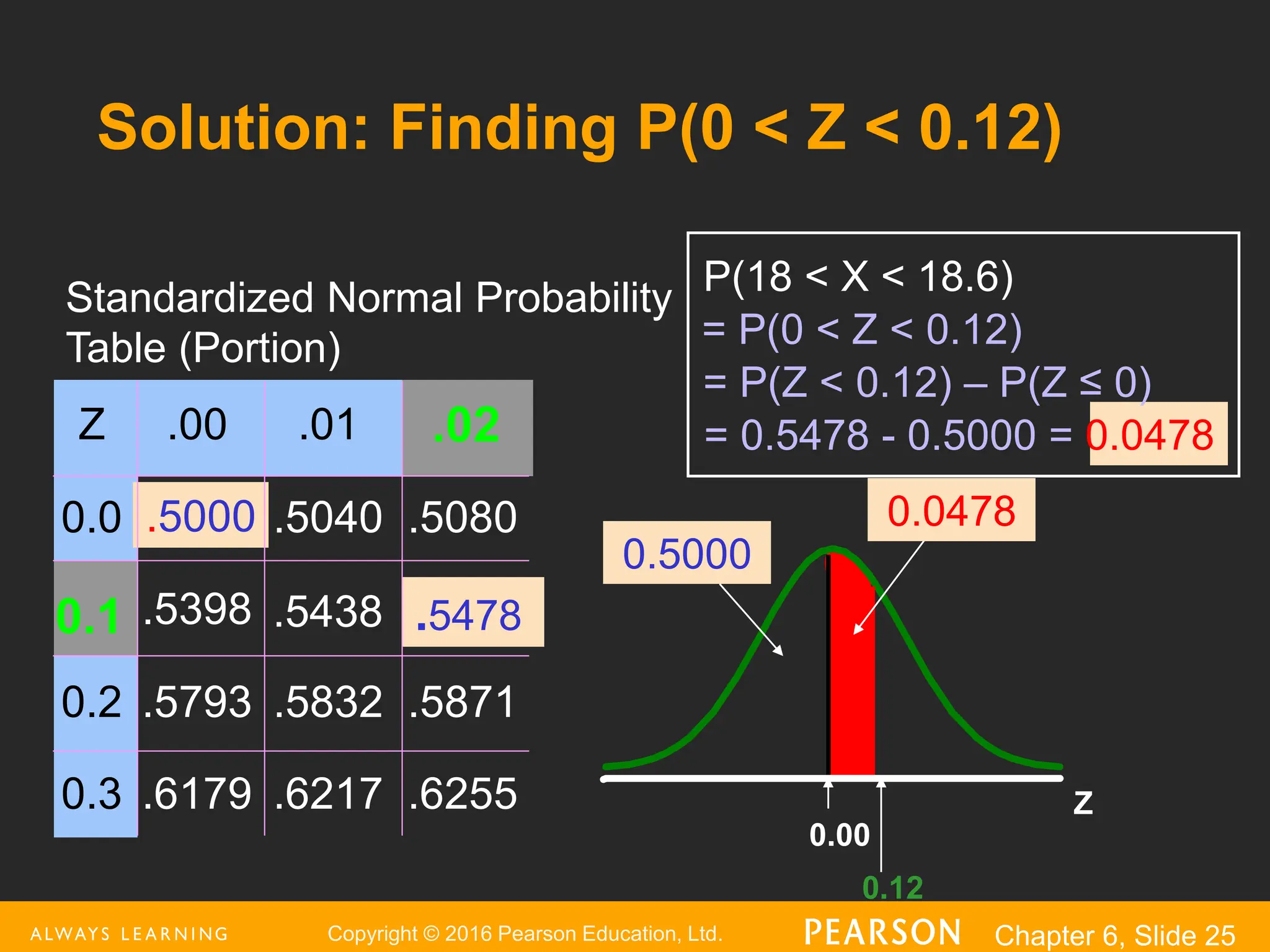
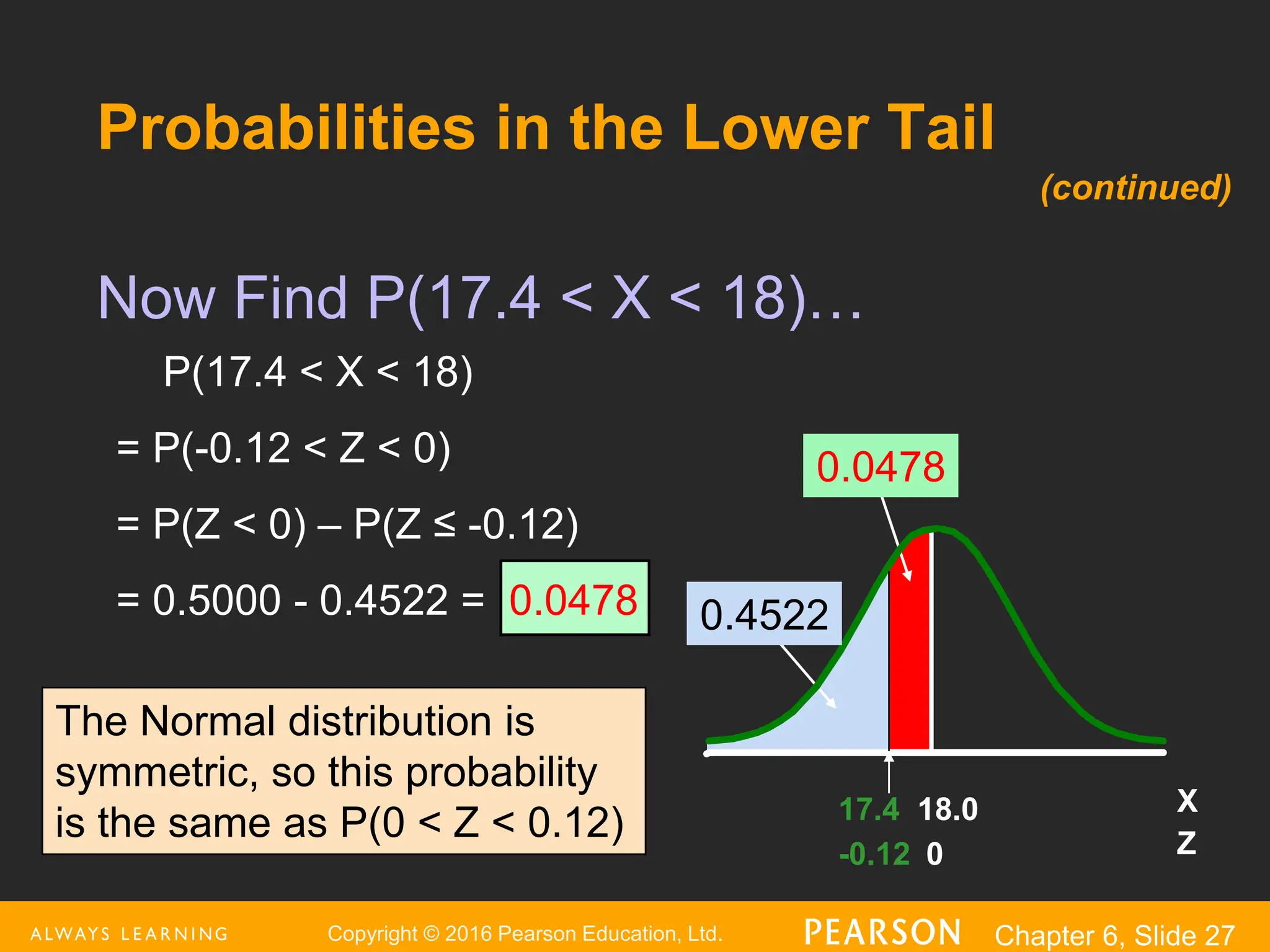
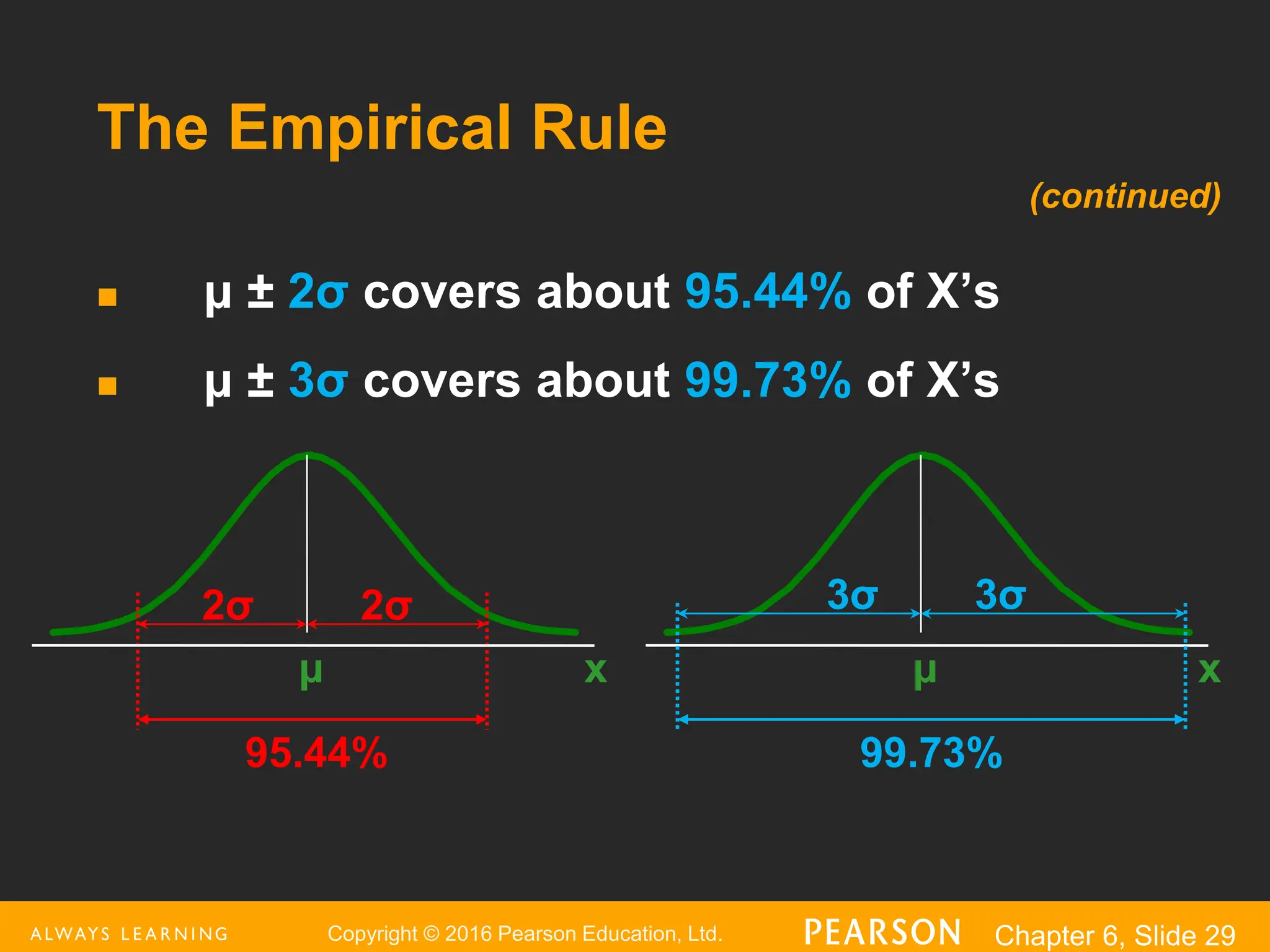
This document provides an overview of the normal distribution. It discusses how the normal distribution is characterized by its mean, median and mode all being equal. It describes how the standard normal distribution is used to compute probabilities by transforming data values into z-scores. Examples are provided to demonstrate how to calculate probabilities using the normal distribution table and how to find data values associated with specific probabilities. Key aspects like the empirical rule and transforming between the original and standardized normal distributions are also covered.