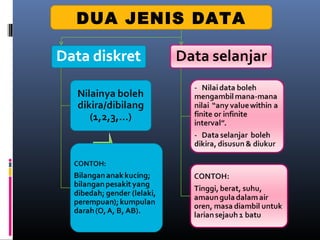
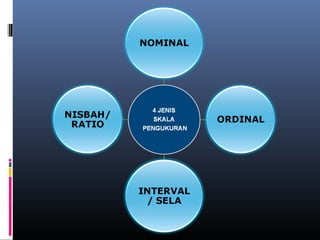
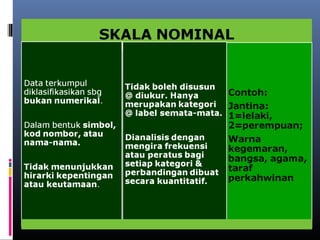
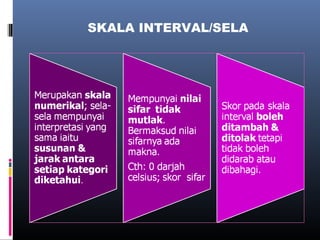
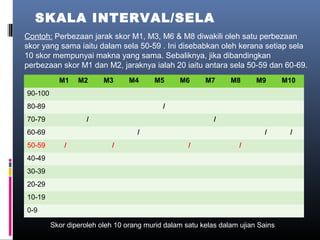
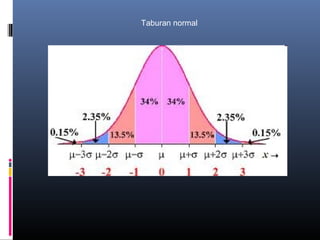
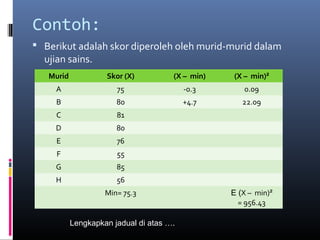
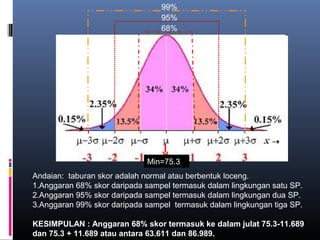
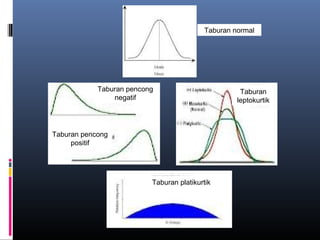
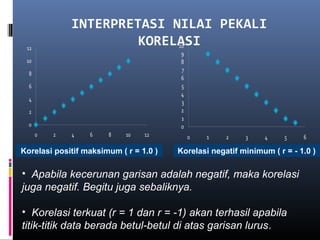
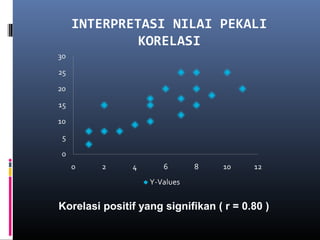
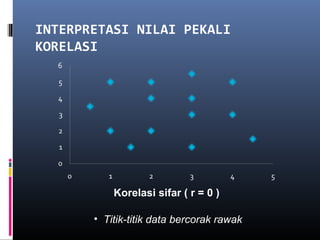
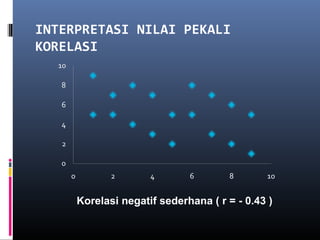
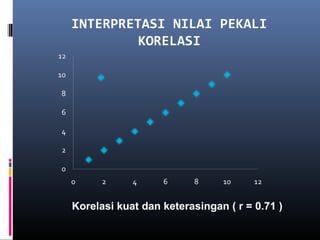
Dokumen ini membincangkan analisis data kuantitatif melalui analisis deskriptif seperti frekuensi, peratusan, min, mod, median, dan sisihan piawai. Ia juga menerangkan konsep dan formula berkaitan statistik yang digunakan untuk meringkaskan hasil ujian yang diperoleh dari pelajar. Selain itu, dokumen tersebut menekankan pentingnya pekali korelasi dalam mengukur hubungan antara dua pembolehubah.

1. Penyelidikan Tindakan:
Analisis Data Kuantitatif

2. Analisis Deskriptif:
 Frekuensi
 Peratusan
 Min
 Mod
 Median
 Sisihan piawai
 Pekali korelasi

3. DUA JENIS DATA

6. SKALA ORDINAL

7. SKALA INTERVAL/SELA

8. SKALA INTERVAL/SELA
Contoh: Perbezaan jarak skor M1, M3, M6 & M8 diwakili oleh satu perbezaan
skor yang sama iaitu dalam sela 50-59 . Ini disebabkan oleh kerana setiap sela
10 skor mempunyai makna yang sama. Sebaliknya, jika dibandingkan
perbezaan skor M1 dan M2, jaraknya ialah 20 iaitu antara sela 50-59 dan 60-69.
M1 M2 M3 M4 M5 M6 M7 M8 M9 M10
90-100
80-89 /
70-79 / /
60-69 / / /
50-59 / / / /
40-49
30-39
20-29
10-19
0-9
Skor diperoleh oleh 10 orang murid dalam satu kelas dalam ujian Sains

9. SKALA NISBAH/RATIO

10. JADUAL FREKUENSI
 Jadual frekuensi digunakan untuk meringkaskan/
merumuskan set data (sama ada data nomimal,
ordinal). Juga boleh digunakan terhadap data selanjar
yang telah dikategorikan dalam kumpulan tertentu.
 Ia merekodkan berapa kerap setiap nilai (atau
satu set nilai-nilai) bagi setiap
pembolehubah dalam soalan itu berlaku .
 Boleh laporkan bilangan ataupun peratus bagi
setiap kategori.

11. JADUAL FREKUENSI
Contoh: Terdapat 30 skor diperoleh oleh seorang penembak adalah seperti
berikut :-
5, 2, 2, 3, 4, 4, 3, 2, 0, 3, 0, 3, 2, 1, 5, 1, 3, 1, 5, 5, 2, 4, 0, 0, 4, 5, 4, 4, 5, 5
Maka, frekuensi bagi skor-skor tersebut diringkaskan
dalam jadual frekuensi seperti berikut :-
Skor Frekuensi
0 4
1 3
2 5
3 5
4 6
5 7
Jumlah 30

12. JADUAL PERATUSAN
Frekuensi skor-skor tersebut juga boleh
diringkaskan seperti berikut :-
Skor Frekuensi Peratus
0 4 13%
1 3 10%
2 5 17%
3 5 17%
4 6 20%
5 7 23%
Jumlah 30 100%

13. MIN
 Adalah hasil purata data-data/skor-skor yang
diperoleh daripada kajian yang dijalankan.
 Min adalah jumlah semua skor dibahagikan
dengan bilangan responden
 Min sampel adalah anggaran digunakan untuk
menganggarkan min populasi
 Simbol : Formula :

14. MIN SAMPEL
Contoh - Set data terdiri daripada :
5, 3, 54, 93, 83, 22, 17, 19.

15. MOD
 Adalah skor/ nilai yang mempunyai kekerapan yang
paling tinggi dalam sesuatu taburan data.
 Kadangkala dalam satu taburan skor akan terdapat dua
mod apabila dua mata nilai muncul lebih kerap.
Contoh - Keputusan ujian statistik adalah seperti berikut :- :
Pelajar Skor
1 94
2 81
3 56
4 90
5 70
6 65
7 90
8 90
9 30
Mod (most common score) ialah 90

16. MEDIAN
 Adalah skor/ nilai tengah bagi sesuatu
taburan skor yang telah disusun mengikut
urutan menaik atau menurun.
Contoh - Taburan skor mempunyai bilangan ganjil
• Data:
96, 48, 27, 72, 39, 70, 7, 68, 99, 36, 95, 4, 6, 13, 34, 74, 65, 42, 28, 54, 69
• Data disusun secara menaik :
4, 6, 7, 13, 27, 28, 34, 36, 39, 42, 48, 54, 65, 68, 69, 70, 72, 74, 95, 96, 99
• Median = 48, leaving ten values below and ten values above

17. MEDIAN
 Jika bilangan skor ialah genap (dua angka tengah),
nilai purata bagi dua skor yang terletak di tengah-
tengah ialah nilai median.
Contoh - Taburan skor mempunyai bilangan genap
Data:
57, 55, 85, 24, 33, 49, 94, 2, 8, 51, 71, 30, 91, 6, 47, 50, 65, 43, 41, 7
Data disusun secara menaik :
2, 6, 7, 8, 24, 30, 33, 41, 43, 47, 49, 50, 51, 55, 57, 65, 71, 85, 91, 94
Median : 47 + 49 ÷ 2 = 48

18. SISIHAN PIAWAI
 SEBARAN : sebaran merujuk kepada serakan
nilai-nilai sekitar kecenderungan
memusat/tengah.
 Dua bentuk sebaran – JULAT & SISIHAN PIAWAI.
 Julat = dihitung dengan menolak nilai
terendah daripada nilai tertinggi.
 Sisihan piawai = menunjukkan hubungan set
skor dengan min iaitu ukuran serakan sesuatu set
data (measure of the spread or dispersion of a set
of data)

19. Taburan normal

20. SISIHAN PIAWAI
 nilai sisihan piawai diperoleh dengan mencari
nilai punca ganda dua varian (s²) dan simbol
sisihan piawai ialah s.d. atau s.
 Formula varian, s² :
 Formula sisihan piawai, s :

21. Contoh:
 Berikut adalah skor diperoleh oleh murid-murid dalam
ujian sains.
Murid Skor (X) (X – min) (X – min)²
A 75 -0.3 0.09
B 80 +4.7 22.09
C 81
D 80
E 76
F 55
G 85
H 56
Min= 75.3 Ε (X – min)²
= 956.43
Lengkapkan jadual di atas ….

22.  Varian = =
= 956.43 = 136.633
8–1
 Sisihan piawai =
= √136.633 = 11.689

23. 99%
95%
68%
Min=75.3
Andaian: taburan skor adalah normal atau berbentuk loceng.
1.Anggaran 68% skor daripada sampel termasuk dalam lingkungan satu SP.
2.Anggaran 95% skor daripada sampel termasuk dalam lingkungan dua SP.
3.Anggaran 99% skor daripada sampel termasuk dalam lingkungan tiga SP.
KESIMPULAN : Anggaran 68% skor termasuk ke dalam julat 75.3-11.689
dan 75.3 + 11.689 atau antara 63.611 dan 86.989.

24. Taburan normal
Taburan pencong Taburan
negatif leptokurtik
Taburan pencong
positif
Taburan platikurtik

25. SISIHAN PIAWAI
 Semakin luas nilai skor disebarkan, semakin besar nilai
sisihan piawai.
 Contoh: Katakan ada dua keputusan ujian daripada kelas
terdiri daripada 30 orang pelajar ;
Keputusan pertamanya ialah antara julat 31% hingga
98%, dan satu lagi, antara 82% hingga 93%,.
Maka, sisihan piawai bagi keputusan yang pertama
adalah lebih besar.

26. PEKALI KORELASI
 Pekali korelasi mengukur sejauh mana atau sekuat
mana dua pembolehubah dapat dikaitkan antara
satu sama lain & arah perkaitan tersebut (the strength
and the direction of a linear relationship)
 Pekali korelasi juga dirujuk dengan nama Korelasi
Pearson (Pearson product moment correlation coefficient )
penghormatan diberi kepada Karl Pearson.
 Formula menentukan nilai pekali korelasi (r) ialah :

27. INTERPRETASI NILAI PEKALI KORELASI
 Julat nilai sesuatu pekali korelasi adalah antara +1 dan -1
 Semakin besar nilai sebenar pekali korelasi, maka semakin kuat
hubungan linear
 Hubungan linear yang paling kuat ditunjukkan oleh pekali
korelasi -1 atau 1
 Hubungan linear yang paling lemah ditunjukkan oleh pekali
korelasi sama dengan 0
 Korelasi positif bermaksud sekiranya nilai satu pebolehubah
meningkat atau menjadi lebih besar, maka nilai pembolehubah
yang lagi satu juga akan meningkat atau menjadi besar
 Korelasi negatif bermaksud sekiranya nilai satu pembolehubah
meningkat atau menjadi lebih besar, maka nilai pembolehubah
yang lagi satu akan mengecil

28. INTERPRETASI NILAI PEKALI
KORELASI
Korelasi positif maksimum ( r = 1.0 ) Korelasi negatif minimum ( r = - 1.0 )
• Apabila kecerunan garisan adalah negatif, maka korelasi
juga negatif. Begitu juga sebaliknya.
• Korelasi terkuat (r = 1 dan r = -1) akan terhasil apabila
titik-titik data berada betul-betul di atas garisan lurus.

29. INTERPRETASI NILAI PEKALI
KORELASI
Korelasi positif yang signifikan ( r = 0.80 )

30. INTERPRETASI NILAI PEKALI
KORELASI
Korelasi sifar ( r = 0 )
• Titik-titik data bercorak rawak

31. INTERPRETASI NILAI PEKALI
KORELASI
Korelasi negatif sederhana ( r = - 0.43 )

32. INTERPRETASI NILAI PEKALI
KORELASI
Korelasi kuat dan keterasingan ( r = 0.71 )

33. INTERPRETASI NILAI PEKALI
KORELASI
 PADA UMUMNYA,
NILAI KORELASI LEBIH DARIPADA 0.8
DIANGGAP KUAT MANAKALA KORELASI
KURANG DARIPADA 0.5 DIANGGAP
LEMAH.

34. PERSEDIAAN TUTORIAL (ISL):
 Dalam kumpulan, sediakan satu soal selidik yang
mengandungi 20 soalan tentang ”Faktor-faktor yang
menyebabkan murid kelas Awana Tahun 5
mengantuk semasa pengajaran dan pembelajaran”.
Edarkan soal selidik kepada 10 rakan anda.
TUTORIAL 11:
Dalam kumpulan, analisiskan data soal selidik
menggunakan jadual kekerapan, min dan peratus.
(1 jam)