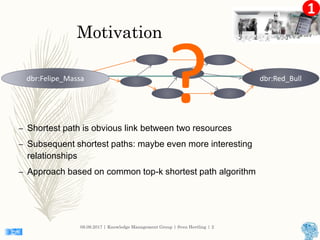
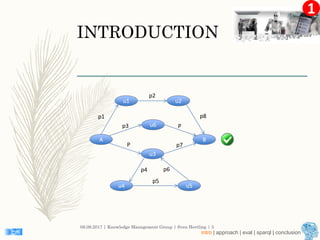
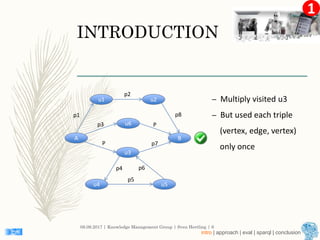
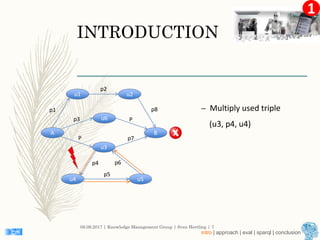
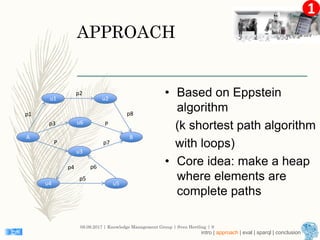
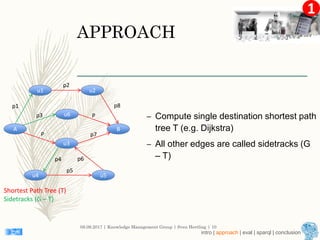
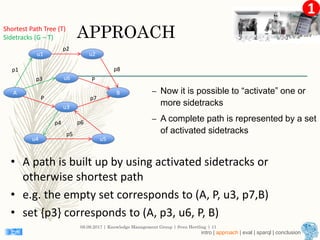
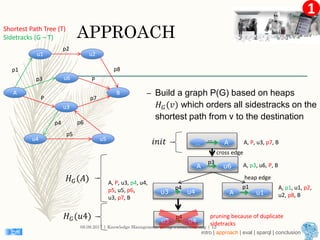
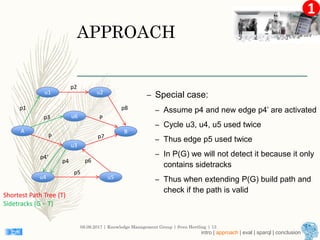
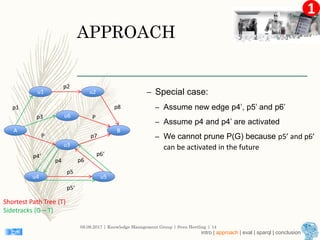
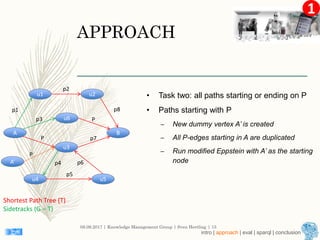
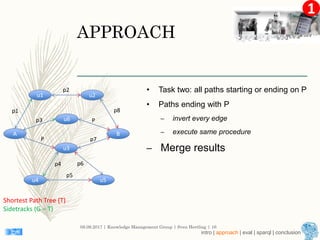
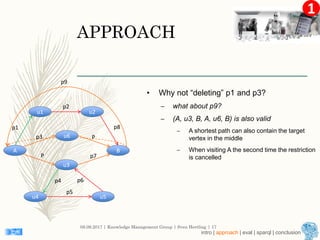
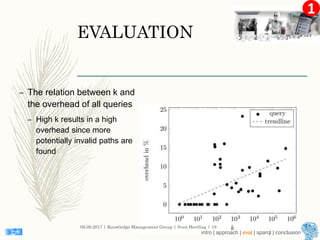
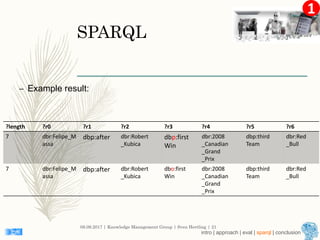
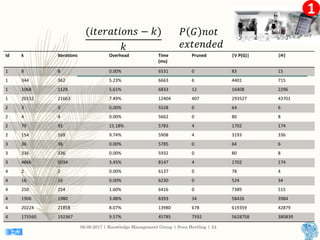
This document describes an approach for finding the top-k shortest paths in large typed RDF graphs. The approach is based on Eppstein's algorithm for finding shortest paths with loops. It represents paths as sets of "activated sidetracks" and builds a graph of paths. Special cases are handled to avoid duplicate edges. The approach was evaluated on the ESWC 2016 Top-k Shortest Path Challenge training data and solved all queries efficiently.