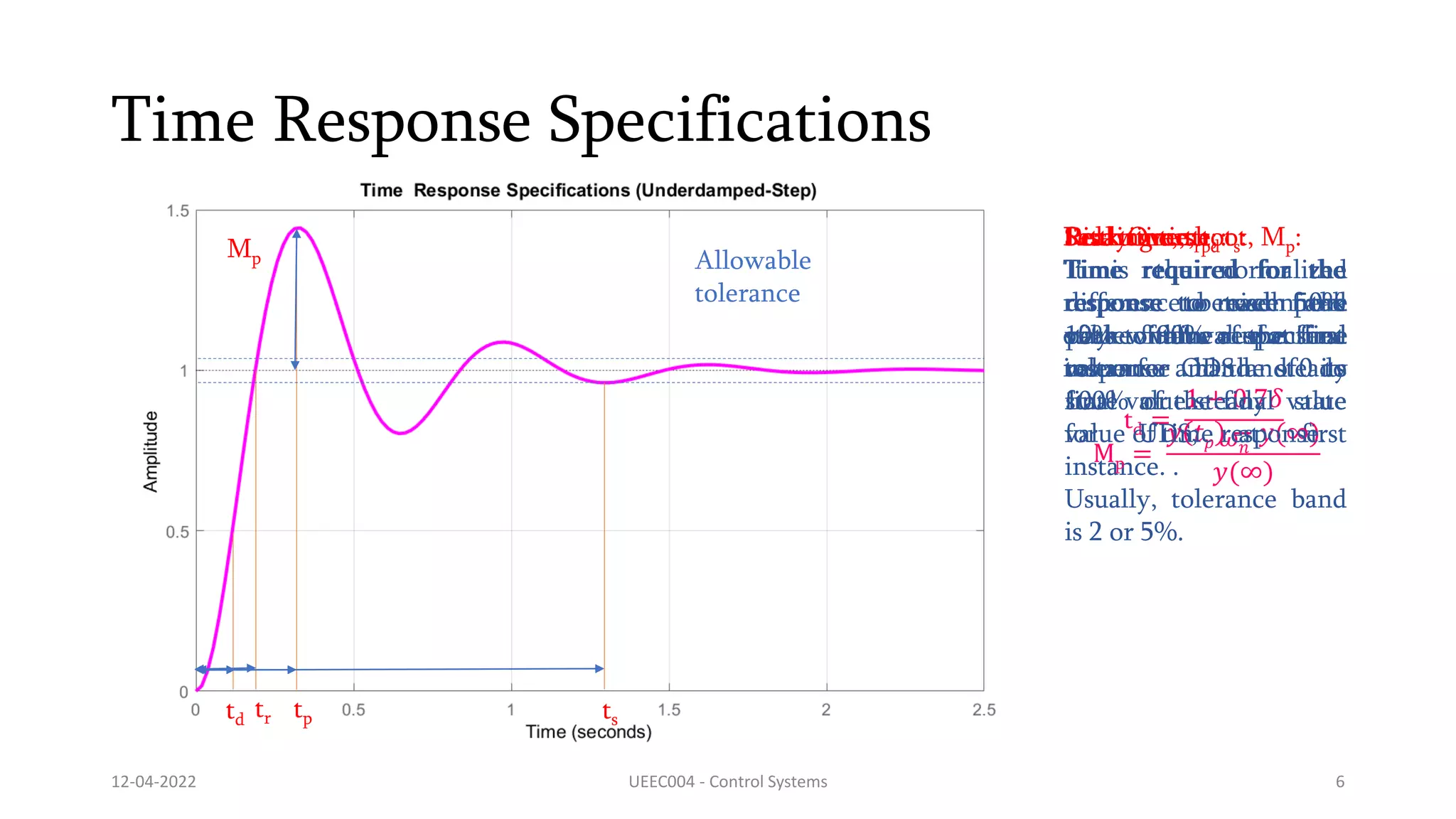
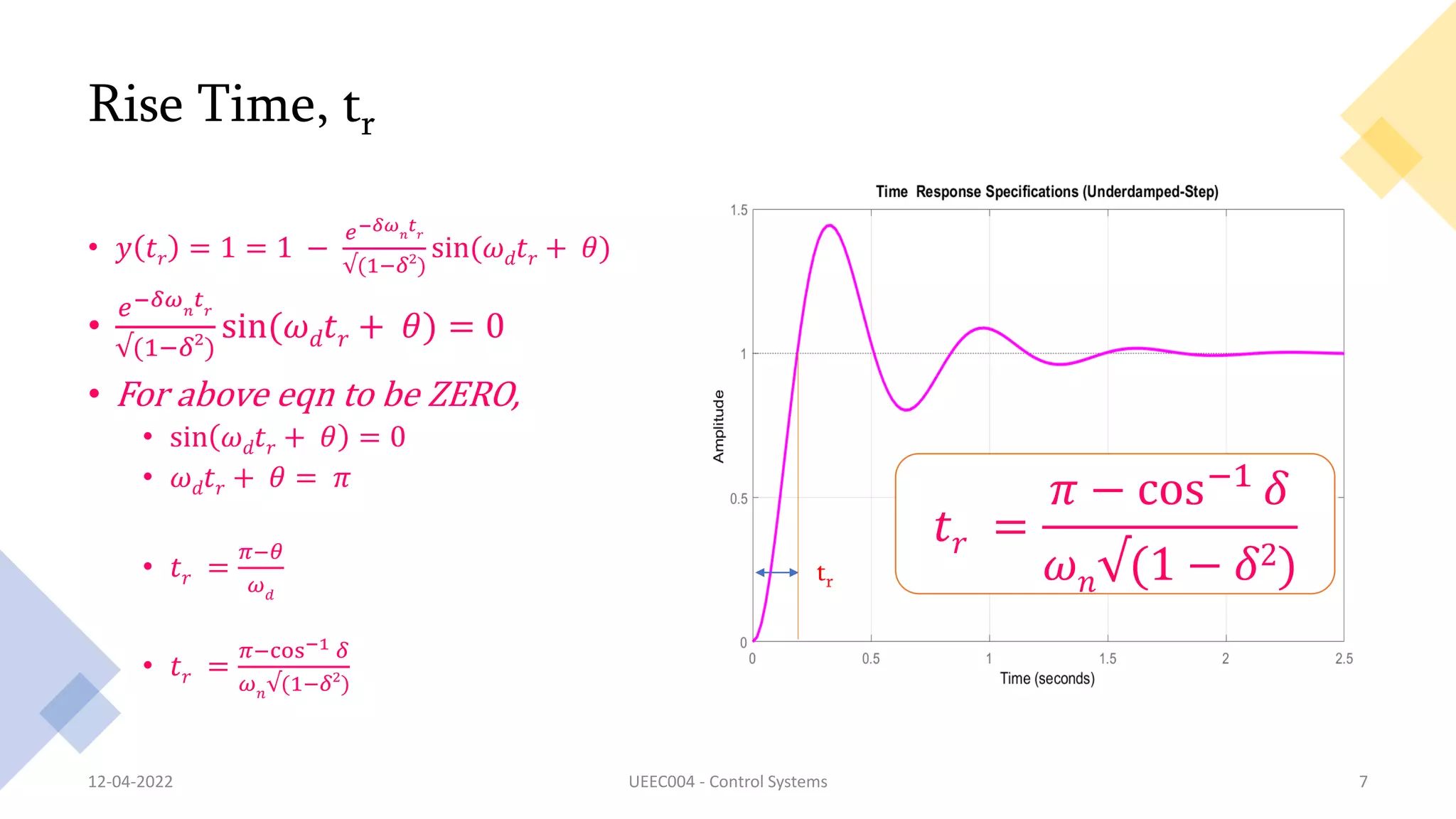
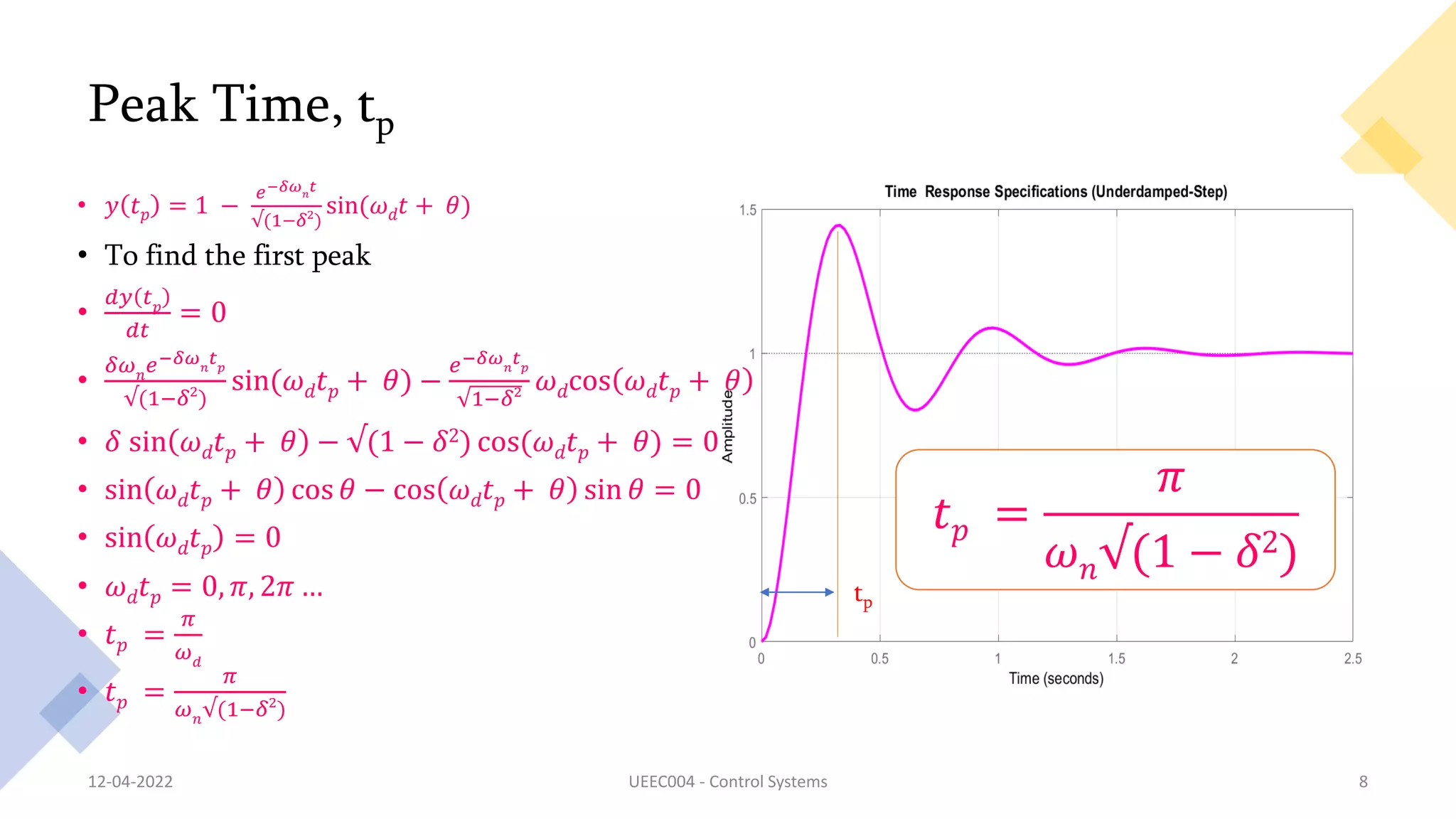
This document discusses time response specifications for second order systems, including delay time, rise time, peak time, and peak overshoot. It provides equations to calculate each specification based on the natural frequency (ωn) and damping ratio (δ) of the system. Rise time is defined as the time to rise from 10-90% of the final value and is calculated as (π - cos^-1δ)/ωn√(1-δ^2). Peak time is the time to reach the first peak and is calculated as π/ωn√(1-δ^2). Peak overshoot is calculated as 100e^(-δπ)/√(1-δ^2)

1. Control Systems
Lecture - 8
E. Ramkumar
Assistant Professor / EEE
12-04-2022 UEEC004 - Control Systems 1

2. Time response of Second Order System
• 𝐶 𝑆 =
ω𝑛 2
𝑆2
+2δω𝑛𝑆+ω𝑛 2
•
𝐶(𝑆)
𝑅(𝑆)
=
100
𝑆2
+0𝑆+100
ω𝑛 2 = 100
ω𝑛 = 10
2δω𝑛 = 0
2δ = 0
δ = 0
12-04-2022 UEEC004 - Control Systems 2

3. Time response of Second Order System
• 𝐶 𝑆 =
ω𝑛 2
𝑆2
+2δω𝑛𝑆+ω𝑛 2
•
𝐶(𝑆)
𝑅(𝑆)
=
100
𝑆2
+10𝑆+100
ω𝑛 2 = 100
ω𝑛 = 10
2δω𝑛 = 10
2δ = 1
δ = 0.5
12-04-2022 UEEC004 - Control Systems 3

4. Time response of Second Order System
• 𝐶 𝑆 =
ω𝑛 2
𝑆2
+2δω𝑛𝑆+ω𝑛 2
•
𝐶(𝑆)
𝑅(𝑆)
=
100
𝑆2
+20𝑆+100
ω𝑛 2 = 100
ω𝑛 = 10
2δω𝑛 = 20
2δ = 2
δ = 1
12-04-2022 UEEC004 - Control Systems 4

5. Time response of Second Order System
• 𝐶 𝑆 =
ω𝑛 2
𝑆2
+2δω𝑛𝑆+ω𝑛 2
•
𝐶(𝑆)
𝑅(𝑆)
=
100
𝑆2
+40𝑆+100
ω𝑛 2 = 100
ω𝑛 = 10
2δω𝑛 = 40
2δ = 4
δ = 2
12-04-2022 UEEC004 - Control Systems 5

6. Time Response Specifications
12-04-2022 UEEC004 - Control Systems 6
Delay time, td:
Time required for the
response to reach 50%
of the final value at first
instance.
td =
1 + 0.7𝛿
𝜔𝑛
Rise time, tr:
Time required for the
response to rise from
10% to 90% of the final
value for ODS and 0 to
100% of the final value
for UDS, at first
instance. .
Peak time, tp:
Time required for the
response to reach peak
value of time response.
Peak Overshoot, Mp:
It is the normalized
difference between the
peak value of time
response and the steady
state value.
Mp =
𝑦 𝑡𝑝 − 𝑦(∞)
𝑦(∞)
Settling time, ts:
Time required for the
response to reach and
stay within a specified
tolerance band of its
final or steady state
value of time response.
Usually, tolerance band
is 2 or 5%.
td tr tp
Mp
ts
Allowable
tolerance

7. Rise Time, tr
• 𝑦 𝑡𝑟 = 1 = 1 −
𝑒−𝛿𝜔𝑛
𝑡𝑟
√(1−𝛿2
)
sin(𝜔𝑑𝑡𝑟 + 𝜃)
•
𝑒−𝛿𝜔𝑛
𝑡𝑟
√(1−𝛿2
)
sin(𝜔𝑑𝑡𝑟 + 𝜃) = 0
• For above eqn to be ZERO,
• sin 𝜔𝑑𝑡𝑟 + 𝜃 = 0
• 𝜔𝑑𝑡𝑟 + 𝜃 = 𝜋
• 𝑡𝑟 =
𝜋−𝜃
𝜔𝑑
• 𝑡𝑟 =
𝜋−cos−1 𝛿
𝜔𝑛
√(1−𝛿2
)
12-04-2022 UEEC004 - Control Systems 7
tr
𝑡𝑟 =
𝜋 − cos−1
𝛿
𝜔𝑛√(1 − 𝛿2)

8. Peak Time, tp
12-04-2022 UEEC004 - Control Systems 8
tp
• 𝑦 𝑡𝑝 = 1 −
𝑒−𝛿𝜔𝑛
𝑡
√(1−𝛿2
)
sin(𝜔𝑑𝑡 + 𝜃)
• To find the first peak
•
𝑑𝑦 𝑡𝑝
𝑑𝑡
= 0
•
𝛿𝜔𝑛
𝑒−𝛿𝜔𝑛
𝑡𝑝
√(1−𝛿2
)
sin(𝜔𝑑𝑡𝑝 + 𝜃) −
𝑒−𝛿𝜔𝑛
𝑡𝑝
1−𝛿2 𝜔𝑑cos 𝜔𝑑𝑡𝑝 + 𝜃
• 𝛿 sin 𝜔𝑑𝑡𝑝 + 𝜃 − √(1 − 𝛿2) cos(𝜔𝑑𝑡𝑝 + 𝜃) = 0
• sin 𝜔𝑑𝑡𝑝 + 𝜃 cos 𝜃 − cos 𝜔𝑑𝑡𝑝 + 𝜃 sin 𝜃 = 0
• sin 𝜔𝑑𝑡𝑝 = 0
• 𝜔𝑑𝑡𝑝 = 0, 𝜋, 2𝜋 …
• 𝑡𝑝 =
𝜋
𝜔𝑑
• 𝑡𝑝 =
𝜋
𝜔𝑛
√(1−𝛿2
)
𝑡𝑝 =
𝜋
𝜔𝑛√(1 − 𝛿2)

9. Peak Overshoot, Mp
12-04-2022 UEEC004 - Control Systems 9
Mp
• 𝑀𝑝 =
𝑦 𝑡𝑝
−1
1
• 𝑦 𝑡𝑝 − 1 = 1 −
𝑒−𝛿𝜔𝑛
𝑡𝑝
1−𝛿2 sin 𝜔𝑑𝑡𝑝 + 𝜃 − 1
• 𝑦 𝑡𝑝 = −
𝑒−𝛿𝜔𝑛
𝑡𝑝
√(1−𝛿2
)
sin(𝜔𝑑𝑡𝑝 + 𝜃)
• 𝑡𝑝 =
𝜋
𝜔𝑑
• 𝑀𝑝 = −
𝑒
−𝛿𝜔𝑛
𝜋
𝜔𝑑
√(1−𝛿2
)
sin(𝜔𝑑
𝜋
𝜔𝑑
+ 𝜃)
• 𝑀𝑝 =
𝑒
−
𝛿𝜋
√(1−𝛿
2
)
√(1−𝛿2
)
sin( 𝜃)
• 𝑀𝑝 = 𝑒
−
𝛿𝜋
√(1−𝛿2
)
𝑀𝑝 = 100𝑒
𝛿𝜋
√(1−𝛿2
)%