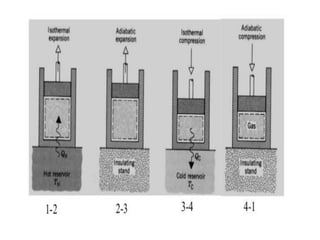
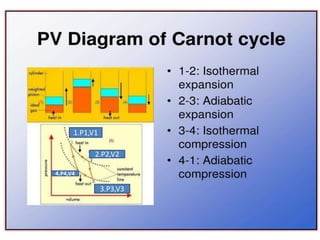
The document discusses the laws of thermodynamics, specifically the first and second laws, explaining concepts such as energy conservation, heat flow direction, and the limitations of the first law. It details the Carnot heat engine and calculations related to its efficiency, as well as introduces the concept of entropy, emphasizing its significance in measuring unavailable energy and disorder in systems. The document also includes mathematical equations and examples related to the principles discussed.




















![.
Similarly along the curve AD
T2V1 (ɤ - 1) = T1V4(ɤ - 1)
(T2/T1) = (V4/V1) (ϒ-1) --------------(7)
Thus From Eq 6 and 7
(V3/V2)(ϒ-1) = (V4/V1) (ϒ-1)
(V3/V1) = (V4/V1)
(V2/V1) = (V3/V4)
Equation (5) becomes
- W net = RT2ln(V2/V1)+RT1ln(V1/V2)
- W net = RT2ln(V2/V1) - RT1ln(V2/V1) ------------(8)
- W net = R(T2 - T1)ln(V2/V1)
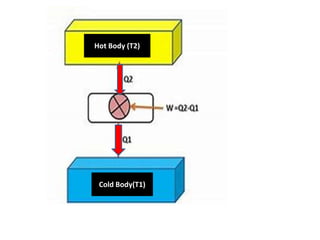
Net heat absorbed by the system in complete cycle is given by
q = { Heat absorbed in various Step –Heat rejected in various step}
= [ q2 – q1 ] -----------------------------(9)
Q = (q2 –q1)
But net heat absorbed = Net work performed
q = -W net = (q2 – q1) = R(T2-T1)ln(V2/V1)
-Wnet = q = (q2 –q1 = R (T2 –T1) ln (V2/V1) ---------(10)](https://image.slidesharecdn.com/thermodynamic3-210517124931/85/Thermodynamic3-24-320.jpg)


























