The document describes the octagon abstract domain, which is used in abstract interpretation of programs. It can represent relationships between two variables, such as X - Y ≤ c, using difference bound matrices. The octagon domain is more precise than the interval domain as it is relational, but has lower complexity than the polyhedra domain. Abstract transfer functions corresponding to semantic operations are used to manipulate elements in the domain. Shortest path closure is used to obtain the smallest representation. An example analysis and conclusion are also outlined.



![Domains The Octagon Domain Abstract Transfer Functions Analysis Example Conclusion
Numerical Domains II
Assumption: Numeric means R
Interval Domain: Xi ∈ [ai , bi ]
Polyhedra Domain: i aij Xi ≤ bj
Zone Abstract Domain: ±Xi ≤ ci , Xi − Xj ≤ cij ∀i = j
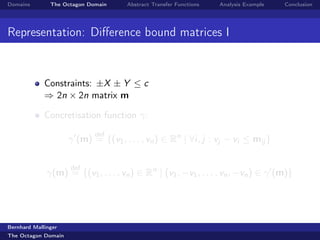
Octagon Domain: ±Xi ± Xj ≤ cij ∀i, j
Bernhard Mallinger
The Octagon Domain](https://image.slidesharecdn.com/octagon-domain-130313093321-phpapp01/85/The-Octagon-Abstract-Domain-6-320.jpg)
![Domains The Octagon Domain Abstract Transfer Functions Analysis Example Conclusion
Numerical Domains II
Assumption: Numeric means R
Interval Domain: Xi ∈ [ai , bi ]
Polyhedra Domain: i aij Xi ≤ bj
Zone Abstract Domain: ±Xi ≤ ci , Xi − Xj ≤ cij ∀i = j
Octagon Domain: ±Xi ± Xj ≤ cij ∀i, j
Bernhard Mallinger
The Octagon Domain](https://image.slidesharecdn.com/octagon-domain-130313093321-phpapp01/85/The-Octagon-Abstract-Domain-7-320.jpg)
![Domains The Octagon Domain Abstract Transfer Functions Analysis Example Conclusion
Numerical Domains II
Assumption: Numeric means R
Interval Domain: Xi ∈ [ai , bi ]
Polyhedra Domain: i aij Xi ≤ bj
Zone Abstract Domain: ±Xi ≤ ci , Xi − Xj ≤ cij ∀i = j
Octagon Domain: ±Xi ± Xj ≤ cij ∀i, j
Bernhard Mallinger
The Octagon Domain](https://image.slidesharecdn.com/octagon-domain-130313093321-phpapp01/85/The-Octagon-Abstract-Domain-8-320.jpg)
![Domains The Octagon Domain Abstract Transfer Functions Analysis Example Conclusion
Numerical Domains II
Assumption: Numeric means R
Interval Domain: Xi ∈ [ai , bi ]
Polyhedra Domain: i aij Xi ≤ bj
Zone Abstract Domain: ±Xi ≤ ci , Xi − Xj ≤ cij ∀i = j
Octagon Domain: ±Xi ± Xj ≤ cij ∀i, j
Bernhard Mallinger
The Octagon Domain](https://image.slidesharecdn.com/octagon-domain-130313093321-phpapp01/85/The-Octagon-Abstract-Domain-9-320.jpg)











![Domains The Octagon Domain Abstract Transfer Functions Analysis Example Conclusion
Assignment I
Handling of assignments depends on the type of the expression
Directly handleable in the octagon domain:
X ← ±[a, b]
X ← ±Y ± [a, b]
e.g. for X ← Y + [a, b], we get a ≤ X − Y ≤ b:
+X − −Y ≤ b − X − +Y ≤ −a
−Y − +X ≤ b + Y − −X ≤ −a
Constraints for X w.r.t. other variables have to be discarded
Bernhard Mallinger
The Octagon Domain](https://image.slidesharecdn.com/octagon-domain-130313093321-phpapp01/85/The-Octagon-Abstract-Domain-25-320.jpg)

![Domains The Octagon Domain Abstract Transfer Functions Analysis Example Conclusion
Test
1 X := [-100, 100]
2 if X ≥ 0 then
3 // X ∈ [0, 100]
4 end if
All tests can be simplified to expr ≤ 0
Octagonally shaped tests can directly be applied
(e.g. X + Y + [a, b] ≤ 0)
More complex forms can be handled in the Interval or
Polyhedra domain (cf. Assignment)
Bernhard Mallinger
The Octagon Domain](https://image.slidesharecdn.com/octagon-domain-130313093321-phpapp01/85/The-Octagon-Abstract-Domain-27-320.jpg)
![Domains The Octagon Domain Abstract Transfer Functions Analysis Example Conclusion
1 X := [-100, 100]
2 Y := X
3 if Y ≤ 0 then
4 1 Y := -Y 2
5 else
6 3
7 end if
8 4
9 if Y ≤ 69 then 5
10 end if
1 −100 ≤ X ≤ 0 ∧ −100 ≤ Y ≤ 0 ∧ X − Y = 0 ∧ −200 ≤ X + Y ≤ 0
2 −100 ≤ X ≤ 0 ∧ 0 ≤ Y ≤ 100 ∧ −200 ≤ X − Y ≤ 0 ∧ X + Y = 0
3 0 ≤ X ≤ 100 ∧ 0 ≤ Y ≤ 100 ∧ X − Y = 0 ∧ 0 ≤ X + Y ≤ 200
4 −100 ≤ X ≤ 100 ∧ 0 ≤ Y ≤ 100 ∧ −200 ≤ X − Y ≤ 0 ∧ 0 ≤ X + Y ≤ 200
5 −69 ≤ X ≤ 69 ∧ 0 ≤ Y ≤ 69 ∧ −138 ≤ X − Y ≤ 0 ∧ 0 ≤ X + Y ≤ 138
Bernhard Mallinger
The Octagon Domain](https://image.slidesharecdn.com/octagon-domain-130313093321-phpapp01/85/The-Octagon-Abstract-Domain-29-320.jpg)
![Domains The Octagon Domain Abstract Transfer Functions Analysis Example Conclusion
1 X := [-100, 100]
2 Y := X
3 if Y ≤ 0 then
4 1 Y := -Y 2
5 else
6 3
7 end if
8 4
9 if Y ≤ 69 then 5
10 end if
1 −100 ≤ X ≤ 0 ∧ −100 ≤ Y ≤ 0 ∧ X − Y = 0 ∧ −200 ≤ X + Y ≤ 0
2 −100 ≤ X ≤ 0 ∧ 0 ≤ Y ≤ 100 ∧ −200 ≤ X − Y ≤ 0 ∧ X + Y = 0
3 0 ≤ X ≤ 100 ∧ 0 ≤ Y ≤ 100 ∧ X − Y = 0 ∧ 0 ≤ X + Y ≤ 200
4 −100 ≤ X ≤ 100 ∧ 0 ≤ Y ≤ 100 ∧ −200 ≤ X − Y ≤ 0 ∧ 0 ≤ X + Y ≤ 200
5 −69 ≤ X ≤ 69 ∧ 0 ≤ Y ≤ 69 ∧ −138 ≤ X − Y ≤ 0 ∧ 0 ≤ X + Y ≤ 138
Bernhard Mallinger
The Octagon Domain](https://image.slidesharecdn.com/octagon-domain-130313093321-phpapp01/85/The-Octagon-Abstract-Domain-30-320.jpg)
![Domains The Octagon Domain Abstract Transfer Functions Analysis Example Conclusion
1 X := [-100, 100]
2 Y := X
3 if Y ≤ 0 then
4 1 Y := -Y 2
5 else
6 3
7 end if
8 4
9 if Y ≤ 69 then 5
10 end if
1 −100 ≤ X ≤ 0 ∧ −100 ≤ Y ≤ 0 ∧ X − Y = 0 ∧ −200 ≤ X + Y ≤ 0
2 −100 ≤ X ≤ 0 ∧ 0 ≤ Y ≤ 100 ∧ −200 ≤ X − Y ≤ 0 ∧ X + Y = 0
3 0 ≤ X ≤ 100 ∧ 0 ≤ Y ≤ 100 ∧ X − Y = 0 ∧ 0 ≤ X + Y ≤ 200
4 −100 ≤ X ≤ 100 ∧ 0 ≤ Y ≤ 100 ∧ −200 ≤ X − Y ≤ 0 ∧ 0 ≤ X + Y ≤ 200
5 −69 ≤ X ≤ 69 ∧ 0 ≤ Y ≤ 69 ∧ −138 ≤ X − Y ≤ 0 ∧ 0 ≤ X + Y ≤ 138
Bernhard Mallinger
The Octagon Domain](https://image.slidesharecdn.com/octagon-domain-130313093321-phpapp01/85/The-Octagon-Abstract-Domain-31-320.jpg)
![Domains The Octagon Domain Abstract Transfer Functions Analysis Example Conclusion
1 X := [-100, 100]
2 Y := X
3 if Y ≤ 0 then
4 1 Y := -Y 2
5 else
6 3
7 end if
8 4
9 if Y ≤ 69 then 5
10 end if
1 −100 ≤ X ≤ 0 ∧ −100 ≤ Y ≤ 0 ∧ X − Y = 0 ∧ −200 ≤ X + Y ≤ 0
2 −100 ≤ X ≤ 0 ∧ 0 ≤ Y ≤ 100 ∧ −200 ≤ X − Y ≤ 0 ∧ X + Y = 0
3 0 ≤ X ≤ 100 ∧ 0 ≤ Y ≤ 100 ∧ X − Y = 0 ∧ 0 ≤ X + Y ≤ 200
4 −100 ≤ X ≤ 100 ∧ 0 ≤ Y ≤ 100 ∧ −200 ≤ X − Y ≤ 0 ∧ 0 ≤ X + Y ≤ 200
5 −69 ≤ X ≤ 69 ∧ 0 ≤ Y ≤ 69 ∧ −138 ≤ X − Y ≤ 0 ∧ 0 ≤ X + Y ≤ 138
Bernhard Mallinger
The Octagon Domain](https://image.slidesharecdn.com/octagon-domain-130313093321-phpapp01/85/The-Octagon-Abstract-Domain-32-320.jpg)
![Domains The Octagon Domain Abstract Transfer Functions Analysis Example Conclusion
1 X := [-100, 100]
2 Y := X
3 if Y ≤ 0 then
4 1 Y := -Y 2
5 else
6 3
7 end if
8 4
9 if Y ≤ 69 then 5
10 end if
1 −100 ≤ X ≤ 0 ∧ −100 ≤ Y ≤ 0 ∧ X − Y = 0 ∧ −200 ≤ X + Y ≤ 0
2 −100 ≤ X ≤ 0 ∧ 0 ≤ Y ≤ 100 ∧ −200 ≤ X − Y ≤ 0 ∧ X + Y = 0
3 0 ≤ X ≤ 100 ∧ 0 ≤ Y ≤ 100 ∧ X − Y = 0 ∧ 0 ≤ X + Y ≤ 200
4 −100 ≤ X ≤ 100 ∧ 0 ≤ Y ≤ 100 ∧ −200 ≤ X − Y ≤ 0 ∧ 0 ≤ X + Y ≤ 200
5 −69 ≤ X ≤ 69 ∧ 0 ≤ Y ≤ 69 ∧ −138 ≤ X − Y ≤ 0 ∧ 0 ≤ X + Y ≤ 138
Bernhard Mallinger
The Octagon Domain](https://image.slidesharecdn.com/octagon-domain-130313093321-phpapp01/85/The-Octagon-Abstract-Domain-33-320.jpg)
![Domains The Octagon Domain Abstract Transfer Functions Analysis Example Conclusion
1 X := [-100, 100]
2 Y := X
3 if Y ≤ 0 then
4 1 Y := -Y 2
5 else
6 3
7 end if
8 4
9 if Y ≤ 69 then 5
10 end if
1 −100 ≤ X ≤ 0 ∧ −100 ≤ Y ≤ 0 ∧ X − Y = 0 ∧ −200 ≤ X + Y ≤ 0
2 −100 ≤ X ≤ 0 ∧ 0 ≤ Y ≤ 100 ∧ −200 ≤ X − Y ≤ 0 ∧ X + Y = 0
3 0 ≤ X ≤ 100 ∧ 0 ≤ Y ≤ 100 ∧ X − Y = 0 ∧ 0 ≤ X + Y ≤ 200
4 −100 ≤ X ≤ 100 ∧ 0 ≤ Y ≤ 100 ∧ −200 ≤ X − Y ≤ 0 ∧ 0 ≤ X + Y ≤ 200
5 −69 ≤ X ≤ 69 ∧ 0 ≤ Y ≤ 69 ∧ −138 ≤ X − Y ≤ 0 ∧ 0 ≤ X + Y ≤ 138
Bernhard Mallinger
The Octagon Domain](https://image.slidesharecdn.com/octagon-domain-130313093321-phpapp01/85/The-Octagon-Abstract-Domain-34-320.jpg)