Downloaded 517 times
Uploaded byGrace Henry
The history of pi
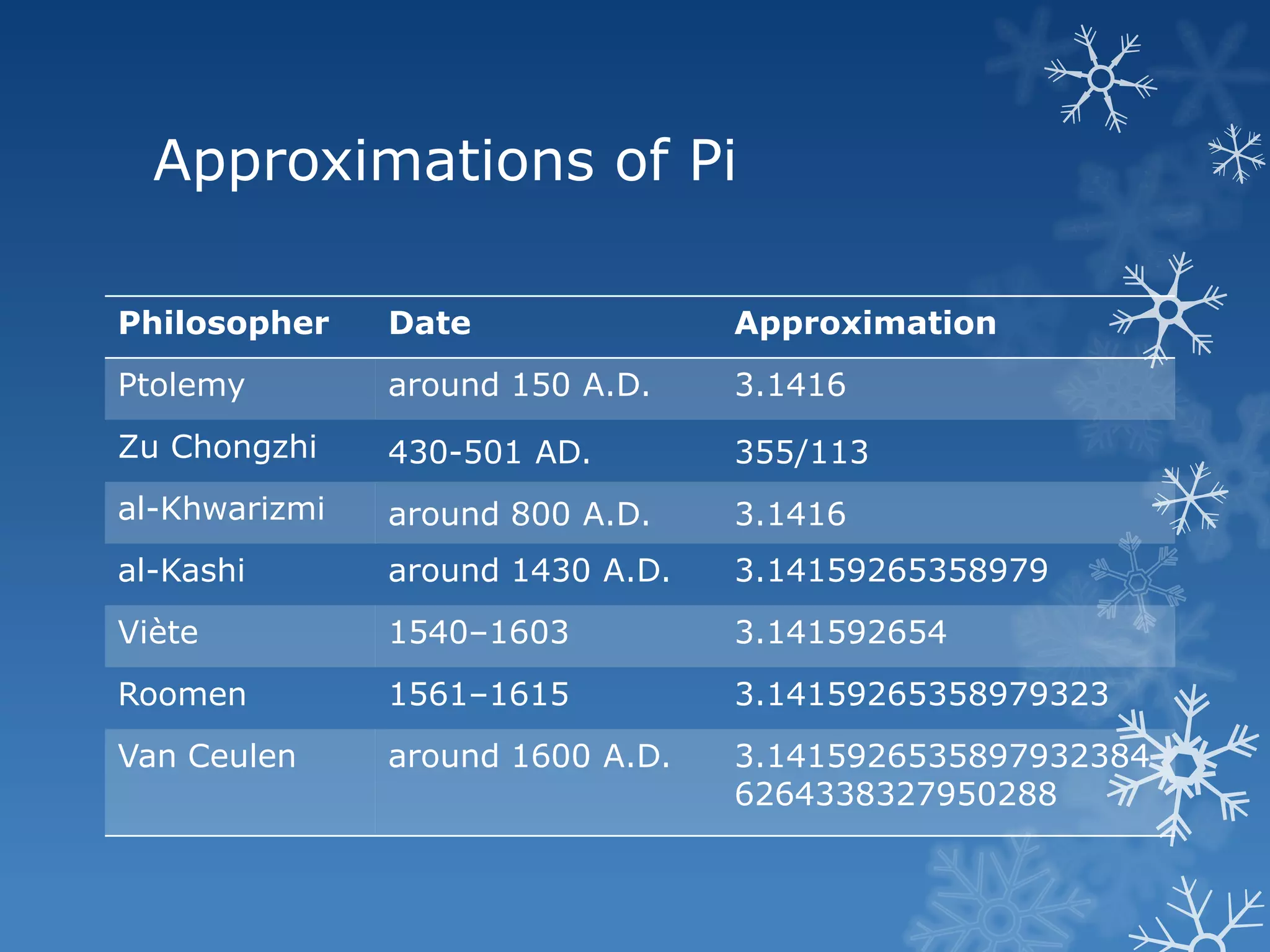
The document discusses the history and properties of pi (π). It describes how various ancient civilizations like the Babylonians, Hebrews, and Egyptians approximated pi. The Greeks studied pi's relationship to circles, cones, and cylinders. Over centuries, mathematicians like Machin, Euler, and Lambert improved approximations of pi and proved its irrationality. With modern computers, pi has been calculated to extreme accuracy. The document also notes how pi is
More Related Content
Similar to The history of pi
The history of pi
- 2. Team Members… Grace Henry HaimaRonald Lekshmi Dev.S Preetha G. Lopez Rahul Lekshman Suriya S. Kumar Shameer Mehboob
- 3. What is pi?? Anumber can be placed into several categories based on its properties. Is it prime or composite? Is it imaginary or real? Is it transcendental or algebraic? These questions help define a number's behaviour in different situations. In order to understand where π fits in to the world of mathematics, one must understand several of its properties: π is irrational and π is transcendental. Another important concept to understand is that of how π is calculated and how the methods have changed over time. π is:- "1: the 16th letter of the Greek alphabet... 2 a: the symbol pi denoting the ratio of the circumference of a circle to its diameter b: the ratio itself: a transcendental number having a value to eight decimal places of 3.14159265"
- 4. The computation ofPi to 10,000 places may be of no direct scientific usefulness. However, its usefulness in training personnel to use computers and to test such machines appears to be extremely important. Thus the mysterious and wonderful Pi is reduced to a gargle that helps computing machines clear their throats.
- 5. The early Babyloniansand Hebrews used “3”as a value for Pi. Later, Ahmed, an Egyptian found the area of a circle . Down through the ages, countless people have puzzled over this same question, “What is Pi? The Greeks found Pi to be related to cones, ellipses, cylinders and other geometric figures.
- 6. LEIBNITZ (1671) Pi=4(1/1-1/3+1/5-1/7+1/9- 1/11+1/13+...) WALLIS Pi= 2(2/1*2/3*4/3*4/5*6/5*6/7*...) MACHIN (1706) Pi=16(1/5- 1/(3+5^3) +1/(5+5^5) - 1/(7+5^7)+...) x - 4(1/239 -1/(3*239^3) + 1/(5*239^5)- ...) SHARP (1717) Pi= 2*Sq.Rt(3)(1-1/3*3 + 1/5*3^2 - 1/7*3^5...) EULER (1736) Pi= Sq.Rt(6(1+1/1^2+1/2^2+ 1/3^2...)) BOUNCKER Pi= 4 --- 1+1 --- 2+9 --- 2+25 +...
- 7. Approximations of Pi PhilosopherDate Approximation Ptolemy around 150 A.D. 3.1416 Zu Chongzhi 430-501 AD. 355/113 al-Khwarizmi around 800 A.D. 3.1416 al-Kashi around 1430 A.D. 3.14159265358979 Viète 1540–1603 3.141592654 Roomen 1561–1615 3.14159265358979323 Van Ceulen around 1600 A.D. 3.1415926535897932384 6264338327950288
- 8. Pi in everydaylife We use it for Drawing, machining, plans, planes, buildings, bridges, g eometry problems, radio, TV, radar, telephones, estimation, testin g, simulation, global paths, global positioning, space science, orbit calculation, Space ships, satellites, Speedometers at vehicles… etc. Pi is used by every career whether you are a electrical engineer, statistician, biochemist, or physicist. Pi is indeed a necessity for life.
- 9. Pi facts ”PiDay” is celebrated on March 14. The official celebration begins at 1:59 p.m. to make an appropriate 3.14159 when combined with the date. Albert Einstein was born on Pi Day (14/3/1879) in Ulm Wurttemberg, Germany. Pi goes on for ever Decimals have no pattern and don’t repeat.
- 11. The development ofhigh speed electronic computing equipment provided a means for rapid computation. Inquiries regarding the number of Pi’s digits -- not what the numbers were individually, but how they behave statistically -- provided the motive for additional research.
- 12. • The earlyBabylonians and Hebrews used three as a value for Pi. Later, Ahmes, an Egyptian found the area of a circle . Down through the ages, countless people have puzzled over this same question, “What is Pi?" • From 287 - 212B.C. there lived Archimedes, who inscribed in a circle and circumscribed about a circle, regular polygons. • The Greeks found Pi to be related to cones, ellipses, cylinders and other geometric figures.
- 13.
- 14. Pi Day isan unofficial holiday commemorating the mathematical constant π (pi). Pi Day is observed on March 14 (or 3/14 in month/day date format), since 3, 1 and 4 are the three most significant digits of π in the decimal form. In 2009, the United States House of Representatives supported the designation of Pi Day. Pi Approximation Day is observed on July 22 (or 22/7 in day/month date format), since the fraction 22⁄7 is a common approximation of π.
- 15. . Pi Pie atDelft University
- 16. 22/7 exceeds π Proofs of the famous mathematical result that the rational number 22/7 is greater than π (pi) date back to antiquity. 22/7 is a widely used Diophantine approximation of π(the approximation of real numbers by rational numbers). It is a convergent in the simple continued fraction expansion of π. It is greater than π, as can be readily seen in the decimal expansions of these values: The approximation has been known since antiquity. Archimedes wrote the first known proof that 22/7 is an overestimate in the 3rd century BCE, although he may not have been the first to use that approximation. His proof proceeds by showing that 22/7 is greater than the ratio of the perimeter of a circumscribed regular polygon with 96 sides to the diameter of the circle. Another rational approximation of π that is far more accurate is 355/113.
- 18. The first recordof an individual mathematician taking on the problem of π (often called "squaring the circle," and involving the search for a way to cleanly relate either the area or the circumference of a circle to that of a square) occurred in ancient Greece in the 400's B.C. (this attempt was made by Anaxagoras) In the late Greek period (300's-200's B.C.), after Alexander the Great had spread Greek culture from the western borders of India to the Nile Valley of Egypt, Alexandria, Egypt became the intellectual centre of the world. Among the many scholars who worked at the University there, by far the most influential to the history of π was Euclid. While π activity stagnated in Europe, the situation in other parts of the world was quite different. The Mayan civilization, situated on the Yucatan Peninsula in Central America, was quite advanced for its time. The Mayans were top-notch astronomers, developing a very accurate calendar. In order to do this, it would have been necessary for them to have a fairly good value for π. The Chinese in the 5th century calculated π to an accuracy not surpassed by Europe until the 1500's. The Chinese, as well as the Hindus, arrived at π in roughly the same method as the Europeans until well into the Renaissance, when Europe finally began to pull ahead.
- 19. Leonardo Da Vinciand Nicolas Copernicus made minimal contributions to the π endeavour, but François Viète actually made significant improvements to Archimedes' methods. The efforts of Snellius, Gregory, and John Machin eventually culminated in algebraic formulas for π that allowed rapid calculation, leading to ever more accurate values of π during this period. In the 1700's the invention of calculus by Sir Isaac Newton and Leibniz rapidly accelerated the calculation and theorization of π. Using advanced mathematics, Leonhard Euler found a formula for π that is the fastest to date. In the late 1700's Lambert (Swiss) and Legendre (French) independently proved that π is irrational. Although Legendre predicted that π is also transcendental in 1882. Also in the 18th century, George Louis Leclerc, Comte de Buffon, discovered an experimental method for calculating π. Pierre Simon Laplace, one of the founders of probability theory, followed up on this in the next century. Starting in 1949 with the ENIAC computer, digital systems have been calculating π to incredible accuracy throughout the second half of the twentieth century.
- 20.