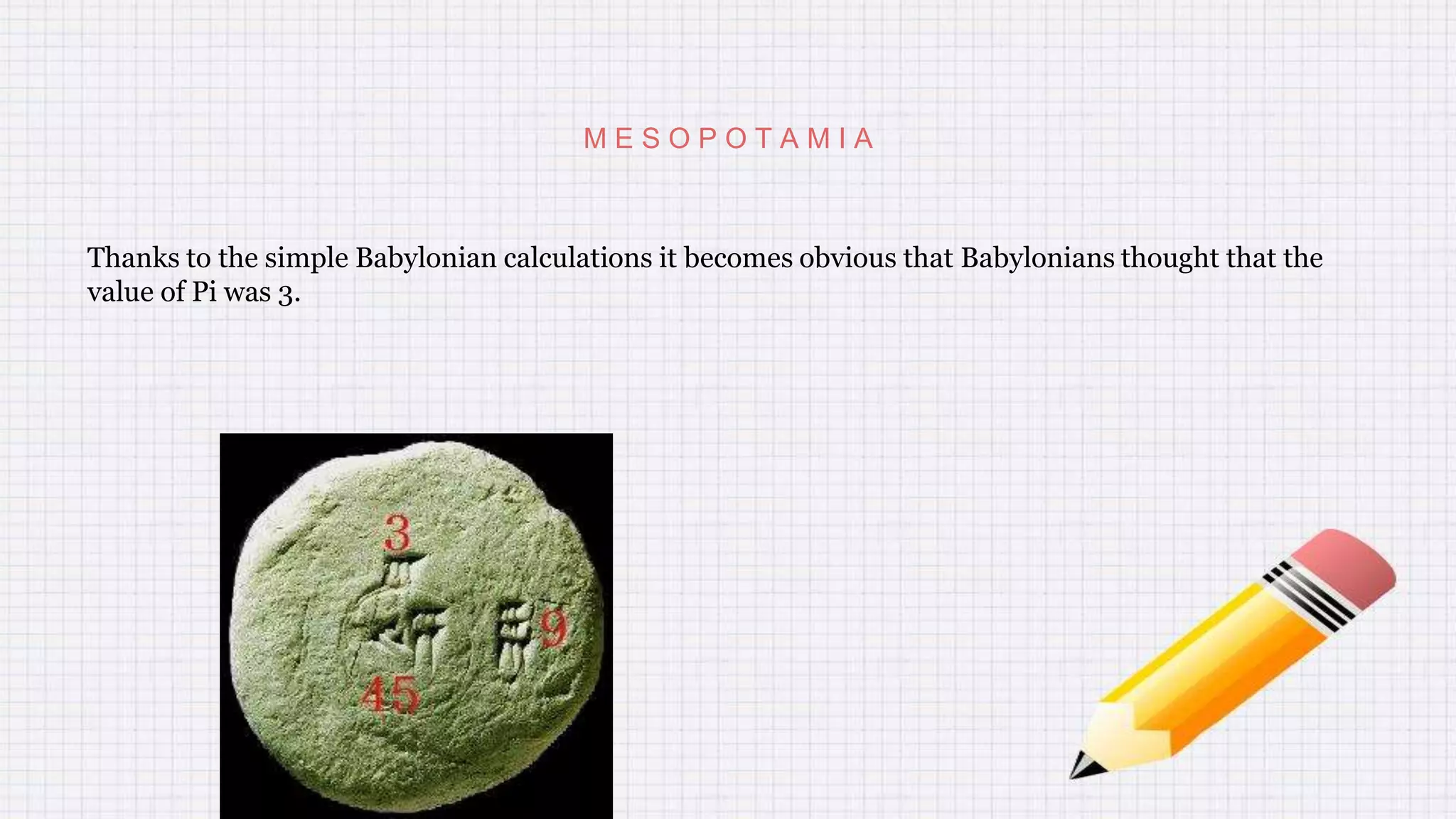
This document provides a history of the number Pi from ancient civilizations to modern times. It discusses how Pi was conceptualized and calculated in ancient Egypt, Mesopotamia, China, and among ancient Greek mathematicians like Archimedes. It then covers the stagnation of math during the Middle Ages, followed by advances during the Renaissance made by mathematicians like Viete and Ludolf van Ceulen. The 18th and 19th centuries saw more accurate calculations of Pi. In the 20th century, computers were used to calculate Pi to increasing levels of precision. The document concludes by noting modern applications of Pi in fields like computing and its cultural significance.

1. History of
Number Pi
Klasické a španělské gymnázium, Brno

2. Dividing time slots
1. Egypt, Mesopotamia, China
2. Ancient Greek
3. Middle age
4. Renaissance
5. 18. Century
6. 19. Century
6. 20. Century
7. Movies
8. Present

3. what is actuallyπ?
Number Pi is an irrational number so it can't be expressed by a mathematical fraction. In basic
problems we can use the fraction 22/7 or more exact 335/13.
A different name for Pi is Ludolf‘s number – named by a Dutch mathematician Ludolafa von
Ceulena.
He was the first who calculated π for 35 decimal places.

4. E G Y P T
We can find some mathematical discoveries even in the
Egyptian civilization.
They used to write with hieroglyphics onto roll paper
(papyrus).
The most important discovery was Rhind's (Ahmos's)
papyrus, which was discovered in Thebes in the middle of
the 19. Century. It includes a collection of 87 mathematical
problems. Because of that we know that Egyptians
handled algebra and geometry perfectly.

5. E G Y P T
Rhind's papyrus includes even the first calculations of area of a circle and because of
That, Egyptian thought that the value of πis 3,1605. Egyptians were also thinking that circle can
be inscribed in a square.

6. E G Y P T

7. M E S O P O T A M I A
One of the oldest Babylonian charts relating to geometry of circles is called YBC7302. There‘s a
diagram of a perfect circle and three figures. Above the diagram there‘s number 3 (perimeter), 9 (32
)
and inside of the circle there‘

8. M E S O P O T A M I A
Thanks to the simple Babylonian calculations it becomes obvious that Babylonians thought that the
value of Pi was 3.

9. C H I N A
Already around the year 200 AD, the major Chinese work, entitled "Mathematics in nine books„ was
created, filling a comparable role, same as the European Euclid‘s collection („Elements„).

10. C H I N A
Thanks to an educated chieftain named Wang Fan, the value of Pi was already known to be
approximately 3.15555. Later on, Chinese knowledge expanded with Liu Hui, who gave us a more exact
value, that is 3.14159.

11. A N C I E N T G R E E C E
Ve starověkém Řecku hrál největší roli Archimédes. Ten vypočítal číslo pí pomoci vepsaných a
opsaných mnohoúhelníků. Původně měly mnohoúhelníky 12 stran, později 24, 48 a 96… Dostal tak pro
pí horní a dolní hranici.
The major mathematician in ancient Greece was Archimedes who calculated the number thanks to
inscribed and circumscribed polygons. Originally, the polygons had 12 sides, then 24, 48, 96… And
Archimedes got to the upper and lower limits.

12. A N C I E N T G R E E C E
Archimedes‘ most important works include: The Method, On Spirals, Measurement of a Circle,
Quadrature of the Parabola, Conoids and Spheroids, On Spheres and Cylinders,…
Archimedova metoda

13. M I D D L E A G E S
Middle Ages were characterized by the "dark interim" between Graeco-Roman medieval and modern
period. The beginning of the Middle Ages, is generally considered to be the fall of Rome in 476 AD and
the end date is considered to be the year 1492nd
The term Middle Ages was first used by the Renaissance thinkers in the late fifteenth century.

14. M I D D L E A G E S
The Middle Ages was a period of significant
cultural decline.
All of the scientific theories were declined by the
church and said to be the devil‘s work.
Because of the church a lot of eminent
mathematicians were burned alive, including
Giordano Bruno, Galileo Galilei, …

15. M I D D L E A G E S
It is no wonder that mathematics registered only a small progress during these ages. Until the
Renaissance, Europe's math knowledge was roughly the same as the Babylonians‘ 2000 years ago.
The history of number Pi wasn‘t an exception as there wasn‘t accomplished any major improvement in
this area.
That was until the year 1593 when Viete discovered the infinite product of nested radicals.

16. Leonardo z Pisy- FIBONACCI (around 1170 - 1250)
can be seen as the most notable mathematician of the Middle Ages. His work wasn‘t outdone until the
Middle Ages – Modern ages turn.
M I D D L E A G E S

17. M I D D L E A G E S
Leonardo‘s book Practica geometriae is also partly
dedicated to geometric problems. This file is divided
into 3 section. The third part mainly deals with the
„measurement of figures“ (e.g. triangle, square,
rectangle, polygon and circle). There‘s also a general
guidance on how to calculate the perimeter and the
area of a circle plus a specific formula for a circle that
is 14 in diameter. Pi is used in the form of 22/7.

18. T H E B E G I N N I N G O F T H E R E N A I S S A N C E
It was the most progressive coup the humanity experienced
so far. Renaissance is saturated with discoveries leading to
the refinement of mathematical methods.
During this time period the number π was mainly associated
with the need of accurate numerical values of constants.
In addition to the Indo-Arabic numerals and decimal fractions
there were another two means of numerical calculations,
namely trigonometric functions and logarithms.

19. T H E B E G I N N I N G O F T H E R E N A I S S A N C E
Francois Viète (1540 - 1603) significantly contributed to
the development of modern algebra by adding lots of new
terminological words, some of which, such as ‚negative‘ or
‚coefficient‘ persisted to modern age. Applying Archimedes'
method he calculated π (using a regular 392,216-square)
accurately up to nine decimal places. Later on he expressed
π as an infinite product. The process was that he put the
area of a polygon with n sides to the area of a polygon with
2n sides.

20. T H E B E G I N N I N G O F T H E R E N A I S S A N C E
Ludolf van Ceulen (1540 - 1610)
In 1596, he published his article Van den Circkel with the
accurate value of π up to 20 decimal places. The paper ends
with: "Whoever wants to, can go even further." And his
work (‚De Aritmetische en Geometrische fondamenten‘)
accurately indicates the value of π even up to 35 digits. His
never ending hunt for numbers made an impression on the
Germans thus they began to call π „The Ludolf‘s number".

21. T H E B E G I N N I N G O F T H E R E N A I S S A N C E
James Gregory (1638 - 1675)
One of the very important discoveries were the arctg
series.Gregory realized that the area under
the curve 1 / (1 + x ^ 2) in the interval (0, x) is the arctan x.
Isaac Newton (1642 - 1727)
He found the converging series for π. He determined a
method of how to calculate the derivative variables and vice
versa and how to find the integral of the function.

22. 1 8 . C E N T U R Y
In 1706 Machin found this mathematical relation:
And the symbol of π set
Thanks to this ralation, π
was refined to 707 decimal places.
In 1761 Lambert describes π as an irracional number

23. 1 9 . C E N T U R Y
Joseph Liouville (1809-1882)
- French professor of Mathematics
- In 1840 he was the first one to prove the existence of the
transcendental numbers
Transcendental number:
a real or complex number that is not algebraic

24. 1 9 . C E N T U R Y
Ferdinand von Lindemann (1852-1939)
- German mathematician
- In 1882, he demonstrated that Pi is a transcendental
number
- his approach was similar to the methods used nine years
earlier by Charles Hermite
- he has also proved that e (the base of natural
logarithms) is transcendental.

25. 2 0 . C E N T U R Y
The technical revolution has helped π to unroll even further.
Eventually, people started to realize that they don‘t need to limit themselves by using only pen and
paper to work with numbers and so the world began operating computers.

26. 2 0 . C E N T U R Y
The last person to calculate Pi on paper and with no technical help is Ferguson.
In 1946 he publishes this number calculated up to 620 decimal places.
And additionally in 1947 (this time using a desktop calculator) he correctly forecasts Pi to 808 digits.

27. 2 0 . C E N T U R Y
In 1949 a computer was used for calculating for the first time (Eniac) and π is determined to 2000
decimal places.

28. 2 0 . C E N T U R Y
Rapid technological innovation and new computer models now enable even faster and more accurate
calculations of π.
http://upload.wikimedia.org/wikipedia/commons/4/4e/Eniac.jpg

29. 2 0 . C E N T U R Y
Computer model The number of decimal places
designated by / for what time / in what
year
ENIAC 2 037/70 hours/1949
NORC 3 089/13 minutes/1955
Pegasus 10 021/33 hours/1957
IBN „704“ 10 000/40 minutes/1958
IBN „7090“ 20 000/39 minutes/1961
CDC „6600“ 500 000/28 hours 10 minutes/1967

30. Film Pi(1998, USA)
“Max is a genius mathematician, who is able to
combine his unique mind with the newest technology.
With the help of one of his inventions, he's trying to
find out how will the shares increase..
His real goals go even further and these activities begin
early interest representatives of the Orthodox Jewish sects
and senior people from Wall Street ... "

31. Film Pipas (2013, Spain )
Short film about 2 girls who don't know what is number Pi, one of the girl's boyfriend o and the
non- existing Pilar.
For watch here

32. Today
Today there isn't any mathematical fild which doesn't use this number. We use number Pi in
geometry, algebra and mathematics analysis. And as a consequence number Pi becomes more
important. With the arrival of modern technology it became obvious that number Pi isn't just in
mathematical world. Computers are dependant on π.

33. Today
People often ask themselves that why number π has so
many digits . In the past like in 17. and 18. Century the
mathematicians were fighting and competing amongst
each other.
Today we use number Pi if we want to test
computers. A computer passes this test if its result is
the same (several thousand digits) as in other
computers.

34. And for conclusion some playthings
Number of letters in the word gives us the value of number Pi.
1. But I must a while endeavour to reckon right (9 digits)
2. How I want a drink, alcoholic of course, after the heavy lectures involving quantum
mechanics (15 digits)

35. Sources
● JUŠKEVIČ, P. Adolf. Dějiny matematiky ve středov ku. Praha: Academia,
1977
● CRILLY, Tony. Matematika. 50 myšlenek, které musíte znát.
Bratislava:Slovart, 2010.
● Bakalářská práce- Bc. Eliška Ponikelská (str.44, 45, 46)
● Internetový portál Pi 314. Francois Viete:
http://www.pi314.net/eng/viete.php
● http://www.studovna4u.cz/matematika/ludolfovo-cislo-pi%CF%80
● http://www.csfd.cz/film/35661-pi