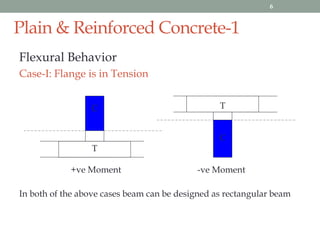
The document provides an analysis of plain and reinforced concrete T and L beams, focusing on their effective widths, flexural behavior, and design considerations. It details the conditions under which beams can be classified based on the position of the neutral axis and discusses various factors affecting tensile and compressive forces within the beams. The analysis includes guidelines for reinforcement ratios and potential failure modes of T-beams.

1. PLAIN & REINFORCED CONCRETE-1
TEE - BEAMS
By
Engr. Rafia Firdous
1

2. Plain & Reinforced Concrete-1
T & L Beams
• With the exception of pre-cast systems, reinforced
concrete floors, roofs, decks, etc., are almost
always monolith.
• Beam stirrups and bent bars extend up into the
slab.
• It is evident, therefore, that a part of the slab will
act with the upper part of the beam to resist
compression.
• The slab forms the beam flange, while a part of the
beam projecting below the slab forms what is
called the “web” or “stem”.
2

3. Plain & Reinforced Concrete-1
T & L Beams (contd…)
d h
b or bf b
hf
bw
b = Effective width
bw = width of web/rib/stem
hf = Thickness of flange
hf
3

4. Plain & Reinforced Concrete-1
Effective With of T & L Beams
T-Beams
Effective width will be minimum of the following:
1. L/4
2. 16hf + bw
3. bw + ½ x (clear spacing of beams (Si) on both sides)
= c/c spacing for beams at regular interval
4

5. Plain & Reinforced Concrete-1
Effective With of T & L Beams
L-Beams
Effective width will be minimum of the
following:
1. L/12
2. 6hf + bw
3. bw + Si/2 on one side
Note: Only above discussion is different for isolated (pre-
cast) T or L beam. Other discussion is same (analysis and
design formula).
5

6. Plain & Reinforced Concrete-1
Flexural Behavior
Case-I: Flange is in Tension
+ve Moment -ve Moment
In both of the above cases beam can be designed as rectangular beam
T
C
C
T
6

7. Plain & Reinforced Concrete-1
Flexural Behavior (contd…)
Case-II: Flange is in Compression and N.A. lies with in
Flange
beam can be designed
as a rectangular beam
of total width “b” and
effective depth “d”.
c N.A.
hf
fhc 
b
T Td
C
7

8. Plain & Reinforced Concrete-1
Flexural Behavior (contd…)
Case-III: Flange is in Compression and N.A. lies out of the
Flange
Beam has to be
designed as a T-Beam.
Separate expressions
are to be developed for
analysis and design.
c
N.A.
hf
fhc 
b
d
C
or
a > β1 hf
8

9. Plain & Reinforced Concrete-1
Flexural Behavior (contd…)
Cw
T = Asfs
N.A.
εcu= 0.003
Strain Diagram Internal Force
Diagram
εs
c
0.85fc
a
Whitney’s
Stress Diagram
(d-a/2)
fs
Cf
d – β1hf/2
hf
Cw
Cf / 2 β1hf/2Cf / 2
Cw = Compression developed in the web = 0.85fc’bwa
Cf = Compression developed in the overhanging flange
= 0.85fc’(b-bw) β1hf
C = Total Compression = Cw + Cf
T = Total Tension = Tw + Tf
Tw = Tension to balance Cw
Tf =Tension to balance Cf
9

10. Plain & Reinforced Concrete-1
Flexural Behavior (contd…)
• It is convenient to divide total tensile steel into two parts. The first
part, Asf represents the steel area which, when stressed to fy, is required
to balance the longitudinal compressive force in the overhanging
portions of the flange that are stressed uniformly at 0.85fc’.
• The remaining steel area As – Asf, at a stress fy, is balanced by the
compression in the rectangular portion web above the N.A.
ssff fAT 
  ssfsssww fAAfAT 
10

11. Plain & Reinforced Concrete-1
Flexural Behavior (contd…)
Majority of T and L beams are under-reinforced (tension
controlled). Because of the large compressive concrete area
provided by the flange. In addition, an upper limit can be
established for the reinforcement ratio to ensure the yielding of
steel.
0F 
For longitudinal equilibrium
ff CT  ww CT &
11

12. Plain & Reinforced Concrete-1
Flexural Behavior (contd…)
ff CT 
  f1wcysf hβbb'f85.0fA 
 w
y
c
f1sf bb
f
'f
hβ85.0A  Only for case-III
ww CT 
  ab'f85.0fAA wcysfs 
 
wc
ysfs
b'f85.0
fAA
a


1β
a
c and
If N.A. is outside the flangefhc 
12

13. Plain & Reinforced Concrete-1
Flexural Behavior (contd…)
Flexural Capacity
From Compression Side
nwnfn MMM 













2
a
dC
2
hβ
dCM w
f1
fn
  












2
a
dab'f85.0
2
hβ
dhβbb'f85.0M wc
f1
f1wcn
13

14. Plain & Reinforced Concrete-1
Flexural Behavior (contd…)
Flexural Capacity
From Tension Side
nwnfn MMM 













2
a
dT
2
hβ
dTM w
f1
fn
  












2
a
dfAA
2
hβ
dfAM ysfs
f1
ysfn
14

15. Plain & Reinforced Concrete-1
Tension Controlled Failure of T-Beam
db
A
ρ
w
s
w  = Total tension steel area (all steel will be in web)
db
A
ρ
w
sf
f  = Steel ratio to balance the flange compressive force
bρ = Balanced steel ratio for the singly reinforced rectangular section
 maxwρ = Maximum steel ratio for T-Beam
maxρ = Maximum steel ratio for the singly reinforced rectangular section
15

16. Plain & Reinforced Concrete-1
Tension Controlled Failure of T-Beam (contd…)
 
db
A
f
'f
8
3
β85.0ρ
w
sf
y
c
1maxw 
  fmaxmaxw ρρρ 
 maxww ρρIf  Tension controlled section
 maxww ρρIf  Transition or Compression controlled section
Or
If a < β1d (3/8) then Tension
controlled section
16

17. Concluded
17