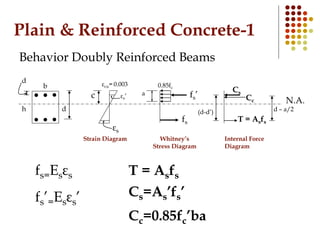
This document discusses the behavior and design of doubly reinforced concrete beams. It describes that doubly reinforced beams have both tension and compression reinforcement to allow for shallower beam depths. There are two possible cases for doubly reinforced beams at the ultimate limit state: 1) both the tension and compression steel yield, or 2) only the tension steel yields, while the compression steel remains elastic. The document provides equations for analyzing each case to determine the forces in the steel and concrete and the beams' moment capacity.

1. Plain & Reinforced
Concrete-1
CE3601
Lecture # 17
3rd April 2012
Flexural Analysis and
Design of Beams
(Ultimate Strength Design of Beams)

2. Plain & Reinforced Concrete-1
Doubly Reinforced Beams
“Beams having both tension and compression reinforcement
to allow the depth of beam to be lesser than minimum depth
for singly reinforced beam”
 By using lesser depth the lever arm reduces and to develop
the same force more area of steel is required, so solution is
costly.
 Ductility will be increased by providing compression steel.
 Hanger bars can also be used as compression steel reducing
the cost up to certain cost.
 For high rise buildings the extra cost of the shallow deep
beams is offset by saving due to less story height.

3. Plain & Reinforced Concrete-1
Doubly Reinforced Beams (contd…)
 Compression steel may reduce creep and shrinkage of
concrete and thus reducing long term deflection.
 Use of doubly reinforced section has been reduced due
to the Ultimate Strength Design Method, which fully
utilizes concrete compressive strength.
Doubly Reinforced Beam

4. Plain & Reinforced Concrete-1
Behavior Doubly Reinforced Beams
Tension steel always yields in D.R.B.
There are two possible cases:
1. Case-I Compression steel is yielding at
ultimate condition.
2. Case-II Compression steel is NOT yielding
at ultimate condition.

5. Plain & Reinforced Concrete-1
Behavior Doubly Reinforced Beams
Cc
T = Asfs
N.A.
εcu= 0.003
Strain Diagram Internal Force
Diagram
εs
h
c
d
b 0.85fc
a
Whitney’s
Stress Diagram
(d-d’)
fs
d
εs’ fs’
Cs
d – a/2
T = Asfs
Cs=As’fs’
Cc=0.85fc’ba
fs=Esεs
fs’=Esεs’

6. Plain & Reinforced Concrete-1
Behavior Doubly Reinforced Beams (contd…)
Case-I Both Tension & Compression steel are yielding at
ultimate condition
fs = fy and fs’=fy
Location of N.A.
Consider equilibrium of forces in longitudinal direction
sc CCT 
yscys f'Aba'f85.0fA 
 
b'f85.0
f'AA
a
c
yss 

1β
a
c and

7. Plain & Reinforced Concrete-1
Case-I Both Tension & Compression steel are yielding at ultimate
condition (contd…)
c
d'c
0.003
'εs 

εcu= 0.003
Strain Diagram
εs
c εs’
d’
B
D
E
C
A
Δ ABC & ADE





 

c
d'c
0.003'εs
1
1
s
β
β
c
d'c
0.003'ε 




 






 

a
d'βa
0.003'ε 1
s
If εs’ ≥ εy compression steel is yielding.
If εs’ < εy compression steel is NOT yielding.
(1)

8. Plain & Reinforced Concrete-1
Case-I Both Tension & Compression steel are yielding at ultimate
condition (contd…)
Cc
T = Asfy
N.A.
Internal Force
Diagram
(d-d’)
Cs
d – a/2
T = total tensile force in the steel
21 TTT 
T1 is balanced by Cs
T2 is balanced by Cc
s1 CT 
c2 CT 

9. Plain & Reinforced Concrete-1
Case-I Both Tension & Compression steel are yielding at ultimate
condition (contd…)
Cc
T = Asfy
N.A.
Internal Force
Diagram
(d-d’)
Cs
d – a/2
Moment Capacity by Compression Steel
   'dd'f'A'ddCM yssn1

 'ddT1 
Moment Capacity by Concrete













2
a
dT
2
a
dCM 2cn2
  






2
a
dTTM 1n 2
  






2
a
d'f'AfAM ysysn 2

10. Plain & Reinforced Concrete-1
Case-I Both Tension & Compression steel are yielding at ultimate
condition (contd…)
Total Moment Capacity
21 nnn MMM 
    






2
a
d'f'AfA'dd'f'AM ysysysn

11. Plain & Reinforced Concrete-1
Case-II Compression steel is not yielding at ultimate
condition
fs = fy and fs’< fy
'εE'f ss 
b'f85.0
'f'AfA
a
c
ssys 

1β
a
c and
a
d'βa
600'f 1
s


Location of N.A.

12. Concluded