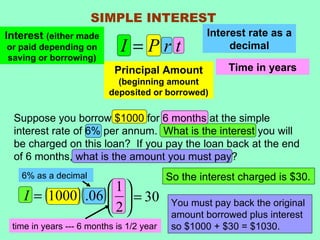
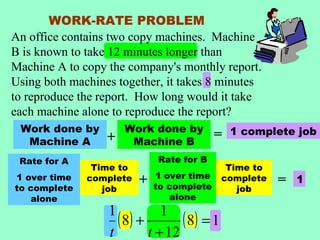
Machine A can copy the monthly report in 12 minutes and Machine B can copy it in 24 minutes. Using both machines together, they can copy the report in 8 minutes. To solve for the individual times, an equation was set up equating the work done by each machine over time to the total work done. This resulted in a quadratic equation that was factored and solved to find the times for each machine alone as 12 and 24 minutes.

1. Mathematical N
Modeling
I O
A T
I C
P L Applied
A P Problems

2. SIMPLE INTEREST
Interest (either made Interest rate as a
or paid depending on
saving or borrowing)
I =Prt decimal
Principal Amount Time in years
(beginning amount
deposited or borrowed)
Suppose you borrow $1000 for 6 months at the simple
interest rate of 6% per annum. What is the interest you will
be charged on this loan? If you pay the loan back at the end
of 6 months, what is the amount you must pay?
6% as a decimal So the interest charged is $30.
1
I = (1000 )( .06 )   = 30 You must pay back the original
2 amount borrowed plus interest
time in years --- 6 months is 1/2 year so $1000 + $30 = $1030.

3. MIXTURE PROBLEMS
+ =
Total Total
Concentration Quantity Concentration Quantity
or price of 1st of first + or price of 2nd of second
= concentration Quantity
or price
How many gallons of a 25% acid Remember total quantity would be
solution would you mix with 4 quantity of 1st + quantity of 2nd
gallons of a 6% acid solution to
We could multiply all terms by
obtain a 15% acid solution? 100 to get rid of decimals.
( .25)( x ) + ( .06)( 4) = ( .15)( x + 4) x = 3.6 gal
25 x + 6( 4 ) = 15( x + 4 ) 10 x = 36

4. PHYSICS: UNIFORM MOTION
You've probably heard: distance equals rate times time
Using the variables from physics the equation becomes:
distance s=vt time
velocity (rate)
These problems are easy if we just have one distance,
velocity and time, but often we'll have two different
situations. The best way to tackle these is to make a
table with the information for each situation.

5. Uniform Motion Problem
A truck traveled the first 100 miles of a trip at one
speed and the last 135 miles at an average speed of
5 miles per hour less. If the entire trip took 5 hours,
what was the average speed for the first part of the trip?
Let's make a table with the information If you used t hours
for the first part of
the trip, then the
distance velocity time total of 5 hours
minus the t would
be the time left for
first part 100 v t the second part.
second part 135 v-5 5-t

6. Use this formula to get an
Distance = velocity x time equation for each part of trip
distance velocity time
first part 100 v t
second part 135 v-5 5-t
first part second part
Solve first equation for t and
substitute in second equation
100 = v t 135 = (v - 5)(5 - t)
v v
100
 100 
135 = ( v − 5)  5 −  v
 v 

7.  100 
135 = ( v − 5)  5 −
FOIL the right hand side

 v 
500 v
Multiply all terms by v 135v= 5vv− 100v 25v+
−
to get rid of fractions
v
5v − 260v + 500 = 0
2 Combine like terms and get
everything on one side
Divide everything by 5 v − 52v + 100 = 0
2
( v − 50)( v − 2) = 0 Factor or quadratic formula
So v = 50 mph. v = 2 wouldn't work
v = 50 or v = 2 because if you subbed in 2 for v to get
velocity of second part you'd get –3.

8. WORK-RATE PROBLEM
An office contains two copy machines. Machine
B is known to take 12 minutes longer than
Machine A to copy the company's monthly report.
Using both machines together, it takes 8 minutes
to reproduce the report. How long would it take
each machine alone to reproduce the report?
Work done by Work done by 1 complete job
Machine A + Machine B
=
Rate for A Rate for B
Time to Time to
1 over time 1 over time
complete + to complete
complete = 1
to complete job job
alone alone
1 1
( 8) + ( 8) = 1
t t + 12

9. 1 1
( 8) + ( 8) = 1
t t + 12
8t(t+12)8t(t+12) t(t+12)
+ =1
clear equation of fractions by
multiplying by common denominator
t t + 12
8( t + 12 ) + 8t = t ( t + 12 ) distribute
8t + 96 + 8t = t + 12t
2 quadratic so get everything on one
side = 0
t − 4t − 96 = 0
2 factor
( t − 12)( t + 8) = 0
So time for Machine A is 12 minutes
and time for Machine B is 12 + 12 or
24 minutes
t = 12 or t = -8 -8 doesn't make sense for time so throw it out