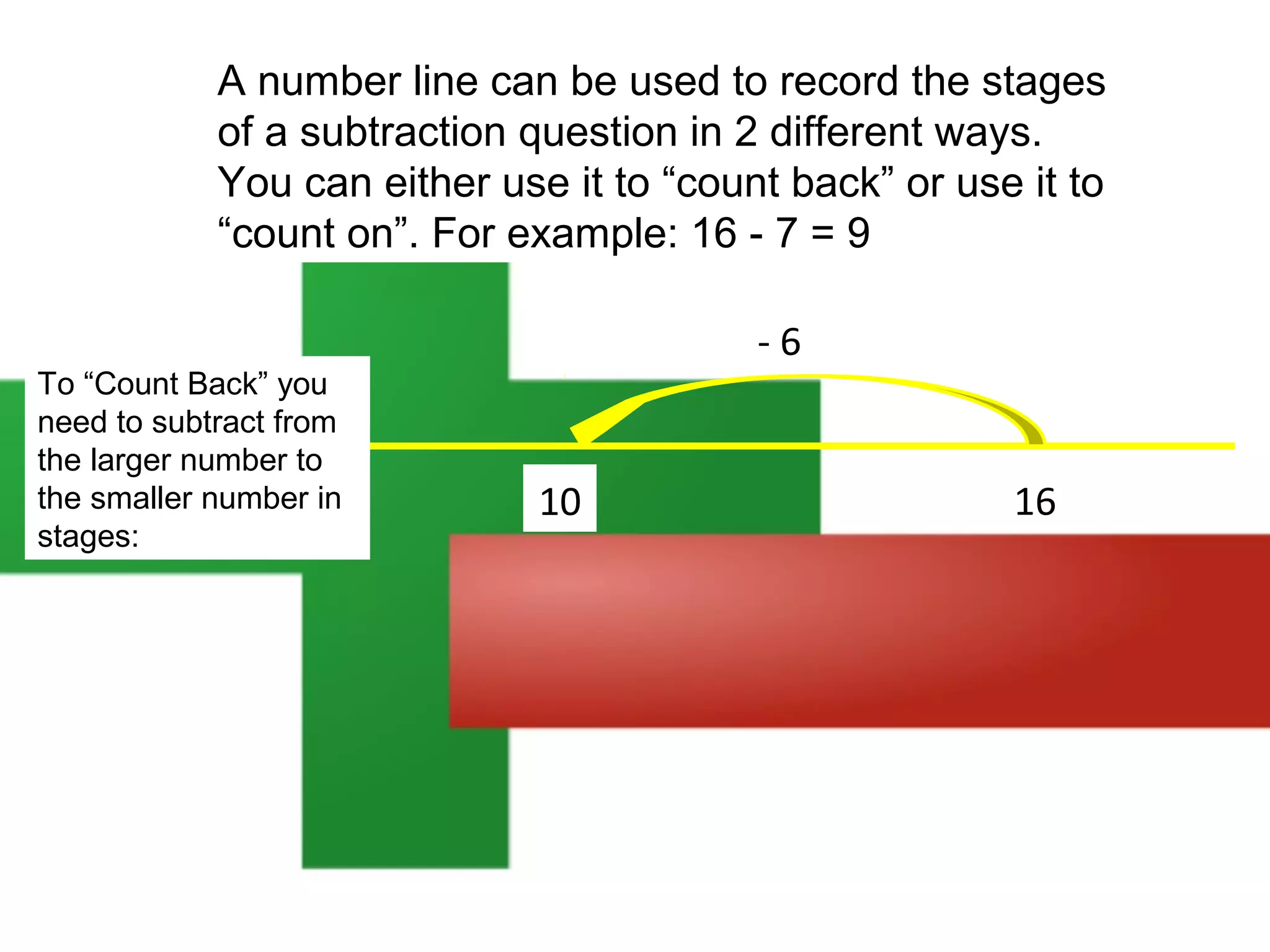
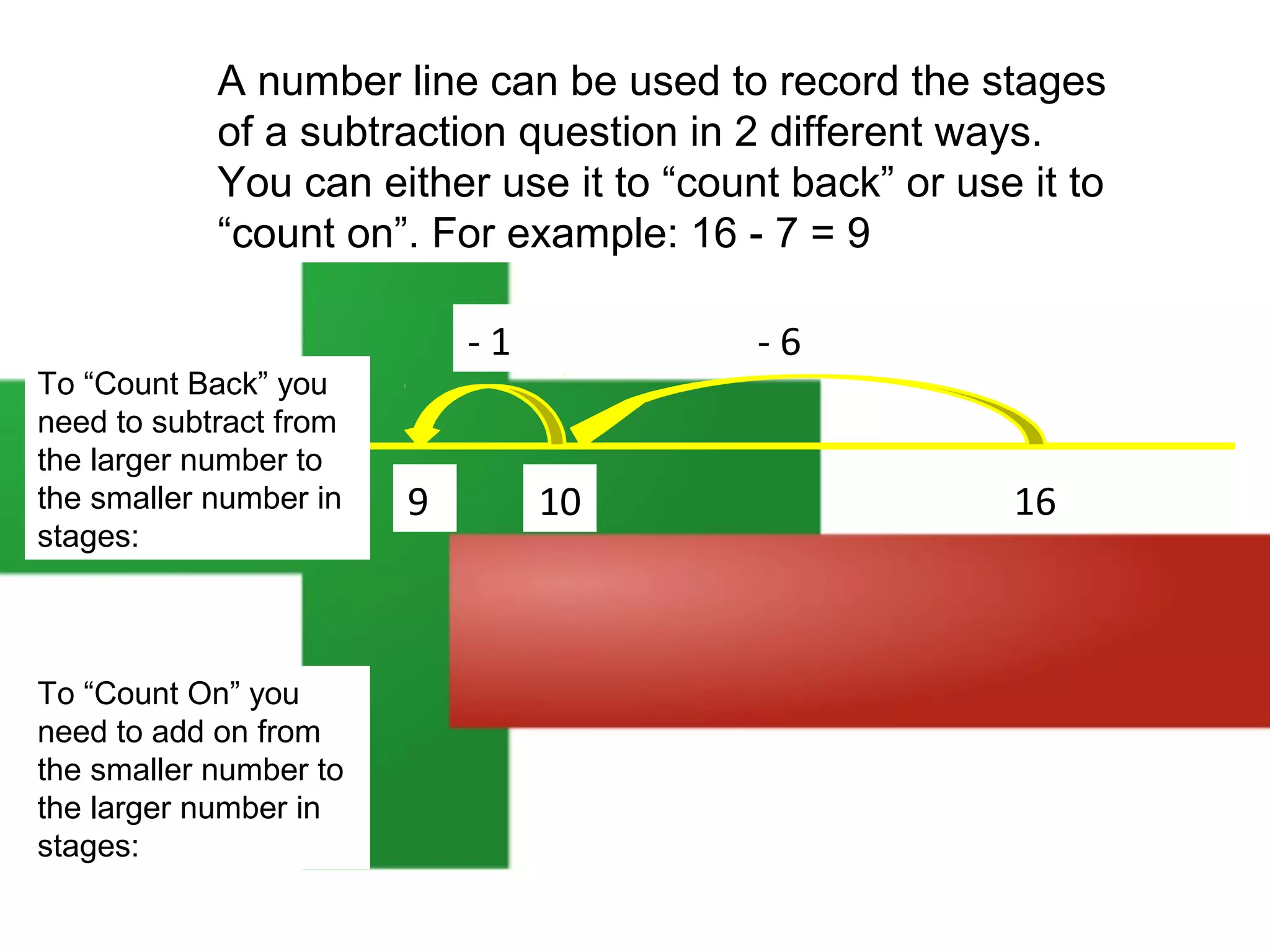
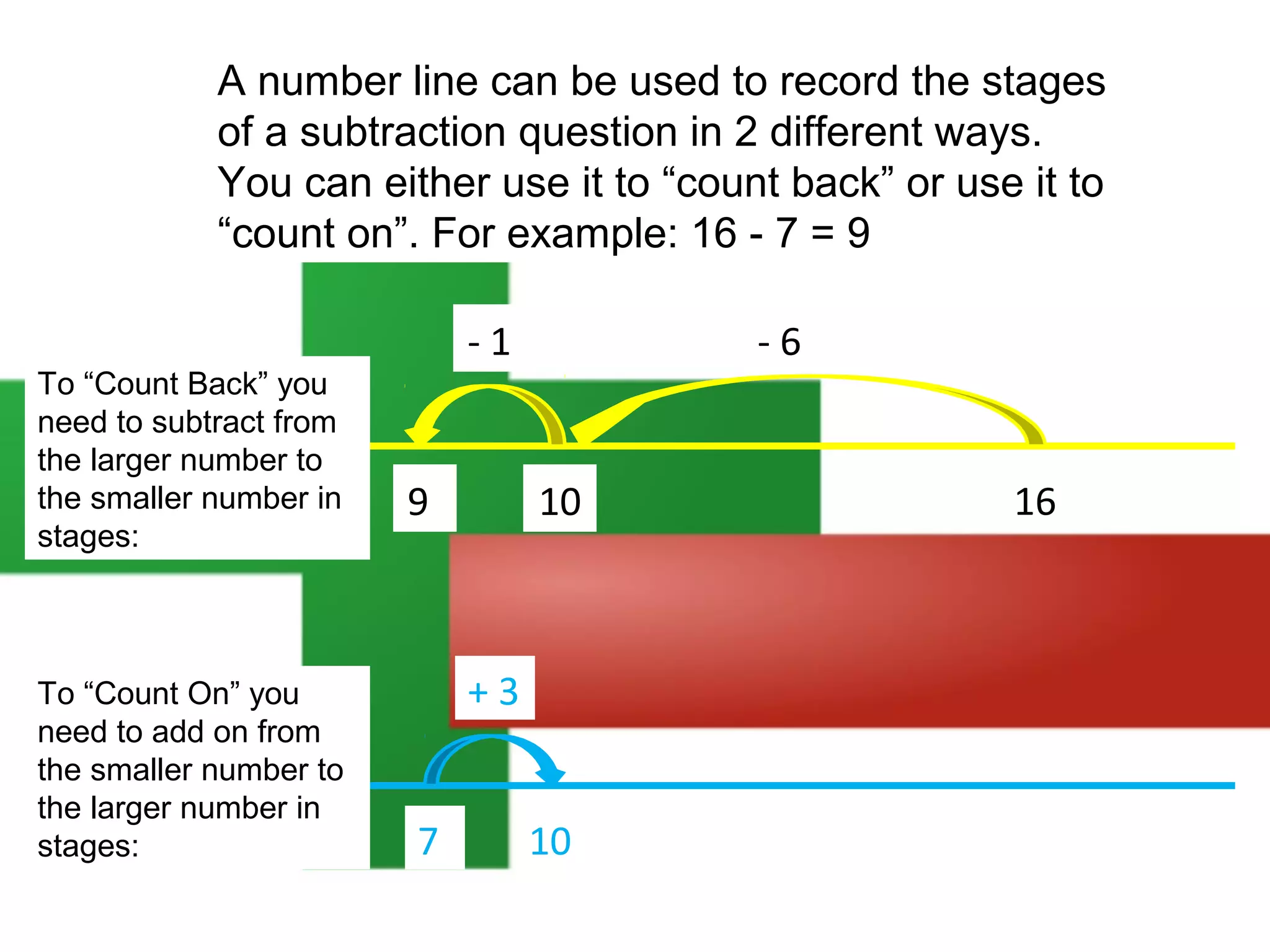
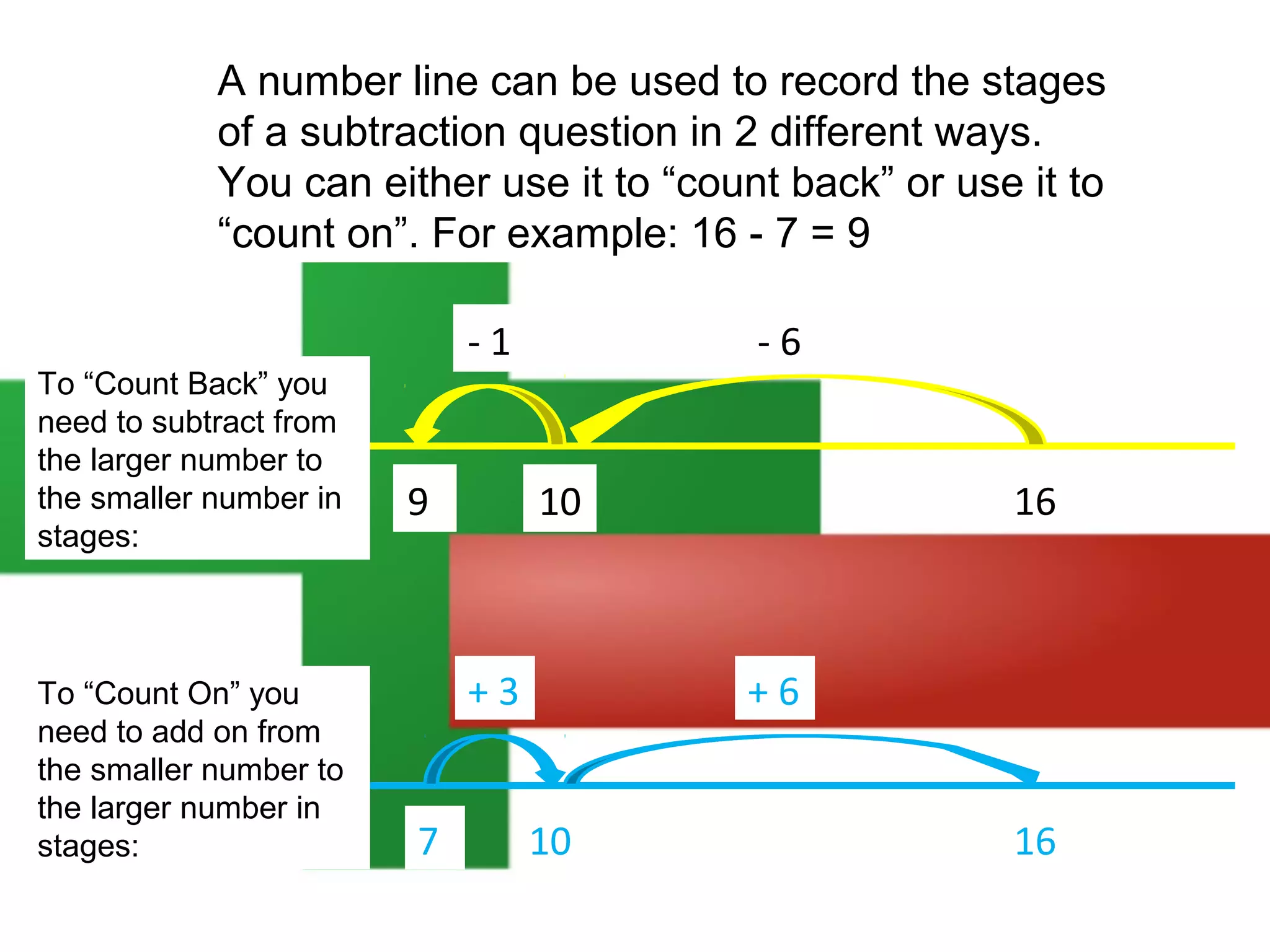
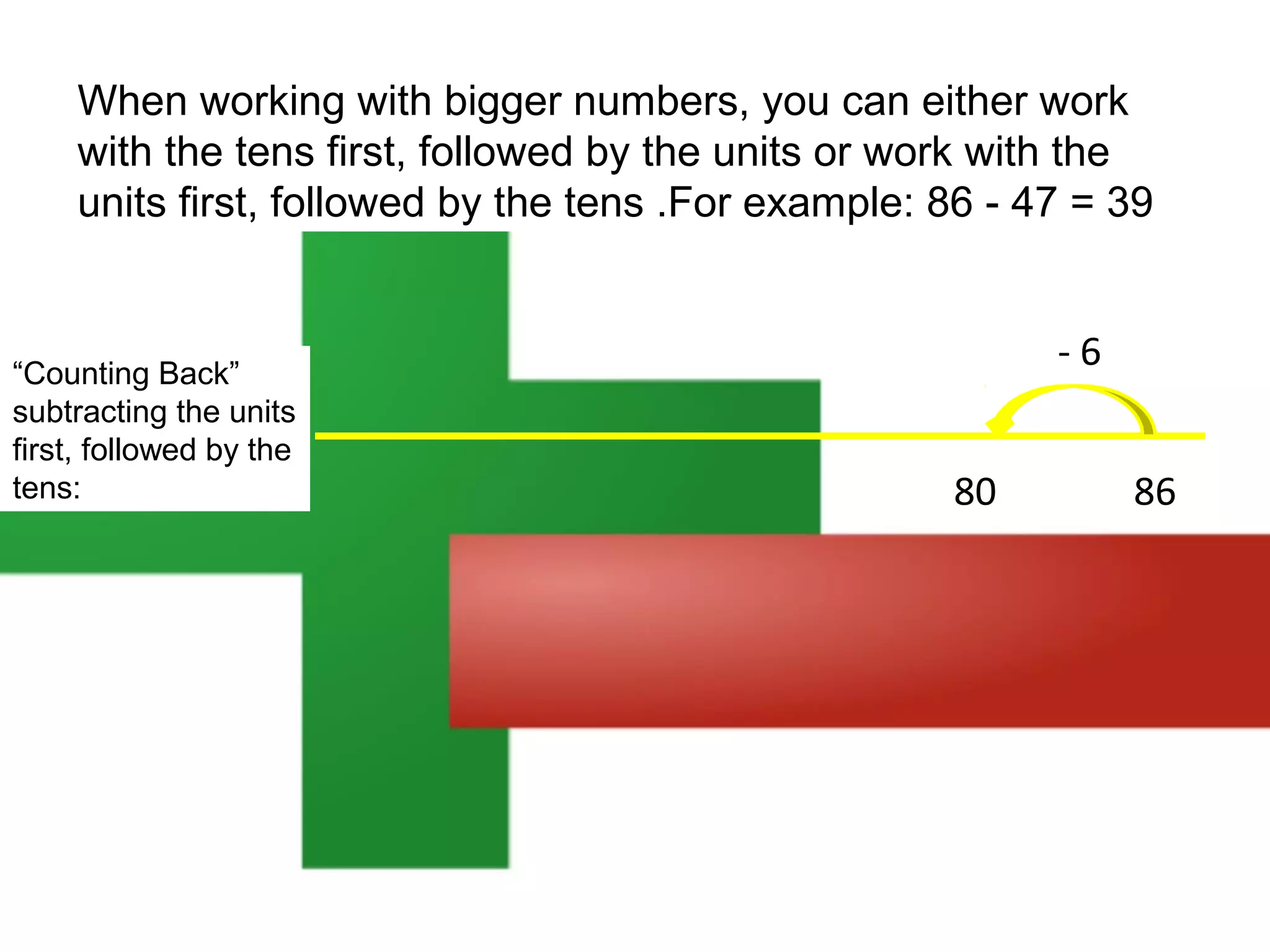
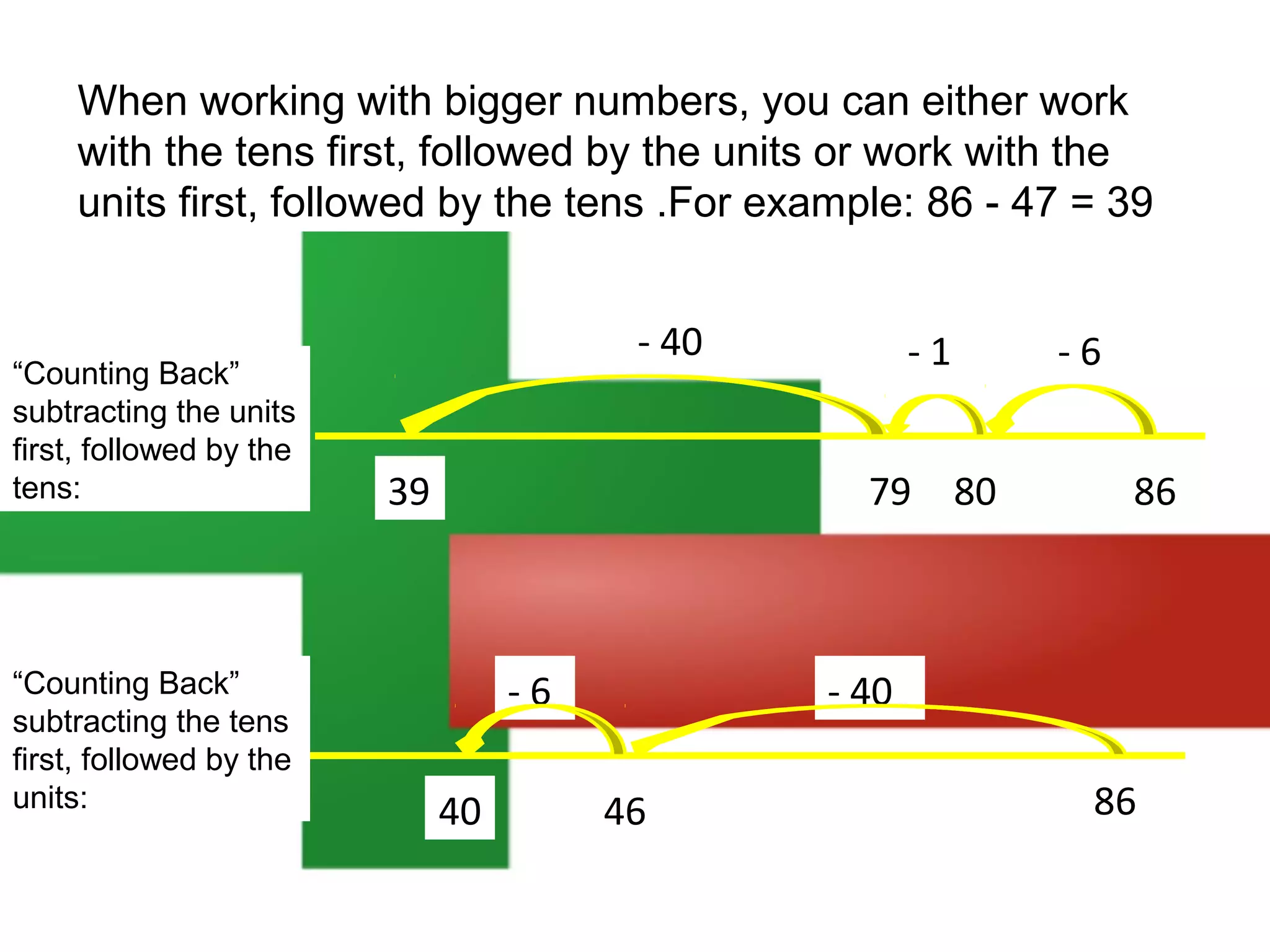
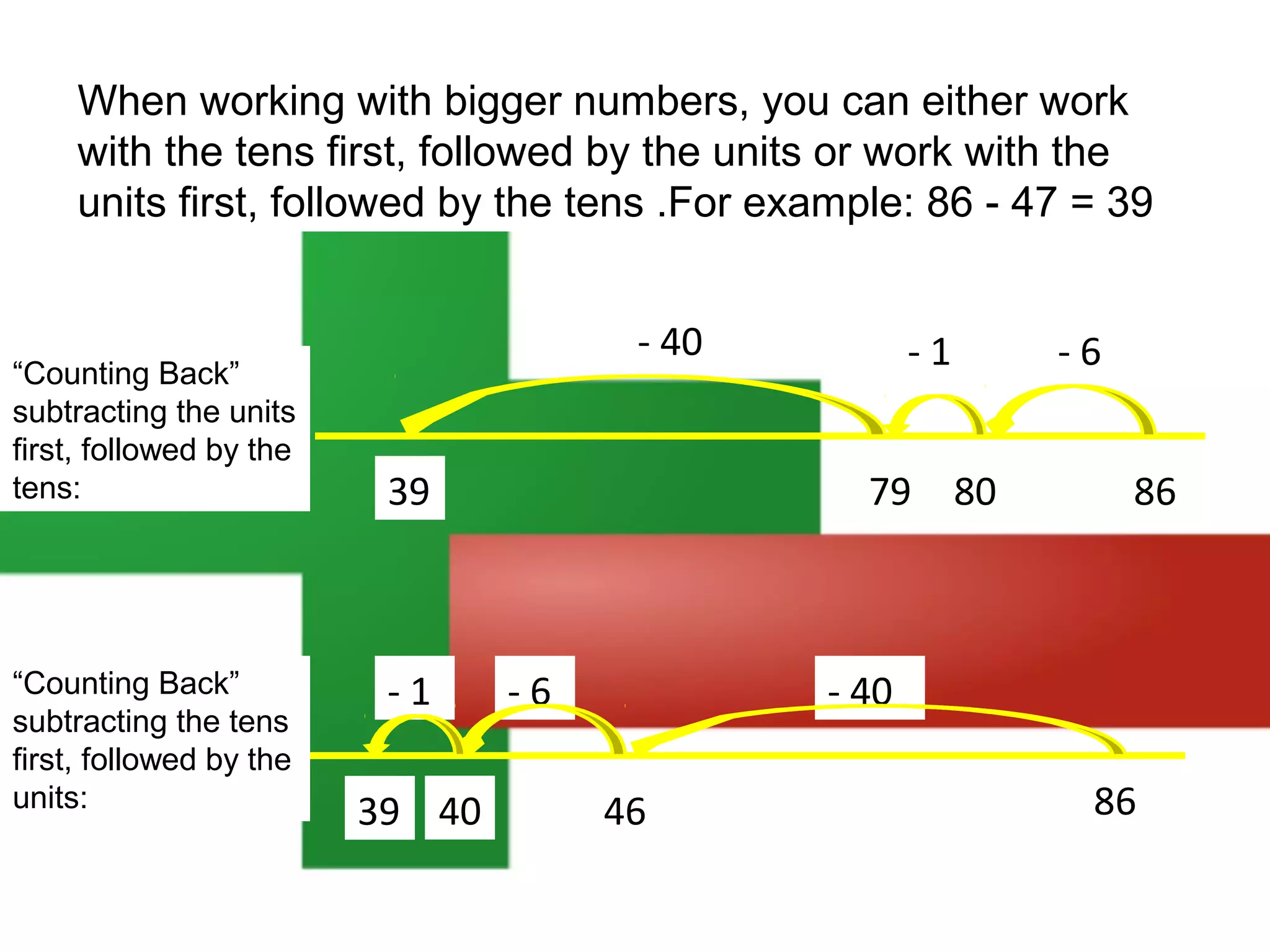
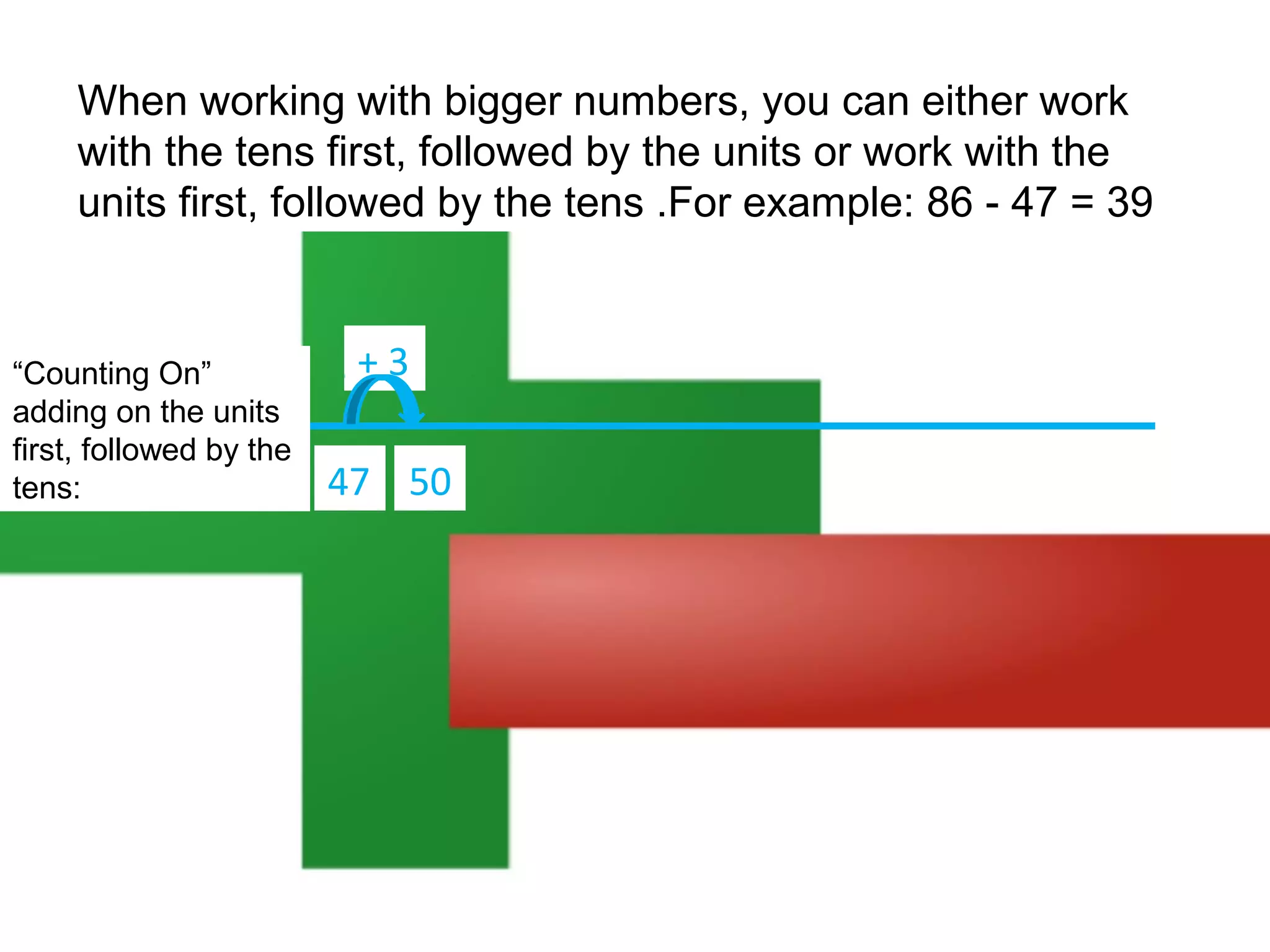
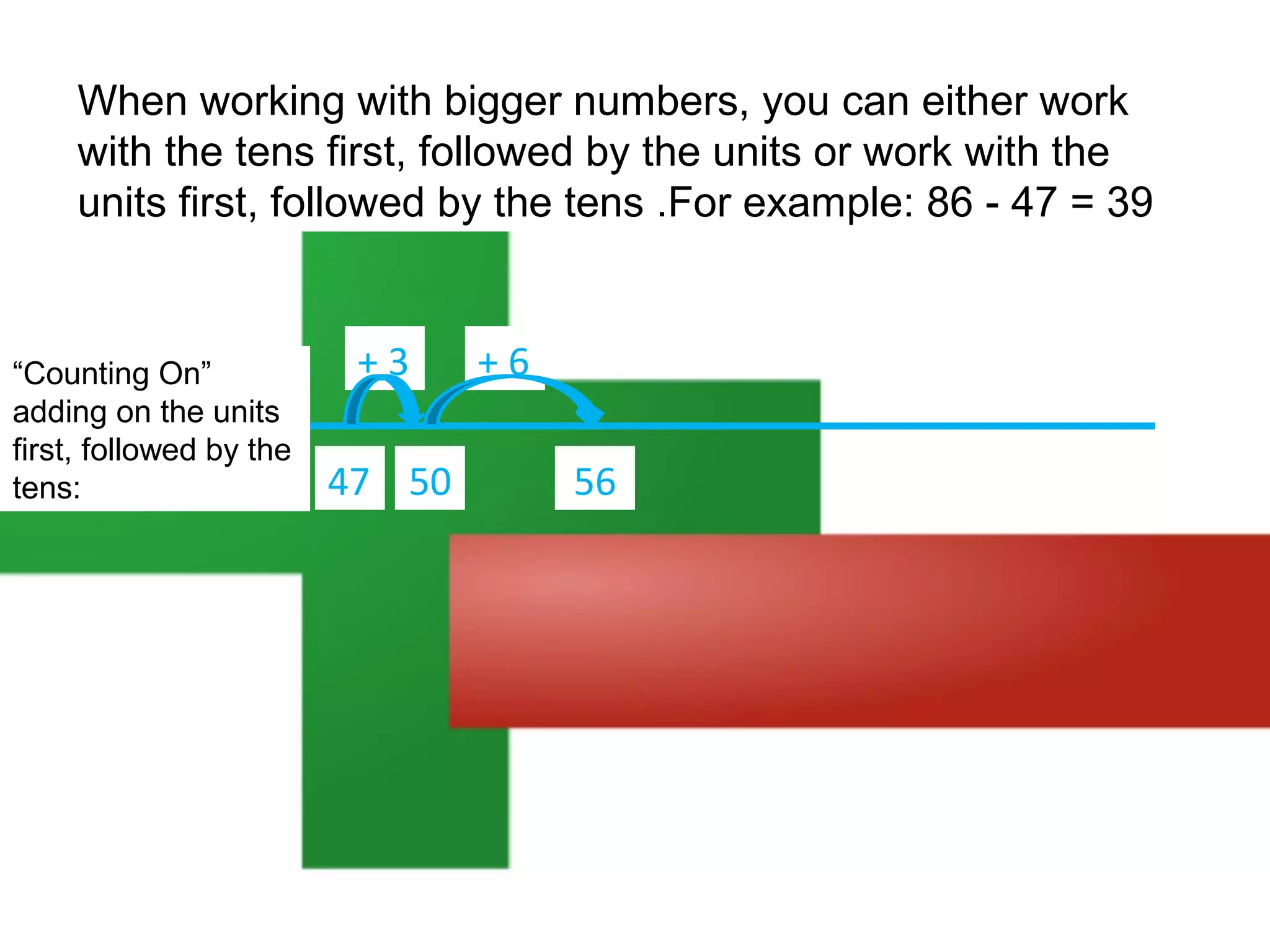
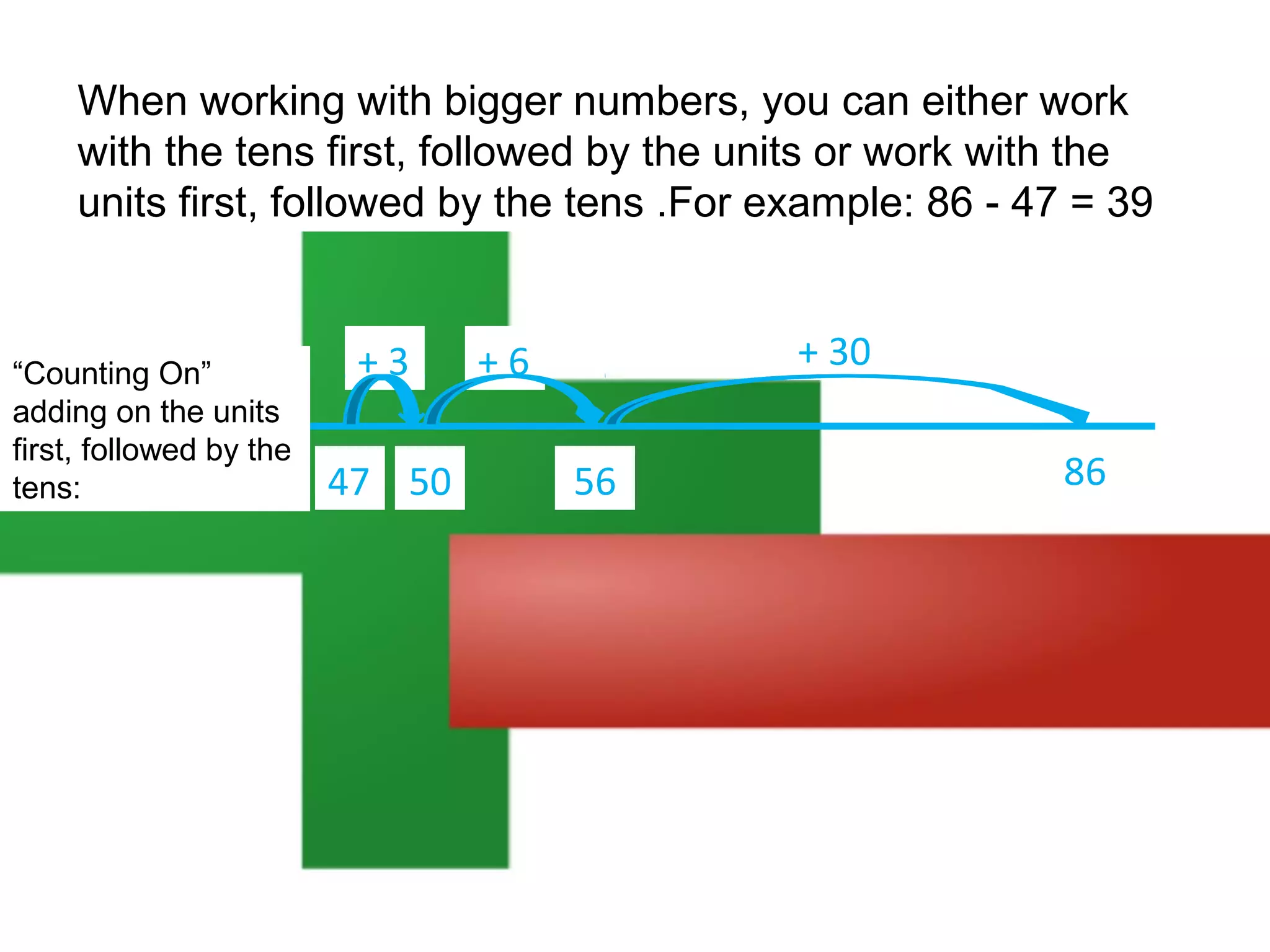
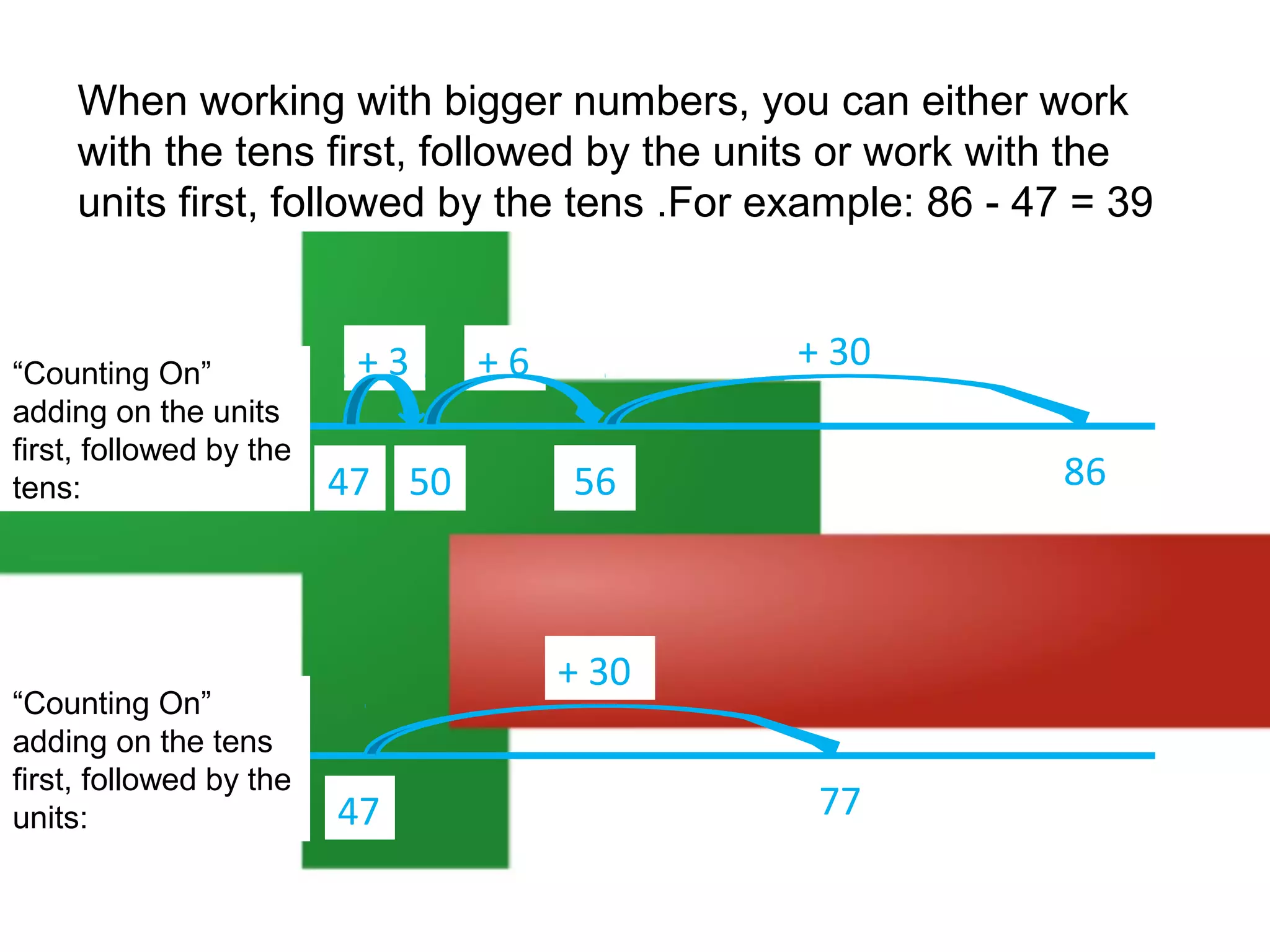
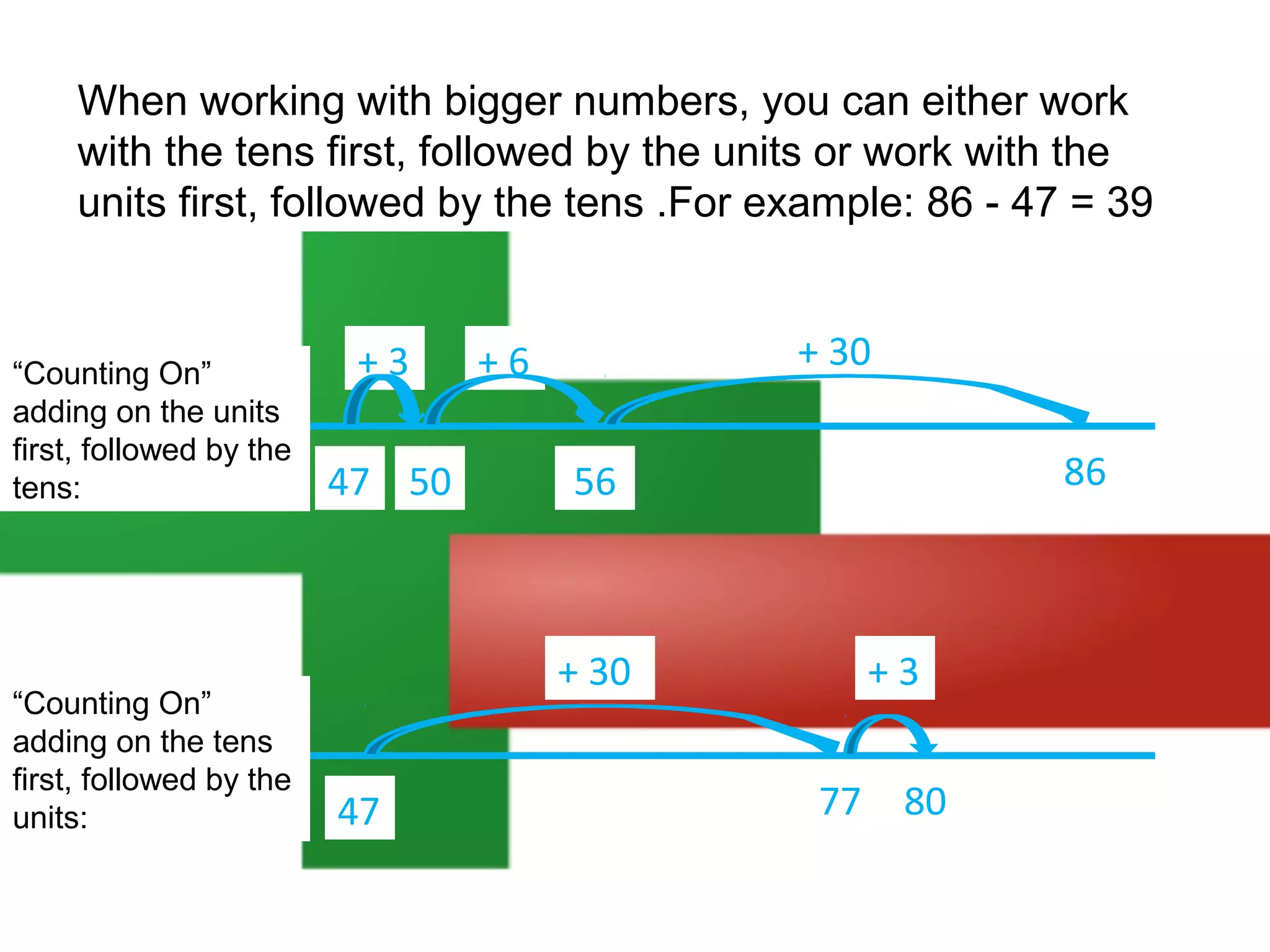
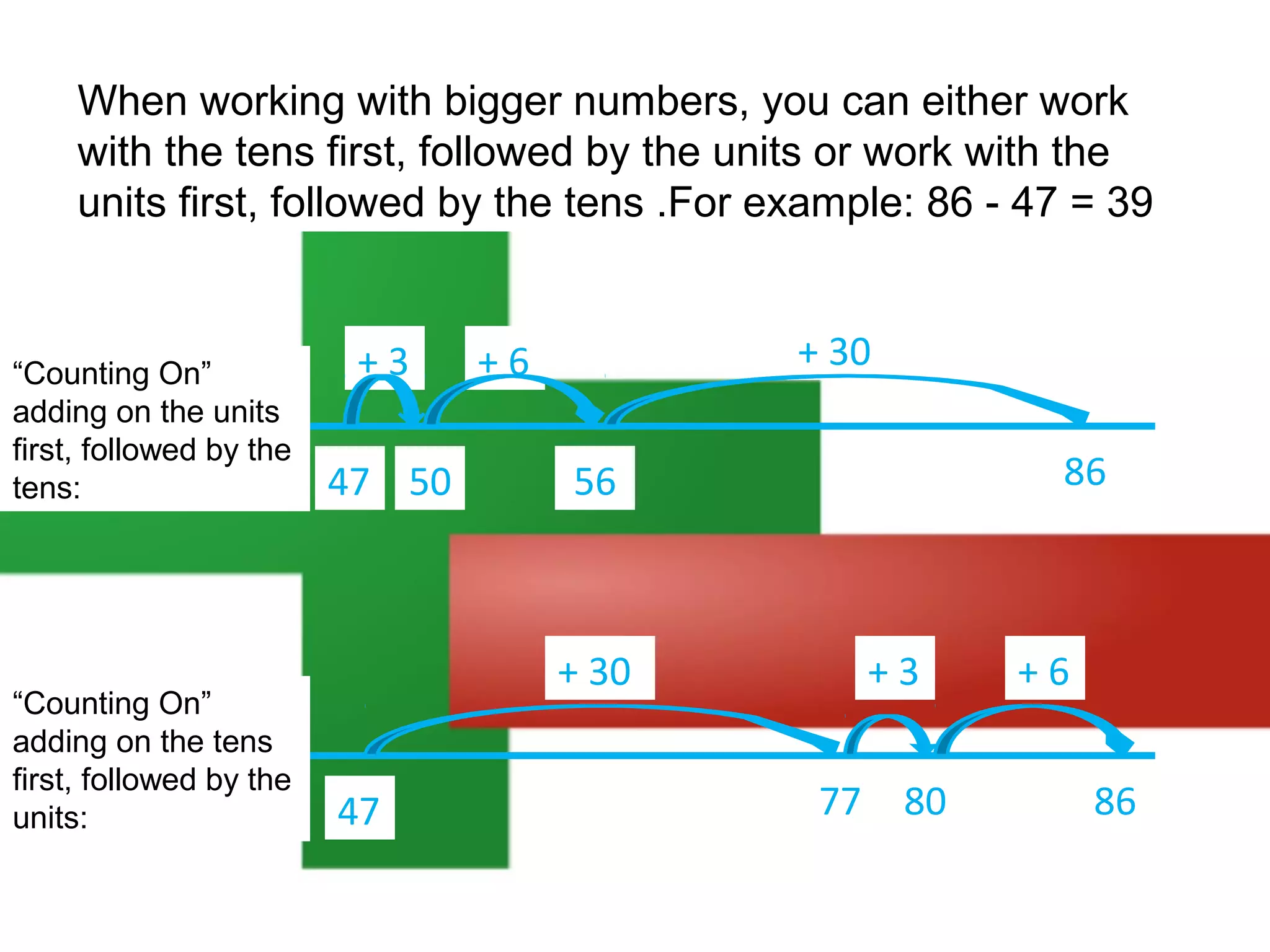
The document discusses using a number line to subtract whole numbers. It explains that a number line can be used to subtract either by counting back, which involves subtracting the numbers in stages moving from the larger to the smaller number, or by counting on, which involves adding the numbers in stages moving from the smaller to the larger number. It provides examples of using counting back and counting on to solve 16 - 7. It also discusses subtracting larger numbers by either working with the tens place value first then the ones, or vice versa.

1. Subtraction Of Whole Numbers Using
A Number Line
(the 1st step towards using a standard written
method for subtraction)
For more maths help & free games related to
this, visit: www.makemymathsbetter.com

2. A number line can be used to record the stages
of a subtraction question in 2 different ways.
You can either use it to “count back” or use it to
“count on”. For example: 16 - 7 = 9

3. A number line can be used to record the stages
of a subtraction question in 2 different ways.
You can either use it to “count back” or use it to
“count on”. For example: 16 - 7 = 9
To “Count Back” you
need to subtract from
the larger number to
the smaller number in
stages:

4. A number line can be used to record the stages
of a subtraction question in 2 different ways.
You can either use it to “count back” or use it to
“count on”. For example: 16 - 7 = 9
To “Count Back” you
need to subtract from
the larger number to
the smaller number in
stages:
-6
10
16

5. A number line can be used to record the stages
of a subtraction question in 2 different ways.
You can either use it to “count back” or use it to
“count on”. For example: 16 - 7 = 9
To “Count Back” you
need to subtract from
the larger number to
the smaller number in
stages:
-1
9
-6
10
16

6. A number line can be used to record the stages
of a subtraction question in 2 different ways.
You can either use it to “count back” or use it to
“count on”. For example: 16 - 7 = 9
To “Count Back” you
need to subtract from
the larger number to
the smaller number in
stages:
To “Count On” you
need to add on from
the smaller number to
the larger number in
stages:
-1
9
-6
10
16

7. A number line can be used to record the stages
of a subtraction question in 2 different ways.
You can either use it to “count back” or use it to
“count on”. For example: 16 - 7 = 9
To “Count Back” you
need to subtract from
the larger number to
the smaller number in
stages:
To “Count On” you
need to add on from
the smaller number to
the larger number in
stages:
-1
9
-6
10
+3
7
10
16

8. A number line can be used to record the stages
of a subtraction question in 2 different ways.
You can either use it to “count back” or use it to
“count on”. For example: 16 - 7 = 9
To “Count Back” you
need to subtract from
the larger number to
the smaller number in
stages:
To “Count On” you
need to add on from
the smaller number to
the larger number in
stages:
-1
9
-6
+3
7
16
10
+6
10
16

9. When working with bigger numbers, you can either work
with the tens first, followed by the units or work with the
units first, followed by the tens .For example: 86 - 47 = 39

10. When working with bigger numbers, you can either work
with the tens first, followed by the units or work with the
units first, followed by the tens .For example: 86 - 47 = 39
“Counting Back”
subtracting the units
first, followed by the
tens:
-6
80
86

11. When working with bigger numbers, you can either work
with the tens first, followed by the units or work with the
units first, followed by the tens .For example: 86 - 47 = 39
“Counting Back”
subtracting the units
first, followed by the
tens:
-1
79 80
-6
86

12. When working with bigger numbers, you can either work
with the tens first, followed by the units or work with the
units first, followed by the tens .For example: 86 - 47 = 39
“Counting Back”
subtracting the units
first, followed by the
tens:
- 40
39
-1
79 80
-6
86

13. When working with bigger numbers, you can either work
with the tens first, followed by the units or work with the
units first, followed by the tens .For example: 86 - 47 = 39
“Counting Back”
subtracting the units
first, followed by the
tens:
“Counting Back”
subtracting the tens
first, followed by the
units:
- 40
39
-1
79 80
-6
86
- 40
46
86

14. When working with bigger numbers, you can either work
with the tens first, followed by the units or work with the
units first, followed by the tens .For example: 86 - 47 = 39
“Counting Back”
subtracting the units
first, followed by the
tens:
“Counting Back”
subtracting the tens
first, followed by the
units:
- 40
39
-1
79 80
-6
40
-6
86
- 40
46
86

15. When working with bigger numbers, you can either work
with the tens first, followed by the units or work with the
units first, followed by the tens .For example: 86 - 47 = 39
“Counting Back”
subtracting the units
first, followed by the
tens:
“Counting Back”
subtracting the tens
first, followed by the
units:
- 40
39
-1
39 40
-1
79 80
-6
-6
86
- 40
46
86

16. When working with bigger numbers, you can either work
with the tens first, followed by the units or work with the
units first, followed by the tens .For example: 86 - 47 = 39
“Counting On”
adding on the units
first, followed by the
tens:
+3
47 50

17. When working with bigger numbers, you can either work
with the tens first, followed by the units or work with the
units first, followed by the tens .For example: 86 - 47 = 39
“Counting On”
adding on the units
first, followed by the
tens:
+3
47 50
+6
56

18. When working with bigger numbers, you can either work
with the tens first, followed by the units or work with the
units first, followed by the tens .For example: 86 - 47 = 39
“Counting On”
adding on the units
first, followed by the
tens:
+3
47 50
+ 30
+6
56
86

19. When working with bigger numbers, you can either work
with the tens first, followed by the units or work with the
units first, followed by the tens .For example: 86 - 47 = 39
“Counting On”
adding on the units
first, followed by the
tens:
“Counting On”
adding on the tens
first, followed by the
units:
+3
47 50
+ 30
+6
86
56
+ 30
47
77

20. When working with bigger numbers, you can either work
with the tens first, followed by the units or work with the
units first, followed by the tens .For example: 86 - 47 = 39
“Counting On”
adding on the units
first, followed by the
tens:
“Counting On”
adding on the tens
first, followed by the
units:
+3
47 50
+ 30
+6
+ 30
47
86
56
+3
77 80

21. When working with bigger numbers, you can either work
with the tens first, followed by the units or work with the
units first, followed by the tens .For example: 86 - 47 = 39
“Counting On”
adding on the units
first, followed by the
tens:
“Counting On”
adding on the tens
first, followed by the
units:
+3
47 50
+ 30
+6
+ 30
47
86
56
+3
77 80
+6
86

22. That’s it for now......
For more help with your maths, try
my book:
mastering multiplication tables
on amazon.com