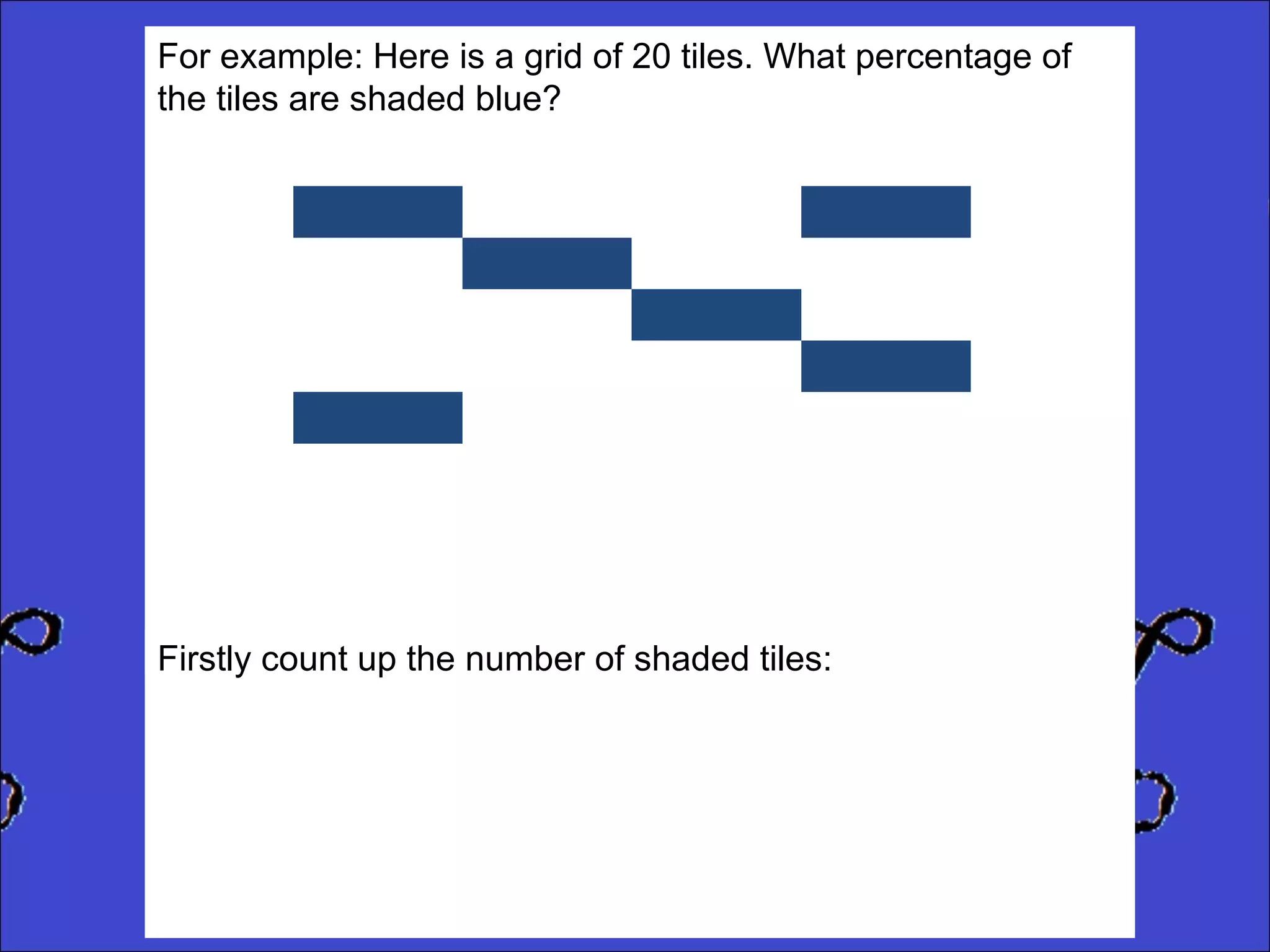
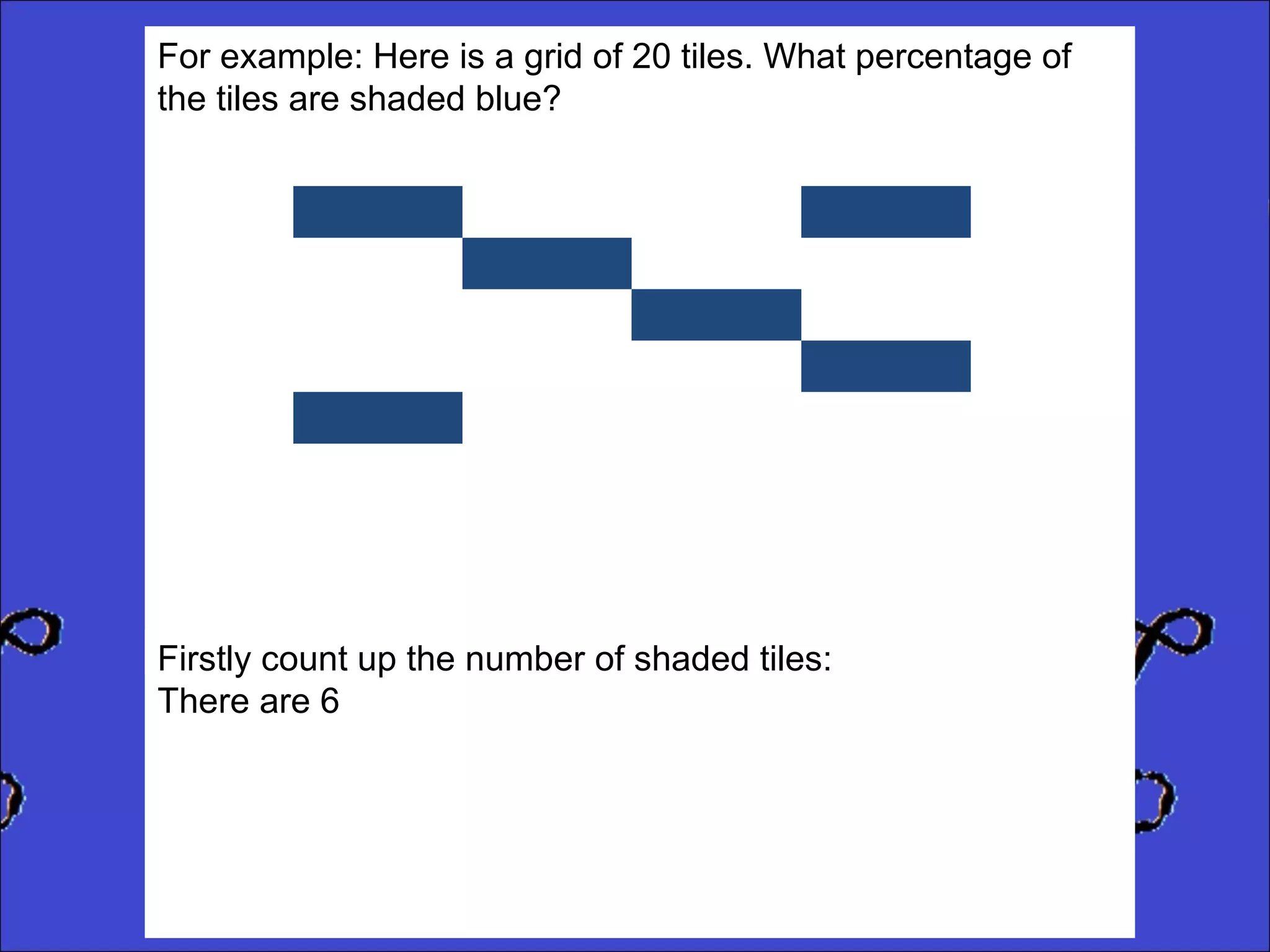
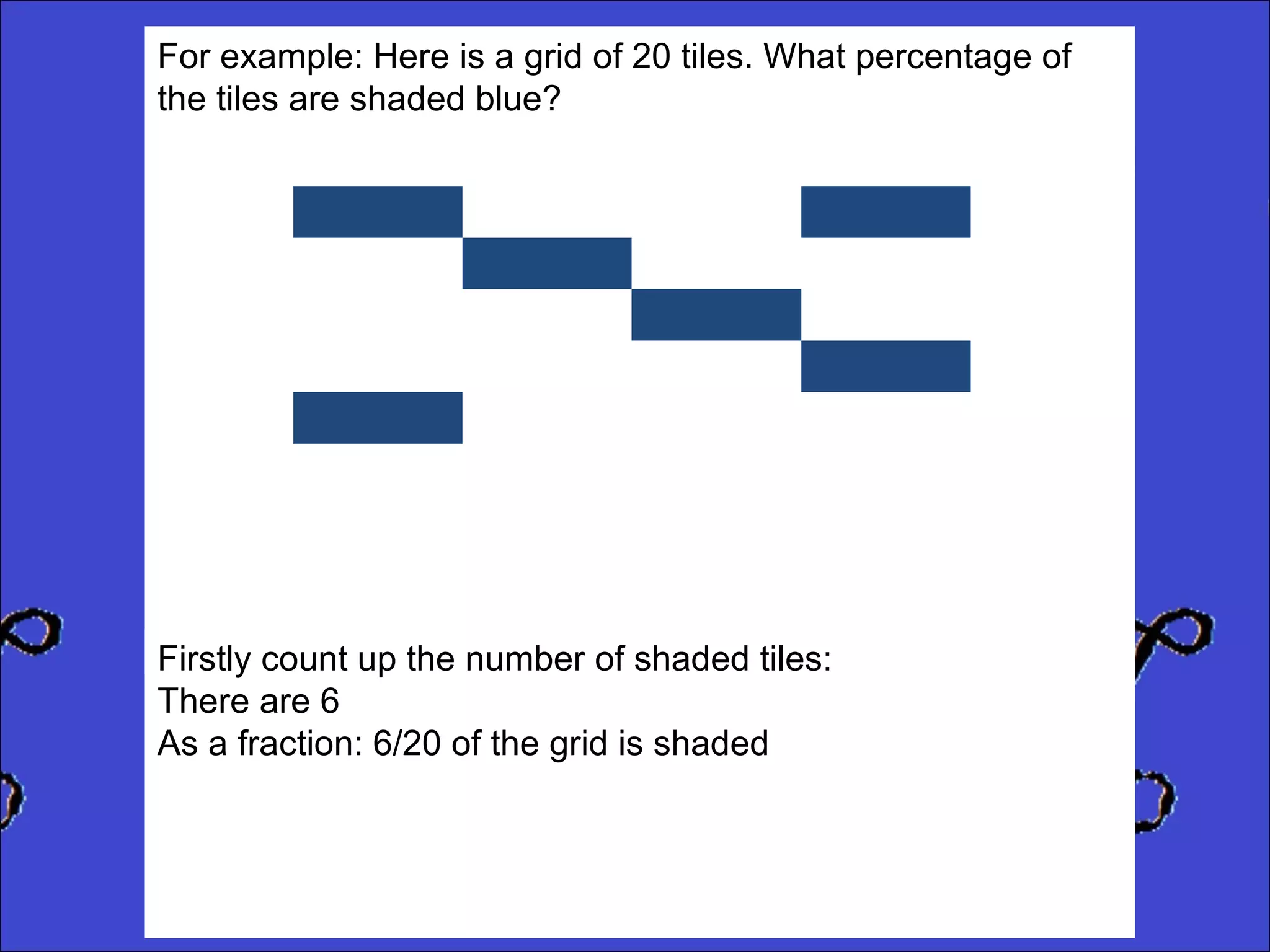
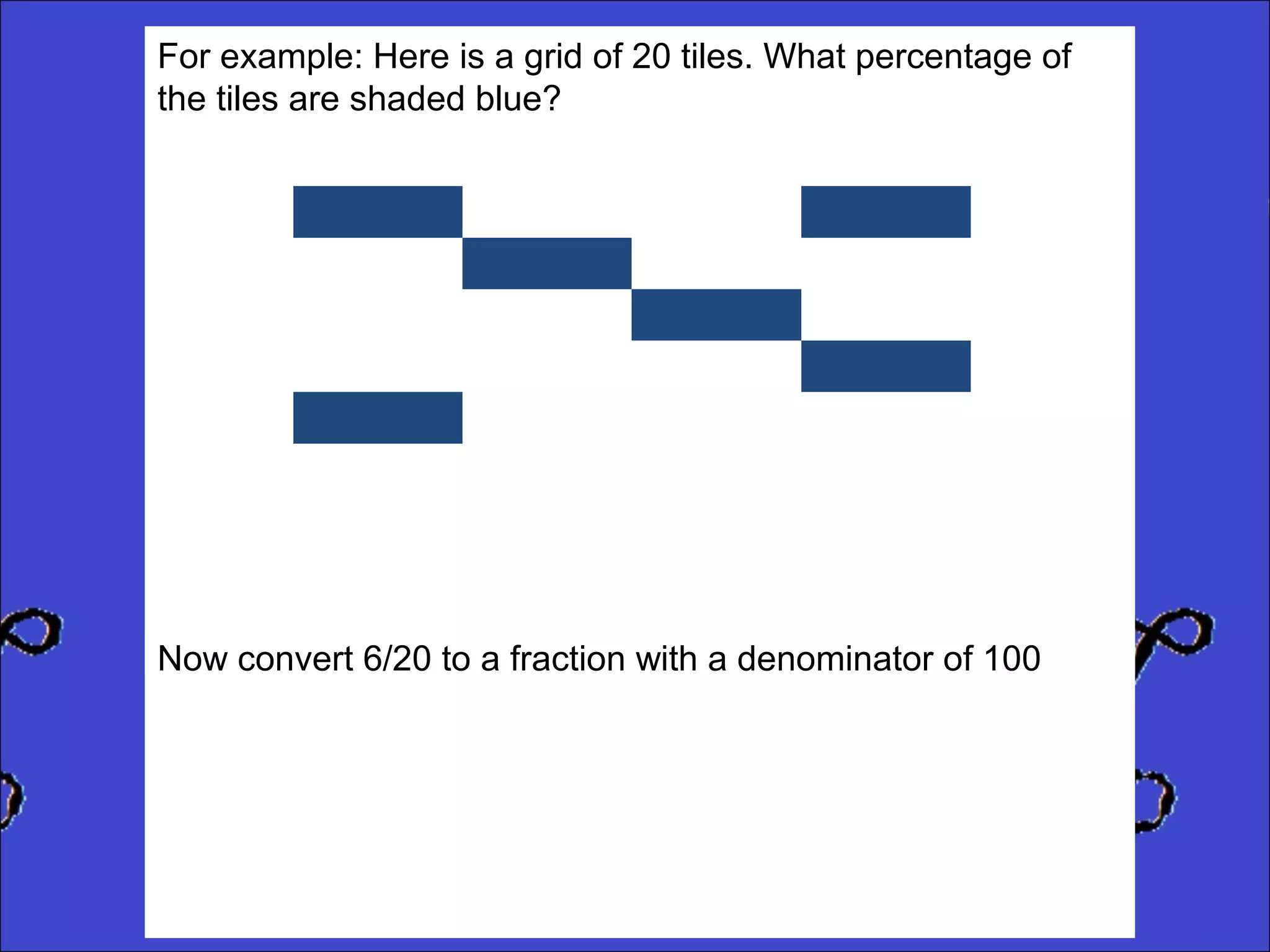
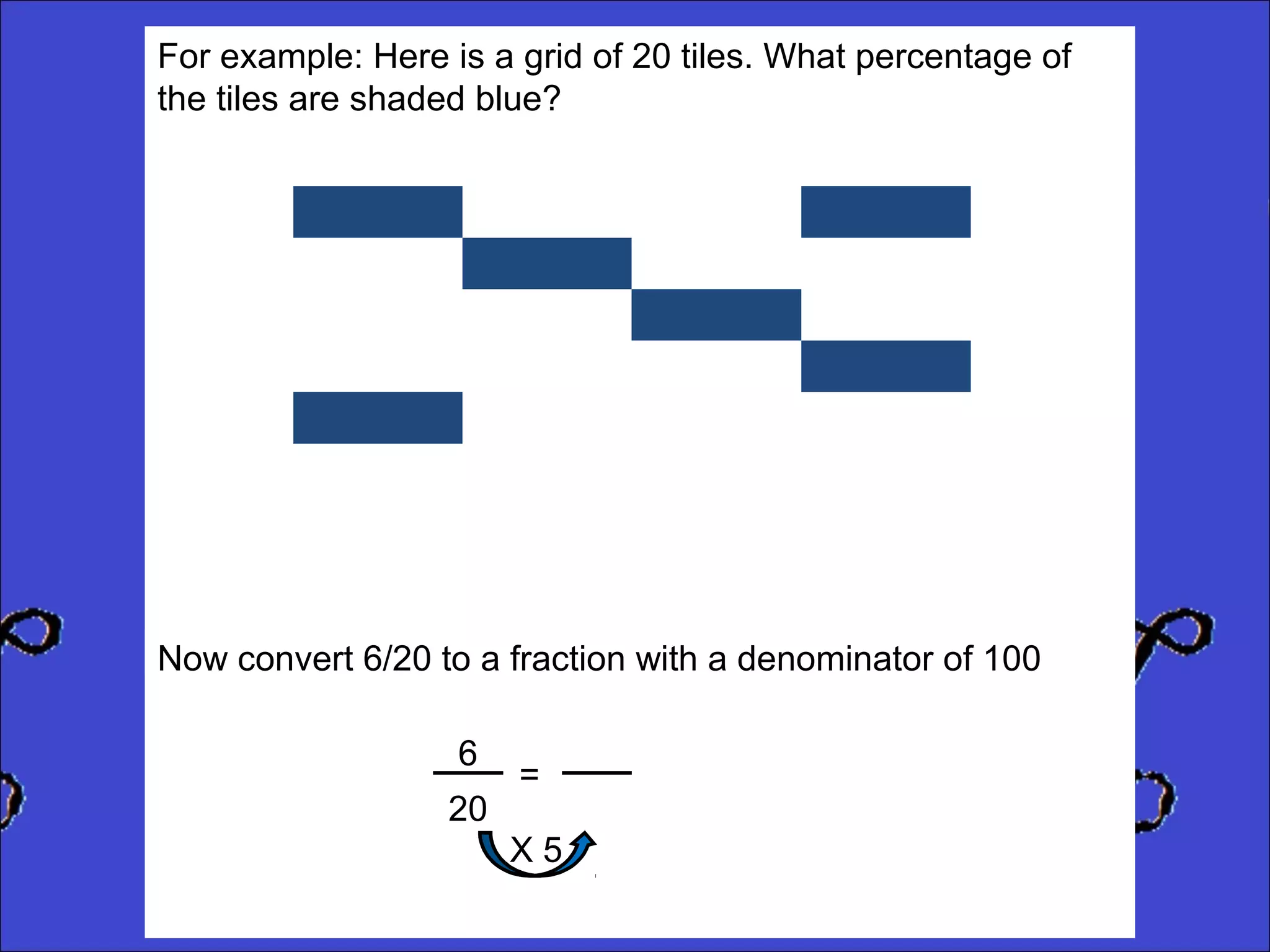
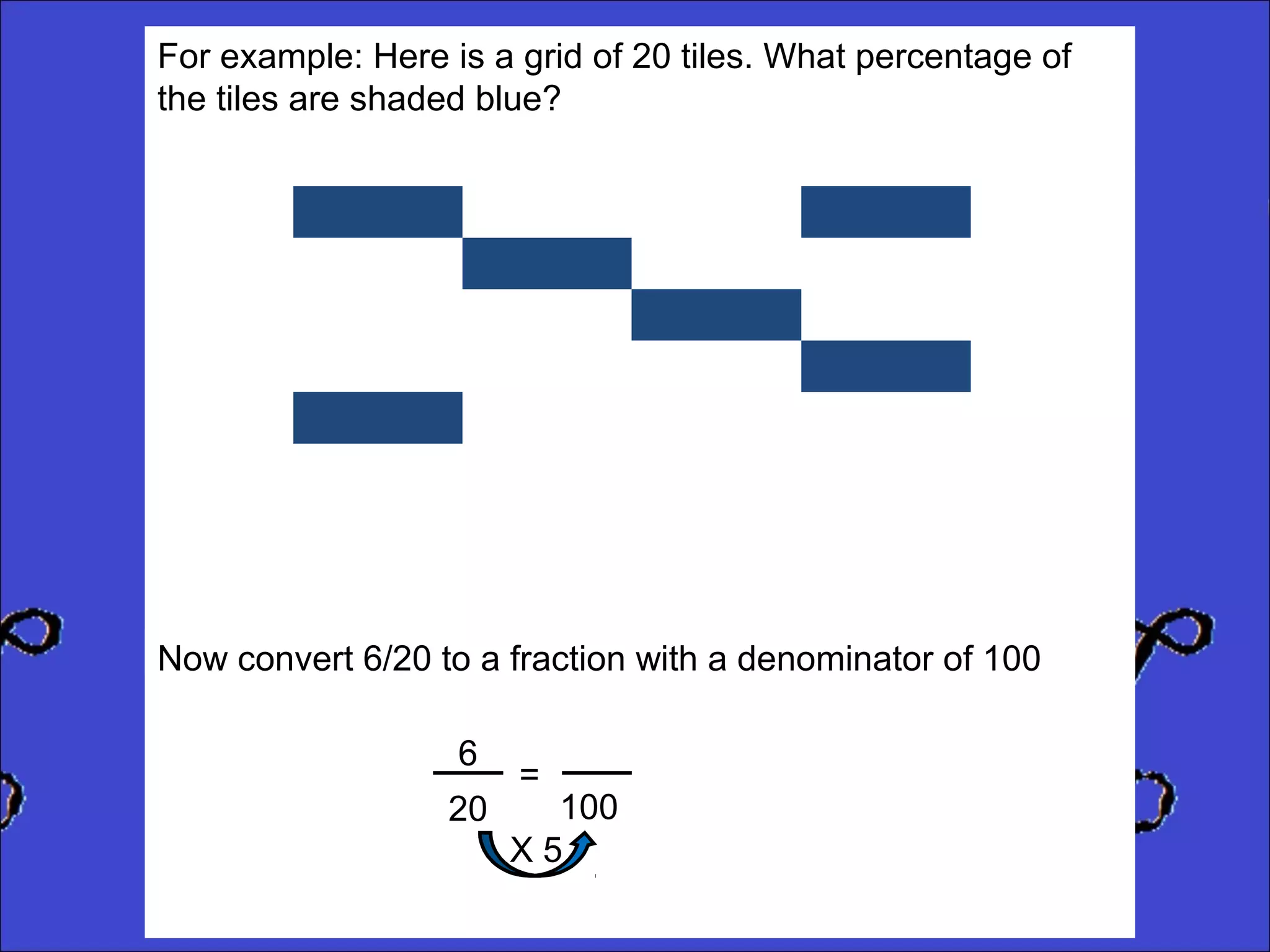
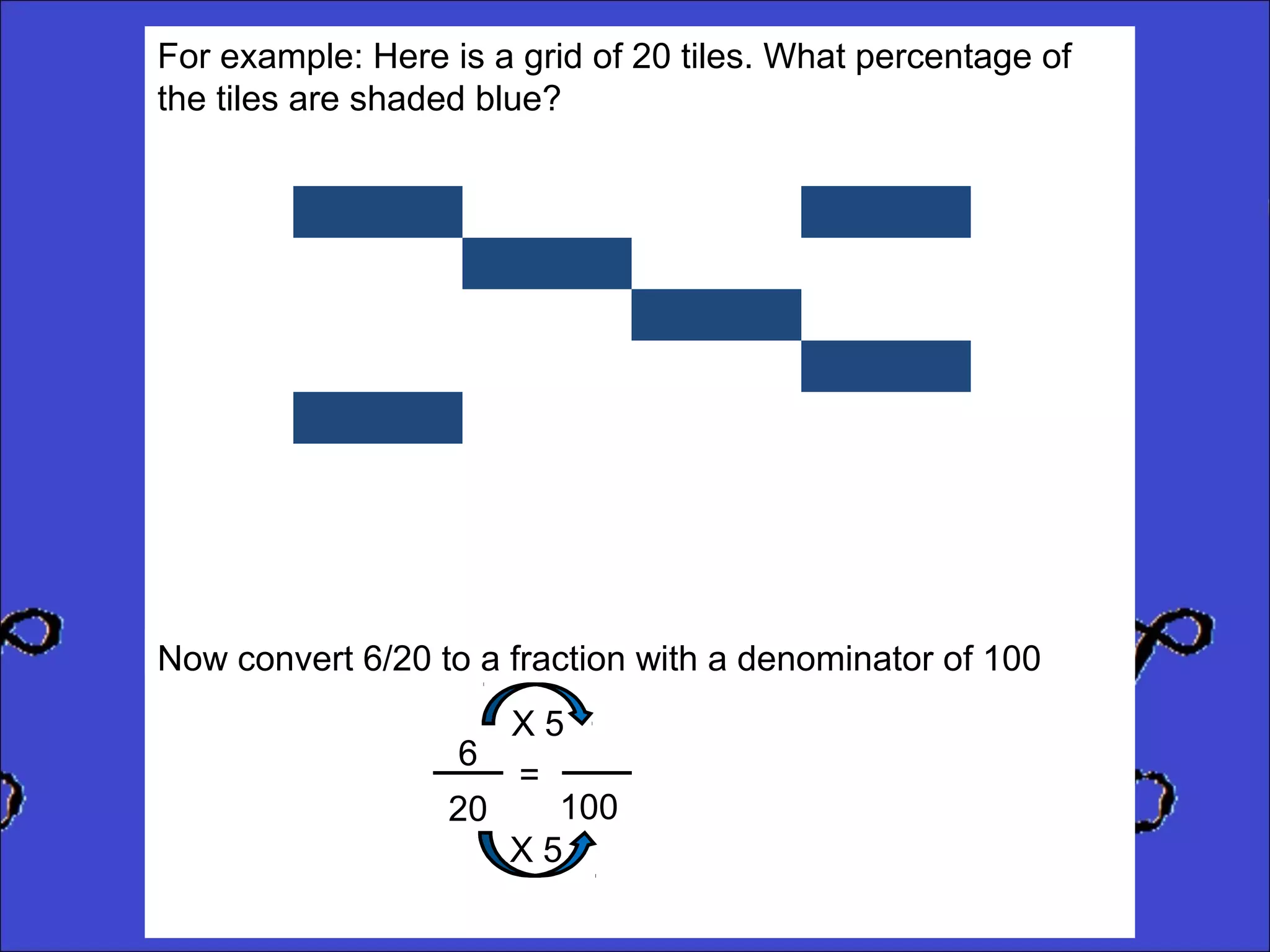
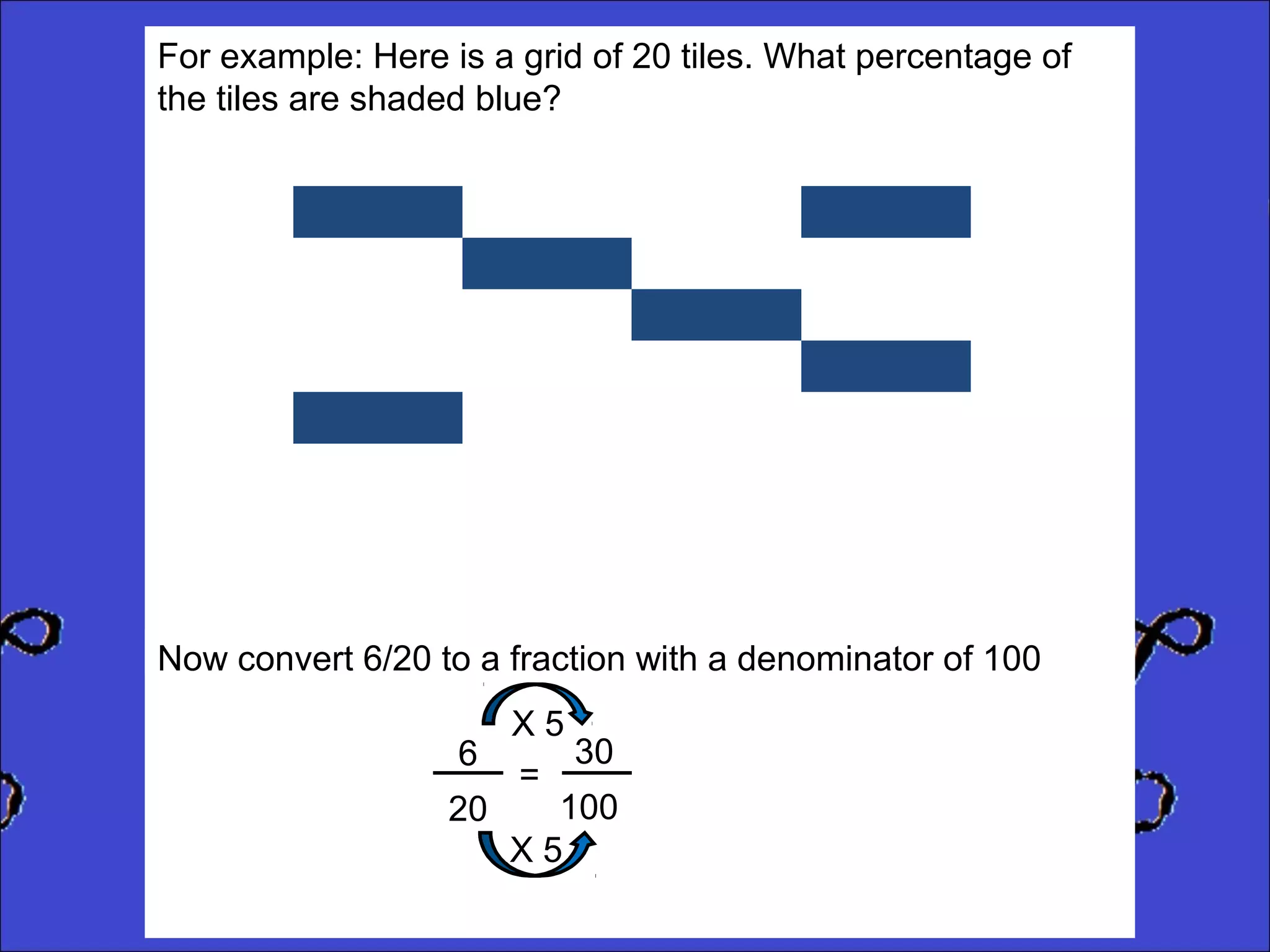
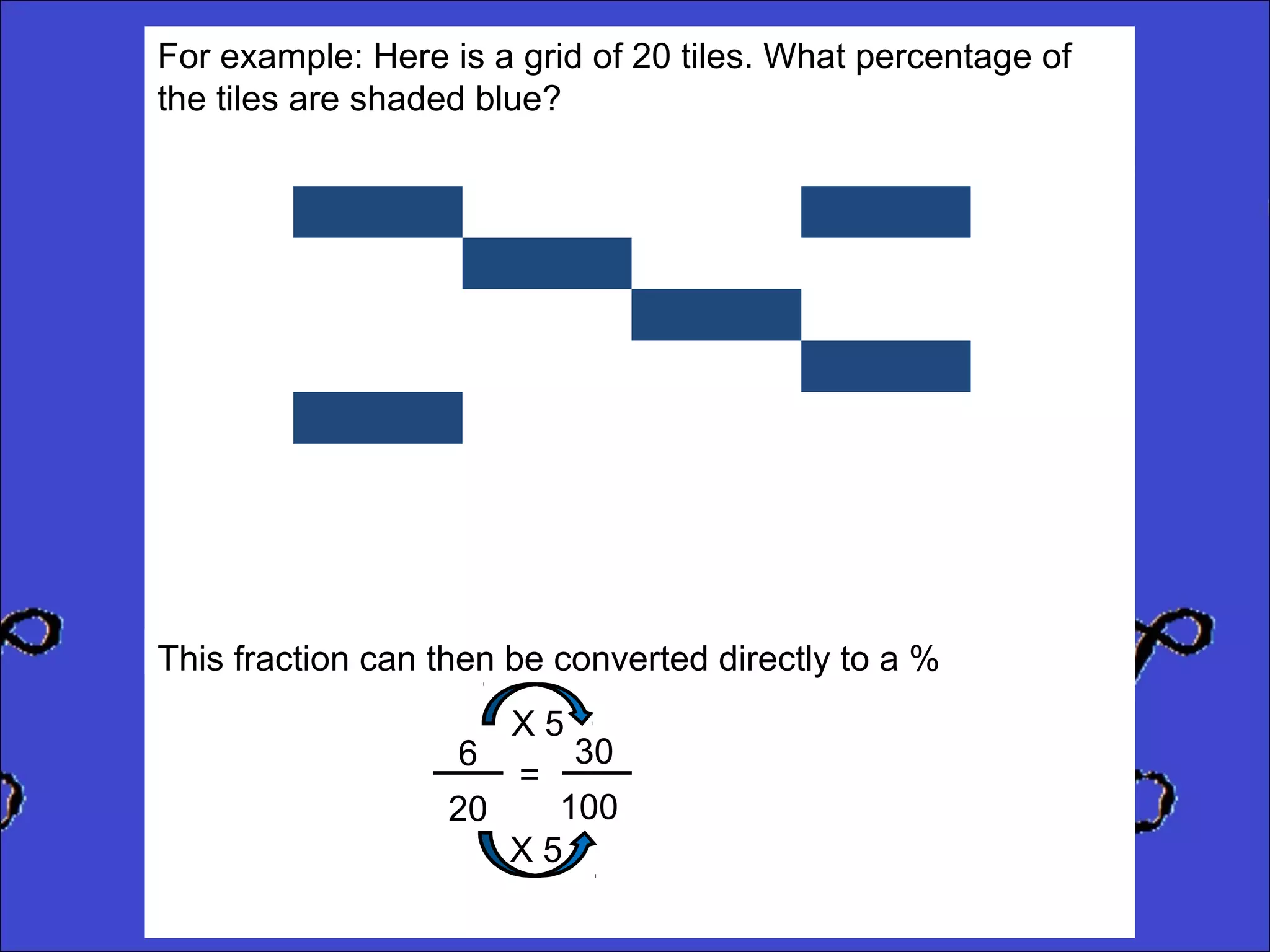
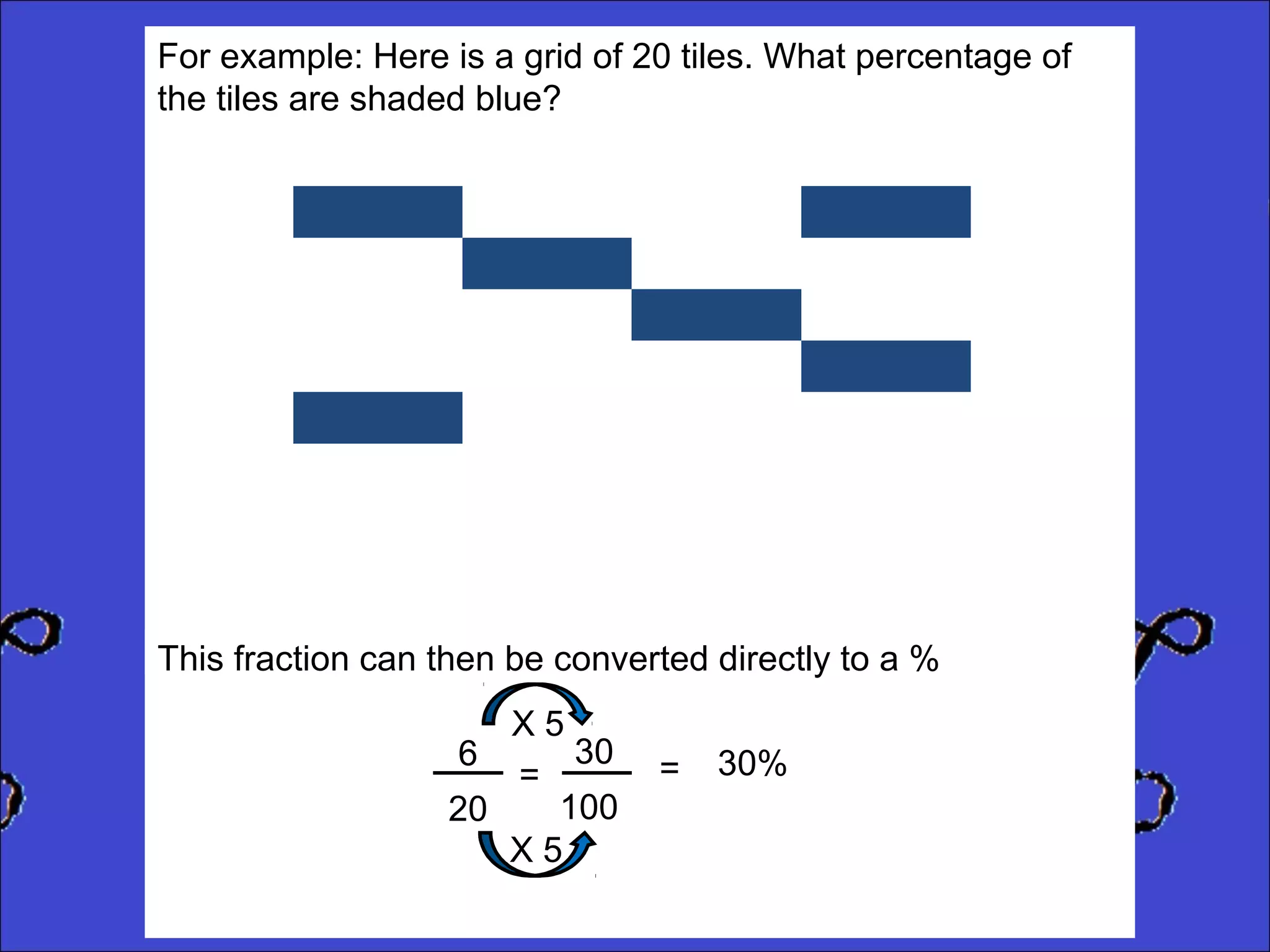
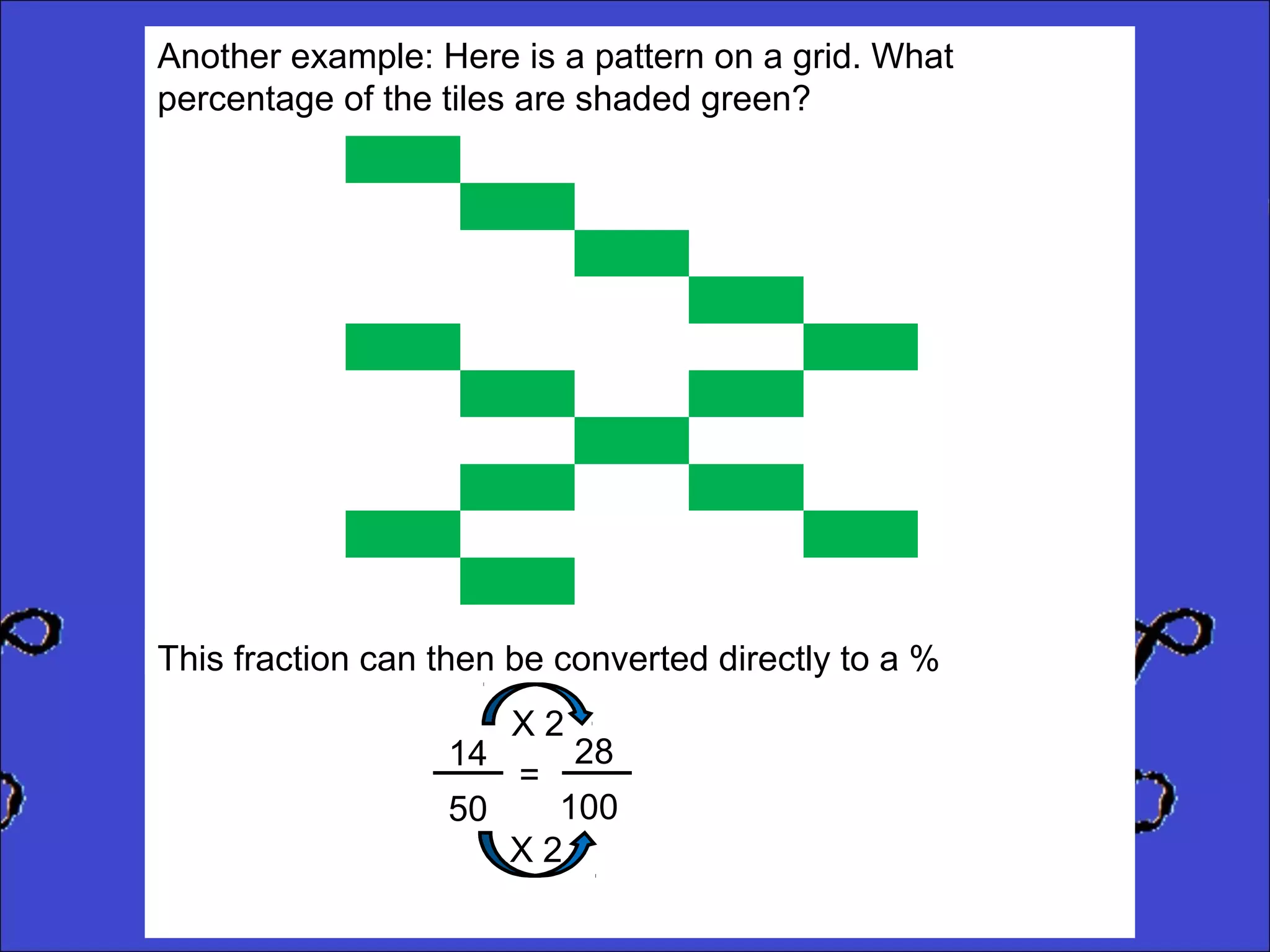
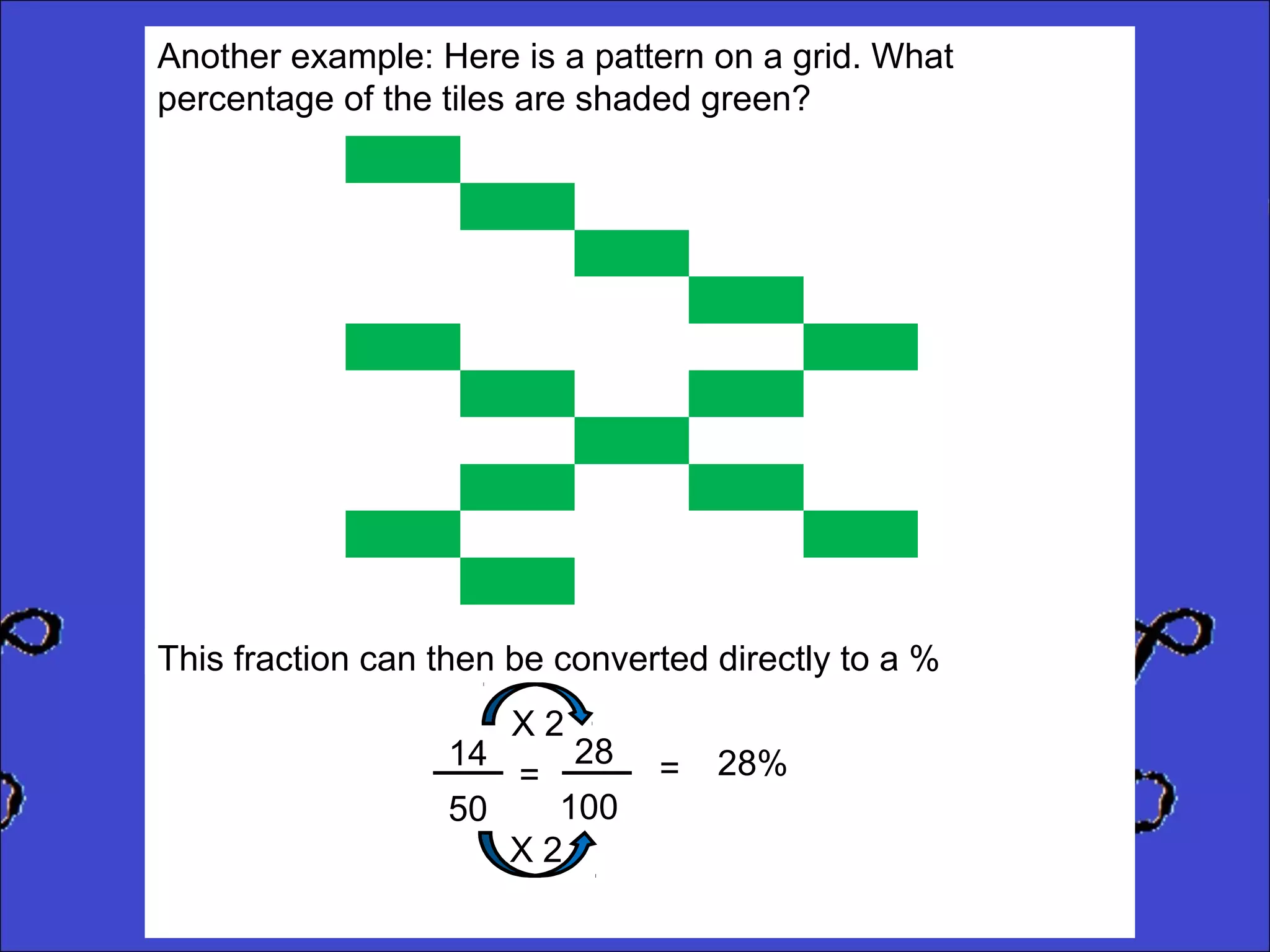
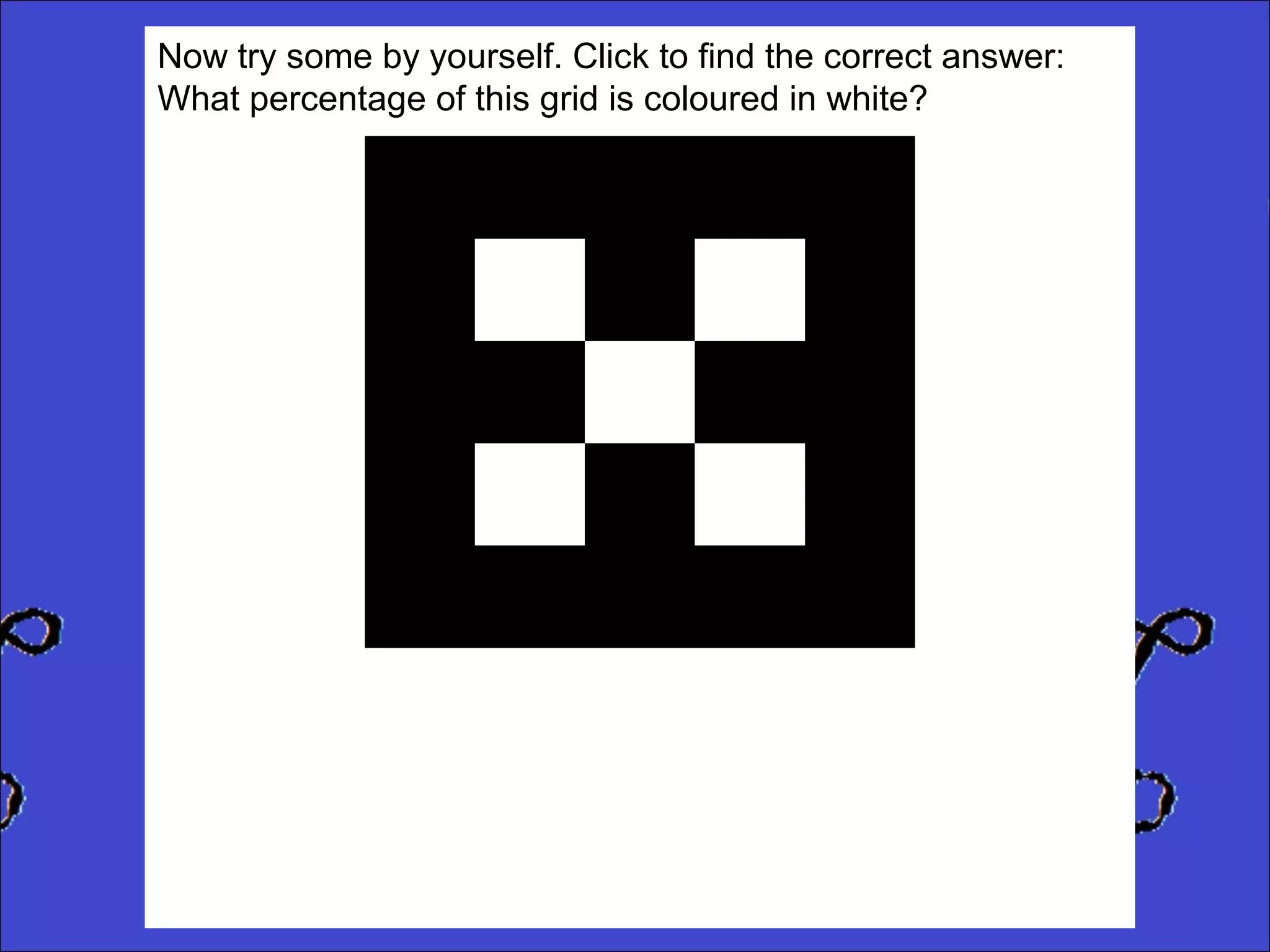
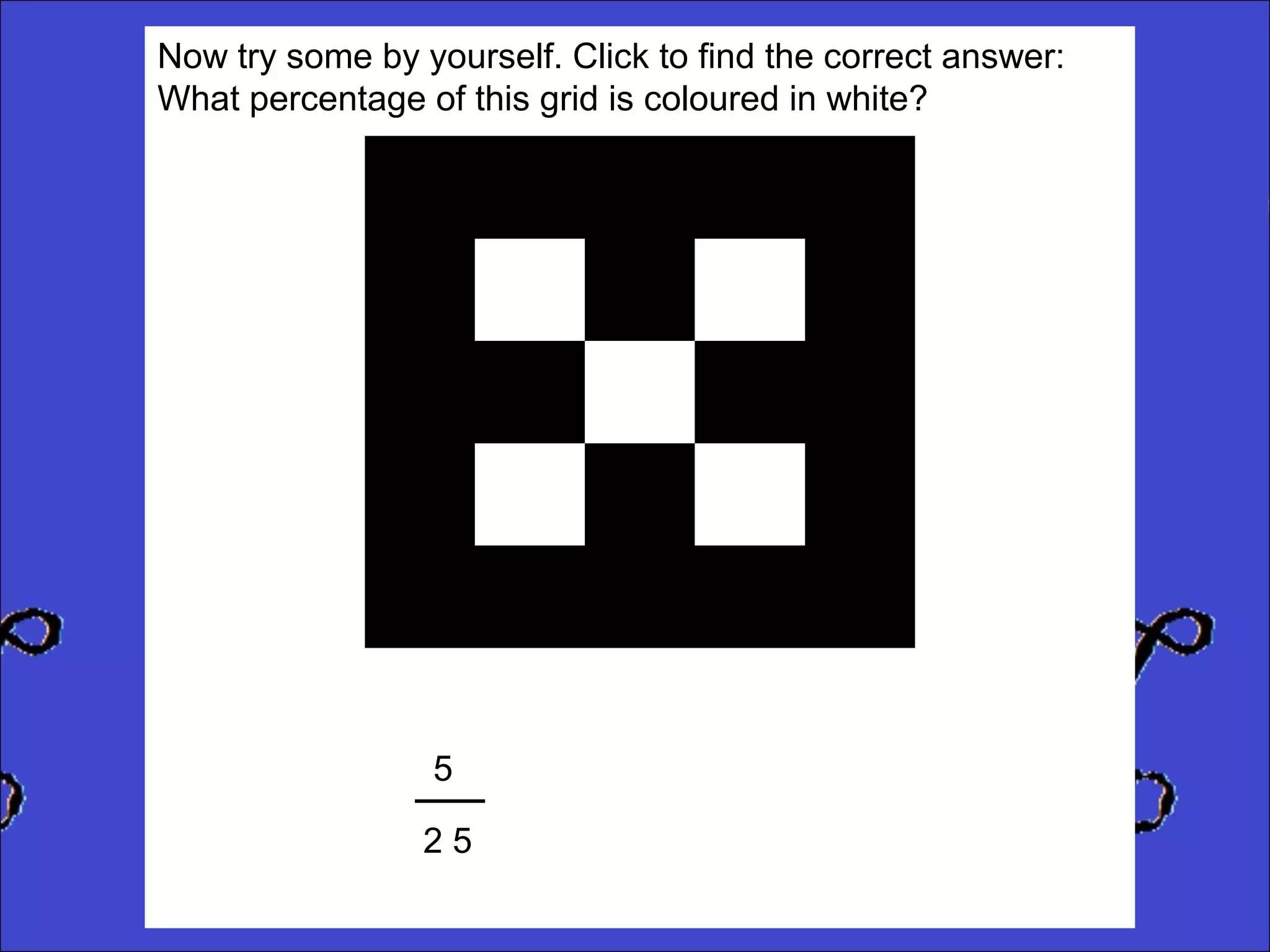
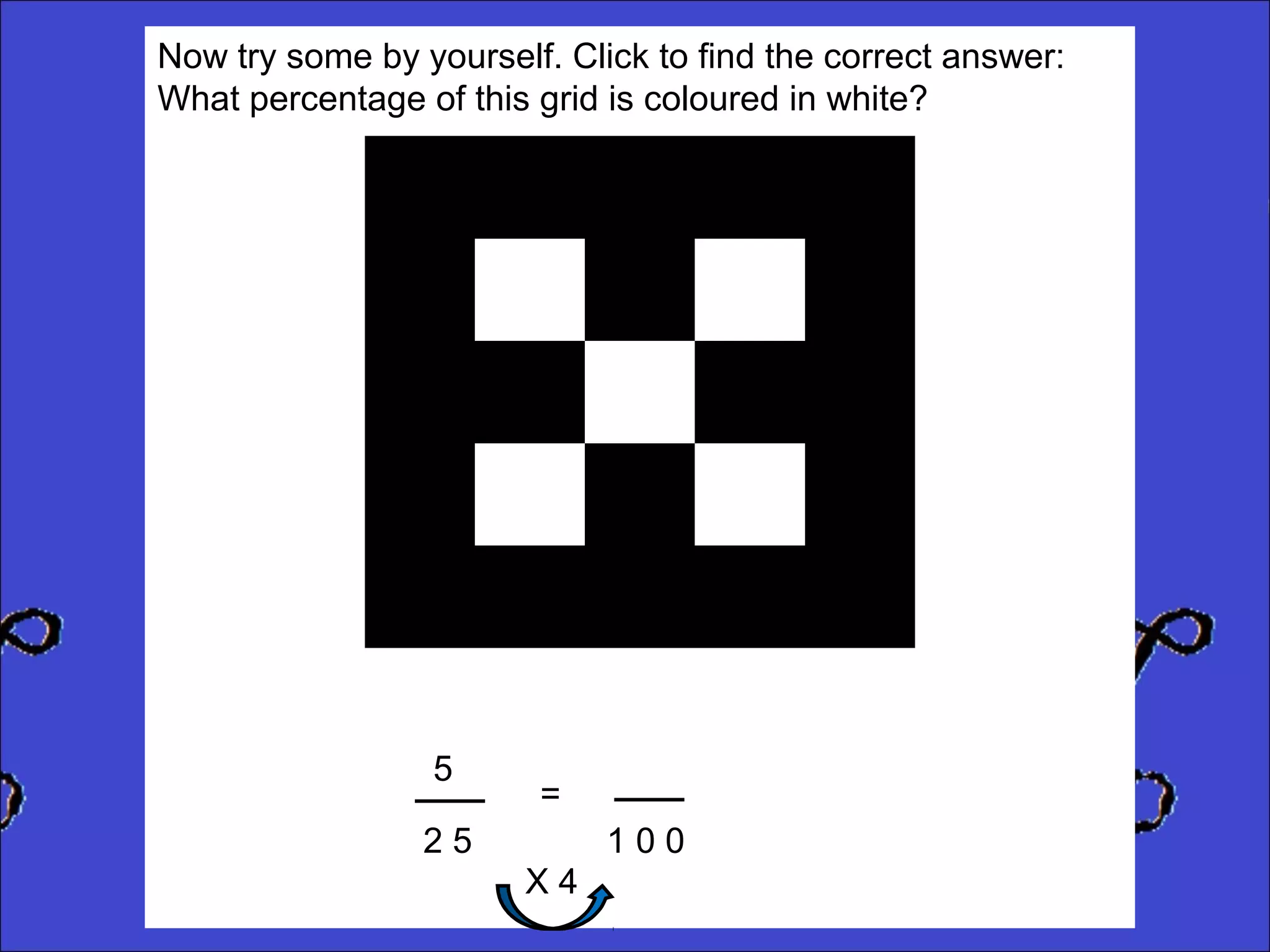
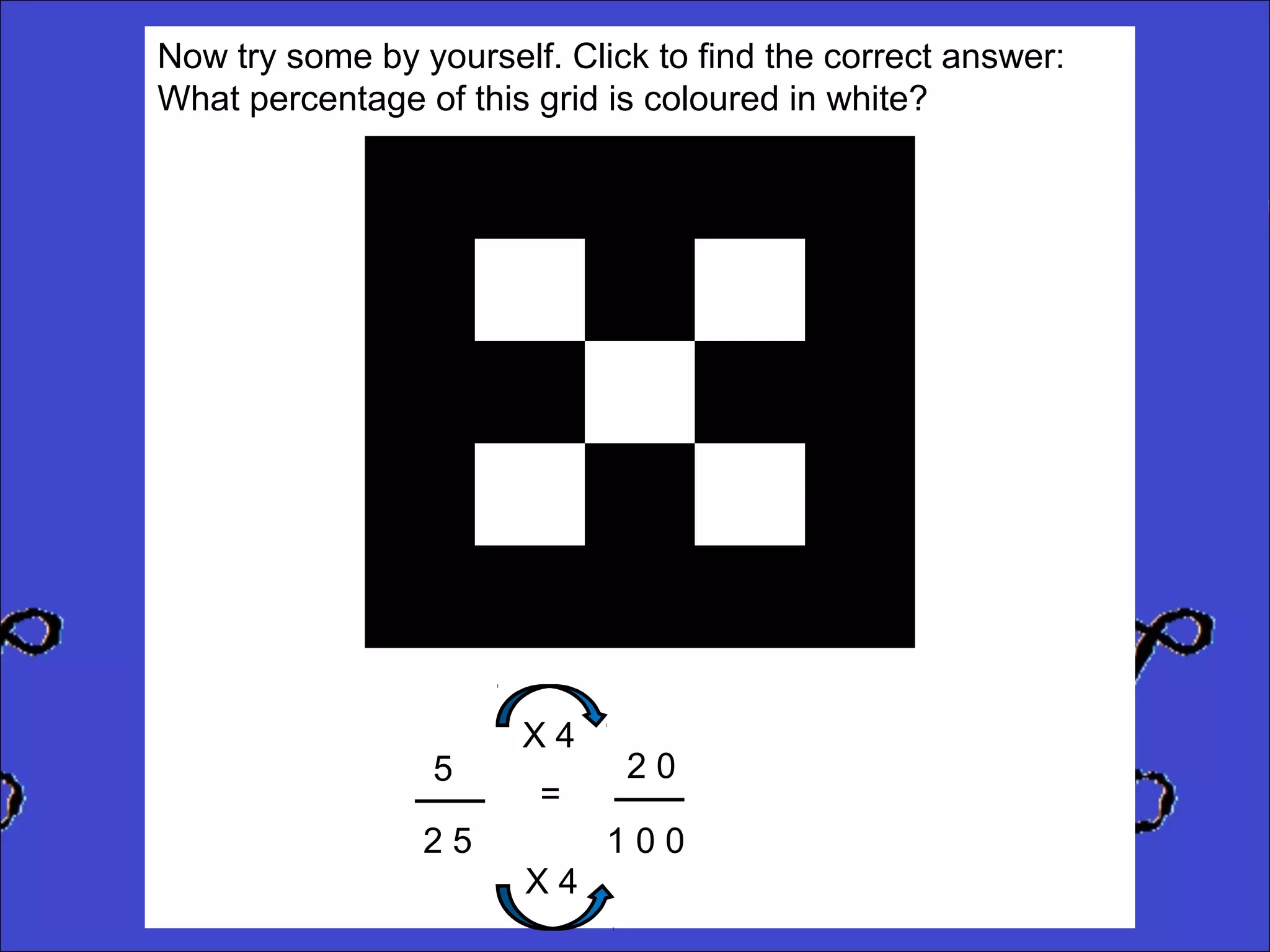
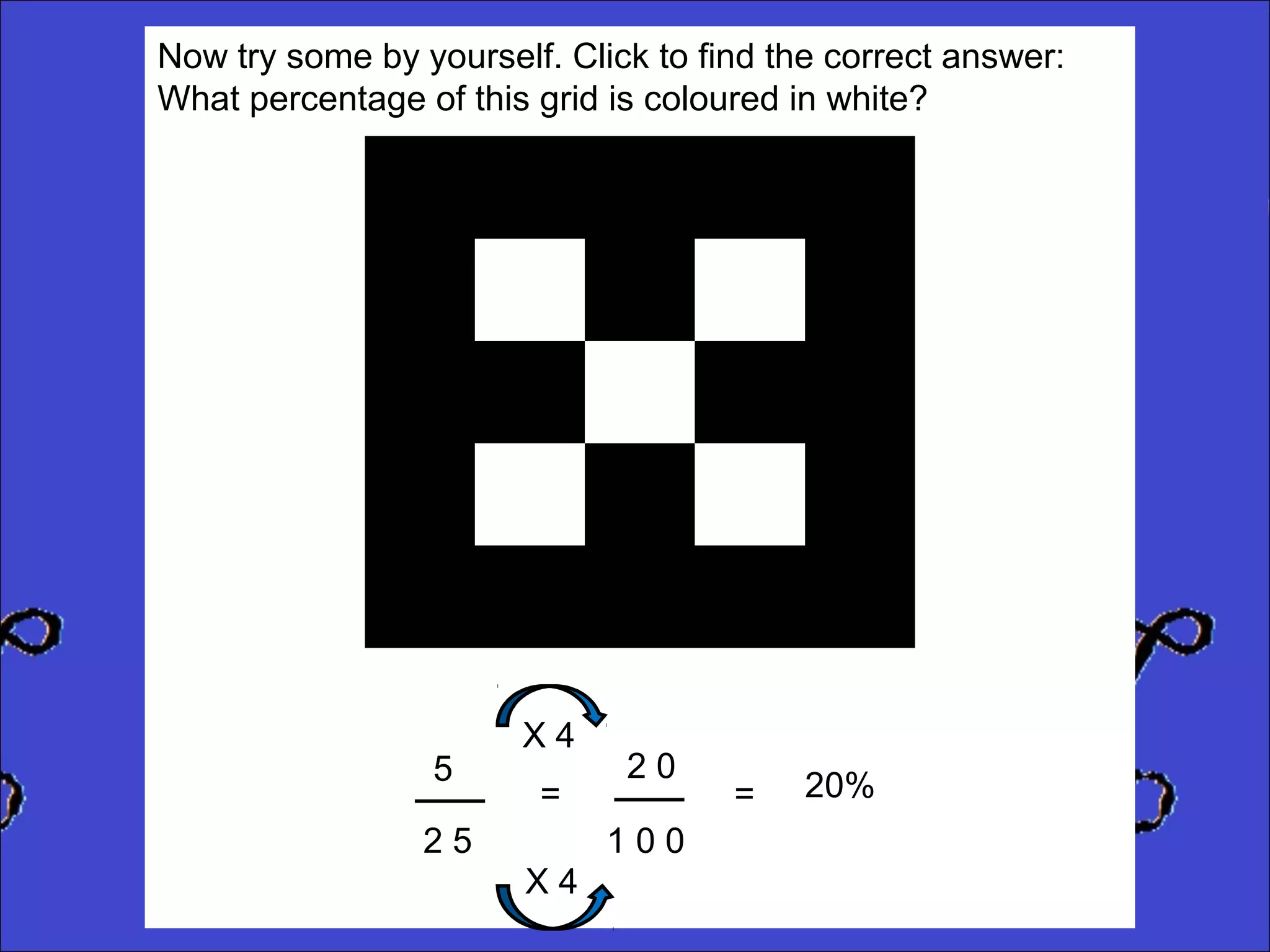
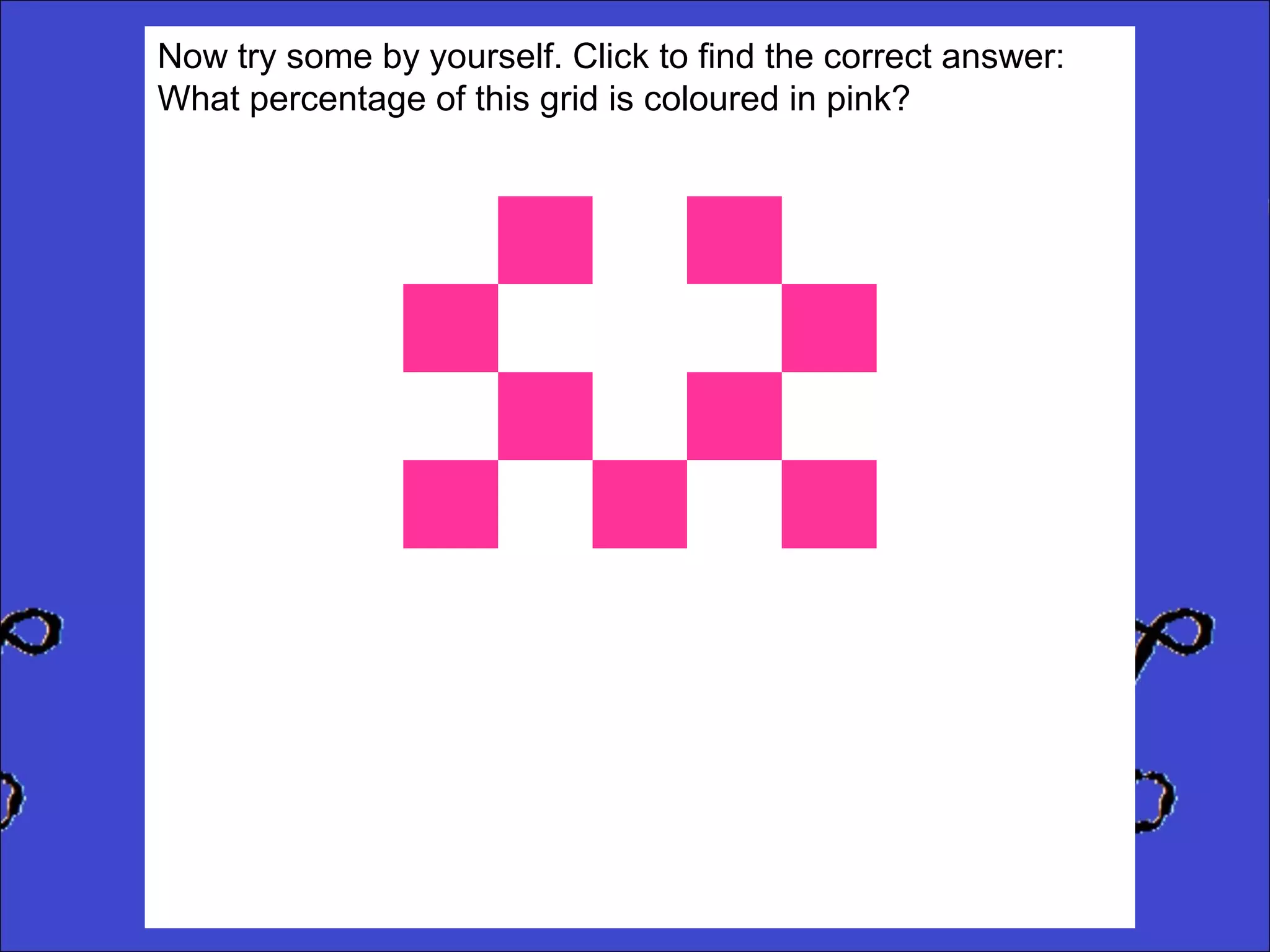
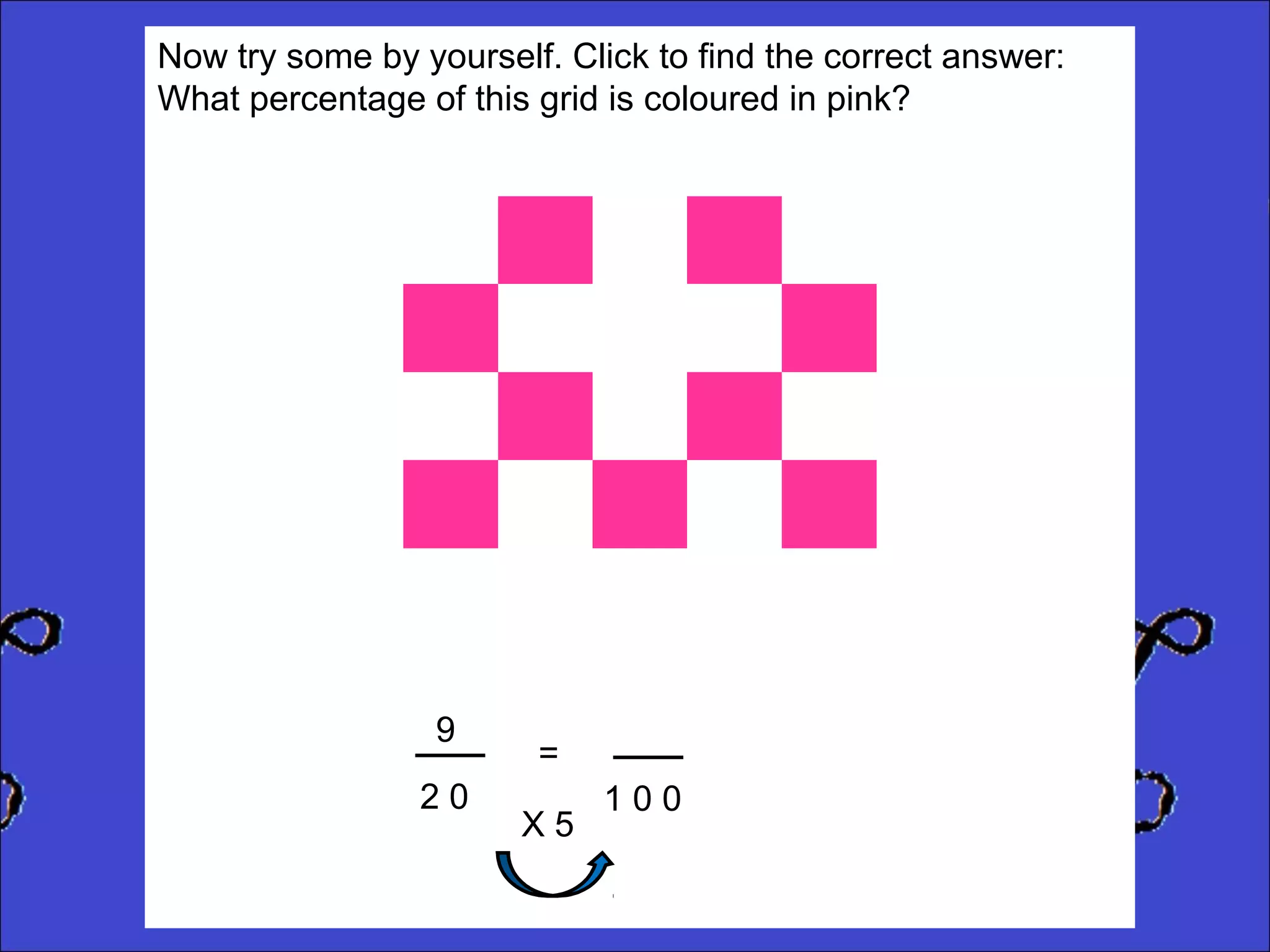
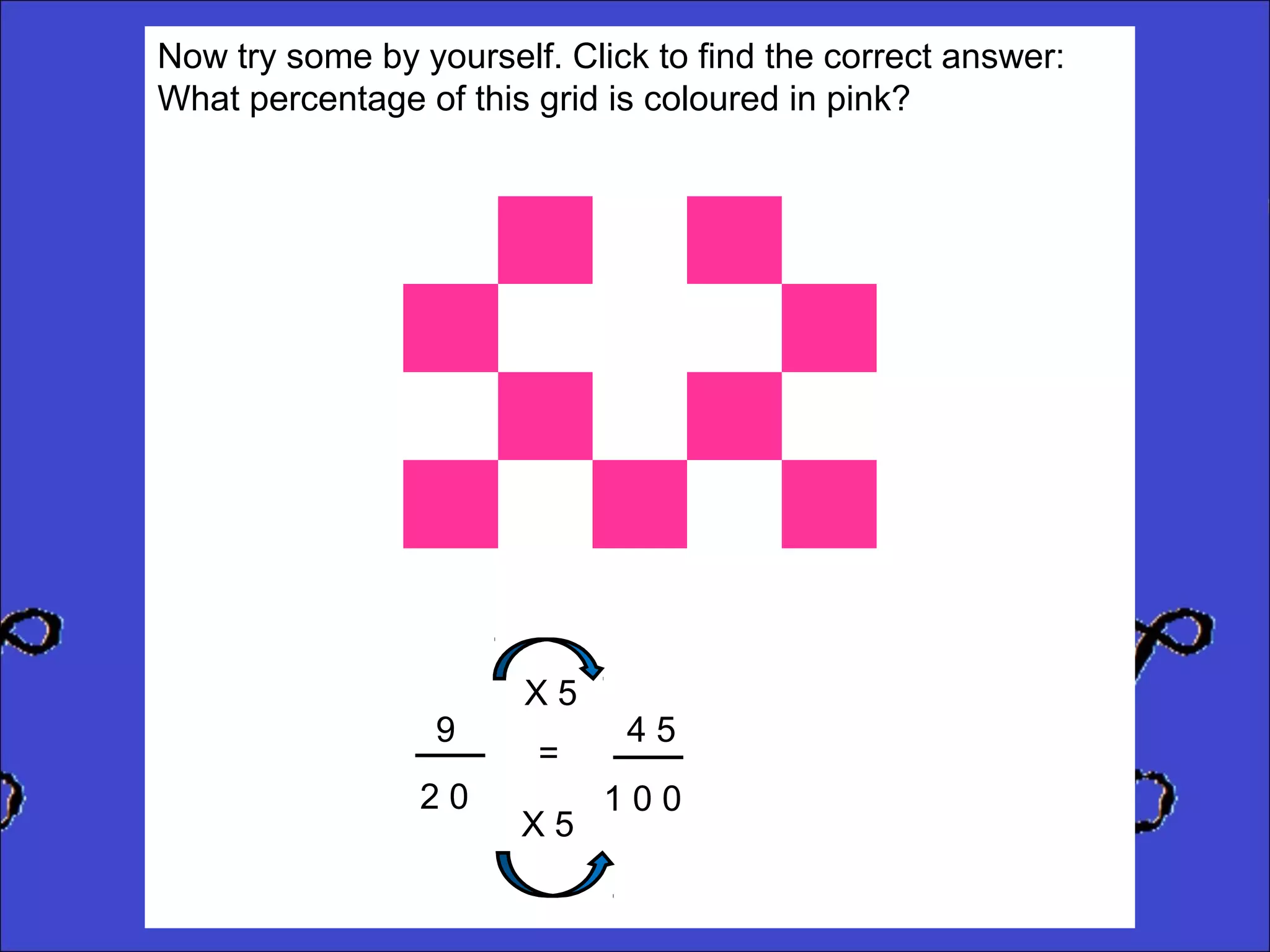
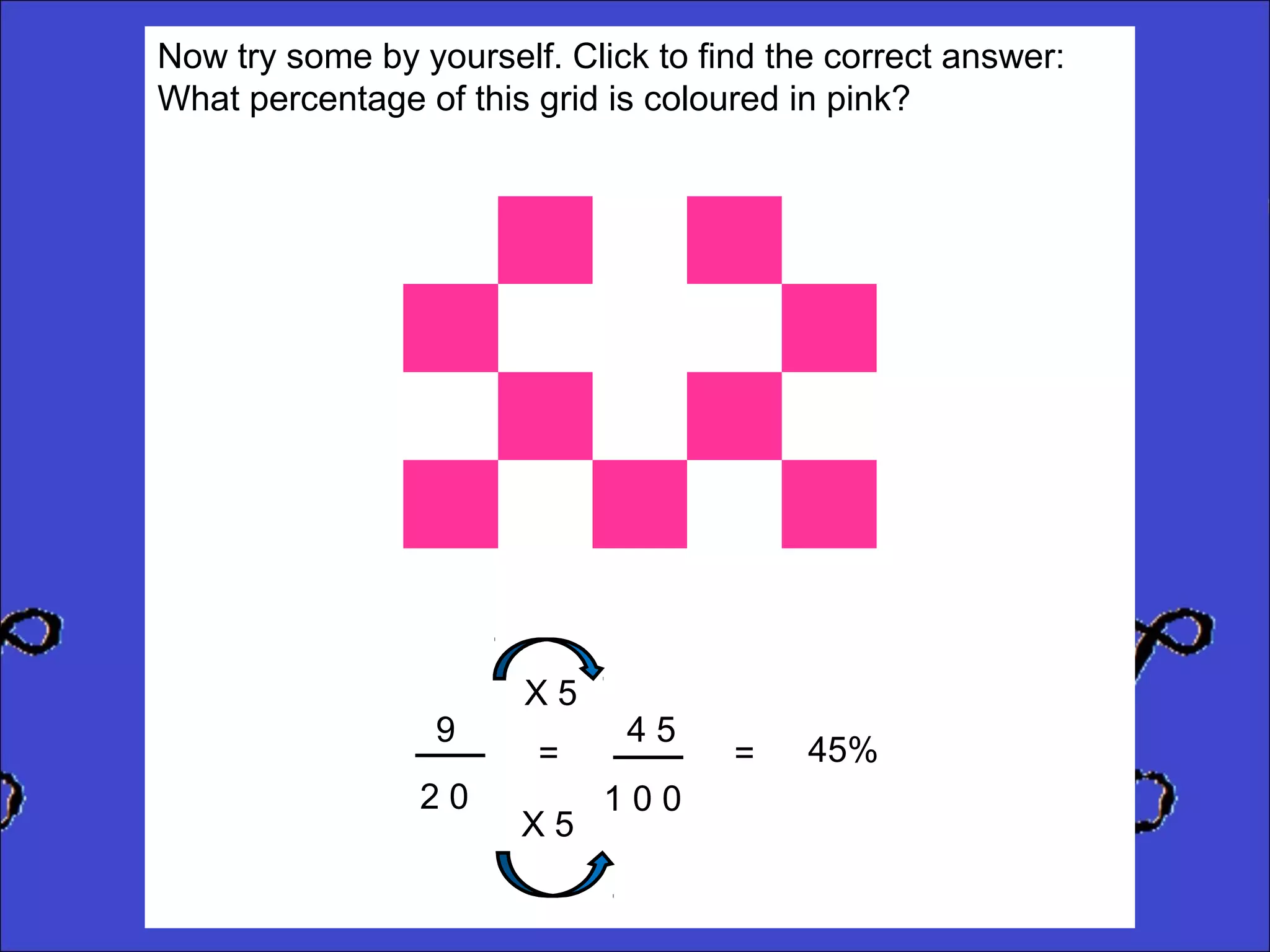
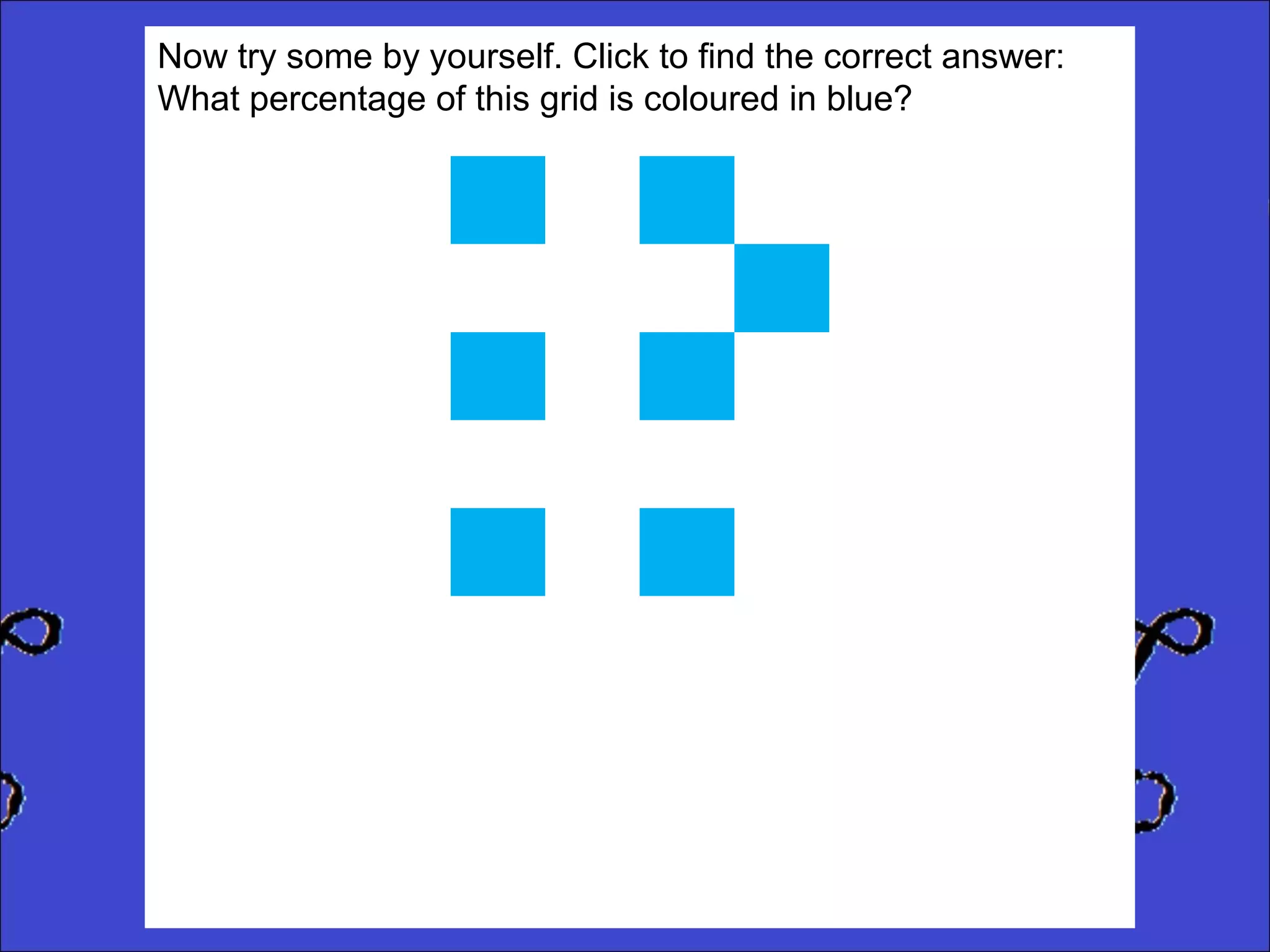
This document provides instructions for calculating percentages from grids for KS2 maths SATs questions. It explains that you count the number of shaded or colored tiles, express it as a fraction of the total tiles, and convert that fraction to a percentage by changing the denominator to 100. Two examples are shown step-by-step: calculating that 6 out of 20 tiles shaded is 30% and 14 out of 50 tiles green is 28%. The document ends by providing three practice problems for the reader to solve.

1. How To Do KS2 Maths SATs
Type Questions
(Paper B – Calculator Allowed)
Percentages 2: Calculating
How Much Of A Grid Is
Shaded
For more maths help & free games related
to this, visit: www.makemymathsbetter.com

2. In a SATs Paper B you might be asked to work out what
percentage of a grid is shaded:

3. For example: Here is a grid of 20 tiles. What percentage of
the tiles are shaded blue?
Firstly count up the number of shaded tiles:

4. For example: Here is a grid of 20 tiles. What percentage of
the tiles are shaded blue?
Firstly count up the number of shaded tiles:
There are 6

5. For example: Here is a grid of 20 tiles. What percentage of
the tiles are shaded blue?
Firstly count up the number of shaded tiles:
There are 6
As a fraction: 6/20 of the grid is shaded

6. For example: Here is a grid of 20 tiles. What percentage of
the tiles are shaded blue?
Now convert 6/20 to a fraction with a denominator of 100

7. For example: Here is a grid of 20 tiles. What percentage of
the tiles are shaded blue?
Now convert 6/20 to a fraction with a denominator of 100
6
20
=
X5

8. For example: Here is a grid of 20 tiles. What percentage of
the tiles are shaded blue?
Now convert 6/20 to a fraction with a denominator of 100
6
20
=
100
X5

9. For example: Here is a grid of 20 tiles. What percentage of
the tiles are shaded blue?
Now convert 6/20 to a fraction with a denominator of 100
X5
6
=
100
20
X5

10. For example: Here is a grid of 20 tiles. What percentage of
the tiles are shaded blue?
Now convert 6/20 to a fraction with a denominator of 100
X5
30
6
=
100
20
X5

11. For example: Here is a grid of 20 tiles. What percentage of
the tiles are shaded blue?
This fraction can then be converted directly to a %
X5
30
6
=
100
20
X5

12. For example: Here is a grid of 20 tiles. What percentage of
the tiles are shaded blue?
This fraction can then be converted directly to a %
X5
30
6
=
100
20
X5
=
30%

13. Another example: Here is a pattern on a grid. What
percentage of the tiles are shaded green?

14. Another example: Here is a pattern on a grid. What
percentage of the tiles are shaded green?
Firstly count up the total number of tiles.

15. Another example: Here is a pattern on a grid. What
percentage of the tiles are shaded green?
Firstly count up the total number of tiles. There are 50.

16. Another example: Here is a pattern on a grid. What
percentage of the tiles are shaded green?
Firstly count up the total number of tiles. There are 50.
Then count up the number of tiles that are shaded green.

17. Another example: Here is a pattern on a grid. What
percentage of the tiles are shaded green?
Firstly count up the total number of tiles. There are 50.
Then count up the number of tiles that are shaded green.
There are 14

18. Another example: Here is a pattern on a grid. What
percentage of the tiles are shaded green?
Firstly count up the total number of tiles. There are 50.
Then count up the number of tiles that are shaded green.
There are 14
As a fraction, this is written as 14/50

19. Another example: Here is a pattern on a grid. What
percentage of the tiles are shaded green?
Now convert 14/50 to a fraction with a denominator of 100

20. Another example: Here is a pattern on a grid. What
percentage of the tiles are shaded green?
Now convert 14/50 to a fraction with a denominator of 100
14
50
=

21. Another example: Here is a pattern on a grid. What
percentage of the tiles are shaded green?
Now convert 14/50 to a fraction with a denominator of 100
14
50
=
X2

22. Another example: Here is a pattern on a grid. What
percentage of the tiles are shaded green?
Now convert 14/50 to a fraction with a denominator of 100
14
50
=
100
X2

23. Another example: Here is a pattern on a grid. What
percentage of the tiles are shaded green?
Now convert 14/50 to a fraction with a denominator of 100
X2
14
=
100
50
X2

24. Another example: Here is a pattern on a grid. What
percentage of the tiles are shaded green?
Now convert 14/50 to a fraction with a denominator of 100
X2
28
14
=
100
50
X2

25. Another example: Here is a pattern on a grid. What
percentage of the tiles are shaded green?
This fraction can then be converted directly to a %
X2
28
14
=
100
50
X2

26. Another example: Here is a pattern on a grid. What
percentage of the tiles are shaded green?
This fraction can then be converted directly to a %
X2
28
14
=
100
50
X2
=
28%

27. Now try some by yourself. Click to find the correct answer:
What percentage of this grid is coloured in white?

28. Now try some by yourself. Click to find the correct answer:
What percentage of this grid is coloured in white?

29. Now try some by yourself. Click to find the correct answer:
What percentage of this grid is coloured in white?
5
25

30. Now try some by yourself. Click to find the correct answer:
What percentage of this grid is coloured in white?
5
=
25
100
X4

31. Now try some by yourself. Click to find the correct answer:
What percentage of this grid is coloured in white?
5
X4
=
25
20
100
X4

32. Now try some by yourself. Click to find the correct answer:
What percentage of this grid is coloured in white?
5
X4
=
25
20
100
X4
=
20%

33. Now try some by yourself. Click to find the correct answer:
What percentage of this grid is coloured in pink?

34. Now try some by yourself. Click to find the correct answer:
What percentage of this grid is coloured in pink?
9
20

35. Now try some by yourself. Click to find the correct answer:
What percentage of this grid is coloured in pink?
9
20
=
X5
100

36. Now try some by yourself. Click to find the correct answer:
What percentage of this grid is coloured in pink?
9
20
X5
=
X5
45
100

37. Now try some by yourself. Click to find the correct answer:
What percentage of this grid is coloured in pink?
9
20
X5
=
X5
45
100
=
45%

38. Now try some by yourself. Click to find the correct answer:
What percentage of this grid is coloured in blue?

39. Now try some by yourself. Click to find the correct answer:
What percentage of this grid is coloured in blue?
7
20

40. Now try some by yourself. Click to find the correct answer:
What percentage of this grid is coloured in blue?
7
20
=
X5
100

41. Now try some by yourself. Click to find the correct answer:
What percentage of this grid is coloured in blue?
7
20
X5
=
X5
35
100

42. Now try some by yourself. Click to find the correct answer:
What percentage of this grid is coloured in blue?
7
20
X5
=
X5
35
100
=
35%

43. That’s it for now......
for more help with your maths,
try my book:
mastering multiplication tables
on amazon.com