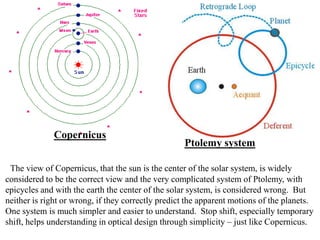
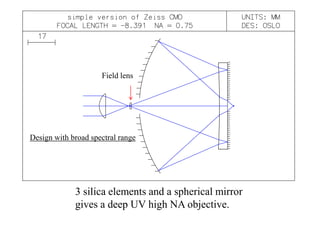
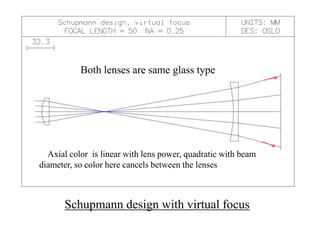
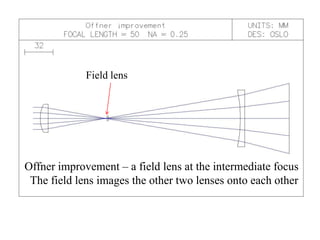
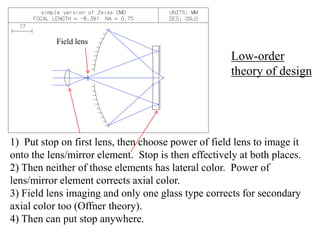
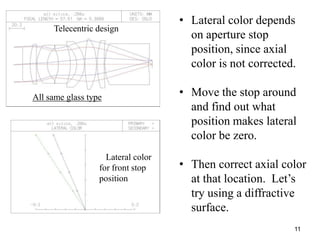
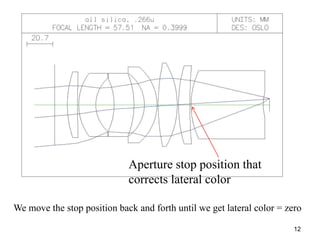
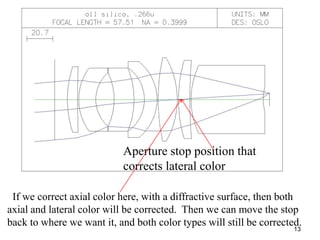
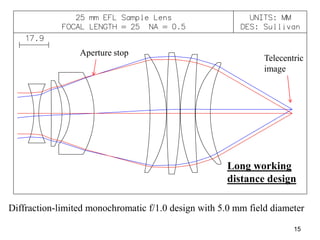
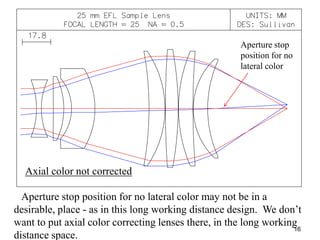
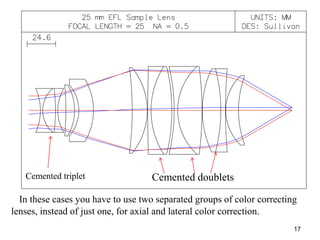
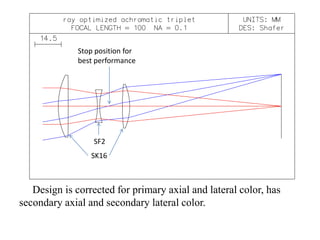
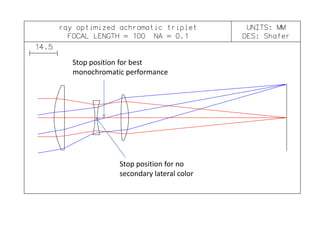
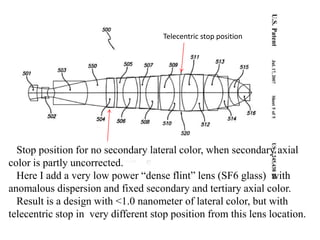
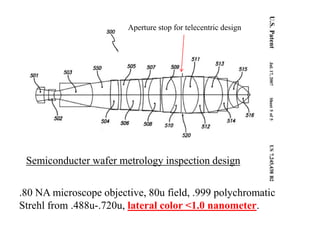
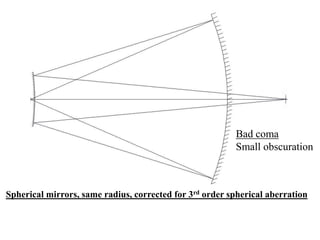
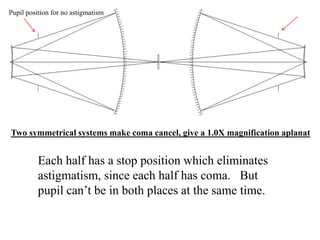
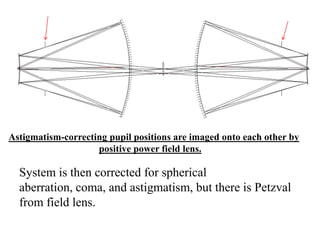
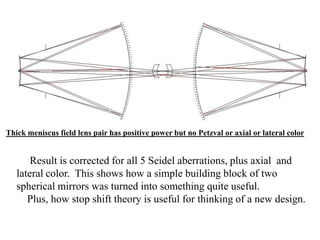
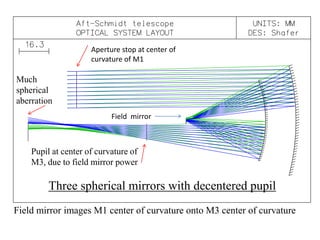
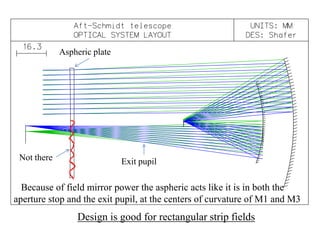
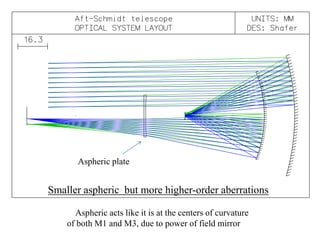
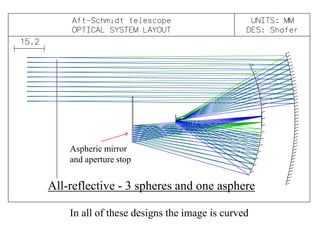
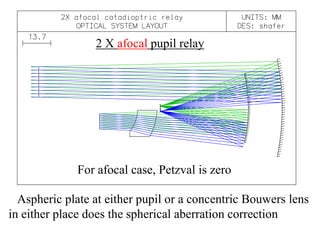
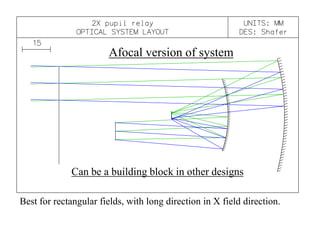
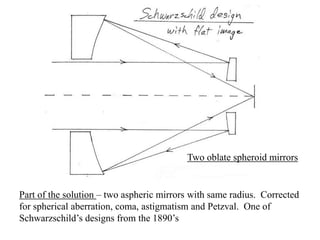
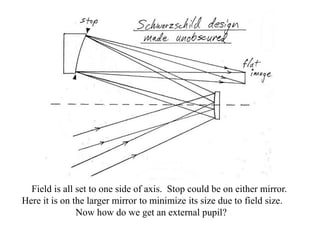
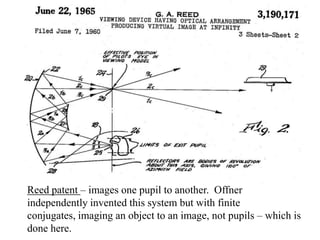
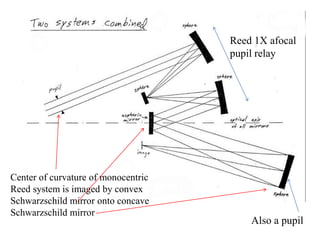
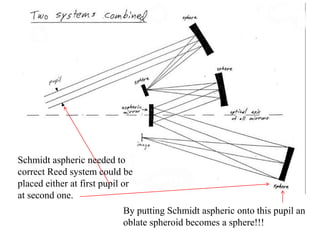
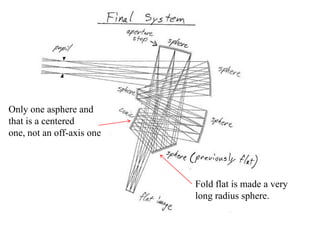
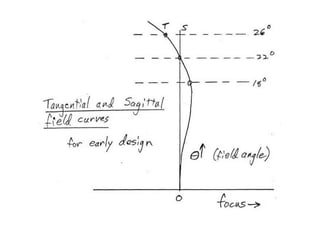
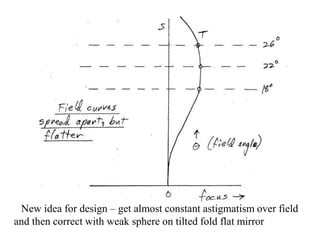
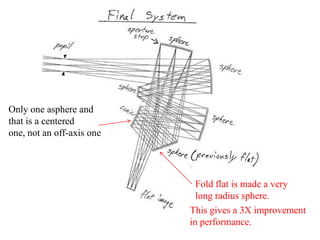
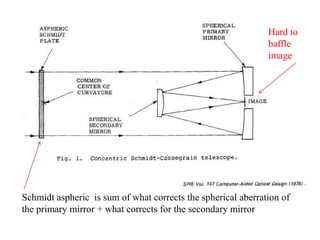
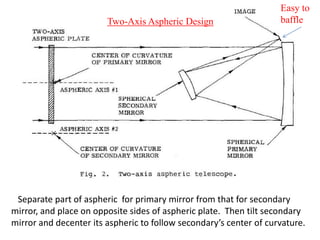
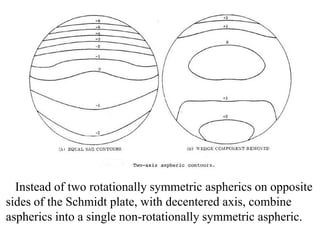
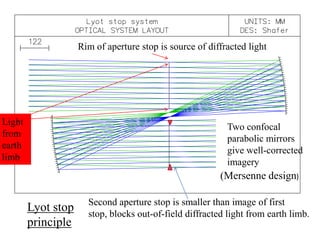
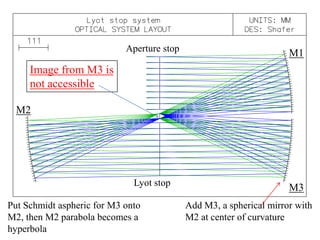
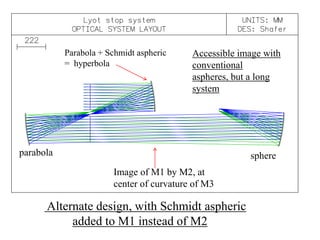
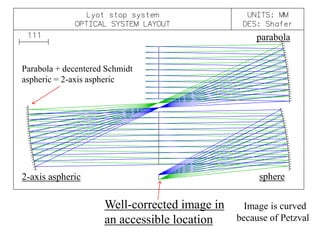
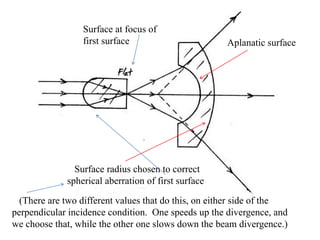
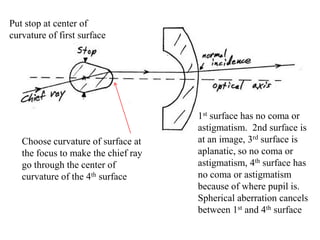
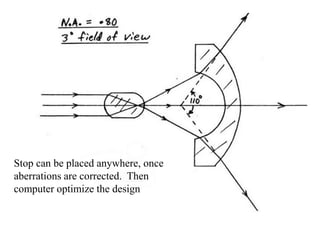
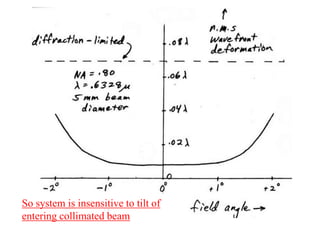
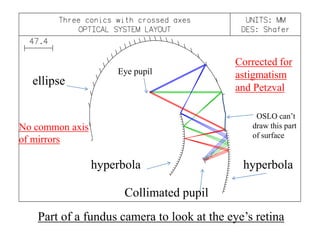
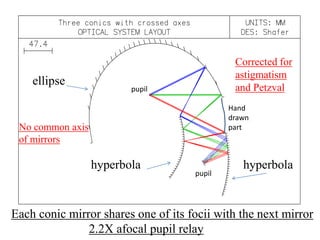
The document explores the application of stop-shift theory in optical design, highlighting its capacity to simplify design processes and enhance understanding of optical aberrations without extensive computations. It discusses various examples, including the Copernican system analogy, designs for semiconductor metrology, and advanced lens configurations, demonstrating how stop position adjustments can optimize correction of axial and lateral colors. Ultimately, it asserts that temporary stop shifts are valuable tools for achieving effective optical systems while maintaining the desired final aperture stop location.

1. Optical Design Using Stop-Shift Theory
Dave Shafer

2. •
The use of first and 3rd order stop shift theory can lead to
new types of designs and a better understanding of existing
designs.
•
No computations are necessary to benefit from stop-shift
theory – it just involves a few basic principles and some
temporary changes in aperture stop position.
•
Experiments can be carried out in your head. Computer
calculations only happen after you are done with the
conceptual work.

3. Copernicus
Ptolemy system
The view of Copernicus, that the sun is the center of the solar system, is widely
considered to be the correct view and the very complicated system of Ptolemy, with
epicycles and with the earth the center of the solar system, is considered wrong. But
neither is right or wrong, if they correctly predict the apparent motions of the planets.
One system is much simpler and easier to understand. Stop shift, especially temporary
shift, helps understanding in optical design through simplicity – just like Copernicus.

4. Let’s start out with 1st order stop-shift theory, which
relates lateral and axial color.
1) If a system has axial color then lateral color is linear
with stop position. That means that there must be a stop
position that makes primary (1st-order) lateral color be zero.
2) If a system is corrected for primary axial color, then
primary lateral color is independent of stop position.
3) A thin lens with the stop in contact has no lateral color.
4) A thin lens at a focus has no axial or lateral color.

5. Field lens
Design with broad spectral range
3 silica elements and a spherical mirror
gives a deep UV high NA objective.

6. What is the aberration theory behind
this very simple design?
Answer – it involves stop-shift theory

7. Both lenses are same glass type
Axial color is linear with lens power, quadratic with beam
diameter, so color here cancels between the lenses
Schupmann design with virtual focus

8. Field lens
Offner improvement – a field lens at the intermediate focus
The field lens images the other two lenses onto each other

9. Field lens
Low-order
theory of design
1) Put stop on first lens, then choose power of field lens to image it
onto the lens/mirror element. Stop is then effectively at both places.
2) Then neither of those elements has lateral color. Power of
lens/mirror element corrects axial color.
3) Field lens imaging and only one glass type corrects for secondary
axial color too (Offner theory).
4) Then can put stop anywhere.

10. •
A key point – the aperture stop was only
temporarily located at a place where the theory is
simple to understand and the aberration correction
method becomes obvious.
• Then later the stop is moved to where it needs to be
– like in order to have a telecentric system.
• Once the aberrations are well-corrected they do not
change (at the lower-order levels) when the stop is
moved.

11. Telecentric design
All same glass type
Lateral color
for front stop
position
• Lateral color depends
on aperture stop
position, since axial
color is not corrected.
• Move the stop around
and find out what
position makes lateral
color be zero.
• Then correct axial color
at that location. Let’s
try using a diffractive
surface.
11

12. Aperture stop position that
corrects lateral color
We move the stop position back and forth until we get lateral color = zero
12

13. Aperture stop position that
corrects lateral color
If we correct axial color here, with a diffractive surface, then both
axial and lateral color will be corrected. Then we can move the stop
back to where we want it, and both color types will still be corrected.
13

14. • This same design method indicates where to add
lenses for color correction
• It minimizes the number of extra lenses needed for
color correction
• But it may indicate adding color correcting lenses
where we don’t want them, because of space
constraints
• Then we rely on conventional color correcting
techniques
14

15. Aperture stop
Telecentric
image
Long working
distance design
Diffraction-limited monochromatic f/1.0 design with 5.0 mm field diameter
15

16. Aperture stop
position for no
lateral color
Axial color not corrected
Aperture stop position for no lateral color may not be in a
desirable, place - as in this long working distance design. We don’t
want to put axial color correcting lenses there, in the long working
16
distance space.

17. Cemented triplet
Cemented doublets
In these cases you have to use two separated groups of color correcting
lenses, instead of just one, for axial and lateral color correction.
17

18. Correcting secondary lateral color

19. Stop position for
best performance
SF2
SK16
Design is corrected for primary axial and lateral color, has
secondary axial and secondary lateral color.

20. • Suppose primary axial and lateral color are corrected.
• If a design has secondary axial color then secondary
lateral color is linear with stop position.
• So there must be a stop position then that corrects for secondary
lateral color.
• If you fix secondary axial color at that stop position, then both
secondary axial and lateral color will be corrected.
• Then you can put the stop anywhere with no effect.

21. Stop position for best
monochromatic performance
Stop position for no
secondary lateral color

22. Semiconducter wafer metrology inspection design

23. • KLA-Tencor in 2005 wanted a “perfect” .80 NA design for
.488u - .720u
• Requires correction of primary, secondary, and tertiary axial
color to get .999 polychromatic Strehl over that spectral range.
• Needs correction of primary lateral color, and secondary lateral
color is a very big problem – doesn’t hurt image quality but
gives wafer measurement error.
• Olympus, Tropel, and ORA all worked on this and could not get
any better than 10 to 20X more secondary lateral color than was
acceptable (needed = 1.0 nanometer over a 80u field diameter).
• I tried a design and also was about 10X too much lateral color

24. • The solution – use stop-shift theory
• I corrected primary axial and lateral color and partially
corrected secondary axial color.
• I found out where the stop position is then where
secondary lateral color is zero
• I corrected the remaining secondary axial color at that stop
position
• Then I moved the stop back to its telecentric position

25. Telecentric stop position
Stop position for no secondary lateral color, when secondary axial
color is partly uncorrected.
Here I add a very low power “dense flint” lens (SF6 glass) with
anomalous dispersion and fixed secondary and tertiary axial color.
Result is a design with <1.0 nanometer of lateral color, but with
telecentric stop in very different stop position from this lens location.

26. Aperture stop for telecentric design
Semiconducter wafer metrology inspection design
.80 NA microscope objective, 80u field, .999 polychromatic
Strehl from .488u-.720u, lateral color <1.0 nanometer.

27. A 1.0X catadioptric relay system
developed using stop shift theory

28. Bad coma
Small obscuration
Spherical mirrors, same radius, corrected for 3rd order spherical aberration

29. • If a design has spherical aberration then coma is
linear with stop position and astigmatism is
quadratic with stop position
• If spherical aberration is corrected then coma is
constant with stop position and astigmatism is
linear with stop position. Then, for non-zero
coma, there is always a stop position that corrects
for astigmatism.
• If both spherical aberration and coma are
corrected then astigmatism is a constant

30. Pupil position for no astigmatism
Two symmetrical systems make coma cancel, give a 1.0X magnification aplanat
Each half has a stop position which eliminates
astigmatism, since each half has coma. But
pupil can’t be in both places at the same time.

31. Astigmatism-correcting pupil positions are imaged onto each other by
positive power field lens.
System is then corrected for spherical
aberration, coma, and astigmatism, but there is Petzval
from field lens.

32. Thick meniscus field lens pair has positive power but no Petzval or axial or lateral color
Result is corrected for all 5 Seidel aberrations, plus axial and
lateral color. This shows how a simple building block of two
spherical mirrors was turned into something quite useful.
Plus, how stop shift theory is useful for thinking of a new design.

33. Aft-Schmidt Design

34. • If spherical aberration is uncorrected then coma is linear
with stop position and astigmatism is quadratic with stop
position.
• So then, for non-zero spherical aberration, there is always
a stop position that corrects for coma and either 2 or none
that correct for astigmatism.
• In some cases (like the Schmidt telescope) the stop
position which corrects coma also corrects astigmatism.

35. Aperture stop at center of
curvature of M1
Much
spherical
aberration
Field mirror
Pupil at center of curvature of
M3, due to field mirror power
Three spherical mirrors with decentered pupil
Field mirror images M1 center of curvature onto M3 center of curvature

36. Aspheric plate
Not there
Exit pupil
Because of field mirror power the aspheric acts like it is in both the
aperture stop and the exit pupil, at the centers of curvature of M1 and M3
Design is good for rectangular strip fields

37. Aspheric plate
Smaller aspheric but more higher-order aberrations
Aspheric acts like it is at the centers of curvature
of both M1 and M3, due to power of field mirror

38. Aspheric mirror
and aperture stop
All-reflective - 3 spheres and one asphere
In all of these designs the image is curved

39. After the system is given good correction, with the
Schmidt aspheric, the aperture stop can be moved if
that is wanted, maybe to minimize the size of M1.
Higher-order aberrations will be affected and the
best stop position is at the centers of curvatures of
M1 and M3

40. 2 X afocal pupil relay
For afocal case, Petzval is zero
Aspheric plate at either pupil or a concentric Bouwers lens
in either place does the spherical aberration correction

41. Afocal version of system
Can be a building block in other designs
Best for rectangular fields, with long direction in X field direction.

42. Infrared Target Simulator Design

43. External pupil of simulator matches internal pupil of missile head
A system from 1984 – customer wanted an infrared target simulator
to test missile heat seeking heads. Requires a distant external pupil.
Goals – all-reflective, inexpensive, 8 X 8 degree square
field, f/4.5, 200 mm aperture, unobscured, .05 to .10 millirad spot on a
flat image

44. Two oblate spheroid mirrors
Part of the solution – two aspheric mirrors with same radius. Corrected
for spherical aberration, coma, astigmatism and Petzval. One of
Schwarzschild’s designs from the 1890’s

45. Field is all set to one side of axis. Stop could be on either mirror.
Here it is on the larger mirror to minimize its size due to field size.
Now how do we get an external pupil?

46. Reed patent – images one pupil to another. Offner
independently invented this system but with finite
conjugates, imaging an object to an image, not pupils – which is
done here.

47. Reed 1X afocal
pupil relay
Center of curvature of monocentric
Reed system is imaged by convex
Schwarzschild mirror onto concave
Schwarzschild mirror
Also a pupil

48. Schmidt aspheric needed to
correct Reed system could be
placed either at first pupil or
at second one.
By putting Schmidt aspheric onto this pupil an
oblate spheroid becomes a sphere!!!

49. Only one asphere and
that is a centered
one, not an off-axis one
Fold flat is made a very
long radius sphere.

51. New idea for design – get almost constant astigmatism over field
and then correct with weak sphere on tilted fold flat mirror

52. Only one asphere and
that is a centered
one, not an off-axis one
Fold flat is made a very
long radius sphere.
This gives a 3X improvement
in performance.

53. Two-Axis Asphere Design

54. Hard to
baffle
image
Schmidt aspheric is sum of what corrects the spherical aberration of
the primary mirror + what corrects for the secondary mirror

55. Two-Axis Aspheric Design
Easy to
baffle
Separate part of aspheric for primary mirror from that for secondary
mirror, and place on opposite sides of aspheric plate. Then tilt secondary
mirror and decenter its aspheric to follow secondary’s center of curvature.

56. Instead of two rotationally symmetric aspherics on opposite
sides of the Schmidt plate, with decentered axis, combine
aspherics into a single non-rotationally symmetric aspheric.

57. Early warning missile defense system
Work I did in 1972, 40 years ago.

58. If a missile comes over
the rim of the earth it will
be seen here by a satellite
against a black sky, but it
will be very close to an
extremely bright
earth, which gives an
unwanted signal that vastly
exceeds the missile’s heat
signal. But that is the easy
case. Much worse is when
the satellite is on the night
side and the missile is seen
against a sun-lit earth’s
limb.

59. With the sun behind the horizon, the earth’s limb is
1.0 e+10 times brighter than the missile signal.

60. Rim of aperture stop is source of diffracted light
Light
from
earth
limb
Two confocal
parabolic mirrors
give well-corrected
imagery
(Mersenne design)
Lyot stop
principle
Second aperture stop is smaller than image of first
stop, blocks out-of-field diffracted light from earth limb.

61. Aperture stop
M1
Lyot stop
M3
Image from M3 is
not accessible
M2
Put Schmidt aspheric for M3 onto
M2, then M2 parabola becomes a
hyperbola
Add M3, a spherical mirror with
M2 at center of curvature

62. Parabola + Schmidt aspheric
= hyperbola
Accessible image with
conventional
aspheres, but a long
system
parabola
sphere
Image of M1 by M2, at
center of curvature of M3
Alternate design, with Schmidt aspheric
added to M1 instead of M2

63. parabola
Parabola + decentered Schmidt
aspheric = 2-axis aspheric
sphere
2-axis aspheric
Well-corrected image in
an accessible location
Image is curved
because of Petzval

64. High NA laser beam expander

65. Surface at focus of
first surface
Aplanatic surface
Surface radius chosen to correct
spherical aberration of first surface
(There are two different values that do this, on either side of the
perpendicular incidence condition. One speeds up the divergence, and
we choose that, while the other one slows down the beam divergence.)

66. Put stop at center of
curvature of first surface
Choose curvature of surface at
the focus to make the chief ray
go through the center of
curvature of the 4th surface
1st surface has no coma or
astigmatism. 2nd surface is
at an image, 3rd surface is
aplanatic, so no coma or
astigmatism, 4th surface has
no coma or astigmatism
because of where pupil is.
Spherical aberration cancels
between 1st and 4th surface

67. Stop can be placed anywhere, once
aberrations are corrected. Then
computer optimize the design

68. So system is insensitive to tilt of
entering collimated beam

69. Cascaded Conic Mirrors

70. •
A conic mirror with the aperture stop at
either of its focii has no astigmatism of any
order.
•
This can be proven mathematically with
the Coddington equations.
•
Some interesting designs are possible
using this fact.

71. Eye pupil
ellipse
Corrected for
astigmatism
and Petzval
OSLO can’t
draw this part
of surface
No common axis
of mirrors
hyperbola
hyperbola
Collimated pupil
Part of a fundus camera to look at the eye’s retina

72. ellipse
Corrected for
astigmatism
and Petzval
pupil
Hand
drawn
part
No common axis
of mirrors
hyperbola
pupil
hyperbola
Each conic mirror shares one of its focii with the next mirror
2.2X afocal pupil relay

73. • Spherical aberration and coma are uncorrected in this
design but the pupil size is very small so they don’t
matter very much
• But still this means that the aperture stop and pupils
cannot be moved from the mirror focii without
hurting the zero astigmatism situation of the system

74. Conclusion
• Stop shift theory gives insight into the aberration theory
of a design and also suggests new design possibilities
• Temporary stop shift is a powerful design tool and does
not usually require changing the actual final position of
the stop, which may be set by the telecentric condition
or other constraints