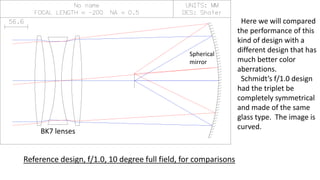
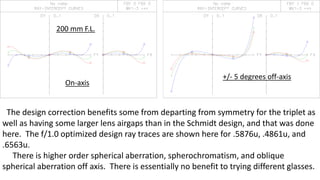
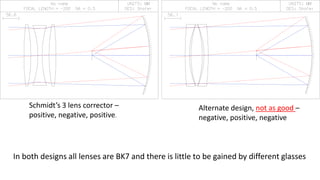
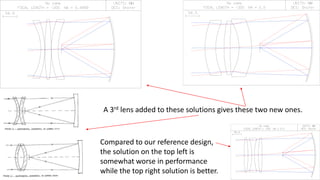
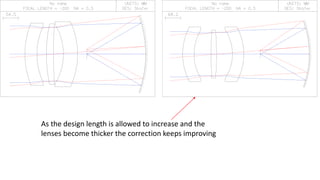
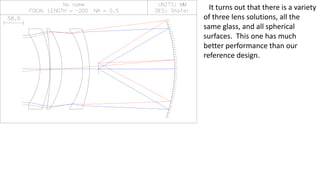
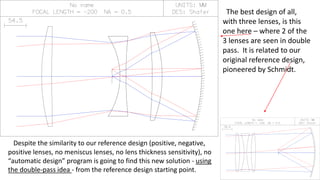
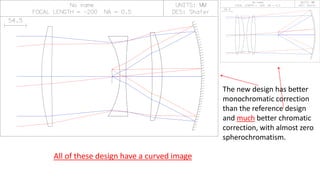
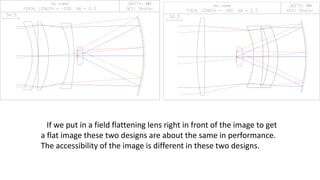
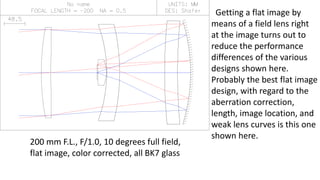
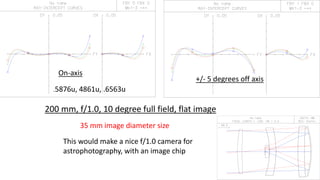
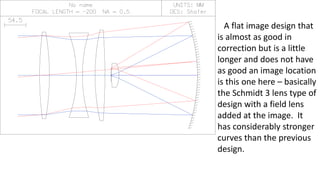
The document discusses Schmidt's 1934 design of a three-lens replacement for an aspheric plate in an f/1.0 Schmidt camera, which predates similar designs by Houghton. It compares the performance of Schmidt's design with new variations that offer better color aberrations and highlights the importance of lens thickness and configuration in achieving better optical correction. The findings suggest that additional lenses or aspherical elements could further improve performance beyond the discussed examples.

1. Schmidt’s 1934 three lens replacement for
an aspheric plate, and some new variations
David Shafer
David Shafer Optical Design
Fairfield, CT. 06824
#203-259-1431
shaferlens@sbcglobal.net

2. Recently a fascinating story from lens design history was chronicled in
this journal article here, about how Schmidt designed and built in 1934 a
three lens replacement for the aspheric plate in a f/1.0 Schmidt camera.

3. This system designed and built
system by Schmidt in 1934 was
10 years before the two and
three lens replacements for an
aspheric Schmidt plate that were
described by Houghton in this
1944 patent. Schmidt died
unexpectedly and was never able
to publish his results, which have
been unknown until very
recently. Later Buchroeder in
1972 published some Houghton
type of designs.

4. Here we will compared
the performance of this
kind of design with a
different design that has
much better color
aberrations.
Schmidt’s f/1.0 design
had the triplet be
completely symmetrical
and made of the same
glass type. The image is
curved.
Reference design, f/1.0, 10 degree full field, for comparisons
BK7 lenses
Spherical
mirror

5. On-axis
+/- 5 degrees off-axis
The design correction benefits some from departing from symmetry for the triplet as
well as having some larger lens airgaps than in the Schmidt design, and that was done
here. The f/1.0 optimized design ray traces are shown here for .5876u, .4861u, and
.6563u.
There is higher order spherical aberration, spherochromatism, and oblique
spherical aberration off axis. There is essentially no benefit to trying different glasses.
200 mm F.L.

6. Schmidt’s 3 lens corrector –
positive, negative, positive.
Alternate design, not as good –
negative, positive, negative
In both designs all lenses are BK7 and there is little to be gained by different glasses

7. In 1983 (SPIE Vol. 0399 -“Optical
Design With Air Lenses”) I showed
how the two lens Houghton corrector
can be replaced with two nearly zero
power meniscus lenses to get a well-
corrected alternate design. And there
are theoretical reasons why the
resulting pair of lenses moves much
closer to the spherical primary mirror,
giving a much shorter design than the
Houghton design. The lens thickness
in this kind of design is an important
parameter that affects axial and lateral
color as well as higher-order spherical
aberration.

8. A 3rd lens added to these solutions gives these two new ones.
Compared to our reference design,
the solution on the top left is
somewhat worse in performance
while the top right solution is better.

9. This is a different solution region than this one, and its has much weaker lens powers and
much better correction. Lens thickness is important for good correction, while it makes no
difference in the other solution on the right. This solution on the top left starts to be close
to the Baker Super-Schmidt design shown on the lower left here,
but that is considerably longer and has one or more aspherics.

10. As the design length is allowed to increase and the
lenses become thicker the correction keeps improving

11. It turns out that there is a variety
of three lens solutions, all the
same glass, and all spherical
surfaces. This one has much
better performance than our
reference design.

12. The best design of all,
with three lenses, is this
one here – where 2 of the
3 lenses are seen in double
pass. It is related to our
original reference design,
pioneered by Schmidt.
Despite the similarity to our reference design (positive, negative,
positive lenses, no meniscus lenses, no lens thickness sensitivity), no
“automatic design” program is going to find this new solution - using
the double-pass idea - from the reference design starting point.

13. Reference
design
New
design
On-axis
On-axis
+/- 5
degrees
+/- 5
degrees
Same scale
on plots

14. The new design has better
monochromatic correction
than the reference design
and much better chromatic
correction, with almost zero
spherochromatism.
All of these design have a curved image

15. If we put in a field flattening lens right in front of the image to get
a flat image these two designs are about the same in performance.
The accessibility of the image is different in these two designs.

16. Getting a flat image by
means of a field lens right
at the image turns out to
reduce the performance
differences of the various
designs shown here.
Probably the best flat image
design, with regard to the
aberration correction,
length, image location, and
weak lens curves is this one
shown here.
200 mm F.L., F/1.0, 10 degrees full field,
flat image, color corrected, all BK7 glass

17. 200 mm, f/1.0, 10 degree full field, flat image
On-axis
+/- 5 degrees off axis
.5876u, 4861u, .6563u
This would make a nice f/1.0 camera for
astrophotography, with an image chip
35 mm image diameter size

18. A flat image design that
is almost as good in
correction but is a little
longer and does not have
as good an image location
is this one here – basically
the Schmidt 3 lens type of
design with a field lens
added at the image. It
has considerably stronger
curves than the previous
design.

19. In summary, Schmidt’s 1934 design makes a good starting
point for finding other simple catadioptric designs. Of
course adding more lenses to the design, or aspherics, will
further improve performance beyond these examples here.