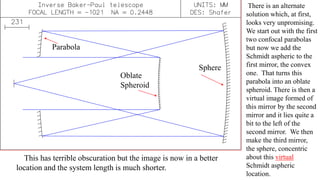
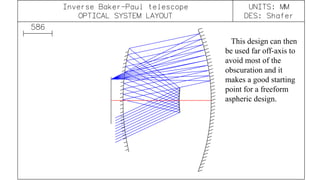
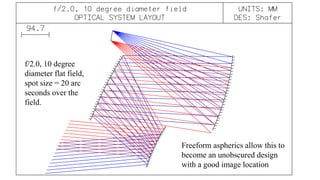
The document discusses design strategies for freeform aspheric telescopes, focusing on variations of the Baker-Paul design with multiple mirror configurations to achieve optimal aberration correction. It outlines the benefits of using reflective telescopes with freeform aspherics, including the development of configurations that improve image accessibility and field sizes. Key designs mentioned feature combinations of parabolic, hyperbolic, and spherical mirrors, ultimately showcasing how conventional aspheric designs serve as effective foundations for advanced freeform designs.

1. Design starting points for freeform aspheric telescopes
David Shafer
David Shafer Optical Design

2. 1) One approach to a good reflective telescope design with
freeform aspherics is to base it on a good design with
conventional aspherics
2) Just as is the case with camera lenses, a combination of wide
angle and fast speed is best served by the retrofocus
configuration, with a negative power first element
3) We will look at a simple three mirror design

3. The Baker-Paul design
combines the great aberration
correction of two confocal
parabolic mirrors with the
Schmidt principle and a spherical
third mirror to get an image with
good correction. The parabolic
secondary mirror becomes a
sphere when the Schmidt
aspheric has its deformation
superimposed on it.
This design is only good for small field
sizes and the image is not accessible.

4. Parabola
Hyperbola Sphere
Image
There is an inverse,
or retrofocus version
of the design, where
the first mirror is a
convex parabola and
the second mirror is a
concave parabola. It
is at the center of
curvature of the third
mirror, which is a
sphere. The Schmidt
aspheric to correct for
the sphere now adds
its deformation to the
second mirror and
turns the parabola
into a hyperbola.
This inverse or retrofocus configuration is much better suited to large
field sizes than the classical Baker-Paul design from the previous slide.

5. There is an alternate
solution which, at first,
looks very unpromising.
We start out with the first
two confocal parabolas
but now we add the
Schmidt aspheric to the
first mirror, the convex
one. That turns this
parabola into an oblate
spheroid. There is then a
virtual image formed of
this mirror by the second
mirror and it lies quite a
bit to the left of the
second mirror. We then
make the third mirror,
the sphere, concentric
about this virtual
Schmidt aspheric
location.
This has terrible obscuration but the image is now in a better
location and the system length is much shorter.
Sphere
Parabola
Oblate
Spheroid

6. This design can then
be used far off-axis to
avoid most of the
obscuration and it
makes a good starting
point for a freeform
aspheric design.

7. Three freeform aspheric
mirrors, f/2.0 and a 10 degree
diameter flat field. Spot size
is 10 arc seconds over field

8. Freeform aspherics allow this to
become an unobscured design
with a good image location
f/2.0, 10 degree
diameter flat field,
spot size = 20 arc
seconds over the
field.

9. These designs are only partially optimized and
better performance is probably possible
This shows how a design with conventional
aspherics can make for a good starting point
for a freeform aspheric design