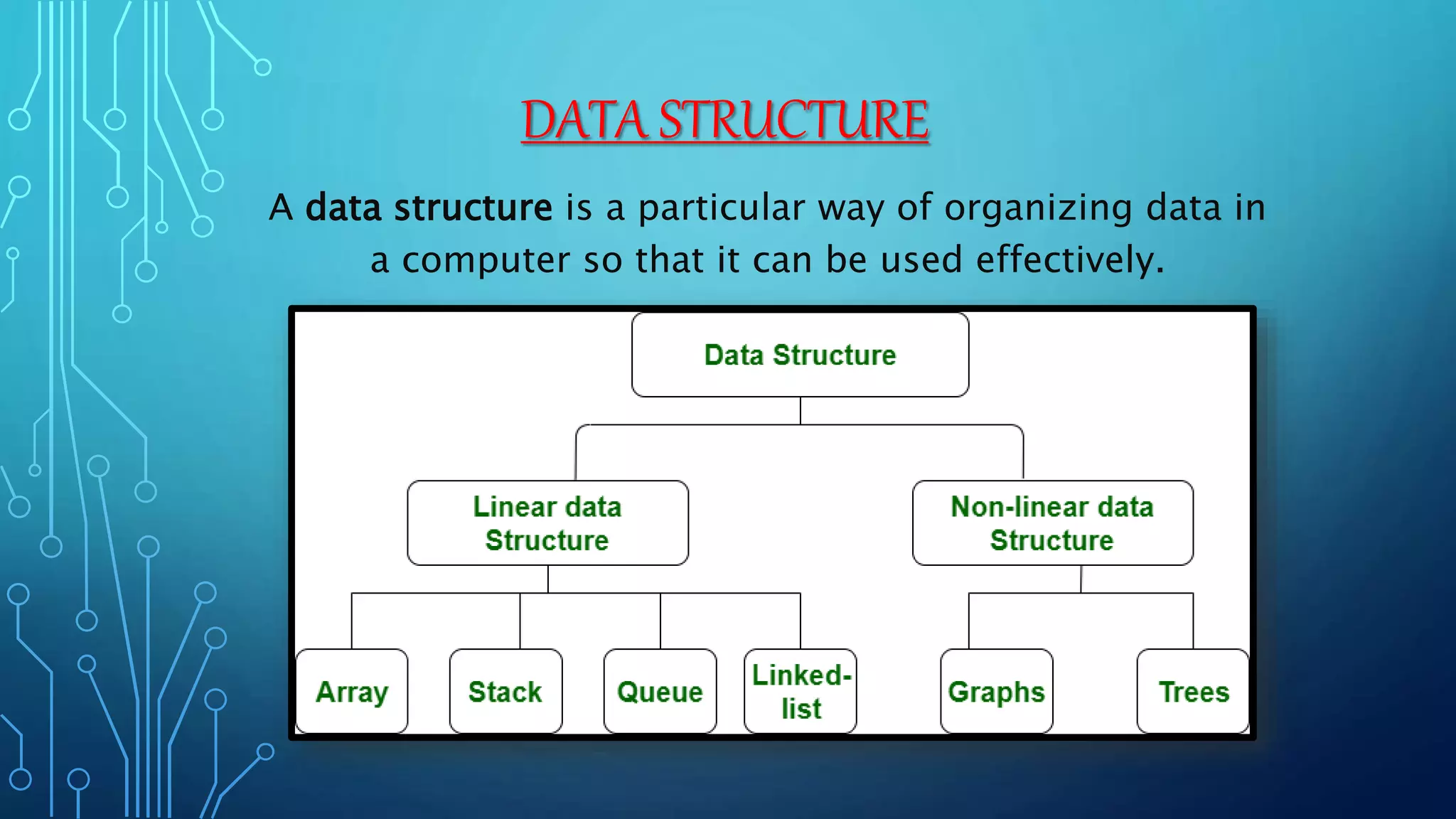
A data structure is a way to organize data in a computer. The document describes a stack data structure, which follows LIFO (Last In, First Out) order. Key aspects of a stack include push and pop operations to add and remove elements from the top of the stack, and functions to check if the stack is full or empty. Algorithms and code examples are provided for implementing push and pop operations on a stack.

1. DATA STRUCTURE
A data structure is a particular way of organizing data in
a computer so that it can be used effectively.

2. STACK
Stack is a linear data structure which follows a particular order
in which the operations are performed.
It follows the LIFO principle which stands for Last In First Out.
Here, the element which is placed (inserted or added) last, is
accessed first.
It has only one pointer TOP that points the last or top most
element of Stack.
Insertion and Deletion in stack can only be done from top only.

3. EXAMPLES OF STACK

4. OPERATIONS OF STACK
Push() − Pushing (storing) an element on the stack.
Pop() − Removing (accessing) an element from the stack.
We also need to check the status of the stack
to use it efficiently :
Overflow( ) – To check if stack is full.
Underflow( ) – To check if stack is empty.

5. ALGORITHM OF PUSH OPERATION
 Step 1 − Start
 Step 2 – Checks if the stack is full.
 Step 3 − If the stack is full, displays “Overflow”.
 Step 4 − If the stack is not full, increments TOP to point to
next empty space.
 Step 5 − Adds data element to the stack location, where top is
pointing.
 Step 6 − End

6. IMPLEMENTATION OF PUSH
10 10
30
10
30
20
10
30
20
15
10
30
20
15
40
0
1
2
3
4 4
3
2
1
0
4
3
2
1
0
4
3
2
1
0 0
1
2
33
4 4
2
1
0
top = -
1
top =
0
top =
1
top =
2
top =
3
top =
4

7. CODE FOR PUSH OPERATION
void push(int data)
{
if (top == arr.length - 1)
System.out.println("Stack is Full");
else
{
arr[++top] = data;
System.out.println("Pushed data :" + arr[top]);
}
}

8. ALGORITHM OF POP OPERATION
 Step 1 − Start
 Step 2 − Checks if the stack is empty.
 Step 3 − If the stack is empty, displays “Underflow”.
 Step 4 − If the stack is not empty, access the data element at
which TOP is pointing.
 Step 5 − Decrease the value of top by 1.
 Step 6 − End.

9. IMPLEMENTATION OF POP
10
30
20
15
40
3
4
2
1
0
top =
4
10
30
20
15
0
1
2
3
4
top =
3
10
30
20
4
3
2
1
0
top =
2
10
30
4
3
2
1
0
top =
1
10
4
3
2
1
0
top =
0
0
1
2
3
4
top = -
1

10. CODE FOR POP OPERATION
int pop()
{
if (top < 0)
{
System.out.println("Stack Underflow");
return 0;
}
else
{
System.out.println("Popped data : " + arr[top]);
return arr[top--];
}
}

11. APPLICATIONS OF STACK
Conversion of expressions.
Function calling and return procedure.
Recursion handling.
Decimal to Binary conversion.

12. TYPES OF ARITHMETIC EXPRESSIONS
Infix Expression : Operator is placed between the operands.
Example : A+B
Prefix Expression : Operator is placed before the operands.
Example : +AB
Postfix Expression : Operator is placed after the operands.
Example : AB+

13. CONVERSION FROM INFIX TO POSTFIX
1. A + (B * C) – (D / E)
= A + B C * - D E /
= A B C * + - D E /
= A B C * + D E / -

14. 2. (A / B + C) * (D / (E - F))
= (A B / + C ) * (D / E F –)
= (A B / C +) * D E F – /
= A B / C + D E F – / *
3. (M – N )/ (P* ( S – T) + K)
= (M N – ) / (P* (S T – ) + K)
= ( M N –) / ((P S T – *) + K)
= ( M N –) / (P S T – * K +)
= M N – P S T – * K + /

15. CONVERSION FROM INFIX TO PREFIX
1. A + (B * C) – (D / E)
= A + * B C - / D E
= + A * B C - / D E
= - + A * B C / D E

16. 2. (A / B + C) * (D / (E - F))
= (/ A B + C) * (D / - E F)
= (+ / A B C) * ( / D – E F)
= * + / A B C / D – E F
3. (M – N )/ (P* ( S – T) + K)
= ( - M N ) / (P * ( - S T ) + K)
= (- M N ) / ( (* P – S T) + K)
= (- M N ) / (+ * P – S T K)
= / - M N + * P – S T K