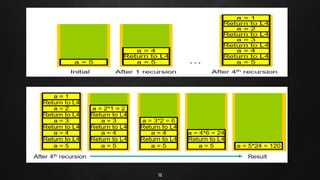
The document discusses stacks, which are linear data structures that follow the LIFO (last in, first out) principle. Elements are inserted and removed from only one end, called the top. Common stack operations are PUSH, which inserts an element at the top, and POP, which removes the top element. Stacks can be implemented using arrays or linked lists. Stacks have applications in recursion, expression evaluation, and showing operator precedence. Recursion uses stacks to call nested functions, with stack frames allowing data to come out in the correct order as frames are popped.

1. Stack

2. Stack?
✘ Non primitive linear data structure
✘ An ordered list in which insertion of new data item and deletion of an existing data item is done
from only one end, known as top of stack (TOS)
✘ The last added element will be the first to be removed from the stack, so a stack is also know as
Last In First Out (LIFO)
✘ When a new element is added to the stack, the top goes on increasing , conversely as the top
most element of the stack is removed the stack top is decrementing
✘ Two operations on a stack :
✘ PUSH: insertion of an item to the top of stack
✘ POP: Deletion of an item from the top of stack
2

3. PUSH and POP operations
3

4. Operations
✘ CREATE(S): Creates S as an empty stack
✘ PUSH (i,S): Inserts an element I on to the stack S and returns the new stack
✘ POP(S): Removes the top element of the stack and returns the new stack
✘ TOP(S): Returns the top element of the stack
✘ ISEMTS(S): Returns true if stack is empty else false.
4

5. Stack implementation
✘ Static implementation
uses arrays to create stack
✘ Dynamic implementation
Uses linked list for stack creation
5

6. Operations
✘ PUSH:
• process of adding a new element to the top of stack.
• Top is incremented by one for each PUSH operation.
• If array is full it is known as stack overflow
✘ POP:
• Process of deleting an element from the top of stack.
• After every POP operation top is decremented by one.
• If array is empty it results stack underflow condition
6

7. Function for PUSH and POP operations [using array]
void push(int stack[ ],int item)
{
/*add an item to the top of stack */
if(top>=MAXSIZE-1)
printf("OVERFLOWn");
else
{
top++;
stack[top]=item;
}
}
int pop( )
{
/*delete and return the top element from the stack*/
if(top==-1)
printf("UNDERFLOWn");
else
{
item=stack[top];
top=top-1;
}
return(item);
}
7

8. Function for PUSH and POP operations [using Linked list]
Void push( )
{
stack *newnode;
newnode=(stack*) malloc (sizeof(stack));
printf(“enter the data”);
scanf(“%d”,&newnode->data);
if (top==NULL)
newnode->next=NULL;
else
newnode->next=top;
top=newnode;
}
int pop( )
{
stack *p; int val;
p=top;
if (top==NULL)
{
printf(“stack is empty”);
return;
}
top=top->next;
val=p->data;
free(p);
Return(val);
}
8

9. Applications of stack
✘ Recursion
✘ Expression evaluation
• Infix notation:- Operator is written in between the operands
Eg: A+B
• Prefix notation:- Operator is written before the operands
(polish notation) Eg: +AB
• Postfix notation:- Operators are written after the operands
(Suffix notation/reverse polish notation) Eg: AB+
✘ Operator of precedence
• ^
• *,/ (left to right)
• +,- (left to right)
9

10. How Recursion Works
✘ By using a stack, we can have functions call other functions which can call other functions, etc.
✘ Because the stack is a first-in, last-out data structure, as the stackframes are popped, the data
comes out in the correct order.
✘ Example: Factorial of a number
n! = 1 * 2 * 3 * ... * (n-1) * n
✘ Note:
n! = n * (n-1)!
✘ remember:
...splitting up the problem into a smaller problem of the same type...
n !
n * (n-1)!
10

11. Tracing the example
public int factorial(int n)
{
if (n==0)
return(1);
else
return(n * factorial( n-1));
}
11

12. 12

13. thanks!
13