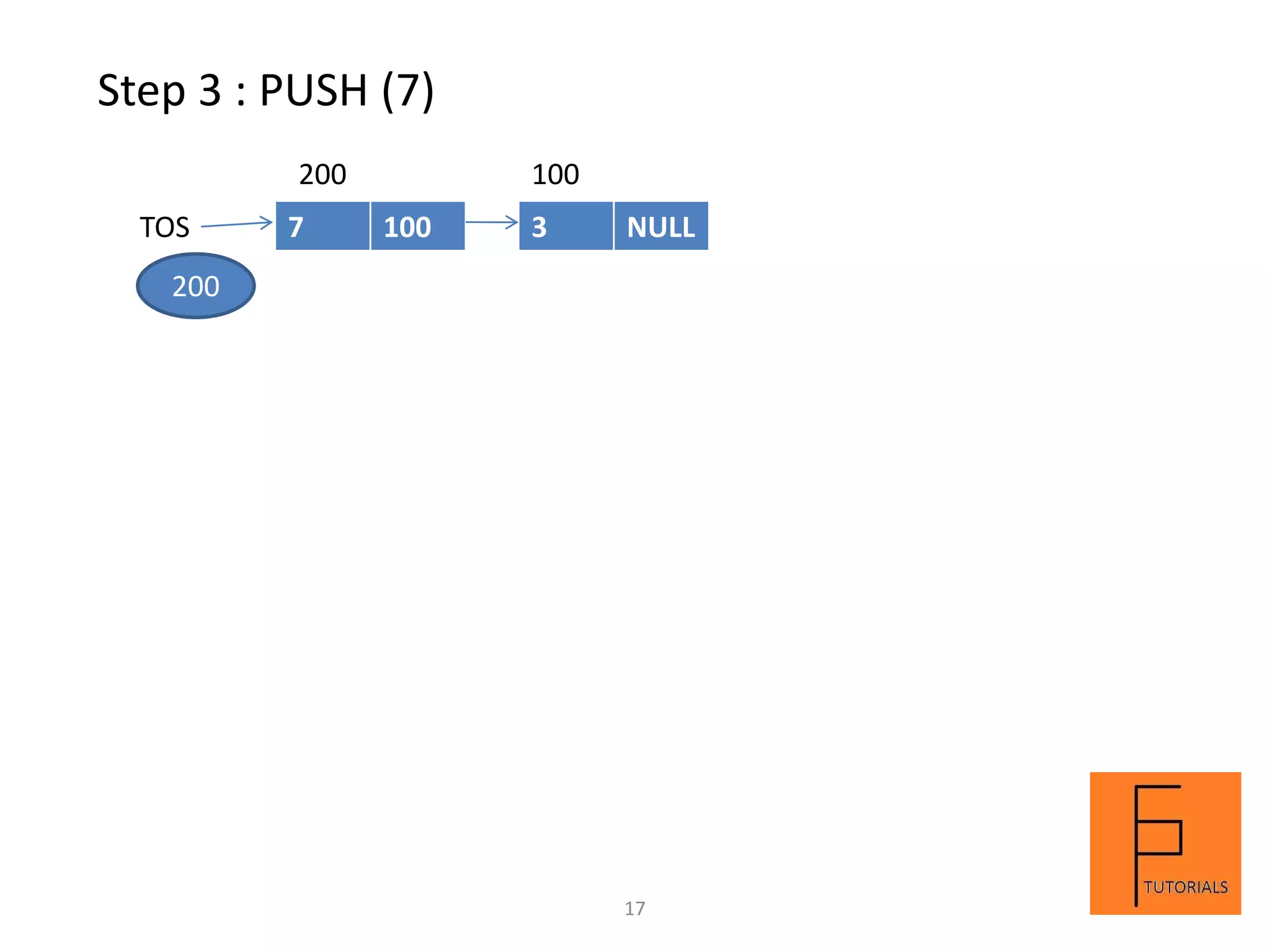
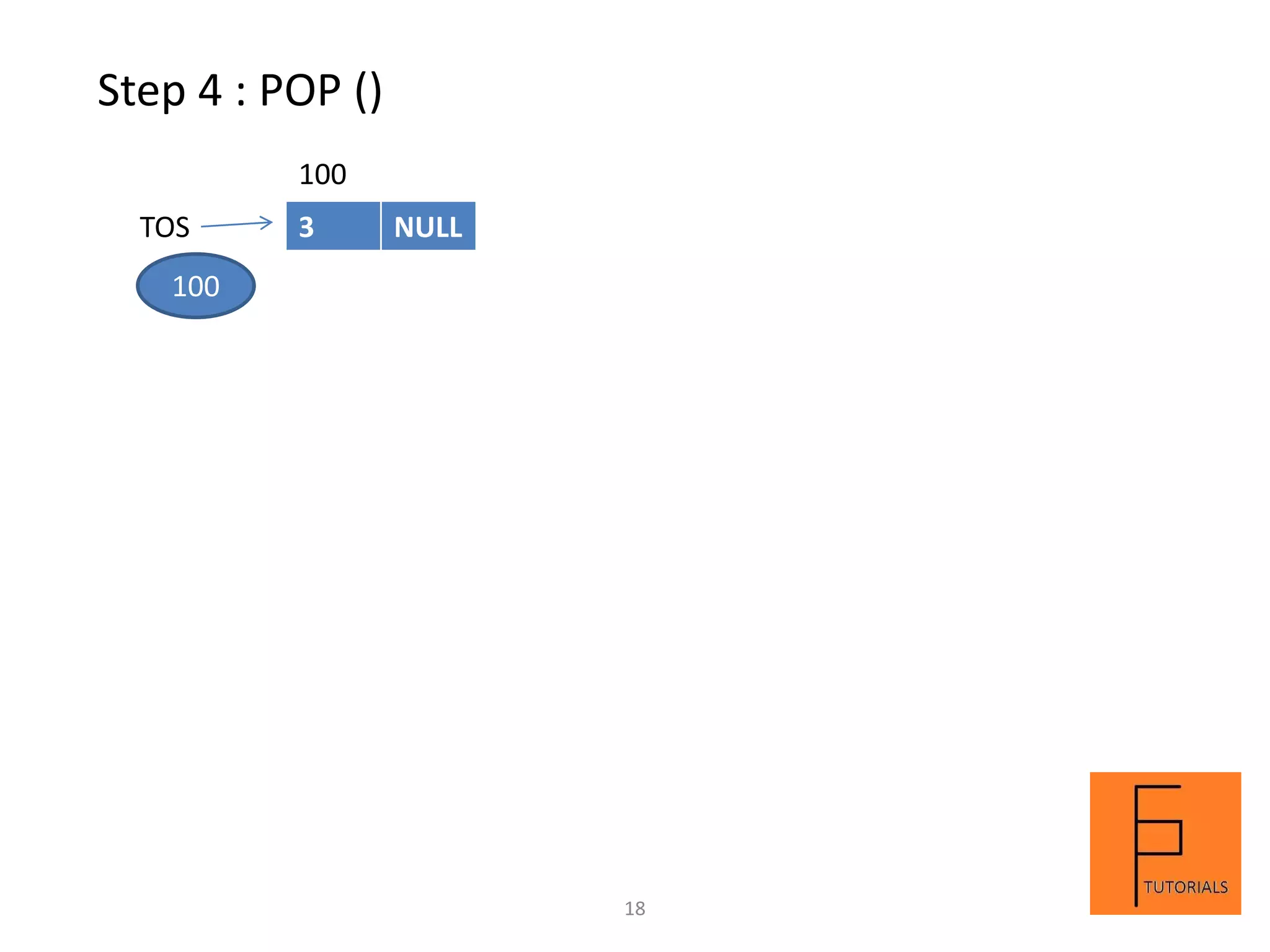
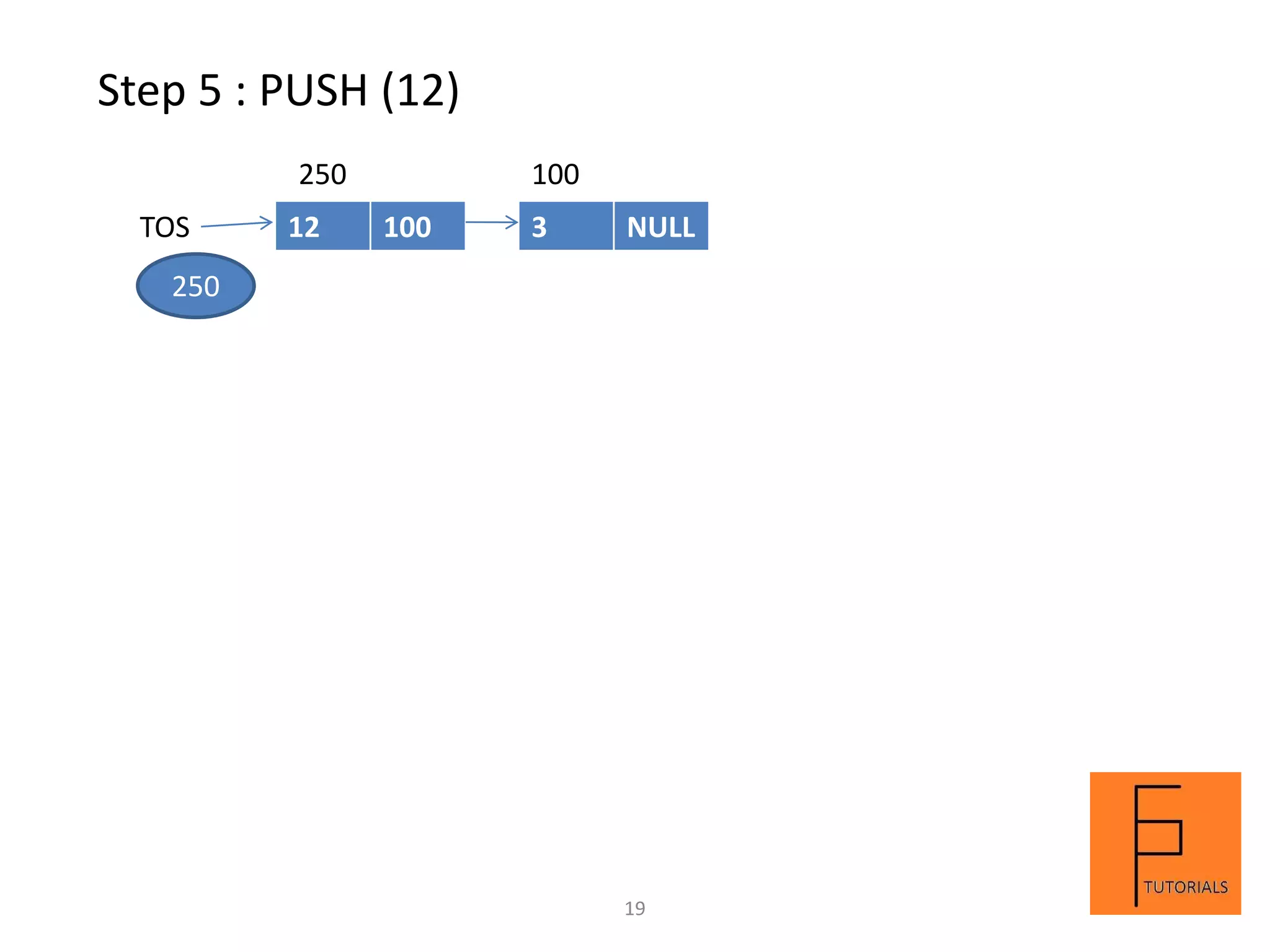
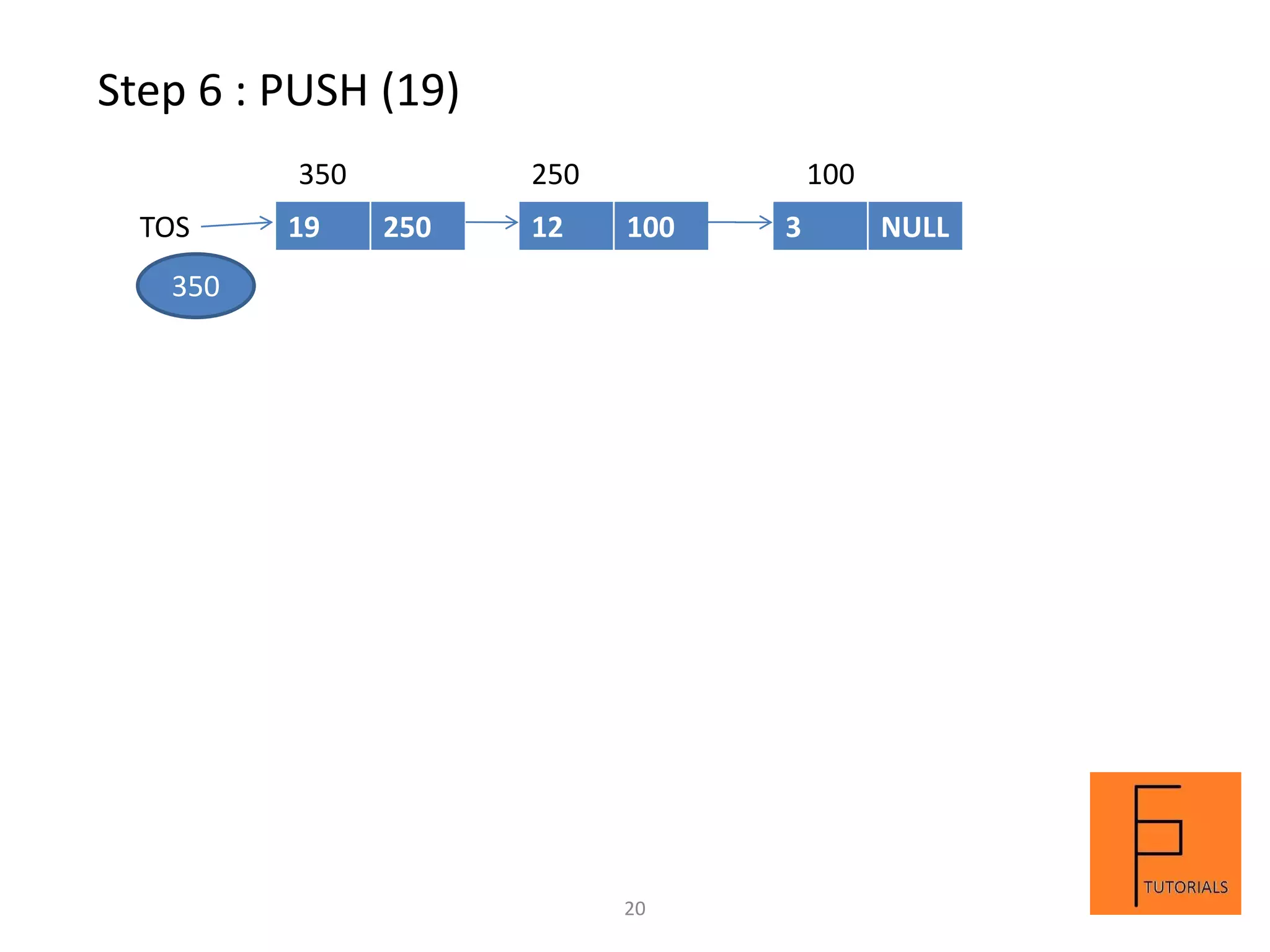
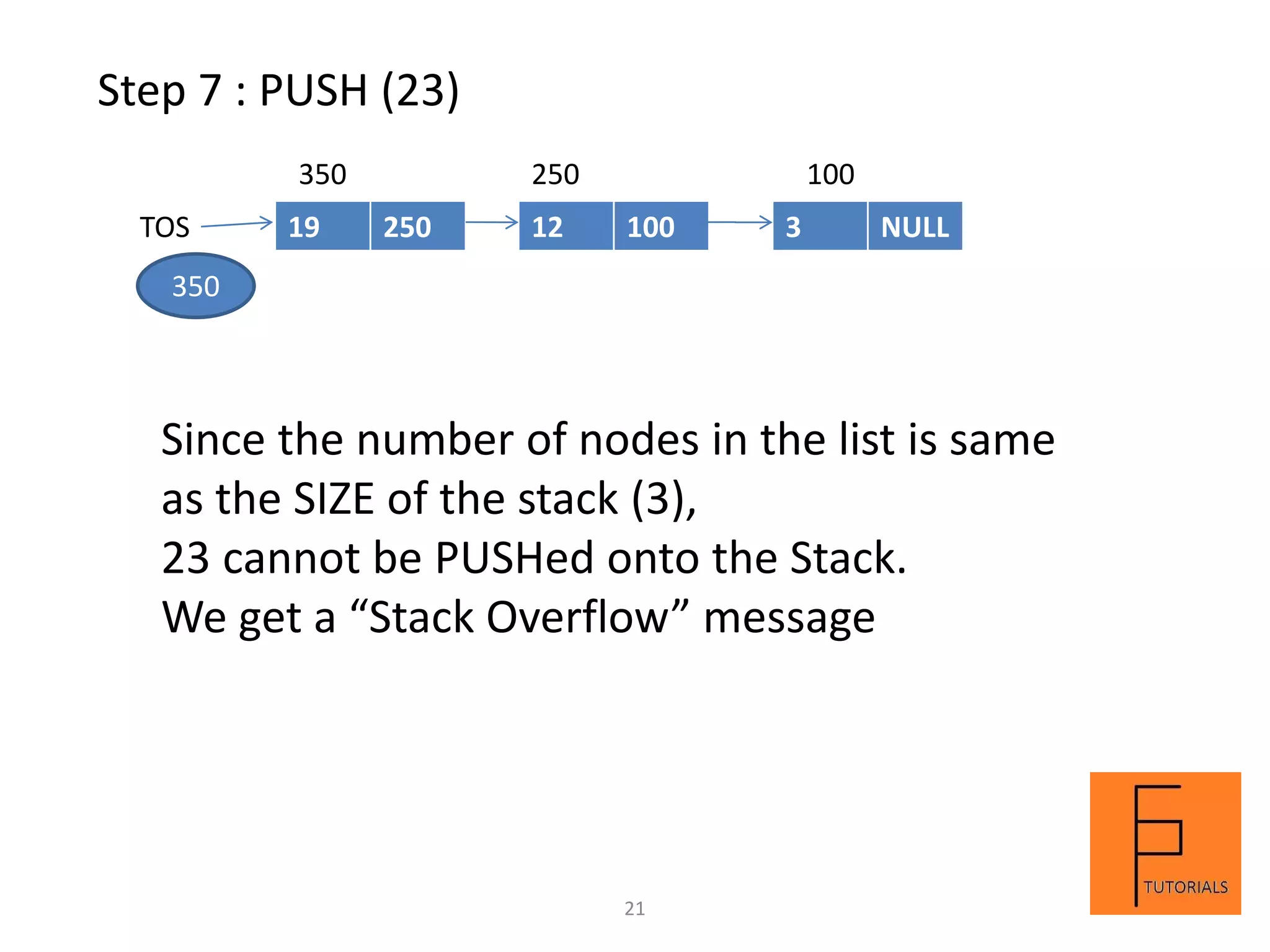
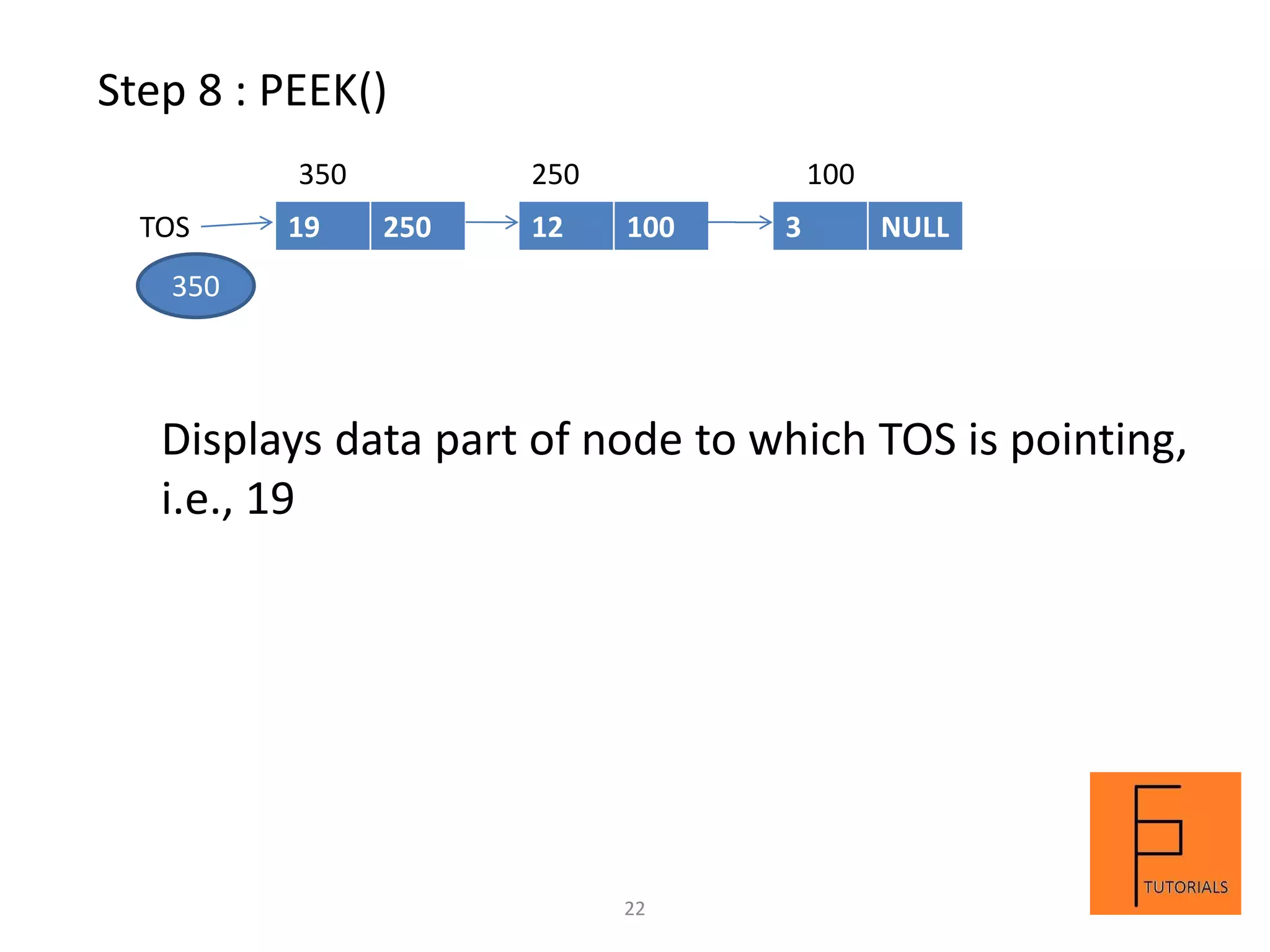
A stack is a linear data structure that follows the LIFO (last in, first out) principle. Elements can be inserted and removed from only one end called the top. Main operations on a stack are push to insert, pop to remove, and peek to view the top element. A stack can be implemented using arrays or linked lists. An example demonstrates the steps and contents of a stack at each step for a sequence of push, pop, and peek operations on an array-based stack of size 3.

1. Stack Data Structure

2. Array
Representation
of
Stack
1

3. 1. Linear Data Structure
2. Follows LIFO (Last In First Out) Algorithm
3. All operations at one end only
4. Insertion : PUSH(item)
5. Deletion : POP()
6. PEEK() : Finds topmost element of stack
7. SIZE denotes maximum number of elements possible in stack
8. TOS (Top of Stack) pointer
9. Initially TOS = -1
10. Implemented through arrays and linked lists
11. Used in recursion, infix to postfix evaluation, etc.
2

4. PUSH(item) involves following two steps:
1. Increment top by 1
2. Insert item at position denoted by value of top
POP() involves following two steps:
1. Remove element at position denoted by value of top
2. Decrement value of top by 1
Before PUSH(item), check if stack is full or not
If stack is full, print “Stack Overflow”
Before POP(), check if stack is empty or not
If stack is empty, print “Stack Underflow”
3

5. Example : Given a Stack S with SIZE = 3, show its contents at each
step for the following sequence of operations:
POP(), PUSH(3), PUSH(7), POP(), PUSH(12), PUSH(19), PUSH(23),
PEEK()
4

6. Step 1 : POP()  Since stack is empty, we have nothing to delete
We get a message : “Stack Underflow”
0 1 2
TOS = -1 Array index shown in red (0, 1, 2)
5

7. 3
Step 2 : PUSH(3)  Since TOS = -1, the stack has empty space.
We can insert 3 on the stack. First increment TOS by 1 and then
Insert element at TOS position, i.e., at index 0
0 1 2
TOS = -1  0 Array index shown in red (0, 1, 2)
6

8. 3 7
Step 3 : PUSH(7)  Since TOS = 0, the stack has empty space.
We can insert 7 on the stack. First increment TOS by 1 and then
Insert element at TOS position, i.e., at index 1
0 1 2
TOS = 0  1 Array index shown in red (0, 1, 2)
7

9. 3
Step 4 : POP()  Since TOS != -1, the stack has elements.
First remove element at TOS position, i.e., remove element
at position 1 and then decrement TOS by 1
0 1 2
TOS = 1  0 Array index shown in red (0, 1, 2)
8

10. 3 12
Step 5 : PUSH(12)  Since TOS = 0, the stack has empty space.
We can insert 12 on the stack. First increment TOS by 1 and then
Insert element at TOS position, i.e., at index 1
0 1 2
TOS = 0  1 Array index shown in red (0, 1, 2)
9

11. 3 12 19
Step 6 : PUSH(19)  Since TOS = 1, the stack has empty space.
We can insert 19 on the stack. First increment TOS by 1 and then
Insert element at TOS position, i.e., at index 2
0 1 2
TOS = 1  2 Array index shown in red (0, 1, 2)
10

12. 3 12 19
Step 7 : PUSH(23)  Since TOS = 2 (SIZE – 1)the stack has
no empty space. We cannot insert 23 on the stack. Instead,
We display the statement “Stack Overflow”
0 1 2
TOS = 2 Array index shown in red (0, 1, 2)
11

13. 3 12 19
Step 8 : PEEK()  This displays the topmost element of Stack
whose position is denoted by value of TOS, i.e., element at
position 2 (19). Nothing is deleted from stack.
0 1 2
TOS = 2 Array index shown in red (0, 1, 2)
12

14. Linked
Representation
of
Stack
13

15. Example : Given a Stack S with SIZE = 3, show its contents at each
step for the following sequence of operations:
POP(), PUSH(3), PUSH(7), POP(), PUSH(12), PUSH(19), PUSH(23),
PEEK()
14

16. Step 1 : POP ()
TOS = NULL Since TOS = NULL, the
Stack is empty and there is
nothing to delete. We get
“Stack Underflow” as the
outcome.
15

17. Step 2 : PUSH (3)
TOS 3 NULL
100
100
16

18. Step 3 : PUSH (7)
TOS 3 NULL
200
200
7 100
100
17

19. Step 4 : POP ()
TOS 3 NULL
100
100
18

20. Step 5 : PUSH (12)
TOS 3 NULL
250
250
12 100
100
19

21. Step 6 : PUSH (19)
TOS 12 100
350
350
19 250
250
3 NULL
100
20

22. Step 7 : PUSH (23)
TOS 12 100
350
350
19 250
250
3 NULL
100
Since the number of nodes in the list is same
as the SIZE of the stack (3),
23 cannot be PUSHed onto the Stack.
We get a “Stack Overflow” message
21

23. Step 8 : PEEK()
TOS 12 100
350
350
19 250
250
3 NULL
100
Displays data part of node to which TOS is pointing,
i.e., 19
22

24. 1. What is Stack? Explain various operations performed using stack
with examples. [6] [MAKAUT 2015 BCA]
Solution : Points 1 and 2 in Slide 2 (stack definition)
Entire slide 3 and point 6 of slide 3 (operations)
Slides 4 to 12 (example of stack operations)
23

25. 2. What is Stack? Explain with an example. [5]
[MAKAUT 2016 BCA]
Solution : Points 1 and 2 in Slide 2 (stack definition)
Slides 4 to 12 (example of stack)
24

26. 3. Write C function to implement push and pop operations [4 + 4]
[MAKAUT 2016 BCA]
Solution :
25

27. 4. Write algorithm to implement push and pop operations in Stack
[7] [MAKAUT 2012 BCA]
26

28. 27

29. 5. What are overflow and underflow conditions?
[3] [MAKAUT 2012 BCA]
Solution : Overflow : Trying to insert more elements than the
capacity of the data structure. Example : Stack Overflow
Underflow : Trying to remove an element from a data structure
which is already empty. Example : Stack Underflow
28

30. 6. Write short note on linked representation of Stack
[3] [MAKAUT 2011 BCA]
Solution : Refer to the example on linked representation of stack
show earlier.
Every element is stored in a node of a linked list. The PUSH
Operation is same as inserting an element at beginning of linked
List. The pop operation is same as deleting an element from the
Beginning of a linked list.
29