数学ハンズオン 2017/12/10

1. すうがくはじめの一歩
PyLadies Tokyo Meetup #27
2017/12/10(Sun) かたよせ りな（せりーな）

2. 自己紹介
 工学修士（航空宇宙学）
 私は飛行機が好きで、航空宇宙学科に行きました。
（最近はドローンを改造して遊んでいます。）
 大学院で物理とか数学を学びました。
 数学の初歩をPythonを用いて計算します。
（当時はPythonなかった）
 主に私は物理計算で使う数学が得意です。
かたよせ りな
片寄 里菜 ＠se_lina08

3. 今日やること
数学とは
Pythonでできる数学
入力（計算）してみよう！
Pythonの数学ライブラリ
やってみよう
グラフを描いてみよう！

4. 数学は何かを考えよう
量
構造
空間
変化
数学は、
これらのパターンを探して、新しい予想を定式化し、
適切に選ばれた公理と定義から厳格な推論により真理を確立することです。
抽象概念と論理的推論を用いることにより、数えること、計算、測定、そして物体の
形と動作の組織的研究から、数学ができています。
𝑓 𝑥 = 𝑎0 +
𝑛=1
∞
𝑎 𝑛 cos
𝑛𝜋𝑥
𝐿
+ 𝑏 𝑛 sin
𝑛𝜋𝑥
𝐿

5. 数学は何かを考えよう
量
自然数
整数
有理数
実数
複素数
𝑥 =
−𝑏 ± 𝑏2 − 4𝑎𝑐
2𝑎
組合せ数学
数論
群論
グラフ理論
順序論
幾何
三角法
微分幾何
位相幾何
フラクタル幾何
測度論
微分積分学
ベクトル解析
微分方程式
力学系
カオス理論
複素解析
構造 空間 変化

6. 数学は何かを考えよう
 っと、いうことで
𝑥 =
−𝑏 ± 𝑏2 − 4𝑎𝑐
2𝑎

7. 数字を入力して計算しよう
 Jupyter Notebookを起動して、
Pythonが入力できるようにしてください。
𝑎2
+ 𝑏2
= 𝑐2

8. 数字を入力して計算しよう
5 + 7 [Shift + Enter] →加算（足し算）
19 - 7 [Shift + Enter] →減算（引き算）
3 * 4 [Shift + Enter] →乗算（かけ算）
365 / 30 [Shift + Enter] →除算（割る）
365 // 30 [Shift + Enter] →整除除算（割って実数のみ）
365 % 30 [Shift + Enter] →剰余（あまり）
𝑎2
+ 𝑏2
= 𝑐2

9. 数字を入力して計算しよう
結果はどうでしたでしょうか？
𝑎2
+ 𝑏2
= 𝑐2

10. 記号に数字を入力してみよう
x = 5 + 7 [Enter]
x [Alt + Enter]
y = x * 30 [Enter]
z = 365 % 30 [Enter]
y + z [Alt + Enter]
さて、何が出るでしょうか？
𝑎2
+ 𝑏2
= 𝑐2

11. 数字を入力して計算しよう
結果はどうでしたでしょうか？
𝑎2
+ 𝑏2
= 𝑐2

12. 考えてやってみよう
イーロン・マスクさんが
時速60km/hの電気自動車に乗っています。
310kmの距離を走るとすると、
何時間かかりますか？
（イーロンさんはストイックなので途中休憩なし、
細かな分minuteは気にしないとする。）
Pythonのプログラムを書いて計算してください。
𝑎2
+ 𝑏2
= 𝑐2

13. 答え
v = 60 （時速）
d = 310 （距離）
t = d //v （かかる時間）
t = d / v （かかる時間）
どちらでもOK
𝑎2
+ 𝑏2
= 𝑐2

14. Input関数を使って計算させよう
input関数を使って、
毎回、代入をしなくても
計算させることができます。
a = input()
kyori = input(‘ここに聞きたいことを入れる: ')
𝑎2
+ 𝑏2
= 𝑐2

15. 考えてやってみよう
イーロン・タスクさんが
時速不明の電気自動車に乗っています。
走りたい距離も不明です。
でも、簡単に求めるプログラムを作りたいそうです。
何時間かかりますかを求めるプログラムを作ってください。
（イーロンさんはストイックなので途中休憩なし、
細かな分minuteは気にしないとする。）
Pythonのプログラムを書いて計算してください。
𝑎2
+ 𝑏2
= 𝑐2

16. 答え
kyori = input('行先までの距離kmを入力してください: ')
jisoku = input('あなたの走りたい時速を入れてください: ')
k = int(kyori)
j = int(jisoku)
jikan = k / j
print(jikan,'時間かかりますね。')
𝑎2
+ 𝑏2
= 𝑐2

17. どうでしたか？
？？？
𝑎2
+ 𝑏2
= 𝑐2

18. 数学ライブラリ
 SymPy
 NumPy
 SciPy
 があります。
𝑓 𝑥 = 𝑎2
+ 𝑏2
+ 𝑐2

19. 数学ライブラリ
 SymPy は、
 プログラミング言語Pythonで記号計算を行うためののライブラリです。
𝑓 𝑥 = 𝑎2
+ 𝑏2
+ 𝑐2

20. 数学ライブラリ
 NumPyは、
 プログラミング言語Pythonにおいて数値計算を効率的に行うための拡張モジュー
ルである。
 効率的な数値計算を行うための型付きの多次元配列（例えばベクトルや行列など
を表現できる）のサポートをPythonに加えるとともに、それらを操作するための
大規模な高水準の数学関数ライブラリを提供します。
𝑓 𝑥 = 𝑎2
+ 𝑏2
+ 𝑐2

21. 数学ライブラリ
 SciPy は、
 配列オブジェクトとその他の基本的な機能を備えた NumPy を基礎にしています。
SciPy は統計、最適化、積分、線形代数、フーリエ変換、信号・イメージ処理、遺
伝的アルゴリズム、ODE (常微分方程式) ソルバ、特殊関数、その他のモジュール
を提供します。
𝑓 𝑥 = 𝑎2
+ 𝑏2
+ 𝑐2

22. 数学ライブラリ
 今回はSymPyとNumPyをつかいます。

23. 数学ライブラリ Sympy
 SymPy で代数と式を計算する。
 SymPyは記号を使って数式を表現し、評価することを可能にします。
 それを使うには、Symbolクラスのオブジェクトを作ります。
from sympy import Symbol
x = Symbol('x’)
from sympy import Symbol
x = Symbol('x')
x + x + 1

24. 数学ライブラリ Sympy
from sympy import Symbol
x = Symbol('x')
y = Symbol('y')
s = x*y +x*y
s
2*x*y
𝑠 = 𝑥𝑦 + 𝑥𝑦

25. 数学ライブラリ Sympy
 SymPy を使って因数分解します。
from sympy import Symbol
x = Symbol('x')
y = Symbol('y')
from sympy import factor, expand
expr = x**2 - y**2
factor(expr)
expr = 𝑥2
+ 𝑦2

26. 数学ライブラリ Sympy
 先ほどの式を元の展開した式に戻します。
factors = factor(expr)
expand(factors)

27. 数学ライブラリ Sympy (init_printing)
 数式をきれいに人が書くようにきれいに表示します。
from sympy import *
init_printing()
# この後に以下のコードを入れてみましょう
x = Symbol('x')
y = Symbol('y')
expr = (x + y)**3
expr

28. 数学ライブラリ Sympy 値の代入
 値に代入してみましょう。
 今までは数式の計算でした。
 実際に数を入れてみましょう。
 Subs()メソッドを使って記号に数値を入れます。
x = Symbol('x')
y = Symbol('y')
x*x + x*y + x*y + y*y

29. 数学ライブラリ Sympy
expr = x*x + x*y + x*y + y*y
res = expr.subs({x:3,y:5})
ここでｘとｙに任意の数を入れます。
res

30. 数学ライブラリ Sympy 2次方程式
 SymPy を使って2次方程式を解きましょう。
𝑥2
+ 5𝑥 + 4 = 0
この式のxを求めましょう。
𝑥 =
−𝑏 ± 𝑏2 − 4𝑎𝑐
2𝑎

31. 数学ライブラリ Sympy 2次方程式
 SymPy を使って2次方程式を解きます。
#solve関数をインポートします。
from sympy import Symbol, solve
x = Symbol('x')
#式を定義します。
expr = x**2 + 5*x +4
#solve関数で計算します
solve(expr, dict=True)
#↓答えが出る

32. 数学ライブラリ Sympy 連立方程式
 SymPy を使って連立方程式を解きましょう。
2𝑥 + 3𝑦 = 6
3𝑥 + 2𝑦 = 12

33. 数学ライブラリ Sympy 連立方程式
 SymPy を使って連立方程式を解きます。
x = Symbol('x')
y = Symbol('y')
expr1 = 2*x + 3*y - 6
expr2 = 3*x + 2*y - 12

34. 数学ライブラリ Sympy 連立方程式
# 2つの式をexpr1とexpr2で定義しました。
# 解を求めるには2つの式をタプルにしてsolve()関数を呼び出します。
solve((expr1,expr2), dict = True)
#値は出ましたか？

35. 数学ライブラリ Sympy グラフ
 SymPy を使ってグラフをプロットします。
from sympy.plotting import plot
from sympy import Symbol
x = Symbol('x')
plot(2*x+3)
𝑓 𝑥 = 2𝑥 + 3

36. 数学ライブラリ Sympy グラフ②
 SymPy を使ってグラフをプロットします。
from sympy.plotting import plot
from sympy import symbol
x = Symbol('x')
plot(2*x*x+3)
𝑓 𝑥 = 2𝑥2
+ 3

37. 数学ライブラリ Sympy グラフ③
 SymPy を使ってグラフをプロットします。
from sympy.plotting import plot
from sympy import symbol
x = Symbol('x')
plot(2*x*x*x+3)
𝑓 𝑥 = 2𝑥3
+ 3

38. 数学ライブラリ Numpy 三角関数
 NumPy を使って三角関数を計算します。
三角関数の（）の中にはラジアンを入れます。
ラジアンとは。
→Python標準ライブラリのmathモジュールで三角関数が使えます。
それはどうするのか
import math
math.sin(math.pi/2)
Pythonでの()の中ではラジアンを使います。
ラジアンはわかる方はいますか？
(2𝜋=360°)
2pi=360°
pi = 180°
1/2 pi = 90

39. やってみよう
import math
math.sin(math.pi/2)
これで、90度の時のsinが求められます。
三角関数とは？

40. 数学ライブラリ Numpy 三角関数
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(0, 6, 0.1)
# 計算式
y = np.sin(x)
plt.plot(x, y)
plt.show()

41. 数学ライブラリ Numpy グラフ
import numpy as np
import matplotlib.pyplot as plt
#0から6まで0.1ずつ
x = np.arange(0, 6, 0.1)
# 計算式
y = np.sin(x)
plt.plot(x, y)
plt.show() #ここで見せます。

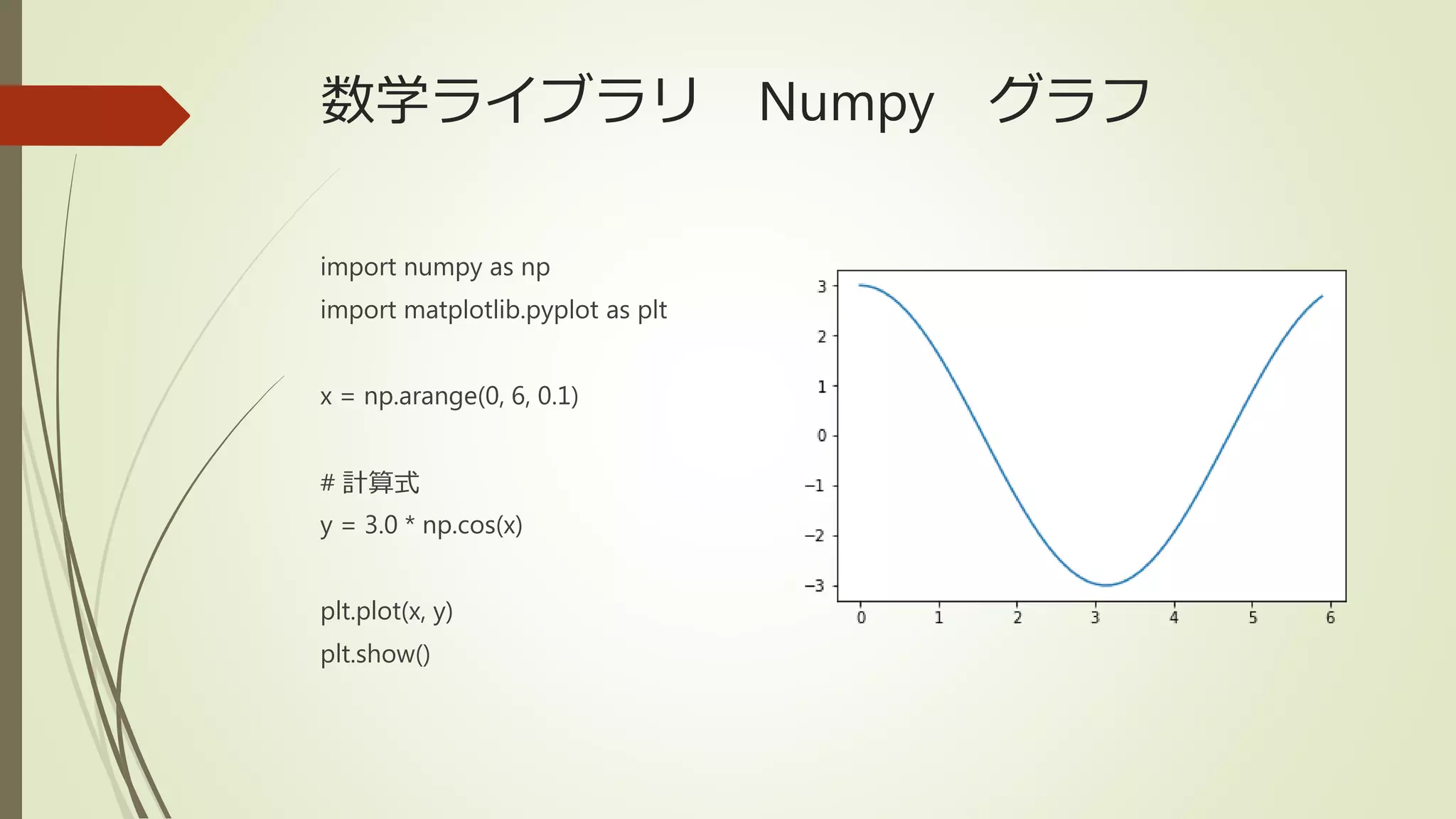
42. 数学ライブラリ Numpy グラフ
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(0, 6, 0.1)
# 計算式
y = 3.0 * np.cos(x)
plt.plot(x, y)
plt.show()

43. Pythonで使う演算子
 http://www.tohoho-web.com/python/operators.html