учебно методическое пособие по дисциплине прикладная голография

1
ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
Федеральное государственное образовательное бюджетное учреждение
высшего профессионального образования
ПОВОЛЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ТЕЛЕКОММУНИКАЦИЙ И ИНФОРМАТИКИ
Кафедра физики
УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ ПО ДИСЦИПЛИНЕ
Прикладная голография
Автор: Петропавловский В. М., канд. ф.-м.н., доцент
Самара, 2014
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

2
УДК 535.43 + 681.069
Петропавловский В.М. Прикладная голография
Самара: ФБГОБУ ПГУТИ, 2014. – 123с.
Рассмотрены современные методы голографии. Излагаются способы записи и
воспроизведения голограмм различных типов, их преимущества и недостатки.
Для студентов, магистров и аспирантов, обучающихся по специальности
200700 ФОТОНИКА И ОПТОИНФОРМАТИКА.
Федеральное государственное образовательное бюджетное учреждение
высшего профессионального образования
Поволжский государственный университет телекоммуникаций и информатики

3
Введение.
Слово голография образовано от греческих слов «целый» и «описание». Его
можно перевести как «полное описание (объекта)». Это означает, что на голограмме
регистрируется (и может быть воспроизведена) информация как об амплитуде волны
так и об ее фазе. Для записи голограммы необходимо использовать источник
когерентного света – лазер. Излучение разделяется на две волны: предметную,
отраженную от объекта, и опорную волну с плоским или сферическим фронтом.
Интерференционная картина от этих волн регистрируется фотопластинкой. При
восстановлении опорная волна, проходя сквозь голограмму, дифрагирует на ней,
создавая изображение предмета.
1. РАСПРОСТРАНЕНИЕ И ДИФРАКЦИЯ СВЕТА
При получении голограммы на пути света, испущенного источником, приходится
помещать различные препятствия. Ими могут быть светоделители, зеркала,
микрообъективы, линзы, диафрагмы, а также объект голографирования и
фотопластинка. Каждый из этих элементов по-своему воздействует на световой
пучок. Так как их размеры конечны, то они оказывают влияние лишь на часть пучка,
вызывая потери оптической информации.
Дифракция на препятствиях не является единственной причиной изменения
световой волны. Даже в процессе обычного распространения света в пространстве
происходит изменение поля его комплексных амплитуд. Примером этого может
служить рассматриваемое далее свойство тонких линз выполнять преобразование
Фурье распределения амплитуд в световой волне. Мы увидим, что для
осуществления преобразования Фурье необходимо не только, чтобы свет прошел
через линзу, но и чтобы он прошел после этого путь, равный фокусному расстоянию
линзы. Процесс получения голограмм и их изображающие свойства можно
объяснить с помощью теории дифракции.
В этой главе мы рассмотрим распространение и дифракцию плоских волн сначала
на препятствиях простой, а затем более сложной формы. Будет установлена связь
между распределением комплексных амплитуд света в плоскости объекта и в
плоскости, удаленной от него на некоторое расстояние в направлении распро-
странения волн. Анализ проводится в области пространственных частот. Хотя этот
подход отличается от принятого во многих учебниках по оптике, мы увидим, что он
естественно вытекает из исходных представлений. При обычном методе анализа, т. е.
в координатной области, связь между амплитудами светового поля в двух плоскостях
устанавливается с помощью интеграла Френеля — Кирхгофа. Покажем
эквивалентность того и другого подхода к решению задач о дифракции.
1.1. Волновое уравнение и его решение для монохроматической
волны
Уравнения Максвелла устанавливают связь между производными по координатам
и времени от векторных величин, характеризующих электромагнитное поле. Для
волн, распространяющихсяв свободном пространстве, из уравнений Максвелла
можно получить волновое уравнение

4
⃗( , , , ) =
⃗( , , , )
(1.1).
Будем рассматривать только вектор электрического поля ⃗ черезс обозначена
скорость света;t — время, V2
— оператор Лапласа, а х, у, z — декартовы координаты.
Из условий интерференции вытекает, что в уравнении (1.1) векторные величины
можно заменить скалярными, т. е.
( , , , ) =
( , , , )
(1.2)
где ( , , , ) — одна из двух взаимно перпендикулярных компонент
электрического поля, колеблющихся в плоскости, перпендикулярной направлению
распространения волны.
Еслирассматривать монохроматический свет с частотойf, то решением
уравнения (1.2) будет синусоидальное скалярное поле
( , , , ) = ( , , ) [ + ( , , )], (1.3)
или, по аналогии с (1.6),
( , , , ) = [ ( , , ) ( )], (1.4)
где а (х, у, z) — комплексная амплитуда, или фазор, определяющий как
амплитуду, так и фазу волны,
( , , , ) = [ ( , , ) ( )], (1.5)
Для удобства математических выкладок символ Re [ ] отбрасывают и в
(1.2) величинуvзаменяют комплексной величиной v. Делая эту замену,
следует помнить, что в действительности физическая величина
электрического поля вещественна.
1 . 2 . Решение волнового уравнения для случая - плоской волны
Волна называется плоской, если ее амплитуда и фаза в любой момент
времени постоянны по всей плоскости, уравнение которой имеет вид
⃗ ∙ ⃗ = (1.6)
где, ⃗— радус-вектор точки в пространстве, a ⃗ — единичный вектор,
нормальный к рассматриваемой плоскости (Рис. 5.1
Положим, что удовлетворяющая волновому уравнению комплексная
величина электрическогополяv имеет вид
( , , , ) = − ⃗ ∙ ⃗ ( ), (1.7)
где a1 — постоянная амплитуда волны, а k — константа, физический смысл
и величину которой мы определим далее. Если произведение ⃗ ∙ ⃗
постоянно по всей плоскости, то, согласно (1.7), фазаволны в любой момент
времени тоже постоянна по всей этой плоскости. Для конкретных значений

5
r=r1 и t=t1 фаза волны будет равна − ⃗ ⃗ = ( , ) В более
поздний момент времен t2 >t1 то же значение фаза будет иметь на большем
расстоянии ⃗ ∙ ⃗ > ⃗ ∙ ⃗, в то время как на прежнем расстоянии ⃗ ∙ ⃗
она возрастет. Таким образом, плоскости постоянных фаз перемещаются в
пространстве, и решение волнового уравнения, имеющее вид (1.7),
представляет собой плоские волны. Направление вектора ⃗, нормального к
плоскости постоянной фазы, является направлением распространения
волны. Если , , — направляющие косинусы вектора ⃗ (Рис.
1.1), то равенство (1.7) можно записать в виде
( , , . ) = [− ( + + ] ( ), (1.8)
Где x, yи z — компоненты вектора⃗в декартовых координатах. Подстановка
решения вида (1.8) в волновое уравнение (1.2) дает
− ( + + ) = − = − (1.9)
где — длина волны света. Поскольку направляющие косинусы
удовлетворяют соотношению
+ + = (1.10)
то v является решением волнового уравнения при условии
= (1.11)
РИС.1.1.Плоская волна в прямоугольной системекоординат х,у,z.

6
Величинаk называется волновым числом. Соотношение (1.8) можно
записать в виде
( , , , ) = − +
+ ( )
= [− ( +
+ )] ( )
= ( , , ) ( ).
(1.12)
В этой главе мы будем рассматривать только монохроматический свет.
Тогда множитель ( ) можно опустить и для описания
электрического поля пользоваться только комплексной амплитудой a(x, y,
z). Величины ξ, η, , определяемые равенствами
= (1.13a)
= (1.13б)
= (1.13в)
Называются пространственными частотами. Они обратны про-
странственным периодам волны, измеренным соответственно по осям x, yи z.
Пространственная частота измеряется в обратных миллиметрах (1/мм).
Следует отметить, что пространственные частоты могут принимать как
положительные, так и отрицательные значения. Если направление распространения
волны составляет с соответствующей осью угол меньше 90°, то пространственная
частота положительна, если больше 90°, то она отрицательна. Если ориентировать
систему координат так, чтобы, например, осьz совпала с направлением
распространения волны (ξ = η = 0, = 1/ λ), то легко видеть, что в (1.12) фаза волны в
фиксированный момент времени уменьшается с увеличением расстояния от
источника. (Читатель должен обратить внимание на то, что в некоторых книгах
введено обратное правило выбора знака, конечно, в равной мере законное.Важно
только в дальнейшем последовательно придерживаться того или иного выбора.)
Пространственные частоты ξ, η и часто выражаются через углы θ1=90° — α,
θ2=90° — β и θ3=90° — γ; тогда они записываются следующим образом:
= (1.14а)
= (1.14б)

7
= (1.14в)
На Рис.1.2 изображена плоская волна, распространяющаяся в плоскостиyz. Мы видим,
что 0 θ2 и θ3 представляют собой углы, образованные направлением распространения
волны с плоскостямиxz иху соответственно. Величины ξ, η, не являются незави-
симыми, их связь можно получить из (1.10). При подстановке (1.13а) — (1.13в) в
(1.10) получаем
+ + = , (1.15)
или
= ± ( − − ) /
, (1.16)
где знак определяется направлением распространения волны в соответствии с
принятым ранее правилом знаков [см. обсуждение после формул (1.13)]. Теперь мы
можем записать комплексную амплитуду а (х, у, z) плоской волны [см. (1.12)] в
следующем виде:
( , , ) = − + + ,
= [− ( + )] − ( − − ) /
== ( , . ) [− ( ( − − ) /
]
(1.17)

8
Выражение (1.17) очень полезно при рассмотрении задач о дифракции волн. Из него
видно, что величина комплексной амплитуды плоской волны на произвольном
расстоянииz равна произведению комплексной амплитуды волны приz = 0 и
экспоненты, убывающей при увеличении z.
1.3. Дифракция на периодических структурах
Рассмотрим теперь, что происходит со световой волной, встречающей на
своем пути какое-либо препятствие. Чтобы получить точное решение
задачи о дифракции волн, необходимо решить волновое уравнение (1.2)
при граничных условиях, соответствующих выбранному препятствию. К
сожалению, такой прямой подход годится только для предметов очень
простой формы. Даже в этом случае решение получается очень сложным и
громоздким. Поэтому обычно представляющие практический интерес
задачи дифракции решают приближенными методами. В большинстве
задач оптики точность этих решений оказывается вполне удовлет-
ворительной. Причины этого выяснятся в дальнейшем.
РИС.1.2.Плоская волна, распространяющаяся в плоскости yz

9
РИС.1.3.Прохождение плоской волны с амплитудой a1 через транспарант,
амплитудное пропускание которого меняется как cosy.Непосредственно за
транспарантом возникают три плоские волны.
Сначала рассмотрим плоскую волну с амплитудойa1 распро-
страняющуюся в направлении положительной полуосиz и падающую на
прозрачный объект (транспарант), находящийся в плоскостиz= 0. Пусть
транспарант, показанный на Рис.1.3, имеет амплитудное пропускание
( , ) = + , (1.18)
являющееся периодической функцией от y с пространственной частотой η,
at0 иt1 — вещественные постоянные. [Предполагается, чтоt (х, у) —
вещественная функция, т. е. транспарант не вносит фазового сдвига.]
Непосредственно за транспарантом амплитуда волны а (х, у, 0) равна
произведению амплитуды падающего света a1 и пропускания t:
( , , ) = ( , ) = +
= + ( ) + (− ). (1.19)
Заметим, что второй член в (1.19) и решение (1.12) волнового уравнения
одинаково зависят отху, если в (1.12) ξ = 0, аη>0. Поэтому можно считать,
что второй член описывает плоскую волну, которая распространяется
параллельно плоскостиyz (т.е. перпендикулярно оси х, а=90°), и
направление ее распространения образует отрицательный угол θ2 с осьюz
(Рис.1.3), поскольку, согласно (1.14,б), sinθ2 = λη. Аналогично третий член
(1.19) описывает плоскую волну, которая также распространяется
параллельно плоскостиyz, образуя при этом с осьюz положительный угол
θ2 (Рис.1.3). Первый член в (1.19) не зависит отху [в (1.12) этому
соответствует ξ = η=0] и описывает плоскую волну, распространяющуюся в
направлении осиz.Итак, при падении плоской волны,

10
распространяющейся вдоль осиz, на транспарант с синусоидальным в
направлении у амплитудным пропусканием за транспарантом возникают
три плоские волны: первая, с амплитудой a1,t0, распространяется вдоль
осиz (недифрагированная волна);вторая, с амплитудойa1,t1/2,
распространяется в плоскости yz вниз от осиz, образуя с осьюz угол | θ2 | =
arcsin(λη) (дифрагированная волна —1-го порядка); третья, с амплитудой
a1,t1/2, распространяется в плоскостиyz вверх от осиz, образуя с осьюzтакой
же угол | θ2 | (дифрагированная волна + 1-го порядка).
Мы рассмотрели один из важных случаев дифракции. Транспаранты с
периодическим распределением амплитудного пропускания называются
дифракционными решетками. В большинстве случаев голограмму можно
рассматривать как транспарант с периодически промодулированным
амплитудным пропусканием. Поэтому можно ожидать, что голограмма
будет воздействовать на падающий свет примерно так же, как обычная
дифракционная решетка.
Продолжим рассмотрение дифракции плоской волны на помещенном в
плоскостиz = 0 транспаранте с синусоидальным амплитудным
пропусканиемt(х, у) и определим комплексную амплитуду света в
плоскостиху приz = d. Непосредственно за транспарантом возникают три
плоские волны, комплексные амплитуды которых в плоскостиz = 0
описываются выражением (1.19). С помощью (1.17) можно определить
комплексные амплитуды этих волн при z = d. Результирующая
комплексная амплитуда приz = dявляется их суммой и имеет вид
( , , ) = − + ( ) − ( − )
+ (− ) − ( − ) .
(1.20)
[Первый член (1.20) получается из (1.17) при ξ=η=0, а второй и третий при
ξ=0.] Поскольку зависящие отz показатели экспонент, взятые в (1.20)
приz=d, являются мнимыми, каждый из трех членов в (1.20) описывает
распространяющуюся волну. Однако для некоторых длин волн λ
показатели экспонент становятся вещественными. При λη→1 угол
дифракции θ2 = arcsinληувеличивается, приближаясь к 90°. Для больших
значений длин волн, удовлетворяющих неравенству
> , (1.21)
Выражение( − ) становится мнимым. Если взять отрицательный знак
перед корнем, то экспоненциальный множитель принимает вид
− (− )( − ) /
= (− ), (1.22)
гдеb имеет положительное и вещественное значение. В этом случае второй
и третий члены в (1.20), соответствующие первому порядку дифракции,
будут описывать поверхностные волны — волны, распространяющиеся
вдоль поверхности транспаранта и затухающие по экспоненте с
увеличением расстояния от нее. (Выбор знака, таким образом,

11
соответствует физически реализуемому явлению.) Если неравенство (1.21)
записать в виде λ>1/η, то видно, что поверхностные волны возникают при
падении на решетку света, длина волны которого больше периода решетки
1/η. Их амплитуда является функцией расстоянияd от решетки и приd>>λ
стремится к нулю [см. (1.22)]. Условие затухания волн, выраженное через
пространственные частоты, может быть записано в виде η>1/λ. Таким
образом, в распределении поля на расстоянии d>λ от транспаранта не
содержится никакой информации о его пространственных частотах,
превышающих1/λ.
1.4. Постановка общей задачи о дифракции
Рассмотрим теперь дифракцию на предметах более сложной формы.
Пусть амплитудное пропускание предмета является периодической
функцией оту, которая может и не быть простой косинусоидальной
функцией вида (1.18). Например, транспарант может состоять из
чередующихся непрозрачных и прозрачных полос. Тогда амплитудное
пропускание можно записать в виде ряда Фурье. В более общем случае,
когда амплитудное пропускание является комплексной периодической
функцией двух переменных х иy, его можно представить в виде суммы
членов, каждый из которых имеет вид ехр (—i2 ξx)ехр(—i2 ξy)[см. (1.5)].
Умножая каждый член на соответствующий коэффициент, получаем для
комплексного амплитудного пропусканияt(x, y), периодически (но в
остальном произвольно) зависящего от х и y, следующий ряд Фурье:
( , ) = (− ) (− ). (1.22)
Суммирование проводится по всем членам, необходимым для описания
двумерной функции. Пусть транспарант с пропусканием t (x, у) помещен
в плоскостьz= 0, и на него падает плоская волна с амплитудой
распространяющаяся в направлении оси z. За транспарантом возникает
набор плоских волн, распространяющихся в различных направлениях. С
помощью (1.17) и (1.23) для суммарной амплитуды а2 (х, у, d) этих волн в
плоскостиz =d имеем
( , , ) = [ (− ) (− )
× (− − − ) =
= [ (− − − )
× (− ) (− ).
(1.24)

12
Еслиt (х, у) — непериодическая функция, то ряд Фурье заменяется
интегралом Фурье [5.2], а коэффициенты tlk — произведением Т (ξ,η)dξdη,
где ( , ) ⊃ ( , ). Тогда (1.24) принимает вид
( , , ) = ( , ) − − − )
× (− ) (− ) ,
(1.25)
где интегрирование производится по всем ξ и η, удовлетворяющим
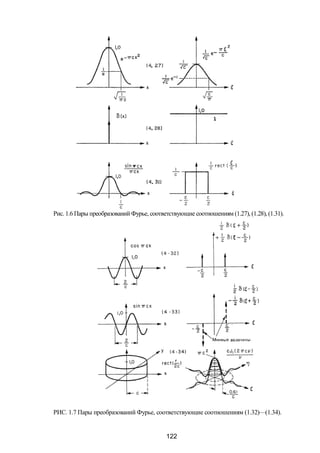
неравенству (ξ2+η2)≤1/λ2. Анализ преобразования Фурье(1.25) дает
следующий результат:
Если плоская волна с амплитудой а1 распространяющаяся в
направлении оси z, падает на помещенный в плоскости z= 0
транспарант с амплитудным пропусканиемt(х, у), то спектр ( , ).
комплексной амплитуды волны в плоскости z=d имеет вид
( , )| = ( , ) − − − ) . (1.26)
Если лучи считать параксиальными, т. е. г] 1А, то квадратный корень в
(1.26) можно записать в виде
( − − ) ≈ − − , (1.27)
а (1.26) заменить приближенным выражением
( , )| ≈ ( , ) [ ( + )]. (1.28)
Фазовый множитель (− / ) ,постоянный в плоскостиху, в (1.28)
опущен. (Отбрасывание фазового множителя, постоянного по всей
плоскости, эквивалентно сдвигу начала отсчета времени.) Поскольку в
(1.28) фаза = ( + ) = является параболической функцией
координат ξ, η, то приближение (1.28) называют параболическим. Мы часто
будем пользоваться этим приближением, поэтому следует установить
границы его применимости. Определим при η= 0 верхний предел значений
пространственной частоты для которых параболическое приближение
справедливо. Заметим, что в (1.27) следующий (опущенный) член
разложения равен / .Для определения искомого предела мы должны
задать допустимую ошибку в фазе. Известное правило Рэлея (см. [1.13])
гласит, что любая хорошая оптическая система не должна искажать фазу
волнового фронта больше чем на / . Принимая этот критерий, запишем
<
(1.29)
откуда
<
(1.30)

13
Приведем числовой пример. Пустьd = 10 см,X = 0,5 мкм. Из условия (1.30)
получим, что верхнее предельное значение пространственной частоты, для
которого справедливо параболическое приближение, равно ξ = 113 мм-1.
1. 5. Связь с интегралом Френеля—Кирхгофа
В координатной области решение задачи о дифракции формулируется с
помощью интеграла Френеля — Кирхгофа следующим образом: если
плоская волна с амплитудой а1, распространяющаяся в положительном
направлении оси z, падает на предмет с амплитудным пропусканием t(x1,
y1), помещенный в перпендикулярной осиz плоскостиz=0, то комплексная
амплитуда света а2 (х2г у2,d) в плоскостиz =d имеет вид
( , , )
= ( , ) ×
×
− [ + ( − ) + ( − ) ] /
[ + ( − ) + ( − ) ] / .
(1.31)
Вывод интеграла Френеля—Кирхгофа приведен, например, в книге [5.3].
Через θ обозначен угол между положительным направлением осиZ и
отрезком прямой, соединяющим точки( , , ) и( , , ),acosθ называют
коэффициентом наклона. Геометрическая схема, используемая при
выводе интеграла Френеля — Кирхгофа, приведена на Рис. 1.4. Следует
отметить, что небольшие изменения граничных условий приводят к
изменению коэффициента наклона. Коэффициент наклона, введенный
Зоммерфельдом, совпадает с входящим в (1.31), тогда как у Кирхгофа он
равен (1+cosθ)/2. Если угол θ не слишком велик, то различие между этими
коэффициентами мало.
РИС.1.4.Схема, поясняющая обозначения в интеграле Френеля-Кирхгофа.
Заметим, что выражение (1.31) имеет форму интеграла свертки, т. е. для
нахождения комплексной амплитуды света приz = dнеобходимо
подвергнуть операции свертки амплитудное пропускание t (х, у) со второй
функцией под знаком интеграла в (1.31). Это соответствует умножению в

14
(1.26) фурье-образа пропусканияt(х, у) на функцию пространственной
частоты. Можно показать, что запись комплексной амплитуды света через
интеграл Френеля — Кирхгофа в виде (1.31) и запись в частотной области в
виде (1.26) полностью эквивалентны. Поскольку доказательство этого
довольно громоздко, оно приведено в приложении I. Здесь мы покажем эту
эквивалентность только для параболического приближения (1.28) и для
приближенной формы выражения (1.31), которую сейчас получим. Пусть в
(1.31) (х2 — х1)<<dи (у2 —у1)<<d; тогда cosθ≈1. Разложим в ряд аргумент
экспоненты в (1.31):
[ + ( − ) + ( − ) ] /
≈ +
( − )
+
( − )
(1.32)
и заменим знаменатель в (1.31) его приближенным значением, равнымd. С
такими приближениями выражение для комплексной амплитуды света
приz = d имеет вид
( , , ) = ( , ) ×
× − ( − ) + ( − )
(1.33)
Здесь опущен постоянный по всей плоскостиz = d множитель. Отсюда
видно, что функция t (x1, y1) подвергается операции свертки с функцией
( , ) = − ( + ) .
(1.34)
Эквивалентность рассматриваемых приближений в координатной и
частотной областях будет доказана, если мы сможем показать, что
амплитуда а2 {х2, у2, d) в виде (1.33) и спектр А2 (ξ, η) в виде (1.28) связаны
преобразованием Фурье. Поскольку, как уже отмечалось, t(x, у)⊃T(ξ, η), то
из теоремы свертки (1.11) следует, чтоh(x, у)⊃H(ξ, η), где
( , ) = [ ( + )]. (1.35)
является третьим сомножителем в (1.28). Запишем функцию H(ξ, η), в виде
произведения
( , ) = ( ) ( ) (1.36)
и вычислим ее обратныйфурье-образ. Мы можем сделать это в два
действия. Сначала проведем преобразование относительно ξ, считая η
постоянной, а затем сделаем преобразование относительно η, считая
постоянной х. С помощью соотношения (1.27) получим искомый обратный
фурье-образ функции Н (ξ, η):

15
=
(− ) (− )
= − ( + ) = ( , ).
что и требовалось доказать.
Комплексную амплитуду дальнего поля (дифракционную картину
Фраунгофера) можно приближенно представить как фурье-образ
амплитудного пропускания транспаранта. Используя (1.33), можно
проверить это утверждение для случая освещения плоской волной
транспаранта с амплитудным пропусканием t(x1, y1). Представим
экспоненциальный множитель в (1.33) в виде
− ( + ) −
( + )
×× + .
.
Первый сомножитель не зависит от переменных интегрирования x1 и y1 и
может быть вынесен из-под знака интеграла. Если дальним полем считать
область, расстояниеd до которой больше размеров транспаранта, так что
выполняется условие дальнего поля
+
≪ ,
(1.37)
то второй сомножитель приблизительно равен единице. Производя замену
= и = (1.38)
получаем
( , , ) = − ( + ) ×
× ( , ) [ ( + )] =
= − ( + ) ( , ),
(1.39)
где фазовый множитель сферической волны медленно меняется в
плоскостих2у2 и где мы использовали определение фурье-образа (1.1).
Если умножить выражение (1.39) на комплексно-сопряженное с ним, то
получим, что интенсивность в дальнем поле равна квадрату абсолютной
величины фурье-образа функции t.
Для дальнего поля, т. е. при выполнении условия (1.37), ξ и η определяются
выражениями (1.38), аналогичными выражениям(1.14а) и (1.146), согласно
которым ξ=(sinθ1)/λ и η=(sinθ2)/λ. На Рис. 5.5 схематически изображена
плоская волна, падающая на прозрачный объект (транспарант),

16
помещенный в плоскости Размеры транспаранта малы по сравнению с
расстоянием от плоскости х1у1 до плоскости наблюдениях2у2. Световые
лучи, дифрагировавшие на транспаранте, можно представить в виде
пучков света с одинаковым поперечным сечением, распространяющихся в
направлениях, соответствующих пространственным частотам
транспаранта. Один из таких пучков, проходящий под угломθ2 к оси z,
изображен на Рис.5.5. Его сечение плоскостью x2y2 представляет собой
сравнительно небольшую область с центром в точке y2.Если расстояние d
достаточно велико, так что y2гораздо больше размеров сечения пучка, то
= ≈ или =
РИС.1.6Схема пояснения дальнего поля
Аналогично
≈
Интеграл Френеля-Кирхгофа и эквивалентная ему запись в частотной
области не дают точного решения задачи с граничными условиями.
Физический смысл основного допущения этой теории можно
проиллюстрировать на примере плоской волны, падающей на
непрозрачный экран с отверстием, причем амплитудное пропускание в
пределах отверстия равно единице, а за его пределами — нулю. На самом
деле это справедливо лишь для участков, удаленных от края отверстия, так
как вблизи них на световое поле оказывают влияние оптические свойства
материала экрана. Именно этим влиянием пренебрегают в теории Френеля
— Кирхгофа, поэтому она справедлива для задач о дифракции на
предметах, размеры которых велики по сравнению с длиной волны света.
Это условие выполняется во многих задачах оптики.
Однако в некоторых случаях, особенно в голографии, интегралом
Френеля — Кирхгофа или его эквивалентом в частотной области
пользуются и тогда, когда отдельные детали предмета ненамного
превышают длину волны света. В этом случае теория дает по крайней мере
качественное решение задачи. Примером этого может служить
рассмотрение синусоидальной амплитудной решетки, описываемой
выражением (1.18). При этом мы не считали, что пространственный период

17
решетки 1/η значительно больше λ. Тем не менее наша теория
предсказывает в соответствии с действительностью существование трех
плоских волн, суммарная амплитуда которых сразу за транспарантом
изменяется с частотой, равной частоте решетки η. Точное решение задачи с
граничными условиями также дает три волны, и в этом смысле
приближенная теория справедлива. Приближенное решение может
отличаться от точного лишь значениями амплитуд этих волн, а что
касается большинства задач голографии, то для них нет необходимости
знать точное значение амплитуды волны.
Вопросы для самоконтроля:
1. Уравнение плоской волны. Уравнение сферической волны.
2. Интеграл Френеля – Кирхгофа.
3. Условие максимумов для дифракционной решетки.

18
2. ОПТИЧЕСКИЕ СИСТЕМЫ СО СФЕРИЧЕСКИМИ
ЛИНЗАМИ
Сферические линзы могут формировать не только распределение
амплитуд света, соответствующее изображению, но и создавать картину,
являющуюся фурье-образом этого распределения. Следовательно, с
помощью простой линзы можно добиться того, чтобы распределение
освещенности, создаваемое предметной волной в плоскости голограммы,
представляло собой фурье-образ некоторого исходного изображения.
Записанный на голограмме фурье-образ обладает свойствами, имеющими
важное значение для оптического опознавания образок и оптической
памяти.
Линзу как устройство, способное формировать изображение, используют
в голографии для получения голограммы сфокусированногоизображеиия. В
этом случае линза фокусирует изображение голографируемого предмета на
плоскость голограммы, где оно интерферирует с опорной волной. Такой
метод получения голограмм позволяет значительно уменьшить требования
к степени когерентности излучения, используемого при восстановлении.
Полученная надлежащим образом голограмма сфокусированного
изображения может быть освещена при восстановлении обычной лампой
накаливания с матовым стеклом
Эти причины, а также возможность использования линз для
формирования световых пучков нужной конфигурации делают
необходимым анализ некоторых свойств оптических систем, содержащих
тонкие линзы. В этой главе мы выведем условия, при которых линза
формирует либо а) фурье-образ входного распределения комплексных
амплитуд, либо б) изображение этого распределения.
Хотя условие формирования изображения можно было бы вывести на
основе принципов геометрической оптики (пренебрегая дифракцией), этого
нельзя сделать для условия формирования фурье-образа, которое должно
быть получено с помощью теории дифракции. Поэтому мы рассмотрим то и
другое условие с точки зрения физической оптики, принимая во внимание
конечность длины волны света и связанные с этим дифракционные
эффекты.
2.1. Сферическая линза
Простая сферическая линза состоит из прозрачного материала,
ограниченного двумя сферическими поверхностями. В материале линзы
свет распространяется в n раз медленнее (n — показатель преломления
материала линзы), чем в вакууме. Такая линза изображена на РИС. 2.1,
причем ее центр и центры ограничивающихее сферических поверхностей
лежат на осиz декартовой системы координат. Пусть на линзу падает
плоская волна с длиной волны λ, распространяющаяся вдоль осиz слева
направо. Определим комплексную амплитуду света аr в плоскости,

19
нормальной к осиzи касательной к поверхности правой половины линзы.
Выразим агчерез аl, где аl — комплексная амплитуда света в аналогичной
плоскости, касательной к левой поверхности линзы. Если считать, что в
линзе отсутствует поглощение, то задача сведется к нахождению фазового
множителя, на который надо затем умножить аl. Для его получения мы
должны вычислить изменение фазы волны при ее прохождении между
плоскостямиz = z2 иz = z3 (РИС. 2.1). Допустим далее, что величинаd = z3 —
z2 столь мала, что плоскостиz2 иz3 почти совпадают, т. е. будем считать
линзу тонкой. При таком условии луч света, падающий в точку с
координатами (x0, у0) на левой поверхности линзы, выходит в точке
практически с теми же координатами (х0,у0) на правой поверхности.
Следовательно, фазовую модуляцию падающей волны, осуществляемую
тонкой линзой, можно рассматривать как модуляцию транспарантом,
который имеет пропускание ( , ) = [ ∆ ( , )] и расположен в
плоскостиху, нормальной оси линзы и проходящей через ее центр.
РИС. 2.1.Сферическая линза.
Правая поверхность линзы описывается уравнением сферы радиусомr1:
+ = .
Здесьzr — координата произвольной точки на правой поверхности линзы.
Решая уравнение относительноzr, получаем
= ( − − ) /
(2.1)
Аналогично левая поверхность описывается уравнением сферы радиусом
г2:
+ + ( − ) =
где — координата произвольной точки на левой поверхности линзы, a
— координата центра кривизны левой поверхности; они связаны
следующим соотношением:
= − ( − − ) /
(2.2)

20
Толщина материала линзы, через которую проходит световая волна,
зависит от х и y, а именно:
( , ) = − = ( − − ) − + ( − − ) / (2.3)
После прохождения линзы в месте с толщиной Т волна будет испытывать
фазовый сдвиг, равный
∆ = −
′
= − ,
(2.4)
где ′ — длина волны в материале линзы;п — показатель преломления
линзы (относительно воздуха); = ′ — длина волны в воздухе. (Знак
«минус» соответствует уменьшению фазы при увеличении расстояния от
источника.)
Путь в воздухе, который проходит световая волна между плоскостямиz =
z2 иz = z3, равенd — Т. Ему соответствует фазовый сдвиг
∆ = − ( − )
(2.5)
гдеd = z3 — z2. Полный фазовый сдвиг при прохождении волны отz2 доz3
выражается суммой
∆ = ∆ + ∆ = − ( − ) − .
(2.6)
Мы можем опустить последний член в (2.6), так как он не зависит от х и у
и представляет собой фазовый сдвиг, постоянный по всей плоскостиху
приz = z3. Тогда (2.6) принимает вид
∆ = − ( − ) ( , ).
(2.7)
Подставляя теперь в (2.7) выражение (2.3) для Т (х,y), получаем
∆ = − ( − )[( − − ) + ( − − ) / (2.8)
Здесь, как и прежде, мы опустили не зависящую от х и у часть фазового
сдвига + ( )z1. Чтобы получить искомое соотношение междуаг и аl,
заменим квадратные скобки в (2.8) их разложениями, в которых
сохраним члены только первого порядка; тогда
( − − ) ≈ ( −
+
)
(2.9)
( − − ) ≈ ( −
+
)
(2.10)

21
Такое параксиальное приближение справедливо, если (х2 +у2)<< или (х2
+ у2)<< . Опять опуская фазовые сдвиги, не зависящие от х и у, получаем
вместо (2.8)
∆ = + ( − )
+
+
+
= ( − ) + ( + ).
(2.11)
Произведение ( − ) + связано с фокусным расстоянием f тонкой
линзы известной формулой (см., например, [6.1])
= ( − ) + ,
(2.12)
и фазовый сдвиг теперь можно записать в виде
∆ = ( + ). (2.13)
Если рассматриваемая линза достаточно тонкая и изменяет только фазу
падающего на нее света, то на основе (2.13) мы можем получить
соответствующее линзе комплексное пропускание t (х, у). Его двумерное
распределение в плоскостиху, проходящей черезцентр линзы,
описывается выражением
( , ) = ( ∆ ) = ( + ) .
(2.14)
Комплексная амплитуда светааr справа от линзы непосредственно
вблизи нее равна произведению пропускания t (х, у) и комплексной
амплитуды аl света, падающего на линзу слева:
= ( + ) .
(2.15)
Если сравнить зависящее от х и у распределение фазовой модуляции ∆ ,
описываемое выражением (2.13), с фазовыми распределениями,
описываемыми выражениями (3.3), (3.4) или (3.26), то видно, что оно в
приближении первого порядка соответствует сферической волне,
схо-дящейся в точку на осиz, расположенную на расстоянии f от линзы (f>
0).
2.2. Простейшая оптическая система
Рассмотрим теперь оптические системы, состоящие из тонких линз и
свободных промежутков между ними. Самые разнообразные оптические
системы, например лупа, микроскоп, телескоп, действительно не содержат
иных элементов, кроме линз и свободных промежутков. (Читателю,
знакомому с материалом гл. 5, не покажется странным включение

22
свободного пространства в число элементов оптической системы.)
Рассмотрим сначала очень простую оптическую систему, которая, однако,
способна выполнять операцию преобразования Фурье. Это поможет нам
понять принцип работы более сложных систем, которые будут рассмотрены
в следующем параграфе. Интересующая нас система изображена на РИС.
2.2. Она состоит из сферической линзы с фокусным расстоянием f,
помещенной в плоскостиz = 0, и расположенного вплотную к ней
транспаранта с комплексным амплитудным пропусканием t(x1, у1). На
линзу падает распространяющаяся в положительном направлении осиz
плоская волна. Ее комплексная амплитуда слева непосредственно вблизи
линзы равнааl. Определим комплексную амплитуду в плоскостиz=f.
Согласно (2.15), комплексная амплитуда ar(x1, у1) справа от линзы
непосредственно вблизи нее описывается формулой
( , ) = ( + ) .
(2.16)
Затем волна проходит через транспарант, и ее комплексная амплитуда
сразу за транспарантом выражается произведением
( , ) = ( , ) ( , )
= ( , ) ( + ) .
(2.17)
[Если линза тонкая, то совершенно неважно, справа или слева от нее
находится транспарант.В любом случае произведение (2.17) будет
состоять из одних и тех же сомножителей.] Справа от транспаранта волна
распространяется в свободном пространстве. Комплексную амплитуду
волны в плоскостиz = f можно выразить через ее амплитуду в плоскостиz =
0 либо в координатной области, либо в области пространственных частот
РИС. 2.2.Простейшая оптическая система, выполняющая преобразование
Фурье.
Выберем координатную область и воспользуемся соотношением (1.33);
тогда комплексная амплитуда а2 (х2, у2) в плоскостиz = fзапишется в
виде

23
( , ) = ( , )
× − [( − ) + ( − ) ]
= ( , ) ( + ) ×
× − [( − ) + ( − ) ] .
(2.18)
Здесь интегрирование производится по всей поверхности линзы.
Упрощая выражение (2.18), получаем
( , ) = ( , )
× + − − .
(2.19)
Поскольку интеграл берется в плоскости , можно вынестииз-под знака
интеграла множитель, зависящий только от х2 и у2;
это дает
( , ) = [− ( + ) ×
× ( , ) ( + )
(2.20)
Если положить
= (2.21)
и
= (2.22)
и подставить эти выражения в (2.20), то комплексную амплитуду приz =f
можно представить в виде
( , ) = [− ( + ) ×
× ( , ) [ ( + )]
(2.23)
В интеграле (2.23) легко узнать двумерное преобразование Фурье при
условии, что функция ( , ) равна нулю за пределами поверхности
линзы. Последнее условие позволяет расширить пределы интегрирования

24
до +∞ и -∞, что и требуется для преобразования Фурье. Множитель,
стоящий перед интегралом, пропорционален пропусканию, которое может
быть приписано тонкой рассеивающей линзе с фокусным расстоянием —f,
помещенной в плоскостиz =f. Экспонента представляет собой фазовый
множитель сферической волны. В данном случае он описывает распре-
деление фазы в плоскости х2у2, которую пересекает сферическая волна,
расходящаяся от расположенного на оси источника. Итак, мы можем
заключить, что если на тонкую линзу с примыкающим к ней
транспарантом падает плоская волна, то в задней фокальной
плоскости линзы образуется распределение комплексных амплитуд,
пропорциональное произведению фазового множителя сферической волны
и фурье-образа пропускания транспаранта.
Выражения (2.21) и (2.22) являются определениями, связывающими
пространственные частоты ξ и η света, дифрагировавшего на
транспаранте, с координатами (х2, у2) формирующегося в фокальной
плоскости линзы фурье-образа пропускания транспаранта. Этим
выражениям, безусловно, можно придать вид, эквивалентный
определениям пространственных частот в гл. 5. В приближении малых
углов, которое согласуется с приближениями, принятыми выше, можно
применять исходные выражения (1.14а)и (1.14б) для ξ и η. Последнее
утверждение иллюстрируется РИС. 2.3, где в соответствии с (1.14б) плоская
волна, испытавшая дифракцию на транспаранте и распространяющаяся
под углом θк оси z, характеризуется пространственной частотой η = (sinθ)/λ.
Луч, проходящий через центр линзы без отклонения (в случае тонкой
линзы), в фокальной плоскости х2у2 встречается с преломленными лучами
на расстоянии +у2 от осиz. Для малых угловимеем / ≈ ≈ = ,
поэтому ≈ / .Аналогичные соображения справедливы для ξ и х2.
РИС. 2.3.Геометрическая схема, поясняющаясоотношение между
пространственными частотами и координатами фокальной плоскости.
Пространственные частоты картины, возникшей в результате
дифракции света на предмете, являются пространственными частотами
двумерныхфурье-компонент предмета. Поэтому если известна
максимальная пространственная частота предмета, то с помощью (2.21)
или (2.22) можно вычислить максимальную протяженность его

25
фурье-образа, сформированного в задней фокальной плоскости данной
линзы. Рассмотрим численный пример только для одной координаты.
Положим максимальную пространственную частоту предмета равной
умеренной величине |ξмакс| = 10 мм-1; кроме того, примем, что f= 500 мм,
а λ= 0,5 мкм = 5*10-4мм. Тогда максимальная протяженность фурье-образа
в положительном направлении оси х получается весьма малой: х2, макс = 2,5
мм.
В некоторых случаях, когда важна только интенсивность света,
эффекты, обусловленные наличием фазового множителя сферической
волны в (2.23), не играют роли. В других случаях от них стараются
избавиться. Для этого в плоскостиz = fпомещают собирающую линзу с
фокусным расстоянием f. Из (2.15) и (2.23) очевидно, что сразу за этой
второй линзой мы получим фурье-образ, не содержащий фазового
множителя сферической волны. Оптическая система, выполняющая такое
преобразование, изображена на РИС. 2.1.
Вернемся к рассмотрению системы, показанной на РИС. 2.2, полагая
при этом, что транспарант совершенно прозрачен, т.е. t(x1y1) =1. Тогда
амплитуда в плоскостиz =f в соответствии с (2.23) будет равна
( , ) = (− )( + ) ×
× [ ( + )] .
(2.24)
РИС. 2.1.Оптическая система, выполняющая точное преобразование Фурье.
Линзы L1 и L2 имеют одинаковые фокусные расстояния f.
Допустим, что линза имеет неограниченные размеры; тогда пределы
интегрирования можно распространить до бесконечности и интеграл будет
представлять собой фурье-образ единицы. Из соотношения (1.30) при с = 0
следует, что интеграл равен ( ) ∙ ( ) ≡ ( , ) = ( / , / ) и
обращается в нуль всюду, кроме х2 = у2 = 0. Тогда (2.24) принимает вид
( , ) = , ;
(2.25)
мы видим, что падающая на линзу с положительным фокусным
расстоянием f плоская волна сходится в математическую точку, лежащую в

26
плоскости, удаленной от линзы на ее фокусное расстояние. Тот факт, что
фокальным пятном линзы оказалась математическая точка, обусловлен
сделанным нами допущением о неограниченности размеров линзы. Линза
конечных размеров образует протяженное световое пятно с центром в точке
с координатами х2=y2=0.
.
2.3. Оптическая система более общего вида
Кроме систем, изображенных на РИС. 2.2 и 6.4, существуют и другие
оптические системы, которые могут выполнять преобразование Фурье. Это
станет очевидным после того, как мы рассмотрим оптическую систему
более общего вида. В этом параграфе мы выведем не только условия
формирования фурье-образа, но и условия формирования изображения.
Рассматриваемая система показана на РИС. 2.5. Сферическая волна
падает на транспарант с комплексным амплитудным пропусканием t(х1,
у1). Радиус кривизны волны равенd1, т. е. волна расходится из точки,
удаленной на расстояниеdl влево от транспаранта t(х1, у1). На расстоянииd2
справа от транспаранта помещена сферическая линза с фокусным
расстоянием f. Наша задача — определить комплексную амплитуду волны
в плоскости, находящейся на расстоянии d3 справа от линзы
РИС. 2.5.Оптическая система более общеговида.Линза имеет фокусное
расстояние f.
.
Для решения задачи воспользуемся приближенной формулой (1.33)
(свертка в координатной области), описывающей распространение волны в
свободном пространстве, и приближенной формулой пропускания линзы
(2.15). Анализировать прохождение света через оптическую систему,
состоящую из свободного пространства и линз, было бы проще с помощью
одних только мультипликативных форм, однако легко убедиться, что это
невозможно. Действительно, если для описания распространения волны в
свободном пространстве мы выберем область пространственных частот, то
можем воспользоваться мультипликативной формой (1.28). Однако
выражение (2.17), описывающее прохождение света через линзу, имеет
мультипликативную форму в координатной области, и в области
пространственных частот мы должны заменить его сверткой. Если же
выбрать в качестве исходной координатную область, то получим, что

27
выражение для распространения света в свободном пространстве имеет
форму свертки, а для прохождения через линзу — мультипликативную
форму. Выбор может быть сделан произвольно, и мы проведем
рассмотрение в координатной области.
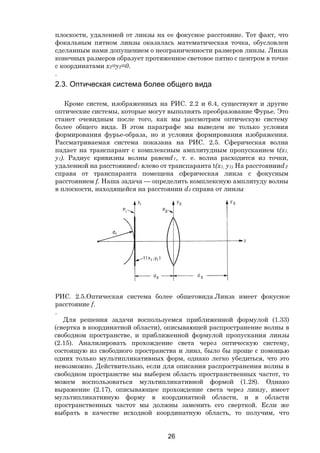
Анализ системы, изображенной на РИС. 2.5, включает в себя две
операции умножения и две операции свертки. Для упрощения записи мы
воспользуемся обозначениями операций и допущениями.введенными
ВандерЛюгтом [6.2]. Это наиболее краткая и удобная форма записи уже
выведенных нами соотношений.
2.3.1. Форма записи операций
Из равенства (2.14) следует, что тонкая линза является транспарантом,
пропускание которого описывается формулой
( , ) = ( + )
(2.26)
Функция g (х, у) по форме очень похожа на функцию h (х, у),
определяемую выражением (1.34). Эта функция, которая подвергается
свертке с входным пропусканием, если распространение волн в свободном
пространстве рассматривается в координатнойобласти, имеет вид
( , ) = − ( + )
(2.27)
Основываясь на сходстве выражений(2.26) и(2.27), можно ввестифункцию:
( , ; ) = − ( + )
(2.28)
гдер — произвольный параметр. Тогда для описания прохождения волны
через сферическую линзу с фокусным расстоянием fкомплексную
амплитуду света, падающего на линзу, нужно умножить на ∗ ( , , ).
Звездочка обозначает комплексно- сопряженную величину, и
=
(2.29)
Волна, прошедшая в пространстве расстояниеd, описывается сверткой
комплексной амплитуды и выражения ∙ ( , , ),где
=
(2.30)
Приведем ряд свойств функции ∗ ( , , ).), которые в дальнейшем
будут нам полезны. В справедливости следующих равенств можно
убедиться подстановкой выражения (2.28):
( , ; ) = ∗ ( , ; − ). (2.31)

28
(− , − ; ) = ( , ; ). (2.32)
( , ; ) ( , ; ) = ( , ; + ). (2.33)
( , ; ) ∗ ( , ; ) = ( , ; − )
=. ∗ ( , ; − )
(2.34)
( , ; ) = ( , ; ). (2.35)
( − , − ; ) = ( , ; )( , ; ) + _.
(2.36)
Соотношение
∗ ( , ; ) = . (2.37)
выражает тот факт, что линза с бесконечно большим фокусным
расстоянием не изменяет распределения амплитуд поля, падающего на
нее.
Применим приведенную форму записи к анализу оптической системы,
изображенной на Рис.6.5. Расходящаяся сферическая волна, падающая на
помещенный в плоскости Р1 транспарант t(x1, y1), описывается функцией
( , , ) [см. обсуждение выражения (2.23)]. Амплитуда света,
прошедшего через транспарант, выражается произведением
( , ) = к( , ) ( − , − ; )
(2.38)
Свертка аt и ( / ) ( , ; ) дает распределение амплитуд на левой
поверхности линзы
( , ) = ( , ) ( − , − ; )
(2.39)
а умножение аl на функцию ( , ; ), описывающую пропускание
линзы, дает распределение комплексных амплитуд на правой
поверхности
( , ) = ( , ) ∗ ( , ; ), (2.40)
Наконец, вычисляя свертку аr с функцией ( / ) ( , ; ), получаем
комплексную амплитуду a(x3, y3) в плоскости xy на расстоянии d3 от
линзы:

29
( , ) = ( , ) ( − , − ; )
(2.41)
Выражение (2.41) можно привести к более удобному виду, если 1)
представить -функции, входящие в (2.39) и (2.41), в виде множителей,
зависящих от координат только одной плоскости [используя(2.36)]; 2)
подставить (2.39) и (2.40) в (2.41); 3) сгруппировать множители,
зависящие от координат х, у одной плоскости [воспользовавшись
равенствами (2.31) — (2.34)]. В результате получим
( , ) = −( ) ( , ; ) ×
× ( , ;
+ ) ( , ) ( , ; − + ) ×
× [ ( + ) + (
+ )] ××
(2.42)
2.3.2. Условие формирования изображения
В первую очередь покажем, что выходная функция а (х3, у3) в (2.42)
имеет такой же вид, как и входная функцияt (X1, Y1), а потому является ее
изображением (если формирование изображения рассматривается в
приближении геометрической оптики). Последнее условие, записанное
через параметры оптической системы, показанной на РИС. 2.5, имеет
вид
+ =
(2.43)
или, используя обозначения, введенные в этой главе,
+ = (2.44)
Подставляя (2.44) во второй множитель, стоящий под знаком интеграла в
(2.42), получаем, что ( , ; − + ) = ,и для интеграла по
плоскости Р2 находим

30
∙ [ ( + )
+ ( + )] =
=
+
,
+
(2.45)
Здесь мы применили соотношение (1.30) при с = 0. Записывая -функцию
следующим образом:
+ , +
и используя свойство (1.13г) для случая двумерной -функции, т. е. б
( , ) = ( /| |) ( , ), получаем
+
,
+
= + , +
(2.46)
Подстановка в (2.42) найденных выше соотношений дает
( , ) = − ( , ; ) ( , ;
+ ) ( , ) ×
× + , + =
= − , ; + ( + ) ×
× (− , )
(2.47)
Здесь мы учли, что свертка любой функции с -функцией равна исходной
функции [см. (1.13д)], а чтобы придать соотношению более компактный
вид, использовали (2.32) — (2.35). В (2.47) -функция является фазовым
множителем сферической волны, который при получении изображения,
как правило, играет незначительную роль. В большинстве случаев в
качестве изображения регистрируется распределение
интенсивностейаа*, так что фазовый множитель выпадает ( * = 1). При
таких условиях на формирование изображения не влияет кривизнаD1
волнового фронта. В (2.47) остается распределение амплитудного
пропускания, т. е.

31
− , − ,
(2.48)
которое является перевернутым увеличенным изображением исходного
распределения t(x1, y1); увеличение равно
= − = − ,
(2.48)
2.3.3. Условие формирования фурье-образа
Возвращаясь к (2.42), определим условия, при которых выходное
распределение комплексных амплитуд а (х3 у3) в плоскости х3у3
является фурье-образом входного пропусканияt
распределения t(x1, y1);Поскольку искомое преобразование Фурье должно
связывать комплексные амплитуды в плоскостях
распределения x1, y1их3уз, то из (2.42) необходимо исключить члены,
зависящие от координат х2, у2 плоскости Р2. Для наглядности запишем
(2.42) в виде
( , ) = −( ) ( , ; ) ×
× ( , ; + ) ( , )
(2.42)
где
= ( , ; −
+ )
+
+
+
=
(2.51)
= ( , ; − + ) { ( + )}
(2.52)
и = , = (2.53)
Переменные x2 и y2 можно исключить, если вычислить интеграл Фурье
(2.52). Функция ( , ; + ) является двумерной функцией Гаусса и
ее фурье-образ І2(x1, x3),определяемый соотношением (1.27), с учетом
свойств - функций приводится к виду

32
( , ) =
( − + )
××
∗ + , + ;
− +
(2.54)
Применяя (2.36) и (2.35), получаем окончательный результат для I2
=
( − + )
∗ , ;
− +
∗ , ;
− +
×
− +
( + )
(2.55)
Подставляя І2 в (2.50) и группируя с помощью (2.34) -функции, зависящие
от координат одной плоскости, получаем следующее выражение для
распределения комплексных амплитуд в плоскости, находящейся на
расстоянииd3 от линзы:
( , ) =
( − + )
, ; −
− +
×
× , ; +
−
− +
( , ) ×
×
( − + )
(
+ )
(2.56)
Интеграл по плоскостиP1 в (2.56) имеет вид фурье-образа, если -функция,
стоящая под знаком интеграла, равна единице. Последнее имеет место при
условии
+ −
− +
=
(2.57)
Положим, что транспарантt(x1, y1) освещается плоской волной, так что D1 =
1/d1= 0 и d1= ∞. Тогда
= или = (2.58)

33
и (2.56) принимает вид
( , ) = , ; −
− +
×
× , ; + − ×
× ( , ) ( + ) (2.59)
РИС. 2.6Другая оптическая система, выполняющая точное преобразование
Фурье. Фокусное расстояние линзы равно f.
Таким образом, когда на помещенный перед линзой транспарант t(x1, y1)
падает плоская волна, в задней фокальной плоскости линзы, если не
учитывать фазовый множитель сферической волны, возникает
распределение комплексных амплитуд, которое имеет вид фурье-образа
функцииt(x1, y1) Это справедливо независимо» от расстоянияd2 между
линзой и транспарантом. Фазовый множитель сферической волны можно
сделать равным единице, положив
D2 = F, (2.60)
т. е. поместив транспарант в переднюю фокальную плоскость линзы. Такая
система, применяемая на практике для получения фурье-образа входного
транспаранта, изображена на РИС. 2.6, С учетом (2.60) выражение (2.59)
принимает вид
( , ) = ( , ) [ ( + )]
(2.61)
где
= и = (2.62)

34
являются координатами в плоскости пространственных частот.
Следует заметить, что еслиξ и ηвзяты положительными, то знак показателя
экспоненты под интегралом в (2.61) соответствует преобразованию
пространственного распределения в частотное, но не наоборот. При
положительных ξ и η показатель экспоненты имеет знак плюс во всех
формулах аналогичных преобразований, осуществляемых оптическими
системами, подобными изображенной на РИС. 2.6. Чтобы привести
оптические преобразования в соответствие с определениями (1.1) и (1.2),
координаты в задней фокальной плоскости линзы, где формируется
пространственное распределение, должны иметь знаки, обратные знакам
координат в передней фокальной плоскости, являющейся плоскостью
пространственных частот. Если же пространственное распределение
образовано в передней фокальной плоскости, то координаты в задней
плоскости берутся с теми же знаками, что и в передней. Иллюстрация этого
правила дана на РИС. 2.7.
РИС. 2.7. Ориентация координатных осей в плоскостях, в которых
формируются фурье-образы.
Если входной транспарант t(x1, y1)освещен сферической волной (D1≠0), то
из (2.56) легко видеть, что плоскость, в которой формируется фурье-образ,
не совпадает с задней фокальной плоскостью линзы [D3 определяется из
соотношения (2.57)]. Кроме того, поскольку теперьD3 иF не равны друг
другу, масштабный множитель преобразования Фурье
( − + )
будет функцией . Это позволяет создавать системы, выполняющие
преобразование Фурье с переменным масштабным множителем [6.2].
2.4. Влияние конечных размеров линзы
2.4.1. Влияние на спектр пространственных частот
Для анализа оптического преобразования Фурье в § 2 было принято
допущение о бесконечном радиусе линзы. Это позволило описывать

35
пропускание линзы чисто фазовым множителем с бесконечными
пределами. Теперь положим, что линза имеет конечный радиус с, и
рассмотрим снова интеграл Фурье в (2.24) для случая t(x1, y1)=1.
= [ ( + )]
Если выразить через цилиндрические координаты как в координатной,
так и в частотной области, а интегрирование проводить а пределах радиуса
линзы c, то для I1 получаем
= [ ( / )] = ( )
( ) (2.63) ,
где обозначает преобразование Фурье. Функция
( )
имеет
максимальное значение, равное единице, при v =0, следовательно,
максимум функции лежит на оси и его значение равно . На Рис.1.7
построены функция и ее фурье-образ ( / ). Таким образом, если
линза с бесконечными размерами фокусирует плоскую волну в
математическую точку [ -функция в (2.25)], то линза с конечным радиусом с
преобразует падающую на нее часть плоской волны в пятно конечной
ширины. За размер пятна обычно принимают половину расстояния между
нулями функции Бесселя, что соответствует интервалу в области
пространственных частот, равному v0 = 0,61/c мм-1 . Пользуясь
соотношением
= ( + ) /
= )( + ) /
=
(2.64)
вытекающим из (2.21) и (2.22), можно перейти от ширины полосы в
частотной области к расстоянию в координатной области; в результате для
ширины (диаметра) пятна в плоскости х2у2 находим
∆= ,
(2.65)
Ширину ∆ в (2.65) можно считать мерой степени неопределенности, с
которой точка плоскости х2у2пространственных частот соответствует
пространственной частоте аксиальной плоской волны, падающей на линзу
конечного радиусас.Эта неопределенность является следствием того, что
линза конечных размеров собирает лишь часть пространственной
информации, которую несет световая волна.
Рассмотрим теперь транспарант, пропускание которого уже не равно
единице и в полярных координатах описывается функцией t (r, θ).
Интеграл Фурье в (2.23), описывающий результат оптического
преобразования Фурье, которое осуществляет система, изображенная на
РИС. 2.2, теперь имеет вид
= [ ( , ) ( / )] = ( , ) ∗
( ) (2.66)

36
где t ( , ) ⊃ ( , ). Как указывалось в гл. 4, § 3, свертка двух функций
представляет собой результат сканирования одной функции с помощью
другой. Функцию ( , ) , являющуюся фурье- образом пропускания
( , ), сформированным бесконечно большой линзой, можно рассматривать
как совокупность идеальных точек или -функций. При свертке каждой
-функции с функцией пятна
( )
, имеющего ширину ∆=
, , -функция уширяется до значения ∆.
2.4.2. Влияние конечных размеров линзы на выбор системы,
формирующей изображение или фурье-образ.
Рассмотрим сначала, как сказывается конечность размеров линзы на
формировании изображения. Для получения качественного изображения
необходимо, чтобы линза собирала всю световую волну, переносящую
информацию о предмете. Заведомо плохая в этом отношении система
изображена на РИС. 2.8. Плоская волна падает на предмет, которым
является транспарант с пропусканием t(x1, y1). Будем рассматривать
распространение волны в плоскостиyz. Можно мысленно представить, что
входное пропусканиеtразложено на фурье-компоненты, описывающие
пропускание синусоидальных решеток. Пусть одна из них имеет
пространственную частоту η. Наша система подобна системе, изображенной
на Рис.2.3, за исключением того, что здесь поперечное сечение падающего
на решетку пучка света ограничивается протяженностью транспаранта t(x1,
y1).
Если плоская волна падает на решетку неограниченных размеров, то
дифрагировавшие волны будут плоскими, а их комплексные амплитуды
справа будут описываться:
( , ) = + ( ) + (− ) (2.67)
РИС. 2.8 Система, формирующая изображение при освещении плоской
волной
А углы дтфракции определяться формулой = ±
Рассмотрим сначала пучок лучей, осью которого является ось z (РИС. 2.8).
Максимальный угол, под которым дифрагируют лучи, щепадающее на
линзу с радиусом r2, определяется отношением r2/ d2=tgθ2. Для
центральных лучей получим, что максимальная пространственная частота

37
ηмакс входной решетки, которую линза может преобразовать в изображение,
определяется условием = ≤ , т. е. не превосходит величины
≤ / (2.68)
Предположим теперь, что транспарант t имеет форму круга радиусом r1 и
рассмотрим пучок лучей, падающих на область, расположенную в
непосредственной близости от края круга у1= r1. Чтобы на линзу попадали
все лучи, идущие от этой области транспаранта, угол дифракции θ'2 не
должен превышать величины ( − )/ т. е.
= = ′ ≤
−
или
′ ≤ /
− (2.69)
Таким образом, максимальная пространственная частота предмета,
преобразуемая в изображение, является линейной убывающей функцией
его радиуса. Если пространственные частоты не удовлетворяют условию
(2.69), то происходит потеря информации.
Прежде чем рассматривать оптическую систему, более полно
передающую информацию о предмете, воспользуемся проведенным выше
анализом системы на РИС. 2.8, чтобы выявить преимущество
осуществляющей преобразование Фурье оптической системы,
изображенной на РИС. 2.2 (или 2.4) по сравнению с системой, показанной
на РИС. 2.6. Если на РИС. 2.8 расстояниеd3 равно фокусному расстоянию
линзы, то мы получим выполняющую преобразование Фурье оптическую
систему, которая при неограниченных размерах линзы будет формировать
фурье-образ Т(ξ, η) в плоскости х3у3 независимо от величиныd2. [От
величины d2 зависит фазовый множитель сферической волны из (2.59),
который мы здесь не учитываем.] Однако в действительности линза имеет
конечный радиус r2, и из (2.68) и (2.69) видно, что максимальная
пространственная частота света, попадающего на линзу, обратно
пропорциональна расстояниюd2 между линзой и транспарантом t(x1, y1).
Если жеd2 = 0 (как на РИС. 2.2 или 6.4), то линза преобразует все
пространственные частоты предмета, и в задней фокальной плоскости
формируется полный спектр функцииt(x1, y1). В этом отношении подобная
система обладает преимуществом перед показанной на РИС. 2.6 системой,
гдеd2 = f.
Система, формирующая изображение и сохраняющая наиболее полно
переносимую светом информацию о предмете, изображена на РИС. 2.9.
Соприкасающаяся с предметом-транспарантомt(x1, y1) первая линза L1
формирует сферический волновой фронт, который фокусируется в
расположенный на оси центр второй линзы L2. Поскольку линза L2
находится в задней фокальной плоскости первой линзы, на поверхности
линзы L2 формируется фурье-образ, или спектр, функцииt(x1, y1). В свою
очередь линза L2 преобразует этот фурье-образ в изображение
транспаранта, возникающее в плоскости х3у3.

38
Ограничиваясь анализом в плоскостиyz, рассмотрим опять
фурье-компоненту [одну из синусоидальных решеток, составляющих
пропускание t(x1, y1) с пространственной частотой η. На этот раз решетка
освещается сферической волной. Если в (2.67) вместо подставить фазовый
множитель, соответствующий сферической волне, которая сходится в
точку, находящуюся на расстоянииd2 от t(x1, y1) то третий член в правой
части; (2.67) примет вид
(− ) ~ ( + ) ×
× − ( )
= [ + − ( ) ]
(2.70)
Для малых углов имеемd2sinθ2≈d2θ2≈y2- Подставляя в (2.70) у2, получаем
для фазы
= [ + − ]
(2.71)
Сравнение выражений (2.71) и (3.26) показывает, что представляет собой
распределение фаз сферической волны, фокусирующейся в расположенную
вне осиz точку с координатами (у2,z = d2), положение которой определяется
углом θ2. Вообще говоря, при освещении синусоидальной
решеткисходящейся сферической волной, как и при освещении плоской
волной, возникают три волны: одна иедифрагированная, фокусирующаяся
в точку на оси, и две другие, дифрагирующие под средними углами θ2 = ±
arcsinλη и фокусирующиеся в плоскостиz = d2 в точки с координатами ±у2.
Рассмотрим опять падающий наt(x1, y1)) узкий пучок лучей с вершиной на
осиz. Как видно из Рис.6.9, максимальный угол, под которым эти лучи могут
дифрагировать, попадая при этом иа линзу, составляет
РИС. 2.9.Система, формирующая изображениепри освещении сферической
волной.

39
≈ = = / (2.72)
РИС. 2.10 Когерентная передаточная функция rect (v/2vмакс) оптической
системы, изображенной на РИС. 2.9.
Однако это же условие справедливо (в пределах наших допущений) и для
лучей, падающих на края предмета. Если обобщить проведенный анализ на
произвольно ориентированные синусоидальные решетки, то (2.72) можно
= /
или
= /
(2.73)
= ( + ) /
Как в (2.64). Из (2.73) следует, что линза в оптической
системе на РИС. 2.9 независимо от расположения предмета во входной
плоскости преобразует в изображение всю световую информацию о
предмете, которую несут компоненты с пространственными частотами
вплоть до - Если- пространственная частота какой-либо компоненты
пропускания превышает ,то соответствующая ей информация теряется.
Если записать полученные результаты, применив понятие частотной
передаточной функции [см. определение (1.6)], то в нашем случае она имеет
постоянное значение для частот вплоть до и равна нулю для частот,
превышающих - Эта функция изображена на РИС. 2.10. Для систем,
формирующих изображение в когерентном свете, ее называют когерентной
передаточной функцией.
2.4.3. Влияние конечных размеров линзы на разрешение изображения
Чтобы получить функцию рассеяния s (х3, у3) для изображенной на
РИС. 2.9 системы, формирующей изображение, мы должны, согласно (1.15),
найти обратный фурье-образ частотной передаточной функции S (v).
Последняя изображена на РИС. 2.10 и является функцией вида ( /
) фурье-образ которой определяется собтношением (1.34). В данном
случае фурье-образ зависит от переменных, принадлежащих координатной
области, и функция рассеяния (нормированная на максимальное значение,
равное единице) имеет вид

40
( ) = ( )/
(2.74)
где = ( + ) /
. График функцииs (r) приведен на РИС. 2.11.
Мы уже знаем, что если пучок света фокусируется в плоскости линзы,
строящей затем изображение, как в системе на РИС. 2.9, то частотная
передаточная функция одинакова для любого положения предмета во
входной плоскости и не зависит от координат входной плоскости.
Следовательно, разрешение изображения, которое определяется функцией
рассеяния, тоже не зависит от положения предмета на входе. Выходная
функция линейной пространственно-инвариантной оптической системы
(изображение) равна свертке входной функции и функции рассеяния. При
свертке каждая точка входной функции, описываемая -функцией,
расширится на выходе в пятно шириной ∆=
,
= , / . Величина ∆
есть ширина наименьшего разрешаемого системой пятна на изображении.
Здесь мы полагаем, что увеличение равно единице. В противном случае А
умножается наd3/d2 см. (2.49).] Показанную на РИС. 2.8 оптическую
систему, в которой для освещения используется плоская волна, а также
системы со сферическими волнами, фокусирующимися вне плоскости
линзы, формирующей изображение, невозможно описать одной только
передаточной функцией. Такие системы,в которых разрешение меняется в
зависимости от положения предмета во входной плоскости, называются
пространственно-неинвариантными.
РИС. 2.11.Функция рассеяния для формирующейизображение системы,
представленной на РИС. 2.9.
Мы рассмотрели некоторые ограничения свойств оптической системы,
обусловленные конечными размерами реальных линз. Если ограничение,
вносимое линзой, вызвано только конечностью ее размеров, то такая линза
называется дифракционно-ограниченной. В нашем анализе мы
неоднократно пользовались приближением малых углов. Если же световые
лучи падают на тонкие линзы под большими углами, значения которых
выходят за рамки этого приближения, то наблюдается ухудшение свойств
системы по сравнению с оптимальными свойствами
дифракционно-ограниченной системы. Это происходит, когда размеры

41
предмета велики и он расположен не на оси, а отношение диаметра линзы
к ее фокусному расстоянию уже нельзя считать малым.
2.5. Когерентные и некогерентные передаточные
функции
Хотя для голографии получение изображений в некогерентном свете
обычно не представляет интереса, здесь уместно сделать краткое
отступление и сравнить частотные передаточные функции оптических
систем, освещаемых когерентным и некогерентным светом.
РИС. 2.12 Сечение когерентной передаточной функции и оптической
передаточной функции для системы, изображенной на РИС. 2.9
Пусть в оптической системе, освещаемой когерентным светом, входным
комплексным амплитудам (х, у) или а2 (х, у) отвечают соответственно
выходные амплитудыb1 (х, у) или b2 (х, у). Если система линейна, то
входной комплексной амплитуде а1(х, у) + а2 (х, у) должна соответствовать
на выходе комплексная амплитуда с (х, у) =b1 (х, у) +b2 (х, у). Выходная
интенсивность I = сс* будет при этом иметь вид многочлена
= ∗
+ ∗
+ ∗
+ ∗
= + + ∗
+ ∗
(2.75)
где — выходная интенсивность при действии на входе только волны а1,
а — при действии только волны а2. При когерентном освещении все
четыре члена в (2.75), вообще говоря, не равны нулю. Следовательно, в
этом случае система нелинейна по интенсивности. Однако при
некогерентном освещении выходная интенсивность складывается только
из входных интенсивностей
= +
т. е. системы, освещаемые некогерентным светом, линейны по
интенсивности. Для характеристики таких систем можно пользоваться
функцией рассеяния и частотной передаточной функцией для
интенсивности. Последнюю называют оптической передаточной
функцией, а ее модуль — модуляционной передаточной функцией.

42
Функция рассеяния для интенсивности описывает распределение
интенсивности света в выходной плоскости, соответствующее импульсной
функции во входной плоскости, и, следовательно, равна квадрату
абсолютной величины комплексной амплитудной функции рассеяния. Для
представленной на РИС. 2.9 системы, формирующей изображение, она
имеет вид
( ) = [ ( )/ ] (2.76)
В соответствии с аналогичными соотношениями для когерентной системы
оптическая передаточная функция является фурье-образом функции ( )
и, согласно (1.18) и (1.34), представляет собой автокорреляцию когерентной
передаточной фунции ( / ) ). Как оптическая передаточная
функция, так и когерентная передаточная функция обладают круговой
симметрией и зависят только от v. Двумерные проекции абсолютных
величин этих функций представлены на РИС. 2.12.
Вопросы для самоподготовки
1. Формула линзы.
2. Как идеальная линза преобразует сферическую волну.
3. Формула фокусного расстояния тонкой линзы.
4. Комплексное пропускание линзы.

43
3. АНАЛИЗ ПЛОСКИХ ГОЛОГРАММ
Расстояние между полосами на небольших осевых голограммах,
зарегистрированных при недиффузном освещении, значительно превышает толщину
фотослоя. Каждый луч, освещающий такую голограмму, при прохождении через нее
взаимодействует только с одной зарегистрированной на ней полосой. Следовательно,
действие, оказываемое голограммой на пучок света, подобно действию плоской
дифракционной решетки, обладающей фокусирующими свойствами. Габор
рассмотрел эти свойства для случая строго двумерной голограммы. Полученные им
выводы оказались в хорошем согласии с экспериментальными данными.
В предложенном Лейтом и Упатниексом методе с наклонным опорным пучком
образуются голограммы с большей частотой полос, чем в случае осевых голограмм.
Разность частот пропорциональна величине угла между предметным и опорным
пучками [см. (3.15)]. Типичное значение расстояния между полосами на голограмме с
наклонным опорным пучком можно получить, рассмотрев интерференцию двух
плоских волн. Расстояние между полосамиd связано с углом θ (равным половине угла
между направлениями пучков) и длиной волны К соотношением (1.10): 2d sinθ = X.
Для θ= 15° и λ = 0,5 мкм (зеленый свет) имеем d — 1 мкм. Толщина фотослоев,
используемых для регистрации внеосевых голограмм, составляет обычно 15 мкм, и,
следовательно, зарегистрированные на них голограммы по сути дела уже нельзя
считать двумерными. Тем не менееЛейт и Упатниекс [8.1, 8.2], используя
представления теории связи, распространили двумерный анализ и на случай
внеосевых голограмм. Несмотря на то что двумерная модель на самом деле обычно не
реализуется, такой подход создал хорошую базу для дальнейшего развития гологра-
фии. Однако его применение к тем голограммам, которые правильнее было бы
рассматривать как объемные дифракционные решетки, дает результаты,
выполняющиеся лишь частично, и оставляет необъясненными многие наблюдаемые
на практике свойства голограмм.
Поэтому важно помнить, что выводы, полученные в результате анализа
плоских голограмм, строго выполняются лишь для голограмм, зарегистрированных
на достаточно тонких слоях. В качестве примера такого слоя можно назвать
термопластик, толщина которого может быть сравнимой с длиной световой волны.
Наблюдаемые свойства голограмм, зарегистрированных на термопластике,
правильно предсказываются теорией плоских голограмм.
Используя математический аппарат, разработанный в теории дифракции
(лекции 1 и 2), рассмотрим теперь те свойства плоских голограмм, которые нельзя
было получить с помощью геометрического анализа. На теории дифракции основано
и обсуждение фурье-голограмм. Мы выведем условие разделения формирующих
изображение волн, дифрагированных внеосевой голограммой, рассмотрим факторы,
влияющие на качество изображения, и найдем максимальное значение диф-
ракционной эффективности амплитудных и фазовых голограмм.
3.1. Получение голограмм с наклонным опорным пучком при
недиффузном предметном пучке
Получение голограммы с помощью опорной волны, интерферирующей с
предметной под некоторым углом это один из наиболее эффективных методов
разделения двойниковых изображений. Пространственно-частотный анализ этого
метода приводит к понятию несущей, или опорной, волны, пространственная частота
которой модулируется информацией о предмете. Таким образом,
выражениеголограмма с несущей частотой эквивалентно выражениювнеосевая

44
голограмма. При использовании метода несущей частоты отпадает необходимость
получения опорной волны за счет света, прошедшего через предмет. Вследствие этого
при применении внеосевых голограмм, в противоположность габоровским
голограммам, нет необходимости ограничиваться транспарантами с большими
прозрачными участками.
На Рис. 3.1 показан простой способ деления волнового фронта, позволяющий
освещать прозрачный транспарант когерентной плоской волной и получать
наклонную плоскую опорную волну от того же источника. В качестве предмета
можно взять полутоновый транспарант. Пусть а(х, у) — комплексная амплитуда
предметной волны в плоскости голограммы, r =r•ехр(2πiξrx) — комплексная
амплитуда плоской опорной волны. Пространственная частота опорной волны ξопорн
=-ξr= - (sinθ)/λ соответствует волновому вектору опорной волны, направленному вниз
от осиz, где θ — угол, образованный им в плоскостиxz с осьюz. Будем рассматривать
получение амплитудной голограммы. Пусть после записи интерференционной
картины, образованной волновыми фронтами а(х, у) и г, и полной фотографической
обработки мы получили голограмму с амплитудным пропусканием
= − , (3.1)
Гдеt0 — пропускание неэкспонированной (но проявленной) пластинки;к —
постоянная, аI — интенсивность интерференционной картины. Согласно (1.15),
интенсивность описывается выражением
= ∗
+ ∗
+ ∗
+ ∗
=
= ∗
+ + exp(−2 ) + ∗
exp(2 ). (3.2)
РИС. 3.1.Простая схема получения голограммыс внеосевым опорным пучком.
Если на стадии восстановления голограмма освещается исходной опорной
волной, для комплексной амплитуды поля сразу за голограммой имеем
( , ) = = exp(2 )
− [ ∗
exp(2 ) + exp(2 ) +
+ ∗
exp(4 )]. (3.3)
3.1.1. Разделение дифрагированных волн
При соответствующем направлении опорной волны можно отделить нужную
восстановленную волну от остальных, дифрагированных голограммой. Для этого
необходимо иметь достаточно большой средний угол между предметным и опорным
пучками. Чтобы связать условие углового разделения дифрагированных волн с

45
максимальной пространственной частотой пропускания предмета, проведем
пространственно- частотный анализ выражения (3.3) [3.1]. Пусть голографируемый
транспарант имеет пропускание s (х, у) и спектр S(ξ, η), где s (х, у) ⊃S(ξ, η).
Протяженность спектра S(ξ, η) лежит в пределахот–ξмаксдо + ξмакс и от –η максдо +η макс.
Возможное спектральное распределение | S(ξ, η) | в плоскости ξηприведено на Рис. 3.2.
При освещении транспаранта распространяющейся вдоль осиz плоской волной
комплексная амплитуда предметнойволны, падающей на голограмму, равна а (х, у).
Соответствующий этой функции спектр определяется выражением (1.26):
( , ) = ( , ) exp −
2
(1 − − ) .
(3.4)
где а1 — постоянная амплитуда плоской волны, падающей на транспарант, аd —
расстояние между транспарантом и голограммой. Заметим, что максимальная
протяженность, или ширина, спектра А(ξ, η) в плоскости пространственных частот
определяется интервалом, в котором функция S (ξ, η)не равна нулю. Выражение (3.3)
содержит не только а (х, у), но и комплексно-сопряженную ей величину а*(х, у) со
спектром
′( , ) = ∗(− , − )
= ∗(− , − ) exp +
2
(1 − − ) .
(3.5)
Здесь было использовано соотношение (4.26). Теперь с помощью (3.4) и (3.5)
найдем абсолютное значение спектра функции w (х, у), определяемой выражением
(3.3).
РИС. 3.2 Спектр транспаранта.
Первый член в правой части (3.3),t0rехр(2πiξrx), описывает
недифрагированный свет, распространяющийся в направлении падающей волны. Для
обычных амплитудных голограмм (с низкой эффективностью) эта компонента, как
правило, очень велика. Ее спектр представляет собой сканирование одной функции
с помощью другой (рис. 3.2). Интервал значений переменных, в котором интеграл не
равен нулю, определяется суммой ширины обеих функций; в случае автокорреляции
максимальная протяженность результирующей функции в два раза больше ширины
функции, подвергаемой операции автокорреляции. Опуская постоянные множители,
получаем фурье-образ второго члена из(3.3):

46
(2 ) ⊃ ∗( , ) ∗ ( + , ) =
= [ ∗( , ) exp
2
(1 − − ) ∗
∗ ( + , ) exp −
2
(1 − ( − ) − )
. (3.7)
Снова возвращаясь к (3.3), мы видим, что второй член в скобках, —kr3
ехр
(2πiξrx), аналогичен первому экспоненциальному члену в правой части формулы,
который, как уже говорилось, преобразуется в -функцию в точке (ξ=-ξr,0). Как
правило, компонента, соответствующая этому члену, меньше компоненты,
опрсываемой первым членом формулы (3.3).
Рис. 3.3 Пространственный спектр излучения, вышедшего из голограммы,
зарегистрированной с наклонным опорным пучком.
Все три члена, которые мы только что рассмотрели, называются членами
нулевого порядка, так как они описывают световые волны, не испытавшие
отклонения, т. е. распространяющиеся за голограммой в том же направлении, что и
падающая на нее волна.
Третий член в квадратных скобках в (3.3) пропорционален исходной волне а (х,
у), которая попадает на голограмму от предмета. Абсолютная величина ее спектра |
А(ξ, η) |, как легко видеть из (3.4), пропорциональна | S(ξ, η) |. Мы считаем, что IS(ξ, η)|
описывает симметричное распределение вокруг центральной пространственной
частотыξ0 = 0, η0 = 0 в интервале ±ξмакси±ηмакс (Рис. 3.2), и, следовательно, то же
частотное распределение соответствует функции а (х, у) в изображении спектра на
Рис. 3.3.
Последний член в (3.3), − ∗
exp(4 ) ⊃ − ∗[−( +
2 ), − ], описывает волновой фронт, комплексно-сопряженный предметному
волновому фронту в плоскости голограммы и промодулированный высокой несущей
частотой. (Заметим, что соответствующая дифрагированная волна не является ни
антипараллельной, ни комплексно- сопряженной исходной предметной волне.)
Спектр рассматриваемого члена определяется соотношением
− ∗
exp(4 ) ⊃ − ∗ [−( + 2 ), − ].
Согласно (3.5), его абсолютная величина пропорциональна [ S* [—(ξ+ 2ξr), -η)]
|, т. е. это частотное распределение подобно распределению на Рис. 3.2, но является

47
его зеркальным отражением и смещено по оси -ξ на величину 2ξr, а граничные
значения частот равныξ =-2ξr ± ξмакс иη = ±ηмакс.
На Рис. 3.3 построены абсолютные значения спектров волн на выходе из
голограммы. Видно, что использование опорной волны с соответствующей высокой
пространственной частотой (т. е. большим углом падения θ) обеспечивает угловое
разделение волн, образующих изображение. Как следует из Рис. 3.3, чтобы избежать
наложения волны нулевого порядка на волны, образующие изображение, опорная
пространственная частотаξопорндолжна удовлетворять соотношению
| опорн − |= | − − | = + ≥ 3 макс. (3.8)
Гдеξ0 — центральная пространственная частота спектра предмета (которую мы
считаем равной нулю). Даже для того, чтобы выполнялось условие минимального
углового разделения волн |ξопорн-ξ0 |= 3ξмакс, светочувствительный материал должен
обладать высоким разрешением в направлении х. Заменим в (3.2) комплексную
амплитуду а (x, у) предметной волны в плоскости голограммы ее компонентой в
направлении +х с наивысшей пространственной частотой
В аргументе косинуса содержится частота полосξr + ξ0 + ξмакс,которая должна
быть записана на светочувствительном материале. Если учесть условие (3.8):ξr +
ξ0=3ξмакc, то оказывается, что пространственная частота будет равна 4ξмакc. е. в 4 раза
превосходит наивысшую пространственную частоту предмета. Высокая
разрешающая способность, которую должна иметь регистрирующая среда при
получении голограммы с наклонным опорным пучком, является своего рода платой за
разделение двойниковыхизображений. Однако достоинства этого метода — высокое
качество изображения и широкий выбор объектов голографирования —
компенсируют его недостатки, особенно если имеются высокоразрешающие
фотоэмульсии. Перекрытие волн, обусловленное интермодуляцией, обычно не играет
существенной роли, так как величина члена, описывающего этот эффект, быстро
падает с удалением частоты от центральной (Рис. 3.3). Ослабить
нежелательныеэффекты, обусловленные перекрытием волн, можно также, делая
амплитуду опорной волны значительно больше амплитуды предметной волны. Тогда
первый член в скобках в (3.3) становится малым по сравнению с третьим и четвертым
членами.

48
РИС. 3.4 Схема, показывающая, что световые пучки могут перекрываться в
плоскости изображения, несмотря на угловое разделение, тогда как в положении 2
перекрытиеотсутствует.
Хотя соотношение (3.8) является условием того, что в области
пространственных частот волны не перекрываются (условие углового разделения), из
него не следует, что в плоскости изображения, образованного одной из
дифрагированных волн, будет отсутствовать нежелательное излучение,
обусловленное другими волнами. Это легко видеть из Рис. 3.4, где показано
образование действительного изображения в плоскости, находящейся сравнительно
недалеко от плоскости голограммы (положение 1). На Рис. 3.4 изображены пучки
света, исходящие из двух точек освещенной голограммы. Здесь выполняется условие
углового разделения дифрагированных волн, тем не менее в область действительного
изображения (положение 1) наряду с волной, формирующей действительное
изображение, попадает нежелательный свет засчет волн нулевого порядка. Наиболее
простой выход из этого положения заключается в выборе достаточно высокой
пространственной частоты опорной волны, а также достаточно большого расстояния
между предметом и голограммой, что устраняет перекрытие волн в плоскости
изображения (положение 2).
Другой, более сложный выход состоит в отфильтровании компонент с
нежелательными пространственными частотами. Это можно сделать, если
использовать линзу, формирующую в задней фокальной плоскости частотный спектр
поля комплексных амплитуд, существующего в непосредственной близости за
голограммой, а затем закрыть весь спектр, кроме его полезной части. Из-за сложности
этого метода он применяется в тех случаях, когда разрешающая способность
регистрирующей среды очень низка. Предположим, например, что мы хотим
зарегистрировать на панхроматической пленке голограмму транспаранта,
центральная пространственная частота которого ξ0= 0, а максимальнаяξмакс =ηмакс= 20
мм-1
(что соответствует детали предмета, имеющей протяженность 0,025 мм). Если
мы хотим записать голограмму с наклонным опорным пучком, то в соответствии с
настоящим параграфом абсолютное значение минимальной пространственной
частоты опорной волны, необходимое для полного углового разделения
дифрагированных волн, составит |ξопорн| = 3ξмакс = 60 мм-1
, а наивысшая частота полос,
которую нужно зарегистрировать, будет 4ξмакс = 80 мм-1
. Эти величины лежат как раз
в пределах разрешающей способности данной пленки. Правда, увеличивая угол
междуопорным и предметным пучками, т. е. увеличивая |ξопорн| можно достигнуть еще
большего углового разделения волн, но тогда будет превзойден предел разрешения
пленки. Найдем угол между пучками в схеме на Рис. 3.1, соответствующий частоте 60
мм-1
:
≈ = опорн = (0,633 ∙ 10 )(6 ∙ 10 ) = 3,79 ∙ 10 рад = 2,16°,
где λ = 0,633*10-3
мм — длина волны излучения гелий-неонового лазера. Поскольку
угол очень мал, опорный пучок должен быть сформирован с помощью светоделителя,
помещенного между голографируемым транспарантом и голограммой. Такая схема
получения голограммы показана на Рис. 3.5. Поскольку θ составляет всего 2,16°,
дифрагированные волны будут наверняка перекрываться в плоскости
действительного изображения, если поперечные размеры транспаранта сравнимы с
расстоянием от него до голограммы. В этом случае нужно применить метод
фильтрации пространственных частот. Были предложены также методы, основанные
на полном внутреннем отражении нежелательных волн.

49
РИС. 3.5. Схема получения внеосевых голограмм при малом угле между
предметным и опорным пучками.
Попутно следует заметить, что если на одной и той же фотопластинке
регистрируются сразу несколько голограмм, то путем надлежащего выбора опорных
волн, используемых при их получении, можно обеспечить угловое разделение
восстановленных воли, формирующих изображения. Предположим, что имеются две
наложенные друг на друга голограммы, каждая из которых является голограммой
предмета, расположенного на осиz и освещенногоаксиальной плоской волной. Оба
предмета имеют среднюю пространственную частотуξо=0, η0 = 0 и полосу
пространственных частот ±ξмакс, ±ηмакс. Одна голограмма получена с плоской опорной
ВОЛНОЙ, имеющей пространственную частотуξопорн = -ξr = -3ξмакс и ηопорн = 0; другая
— с плоской опорной волной, имеющей пространственные частотыξопорн = -ξr - 2ξмакс=
-5ξмакс и ηопорн = 0.Основываясь на анализе, подобном тому, с помощью которого были
получены спектры на Рис. 3.3, мы найдем, что спектральный отклик каждой
отдельной голограммы, освещаемой соответствующей ей опорной волной, имеет вид,
показанный на Рис. 3.6, а и б. При освещении двух наложенных друг на друга
голограмм плоской волной с пространственной частотой ξ = —ξr получается спектр,
изображенный на Рис. 3.6, в.

50
РИС. 3.6. Пространственный спектр излучения,прошедшего через голограмму: а — на
стадии регистрации и восстановления использовалась опорная волна с простран-
ственной частотой –ξr == -3ξмакс; б — пространственная частота –ξr –ξмакс; в — спектр
света, прошедшего через две голограммы а и б, освещенные плоской волной с
пространственной частотой – ξr .
Волны, формирующие изображение, не перекрываются, причем условие
углового разделения имеет вид
∆ опорн ≥ 2 макс, (3.9)
где∆ опорн — разностьпространственных частот опорныхволн, а макс — ширина
полосыпространственных частот предмета в направлении х. Пространственная
частота восстанавливающей волны может быть произвольной.
3.1.2. Формирование действительного изображения
Если транспарант освещается плоской волной, то возникающая в ближнем
поле дифракционная картина является проекцией голографируемого транспаранта.
Каждый малый участок голограммы, на которой регистрируется эта картина,
содержит информацию только о малой части предмета. Предположим, что голо-
грамма, полученная по схеме, показанной на Рис. 3.1, освещается теперь исходной
плоской опорной волной. На Рис. 3.7 показаны освещающие голограмму и
восстановленные волны, а также расположенное на оси мнимое изображение.
(Предполагается, что предметом является простой транспарант, представляющий
собой непрозрачный экран с тремя небольшими отверстиями.) Так как освещение

51
предмета не является диффузным, а сам предмет не вызывает диффузного рассеяния
падающей на него плоской волны, то наблюдатель из данного положения будет
видеть свет только от одного из пятен мнимого изображения. Он может обнаружить
все три пятна, поворачивая голову, т. е. переводя взгляд с одного места изображения
на другое. Это утомительный и практически непригодный способ. Поэтому, когда
предмет не вызывает диффузного рассеяния света, лучше наблюдать проекцию
действительного изображения. Для этого в плоскость действительного изображения
следует поместить диффузно рассеивающий экран из матового стекла; в этом случае
можно рассматривать все изображение из одного положения. (Менее удобный способ
наблюдения состоит в превращении мнимого изображения в действительное с
помощью линзы.
РИС. 3.7 Наблюдение мнимого изображения предмета, освещавшегося на
стадии получения голограммы недиффузным светом.
При освещении голограммы исходной опорной волной, как на Рис. 3.7, мнимое
изображение возникает на оси там, где находился исходный предмет, и не имеет
сферических аберраций и аберраций косых пучков. Для действительного
изображения, которое образуется не на оси, это не так. Рассмотрим теперь два способа
освещения голограммы, позволяющие получить свободное от аберраций и
расположенное на оси действительное изображение. Мы полагаем, что
голограммабыла получена по схеме Рис. 3.1, где центр предмета располагается на
осиz, а опорная плоская волна распространяется под углом – θ к ней.В первом
способе голограмма освещается плоской волной, составляющей с осьюz угол +θ, как
показано на Рис. 3.8.

52
РИС. 3.8 Формирование действительного изображения, расположения на оси.
Такое освещение голограммы соответствует умножению ее амплитудного
пропускания, описываемого формулами (3.1) и (3.2), на множитель rехр (—2πiξrx),
гдеξr = (sinθ)/λ,. Из всех дифрагированных волн мы будем рассматривать только
волну, формирующую действительное изображение. Эта волна имеет в плоскости
голограммы комплексную амплитуду а*r2
, сопряженную с амплитудой исходной
предметной волны в этой же плоскости. Анализ легко проводится в плоскости
пространственных частот. Частотный спектр функции а* {х, у) определяется
выражением (3.5):
( , ) = ∗(− , − )
= ∗(− , − ) +
2
(1 − − ) ,
Предположим, чтоБОЛНОВОЙ фронт с комплексной амплитудой а* (х, у)
переместился на расстояниеd вдоль осиz вправо от голограммы. Согласно (5.26),
спектр пространственных частот комплексной амплитуды волны на расстоянииd
имеет вид
′( , ) = ( , ) −
2
(1 − − ) ,
(3.10)
Если мы совершим обратное фурье-преобразоваиие обеих частей
•соотношения (3.10), то получим, что комплексная амплитуда в плоскости, удаленной
на расстояние d от голограммы, пропорциональна величине, комплексно-сопря-
женной пропусканию s* (х, у) голографируемого транспаранта. Следовательно,
интенсивность на расстоянииd пропорциональна интенсивности в плоскости
транспаранта. Таким образом, голограмма формирует изображение исходного
транспаранта, которое является действительным (волны, формирующие изображение,
сходятся к изображению) и располагается на осиz. Плоскость изображения находится
справа от голограммы на том же расстоянииd, на котором слева от нее был помещен
голографируемый предмет. Фотопластинка, помещенная в плоскости изображения,
зарегистрирует изображение без использования линзы.
.

53
РИС. 3.9 Другой метод получения действительного изображения, расположенного на
оси.
Второй способ образования действительного изображения показан на Рис. 3.9.
Следует обратить внимание на то, что восстанавливающий пучок падает на
голограмму справа (в то время как исходный опорный пучок падал на нее слева) и
является антипараллельным, а следовательно, сопряженным исходному опорному
пучку. Однако в плоскости голограммы комплексная амплитуда освещающего ее
волнового фронта естьrехр (—і2пξr x), т. е. совпадает с амплитудой освещающего
пучка, показанного на Рис. 3.8. Пучок на Рис. 3.9 отличается от пучка на Рис. 3.8
только тем, что распространяется справа налево. Поскольку комплексные амплитуды
в плоскости голограммы одинаковы в обеих схемах, к схеме на Рис. 3.9 применимы
наши предыдущие рассуждения. Единственное различие заключается в том, что
теперь действительное изображение формируется на оси на расстоянииd слева от
голограммы, в соответствии с направлением распространения освещающего пучка, и
положение изображения совпадает с исходным положением предмета. Для этого
лучи, формирующие изображение, должны быть антипараллельны лучам,
исходившим из объекта, а соответствующие волны должны быть сопряженными.
Схемы на Рис. 3.8 и 8.9 можно с равным успехом использовать для получения
действительного изображения при условии, что голограмма тонкая. Для толстых
голограмм больше подходит схема на Рис. 3.9, поскольку закон Брэгга (критерий
максимальной интенсивности волны, дифрагированной объемной решеткой)
одинаково удовлетворяется при использовании как исходной опорной волны, так и
сопряженной волны (см. гл. 1, § 6). Если регистрирующую среду нельзя считать
строго двумерной, то схема на Рис. 3.7 больше подходит для получения мнимого
изображения,, а схема на Рис. 3.9 — для получения действительного изображения.
3.1.3. Требования к когерентности излучения при получении внеосевых
голограмм
Длина когерентности лазерного излучения, используемого для получения
голограммы по схеме.Рис. 3.1 с наклонным опорным пучком, должна быть больше,
чем при применении схемы с осевым опорным пучком. Мы можем найти связь между
необходимой длиной когерентности и геометрией схемы получения голограммы,

54
рассмотрев сначала интерференцию двух плоских волн (Рис. 3.10). Смодулированный
предметный (сигнальный) пучок распространяется по оси, а опорный пучок
составляет с ним угол θ. Отсюда следует, что длины путей от источника до
фотографической пластинки для всех лучей пучка одинаковы, в то время как для
опорного они различны; наибольшая разность равнаl1.
Рис. 3.10. Максимальная разность хода l1лучейв плоскости голограммы для
наклонной плоской опорной волны.
Мы можем сделать так, чтобы длина пути центрального опорного луча была
равна длине пути сигнальных лучей; в таком случае максимальная разность хода
сигнального и опорного пучковбудет составлять
2
=
2
sin| | =
2 (3.11)
где а — размер пластинки; | θ | — величина угла, который опорный пучок составляет с
осью z, и — соответствующая пространственная частота опорной волны. Таким
образом, даже при отсутствии какой-либо информации в предметном пучке длина
когерентности должна быть по крайней мереl1/ 2.
Теперь рассмотрим дополнительную разность хода сигнального пучка,
обусловленную дифракцией на транспаранте, содержащем некоторую информацию
(Рис. 3.11). При малых значениях θмакс наибольшая длина пути предметных лучей
отличается от длины пути немодулированного сигнального пучка на величину
=
макс
− ≈
2 макс (3.12)
Здесьd — расстояние между транспарантом и пластинкой; θмакс —
максимальный угол дифракции плоской волны на транспаранте и ξмакс —
максимальная пространственная частота транспаранта. Таким образом, если длина
пути центрального луча опорного пучка равна длине пути центрального луча сигналь-
ного пучка, то окончательное требование к длине когерентностилазерного излучения
принимает вид
∆ >
2
+ =
2
+
2 макс (3.13)

55
РИС. 3.11. Максимальная разность хода l2 для сигнального пучка, несущего
информацию о предмете.
При осевом расположении Габора ξr= 0 и необходимая длина когерентности LH
должна быть всего лишь равна или больше 12. Существует несколько методов
получения внеосевыхголограмм, которые позволяют использовать излучение
примерно с такой же длиной когерентности. В этих методах применяется особое рас-
положение оптических элементов, и они предназначены для получения голограмм в
тех случаях, когда для освещения используется нелазерный свет или излучение
многомодовых импульсных лазеров.
3.2. Голографирование с наклонным опорным пучком при
диффузном освещении предмета
Как уже указывалось, один из недостатков метода освещения
голографируемого транспаранта плоской (или сферической) волной заключается в
трудности наблюдения мнимого изображения. Другой недостаток проявляется, даже
когда мы наблюдаем действительное изображение. Пылинка или дефект на
поверхности какого- либо оптического элемента, используемого для расширения
освещающего предмет пучка, при восстановлении может вызвать появление
концентрических колец, локализованныхв плоскости изображения. Эта кольцевая
структура видна на Рис. 3.12. Она напоминает зонную пластинку и представляет
собой спроецированную на плоскость предмета картину интерференции сферических
волн (возникших при рассеянии света на пылинке) с невозмущенной волной,
освещающей транспарант.
Третий недостаток заключается в том, что при освещении голографируемого
транспаранта плоской волной интенсивностьпрошедшего через него света изменяется
в широких пределах, определяемых вариациями пропускания предмета. Этот недоста-
ток также является следствием проецирования сигнальной волны на голограмму.
Если необходимо произвести линейную голографическую запись, то интенсивность
опорного пучка должна быть больше интенсивности сигнального пучка по всей
плоскости голограммы. В тех местах, где сигнальный пучок слаб, отношение
интенсивностей пучков будет слишком большим и, следовательно, дифракционная
эффективность соответствующего участка голограммы мала.

56
Рис.3.12. Действительное изображение транспаранта, восстановленное с
голограммы, полученной при недиффузном освещении. (По Лейту и Упатниекс[3.2].)
Видны шумы в виде системы колец.
Эти недостатки можно устранить, если использовать диффузное освещение
голографируемого транспаранта. Для этого между лазерным источником и
транспарантом обычно помещают диффузный экран, например матовое стекло. Так
как диффузный экран рассеивает свет в широком телесном угле, то теперь
наблюдателю не нужно менять положения головы, чтобы видеть весь транспарант. То
же справедливо и для наблюдения мнимого изображения, образованного
восстановленной предметной волной, по крайней мере в том интервале углов, в
который попадают падающие на голограмму и регистрируемые ею лучи.
Хотя фаза диффузного света, идущего от предмета, представляет собой быстро
меняющуюся пространственную функцию координат в плоскости голограммы, свет в
этой плоскости может сохранять когерентные свойства. Это происходит, если 1)
исходная волна, освещающая диффузный экран, пространственно когерентна по всей
площади экрана, 2) максимальная длина пути света от источника до голограммы через
диффузный экран отличается от длины пути опорного пучка не больше, чем на длину
когерентности и 3) экран остается неподвижным. Схема установки для получения
голограммы при диффузном освещении транспаранта показана на Рис. 3.13, а, а схема
наблюдения мнимого изображения — на Рис. 3.13, б.

57
РИС. 3.13. Освещение голографируемого транспаранта через диффузный
экран.а — получение голограммы; б — наблюдение мнимого изображения.
РИС. 3.14. Фотографии действительных изображений диффузно освещенного
предмета, которые получены при освещении голограммы пучком уменьшающего
диаметра.
Голограмма, полученная при диффузном освещении, обладает рядом
замечательных свойств. Поскольку диффузный экран имеетболее широкий спектр
пространственных частот, чем транспарант, он рассеивает свет в широком телесном
угле, так что каждая точка в плоскости голограммы получает свет от всех точек
транспаранта. На стадии восстановления через любую часть голограммы можно
наблюдать все мнимое изображение предмета. При смещении направления
наблюдения изображение видно с другой стороны. Если мы имеем голограмму

58
двумерного транспаранта и хотим наблюдать в некоторой плоскости его
действительное изображение, то сможем получить его целиком даже в том случае,
когда голограмма оказалась разбитой или поврежденной, так что сохранился лишь
небольшой участок. Конечно, разрешение изображения тем хуже, чем меньше
площадь оставшейся части голограммы (как и в случае линзы конечных размеров). На
Рис. 3.14 представлены фотографии трех действительных изображений, восста-
новленных с одной и той же голограммы, освещаемой лазерным пучком
уменьшающегося диаметра. Способность нелокально регистрировать информацию,
свойственная голограммам, полученным при диффузном освещении предмета, может
оказаться ценной для хранения информации. В то время как при использовании
микроизображений царапина или пятно на них приводит к полному уничтожению
части информации, информация, записанная на голограмме при диффузном
освещении, оказывается сравнительно невосприимчивой к подобным дефектам
регистрирующей среды.
РИС. 3.15. Максимальные углы между опорными и предметными лучами,
Использование диффузного освещения выдвигает повышенные требования к
разрешающей способности регистрирующей среды. Максимальная частота полос,
которая должна быть зарегистрирована на голограмме, определяется максимальным
углом, образованным предметными лучами с направлением распространения

59
опорного пучка. На Рис. 3.15, а показан угол ,образованный плоской опорной волной
и лучами недиффузного света, прошедшего через транспарант. Помещая диффузный
экран между источником света и транспарантом, можно существенно увеличить угол
(Рис. 3.15, б).
3.2.1. Трехмерные изображения
Большинство трехмерных объектов отражает свет более или менее диффузно,
так что их голограммы обладают только что рассмотренными свойствами. Кроме этих
свойств, существуют другие, связанные с трехмерностью предмета. Так как
голограмма может восстанавливать волну, являющуюся точной копией исходной
предметной волны, то мнимое изображение, из которого кажется исходящей
восстановленная волна, будет обладать такой же глубиной и параллаксом, как и
исходный объект. Изображение, которое воспринимает наблюдатель правым и левым
глазом, формируется лучами, проходящими через различные участки голограммы;
таким образом, каждый глаз наблюдателя воспринимает изображение из разных точек
зрения (Рис. 3.16).
Эти точки зрения совпадают с теми, из которых видел исходный предмет
наблюдатель, рассматривавший его через отверстие, определяемое размерами
голограммы. Как при наблюдении изображения, так и при наблюдении самого
объекта создается одинаковое ощущение глубины. При перемещении наблюдателя
смещается его точка зрения и, так же как при рассматривании исходного объекта,
наблюдается параллакс. На Рис. 3.17 для демонстрации параллакса приведены две
фотографии одного и того же мнимого изображения, полученные под разными
углами. Конечно, полное представление о трехмерности изображения можно
получить, только рассматривая его через голограмму своими глазами.
РИС. 3.16. Наблюдение мнимого
изображения трехмерного объекта.

60
РИС. 3.17 Две фотографии одного и того же мнимого изображения сделанные
под разными углами зрения.
Действительное изображение трехмерного предмета, восстановленное с
помощью голограммы, обладает одним удивительным свойством — его глубина
инвертирована. В этом случае мы говорим, что изображение
являетсяпсевдоскопическим. Рассмотримполучение голограммы простого
трехмерного предмета, представляющего собой два разделенных в пространстве
точечных источника (Рис. 3.18, а), и последующее восстановление действительного
изображения при освещении голограммы волной, сопряженной исходной опорной
волне (Рис. 3.18, б).
РИС. 3.18, а — получение голограммы предмета,состоящего из двух точек,
находящихся на разных расстояниях от голограммы; б — формирование
действительного изображения.

61
На стадии получения голограммы точка P1 расположена ближе к плоскости
голограммы, чем точка Р2. На стадии восстановления действительные изображения
точек Р1 и Р2 образуются в их исходных положениях (в соответствии с изложенным в
§ 1, п. 2, настоящей главы). Однако чтобы наблюдатель увидел действительное
изображение, т. е. воспринял свет, распространяющийся справа налево и испытавший
дифракцию наголограмме, он должен занять положение, показанное на Рис. 3.18, б.
Точка Р2 будет для него ближе, чем Р1 Таким образом, наблюдатель увидит обратное
по глубине расположение точек по отношению к исходной картине, которую он видел
при регистрации света, распространявшегося через фотопластинку слева направо. Это
свойство приводит к ряду необычных визуальных эффектов. Предположим, что Р1 и
Р2 — точки наповерхности некоторого трехмерного предмета и что существует
диапазон углов наблюдения, в котором часть поверхности вблизи точкиP1 заслоняет
окрестность точки Р2. При освещении предмета под углами в пределах этого
диапазона на голограмме регистрируется информация только о поверхности вблизи
Р1. При восстановлении наблюдатель, смотрящий под соответствующими углами, но
с другой стороны голограммы, видит только область вокруг Ему кажется, что точка
Р2, находящаяся на переднем плане изображения, заслоняется областью,
расположенной позади нее,— чувство, противоречащее повседневному опыту.
Противоречие между воспринимаемым изображением и действительным видом
предмета, каким его запомнил наблюдатель, вызывает ощущение неудов-
летворенности при наблюдении псевдоскопических изображений.
Рис. 3.19. Получение голограммы, формирующей ортоскопическое действительное
изображение.
От псевдоскопичности действительного изображения можно избавиться.
Предположим, что на стадии получения голограммы используется линза, с помощью
которой формируется действительное изображение освещенного лазерным светом
предмета, т. е. фотопластинка помещается в сходящуюся волну, как на Рис. 3.19, и с
помощью соответствующего опорного пучка записывается голограмма сходящейся
волны. При освещении голограммы исходной опорной волной восстанавливается
исходная предметная волна. Восстановленная волна сходится, образуя, как и
исходная, действительное изображение справа от голограммы. Поэтому изображение
имеет нормальную глубину, т. е. являетсяортоскопическим. Если же голограмму
осветить сопряженной опорной волной, распространяющейся справа налево, то из
исходного положения предмета будет расходиться волна, сопряженная исходной

62
предметной волне. Это значит, что для рассматриваемого случая в плоскости, в
которой строила изображение линза, будет теперь формироваться мнимое
изображение этого изображения. Наблюдателю, смотрящему через голограмму слева,
точки, находившиеся на заднем плане изображения, сформированного линзой, теперь
будут казаться расположенными ближе точек, располагавшихся на переднем плане,
следовательно, мнимое изображение будет в этом случае псевдоскопическим.
Если с помощью голографического процесса формируется псевдоскопическое
изображение некоторого изображения, которое уже является псевдоскопическим по
отношению к исходному предмету, то результирующее голографическое
изображение будет ортоскопическим по отношению к этому предмету.
Следовательно, если в качестве предметной волны для получения первой голограммы
использовать восстановленную другой голограммой волну, образующую
псевдоскопическое изображение, то освещение первой голограммы волной,
сопряженной ее опорной волне, приведет к образованию ортоскопического
изображения. Тех же результатов можно добиться с помощью автоколлимационных
устройств, которые позволяют обойтись без получения второй голограммы,
необходимой для обращения псевдоскопическогоизобраячения в ортоскопическое и
наоборот.
3.2.2. Пятнистая структура.
Поскольку волны, восстанавливаемые с голограмм, полученных с
диффузными предметными пучками, являются копиями волн, испускаемых
предметами, освещенными лазерным светом, в этом случае возникают те же
проблемы, что и при наблюдении диффузно рассеивающих объектов, освещенных
лазером. Наблюдателю, рассматривающему либо изображение, либо предмет, мешает
пятнистая структура, из-за которой наблюдаемая поверхность кажется состоящей
из отдельных светящихся точек.
Размер отдельных пятен определяется наименьшей апертурой приемника
(например, радужной оболочки глаза) и расстоянием до наблюдаемой поверхности. В
любой области поверхности, меньшей предела разрешения, имеется множество
рассеивающих центров. Компоненты комплексной амплитуды света, рассеянного
разными центрами, будут иметь разные фазы, но так как свет когерентен, то разность
фаз постоянна во времени и компоненты амплитуды складываются. Наблюдатель,
неспособный разрешить отдельные рассеивающие центры, воспринимает свет,
исходящий от (этой) малой области, как небольшое пятно равномерной интен-
сивности, величина которой определяется результирующей фазой складывающихся
амплитуд. Даже при равномерном освещении поверхности будет казаться, что
интенсивность наблюдаемого отраженного света хаотически меняется от пятна к
пятну, так как интенсивность в каждом из них определяется суммарной амплитудой,
возникающей при когерентном сложении амплитуд рассеянного света, имеющих
случайные фазы. Если наблюдатель изменит свое положение так, чтобы видеть
поверхность под другим углом, то световые лучи, идущие от поверхности к
наблюдателю, пройдут по другому пути. Фазы компонент, образующих суммарную
амплитуду света, идущего от каждого из предельно разрешимых при наблюдении
пятен, также изменяются, и соответственно с этим изменяется яркость пятен.
Непрерывное смещение наблюдателя ведет к усреднению интенсивности,
изменениями которой обусловливается пятнистая структура, в результате чего
улучшается качество восприятия. Однако такой способ не очень удобен при
рассмотрении мелких деталей, и наличие пятнистой структуры в этом случае будет
препятствовать качественному восприятию и создавать неудобства при наблюдении

63
3. 3. Схемы получения голограмм различного типа
3.3.1. Голограммы Френеля.
Если светочувствительный материал, предназначенный для регистрации
голограммы, например фотопластинка, помещается в области дифракции ближнего
поля (области дифракции Френеля) на произвольном расстоянии от источника
опорной волны, то получается голограмма, которую называют голограммой Френеля.
Это наиболее простой способ регистрации голограммы, так как он позволяет получать
голограмму и затем восстанавливать волновой фронт без использования линз или
каких-либо других оптических устройств. За исключением некоторых особенностей,
свойственных безлинзовым фурье-голограммам, которые мы обсуждали ранее, все
рассмотренные ранее свойства голограмм представляют собой свойства голограмм
Френеля. Последние относятся к наиболее распространенному типу голограмм и
могут быть получены по схемам, представленным на рис. 3.19; общий вид установки
представлен на рис. 3.20, а фотография полученной голограммы — на рис. 3.21. Для
освещения голограммы на стадии восстановления можно использовать установку,
схема которой показана на рис. 3.22; при этом образуется трехмерное изображение
предмета, подобное показанному на рис. 3.23. На рис3.24 приведена
использовавшаяся на ранней стадии развития голографии схема получения
голограммы с осевым опорным пучком.
3.3.2. Голограммы сфокусированных изображений
При использовании в схеме получения голограмм линз или других оптических
элементов, формирующих изображение, и соответствующем их расположении можно
получить голограмму, обладающую рядом полезных свойств.
Предположим, что фотопластинку на Рис. 3.19 смещают так, что она
оказывается в плоскости центрального сечения изображения, сформированного
линзой (Рис. 3.20). Если теперь ввести опорный пучок, то мы получаем голограмму
сфокусированного изображения.
РИС. 3.20. Получение голограммы сфокусированного изображения.
На стадии восстановления с исходной опорной волной часть изображения,
восстановленного с помощью голограммы, будет мнимой, а часть — действительной.
Наблюдатель не заметит существенного различия между этим изображением и
изображением, восстанавливаемым с помощью безлинзовой голограммы Френеля.

64
Однако теперь угол, под которым может рассматриваться изображение, ограничен
апертурой линзы, и центр трехмерного изображения будет казаться расположенным в
плоскости голограммы. Достоинство этого способа заключается в уменьшении
требований к когерентности излучения источника, используемого на стадии восста-
новления. Связь между размером минимального разрешаемого элемента изображения
∆ s, степенью пространственной когерентности излучения (определяемой
протяженностью источника ∆ r) и расстоянием от источника до голограммыzr
описывается формулой:
∆ = ∆
РИС. 3.21. Изображение, восстановленное с голограммы сфокусированного
изображения, освещенной протяженным источником.
При z1 —> 0 (голограмма сфокусированного изображения) на стадии
восстановления можно использовать источник больших размеров с низкой
пространственной когерентностью излучения и получить при этом изображение с
достаточно хорошим разрешением. Следовательно, голограмму сфокусированного
изображения можно ярко осветить с помощью протяженного источника. Конечно, z1=
0 только для какой-то одной плоскости предмета, и при восстановлении с
протяженным источником разрешение элементов изображения, расположенных по
разные стороны от этой плоскости, будет ухудшаться (Рис. 3.21).
Следующая формула связывает разрешение ∆ восстановленного
изображения со спектральной шириной ∆ излучения, используемого для освещения
голограммы:
∆ =
∆
где z1— снова расстояние между голограммой и изображением; λ — длина волны,
соответствующая середине интервала ∆ , а θr — угол между опорным пучком и
нормалью к плоскости голограммы (считается, что предмет и изображение
расположены на оси). Мы видим, что при малых θr и z1 спектральная ширина

65
источника, используемого при восстановлении изображения, может быть большой —
это не оказывает значительного влияния на размер предельно разрешаемого элемента
изображения. Можно воспользоваться даже источником белого света; в этом случае
центральное сечение изображения, локализованное в плоскости голограммы, будет
казаться ахроматическим в то время как точки изображения, находящиеся вне этой
плоскости, будут обладать цветовой дисперсией и казаться размытыми, что
свидетельствует об уменьшении разрешения.
3.2.3. Фурье-голограммы
В последующих трех пунктах мы сравним несколько методов получения
голограмм, которые позволяют формировать в плоскости голограммы распределение
амплитуд, соответствующее либо точному фурье-образу предмета, либо
произведению фурье-образа на медленно меняющийся фазовый множитель. Общим
для указанных методов является следующее требование: опорный источник должен
располагаться строго в той же (входной) плоскости, чтои предмет. Поэтому наш
анализ относится, строго говоря, к плоским предметам (т. е. транспарантам) и теряет
силу, если размеры предмета заметно выходят за пределы входной плоскости. Как
правило, мы считаем, что предмет освещается плоской волной. В некоторых
исследуемых здесь схемах получения голограмм используется линза. Если линза
расположена перед предметом, то плоской волной освещается линза. Если линза
расположеназа входной плоскостью, то предполагается, что она воздействует на свет,
идущий как от предмета, так и от опорного источника.
РИС. 3.22. Схема получения фурье-голограммы(размеры линзы
даны не в масштабе).
Фуръе-голограммой мы называем голограмму в том случае, если на ней
регистрируется интерференция двух волн, комплексные амплитуды которых в
плоскости голограммы являются фурье- образами предмета и опорного источника.
Как мы увидим в гл. 14, такие голограммы применяются в качестве пространственных
фильтров для опознавания образов, а свойства преобразования Фурье лежат в основе
процесса опознавания. В этом случае пропускание опорного источника
пространственно модулировано (протяженный источник). Здесь же мы ограничимся
рассмотрением точечных опорных источников.

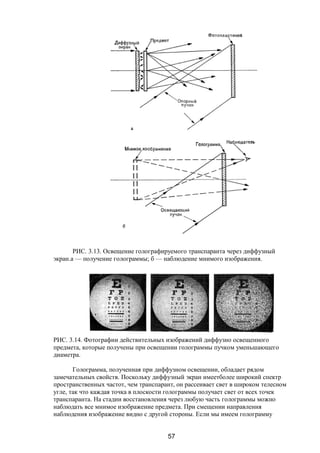
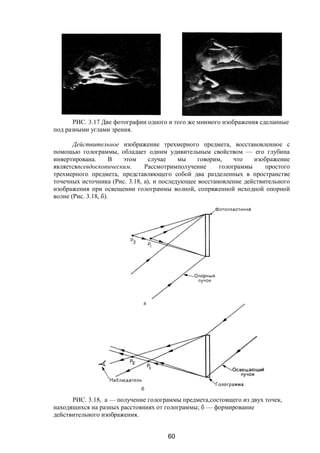
66
Фурье-образ двумерного предмета может быть сформирован в задней
фокальной плоскости линзы. Схема получения фурье-голограмм по методу
ВандерЛюгта показана на Рис. 3.22. Если s (х, у) — пропускание транспаранта,
помещенного в передней фокальной плоскости линзы, то амплитуда предметной
волны в плоскости голограммы, совпадающей с задней фокальной плоскостью линзы,
есть S(ξ. η), где s (,х, у) ⊃S(ξ. η),. В передней фокальной плоскости расположен также
точечный источник ( + , ), фурье-образом которого является плоская волна с
амплитудой ехр(-2πiξb). Это плоская волна играет роль опорной волны и так же, как и
S(ξ. η), освещает заднюю фокальную плоскость линзы. Интенсивность
интерференционной картины, образованной двумя фурье-образами, описывается
выражением
= [exp(−2 ) + ( , )][exp(−2 ) + ∗( , )]=
=1+| ( , )| + + ( , ) exp(2 ) + ∗( , ) exp(−2 ). (3.14)
Предположим, что проявленная голограмма имеет пропускание t (х, y) ~I. Если
голограмма освещается распространяющейся вдоль осиz плоской волной с
постоянной амплитудой r0, то произведениеr0t(х,у) представляет собой комплексную
амплитуду W дифрагированного света непосредственно за голограммой:
~ ( , )~ = 1 + | | + (2 ) + ∗ (−2 ) (3.15)
Линза, расположенная непосредственно перед голограммой или
непосредственно после нее (Рис. 3.23), будет создавать в задней фокальной плоскости
поле, соответствующее произведению обратногофурье-образа функции W на
фазовый множитель сферической волны. Если мы регистрируем только
интенсивность света в задней фокальной плоскости линзы, то можем опустить
фазовый множитель сферической волны. Как показано на Рис. 3.23, члены нулевого
порядка из (3.15) будут фокусироваться в этой плоскости примерно в начале
координат. Обратный фурье-образ третьего члена в правой части выражения (3.15),
s(х -b, у), представляет собой исходное пропускание, смещенное на величину Ъ от
начала координат в положительном направлении оси х. Фурье-образ четвертого члена
есть S* [-(х + b), -у], т. е. представляет собой функцию, сопряженную и зеркально
симметричную исходному пропусканию, смещенную на расстояниеb от начала
координат в отрицательном направлении оси x. Ив том и в другом случае
дифрагировавший на голограмме свет сходится, образуя действительные изображе-
ния, расположенные в одной плоскости. Фотография изображений, формируемых
фурье-голограммой в задней фокальной плоскости восстанавливающей линзы,
показана на Рис. 3.24. Поскольку фотопленка регистрирует только интенсивность, то
изображения отличаются лишь тем, что одно является зеркальным отражением
другого.

67
РИС. 3.23. Восстановление двух действительных изображений с
фурье-голограммы.
Полезное свойство фурье-голограмм, записанных с плоской опорной волной,
состоит в том, что формируемые ими изображения остаются неподвижными при
перемещении голограммы. Благодаря этому с голограмм, записанных на пленке,
намотанной на барабан, можно было бы восстанавливать
неподвижныеизображенияпри вращении барабана. Для доказательства
нечувствительности положения изображения к перемещению голограммы
представим себе, что комплексная амплитуда, выражаемая третьим членом (3.15),
смещена на величину ξ0 в направлении + ξ, так что теперь она описывается
выражением
( − , ) exp[2 ( − ) ].
Если условия освещения голограммы остались прежними и формируется
соответствующая им дифрагированная волна, то комплексная амплитуда поля в
задней фокальной плоскости линзы будетравна
ℱ [ ( − , ) exp[2 )] exp(−2 ) =
= [ ( , ) exp(−2 ) ∗ ( − )] exp(−2 ) =
= ( − , ) exp(−2 ),
где означает обратное преобразование Фурье и где мы использовали
соотношения (4.11), (4.21), (4.29) и учли, что свертка любой функции с б-функцией
дает исходную функцию. Фазовый множитель ехр(− ) не входит в выражение
для интенсивности, и интенсивность изображения
s(х — b, у)s* (х — b, у)
совпадает с наблюдающейся при неподвижной голограмме.
Голограмма фурье-образа транспаранта должна регистрировать
интенсивность, изменяющуюся в широких пределах. Свет, прошедший через
транспарант без отклонений (нулевой порядок), фокусируется линзой в яркую точку в
начале координат частотной плоскости (плоскость голограммы). Гармоники с более

68
высокими пространственными частотами, дифрагировавшие на транспаранте и
фокусирующиеся в других местах частотной плоскости, имеют гораздо меньшую
интенсивность. Если интенсивность опорногопучкадостаточна для линейной записи
низкочастотной компоненты, то она может оказаться слишком большой для
линейной записи слабых высокочастотных гармоник. В результате дифракционная
эффективность для высоких частот может оказаться низкой. Если на стадии
восстановления комплексные амплитуды высокочастотных компонент не превышают
амплитуд шумов, обусловленных рассеянием света на голограмме, то информация о
предмете теряется.
РИС. 3.24, Фотография плоскости изображенияфурье-голограммы.
3.2.4. КВАЗИ-ФУРЬЕ-ГОЛОГРАММЫ
Квази-фуръе-голограммой мы называем голограмму, которая регистрируется
при соблюдении следующих условий: 1) фотопластинка расположена в задней
фокальной плоскости линзы и 2) предмет-транспарант и опорный точечный
источник находятся в одной и той же плоскости, расположенной перед линзой или за
ней, но не являющейся передней фокальной плоскостью линзы. Предмет или линза (в
зависимости от того, что помещено ближе к источнику) освещается плоской волной.

69
РИС. 3.25. Образование квази-фурье-голограммы;входная плоскость
расположена вплотную к линзе.
Такая схема с транспарантом и опорным точечным источником,
расположенным вплотную к линзе, показана на Рис. 3.25. Мы знаем (см. гл. 6, § 2),
что в этом случае амплитуда предметной волны на голограмме есть фурье-образ
транспаранта, умноженный на фазовый множитель сферической волны. Выясним
теперь роль этого множителя. Комплексную амплитуду предметной волны в
плоскости голограммы можно представить в виде:
( , ) = exp − ( + ) ( , ) =
= − ( + ) ( , ),
(3.16)
Гдес=ia/λf, ξ=x2/λf, η=y2/λf, S(ξ, η)⊂s(x1, y1) и ехр [— (iπ/λf) (х2
2 + y2
2)] —
фазовый множитель сферической волны. Множитель ехр [— (iπ/λf) (х2
2 + y2
2)], как
нетрудно видеть, представляет собой пропускание тонкой рассеивающей линзы с
фокусным расстоянием — f [см. (6.15)]. Таким образом,а (х2, у2) можно рассматривать
как пропускание системы, состоящей из транспаранта с пропусканием S (ξ, η) и
помещенной вплотную к нему рассеивающей линзы с фокусным расстоянием — f.
Аналогично а * (х2, у2) соответствует пропусканию системы, состоящей из
транспаранта с пропусканием S* (ξ, η), расположенного вплотную к собирающей
линзе с фокусным расстоянием + f.
Если для получения голограммы используется опорный точечный источник,
лежащий в одной плоскости с транспарантом, то фазовый множитель сферической
волны в выражении для а (х2, у2) выпадает. На Рис. 3.25 показан точечный источник,
смещенный по оси x1 на - b от начала координат плоскости х1у1. Он создает
сферическую волну, распределение фаз которой в плоскости х2у2 (если в точке с
координатами х2 = 0, у2 = 0 мы приписываем фазе нулевое значение) выражается
формулой (3.3)

70
( , ) = + + 2 .
(Тонкая линза с малой кривизной ее поверхностей создает лишь почти
постоянный фазовый сдвиг световой волны, испускаемой точкой плоскости,
расположенной вплотную к линзе.) Вспомним, что в (3.3) z1 — отрицательная
величина. В схеме на Рис. 3.25 z1 =-f. Следовательно, комплексная амплитуда
сферической опорной волны на голограмме имеет вид:
= exp − + + 2 .
(3.17)
В результате интерференции волн с амплитудамиr и а (х2, у2) возникает
картина со следующим распределением интенсивностей:
= + ∗
+ + S(ξ,η)exp − + exp − + + 2 +
+ ∗ ∗( , ) exp − + exp − + + 2
= = + ∗
+ ( , ) exp 2
+ ∗ ∗( , ) exp − 2
= + | | + (ξ, η) exp(2 ) + ∗ ( , ) exp(−2 ).
(3.18)
Полученное выражение тождественно выражению (3.14), которое описывает
фурье-голограмму, следовательно, голограмма, зарегистрированная по схеме Рис.
3.25, обладает теми же свойствами.
Можно показать, что такими же свойствами обладает
квази-фурье-голограмма, при получении которой предмет и источник уже не
располагаются в плоскости, прилегающей вплотную к линзе.
Оно описывает комплексную амплитуду света, приходящего от транспаранта
с пропусканием t(x1, y1) в заднюю фокальную плоскость линзы, где находится
голограмма. Транспарант помещен на произвольном расстоянииd перед линзой и
освещается плоской волной. Мы видим, что комплексная амплитуда равна
произведению фурье-образа функции t (x1, y1) на фазовый множитель сферической
волныexp − − ( + ) , который не зависит от вида t (х1, у1). Вид фазового
множителя не зависит от того, предмету или опорному источнику мы приписываем
пропускание t (х1, у1), поскольку и тот и другой находятся на одном и том же
расстоянииd от линзы. Следовательно, в произведениях аr* и а*r, определяющих
интерференционную структуру голограммы, фазовые множители будут
отсутствовать и останутся только фурье-образы предмета и опорного источника в
соответствии с (3.18).
Предположим теперь, что предмет и опорный источник находятся позади линзы
и расположены на расстоянииd от ее задней: фокальной плоскости и что линза
освещается плоской волной. Выражения (3.16) — (3.18) и вытекающие из них
следствия останутся справедливы, если заменить f наd. В этом случае можно»
считать, что падающий на предмет сходящийся пучок света возникает из
параллельного пучка, освещающего расположенную вплотную к предмету линзу с
фокусным расстояниемd.

71
3.2.5. Безлинзовые фурье-голограммы
Предположим, что из схемы на Рис. 3.25 удалена линза, а опорный точечный
источник по-прежнему располагается в той же плоскости, что и предмет-транспарант
(Рис. 3.26). Предметный волновой фронт, который будет записан на голограмме,
теперь представляет собой картину ближнего поля, или картину дифракции Френеля
от транспаранта. Тем не менее мы увидим, что пропускание голограммы, полученной
по схеме, показанной на Рис. 3.26, похоже на пропускание фурье-голограммы.
Члены, формирующие изображение, опять представляют собой произведения фурье-
образов и фазовых множителей, линейно зависящих от координат
РИС. 3.26. Схема получения безлинзовой фурье-голограммы.
плоскости голограммы. Поэтому термин безлинзовая фуръе-голограмма
применяется для голограмм, получаемых без использования линз, но с
расположенным в плоскости предмета точечным опорным источником. Как и прежде,
предмет освещается плоской волной.
Согласно (5.33) и соображениям, изложенным в гл. 5, § 5, комплексная
амплитуда света предметной волны в плоскости х2у2 голограммы на Рис. 3.26 может
быть записана в виде
( , ) = exp [− ( + )] ×
× ( , ) exp − ( + ) ×
× exp[2 ( + )] =
= exp − ( + ) ( , ),
(3.19)
Где ( , ) ⊂ ( , ) − + , = ,
d — расстояние между плоскостями , их2у2и ξ’=x2'/λd=η’=y2/λd. Если голограмма
была зарегистрирована с опорной волной = exp [−( / )( + )]exp (−2 ′ )
[выражение (3.17) при f =d], то компоненты пропускания голограммы, ответственные
за формирование изображения, выражаются формулой, аналогичной (3.18):
( , ) ∗
+ ∗( , ) =
= ( , ) exp(2 ) + ∗ ∗
( , ′)exp (−2 ′ )
(3.20)

72
Здесь тоже отсутствует фазовый множитель сферической волны, зависящий от
координат плоскости голограммы х2 и у2. Таким образом, изображение, формируемое
голограммой, будет оставаться неподвижным при ее перемещении. Зависящий от x1 и
у1 фазовый множитель сферической волны, на который в выражении для
фурье-образа умножается пропускание предмета s (х1, y1), не оказывает влияния на
свойства восстановленного изображения. Его можно рассматривать просто как часть
пропускания предмета, а именно считать, что он соответствует линзе, расположенной
вплотную к транспаранту.
Если голограмма освещается аксиальной плоской волной, то комплексные
амплитуды дифрагированных голограммой волн, формирующих изображение,
пропорциональны правой части выражения (3.20). Пропускание голограммы (3.20)
подобно пропусканию фурье-голограммы, за исключением того, что F(ξ', η') и
комплексно-сопряженная функция не являются фурье-образами функций s(x1, y1) и s*
(-x1, -y1), а представляют собой фурье-образы произведений этих функций на фазовые
множители сферических волн. Чтобы, освещая голограмму плоской волной, получить
фурье-образ ее пропускания, необходима линза, как на Рис. 3.23. [Заметим, что ξ’ и η'
в (3.20) отличаются постоянным масштабным множителем=d/f от пространственных
частот ξ=x2/λfи η=y2/λf, входящих в выражение (3.16), которое описывает
преобразование Фурье, осуществляемое линзой с фокусным расстоянием f. Запишем
ηи ξ' в виде ξ'= ξ/ и η' = η/ и воспользуемся теоремой подобия, соотношение (4.22).
Тогда найдем, что преобразование Фурье, которому подвергаются члены выражения
(3.20) и которое осуществляет линза с фокусным расстоянием f, приводит к
уменьшению изображения в  раз по сравнению со случаемd = f]. В результате
преобразования получаем, что комплексные амплитуды света в плоскости х3у3
изображения, находящегося в задней фокальной плоскости линзы, пропорциональны
выражениям
[( − ), ] exp − [( − ) + ] ,
∗[−( − ), − ] exp [( − ) + ] ,
умноженным на фазовые множители сферической волны, которые вводит линза,
используемая на стадии восстановления. Если регистрируется интенсивность
изображения, то фазовые множители роли не играют. Интенсивности | s [(x3–b), у3]
|2
и | s[ - (ах3 + b), -у3]|2
соответствуют расположенным в плоскости х3уз прямому и
перевернутому изображениям с координатами центров (b/, 0) и (-b/, 0).
Несмотря на то, что при освещении плоской опорной волной безлинзовая
фурье-голограмма формирует изображение, подобное тому, которое восстанавливает
фурье-голограмма, на практике часто бывает проще осветить голограмму исходным
точечным опорным источником. Тогда, как и у других голограмм, положение
мнимого изображения совпадает с исходным положением предмета.
Основным в безлинзовой фурье-голографии является следующее требование:
кривизна сферического фронта, описываемого фазовым множителем сферической
опорной волны, должна быть такой же, как кривизна сферического фронта,
описываемого фазовым множителем предметной волны. Нечувствительность
положения изображения к перемещению голограммы успешно использовалась для
получения составных голограмм, информационная емкость которых снижена до
необходимого минимума и которые позволяют осуществлять стереоскопическое
наблюдение трехмерных изображений.

73
3.2.6. Безлинзовые голограммы Фраунгофера
Осевые голограммы, зарегистрированные в области дальнего поля предмета,
позволяют наблюдать одно изображение без искажающего влияния со стороны
другого. Томпсон и др. [3.15] использовали эту возможность для исследования
размеров и формы движущихся аэрозольных частиц, что, по-видимому, явилось
одним из первых практических применений голографии. Картина дифракции
Фраунгофера (картина дальнего поля) может быть зарегистрирована на
фотопластинке, помещенной на расстоянииd от предмета, при условии [см. (5.37)]
+
≪ , (3.21)
Здесь x1 и y1 — координаты произвольной точки предмета, а λ— длина волны света.
Предположим, что предмет, пропускание которого описывается функцией s
(х1, у1), имеющей фурье-образом функцию S (ξ, η), освещается плоской волной в
направлении, нормальном к плоскости х1, у1(Рис. 3.27). Выражение (5.39) описывает
комплексную амплитуду а (х2, у2) света, падающего на плоскостьх2у2, располо-
женную в области дальнего поля на расстоянииd отх1у1
( , ) = exp − ( + ) ( , ),
(3.22)
В работе [3.15] голограмма Фраунгофера регистрировалась при освещении
предмета плоской когерентной волной. Фотопластинка экспонировалась в области
дальнего поля. Свет, прошедший через предмет без дифракции, служил опорной
волной. Тогда, так же как и для других осевых голограмм, при условии надлежащего
экспонирования и обработки позитивной голограммыконтраст восстановленного
изображения совпадает с контрастом объекта. На стадии восстановления голограмма
освещается плоской волной, тождественной той, что использовалась для освещения
предмета.
РИС. 3.27. Образование безлинзовой голограммыФраунгофера.
Поскольку на стадии регистрации голограммы используется плоская опорная
волна, фазовый множитель сферической волны [см. (3.22)] не устраняется и
изображение, формируемое голограммой Фраунгофера, смещается при перемещении
голограммы. Можно считать, что в голограмму как бы встроена линза, соответ-

74
ствующая сферическому фазовому множителю. При перемещении голограммы линза
перемещается вместе с ней и в свою очередь перемещает изображение.
Если предмет настолько мал, что его можно рассматривать как расположенный
на оси точечный рассеиватель (как в случае аэрозольной частицы), то при записи
формируется интерференционная картина, напоминающая зоннуюпластинку. Если
пропускание небольшого предмета можно аппроксимировать -функцией ( ) ⊃
( , ) = , то амплитуда a(x2,y2) описываемая выражением (3.22), будет
представлять собой немодулированную сферическую волну. На стадии восстанов-
ления амплитуды а(x2,y2), записанной на голограмме Фраунгофера, будет
формироваться идентичная волна, исходящая из мнимого изображения. В плоскости
действительного изображения с обратной стороны голограммы эта волна создает
только однородный фон, который почти не мешает наблюдению действительного
изображения.
Мы можем определить голограмму Фраунгофера как голограмму, на которой
регистрируется интерференционная структура, образованная дифракционной
картиной от предмета в области дальнего поля и сферической волной от опорного
источника, некомпланарного предмету. Как правило, опорный источник рас-
полагается на бесконечности и опорная волна является плоской.
3.2.7. Голограммы Фраунгофера, полученные с линзой
Выражение (3.22) для комплексной амплитуды а (х2, у2) дифракционной
картины дальнего поля совпадает с формулой (3.16),которая описывает комплексную
амплитуду света, наблюдаемого в задней фокальной плоскости линзы с фокусным
расстоянием f, расположенной непосредственно перед когерентно освещенным
предметом. Следовательно, очевидно, что с помощью линзы регистрируется
голограмма Фраунгофера, если 1) расположенный вплотную к линзе транспарант
освещается плоской волной, 2) используется плоская (например, внеосевая) опорная
волна и 3) предметная и опорная волны интерферируют в плоскости голограммы,
помещенной в задней фокальной плоскости линзы. Полученная таким образом
голограмма будет иметь свойства, подобные свойствам безлинзовой голограммы
Фраунгофера. На Рис.
ЛИТЕРАТУРА
3.1. LEITH Е. N., UPATNI- EKS J., Journ. Opt. Soc. Amer., 57, 975 (1967). Получение
голограмм с помощью систем, создающих ахроматические полосы.
3.2.LEITH Е. N., UPATNI- EKS J., Journ. Opt. Soc. Amer., 54, 1295 (1964).
Восстановление волнового фронта при диффузном освещении и для трехмерных
объектов.
4. Виды голограмм.
5. Действительное и мнимое изображения.
6. Схемы получения голограмм.
7. Требования к когерентности излучения.

75
4. Роль разрешающей способности регистрирующей
среды и размеров голограммы
Рассмотрев основные типы плоских голограмм, вернемся к ограничениям,
которые налагает регистрирующая среда на свойство голограмм формировать
изображение. Рассмотрим с помощью простой модели мы, как сказывается
ограниченность разрешающей способности на качестве изображения.
4.1. Ограниченная разрешающая способность регистрирующей
среды
Начнем анализ с рассмотрения плоскостиxz на Рис. 4.1, где показан предмет,
точечный опорный источникR (хr, 0, — zr) и фотопластинка. Плоскость, нормальная к
оси и содержащая точечный опорный источник, находится от регистрирующей
пластинки на расстоянииzr. Как показано на Рис. 4.1, луч, идущий от опорного
источника до произвольной точкиQ (х2, 0, 0) на поверхности пластинки, образует угол
θr с нормалью к пластинке (осьюz) и, следовательно, характеризуется
пространственной частотой Предположим, что тонкий пучок таких лучей от
опорного источника интерферирует в окрестности точкиQ с аналогичным пучком
лучей от предмета, образующим угол θ0 с осьюz. Последнему соответствует
пространственная частота Интенсивность интерференционной картины, которая
должна быть зарегистрирована, выражается формулой
= [exp(2 ) + exp(2 )][exp(−2 ) + + exp(−2 )]
= 2 + 2 cos[2 ( − ) ].
(4.1)
РИС. 4.1. К рассмотрению влияния ограниченности разрешающей
способности регистрирующей среды.
Здесь мы предположили, что волны имеют единичные амплитуды. Частота
косинусоидального члена ξ0 —ξrпредставляет собойчастоту полос
интерференционной структуры. Для малых углов ее можно представить следующим
образом:

76
− =
−
≈
−
(4.2)
Предположим теперь, что среда идеально регистрирует все пространственные
частоты, не превышающие некоторой предельной частоты ξc,но в то же время
абсолютно не в состоянии зарегистрировать компоненты структуры с частотой,
превышающейξc. Если предмет рассеивает свет в широкой полосе пространственных
частотξ0 это означает, что при данном значении ξrне все пространственные частоты
могут быть зарегистрированы голограммой. Другими словами, на голограмме будут
зарегистрированы только те лучи, углы которых с осьюz не выходят за пределы
некоторого интервала значений. На Рис. 4.1 один такой предельный луч, ждущий от
предмета к произвольной точкеQ плоскости голограммы, пересекает плоскость
опорного источника в точке xмакс. Мы будем называть такой луч краевым;
соответствующая ему пространственная частота ξо,макс удовлетворяет соотношению
,макс − = с (4.3a)
Если краевой луч составляет с осьюz угол θ0,макс, то, используя (3.24), можно
написать
,макс
≈ с =
с
(4.3б)
или
,макс − ≈ (4.3в)
С помощью Рис. 3.29 можно определитькоординатуxмакс
:
макс −
= ( + ) ≈ + ≈
−
+
откуда
макс ≈ + (4.4)
Аналогично для координаты ξмин точки пересечения другого краевого луча
имеем
мин ≈ − (4.5)
Заметим, что краевые лучи пересекают плоскость опорного источника в
точках, координаты которых в использованном здесь приближении малых углов не
зависят от координат точки Q плоскости регистрации.
Введем теперь гипотетический непрозрачный экран, помещенный в плоскости,
нормальной к осиz и содержащей опорный источник. Экран имеет отверстие с
центром в точкеR, где находится опорный источник. Края отверстия определяются
точками (XМАКС, 0,-ZR) И (XМИН, 0, -ZR). Через отверстие проходят все тепредметные лучи,
в результате интерференции которых с опорными лучами в некоторой точкеQ
плоскости голограммы образуются полосы, разрешаемые и регистрируемые
светочувствительной средой. Если же луч, идущий от предмета к произвольной
точке Q плоскости голограммы, или продолжение этого луча пересекает наш
гипотетический экран, то этот луч не будет зарегистрирован голограммой.
Некоторые из таких лучей показаны на Рис. 4.2. Это правило справедливо для
предметов, расположенных как перед плоскостью опорного источника, так и за ней.

77
Мы можем распространить свой анализ и на случай двумерного экрана, вводя про-
странственные частоты v, где v2
= ξ2
+ η2
, и предельную частоту vc; тогда отверстие в
экране представляет собой окружность радиусомzrλvc с центром в точкеR.
Обратимся теперь к рассмотренным ранее схемам получения голограмм
различного типа и, применив наглядный способ экрана, покажем, как сказывается
наличие предельной пространственной частоты на свойствах регистрируемых
голограмм. Начнем со схемы получения безлинзовой фурье-голограммы, показанной
на Рис. 3.26. Так как голографируемый транспарант и точечный опорный источник
находятся в одной и той же плоскости — плоскости экрана, то отверстие в экране
ограничивает только размерпредмета, который может быть зарегистрирован. В
пределах этого размера лучи всех направлений (всех пространственных частот) будут
полностью зарегистрированы голограммой (опять-таки в приближении малых углов).
То же выполняется для схемы на Рис. 3.25, содержащей линзу. Таким образом, эти две
схемы позволяют осуществлять голографическую регистрацию предметов,
содержащих высокие пространственные частоты, на материалах с низкой
разрешающей способностью.
РИС. 4.2. Лучи от предмета, которые не регистрируются голограммой.
Теперь рассмотрим схему для получения осевой голограммы Френеля при
освещении голографируемого транспаранта аксиальной плоской волной. Опорный
источникR лежит на осиz на бесконечности (хr = 0,zr = ∞). Действие нашего
гипотетического экрана, расположенного на бесконечности, выражается в том, что он
устанавливает предельные значения углов, образуемых лучамис осью Z. Если
обозначитьθмакс=xмакс/zr и θмин=xмин/zrто (3.26) и (3.27) принимают вид
макс ≈ , мин ≈ , (4.6)

78
РИС. 4.3. Влияние ограниченности разрешающей способности
регистрирующей среды при получении осевых голограмм.
Эти соотношения показывают,что экстремальные углыθмаксиθмин, которые
составляют краевые лучи с осьюz, непосредственноопределяются предельным
угломθс (Рис. 4.3). Плоская предметная волна, распространяющаяся в направлении |
θс | и имеющая пространственную частоту |ξс | = | θс |/λ соответствует компоненте
пропускания предмета с той же пространственной частотой | ξс |. Следовательно,
голограмма не будет регистрировать те компоненты пропускания предмета,
пространственная частота которых превышает | ξс| , что в свою очередь ведет к огра-
ничению разрешения изображения. Разрешение изображения, достижимое в этом
случае, эквивалентно тому, которое может иметь контактный снимок предмета,
полученный на том же регистрирующем материале.
С помощью Рис. 4.4 можно понять, к чему приводит ограниченность
разрешающей способности регистрирующей среды в том случае, когда
дифрагировавший на предмете аксиальный плоский волновой фронт интерферирует
с наклонной плоской опорной волной. В такой схеме формируется голограмма
Френеля с несущей частотой. Соотношения (3.26) и (3.27), записанные через предель-
ные углы θмакс и θмин, которые определяются экраном, принимают вид
макс = − , мин ≈ − , (4.7)
Из Рис. 4.4 мы видим, что если уголθс не слишком велик, то лишь
ограниченный диапазон положительных пространственных частот,
дифрагированных предметом, попадет на фотопластинку,не пересекая экрана,
ограничивающего интервал углов. Один из таких лучей, идущий от предмета под
углом θс к оси z, показан на Рис. 3.32. Отрицательные пространственные частоты
предмета обрезаются значительно в меньшей степени, чем положительные (и
наоборот, если опорная волна имеет положительную пространственную частоту).
Такая неравномерность записи положительных и отрицательных пространственных
частот может ухудшить

79
РИС. 4.4 Влияние ограниченности разрешающей способности среды при получении
голограмм с наклонной плоской опорной волной разрешение изображения. Чтобы
избежать этого, предельная частота ξс должна быть высокой. Более того, для полного
разделения волн нулевого порядка и дифрагированных волн, формирующих
изображение, частота ξс должна примерно в 4 раза превышать наибольшую
пространственную частоту предмета
4.2. Размер голограммы
Если матрица голограмм предназначается для хранения информации, причем
количество сохраняемой информации велико, то очевидно, что размер каждой
отдельной голограммы должен быть мал. Мы считаем, что влияние размеров
голограммы на качество изображения аналогично влиянию линзы конечных
размеров. Основной результат справедлив и для голограммы, если только заменить
апертуру линзы апертурой голограммы.
Разрешение изображения, формируемого как голограммой, так и линзой,
определяется фурье-образом когерентной передаточной функции оптического
устройства, т. е. функцией рассеяния. Чем больше размеры голограммы, тем выше
максимальная пространственная частота предмета, которая может быть ею
воспринята и тем уже функция рассеяния. Если размер голограммы должен быть
ограничен по таким соображениям, как получение максимальной плотности хранения
информации, то важно наиболее выгодно использовать имеющуюся в распоряжении
поверхность регистрирующей среды. Если мы примем, что разрешающая спо-
собность среды достаточно высока, чтобы среда могла воспринять все
пространственные частоты, идущие от предмета, то наша задача сводится к
равномерной регистрации всех частотных компонент от всех частей предмета.
Линзовая оптическая система, в которой предмет освещается аксиальной
плоской волной, дает максимальное разрешение изображения только для точек
предмета, расположенных вблизи оптической оси. Разрешение изображения линейно
падает с увеличением расстояния от оси. Наилучший способ освещения предмета
состоит в использовании сходящейся сферической волны, фокусирующейся в
плоскости линзы L2. В этом случае для всех точек предмета достигается наивысшее
возможное разрешение изображения, отвечающее данному размеру линзы. Схемы
аналогичных пространственно-инвариантных голографических систем показаны на
Рис. 3.25 и Рис. 3.28. Эти системы позволяют оптимально использовать ограниченную
площадь голограммы, так как на небольшую по размерам голограмму падают от всех
точек предмета лучи в одном и том же диапазоне пространственных частот, благодаря

80
чему разрешение изображения имеет одинаковую достаточно высокую величину на
всех участках. Поскольку пучок лучей от каждой точки предмета перекрывает всю
площадь голограммы, то информация о каждой точке предмета хранится всеми
точками голограммы. Таким образом, голограммы, полученные по схемам Рис. 3.25 и
Рис. 3.28, не чувствительны к пыли и царапинам, подобно голограммам, полученным
при диффузном освещении предмета, и, кроме того, не обладают пятнистой
структурой. Основная проблема, связанная с получением голограмм по схемам Рис.
3.25 и 3.28, заключается в регистрации интенсивности света, меняющейся в широком
диапазоне. Как уже отмечалось, нулевой пространственной частоте соответствует
большой пик интенсивности.
4.3. Максимальная эффективность плоских голограмм
Если нужно восстановить максимально яркое изображение, то полезно знать
максимальную дифракционную эффективность, которой обладают голограммы
различного типа. Здесь мы определим эффективности [3.18] плоских амплитудных и
фазовых голограмм, образующихся в результате интерференции плоской наклонной
опорной волны r = rехр (2πiξх) и аксиальной смодулированной плоской предметной
волны с амплитудой а.
Начнем с рассмотрения амплитудной голограммы. Если предположить, что
зависящая от экспозиции частьtE амплитудного пропускания проявленной
голограммы пропорциональна интенсивности регистрируемой интерференционной
картины, то
~ = [ + exp(2 )][ + exp(−2 )] = + + 2 (2 )
или
= + (2 ) (4.8)
Для плоской амплитудной голограммы полное амплитудное пропусканиеt в
соответствии с формулой (1.14) определяется какt= t0 — tE, гдеt0 — пропускание
неэкспонированной пластинки. Как правило,t может изменяться от 0 до 1 (еслиt0 = 1).
Максимальный диапазон измененияt достигается приtEo =1
/2 иt1 =1
/2. При этих
условиях
= − = 1 −
1
2
−
1
2
(2 ) =
1
2
−
1
2
(2 ) =
=
1
2
−
1
4
(2 ) −
1
4
exp (−2 )
(4.9)
Пусть голограмма освещается аксиальной плоской волной единичной
амплитуды. Тогда амплитуда волны, распространяющейся за голограммой, равна
пропусканию t, определяемому формулой (4.9). Мы видим, что свет дифрагирует
только в нулевой и +1-й и —1-й порядки. Поскольку амплитуда дифрагированной
волны первого порядка составляет х
/4 амплитуды падающего света, то интенсивность
волны первого порядка равна х
/16 интенсивности падающего света. Дифракционная
эффективность определяется как отношение мощности дифрагированной волны
первого порядка к мощности излучения, освещающего голограмму. В настоящем
случае, когда голограмма освещена равномерно, мы можем в этом определении
заменить мощность излучения на его интенсивность. Итак, эффективность равна
1/16, или 6,25%. На практике регистрирующие среды не являются линейными во всем
диапазоне экспозиций, соответствующем изменению пропусканияt от 0 до 1.

81
Поэтому, если требуется восстановить волновой фронт без нелинейных искажений, то
максимальная эффективность, равная 6,25%, не может быть достигнута.
Несколько большей дифракционной эффективностью могут обладать
голограммы, пропускание tE которых описывается не ко синусоидальной, а
прямоугольной периодической функцией х. (Таким пропусканием могут обладать
голограммы, синтезированные с помощью вычислительных машин.) В этом случае в
одной половине периода пропусканиеtE равно нулю, а во второй - единице. Первые
два члена разложения прямоугольной функции в ряд Фурье имеют вид [3.19, 8.21*]:
=
1
2
+
2
(2 ) − ⋯ + ⋯ =
1
2
+
1
[ (2 ) + (−2 )] − ⋯
(4.10)
Приt = 1 —tE дифракционная эффективность равна (1/π)2
= = 10,1%. Кроме
того, на решетках прямоугольного профиля возможна и дифракция более высоких
порядков.
Запишем комплексное пропускание светочувствительной среды в виде
= [ ( )].
Для фазовой голограммы в отсутствие потерь мы можем считать t постоянной
величиной, равной единице;
= [ ( )]. (4.11)
Хотя фазовые голограммы осуществляют линейную запись только при малых
значениях , для нахождения максимально возможной эффективности голограммы
снимем с это ограничение. Светочувствительный материал экспонируется таким
образом, что фазовый сдвиг (х), приобретаемый плоской волной при
прохождении обработанной голограммы, пропорционален интенсивности света,
действовавшей при экспозиции, т. е.
( )~ + = 2 (2 ) = + (2 ). (4.12)
Пропускание голограммы t принимает вид
= exp( ) exp[ (2 )] ~ + (2 ) (4.13)
Если опустить постоянный фазовый множитель exp( ), то (3.35) можно
представить в виде ряда Фурье:
= [ ( )] = ( ) ( ),
гдеJn — функция Бесселя первого рода n-го порядка. Если голограмма t освещается
аксиальной плоской волной единичной амплитуды, то амплитуда дифрагированной
волны + 1-го порядка описывается функцией J1 ( ), которая показана на Рис. 4.5. Ее
максимальное значение равно 0,582, а максимальная эффективность составляет
33,9%.

82
Фі
РИС. 4.5. Амплитуда J1 ( ) дифрагированной волны первого порядка для
синусоидальной фазовой решетки.
Несколько больше света дифрагирует в первый порядок, если фаза меняется
как прямоугольная функция х и принимает значение = 0 в течение одной половины
периода и значение = π — в течение другой. Тогда пропускание t равно +1 при = 0
и —1 при = π. Такая голограмма подобна амплитудной голограмме, пропускание
которой описывается прямоугольной функцией, причем амплитуда света,
дифрагированного в первый порядок, в два раза больше, чем при амплитудной
модуляции. Следовательно, такая голограмма обладает в 4 раза большей
эффективностью, равной 40,4%.
1. Разрешающая способность регистрирующей среды.
2. Размер голограммы.
3. Эффективность плоских голограмм.

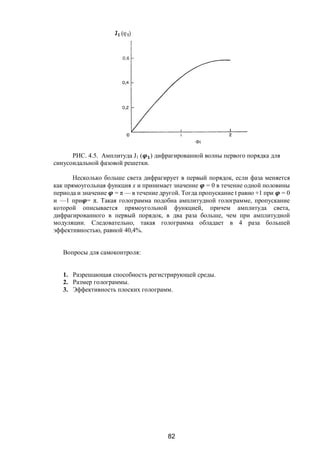
83
5. ДИФРАКЦИЯ СВЕТА НА ОБЪЕМНЫХ
ГОЛОГРАММАХ
Отклик элементарной объемной голограммы при ее освещении когерентным
излучением можно рассматривать с точки зрения теории связанных волн. Однако,
прежде чем применить эту теорию, воспользуемся пространственно-частотными
представлениями, введенными в гл. 5, чтобы понять, как образуется элементарная
объемная голограмма, и вывести аналитические выражения, описывающие ее
дифракционную периодическую структуру.
5.1. Голограмма, образованная двумя плоскими волнами.
Рассмотрим две плоские волны единичной амплитуды, распространяющиеся в
плоскостиyz. Проникая в регистрирующую среду, они интерферируют (Рис. 5.1).
Согласно закону Снеллиуса,
= exp( ) exp[ (2 )] ~ + (2 ) (5.1)
где n — показатель преломления регистрирующей среды. Здесь ΩsиΩr — углы
между направлениями распространения волн и осью z в воздухе, а и ярд —
соответствующие углы в регистрирующей среде. Как и в гл. 3, § 1, мы начнем со
сложения комплексных амплитуд плоских волн в среде и затем, чтобы найти
интенсивность, умножим результирующую комплексную амплитуду на ком-
плексно-сопряженную ей величину. В результате получаем следующее выражение
для комплексной амплитуды в среде:
( , ) = exp[− 2 ( + )] + exp [− 2 ( + )]
и
∗
= = 2 + 2 2 [( + ) + ( − ) ], (9.2)
где
= , = ,
=
(1 − ) /
, =
(1 − ) /
,
и λ — длина волны в среде.
Предположим сначала, что среда обладает фоточувствительностьютолько в
одной плоскости z=z1=const. В этой плоскости второй член в аргументе косинуса в
(5.2) ( − ) представляет собой постоянную добавку к фазе и его можно
положитьравным нулю. Оставшееся слагаемое соответствует фазовому члену,
определяющему частоту интерференционных полос в направлении у:
=
1
= − =
−
,
(5.3)
гдеdy — расстояние между соседними максимумами косинусои-дального
распределения интенсивности в интерференционных полосах в направлении осиу.

84
РИС. 5.1. Образование элементарной голограммы
.
Поскольку распределение интенсивности, описываемое формулой (5.2), не
зависит от х, максимумы интенсивности полос располагаются на лежащих в
плоскости z=z1 линиях, параллельных оси х и находящихся на расстояниях dy друг от
друга. Формула (5.3) дает связь междуdy, длиной волны и направлениями волн в
среде. Аналогичная формула справедлива и для соответствующих величин вне
регистрирующей среды, т. е. в воздухе. Это нетрудно показать, используя закон
Снеллиуса:
=
−
=
/
(1/ ) Ω − Ω
=
Ω − Ω
, (
5.4)
где = — длина волны в воздухе.
Аналогичное выражение дляdy получается для объемной голограммы, если
волновые векторыS иR составляют равные углы с нормалью к поверхности (фиг. 1.4).
В этом случае = − , = − = и − = 0 . В объемной среде
интерференционная картина представляет собой совокупность поверхностей
постоянной фазы косинусоидального члена в формуле (5.2). Эти поверхности
описываются уравнением
2 ( − ) + 2 ( − ) = , (
5.5)
В случае, соответствующем фиг. 1.4, второй член в (5.5) равен нулю,a( −
) = 2 . Тогда для оставшейся части фазового члена получим
(2 ) =
В этом случае уравнение поверхностей постоянной фазы сводится ку = const.
Таким образом, эти поверхности представляют собой плоскости,
параллельные плоскостиxz. Расстояния между поверхностями, соответствующими
максимальным значениям интенсивности (поверхностями пучностей), в направлении
осиу равныdy. Если = − = ,то

85
=
1
=
1
2
, или =
2 (5.6)
что совпадает с выражением (1.10). Поскольку плоскости пучностей параллельны
осиz, то θ соответствует углам, которые каждая из интерферирующих плоских волн
составляет с этими плоскостями в среде.
Возвращаясь к (5.5) и более общему выражению для поверхностей постоянной
фазы, отметим, что уравнение (5.5) описывает плоскости, перпендикулярные
плоскостиyz [линии пересечения этих плоскостей с плоскостьюyz представляют
собой прямые линии, и в (5.5) отсутствует зависимость от х]. Угол между этими
плоскостями и осью можно определить, дифференцируя (5.5) поz:
( − ) + ( − ) = 0
или
= = −
( − )
( − )
.
(5.7)
Воспользовавшись введенными ранее обозначениями для пространственных
частот [см. (5.2)], получим
= −
(1 − ) /
− (1 − ) /
−
= −
−
−
= (
+
2
).
или
=
+
2 (5.8)
Как видно из Рис. 5.1 и формулы (5.8), поверхности пучностей элементарной
голограммы делят пополам угол между волновыми векторами интерферирующих
волн. Оси у иz на Рис. 5.1 можно, конечно, повернуть вокруг оси я на угол ф так,
чтобы осьz совпала с плоскостью пучностей. Если теперь обозначить через θ угол,
который каждый из пучков составляет с плоскостью пучностей в среде, то
соотношение (1.10) будет справедливо независимо от ориентации пучков
относительно нормали к голограмме, т. е.
2dsinθ = λ,
Из Рис. 5.1 видно также, что расстояние между соседними плоскостями
пучностей определяется соотношением
= =
− (5.9)
5.2. Закон Брэгга.
На Рис. 5.2 в соответствующем масштабе представлено поперечное сечение
элементарной голограммы, образованной в объемной светочувствительной среде.
Обычно толщина эмульсионного слоя составляет около 15 мкм. Горизонтальные
линии представляют собой следы пересечения плоскости чертежа с плоскостями

86
максимальной плотности серебра, которые соответствуют плоскостям пучностей
интерференционной картины, существовавшей в эмульсии во время экспозиции.
Предположим, что в воздухе углы между пучками при получении голограммы
составляли 30° (Рис. 5.2) и длина волны Ха = 0,633 мкм. Подставляя эти значения в
(5.4), получим, что постоянная решеткиd = 1,22 мкм. Если такую решетку осветить
исходным опорным пучком, то каждый луч до выхода из эмульсии пересечет по
крайней мере три плоскости максимальной плотности. Было бы удивительно, если бы
теория плоских голограмм, изложенная в гл. 8, описывала бы все свойства такой
объемной голограммы. Кроме того, толщина 15 мкм относительно невелика, если
сравнивать ее с толщиной других регистрирующих сред, например фотохромных
кристаллов. Поэтому при рассмотрении дифракции на таких голограммах необ-
ходимо учитывать, что каждый луч последовательно рассеивается от большого числа
периодически расположенных поверхностей максимумов плотности. Чтобы
амплитуда результирующей дифрагированной волны была максимальной, волны,
рассеянные последовательными слоями, должны быть синфазны. Для этого необхо-
димо, чтобы выполнялось определенное соотношение между длиной волны Я, углом
θ, который составляет освещающий голограмму пучок с рассеивающими
поверхностями, и расстояниемd между этими поверхностями. Это соотношение
представляет собой закон Брэгга [см. (1.12)], который можно записать в виде
2 = (5.10)
Здесь — длина волны в воздухе; — средний показатель преломления
светочувствительной среды и θ — угол, которыйосвещающий и дифрагированный
пучки составляют с рассеивающими слоями в светочувствительной среде. Закон
Брэгга определяет угол падения, если длина волны и расстояние между слоями
заданы. Если же угол падения и постоянная решетки выбираются независимо, то
закон Брэгга определяет длину волны. Таким образом, объемные голограммы,
свойства которых описываются законом Брэгга, являются селективными по
отношению к освещающему их излучению. В настоящей главе мы постараемся найти
функциональную связь между амплитудой дифрагированной волны и углом падения
(или длиной волны) восстанавливающего пучка. Мы также вычислим максимальную
возможную величину дифракционной эффективности элементарной пропускающей
или отражающей голограммы. Результаты этих расчетов существенным образом
отличаются от полученных в лекции 4 результатов для элементарных плоских
голограмм.
РИС. 5.2. Изображенная в масштабе интерференционная картина,
зарегистрированная в фотоэмульсии.

87
5.3. Теория связанных волн
Большинство теоретических работ хорошо описывают наблюдаемую угловую
и спектральнуюселективность объемных голограмм. Однако в том случае, когда
дифракционная эффективность голограммы высока, в теоретических расчетах
обязательно нужно учитывать ослабление освещающей волны при прохождении
через голограмму. Выполненные с помощью электронно- вычислительных машин
расчеты для объемных голограмм [9.2, 9.3] показали, что такие голограммы могут
обладать высокой дифракционной эффективностью; это предсказание было затем
подтверждено экспериментально. Таким образом, линейная теория [9.1, 9.6] не
объясняет всех свойств объемных голограмм. Наоборот, теория связанных волн не
только предсказывает селективный отклик объемных голограмм, но также правильно
описывает их высокую дифракционную эффективность. Согласно этой теории, в
некоторых случаях дифракционная эффективность может приближаться к 100%, что
соответствует почти полному гашению освещающей волны. При дальнейшем
изложении в настоящей главе мы будем придерживаться теории, разработанной
Когельником. Преимущество примененного им подхода состоит в том, что он
позволяет получить как аналитические, так и численные результаты и применим к
разным типам объемных голограмм (поглощающих и непоглощающих).
Здесь мы остановимся только на анализе голограмм, образованных двумя
плоскими волнами, т. е. голограмм с синусоидальной записью. В гл. 1, § 6, мы уже
приводили соображения, поясняющие, почему достаточно ограничиться
рассмотрением синусоидальных голограмм. Дело в том, что произвольная функция
пространственных координат, в данном случае голограмма, может быть разложена в
ряд Фурье, т. е. представлена в виде суммы синусоидальных решеток, каждая из
которых взаимодействует с падающим на нее светом в соответствии с предсказанием
данной теории.
5.4. Волновое уравнение
РИС. 5.3. Геометрическая схема объемной голограммы.

88
Рассмотрим объемную голограмму, схематически изображенную на Рис. 5.3.
Границы голограммы обозначены вертикальными линиямиz = 0 и z = T,
параллельными оси у. Предположим, что в результате экспонирования и проявления
голограммы в ее объеме либо диэлектрическая проницаемость, либо коэффициент
поглощения становятся синусоидальными функциями координат у иzи не зависят от х.
Отсюда следует, что плоскости постоянной диэлектрической проницаемости или
коэффициента поглощенияориентированы перпендикулярно плоскостиyz (плоскости
чертежа). Величина диэлектрической проницаемости (или
коэффициентапоглощения) меняется по закону косинуса в
направлениивекторарешетки К, лежащего в плоскостиyz и перпендикулярного
плоскостям постоянной фазы. Линии на Рис. 5.3 представляют собой следы
пересечения плоскостиyz с поверхностями, в которых синусоидально изменяющаяся
величина коэффициента поглощения или диэлектрической проницаемости имеет
максимум; они расположены на расстоянииd друг от друга и составляют угол ф' с
поверхностями голограммы. Будем считать, что абсолютнаявеличина вектора
решетки К, перпендикулярного к этим поверхностям, равна
= ⃗ =
2
(5.11)
Слева на голограмму падает плоская монохроматическая световая волна,
вектор ⃗ электрического поля которой перпендикулярен плоскости падения, т. е.
направлен параллельно оси х, нормальной к плоскости чертежа. Внутри голограммы
направление распространения волны определяется вектором ⃗, который составляет
угол с нормалью к поверхности голограммы (т. е. с осьюz).
Вектор ⃗ соответствует направлению распространения дифрагированной
волны. (Когельник показал, что с небольшими изменениями эта теория может быть
применена и в случае, когда вектор электрического поля лежит в плоскости падения.)
Прохождение волны через толстую голограмму можно описать с помощью
уравнений Максвелла для немагнитной среды, относительная магнитная
проницаемость которой μ= 1. Эти уравнениясвязывают между собой вектор
электрического поля ⃗, вектор магнитного поля ⃗ и вектор смещения ⃗в среде. В
системе единиц МКС эти уравнения имеют вид
⃗ = −
⃗
. (5.12a)
⃗ = −
⃗
+ ⃗. (5.12б)
⃗=0 (объемные заряды отсутствуют) (5.12в)
⃗=0 (5.12г)
где — магнитная проницаемость вакуума; s0 — диэлектрическая проницаемость
вакуума; — относительная диэлектрическая проницаемость материала голограммы
и — проводимость среды.
Беряrot от обеих частей уравнения (5.12а)
⃗ = −
⃗
= − ⃗
(5.13)
и дифференцируя уравнение (5.12б)

89
⃗ = −
⃗
+
⃗
(5.14)
получаем
⃗ = − (
⃗
+
⃗
) (5.15)
С другой стороны ⃗ можно записать в следующем виде:
⃗ = ( )⃗ − ∇ ⃗ (5.16)
где — оператор Лапласа. Прежде чем приравнять (5.15) и (5.16), покажем, что
первый член в правой части (5.16) равен нулю. Рассмотрим для этого уравнение
(5.12в)
⃗ = ( ⃗) = 0
Это соотношение можно записать иначе с помощью другого векторного
тождества (см. [9.7, 9.17*]), которое в нашем случае имеет вид
( ⃗) = ⃗ ( ) + ⃗ (5.17)
Поскольку вектор ⃗ параллелен оси х, а изменение диэлектрической
проницаемости происходит только в плоскостиyz, то скалярное произведение равно
нулю:
⃗ ( ) = 0 (5.18)
и из (5.17) следует, что
⃗ = 0 (5.19)
Комбинируя (5.19), (5.16) и (5.15), получаем
∇ ⃗ −
⃗
−
⃗
= 0 (5.20)
Теперь мы можем подставить в (5.20) выражения для ⃗, и соответствующие
нашему частному случаю. Так же, как и в гл. 5,§ 1, мы можем записать вектор
электрического поля у, направленный параллельно оси х, в виде скалярной величины
( , , ) = [ ( , )exp ( )], (5.21)
которая не зависит от х и осциллирует с постоянной угловой частотой со.
Опустив, как и ранее, символ действительной величины Re [ ], решим уравнение
(5.20) для комплексной величины а (y,z). Подставляя (5.21) в (5.20), получаем
∇ − + = 0, (5.22)
Можно считать, что относительная диэлектрическая проницаемость ̅
складывается из среднего значения є и синусоидально изменяющейся компоненты,
имеющей амплитуду Вектор, идущий из начала координат в любую точку среды,
можно представить в ⃗ = ⃗ + ⃗ + ⃗ (і,⃗ ⃗ и ⃗— единичные векторы, направленные
соответственно по осям х,у иz). Для принятого нами пространственного
распределения диэлектрической проницаемости поверхности = const представляют
собой плоскости,уравнения которых по аналогии с (5.6) можно записать в виде
⃗ ∙ ⃗ = ,
где вектор ⃗ — единичный вектор нормали к этим плоскостям,равный
⃗
| ⃗|
. Величина
в каждой из таких плоскостей определяется пространственной фазой 2
⃗ ⃗
= ⃗ ⃗,
где ⃗ ⃗ представляет собой расстояние плоскости = const от начала координат и

90
гдеd— измеренное вдоль направления нормали расстояние между плоскостями,
соответствующее изменению фазы на 2π.
Все вышесказанное применимо и к проводимости о, которая определяет
поглощение; изменение этих величин в пространстве описывается следующими
соотношениями:
= ̅ + ⃗ ⃗, (5.23)
= + ⃗ ⃗, (5.24)
Подставляя (5.23) и (5.24) в (5.22), получаем волновое уравнение
∇ + = 0, (5.25)
где
q = ̅ − 2 + ( − 2 ) ⃗ ⃗, (5.26)
В (5.26)
= ( ) /
= =
2
,
= ( ) /
— скорость света в вакууме (очень близкая к скорости света в
воздухе) и — длина волны в воздухе. Чтобы упростить наши расчеты, запишем
q = ( ̅) ( ̅) −
2
( ̅)
+ 2
2( ̅)
−
2( ̅)
⃗ ⃗ =
= − 2 + 2 exp ⃗ ⃗ + exp − ⃗ ⃗ =
= − 2 + 2 [exp ⃗ ⃗ + exp − ⃗ ⃗ ],
(5.27)
(5.28)
где
β = ( ̅) (5.29)
α =
2 ( ̅) (5.30)
χ =
1
2 2( ̅)
−
2( ̅)
=
1
2
(
2( ̅)
− )
(5.31)
и
α =
( )
,
(5.32)
Как будет показано ниже, параметр взаимодействия имеет особое значение в
теории связанных волн. Он описывает взаимодействие между падающей и
дифрагированной волнами. Если = 0, то нет ни взаимодействия, ни дифракции.
Оптические свойства среды обычно принято характеризовать не значением
диэлектрической проницаемости, а показателем преломления. Чтобы перейти к
такому описанию, рассмотрим сначала распространение световой волны в
однородной диэлектрической среде с большим затуханием. Решение волнового
уравнения, соответствующее плоской волне, проходящей через среду в направлении
имеет вид
= (− ),

91
где А — постоянная амплитуда и где комплексная постоянная определяется
соотношением
= ( ̅ − ) /
,
(μ= 1 и однородной среде и равны нулю.) Мы можем установить смысл величин
в (5.29) и в (5.30), выразив через эти параметры, что дает
= ( − 2 ) /
≈ + .
Это справедливо при условии ≪ , которое в большинстве случаев
выполняется. Тогда волновая функция в однородной среде принимает вид
f = (− ) exp(− ),
где — так называемая постоянная распространения, а — коэффициент
поглощения. Поскольку и определены через средние значения диэлектрической
проницаемости и проводимости голограммы, то мы можем считать,что и
представляют собой постоянную распространения и коэффициент поглощения в
эквивалентной однородной среде, где = ̅ = в и = . Это справедливо при условии
≪ .
Обозначим черезn средний показатель преломления голограммы и показатель
преломления эквивалентной однородной среды. Напомним, что показатель
преломления равен отношению скорости света в вакууме к скорости света в среде.
Поскольку при (μ= 1 последняя величина равна ( ̅ ) /
, то мы имеем
n =
( ) /
( ) / = /
, (5.33)
Подставляя это значение в (5.29), получаем
β ≪ , (5.34)
Как видно из (5.34), ограничение ≪ соответствует условию
α ≪ , (5.35)
Следует отметить, что множитель ехр (—z) в волновой функцииfпри а> 0
соответствует ослаблению. Предположим, что в результате регистрации
амплитудной голограммы величина  оказалась промодулированной; однако при
фотографической регистрации коэффициент поглощения не может стать
отрицательным. Используя (5.30) и (5.31), равенство (5.24) можно выразить через 1 и
амплитуду модуляции и показать, что, когда не выполненоусловие ≪ ,
результирующее значение поглощения можетоказаться отрицательным (при
⃗ ∙ ⃗ = 1). Поэтому введем добавочное ограничение
α ≪ , (5.36)
Аналогично (5.33) показатель преломления голограммы п представим в виде
n = ε (5.37)
Выражая n через его среднее значение и амплитуду модуляции
n1 и используя (5.23), запишем

92
n = (n + n cos ⃗ ∙ ⃗) = ε + ε cos ⃗ ∙ ⃗ (5.38)
Допустим, что
n ≪ n (5.39)
Тогда, возведя в квадрат + ⃗ ∙ ⃗ в (5.38) и пренебрегая членом
получим, что = ( ̅) [выражение, совпадающее с (5.33)] и
n =
ε
2n
=
ε
2( ̅) / (5.40)
'
Для объемных голограмм условие (5.39) обычно выполняется. Подставляя
(5.40) в (5.31), постоянную взаимодействия можно представить в виде
χ =
πn
λ
−
iα
2
(
5.41)
5.5. Решение волнового уравнения
Теперь мы должны решить уравнение в частных производных (5.25), т. е.
волновое уравнение. Для этого введем некоторые упрощающие предложения.
Во-первых, будем решать уравнение (5.25) только для углов падения, близких к тем,
которые удовлетворяют закону Брэгга. Именно при таких углах наблюдается
дифрагированная волна заметной интенсивности. Во-вторых, предположим, что в
голограмме распространяются только две волны — падающая волна и волна,
дифрагированная под углом, близким к брэгговскому. Последнее предположение
определяет нижний предел толщины голограммы, для которого справедлива данная
теория. Следствия, к которым приводит введение этих ограничений,будут
рассмотрены в конце главы.
Комплексную амплитуду падающей волны в толще голограммы можно
a = R(z)exp (−iρ⃗r⃗) (5.42)
где ⃗ имеет направление распространения волны (Рис. 5.3). Здесьфазовый множитель
exp (− ⃗ ⃗) соответствует плоской падающей волне, распространяющейся в среде, в
которой нет пространственных вариаций диэлектрической проницаемости и
отсутствует поглощение. Из (5.7) и (5.11) и рассмотренной нами в § 4 настоящей
главы теории распространения волн в однородной среде следует, что
ρ = |ρ⃗| = β (5.43)
где β дается формулой (5.34). Фазовый множитель exp (− ⃗ ⃗) соответствует
быстрым вариациям фазы, связанным с любой бегущей волной. С другой стороны,
амплитудный множитель R(z) учитывает медленные изменения фазы и амплитуды
волны при ее прохождении через толщу голограммы (т. е. является функциейz). Эти
изменения обусловливаются пространственными вариациями диэлектрической
проницаемости и коэффициента поглощения. Аналогично мы можем записать
комплексную амплитудудифрагированной на голограмме волны:
a = S(z)exp(−iσ⃗r⃗), (5.44)
где ⃗ — вектор, показанный на Рис. 5.3. Если свет падает на голограмму под углом
Брэгга, то особое значение приобретает векторное соотношение

93
σ⃗ = ρ⃗ − K⃗ (5.45)
между векторами распространения падающей и дифрагированнойволн и вектором
решеткиК⃗. На Рис. 5.3 вверху справа приведена векторная диаграмма, графически
представляющая равенство (5.45).
Если свет падает под углом Брэгга, то и вектор падающей волны ⃗ и вектор
дифрагированной волны ⃗ составляют с плоскостями пучностей синусоидальной
голографической решетки угол θ0 (угол Брэгга). Как было показано в предыдущем
параграфе, векторК⃗ лежит в плоскости yz, перпендикулярной плоскостям пучностей.
Поскольку вектор электрического поля падающей волны направлен по оси х,
соответствующий волновой вектор (вектор распространения) ⃗ также должен лежать
в плоскости yz. Каквидно из (5.45), вектор а лежит в той же плоскости.
Треугольник,образованный тремя компланарными векторами, для случая, когда как
⃗ , так и ⃗ образуют угол θ0 с рассеивающими плоскостями, показан в нижней
правой части Рис. 5.3. Поскольку этот треугольник равнобедренный, = = , то
K
2
= ρsinθ (5.46)
Используя (5.11) и (5.34), получаем
π
d
= βsinθ =
2πn
λ
sinθ
(5.47)
Соотношение (5.47) можно также записать в виде
2dsinθ = (закон Брэгга)
Таким образом, (5.45) выражает закон Брэгга для света, падающего под углом
Брэгга.
Вернемся теперь к проблеме решения волнового уравнения (5.25).
Комплексную амплитудуа электрического поля в любой точке голограммы можно
представить как сумму амплитуд падающей волны аi и дифрагированной волныad:
a = a + a = ( ) exp(− ⃗ ⃗) + ( )exp (− ⃗ ⃗) (5.48)
Подставим (5.48) в (5.25). При взятии частных производных используем
следующие соотношения
⃗ ⃗ = + , ⃗ ⃗ = + ; (5.49)
= + , = + . (5.50)
Члены, получающиеся после выполнения действий над а, указанных в (5.25),
можно сгруппировать как коэффициенты либо приexp(− ⃗ ⃗), либо при exp (− ⃗ ⃗).
При рассмотрении второгочлена в (5.25), q2
a, членами с экспоненциальными
множителями
[− ( ⃗ + ⃗) ⃗] и [− ( ⃗ − ⃗) ⃗]
можно пренебречь,поскольку волны с векторами распространения ⃗ + ⃗
или ⃗ − ⃗ не удовлетворяют векторному соотношению Брэгга (5.45). Чтобы
одновременно выполнялось и уравнение (5.25), и соотношение(5.45) для
произвольных ⃗, коэффициенты как при (− ⃗ ⃗),так и при (− ⃗ ⃗) должны
равняться нулю. Следовательно, должны выполняться два равенства:

94
− 2 − +β R − 2iαβR + 2χβS = 0 (5.51)
− 2 − +β S − 2iαβS + 2χβR = 0 (5.52)
Штрихи обозначают дифференцирование по z.
Сделав некоторые предположения и введя новые обозначения, можно
упростить (5.51) и (5.52). Ранее уже было отмечено, что» быстрые вариации
волновых функций в (5.42) и (5.44) описываются фазовыми множителями, в то время
как R (z) и S (z) меняются сравнительно медленно. Предположим теперь, что R(z) и
S (z) меняются настолько медленно, что величинами R" и S" можно пренебречь. В
дальнейшем мы проверим справедливость такого приближения. Уравнение (5.51)
упрощается, если заметить, что сумма третьего и четвертого членов равна нулю [см.
(5.43)]. Рассмотрим теперь сумму третьего и четвертого членов в (5.52), равнуюS (β2
— 2
), и оценим величину множителя β2
— 2
для случая, когда угол падения θ
отличается от угла Брэгга θ0 только на малую величину , т. е.
θ = θ + δ. (5.53)
Воспользовавшись выражением (5.45), можно написать
β − σ = β − ρ⃗ − ⃗ = β − ρ + 2ρ⃗ ⃗ − =
= 2
2
− − = 2 − . (5.54)
Угол между ⃗ и ⃗, равный π/2 — θ, показан на Рис. 5.3. В соответствии с (5.53)
sinθ можно записать в виде
sinθ = sin (θ + δ) = sinθ cosδ + sinδcosθ ≈ sinθ + δcosθ ≈
K
2β
+ δcosθ .
(5.55)
где мы положили ≈ δ, cos ≈ 1, Ї использовали(5.46) и (5.43), чтобы
показать, что
sinθ =
K
2β (5.56)
Подставляя (5.55) в (5.54), получаем
β − σ ≈ 2ρK
K
2β
+ δcosθ − ≈≈ 2ρKδcosθ ≈ 2ρ(2βsinθ )δcosθ ,
(5.57)
β − σ ≈ 2β δsin2θ (5.58)
Обозначим
Γ = βδ sinθ (5.59)
так что
β − σ = 2βΓ (5.60)
Тогда, пренебрегая производными R" и S", используя(5.60) и вводя
обозначения
c =
ρ
β
=
ρcosψ
β
= cosψ,
(5.61)
c =
σ
β

95
мы можем преобразовать (5.51) и (5.52) к виду
c R + αR = −iχS (5.62)
c S + (α + iΓ)S = −iχR (5.63)
где = и = / .
Эти уравнения связанных волн позволяют понять физику процесса
дифракции. Когда при распространении падающей и дифрагированной волн сквозь
голограмму пройденное ими расстояние увеличивается наdz, комплексные
амплитуды этих волн меняются на dR или dS. Это изменение вызвано поглощением,
которому соответствуют члены R и S, или взаимодействием волн друг с другом,
описываемым членами взаимодействия S и R. Как мы увидим, член S в (5.63)
соответствует добавочному фазовому множителю в дифрагированной волне. Если
угол, под которым распространяется падающая волна, сильно отличается от угла
Брэгга, то величина Г будет большой. В результате накопления этой добавочной
фазы дифрагированная волна выходит из синхронизма с падающей волной, что
приводит к ослаблению взаимодействия.
Уравнения (5.62) и (5.63) представляют собой систему двух линейных
дифференциальных уравнений первого порядка. Подставляя (5.62) в (5.63), получаем
для R одно дифференциальное уравнение второго порядка
R +
α
c
+
α
c
+
iΓ
c
R +
(α + iΓα + χ )
c c
= 0
(5.64)
Решение этого дифференциального уравнения второго порядка с постоянными
коэффициентами ищем в виде
R(z) = exp(γz). (5.65)
Подставляя (5.65) в (5.64), получаем квадратное уравнение для
γ +
α
c
+
α
c
+
iΓ
c
γ +
(α + iΓα + χ )
c c
= 0,
(5.66)
решение которого имеет вид
γ +
α
c
+
α
c
+
iΓ
c
±
1
2
α
c
−
α
c
−
iΓ
c
−
4χ
c c
/
,
(5.67)
где индекс 1 соответствует знаку плюс перед квадратным корнем, а 2 — знаку минус.
Частными решениями уравнения (5.64) являются функции exp( ) и exp( ), а
полное решение дается их линейной комбинацией
S(z) = S exp(γ z) + S exp(γ z). (5.68)
где Ri и R2 — постоянные, которые можно вычислить, исходя из граничных условий.
Подставляя (5.68) в (5.62), получаем аналогичное уравнение для S (z):

96
S (z) = SAехр (viz) + S2ехр (y2z).
(5.69)
В двух следующих параграфах мы вычислим постоянные R1, R2, S1 ИS2
ДЛЯпропускающих и отражательных голограмм. При рассмотрении пропускающих
голограмм предполагается, что решетка не наклонная, т. е. плоскости решетки
перпендикулярны к поверхности объемной голограммы. При рассмотрении отража-
тельных голограмм предполагается, что плоскости решетки параллельны
поверхности. Мы здесь остановимся только на диэлектрических решетках без потерь, или
чисто фазовых решетках, для которых меняется показатель преломления и потери
равны нулю, и чисто абсорбционных решетках, у которых меняется коэффициент
поглощения, а показатель преломления постоянен. Прежде чем продолжить
обсуждение, заметим, что с помощью выражений (5.65) и (5.67) можно установить,
действительно ли мы имели право пренебречь величиной R" по сравнению с pzR' в
уравнении (5.51). Из (5.65) находим, что = exp( ), из (5.61) получаем =
exp( ). Таким образом, для < 90° условие R" <pzR' означает, что ≪ . Как
видно из (5.67), условие ≪ выполняется, если величина Г (пропорциональная )
очень мала и если удовлетворяются неравенства (5.35), (5.36) и (5.39). Аналогичным
образом можно показать, что при тех же условиях можно пренебречь производной S"
по сравнению с я ′.
5.6. Пропускающие голограммы
Пусть слева на пропускающую голограмму падает освещающая волна (Рис.
5.4). Как освещающая, так и дифрагированная волны распространяются сквозь
голограмму слева направо. Нормируем амплитуду падающей волны R (z) так, чтобы
R (0) = 1
РИС. 5.4 Пропускающая голограмма.
Приz = 0. Первоначально амплитуда дифрагированной волны равна нулю, так
что S(0) = 0 приz = 0. Записав (5.68) и (5.69) дляz = 0, получим граничные условия
R(0) = R + R = 1. (5.70)
S(0) = S + S = 0. (5.71)
Используя (5.70) и (5.71) и добавочное соотношение, которое следует из (5.69),
а именно
(0) = γ + γ ,

97
мы можем решить уравнение взаимодействия волн (5.63) для S1 = -S2; тогда дляz = 0
получаем
c (γ S + γ S ) = −iχ,
или
S = −S = −
iχ
c (γ − γ )
.
(5.72)
При таких значенияхS1 иS2 из (5.69) можно вычислить амплитуду
дифрагированной волны на другой поверхности голограммы приz = Т (Т — толщина
голограммы). Этодает
S(T) =
c (γ − γ )
[exp(γ ) − exp (γ )].
(5.73)
В соответствии с ранее намеченным планом ограничимся случаем, когда
плоскости решетки ориентированы перпендикулярно поверхности голограммы и,
следовательно, вектор решеткиК⃗параллелен поверхности. На Рис. 5.5 приведены
схема расположения векторов и векторный треугольник, соответствующий
соотношению ⃗ = ⃗ − ⃗, для брэгговского угла падения. Вектор падающей волны
⃗образует угол θ с плоскостямирешетки и такой же угол = с осью z. Если
выполнено условие Брэгга, то θ = θ0, треугольник становится равнобедренным и
выполняется соотношение
c = = = = .
(5.74)
РИС. 5.5. Геометрическая схема пропускающей голограммы с плоскостями
пучностей, перпендикулярными поверхности голограммы.
Мы будем считать, что равенство(5.74) справедливо для всех углов падения
(близких к углу Брэгга), которые мы будем рассматривать.

98
5.6.1. Фазовые пропускающие голограммы
Теперь наша цель состоит в том, чтобы найти амплитуду S(T)
дифрагированной волны, исходящей из голограммы, для диэлектрической фазовой
решетки без потерь. При выполнении вычислений удобно ввести параметры ξ и v,
определяемые соотношениями
c = = = = .
(5.75)
c = = = = .
(5.76)
Из (5.73) видно, что прежде всего нужно выразить через и величины
γ − иγ ,
γ − =
2
( + ) /
. (5.77)
γ , = − ± ( + ) /
. (5.78)
Подставляя (5.77) и (5.78) в (5.73), получаем
S(T) = −
exp(− ) ( + ) /
( + ) /
.
(5.79)
Поскольку амплитуду падающей волны приz = 0 мы положили равной
единице, эффективность голограммы составляет
=
| ( )|
| (0)|
= | ( )|
Сначала рассмотрим случай, когда свет падает под углом Брэгга, так что = 0
и = 0. Эффективность будет равна 100%, если sinv = 1 или если
v =
πn T
λ cosθ
=
π
2
(5.80)
Соотношение (5.80) можно также записать в виде
v =
n T
cosθ
=
λ
2
(5.81)
Левая часть равенства (5.81) эквивалентна приращению оптического пути
падающего луча, которое наблюдалось бы в том случае, если бы среднее изменение
показателя преломления среды голограммы было равно щ (Рис. 5.5). Если
эквивалентное изменение длины пути равно половине длины волны падающего
излучения (в воздухе), то эффективность становится равной 100%. Таким образом,
если голограмма образуется в диэлектрической среде без потерь, то даже при
небольших вариациях показателя преломления дифракционная эффективность может
достигать 100% при условии, что толщина среды Т достаточно велика, чтобы
выполнялось равенство (5.81).
Если угол падения отличается от угла Брэгга, то получить 100%-ную
дифракционную эффективность невозможно. На Рис. 5.6 представлены результаты
расчетов, выполненных по формуле (5.79). По вертикальной оси отложена
эффективность η, деленная на η0 — эффективность, получаемую при падении
освещающего пучка под углом Брэгга. По горизонтальной оси отложен
параметрпропорциональный угловому отклонению от угла Брэгга. На Рис. 5.6

99
приведены три кривые, соответствующие трем значениям параметра v. При
постоянной толщине Т и данной геометрии пучков, образующих голограмму,
параметр v пропорционален амплитуде вариаций показателя преломления,
образующихся в результате экспонирования и обработки голограммы. Каждой из
кривых на Рис. 5.6 соответствует своя максимальная величина эффективности η0,
которая достигается при ξ = 0. Отметим, что при v=π/2 эффективность ηо составляет
100%, тогда как при v = π/4 и v = 3π/4 она равна 50%. Рис. 5.6 иллюстрирует зави-
симость эффективности голограммы от угла падения для трех значений
модуляционного параметра v.
РИС. 5.6. Зависимость относительной эффективности / диэлектрической
пропускающей голограммы (без потерь) от = (2 / ) для различных
значений параметра м = / .
В качестве практического примера использования изложенной здесь теории
вычислим, при каком отклонении угла падения от угла Брэгга дифракционная
эффективность падает до нуля. Предположим, что голограмма образована в
хромированном желатине (см. гл. 10) в результате интерференции двух плоских
волн,угол между направлениями распространения которых в воздухе равен 60°. Угол
Брэгга в воздухе равен 30°, а в желатине 19,2° (если считать, что показатель
преломления желатина n = 1,52). Пусть длина волны в воздухеλа = 4880 А, толщина
слоя Т = 15 мкм и v = π/2, так что при падении света под углом Брэгга эффективность
составляет 100%. Из (5.75) имеем
=
2
= 96,5

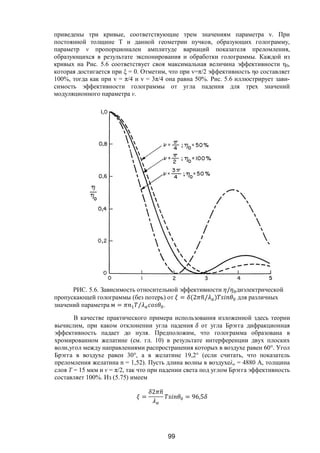
100
Поскольку кривая для v = π/2на Рис. 5.6 падает до нуля при ξ = 2,7, имеем =
2,7/96,5 = 0,028 рад = 1,6° (внутри желатина). В воздухе = 2,45°.
Кривыми, изображенными на Рис. 5.6, можно пользоваться: также, чтобы
определить, как меняется дифракционная эффективность при отклонении длины
волны от значения, удовлетворяющего закону Брэгга. Пусть голограмма образована
двумя плоскими волнами с длиной волны угол между которыми в регистрирующей
среде с показателем преломления равен 2θо. При освещении плоской волной с
длиной волныλа , удовлетворяющей закону Брэгга (5.10) ( 2 = ),
голограмма имеет максимальную эффективность. Пусть теперь длина волны,
падающей на голограмму, стала равной + ∆ , где ∆ / ≪ 1. Максимальная
эффективность теперь наблюдается при освещении не под углом θ0, а под новым
углом Брэгга θ’0= θ0 + . Если мы по-прежнему будем освещать голограмму под
исходным углом θ0= θ0- , то дифракционная эффективность уменьшится, поскольку
теперь угол θ0 отличается от брэгговскогоθ’0угла на - и соответственно параметр ξ =
- βTsinθ0 имеет отрицательную величину. Кривые η/η0 = |S (T) |2
на Рис. 5.6
симметричны относительно ξ (б) [см. (5.79)], так что, зная , мы можем определить
уменьшение эффективности, соответствующее Величину можно выразить через
∆ , введя в (5.10) новые «брэгговские параметры θ0+ и λa+ ∆ :
2ndsin(θ + δ) = λ + ∆λ (5.82)
Полагая sin δ ≈ δи cos δ ≈ 1 и используя (5.10), получаем
δ =
∆λ
2ndcosθ
(5.83)0
или
δ =
∆λ
λ
tgθ
2πn
λ
Tsinθ (5.84)
Для параметра ξ (при положительных∆ ) имеем
ξ = −
∆λ
λ
tgθ
2πn
λ
Tsinθ (5.85)
Вычислим, при каком значении ∆λ эффективность голограммы в
хромированном желатине падает до нуля (для ранее приведенного примера).
Подставляя в (5.85) ξ= 2,7, = 1,52, Т=15мкм, λa = 0,488 мкм и θ0 = 19,2°, найдем, что
| ∆λ | = 0,0393 мкм - = 393 А. [Для малых ∆λизменением v можно пренебречь. Это
становится очевидным, еслипродифференцировать (5.76) по А, и рассмотреть Рис.
5.6.]
С помощью кривых на Рис. 5.6 можно установить простое правило,
определяющее чувствительность фазовых голограмм к изменению угла падения.
Если ≈ 3, то дифракционная эффективность практически равна нулю (по крайней
мере для π/2 ≥v≥π/4).
Воспользовавшись равенством (5.75), вычислим величину 0,
соответствующую ξ = 3:
δ =
3
βTsinθ
=
3λ
2πnTsinθ
≈
λ
2nTsinθ
(5.86)
Используя (5.10), получаем

101
≈
(5.87)
Подставляя (5.87) в (5.84), приходим к приближенному соотношению для
чувствительности к изменению длины волны:
∆λ
λ
≈
d ctgθ
T
(5.88)
Здесь отклонение на ∆λ соответствует уменьшению эффективности до нуля.
5.6.2. Абсорбционные пропускающие голограммы
Если пропускание голограммы, изображенной на Рис. 5.5, характеризуется
величиной = 0 и конечными значениями α и α1, то дифракция света на ней
обусловлена только вариациями коэффициента поглощения. В дальнейшем
рассмотрении можно продолжать пользоваться параметром который определяется
соотношением (5.75), однако вместо параметраv удобнее ввести новый параметр va.
Константа взаимодействия [см. (5.41)] дается теперь соотношением
χ = −
iα
2
(5.89)
и va мы определим следующим образом:
v = −
α T
2cosθ
(5.90)
Снова, как и выше, мы должны вычислить S (Т) по формуле (5.73). Как и
прежде, сначала нужно выразить − и . черезξ иva. Из (5.67) имеем
γ − γ = −
Γ
c
+
α
c c
/
=
α
cosθ
−
Γ
cosθ
/
=
2
T
(v − ξ ) /
(5.91)
и
γ . T = −
α T
2cosθ
− iξ ± (v − ξ ) / (5.92)
Подставляя эти значения в (5.73), получаем амплитуду S (Т) волны,
дифрагированной на чисто абсорбционной пропускающей голограмме:
S(T) = − exp −
αT
cosθ
exp (−iξ)
sh(v − ξ ) /
(1 − ξ /v ) /
(5.93)
Для случая падения под углом Брэгга (ξ = 0) амплитуда дифрагированной
волны принимает вид
S(T) = − exp −
αT
cosθ
sh
α T
2cosθ
(5.94)
На Рис. 5.7 абсолютные величины S (Т) представлены в зависимости от
для различных значений отношения α/α1.Чтобы найти дифракционную
эффективность (для падающей волны единичной амплитуды), нужно возвести
в квадрат |S(Т)|. При увеличении α1 величина |S(Т)| возрастает. Поскольку мы

102
исключаем здесь возможность усиления (или отрицательного поглощения),
при увеличении α1 значение α также должно возрастать, чтобы выполнялось
условие α≥ α1. Как видно из (5.94), увеличениеα приводит к уменьшению
|S(Т)|. Положим величину α1 равной ее максимально возможному значению
α1= α; подставим это значение в (5.94) и найдем максимум |S(Т)| по
отношению к . Максимальное значение амплитуды дифрагированной
волны достигается при = ln3 и равно |S (T)| = (3√3) -1
. Возводя в квадрат
|S (Т)|макс, найдем максимальную дифракционную эффективность ηмакс = 1
/27 =
3,7 %, что несколько больше половины максимальной дифракционной
эффективности тонкой абсорбционной голограммы .
α T
cosθ
РИС. 5.7. Зависимость абсолютной величины амплитуды дифрагированной волны от
для абсорбционных (пропускающих) голограмм при различных значениях
параметра α/α1.
Интересно вычислить оптическую плотность абсорбционной голограммы,
обладающей максимальной дифракционной эффективностью. Предположим, что
средний коэффициент поглощения равен α, а толщина голограммы Т. Измеряемая
оптическая плотность голограммы практически равна плотности равномерно
засвеченной фотопластинки толщиной Т с коэффициентом поглощения α.
Амплитудное пропускание такой пластинки можно определить как отношение
амплитуды световой волны, прошедшей через пластинку в направлении нормали, к
амплитуде волны, падающей на пластинку. Для однородной среды амплитуда волны
(действительная) имеет видАехр (—az), так что
t=ехр (—α Т).
Возводя в квадрат t, получаем пропускание по интенсивности
J= t2
=ехр (-αТ).

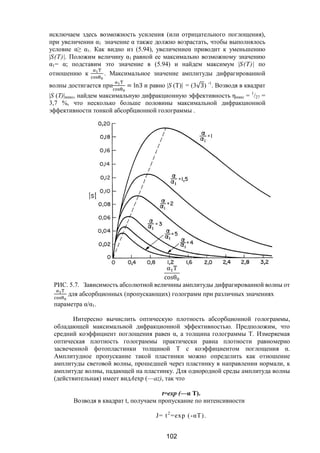
103
В соответствии с определением оптической плотности имеем
D = −lg J
или
D = −lg [exp (2αT)]
(5.95)
ξ
РИС. 5.8. Зависимость относительной эффективности η/ηо абсорбционной
пропускающей голограммы от ξ = (2 / ) .
Положив = ln3 (величина, при которой достигается максимальная
дифракционная эффективность), получим
D = (2ln3)cosθ lge = 0,955cosθ
где е — основание натуральных логарифмов. Мы видим, что оптимальной для
абсорбционной пропускающей голограммы является оптическая плотность, меньшая
единицы. Эта величина мала по сравнению с оптической плотностью, используемой в
обычной фотографии, однако согласуется с результатами экспериментов, которые
показывают, что оптическая плотность хороших абсорбционных голограмм
соответствует плотности недодержанных фотоснимков. На Рис. 5.7 проведена
пунктирная кривая, соединяющая все точки, которым соответствует оптическая
плотность D = 0,955 cosθ0. Мы видим, что эта оптическая плотность является
оптимальной для всех отношений α/α1.
На Рис. 5.8 изображена полученная с помощью (5.93) зависимость
относительной эффективности η/η0от ξ для абсорбционной пропускающей

104
голограммы. Обе кривые соответствуют α=α1; по виду кривые аналогичны кривым на
Рис. 5.6 для v=π/2. Вид кривых слабо зависит от параметра .
5.7. Отражательные голограммы.
Отражательные голограммы с плоскостями пучностей, параллельными
поверхности голограммы, образуются при интерференции двух волн,
распространяющихся в противоположных направлениях относительно осиz.
Действительно, из уравнения (5.5)
2 ( + ) + 2 ( − ) =
следует, что если = и = то уравнение, описывающее плоскости пучностей,
имеет в этом случае вид
2 (2 )z =const,
или
z =const,
т. е. плоскости пучностей параллельны плоскостиху. Они расположены на расстоянии
=
1
2
=
2(1 − ) /
Если отражательная голограмма освещается световой волной*, падающей
слева, то ее отклик характеризуется дифрагированной волной, распространяющейся
справа налево (Рис. 5.9). Поэтомуамплитуда дифрагированной волны приz — Т равна
нулю. Если, как и прежде, положить амплитуду
РИС. 5.9.Отражательная голограмма.
R(0) = R + R = 1, (5.96)
S(T) = S exp (γ T) + S exp (γ T) = 0,
(5.97)

105
Используя эти граничные условия в уравнениях связанных волн, найдем
амплитуду S(0) дифрагированной волны, идущей от голограммы, при z = 0. Мы
можем сделать это, подставляя (5.96) и (5.97) в (5.63). Для z = 0 тогда получим
−iχ(R + R ) = iχ = c (γ S + γ S ) + (α + iΓ)(S + S ),
(5.98)
Поскольку (0) = (S + S ), мы должны представить первый член в правой
части (5.98) как функцию S + S , после чего (5.98) даст искомое решение. После
некоторых преобразований граничных условий (5.97) это удается сделать. Прежде
всего запишем (5.97) в виде
−S = exp(γ T) = S exp(γ T) . (5.99)
Теперь к обоим частям равенства (5.99) прибавим S (γ T). Тогда получим
S [exp(γ T) − exp(γ T)] = (S + S ) exp(γ T) .
(5.100)
Затем умножим обе части (5.99) на -1 и прибавим к ним S (γ T); это дает
S [− exp(γ T) + exp(γ T)] = (S + S ) exp(γ T).
(5.101)
РИС. 5.10. Геометрическая схема отражательнойголограммы с
плоскостями пучностей, параллельными ее поверхности.
Тогда первый член в правой части равенства (5.98) принимает вид
c (γ S + γ S )S = c
γ (S + S ) exp(γ T) − γ exp(γ T)
exp(γ T) + exp(γ T)
. (5.102)
и
S(0)(S + S ) = −iχ α + iΓ + c
γ exp(γ T) − γ exp(γ T)
exp(γ T) + exp(γ T)
. (5.103)

106
Вычислим теперь (5.103) при условии, что вектор решеткиК⃗ перпендикулярен
поверхности голограммы, как это показано на Рис. 5.10. Вектор ⃗образует угол θ с
плоскостями решетки, и векторная диаграмма, изображенная справа на Рис. 5.10,
соответствует равенству (5.45) ⃗ = ⃗ − ⃗для падения под углом Брэгга. Если угол
θравен углу Брэгга θ0, то треугольник равнобедренный, и мы имеем
c =
ρ
β
= −c = −
σ
β
= cosψ . (5.104)
где ψ — показанный на Рис. 5.10 угол между ⃗ и осьюz при падении света под углом
Брэгга. В дальнейшем мы будем считать, что угол падения θ близок к θ0, так что
равенство (5.104) выполняется достаточно точно.
5.7.1. Фазовые отражательные голограммы
Фазовые отражательные голограммы характеризуются значением α=α1=0. В
этом случае удобно ввести параметры
ξ =
ΓT
2cosψ
=
βTδsin2θ
2cosψ
= δβTcosθ (5.105a)
v =
χT
2cosψ
=
πn T
λ cosψ
(5.105б)
В (5.105a) было использовано определение (5.59) величины Г и соотношение
ψ = − . Чтобы выразить S (0) через и ξr, нужно подставить (5.104), (5.105а) и
(5.1056) в выражение (5.67) для vr. Тогда получим
γ , T = iξ ± (v − ξ ) /
(5.106)
Непосредственная, но довольно длительная процедура подстановки (5.105а),
(5.1056) и (5.106) в (5.103) приводит к следующему выражению для амплитуды
дифрагированной волны приz = 0:
S(0) = −
i
( + [1 − (ξ /v ) ] / cth (v − ξ ) /
(5.107)
Для падения под углом Брэгга = 0 и дифракционная эффективность может
достигать 100%, так же как и для диэлектрических пропускающих голограмм при
отсутствии потерь. Однако в противоположность пропускающим голограммам, для
которых η0 достигает 100% при определенном значении произведения толщины на
постоянную взаимодействия, в данном случае при увеличении vr дифракционная
эффективность асимптотически приближается к максимальной
величине.Соответствующее различие кривыхиллюстрируется Рис. 5.11, на которой
приведены экспериментальные зависимости дифракционной эффективности от
экспозиции, полученные в работе [9.10] для хромированного желатина. На кривых 1 и
2, соответствующих пропускающим голограммам, имеется максимум
эффективности, положение которого зависит от экспозиции (и, таким образом, от v), в
то время как эффективность отражательной голограммы (кривая 3) непрерывно
возрастает по мере увеличения экспозиции.

107
РИС. 5.11.Зависимость амплитуды дифрагированной волны от
экспозиции для решеток в хромированном желатине.
РИС. 5.12. Зависимость относительной эффективности η/η0 диэлектрической
отражательной голограммы без потерь от ξr= ( )Tsinθ для разных значений
параметра vr.
На Рис. 5.12 относительная эффективность η/η0 представлена как функция ξr
для трех значений параметра vr, а именно: vr = π/4, 3π/2 и 3π/4; для этих кривых
значения η0 составляют соответственно 43, 84 и 96%. Заметим, что по мере
увеличения vrпроисходит значительное уширение максимума зависимости

108
эффективности отражательной голограммы от угла падения. Рассмотрим кривую для
vr = π/2 и оценим селективность отражательной голограммы по отношению к длине
волны. Из (5.84) (считая отрицательным) и (5.105а) имеем
ξ = −
∆λ
λ
βTtgθ cosθ = −
∆λ
λ
βTsinθ = −
∆λ
λ
(
2πn
λ
)Tsinθ (5.108)
В соответствии с кривой для vr =π/2 на Рис. 5.12, η/η0 = 0, когда ξr0 = 3,5.
Положив λ = 0,488мкм, Т = 15 мкм, n=1,52 иθ0 == 80° (в желатине) и найдя ∆ из
(5.108), получим |∆ | = , мкм = 59 А. Благодаря такой высокой спектральной
селективности отражательных голограмм для их освещения можно использовать
источники белого света.
5.7.2. Абсорбционные отражательные голограммы
Здесь = , тогда как а и имеют конечные значения, а постоянная =
− /
РИС. 5.13. Зависимость абсолютной величины амплитуды дифрагированной волны
от / для абсорбционной отражательной голограммы при различных
значениях параметра α/ α1
Определим параметры vra и ξrа следующим образом:
v = α T/2cosψ (5.109a)
ξ =
αT
cosψ
+
iΓT
2cosψ
(5.109б)
Тогда, выражая , в (5.67) через vra и ξra, получаем

109
γ , T =
iΓT
2cosψ
± (ξ + v ) / (5.110)
Здесь использовано условие (5.104), выполняющееся для отражательной
голограммы:
c = −c = cosψ (5.103)
Если подставить , в выражение для S (0), то для амплитуды
дифрагированной волны, исходящей из голограммы, получим
S(0) = −
ξ
v
+
ξ
v
− 1 cth(ξ + v )
(5.111)
При падении под углом Брэгга Г = 0 и
=
и выражение для S (0) принимает вид
S(0) = − + − 1 cth
T
cosψ
α +
(5.112)
РИС. 5.14. Зависимость относительной эффективности η/η0 для
абсорбционной отражательной голограммы от ГT/2 при различных
значениях параметра / и α1=α.
Оптимальная величина |S (0) | достигается, когда α1 принимает максимальное
значение α1=α. Тогда

110
| (0)| = 2 + 3√3 ℎ −
√3
2
Если α1=α. —>∞, то достигается максимальная эффективность ηмакс = | S (0)
|2
-> (2 + 1√3) -2
=7,2%. Это отражает тот экспериментально установленный факт, что
дифракционная эффективность отражательных абсорбционных голограмм достигает
максимальной величины, когда фотопластинка совсем темная. На Рис. 5.13
изображены кривые зависимости |S (0) | от / для нескольких значений α /α1
Мы видим, что при = 2 амплитуда дифрагированной волны достаточно близка к
своему асимптотическому максимальному значению. В соответствии с (5.95)
оптическая плотность пластинки при этом равна 1,7. Эта величина представляет
собой минимальную оптическую плотность, которую нужно получить (путем
соответствующего выбора экспозиции), чтобы достичь близкой к максимальной
дифракционной эффективности.
На Рис. 5.14 приведена зависимость относительной эффективности отГT/2
для α=α1 и разных значений / .
5.8. Обсуждение свойств объемных голограмм
В табл. 5.1 сравниваются теоретические и наблюдаемые максимальные
значения дифракционной эффективности для плоских и объемных голограмм при
условиях, рассмотренных в настоящей главе. Максимальные теоретические значения
дифракционной эффективности близки к наблюдаемым; исключение составляют
только абсорбционные отражательные голограммы. Поскольку часть предсказанных
значений получена с помощью теории, изложенной в настоящей главе, а часть — с
помощью результатов анализа плоских голограмм, проведенного в гл. 8, необходимо
установить, какой толщиной должна обладать голограмма, чтобы ее можно было
считать объемной. Нижний предел толщины объемных голограмм определяется через
параметр
Q =
2πλaT
nd
2
(5.113)
Теория связанных волн начинает давать хорошие результаты при Q> 10.
Рассмотрим типичный случай: Т = 15 мкм,λа = = 0,633 мкм, n= 1,52 (для желатина).
ПоложивQ = 10, найдем, что расстояние между интерференционными плоскостями
равно d = 1,98 мкм. Подставляя это значение и величину = √ =0,416 мкм в (1.10)
(2dsinθ= λ), находим минимальный угол между пучками 29≈12°, необходимый для
получения объемной голограммы в слое желатина толщиной 15 мкм. Как отмечалось
в § 1, если в (1.10) подставить = , то мы получим угол между пучками в воздухе.
Таким образом, угол 20 между пучками в воздухе, необходимый для получения
объемной голограммы с помощью излучения гелий-неонового лазера в
фотографической эмульсии толщиной 15 мкм, составляет 18,4°.
Голограмма, полученная при таком минимальном угле между пучками,
обладает заметной селективностью к углу падения освещающего пучка. Для фазовой
голограммы значение 0 в среде, согласно (5.86) и (5.87), составляет
=
2
= ≈ 0,13 рад ≈ 7,5°
Однако такие голограммы почти не обладают спектральной селективностью.
Для использованных выше параметров и θ0 = 6°
∆ ≈ ≈ 8000

111
Дифракционная эффективность таких голограмм превышает 50% для всего
видимого спектра.
Т а б л и ц а 5 . 1
Максимальная дифракционная эффективность голограмм разных типов
С ростом 0 селективность голограммы по отношению к углу падения
возрастает. Например, если θ0= 30°, в то время как T, и имеют прежние значения,
то 0≈1,6° в среде. При такой большой угловой селективности на одной
фотопластинке можно получать большое число голограмм, причем наблюдатель
будет видеть одновременно только одно изображение. Все голограммы могут быть
получены с предметным пучком, имеющим одинаковую среднюю пространственную
частоту, тогда как направления опорных пучков должны отличаться по крайней мере
на 0. Если проявленную фотопластинку осветить одним из исходных опорных пуч-
ков (удовлетворяющим условию Брэгга лишь для одной из зарегистрированных на
пластинке голограмм), то восстановится только предметная волна, соответствующая
данному опорному пучку.
Другой метод, позволяющий зарегистрировать на одной фотопластинке много
предметных волы и затем восстанавливать их поочередно, состоит в том, что каждый
предметный пучок интерферирует с одним и тем же опорным пучком, однако фото-
пластинка в этом случае после каждой экспозиции поворачивается на угол 0.
В соответствии с (5.88) при увеличении угла Брэгга θ0 возрастает спектральная
селективность голограммы. Когда угол между пучками увеличивается настолько,
чтобы образовалась отражательная голограмма, селективность по отношению к
длине волны описывается выражением (5.108). Отражательные голограммы
обладают настолько высокой селективностью к длине волны, что их можно
восстанавливать в белом свете. Отражательные голограммы могут восстанавливать
многоцветные изображения при освещении белым светом. Однако при увеличении θ0
из-за наличия множителя cosθ0 в (5.105а) падает селективность таких голограмм по
отношению к углу падения восстанавливающего пучка.
Толщина
регистрирующе
й среды
Тонкая Толстая
Вид голограмм Пропускающи
е
Пропускающие Отражательные
Модулируемая
величина
Ампли-
туда
Фаза Коэфф.
поглощен
ия
Показатель
преломлен
ия
Коэфф.
поглощен
ия
Показатель
преломлен
ия
Максимальная
теоретическая
эффективность,
%
6,25 33,9 3,7 100 7,2 100
Максимальная
эффективность,
достигнутая
экспе-
6,0 32,6 3,0 90 3,8 80

112
1. Закон Брэгга.
2. Геометрическая схема объемной голограммы.
3. Фазовые пропускающие голограммы.
4. Абсорбционные пропускающие голограммы
5. Отражательные голограммы
6. Свойства объемных голограмм.

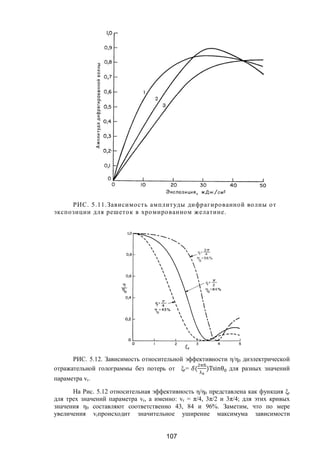
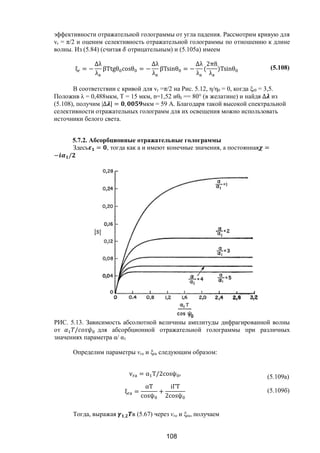
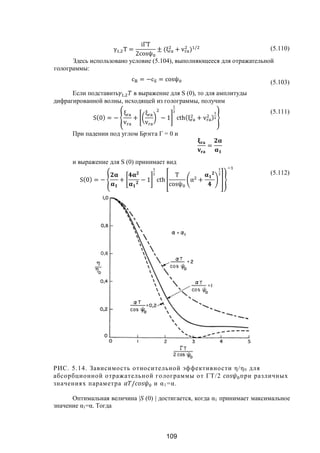
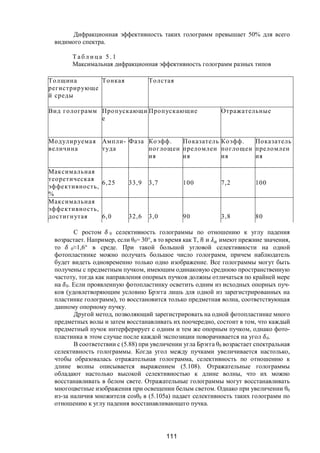
113
Приложение 1
ПРЕОБРАЗОВАНИЕ ФУРЬЕ
В основу анализа голограмм точечного источника было полошено
рассмотрение разности хода лучей от источника до голограммы, образуемой
сферическими или плоскими волнами. Для таких простых волн нетрудно найти
распределение комплексных амплитуд света непосредственно вблизи голограммы,
поэтому такая характеристика поля используется далее для описания основных
принципов записи и восстановления волнового фронта.
Однако если во входной плоскости имеется более сложное распределение
комплексных амплитуд и требуется определить, как оно изменяется при
прохождении света через однородное пространство, оптические элементы,
голограмму и т . п., то рассмотрение следует проводить в более общем виде.
Электромагнитные волны могут быть промодулированы во времени или, что
характерно для волн в оптическом диапазоне, в пространстве. При временной
модуляции распространение волны можно рассматривать в любой из двух
областей: временной или частотно-временной. Аналогично распространение
пространственно-модулированной волны, которое нас здесь интересует, можно
рассматривать либо в координатной области, либо в пространственно-частотной. В
координатной области комплексная амплитуда а' (х, у) выражается как функция
пространственных координат х, у плоскости наблюдения, через которую проходит
свет. То же самое распределение может быть выражено через ортогональные
пространственные частоты ξ и η.
Если к произвольному двумерному распределению комплексных амплитуд
света применить основную теорему анализа Фурье, то это распределение можно
записать в виде дискретной или непрерывной суммы синусоидальных
составляющих. Величина, обратная пространственному периоду любой из
компонент суммы, измеренному в выбранном направлении в плоскости
наблюдения, называется пространственной частотой этой компоненты в ука-
занном направлении. Разлагая пространственный период по ортогональным
направлениям х и у, получаем соответствующие компоненты ξ и η
пространственной частоты. Таким образом, мы можем выразить распределение
комплексных амплитуд а (х, у) в координатной области через другую функцию
( , ) в области пространственных частот. Функция ( , ) определяется
двумерным фурье-образом [ а (х, у) ]функции а (х, у):
[а (х, у)] = а (х, у) ( ) ( )
= ( , ).
(1.1)
Соотношение (1.1), из которого следует, ЧТО ( , ) есть фурье-образ функции а (х,
у), в символической записи имеет вид а (х, у) ⊃ ( , ). С другой стороны, а (х, у)
есть обратный фурье-образ [ ( , )] функции ( , ):
[ ( , )] = ∬ ( , ) (− ) (− ) =
а (х, у).
(1.2)
То обстоятельство, что функция а (х, у) является обратным фурье-образом функции
( , ), символически можно записать как ( , ) ⊂ а (х, у) . Заметим, что если
знак ⊃указывает на прямое преобразование Фурье, a⊂ — на обратное, то запись а (х,
у) ⊃ ( , ) может читаться в обоих направлениях. При этом говорят, что ( , ) и
а (х, у) образуют пару преобразований Фурье

114
Операция преобразования Фурье, связывающая координатную и частотную
области, отражает физическую сущность действия оптических систем.
Преобразование можно рассматривать как разложение сложной световой волны на
множество плоских солн, направляющие косинусы которых соответствуют
пространственным частотам. Анализ распространения и дифракции плоской
волны достаточно прост, но в то же время позволяет понять основные физические
принципы этих явлений.
Хотя прямой (1.1) и обратный (1.2) фурье-образы определяются интегралами с
бесконечными пределами, в большинстве случаев их можно заменить интегралами с
конечными пределами и выполнить преобразование оптическим методом. В гл. 6,
например, показано, что пространственные распределения комплексных амплитуд
света в передней и задней фокальных плоскостях сферической линзы образуют пару
преобразований Фурье. Это позволяет получать голограммы Фурье, интересные
особенности которых связаны с преобразованием Фурье. В настоящей главе мы
рассмотрим основные свойства преобразования Фурье, предполагая, что читатель
уже знаком в общих чертах с этой теорией. Более полное изложение вопроса можно
найти в работах [1.1 — 1.3].
1.1.Линейные пространственно-инвариантные системы и
преобразование Фурье
Будем рассматривать оптическую систему, показанную на Рис. 1.1, как «черный
ящик»; иными словами, нас будет интересовать не содержимое ящика, а только то,
как он действует.
РИС. 1.1.Оптическая система, рассматриваемая как «черный ящик».
Мы хотим знать выходную функцию в плоскости Р2 при заданной входной функции в
плоскости Р1При использовании когерентного света входной и выходной функциями
могут быть, например, функции распределения комплексных амплитуд света в
плоскости предмета и в плоскости изображения. Предположим, что входной
функции а1(х, у)соответствует выходная функция b1(х, у) ,а входной функции а2 (х, у)
соответствует выходная функция b2(х, у). Систему называют линейной, если
выполняется свойство суперпозиции, т. е. для всех входных функций а1(х, у)и а2 (х, у)
и для всех постоянных с1 и с2 входная функцияc1а1(х, у)+c2а2(х, у) преобразуется в
выходную функциюc1b1(х, у)+c2b2(х, у). Систему называют
пространственно-инвариантной, если входная функция а1(х — u, у — v)
преобразуется в выходную b1(х —u, у —v) для всех a1 (х, у). Здесь и иv —
постоянные; масштаб системы координат на выходе выбран так, что увеличение
равно единице. Заметим, что оптические системы очень часто не являются

115
пространственно-инвариантными по всей входной и выходной плоскости. Однако
обычно они пространственно-инвариантны внутри достаточно малых областей,
которые называютизопланарными участками. Тогда для любого изопланарного
участка систему считают линейной и пространственно-инвариантной.
РИС. 1.2.Двумерная синусоидальная функцияс периодом А и пространственными
частотами ξ и η.
Линейные и пространственно-инвариантные системы обладают свойством
преобразовывать синусоидальный сигнал на входе
в синусоидальный сигнал той же частоты на выходе. Синусоидальная двумерная
функция показана на Рис. 1.2. Такая зависящая от x иу функция с периодом A
описывается формулой
( , ) = ( ⃗, ⋀) (
⃗ ∙ ⃗
⋀
)
(1.3)
где ( ⃗, ⋀) — амплитуда косинусоидальной функции; ⃗ = ⃗ + ⃗ радиус-вектор; і и
j — единичные векторы в направлении осей х и у, а ⃗ — единичный вектор в
направлении, соответствующем периоду ⋀.
Из Рис. 1.2 видно, что ⃗ = ⃗ + ⃗ ;
тогда
( , ) = ( , ) ( + ) (1.4)
где пространственные частоты
=
⋀
, =
⋀
есть величины, обратные пространственным периодам, измеренным по осям х иу
соответственно. Вещественную функцию а (x, у) можно представить в виде Re [а (x,
у)] (гл. 1, § 3), гдеa (х, у) — комплексная величина, и затем использовать в расчетах
величину а (x, у), опуская символ Re. Тогда получим
( , ) = ( , ) ( , ) (− ) (− ), (1.5)
У

116
Таким образом, для линейной пространственно-инвариантной системы выходная
функция b(х, у), соответствующая входной функции a(х, у), имеет те же
пространственные частоты, что иa(х, у), и
( , ) = ( , ) ( , ) (− ) (− ), (1.6)
где ( , ) — частотная передаточная функция.
Это простое соотношение между входной и выходной синусоидальными
функциями показывает, что для описания линейной пространственно-инвариантной
оптической системы может служить частотная передаточная функция ( , ) ).
Обычно входные функции оптических систем не являются синусоидальными, но в
соответствии с (1.1) и (1.2) их можно разложить по синусоидальным функциям с
помощью прямого и обратного преобразований Фурье:
( , ) = а (х, у) ( ) ( ) ,
и
а (х, у) = ( , ) (− ) (− ) ,
Функцию ( , ) часто называют спектром функции а(х, у). Предположим, что в
формуле (1.2) а(х, у) является входной функцией линейной
пространственно-инвариантной системы, и нас интересует выходная функция b(х, у).
В соответствии с (1.6) мы должны каждую фурье-компоненту умножить на
соответствующую частотную передаточную функцию ( , ) . Выполняя эту
операцию, получаем следующее выражение для выходной функции b(х, у):
( , ) = ( , ) ( , ) (− ) (− ) , (1.7)
Из формулы (1.7) следует, что выходная функция линейной про-
странственно-инвариантной системы есть фуръе-образ произведения спектра
входной функции на частотную передаточную функцию. Выражая тот же результат
через пространственные частоты (в пространстве Фурье), получаем, что спектр
выходной функции линейной пространственно-инвариантной системы равен произ-
ведению спектра входной функции на частотную передаточную функцию, т. е.
( , ) = ( , ) ( , ), (1.8)
1.2.Формулы соответствия и преобразования Фурье
Формула (1.8) устанавливает связь между входным и выходным сигналами
линейной пространственно-инвариантной системы посредством операции
умножения в области пространственных частот. Как мы увидим, в координатной
области тоже существует операция, определяющая связь между входным и
выходным сигналами. Такое соответствие между операциями в двух областях
обусловлено общими свойствами преобразования Фурье; можно было бы привести
много других подобных примеров. Вообще говоря, существует два типа соответствий

117
между частотной и координатной областями. К первому типу относится соответствие
операций. Каждой операции в координатной области, например сложению или
умножению двух функций, соответствует операция в области пространственных
частот, причем не обязательно совпадающая с операцией в координатной области. Ко
второму типу соответствий относится соответствие функций. Каждой функции в
координатной области соответствует другая функция в частотной области.
(Существуют такие нерегулярные функции, которые не имеют фурье-образов, но мы
их здесь не рассматриваем.)
Хотя входные и выходные функции оптических систем обычно являются
двумерными, основные задачи оптики часто могут быть рассмотрены с помощью
одномерного анализа. Это упрощает математические выражения и графическое
представление. Кроме того, двумерную функцию, записанную в соответствующей
системе координат, часто можно представить как произведение двух одномерных
функций. Фурье-образ такой функции равен произведению фурье-образов двух
одномерных функций. Прямое и обратное фурье-преобразования одномерной
функции имеют вид
( ) = ( ) ( ) , (1.9)
( ) = ( ) (− ) , (1.10)
Некоторые функции, являющиеся двумерными в прямоугольной системе
координат, могут быть представлены как одномерные в полярной системе координат.
Примерами таких функций, интересных для голографии, являются функция Гаусса и
функция круговой апертуры. Функцию Гаусса (− ), гдеg — постоянная и
= + можно представить как произведение
(− ) (− ),
так что ее фурье-образ можно найти путем двукратного применения соотношения
(1.9). Вычисление фурье-образа одномерной функции производится следующим
образом:
( ) = (− ) ( ) = [− ( − )]
= − − −
= − − − =
= − ,
(1.9)
где интеграл с бесконечными пределами в предпоследней строке равен единице.
Тогда для функции A (v), являющейся фурье-образом функции (− ), имеем
( ) = − − = −

118
где
= + .
Функция круговой апертуры rect(r/2c) равна единице в круге радиусомс и нулю
при r>c. Чтобы найти ее фурье-образ, следует записать (1.1) в цилиндрических
координатах. Положим
= , = ,
= , = ,
( , ) = =
для < ,
для > .
Тогда формула (1.1) принимает вид
( ) = ∫ ∫ [ ( − )] = ∫ [ ( )] =
∫ ( ) ( ) ( ) = ( ) =
( )
.
Здесь мы воспользовались следующими соотношениями:
2 ( ) = ∫ ( ) и ∫ ( ) = ( ),
где J0 И J1 — функции Бесселя первого рода соответственно нулевого и первого
порядков. Функция
( )
.
имеет максимальное значение, равное единице, при v = 0, следовательно, функция A
(v) достигает своего максимального значения, равного , в начале координат
частотной плоскости. Функция A (v) показана на Рис. 1.7. Ширину кривой A (v)
принимают равной величине v0 = 0,61 /с, т. е. полуширине центрального пика.
В литературе имеются подробные таблицы фурье-преобразований (см., например,
[1.5]), на которые мы при необходимости будем ссылаться. Однако полезно
рассмотреть здесь некоторые из основных операций фурье-анализа и привести в
наших обозначениях наиболее употребительные соотношения между функциями.
Для обозначения функций в координатной области мы будем пользоваться
строчными буквами, для обозначения функций в частотной области — прописными, а
символом ⊃ будем указывать на фурье-соответствие функций в частотной и
координатной областях. Каждому соответствию, обозначенному символом⊃ отве-
чает обратное соответствие, обозначаемое символом ⊂ , за исключением
соотношений (1.20) и (1.21), относящихся к операции сдвига, а также соотношения
(1.33).
1.3.Операция свертки
Рассмотрение операций, устанавливающих соответствие между функциями в
разных областях, начнем со следующего соотношения:
( ) = ( ) ( − ) ⊃ ( ) ( ) = ( ). (1.11)
Интеграл, стоящий слева, называется интегралом свертки; его часто записывают
следующим образом:

119
( ) ( − ) = ( ) ∗ ( ),
где символ * означает операцию свертки. Соотношение (1.11) выражает очень
важную теорему свертки, согласно которой фуръе-образ свертки двух функций равен
произведению их фуръе-образов. Соотношение (1.11) легко доказать с помощью
определений фурье-образа (1.9) и (1.10):
( ) ( − ) = ( ) ( ) [– ( − ) ] =
= ( ) ( ) ( ) (− ) =
= ( ) ( ) (− ) ⊃ ( , ) ( , ).
Заметим, что по виду последнего интеграла нельзя сказать, которая из функций,
стоящих под интегралом свертки, имеет сдвиг. Следовательно, операция свертки
коммутативна, т. е.
( ) ∗ ( ) = ( ) ∗ ( ).
РИС. 1.3. Иллюстрация операции свертки.Площадь под кривой а (и) s (х — и)
численно равна значению сверткиB(Х) в точке Х.
Если функция а (х) смещена на расстояние с относительно своего начального
положения, то свертка а (х — с) * s (х) может быть выражена через смещенную
свертку начальных функций а (х) и s (х). Пусть
( ) ∗ ( ) = ( ) ( − ) = ( ),
Тогда
f (u)

120
( − ) ∗ ( ) = ( − ) ( − )
= ( ) [( − ) − ] = ( − ),
(1.12)
где = − ,
Смысл интеграла свертки можно уяснить с помощью Рис. 1.3, на которой показаны
вещественные функции a (u), s(u), а также функцияs(-u), являющаяся зеркальным
отражением функции s(и) относительно оси ординат. Для нахождения интеграла
(1.11) нужно построить зеркальное отражение функцииs (и), полученную функцию
сдвинуть по оси и вправо на отрезок х, умножить сдвинутую функциюs (х — и) на а
(и) и вычислить площадь под кривой а(и)s(х — и). В результате мы получим одно
значение функции b(х). Повторяя указанные действия для различных значений
сдвига х, можно построить функциюb(х).
Рис. 1.4 иллюстрирует операцию свертки двух простых прямоугольных функций.
Сдвинутая функцияs (х — и) перемещается вдоль функции а (и) (верхняя часть Рис.
1.4). Свертка этих двух функций отлична от нуля только для тех значений сдвига х,
при которых функции перекрываются. Ширина свертки, изображенной как функция
от х (нижняя часть Рис. 1.4), равна сумме ширин функций, подвергаемых операции
свертки. Последнее справедливо для функций произвольной формы.
Если функцию ( )стоящую в правой части соотношения (1.11), рассматривать
как частотный спектр входной функции линейной пространственно-инвариантной
системы, a ( ) как частотную передаточную функцию, то ( ), согласно равенству
(1.8), есть частотный спектр выходной функции b(х). Вид выходной функции,
выражаемой интегралом свертки, определяется видом входной функции и
передаточными характеристиками системы. В соотношении (1.11) а (х) можно
рассматривать как входную функцию, фурье-образ которой равен ( ) ;
следовательно, для нахождения выходной функции остается определить вид функции
s(х). Для этого сначала рассмотрим некоторые полезные свойства -функции Дирака:
( ) = при ≠ , (1.13a)
( ) = (− ), (1.13б)
( ) ( ) = , (1.13в)
( ) =
| |
( ), (1.13г)
( ) ( − ) ( ) = ( ), (1.13l)
Свойство (1.13д) называют фильтрующим свойством - функции. Оно выражает тот
факт, что свертка какой-либо функции с - функцией равна самой функции.
Предположим, что на вход системы подан импульс, т. е. входная функцияа(х)
представляет собой -функцию. Заменяя в (1.11)a (и) на (и), получаем

121
( ) = ( ) ( − )
= ( ) ( − ) = ( ) ( − ) = ( ).
(1.14)
Здесь мы использовали соотношение (1.13д), коммутативность операции свертки [см.
доказательство соотношения (1.11)] и симметричность -функции. Итак, видно, что
s(x), представляет собой выходную функцию, или отклик системы, соответствующий
импульсу на входе. Импульсный откликs(x) в оптике называют функцией рассеяния.
Она характеризует распределение комплексной амплитуды света в выходной
плоскости, соответствующее точечному источнику света, т. е. -функции во входной
плоскости. Согласно (1.11),
( ) ⊃ ( ), (1.15)
т. е. для линейной пространственно-инвариантной системы фуръе- образ функции
рассеяния есть частотная передаточная функция.
РИС. 1.4.Свертка двух прямоугольных функций.Вверху показано перемещение одной
функции относительно другой. Внизу представлена свертка как функция отя, откуда
видно, что ширина свертки равна сумме ширин функций, подвергаемых операции
свертки.
Кроме того, соотношение (1.11) можно интерпретировать следующим образом:
выходная функция линейной пространственно- инвариантной системы равна
свертке входной функции и функции рассеяния.
Другим примером, поясняющим смысл операции свертки и ее связь с линейной
пространственно-инвариантной системой, может служить функция
( ) = /∆ /∆ , (1.16)

122
т. е. симметричная относительно оси ординат узкая прямоугольная функция,
определенная в области от — ∆ /2 до + ∆ / и имеющая высоту /∆ (Рис. 1.5, a).
Пусть функции I(х) на входе системы соответствует функция s(x) на выходе (Рис. 1.5,
б). Выразим через I(x) произвольную входную функцию a(х).Вещественная входная
функция a (х), показанная на Рис. 1.5, в, представлена в виде совокупности
прямоугольных функций шириной ∆ . Для каждого значения x, x=u, высота
прямоугольной функции равна a(u) и функция сдвинута на u от центра функции I(x).
Высота a(u) в a(u) ∆ раз больше высоты I(x). Следовательно прямоугольную
функцию при х = и можно представить в виде
( ) ( − )∆ .
РИС.1.5 Свертка входной функции с откликом системы на узкую прямоугольную
функцию.а – прямоугольная функция I(x); б – отклик линейной
пространственно-инвариантной системы на входную функцию I(x); в входная
функция, представленная в виде совокупности прямоугольных функций; г – схема,
показывающая, что для любого значения x равна сумме ординат при данном x всех
кривых, представляющих собой отклики.
Учитывая свойство линейности, получаем, что выходная функция, соответствующая
такой входной, будет вa(u) ∆ раз больше выходной функции, соответствующей I
(х). Из пространственной инвариантности системы следует, что смещение входной
функции на и вызывает в свою очередь такое же смещение выходной функции s(x),
не изменяя ее вида. Следовательно, выходная функция, соответствующая функции а
(и) I (х — и)∆ , равна
( ) ( − )∆ ..
Тогда совокупности прямоугольных функций, составляющихa(x),соответствует
сумма выходных функций
( ) ( − )∆ ,
что и показано на Рис. 1.5, г.

123
Совершим теперь переход ∆ → , т. е. заменим конечное приращение ∆
бесконечно малымdu. При этом сумма переходит в интеграл, стоящий в соотношении
(1.11)
( ) = ( ) ( − ) , (1.17)
где для общности функции а(х) и s(x) взяты комплексными. Таким образом,
вследствие линейности и пространственной инвариантности системы выходная
функция представляет собой свертку входной функции и отклика на узкую
импульсную функцию.
1.4. Другие виды соответствия операций
Ниже мы рассмотрим некоторые операции в координатной области и те операции,
которые соответствуют им в частотной области. Для первой из них, операции
корреляции, теорема фурье-преобразования доказывается аналогично теореме
свертки.
а. Операция корреляции
∗( ) ( + ) ) ⊃ ∗( ) ( ), (1.18)
Интеграл слева называется кросс-корреляцией функций а(x) и s(х) и может
быть записан в виде
( ) = ∗( ) ( + ) = ∗( ) ∗ ( ), (1.19)
где символ * означает операцию корреляции. Заметим, что операция корреляции
не является коммутативной, она отличается от операции свертки тем, что для ее
нахождения берется комплексно-сопряженная функция а*(х) и функция s(х), а не
ее зеркальное отражение относительно оси ординат. Соотношение (1.18) означает,
чтофуръе-образ кросс-корреляции двух функций есть произведение
комплексно-сопряженного фуръе-образа одной функции и фуръе- образа другой.
Если в (1.19) а(х) = s(х), то с(х) называется автокорреляцией.
б. Операция сдвига
Смещение функции в координатной области приводит не к смещению
соответствующей функции (ее фурье-образа) в частотной области, а к умножению
фурье-образа несмещенной функции на фазовый множитель, фаза которого
является линейной функцией частоты:
( − ) ⊃ ( ) ( ). (1.20)
Соотношение (1.20) используется для описания оптических схем опознавания
образов. Если мы теперь произведем смещение функции в частотной области, то
найдем, что в координатной области это приведет к умножению соответствующей
функции (обратногофурье-образа) на фазовый множитель, являющийся линейной
функцией координат:

121
( − ) ⊂ ( ) (− ). (1.21)
Заметим, что показатели экспоненты в соотношениях (1.20) и (1.21) отличаются
знаками.
в. Теорема подобия
Если в координатной области произведено «сжатие» координат,
то в частотной области это вызовет «растяжение» координат:
( ) ⊃
| |
( ). (1.22)
г. Сложение и умножение на число
( ) + ( ) ⊃ ( ) + ( ) (1.23)
и
( ) ⊃ ( ). (1.24)
д. Инверсия
Инверсия функции в координатной области вызывает инверсию в частотной
области
(− ) ⊃ (− ). (1.25)
е. Фуръе-образ комплексно-сопряженной функции и свойство симметрии
∗(± ) ⊃ ∗ (− ± ). (1.26)
Если функция в координатной области действительная и четная, т. е.а(х)=а(—х),
то из (1.25) следует, что А (ξ) = А (—ξ). Из соотношения (1.26) имеем А (ξ) = А * (ξ).
Следовательно,действительной и четной функции в координатной области соот-
ветствует действительный и четный фуръе-образ. С учетом этого Брэгг выбрал для
своих экспериментов по рентгеновской микроскопии объекты, имеющие центр
симметрии, т. е. объекты, структура которых описывается действительными четными
функциями.
Еслиа (х)⊃ А (ξ) и а (х) —действительная функция, то, согласно (1.26), имеем
a(x) ⊃ А*(- ξ). Из последнего выражения следует, что функция А (ξ) эрмитова.
Следовательно,фурье-образом действительной в координатной области функции
является эрмитова функция. Это значит, что фурье-образ действительного сигнала
можно полностью определить, если известны его частоты в положительной области, и
при решении задач, в которых рассматриваются действительные сигналы (например,
электрические), можно ограничиться только этими частотами.

122
Рис. 1.6 Пары преобразований Фурье, соответствующие соотношениям (1.27), (1.28), (1.31).
РИС. 1.7 Пары преобразований Фурье, соответствующие соотношениям (1.32)—(1.34).

123
1.5.Некоторые соответствия функций
Ниже приводятся наиболее важные пары преобразований Фурье; большая часть
из них изображена на Рис. 1.6 и Рис. 1.7. В каждой из этих пар возможна взаимная
замена переменных х и ξ, за исключением соотношений (1.29) и (1.30), являющихся
наиболее простыми примерами операции сдвига, а также соотношения (1.33)
(− ) ⊃ /
− . (1.27)
( ) ⊃ (1.28)
( + ) ⊃ (− ) (1.29)
( ) ⊃ ( + ) (1.30)
⊃ ( ) (1.31)
⊃ + − ( − ) (1.32)
⊃ − − ( + ) (1.33)
⊃
( )
(1.34)
В соотношении (1.34) функции rect(r/2c) и cJ1 (2 cv)/v, где r2
= х2
+ у2
и v2
=ξ2
+η2
, обладают осевой симметрией; через J1 обозначена функция Бесселя первого
рода первого порядка.

учебно методическое пособие по дисциплине прикладная голография

More Related Content

What's hot

Viewers also liked

Similar to учебно методическое пособие по дисциплине прикладная голография

More from Иван Иванов

учебно методическое пособие по дисциплине прикладная голография