Recommended
PDF
DOC
เอกสารประกอบการสอนบทที่ 1
PDF
PDF
DOCX
PDF
PDF
PDF
PDF
PDF
DOCX
สถิติ ม.6 เรื่องการวิเคราะห์ข้อมูลเบื้องต้น
PPTX
PPT
การวิเคราะห์ข้อมูลเชิงปริมาณ
PDF
PDF
วิชาโปรแกรมสำเร็จรูปทางสถิติเพื่อการวิจัย
PPT
1. ความร เบ__องต_นเก__ยวก_บสถ_ต_และการว_จ_ย
PDF
PDF
มอค.3คณิตและสถิติในชีวิตประจำวัน ญาติกา
PDF
PDF
73 สถิติและการวิเคราะห์ข้อมูล บทนำ
PDF
การวิเคราะห์ข้อมูลเบื้องต้นคืออะไร
PDF
PPTX
PDF
วิธีวิทยาการวิจัยขั้นสูงด้านการวิจัยและสถิติ
PDF
DOCX
PDF
PDF
75 สถิติและการวิเคราะห์ข้อมูล ตอนที่2_แนวโน้มเข้าสู่ส่วนกลาง1
PPTX
PDF
More Related Content
PDF
DOC
เอกสารประกอบการสอนบทที่ 1
PDF
PDF
DOCX
PDF
PDF
PDF
What's hot
PDF
PDF
DOCX
สถิติ ม.6 เรื่องการวิเคราะห์ข้อมูลเบื้องต้น
PPTX
PPT
การวิเคราะห์ข้อมูลเชิงปริมาณ
PDF
PDF
วิชาโปรแกรมสำเร็จรูปทางสถิติเพื่อการวิจัย
PPT
1. ความร เบ__องต_นเก__ยวก_บสถ_ต_และการว_จ_ย
PDF
PDF
มอค.3คณิตและสถิติในชีวิตประจำวัน ญาติกา
PDF
PDF
73 สถิติและการวิเคราะห์ข้อมูล บทนำ
PDF
การวิเคราะห์ข้อมูลเบื้องต้นคืออะไร
PDF
PPTX
PDF
วิธีวิทยาการวิจัยขั้นสูงด้านการวิจัยและสถิติ
PDF
DOCX
PDF
PDF
75 สถิติและการวิเคราะห์ข้อมูล ตอนที่2_แนวโน้มเข้าสู่ส่วนกลาง1
Similar to statistics
PPTX
PDF
PDF
สถิติเบื้องต้นกลุ่ม 2 สำรอง
PDF
สถิติเบื้องต้นกลุ่ม 2 สำรอง
PPT
PDF
74 สถิติและการวิเคราะห์ข้อมูล ตอนที่1_เนื้อหา
PDF
PDF
บทที่ 1 สถิติและการวิเคราะห์ข้อมูล
PDF
สถิติประยุกต์สำหรับงานวิจัย Ok
PDF
สถิติประยุกต์สำหรับงานวิจัย 169
PDF
สถิติและข้อมูลเตรียมอบรม (1)
PDF
ข้อสอบปลายภาค คณิต ม.5 ฉบับที่ 1
PDF
PPT
Week 5 scale_and_measurement
PPTX
สถิติและคอมพิวเตอร์ การทดสอบสมมติฐาน
PPT
PPT
PPT
PDF
DOCX
statistics 1. 2. คํานํา
เอกสารทางวิชาการที่ผูเขียนเรียบเรียงขึ้นเพื่อใชประกอบการเรียนการสอนในวิชาสถิติระดับ
ปริญญาโท เนื้อหาในเลมประกอบดวย 5 บท ไดแก บทที่ 1 มโนทัศนเบื้องตนของสถิติในการประยุกตใช
ในการวิจัย ประกอบดวยมโนทัศนเกี่ยวกับความหมายของสถิติ ตัวแปร ประเภทของขอมูล เครื่องมือ
การตรวจสอบความเชื่อถือไดของขอมูล การเก็บขอมูล และการวิเคราะหขอมูล บทที่ 2 สถิติบรรยาย
ประกอบดวย การแจกแจงความถี่ การวัดแนวโนมเขาสูสวนกลาง การวัดการกระจาย คะแนนมาตรฐาน
คะแนนที เปอรเซ็นไทล บทที่ 3 สถิติอางอิง ประกอบดวย การเลือกตัวอยาง การประมาณคา และการ
ทดสอบสมมติ ฐานด วยสถิ ติทดสอบ ที ซี ไคสแควร เอฟ และการวิ เคราะห ความแปรปรวน บทที่ 4
ความสัมพันธระหวางตัวแปรและการทํานายตัวแปร ประกอบดวย สหสัมพันธอยางงายแบบตาง ๆ การ
วิเคราะหความถดถอยอยางงาย บทที่ 5 การทดสอบไคสแควร โดยเนนการวิเคราะหขอมูลดว ย
คอมพิวเตอร และการแปลความหมายผลวิเคราะห
เอกสารเลมนีสําเร็จลงไดดวยดี เนื่องจากผูเขียนไดรับความรูในวิทยาการจากคณาจารยภาควิชา
้
วิจัยและจิตวิทยาการศึกษา คณะครุศาสตร จุฬาลงกรณมหาวิทยาลัย โดยเฉพาะทานศาสตราจารยกิตติคุณ
ดร.อุทุมพร จามรมาน ศาสตราจารย กิตติคณ ดร.นงลักษณ วิรัชชัย และศาสตราจารย ดร.ศิริชย
ุ
ั
กาญจนวาสี จึงขอกราบขอบพระคุณมา ณ ที่นี้ดวย
อนึ่งเอกสารเลมนี้ผูเขียนไดพยายามเขียนใหมีความสมบูรณแลวก็ตามอาจมีขอบกพรองอยูบางจึง
ขออภัยไว ณ ที่นี้ดวย
เอมอร จังศิริพรปกรณ
ภาควิชาวิจยและจิตวิทยาการศึกษา
ั
คณะครุศาสตร จุฬาลงกรณมหาวิทยาลัย
3. 4. ค
สารบัญ(ตอ)
- χ2 - distribution
- F – distribution
Sampling Distribution ของสถิติทดสอบแบบตาง ๆ
- คาเฉลียเลขคณิตของกลุมตัวอยาง
่
- สัดสวนของกลุมตัวอยาง
- ความแปรปรวนของกลุมตัวอยาง
การเลือกกลุมตัวอยางและขนาดของกลุมตัวอยาง
- ประเภทของการเลือกกลุมตัวอยาง
- ขนาดของกลุมตัวอยาง
การประมาณคา (Parameters estimation)
การทดสอบสมมติฐาน (Hypothesis testing)
- การทดสอบสมมติฐานเกี่ยวกับคาเฉลียของประชากรเดียว
่
- การทดสอบสมมติฐานเกี่ยวกับคาสัดสวนประชากร
- การทดสอบสมมติฐานเกียวกับคาแปรปรวนประชากร
่
- การทดสอบสมมติฐานเกียวกับผลตางระหวางคาเฉลียของสองประชากร
่
่
- การทดสอบความแตกตางระหวางสัดสวนสองประชากร
- การทดสอบความแตกตางระหวางคาความแปรปรวนสองประชากร
การทดสอบสมมติฐานโดยใชโปรแกรม SPSS for Windows
การวิเคราะหความแปรปรวน (Analysis of Variance)
การวิเคราะหความแปรปรวน โดยใชโปรแกรม SPSS for Windows
แบบฝกหัด
บทที่ 4 ความสัมพันธระหวางตัวแปรและการทํานายตัวแปร
Phi Coefficient
Tetacholic Coefficient
Rank Biserial Correlation Coefficient
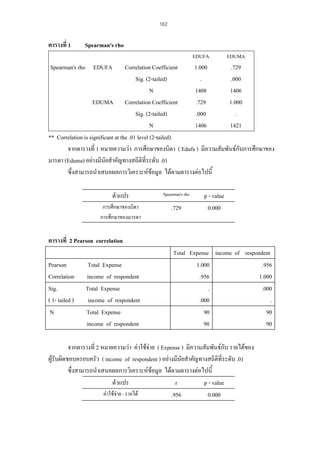
Spearman's Rank Correlation Coefficient
Kendall’s Tau
Point Biserial Correlation coefficient
หนา
88
89
91
91
92
93
94
94
98
100
107
108
109
111
112
117
119
120
127
138
145
150
152
153
153
155
156
5. ง
สารบัญ(ตอ)
Biserial Correlation Coefficient
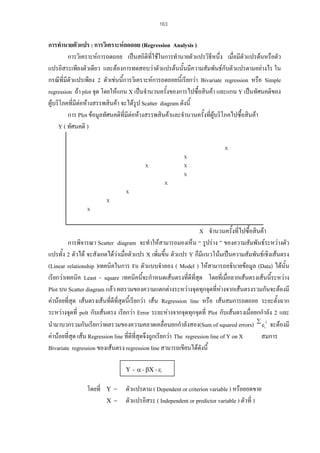
Pearson Product Moment Correlation Coefficient
การทดสอบความสัมพันธโดยใชโปรแกรม SPSS for Windows
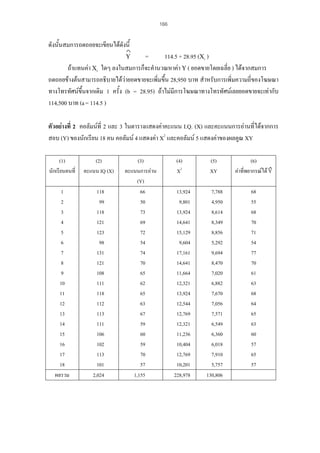
การทํานายตัวแปร : การวิเคราะหถดถอย
การวิเคราะหถดถอยเชิงซอน
การทดสอบการทํานายตัวแปรโดยใชโปรแกรม SPSS for Windows
แบบฝกหัด
บทที่ 5 การทดสอบไคสแควร(χ2)
การทดสอบสมมติฐานสําหรับขอมูลทีจําแนกทางเดียว
่
การทดสอบความแตกตางระหวางความถี่
การทดสอบสัดสวนประชากรวาเปนไปตามคาดหวัง
การทดสอบการแจกแจงของประชากรวาเปนไปตามที่คาดหวัง
การทดสอบสมมติฐานสําหรับขอมูลทีจําแนกสองทาง
่
การทดสอบχ2 โดยใชโปรแกรม SPSS for Windows
แบบฝกหัด
แบบฝกหัดทบทวน
บรรณานุกรม
ภาคผนวก ก การประมวลผลขอมูล
ภาคผนวก ข ตารางเลขสุม
ภาคผนวก ค ตารางการแจกแจงแบบตางๆ
หนา
156
157
161
163
169
171
180
183
183
184
185
187
189
193
195
197
198
214
216
6. บทที่1
บทนํา
มโนทัศนเบื้องตนของสถิติในการประยุกตใชในการวิจัย
องคความรูตางๆที่ไดจากการวิจัยจะชวยใหผูประกอบวิชาชีพพัฒนาความรูไดอยางตอเนื่อง
ดังนั้นความสามารถที่จะเขาใจผลงานวิจัยจึงเปนความสามารถพื้นฐานที่สําคัญของผูประกอบวิชาชีพ
ผลงานวิจัยสวนใหญจะใชสถิติในการนําเสนอผลวิเคราะหและสรุปผล จึงเปนความสําคัญอยางยิ่งที่
จะต องทําความเข าใจกับความรู และแนวคิ ดพื้นฐานทางสถิติ ดังนั้นในบทนี้จึ งไดนําเสนอมโนทัศน
เบื้องตนที่เกี่ยวของกับสถิติ ซึ่งไดแก ความหมายของสถิติ ประชากร กลุมตัวอยาง คาพารามิเตอร คาสถิติ
สถิติบรรยาย และสถิติอางอิง
ความหมายของสถิติ
คําวา สถิติมีหลายความหมาย ในทีนี้ขอสรุปความหมายของสถิติเปน 4 นัย ดังนี้
่
นัยแรก หมายถึง ขอมูลสถิติ ซึ่งเปนตัวเลขที่แทนขอเท็จจริงของสิ่งทีเ่ ราสนใจ เชน สถิติความเร็ว
ในการวิ่งแขงขัน สถิติปริมาณน้ําฝนที่ตกในรอบป สถิตจํานวนผูปวยในโรงพยาบาล สถิติการมาโรงเรียน
ิ
ของผูเรียน สถิติการลาปวยของเจาหนาที่ เปนตน
นัยที่สอง หมายถึง สถิติศาสตร ซึ่งเปนศาสตรที่เกียวกับวิธการที่ใชในการศึกษาขอมูล ไดแกการ
่
ี
เก็บรวบรวมขอมูล การนําเสนอขอมูล การวิเคราะหขอมูลและการแปลความหมาย
นัยที่สาม หมายถึง คาสถิติ ซึ่งเปนคาตัวเลขที่คํานวณไดจากขอมูลกลุมตัวอยาง เชนคาเฉลี่ย คาสวน
เบี่ยงเบนมาตรฐาน
นัยที่สี่ หมายถึง สาขาวิชาสถิติ ซึ่งเปนวิชาวิทยาศาสตรแขนงหนึ่งซึ่งมีเนื้อหาและรากฐานมาจากวิชา
คณิตศาสตรและตรรกวิทยา
ประชากร (Population) หมายถึง สมาชิกทุกหนวยของสิ่งที่สนใจศึกษา ซึ่งไมไดหมายถึงคน
เพียงอยางเดียว ประชากรอาจจะเปนสิ่งของ เวลา สถานที่ ฯลฯ เชนถาสนใจวาความคิดเห็นของคนไทย
ที่มีตอการเลือกตั้ง ประชากร คือคนไทยทุกคน หรือถาสนใจอายุการใชงานของเครื่องคอมพิวเตอรยี่หอ
หนึ่ง ประชากรคือเครื่องคอมพิวเตอรยี่หอนั้นทุกเครื่อง แตการเก็บขอมูลกับประชากรทุกหนวยอาจทําให
เสียเวลาและคาใชจายที่สูงมากและบางครังเปนเรื่องที่ตองตัดสินใจภายในเวลาจํากัด
้
การเลือกศึกษา
เฉพาะบางสวนของประชากรจึงเปนเรื่องทีมีความจําเปน เรียกวากลุมตัวอยาง
่
กลุมตัวอยาง (Sample) หมายถึง สวนหนึ่งของประชากรทีนํามาศึกษาซึ่งเปนตัวแทนของ
่
ประชากร การที่กลุมตัวอยางจะเปนตัวแทนที่ดีของประชากรเพื่อการอางอิงไปยังประชากรอยางนาเชื่อถือ
7. 10
ไดนั้น จะตองมีการเลือกตัวอยางและขนาดตัวอยางที่เหมาะสม ซึ่งจะตองอาศัยสถิติเขามาชวยในการสุม
ตัวอยางและการกําหนดขนาดของกลุมตัวอยาง
การสุมตัวอยาง (Sampling) หมายถึง กระบวนการไดมาซึ่งกลุมตัวอยางที่มีความเปนตัวแทนที่ดี
ของประชากร
คาพารามิเตอร(Parameters) หมายถึง คาตางๆที่คํานวณไดจากประชากร เปนคาที่บรรยาย
ลักษณะของประชากร แตในสถานการณทั่วไปมักไมไดคาพารามิเตอร เนื่องจากเปนเรื่องยากที่จะได
ขอมูลจากกลุมประชากรทุกหนวย จึงตองมีการประมาณคาพารามิเตอรจากคาสถิติโดยใชการประมาณคา
ทางสถิติ สัญลักษณทใชแทนคาพารามิเตอร เชน คาเฉลี่ยของประชากร(µ) คาความแปรปรวนของ
ี่
ประชากร(σ2) คาสวนเบียงเบนมาตรฐานของประชากร(σ) คาสัดสวนของประชากร(¶) คาสัมประสิทธิ์
่
์
สหสัมพันธระหวางตัวแปร 2 ตัวแปรในประชากร ( ρ ) คาสัมประสิทธิการถดถอยของการทํานายตัวแปร
ตามจากตัวแปรตนในกลุมประชากร ( β )
คาสถิติ (Statistics) หมายถึง คาตางๆที่คํานวณไดจากกลุมตัวอยาง เชน คาเฉลียของกลุมตัวอยาง
่
( x ) ความแปรปรวนของกลุมตัวอยาง(s2) คาสวนเบี่ยงเบนมาตรฐานของกลุมตัวอยาง (s) คาสัดสวนของ
กลุมตัวอยาง (p) คาสัมประสิทธิ์สหสัมพันธระหวางตัวแปร 2 ตัวแปรกลุมตัวอยาง (r) คาสัมประสิทธิ์
การถดถอยของการทํานายตัวแปรตามจากตัวแปรตนในกลุมตัวอยาง (b)
ในการเก็บขอมูลตางๆไมวาจากประชากรหรือกลุมตัวอยางจะตองมีคาของตัวแปรทีสนใจอยู
่
หลายคา ซึ่งจะมีการนําคาของตัวแปรมาสรุปถึงลักษณะประชากรหรือกลุมตัวอยาง เชน สรุปเปน คาเฉลี่ย
ความแปรปรวน สัดสวน เปนตน ถาตัวแปรที่สนใจคือ รายไดตอเดือนของคนไทย คาพารามิเตอร ไดแก
คาเฉลี่ยของประชากร (µ ) ความแปรปรวนของประชากร(σ2) คาสถิติ ไดแกคาเฉลี่ยของตัวอยาง( x )
ความแปรปรวนของตัวอยาง( s2 )
คาพารามิเตอรกับคาสถิติมีความสัมพันธกน เพราะคาพารามิเตอรสวนใหญจะคํานวณหาโดยตรง
ั
ไมได ตองใชวิธีที่สรุปอางอิงจากคาสถิติทคํานวณไดจากกลุมตัวอยาง
ี่
สถิติบรรยาย (Descriptive statistics) หมายถึง สถิติทใชในการศึกษาขอเท็จจริงจากกลุมขอมูลที่
ี่
รวบรวมมาได อาจเปนขอมูลจากกลุมตัวอยางหรือกลุมประชากรก็ได ทําใหทราบรายละเอียดเกียวกับ
่
ลักษณะของขอมูลกลุมนั้นโดยไมไดสรุปอางอิงผลการศึกษาไปยังกลุมขอมูลกลุมอืนหรือสรุปอางอิงไป
่
ยังกลุมประชากรที่ศกษา การบรรยายสรุปลักษณะของกลุมขอมูลไดแก การแจกแจงความถี่ การจัด
ึ
ตําแหนงเปรียบเทียบ การวัดแนวโนมเขาสูสวนกลาง การกระจายขอมูล การวัดการแจกแจง เปนตน
สถิติอางอิง (Inferential statistics) หมายถึง สถิตที่ใชัในการสรุปอางอิงขอมูลที่ไดจากกลุม
ิ
ตัวอยางไปยังขอมูลของประชากร โดยใชทฤษฎีความนาจะเปน การประมาณคาพารามิเตอร การทดสอบ
8. 11
สมมุติฐาน สําหรับความสัมพันธระหวางประชากร กลุมตัวอยาง คาพารามิเตอร คาสถิติ สถิติบรรยาย
และสถิติอางอิง อธิบายไดตามรูปมโนทัศนพื้นฐานของการวิเคราะหทางสถิติ ดังตอไปนี้
ประชากร
(Population)
การสุมตัวอยาง (Sampling)
สถิติบรรยาย
(Descriptive Statistics)
กลุมตัวอยาง
(Sample)
สถิติบรรยาย
(Descriptive Statistics)
สถิติอางอิง ( Inferential Statistics )
Parameters
µ σ² σ ¶ ρ
การประมาณคาพารามิเตอร ( Estimation)
การทดสอบสมมุติฐาน ( Hypothesis testing )
Statistics
x s² s.d. p r
รูปที่1 มโนทัศนพื้นฐานของการวิเคราะหทางสถิติ
จากรูปที่ 1 จะเห็นวาในการเก็บขอมูลเพื่อนํามาวิเคราะหทางสถิตินั้น เมื่อไมสามารถเก็บขอมูลได
จากประชากรทั้งหมด จําเปนจะตองมีการสุมตัวอยางทีถกวิธี เพื่อใหไดกลุมตัวอยางที่จะเปนตัวแทนที่ดี
ู่
ของประชากร ขอมูลทีไดจากกลุมตัวอยางสามารถนําไปวิเคราะหคาสถิติบรรยาย และสถิติอางอิง โดยที่
่
สถิติบรรยายทําใหทราบรายละเอียดเกี่ยวกับลักษณะของขอมูลกลุมนั้นโดยไมไดสรุปอางอิงผลการศึกษา
ไปยังกลุมขอมูลกลุมอื่นหรือสรุปอางอิงไปยังประชากรที่ศึกษา
สวนสถิติอางอิงสามารถสรุปอางอิง
ขอมูลที่ไดจากกลุมตัวอยางไปยังขอมูลของกลุมประชากร โดยใชทฤษฎีความนาจะเปน การประมาณ
คาพารามิเตอร การทดสอบสมมุติฐาน
จากมโนทัศนดังกลาวในการใชสถิติเพื่อการวิจัยจําเปนที่จะตองทราบความหมายที่เกี่ยวของกับ
การวิจยและสถิติ ไดแก ตัวแปร ประเภทของขอมูล ประโยชนของขอมูล การเก็บรวบรวมขอมูล
ั
9. 12
เครื่องมือและคุณภาพของเครื่องมือที่ใชในการเก็บขอมูล การสุมตัวอยาง การใชสถิติเพื่อการออกแบบการ
วิจัย และประเภทของสถิติทใชในการวิจย ดังนี้
ี่
ั
ตัวแปร(Variable) หมายถึง คุณลักษณะ หรือเงื่อนไขทีแปรเปลียนคาไปตามบุคคลหรือเวลา ที่
่
่
ผูวจัยจัดกระทํา(Manipulate) ควบคุม(Control) หรือสังเกต (Observe) ซึ่งแปรเปลียนคาไดตั้งแต 2 คา
ิ
่
ขึ้นไป เชน เพศ มี 2 ลักษณะ คือ ชาย และหญิง ฐานะเศรษฐกิจของครอบครัว อาจแบงเปน 3 ลักษณะ
ฐานะร่ํารวย ฐานะปานกลางและฐานะยากจน คะแนนผลสัมฤทธิ์ทางการเรียน เปนคาของตัวเลขชุดหนึ่งที่
มีหลายๆคา เปนตน
ตัวแปรอาจแบงเปนประเภทตางๆ แตตวแปรที่ศึกษาในงานวิจย มักแบงเปน 2 ประเภท ไดแก ตัว
ั
ั
่
ั
แปรตน และตัวแปรตาม แตก็มีตัวแปรอืนที่มีผลกระทบตอขอสรุปของการวิจย เรียกวา Confounding
Variable ดังนัน ในที่นจึงขอแบงประเภทของตัวแปรเปน 3 ประเภท คือ
้
ี้
1. ตัวแปรตน (Independent Variable) หมายถึง คุณลักษณะที่เกิดกอน หรือเปนสาเหตุของตัว
แปรตาม หรืออาจจะเรียกวา ตัวแปรอิสระ สามารถจําแนกไดเปน 2 แบบ คือ ตัวแปรอิสระที่สามารถจัด
กระทําได(Active Variable) และตัวแปรอิสระที่ไมสามารถจัดกระทําได(Attribute Variable) โดยตัวแปร
อิสระทั้ง 2 ชนิดเปนตัวแปรสาเหตุเชนเดียวกัน แตแตกตางกัน คือตัวแปรอิสระทีไมสามารถจัดกระทําได
่
(Attribute Variable) ผูวจยเปนเพียงผูเลือกวากลุมใดมีลักษณะอยางไร แตไมสามารถสรางลักษณะนัน
ิั
้
ขึ้นมา ในขณะที่ตัวแปรอิสระที่สามารถจัดกระทําได (Active Variable) ผูวิจยสามารถสรางลักษณะนั้น
ั
ขึ้นมาได ตัวอยางเชน การวิจัยที่ศึกษาอายุของผูสอนและสภาพของหองเรียนวามีผลตอผลสัมฤทธิ์ทางการ
เรียนหรือไม อายุของผูสอนที่แบงเปนชวงๆและสภาพของหองเรียนที่แบงเปนหองที่มีเครื่องปรับอากาศ
กับไมมีครื่องปรับอากาศ ตางก็เปนตัวแปรอิสระ แตอายุเปนตัวแปรอิสระที่ไมสามารถสรางลักษณะนั้น
ขึ้นมาได เรียกวา Attribute Variable ในขณะที่สภาพของหองเรียนเปนตัวแปรอิสระที่สามารถสราง
ลักษณะนั้นขึนมาได เรียกวา Active Variable
้
2. ตัวแปรตาม (Dependent Variable) หมายถึง คุณลักษณะที่คาดวาจะไดรับ หรือเปนผลที่ได
รับจากตัวแปรอิสระ ตัวอยางเชน การวิจยที่ศึกษาอายุของผูสอนและสภาพของหองเรียนวามีผลตอ
ั
ผลสัมฤทธิ์ทางการเรียนหรือไม ที่กลาวมาแลวขางตน ตัวแปรตามไดแก ผลสัมฤทธิทางการเรียน
์
3. ตัวแปรที่มผลกระทบตอขอสรุปของการวิจัย (Confounding Variable) หมายถึง ตัวแปรที่มี
ี
ผลกระทบตอการสรุปความเปนสาเหตุของตัวแปรตนทีมีตอตัวแปรตาม จําแนกเปน 2 ชนิดใหญๆ คือ
่
3.1 ตัวแปรแทรกซอน (Extraneous Variable) เปนตัวแปรที่สงผลตอตัวแปรตามเชน
10. 13
เดียวกับตัวแปรอิสระ แตเปนสิ่งที่ผูวจัยไมไดสนใจทีจะศึกษา ดังนันจึงตองมีการควบคุม ไมเชนนั้นตัว
ิ
่
้
แปรแทรกซอนอาจทําใหผลที่ศึกษาไมไดขอสรุปอยางทีสรุปไวก็ได ทําใหผลทีไดคาดเคลื่อนไปจากความ
่
่
เปนจริง
3.2 ตัวแปรสอดแทรก(Intervening Variable) เปนตัวแปรทีสอดแทรกอยูระหวางตัว
่
แปรตนและตัวแปรตาม มองได 2 ลักษณะ คือ
ลักษณะแรก เปนตัวแปรคันกลางระหวางตัวแปรตนกับตัวแปรตาม เปนตัวแปรทีไดรับผลมาจาก
่
่
ตัวแปรตนแลวจึงสงผลตอไปที่ตัวแปรตาม เชน การศึกษาความสัมพันธระหวางสภาพเศรษฐกิจสังคมของ
ครอบครัวกับผลสัมฤทธิ์ทางการเรียนของนักเรียน พบวามีความสัมพันธกนสูง ซึ่งอาจเปนไปไดวาสภาพ
ั
เศรษฐกิจสังคมของครอบครัวสูงมีผลใหความคาดหวังของครอบครัวตอผลสัมฤทธิ์ทางการเรียนของ
์
นักเรียนสูง แลวการมีความคาดหวังของครอบครัวตอผลสัมฤทธิทางการเรียนของนักเรียนสูง ทําให
นักเรียนตั้งใจเรียนทําใหผลสัมฤทธิ์ทางการเรียนของนักเรียนสูง ดังนัน ความคาดหวังของครอบครัวตอ
้
ผลสัมฤทธิ์ทางการเรียนของนักเรียน จึงเปนตัวแปรสอดแทรก(Intervening Variable)
ลักษณะที่สอง เปนตัวแปรสอดแทรกที่ทาใหผลของตัวแปรตนมีตอตัวแปรตามตางไปจากสภาพ
ํ
จริงที่ควรจะเปน เชน ความวิตกกังวล ความเมื่อยลา หรือความตื่นเตนของผูสอบที่มีตอคะแนนสอบ
ประเภทของขอมูล
ขอมูล (Data) คือ ขอเท็จจริงที่ตองการ ขอมูลทางสถิติสวนใหญมกเปนตัวเลข เชน จํานวน
ั
นักเรียน คะแนนสอบ รายได รายจาย เปนตน การพิจารณาแบงประเภทของขอมูลพิจารณาไดตาม
ลักษณะตางๆกัน ดังนี้
1. การแบงประเภทของขอมูลตามลักษณะของสิ่งที่แปร เปนการแบงขอมูลตามลักษณะของ
ตัวแปร จําแนกเปน 2 ชนิด คือ
1.1 ขอมูลเชิงปริมาณ (Quantitative data) เปนขอมูลที่วดคาไดวามีคามาก หรือนอยเทาไร
ั
แสดงไดเปนตัวเลข เชน อายุ น้ําหนัก สวนสูง รายได ซึ่งแบงไดเปน 2 แบบ คือ
1.1.1 ขอมูลแบบตอเนื่อง (Continuous data) หมายถึง ขอมูลที่มีคาไดทุกคาในชวงที่
กําหนดอยางมีความหมาย เชน รายไดของครอบครัวตอเดือน ความสูงของนิสิต ความยาวของวัตถุ ดังนั้น
คาของขอมูลแบบนี้จะเปน 150.5 150.6 150.7 150.8………………..
1.1.2 ขอมูลแบบไมตอเนื่อง (Discrete data) หมายถึง ขอมูลที่มีคาเปนจํานวนเต็ม
หรือจํานวนนับ เชน จํานวน คน จํานวนสาขาวิชา จํานวนสินคา เปนตน ดังนันคาของขอมูลแบบนีจะเปน
้
้
0,1,2,3…….
1.2 ขอมูลเชิงคุณภาพ (Qualitative data) เปนขอมูลที่ไมสามารถระบุคาไดวามาก หรือนอยเทา
11. 14
ไร มักเปนคุณลักษณะของขอมูล เชน สีของตา เพศ ลําดับที่ของการแขงขัน คุณภาพของอาหาร เปนตน
2. การแบงประเภทของขอมูลตามแหลงที่มาของขอมูล เปนการแบงขอมูลตามแหลงที่มาของ
ขอมูล จําแนกเปน 2 ชนิด คือ
2.1 ขอมูลปฐมภูมิ (Primary data) เปนขอมูลที่ผใชหรือหนวยงานที่ใชเปนผูเก็บรวบรวมขอมูล
ู
เอง ซึ่งจะไดรายละเอียดตรงตามความตองการของผูใชขอมูล แตจะเสียเวลาและคาใชจายมาก
2.2 ขอมูลทุตยภูมิ (Secondary data) เปนขอมูลทีผใชหรือหนวยงานที่ใชไมไดเก็บรวบรวม
ิ
่ ู
ขอมูลเอง แตมีผูอื่นหรือหนวยงานอื่นเก็บขอมูลไวแลว ผูใชเพียงแตนาขอมูลที่เก็บไวแลวมาใชเทานั้น ซึ่ง
ํ
เปนการประหยัดเวลาและคาใชจาย แตการนําขอมูลทุติยภูมิมาใชบางครั้งจะไมตรงกับความตองการ หรือ
ขาดรายละเอียดที่ตองการ ผูใชไมทราบขอผิดพลาดของขอมูล อาจมีผลทําใหขอสรุปผิดพลาดได ดังนั้น
การใชขอมูลทุติยภูมิ จึงตองใชดวยความระมัดระวัง
3. การแบงประเภทของขอมูลตามมาตรการวัด แบงเปน
3.1 มาตรการวัดแบบนามบัญญัติ (Nominal data) เปนการจําแนกลักษณะของขอมูลที่ได
ออกเปนประเภทตางๆหรือเปนพวกๆ โดยจัดลักษณะทีเ่ หมือนกันไวดวยกัน เชน ตัวแปร เพศ เชื้อชาติ
สถานภาพสมรส เปนตน การจําแนกลักษณะของขอมูลเชน เพศ แบงเปน 2 ลักษณะ คือ ชาย และ หญิง
ซึ่งอาจจะกําหนดคาใหกับลักษณะของตัวแปรเปน 1 และ 2 การกําหนดคาใหกับตัวแปรมีคุณสมบัติเพียง
จําแนกความแตกตางและสะดวกตอการบันทึกลงในคอมพิวเตอรเทานั้น ไมมีความหมายในเชิงปริมาณ ที่
จะนํามา บวก ลบ คูณ หารกันได
3.2 มาตรการวัดแบบอันดับ(Ordinal data) เปนการกําหนดลักษณะของขอมูลทีได ออกเปน
่
อันดับที่ บอกความมากนอยระหวางกันได เชนลําดับที่ของนักเรียนมารยาทดี คาลําดับที่ 1 , 2 , 3
สามารถบอกไดวาใครมารยาทดีกวาใคร แตไมสามารถบอกไดวาคนที่ไดมารยาทดีลําดับที่ 1 ดีกวาลําดับ
ที่ 2 อยูเทาไร และไมสามารถบอกไดวาความแตกตางระหวางคนทีไดมารยาทดีลาดับที่ 1 และ 2 จะ
่
ํ
เทากับความแตกตางระหวางคนที่ไดมารยาทดีลําดับที่ 2 และ 3 หรือชวงความหางของคาตัวแปรแตละคา
ไมเทากัน
3.3 มาตรการวัดแบบอันตรภาค (Interval data ) เปนการกําหนดตัวเลขใหกับลักษณะของขอมูล
ตามความมากนอย โดยตัวเลขทีกําหนดสามารถบอกความมากนอยระหวางกันแลวยังมีชวงหางระหวาง
่
คาที่เทากันดวย แตคาศูนยทกําหนดตามมาตรการวัดนีไมใชศูนยแท ตัวอยาง เชน คะแนน อุณหภูมิ เปน
ี่
้
ุ
ตน คาของอุณหภูมิ 80°C สูงกวาอุณหภูมิ 50 °C อยู 30°C แตอณหภูมิ 0 °C มิไดแปลวาไมมีความรอน
ความจริงมีความรอนระดับหนึ่งแตถูกสมมุติใหเปน 0 °C
12. 15
3.4 มาตราการวัดแบบอัตราสวน(Ratio data) เปนการกําหนดตัวเลขใหกับลักษณะของขอมูล
เชนเดียวกับมาตรการวัดแบบอันตรภาค แตมาตรการวัดระดับนีจะมีคา 0 ที่แทจริงดวย เชน อายุ รายได
้
น้ําหนัก สวนสูง เปนตน สวนสูง 0 เซนติเมตรก็แปลวาไมมีความสูงเลย
การเก็บรวบรวมขอมูล
การเก็บรวบรวมขอมูลทางพฤติกรรมศาสตร ไมวาจะเก็บกับทุกหนวยประชากรหรือเก็บจากกลุม
ตัวอยาง มีวิธการเก็บขอมูล ดังนี้
ี
1. การเก็บรวบรวมขอมูลโดยใชแบบสอบถาม การเก็บขอมูลดวยวิธนผตอบจะตองมีความ
ี ี้ ู
สามารถในการอาน เปนวิธที่ประหยัดและสะดวก แตอาจจะมีปญหาในเรื่องอัตราการตอบกลับและความ
ี
จริงใจในการตอบ
2. การเก็บรวบรวมขอมูลโดยการทดสอบ เปนการเก็บขอมูลโดยสรางเงือนไขหรือสถาน
่
การณใหผรับการทดสอบแสดงความสามารถสูงสุดของตนออกมา
ู
3. การเก็บรวบรวมขอมูลโดยการสัมภาษณ แบงเปน 2 ลักษณะ คือการสัมภาษณที่กําหนดคํา
ถามการสัมภาษณไวอยางแนนอน เรียกวา การสัมภาษณแบบมีโครงสราง(Structured interview) ซึ่งมี
ขอดีคือไดประเด็นทีตองการครบถวนเปนรูปแบบเดียวกัน งายตอการวิเคราะหขอมูล แตมีขอจํากัดที่วาจะ
่
ไดขอมูลที่มในกรอบคําถามเทานั้น อีกลักษณะหนึ่งคือการสัมภาษณที่ไมไดกําหนดคําถามการสัมภาษณ
ี
ไวแนนอน
อาจจะกําหนดประเด็นหลักๆที่ตองการ
เรียกวาการสัมภาษณแบบไมมโครงสราง
ี
(Unstructured interview) การสัมภาษณแบบนี้มีขอดีที่วาไดขอมูลที่หลากหลาย กวางขวาง ลึกซึ้ง แต
ตองอาศัยผูสัมภาษณที่มีทักษะสูง และการวิเคราะหขอมูลจะมีความยุงยากกวา
4. การเก็บรวบรวมขอมูลโดยการสังเกต การเก็บขอมูลดวยการสังเกต เหมาะสําหรับเหตุ
การณหรือพฤติกรรมที่ไมสามารถวัดไดโดยตรง แบงเปน 2 ลักษณะ คือ การสังเกตอยางมีสวนรวม โดยผู
สังเกตเขาไปเปนสวนหนึ่งของกลุมหรือสถานการณที่จะสังเกต ซึ่งจะไดขอมูลทีลึกซึ้ง อีกลักษณะหนึ่งคือ
่
การสังเกตอยางไมมีสวนรวม ผูสังเกตจะทําตนเปนบุคคลภายนอก ผูถูกสังเกตอาจจะรูตัวหรือไมรูตัวก็ได
แตขอมูลที่ไดอาจไมลึกซึ้งมากนัก
5. การเก็บรวบรวมขอมูลโดยการทดลอง ผูวิจัยตองจัดกระทําหรือสรางเงื่อนไข สถานการณ
อยางใดอยางหนึ่ง เพื่อดูผลที่เกิดขึ้นกับตัวแปรตาม ซึ่งมีความจําเปนอยางยิ่งในการออกแบบการทดลอง
ใหดีวาความผันแปรที่เกิดในตัวแปรตาม เปนผลเนื่องมาจากตัวแปรอิสระที่แทจริง
13. 16
เครืองมือและคุณภาพของเครืองมือที่ใชในการเก็บขอมูล
่
่
การสรางเครื่องมือเพื่อใชในการเก็บขอมูลขึ้นอยูกับวิธการที่ใชในการเก็บขอมูล เครื่องมือที่ใช
ี
ไดแก แบบสอบถาม (Questionnaire ) แบบสอบ (Test ) แบบสัมภาษณ (Interview form) แบบสังเกต
(Observation form ) ตลอดจนเครื่องมือตางๆที่สรางขึ้นเพื่อเก็บขอมูลโดยการทดลอง
สําหรับคุณภาพของเครื่องมือที่ใชในการเก็บขอมูล จะตองตรวจสอบคุณภาพรายขอและคุณภาพ
ของเครื่องมือทั้งฉบับ โดยการตรวจสอบคุณภาพรายขอ ตองดูความสอดคลองกับตัวแปรที่มุงวัด ความ
เปนปรนัย ความยากงาย และอํานาจจําแนก สวนการตรวจสอบคุณภาพของเครื่องมือทั้งฉบับตองดูความ
ตรงและความเที่ยงของเครื่องมือ โดยความตรง ตองตรวจสอบ ความตรงตามเนือหา ความตรงตาม
้
โครงสราง ความตรงตามเกณฑ สวนความเที่ยง ตองตรวจสอบความเที่ยงแบบความคงที่ ความเที่ยงแบบ
ความทัดเทียมกัน ความเที่ยงแบบความสอดคลองภายใน โดยมีรายละเอียดของการตรวจสอบคุณภาพของ
เครื่องมือ ดังนี้
ความเที่ยง (Reliability)
ความเที่ยง หมายถึง ความคงเสนคงวาของผลการวัดจากเครื่องมือชนิดเดียวกันที่ทําการวัดซ้ํา
หรือ คือ อัตราสวนระหวางความแปรปรวนของคะแนนจริงกับความแปรปรวนของคะแนนที่สังเกตได
สวนความหมายของความเที่ยงในทางปฏิบัติ คือ คาสัมประสิทธิ์สหสัมพันธระหวางคะแนนจากแบบสอบ
คูขนาน 2 ชุด ซึ่งสอบโดยกลุมผูสอบกลุมเดียวกัน
วิธการตรวจสอบความเที่ยง
ี
1. การหาความเที่ยงเชิงความคงที่ (Stability) ทําไดโดยใชวิธีวัดซ้ํา คือใหผูตอบกลุมเดียวทําแบบ
วัดชุดเดียวกันสองครั้งในเวลาหางกันพอสมควร (test-retest method )แลวนําคะแนนทั้งสองชุดมาหา
ความสัมพันธกัน ถาคาสัมประสิทธิ์สหสัมพันธมีคาสูง แสดงวามีความเที่ยงสูง การวัดความคงที่โดยการ
วัดซ้ําสามารถใชไดกับเครื่องมือวัดที่เปนแบบสอบ แบบสอบถามหรือแบบวัดเจตคติชนิดมาตราสวน
ประมาณคา โดยคํานวณหาคาสัมประสิทธิ์สหสัมพันธอยางงาย (Pearson Product moment Correlation
Coefficient) มีสูตร ดังนี้
[N
r
∑
N
r =
∑
X
2
XY − [( ∑ X )( ∑ Y )]
− ( ∑ X ) 2 ][ N
∑Y
2
− (∑ Y ) 2 ]
= คาสัมประสิทธิ์สหสัมพันธในที่นี้คือคาความเที่ยง
= จํานวนผูสอบ
14. 17
= ผลบวกของผลคูณคะแนนครั้งแรกและครั้งที่สองเปนคู ๆ
= ผลบวกของคะแนนการสอบครั้งแรก
= ผลบวกของคะแนนการสอบครั้งที่สอง
= กําลังสองของคะแนนครั้งแรก
= กําลังสองของคะแนนครั้งที่สอง
2. การหาความเที่ยงเชิงความเทาเทียมกัน (Equivalence) ทําไดโดยวิธีใชแบบทดสอบสมมูลกัน
(Equivalent -form) หรือ เปนแบบสอบคูขนาน (Parallel-form) ไปทดสอบพรอมกันหรือเวลาใกลเคียงกัน
สองฉบับกับกลุมเดียวกันแลวนําคะแนนทั้งสองชุดมาหาความสัมพันธกัน ถาคาสัมประสิทธิ์สหสัมพันธมี
คาสูง แสดงวามีความเที่ยงสูง คํานวณ โดยหาคาสัมประสิทธิ์สหสัมพันธอยางงาย (Pearson Product
moment Correlation Coefficient) มีสูตรคํานวณ ดังนี้
∑
N
r =
[N
∑
X
2
XY − [( ∑ X )( ∑ Y )]
− ( ∑ X ) 2 ][ N
∑Y
2
− (∑ Y ) 2 ]
r = คาสัมประสิทธิ์สหสัมพันธในที่นี้คือคาความเที่ยง
= จํานวนผูสอบ
ในที่นี้ X และ Y เปนแบบสอบที่คูขนานกัน
3. การหาความเที่ยงเชิงความสอดคลองภายใน (Internal Consistency)
เปนวิธีที่ใชการวัดครั้งเดียวและมีวิธประมาณคาความเทียงไดหลายวิธีคือ
ี
่
3.1 วิธแบงครึ่ง (Split-Half Method) วิธีนใชแบบวัดเพียงฉบับเดียวทําการวัดครั้งเดียว แตแบง
ี
ี้
้
ตรวจเปนสองสวนที่เทาเทียมกัน เชน แบงเปนชุดขอคูกับขอคี่ หรือแบงครึ่งแรกกับครึ่งหลัง ทังนี้ตอง
วางแผนสรางใหสองสวนคูขนานกันกอน วิธวิเคราะหคาความเที่ยงโดยหาคาสัมประสิทธิ์สัมพันธอยาง
ี
งายระหวางคะแนนทั้งสองครึ่งกอนดังนี้
N
r =
[N
∑
X
∑
2
XY − [( ∑ X )( ∑ Y )]
− ( ∑ X ) 2 ][ N
∑Y
2
− (∑ Y ) 2 ]
15. 18
r = คาสัมประสิทธิ์สหสัมพันธในที่นี้คือคาความเที่ยง
N = จํานวนผูสอบ
ในที่นี้กําหนดให X เปนคะแนนขอคูหรือครึ่งแรกแลวแตกรณี
Y เปนคะแนนขอคีหรือครึ่งหลังแลวแตกรณี
่
r ที่ไดเปน r hh คือ สหสัมพันธระหวางคะแนนครึ่งฉบับกับอีกครึงฉบับแลวปรับขยายเปน
่
สหสัมพันธทั้งฉบับ (r tt ) ดวยสูตรของ Spearman Brown ดังนี้
=
2rhh
1 + rhh
การประมาณคาความเที่ยงดวยวิธีนี้มจุดออนคือผลที่ไดไมคงที่ขึ้นอยูกบวิธีทใชแบงครึ่งขอสอบ
ี
ั
ี่
ตัวอยาง การหาความเที่ยงของแบบสอบเลือกตอบ 20 ขอ โดยใชวิธแบงครึ่ง (Split-Half
ี
Method)แบงแบบสอบเลือกตอบ 20 ขอ เปน 2 ชุด คือ ชุดขอคู (X) 10 ขอ และชุดขอคี่(y ) 10 ขอ ทําการ
ทดสอบกับผูเรียน 5 คน ไดคะแนน ดังตาราง
คนที่
1
2
3
4
5
รวม
การคํานวณคา rhh
X
5
5
4
3
3
20
rhh =
N
=
=
rhh
X2
25
25
16
9
9
84
Y
8
9
8
6
7
38
=
[N
∑
X
∑
2
Y2
64
81
64
36
49
294
XY − [( ∑ X )( ∑ Y )]
− ( ∑ X ) 2 ][ N
∑Y
2
− (∑ Y ) 2 ]
5(156) − (20)(38)
(5(84) − 400))((5(294) − (1444))
20
(20)(26)
0.877
XY
40
45
32
18
21
156
16. 19
หาคาสหสัมพันธทั้งฉบับ (r tt ) ดวยสูตรของ Spearman Brown ดังนี้
=
2rhh
1 + rhh
=
2 × 0.87
1 + 0.87
=
0.93
ความเที่ยงของแบบสอบเลือกตอบ ชุดนี้ = 0.93 แสดงวามีความเที่ยงของเครื่องมือสูง
3.2 วิธีของคูเดอร-ริชารดสัน( Kuder-Richardson Method) เปนวิธที่แกจดออนของวิธแบงครึ่ง
ี
ุ
ี
ผลทีไดมีคาแตกตางกัน วิธนี้ที่ทําการวัดเพียงครังเดียวเชนกัน ใชไดกบเครื่องมือที่ใหคะแนน 0-1 แลวนํา
่
ี
้
ั
คะแนนมาวิเคราะหโดยใชสตรของ Kuder-Richardson ซึ่งมี 2 สูตร คือ KR20 และ KR21 ซึ่งสูตร KR20
ู
และตองทราบผลการตอบรายขอ ดังนี้
=
เมื่อ rtt
k
pi
qi
คือ คาประมาณความเทียงของเครื่องมือจากสูตร KR20
่
คือ จํานวนขอสอบ
คือ สัดสวนของผูตอบถูกในขอi
คือ 1-pi
คือ คาความแปรปรวนของคะแนนรวม
ั
สวนสูตร KR21ใชไดกบเครื่องมือที่ใหคะแนนแบบ 0-1 และขอสอบทุกขอตองยาก เทากัน หรือ
อนุโลมใหใกลเคียงกัน โดยมีสูตรดังนี้
rtt =
เมื่อ rtt คือ คาประมา ณคาความเที่ยงของแบบทดสอบทั้งฉบับจากสูตร KR21
17. 20
k คือ จํานวนขอสอบ
คือ คาเฉลี่ยของคะแนนรวม
คือ คาความแปรปรวนของคะแนนรวม
ตัวอยางการคํานวณหาคา Reliability ดวยสูตรคูเดอร-ริชารดสัน 20 ( KR-20 )
โดยมีขอสอบ 8 ขอ ผูสอบ 6 คน ดังนี้
คนที่
ขอที่
1
2
3
4
5
6
7
1
1
1
0
1
1
1
1
2
1
1
1
1
0
0
1
3
0
1
0
1
1
0
0
4
1
1
1
0
1
0
0
5
0
1
1
1
1
1
0
6
0
0
1
1
0
0
0
จํานวนนักเรียนตอบถูก
3
5
4
5
4
2
2
สัดสวนที่ตอบถูก (p)
.50 .83 .67 .83 .67 .33 .33
สัดสวนที่ตอบผิด (q)
.50 .17 .33 .17 .33 .67 .67
pq
.25 .14 .22 .14 .22 .22 .22
x
= 4.5
σ2 = Σ ( x - x ) 2
n-1
= (7-4.5)2+(5-4.5) 2+(4-4.5) 2+(4-4.5) 2+(5-4.5) 2+(2-4.5) 2
5
=
2.7
=
=
=
8
7
8
1
0
1
0
0
0
2
.33
.67
.22
(. 25 + . 14 + . 22 + . 14 + . 22 + . 22 + . 22 + . 22 )⎫
⎧
⎨1 −
⎬
2 .7
⎩
⎭
.287
รวม
7
5
4
4
5
2
18. 21
3.3 วิธการหาดวยสูตรสัมประสิทธิแอลฟา (Alpha coefficient) Cronbach เปนผูคิดคนวิธการ
ี
์
ี
หาความเที่ยงแบบ ความสอดคลองภายในเหมือนกับวิธของ Kuder-Richardson แตจะใชไดกับเครืองมือที่
ี
่
เปนแบบอัตนัยหรือมาตราสวนประมาณคา ซึ่งไมไดมีการใหคะแนนแบบ 0 - 1 มีสูตรในการคํานวณดังนี้
=
สูตร
k
= คาความเที่ยงของเครื่องมือ
= จํานวนขอของเครื่องมือ
= ความแปรปรวนของคะแนนแตละขอ
= ความแปรปรวนของคะแนนทั้งฉบับ
ตัวอยางการหาคา Reliability ดวยสูตร Cronbach
นักเรียน
คนที่
1
2
3
4
5
6
7
8
9
10
si
si2
ขอที่
1
1
4
3
1
2
3
5
5
2
4
1.5
2.2
2
2
1
4
2
1
4
1
5
3
4
1.5
2.2
3
4
2
5
3
4
1
2
4
3
5
1.3
1.7
4
2
4
4
4
5
5
3
3
1
4
1.2
1.6
5
5
2
5
5
1
4
4
2
1
5
1.7
2.9
6
3
1
1
4
2
3
5
1
2
4
1.4
2.0
7
1
1
2
3
4
2
1
2
2
5
1.3
1.7
8
2
2
3
2
4
1
2
3
4
5
1.2
1.5
9
4
1
4
1
3
1
3
4
2
5
1.4
2.1
10
4
1
5
3
2
2
4
5
1
3
1.5
2.2
รวม
28
19
36
28
28
26
30
34
21
44
S t2 =52.71
2
∑ s =20.1
i
19. 22
r
tt
=
= (10/10-1)(1-(20.1/52.71)
= (10/9)(1-0.381)
= 0.687
การแปลความหมายของความเที่ยง
คาความเที่ยงที่ประมาณไดตามวิธีดังกลาวเปนสัมประสิทธิ์ของความเที่ยง ซึ่งมีความหมายคลาย
กับคาสัมประสิทธิ์สหสัมพันธ กลาวคือ เมื่อเอาคาสัมประสิทธิ์สหสัมพันธยกกําลังสอง และคูณดวย 100
ทําเปนรอยละจะกลายเปนคาสัมประสิทธิ์ของความแปรผันรวม ซึ่งจะบอกถึงสัดสวนหรือรอยละของ
ความแปรผันรวมกันของตัวแปรสองตัว เชน r xy = 0.9 ฉะนั้น (0.9)2 x 100 เทากับ 81% จะแปลวาตัวแปร
X กับตัวแปร Y มีความแปรผันรวมกันอยู 81% ทํานองเดียวกับคาสัมประสิทธิ์ของความเที่ยงก็สามารถ
แปลความหมายไดเชนกัน ถาพบวาเครื่องมือรวบรวมขอมูลมีคาสัมประสิทธิ์ความเที่ยง (r tt) เทากับ 0.9 ก็
แสดงวาเครื่องมือนั้น ใชวัดครั้งแรกกับวัดครั้งหลัง จะมีความแปรผันรวมกัน 81% หรือถานําเครื่องมือนั้น
ไปวัดซ้ําอีกครั้งจะไดผลเหมือนเดิม 81% (Kerlinger , 1986 : 428)
ความตรง (Validity)
ความตรง หมายถึง ความถูกตองแมนยําของเครื่องมือในการวัดสิ่งที่ตองการวัดความตรง หรือ
เปนคาสัมประสิทธิ์สหสัมพันธระหวางคะแนนที่ไดจากเครื่องมือกับเกณฑภายนอกที่เปนอิสระอื่นๆซึ่ง
สามารถวัดสิ่งที่ตองการวัดได
ประเภทและวิธีตรวจสอบความตรง
ความตรงปนคุณสมบัติที่เกียวของกับจุดมุงหมายสําคัญของการนําเครื่องมือไปใชเปนคุณลักษณะ
่
ที่อาศัยการตรวจสอบไดหลายวิธี ดังนั้นจึงสามารถแบงความตรงไดหลายประเภท ดังนี้
1. ความตรงเชิงเนื้อหา (Content Validity) หมายถึง ความสามารถของเครืองมือที่วัดไดตรงและ
่
ครอบคลุมเนื้อหาตามที่ตองการวัดและเนื้อหาที่วัดเปนตัวแทนของเนื้อหาทั้งหมดและครอบคลุม
องคประกอบของคุณลักษณะที่ตองการ
การตรวจสอบความตรงตามเนื้อหาของเครื่องมือจะกระทําดวยการวิเคราะหเชิงเหตุผล อาศัยดุลย
พินิจทางวิชาการของผูเ ชี่ยวชาญทางเนื้อหาเปนเกณฑ ซึ่งถาเปนเครื่องมือวัดความรูหรือเปนแบบสอบ
วัดผลสัมฤทธิ์ การพิจารณาของผูเชี่ยวชาญจะอาศัยตารางวิเคราะหหลักสูตร ซึ่งจะจําแนกสองทางตาม
20. 23
เนื้อหาและพฤติกรรมที่ตองการวัด แตถาเปนเครื่องมือที่มิใชวัดผลสัมฤทธิ์ เชน แบบวัดเจตคติ แบบวัด
บุคลิกภาพ เนือหาที่วัดไมแนนอน การตรวจสอบจึงตองทําตารางโครงสรางของสิ่งที่ตองการวัด ใหนิยาม
้
ความหมายกําหนดขอบเขตและองคประกอบของเนื้อหาใหชัดเจน โดยยึดกรอบแนวคิดใดแนวคิดหนึ่งที่
เชื่อถือไดเปนเกณฑ จากนั้นก็ตรวจสอบดูวาขอคําถามหรือขอความแตละขอถามไดตรง ครอบคลุม
ครบถวนและเปนตัวแทนตามแนวคิดที่นํามาเปนกรอบของการวิจยเรื่องนั้นหรือไม ถาครบถวนก็ถือวา
ั
เครื่องมือนั้นมีความตรงตามเนื้อหา
วิธีตรวจสอบความตรงเชิงเนื้อหา
เปนวิธีที่ใหผเู ชี่ยวชาญตัดสินขอคําถามทีสรางขึ้นเปนไปตามเนื้อหาและวัตถุประสงคที่ตองการ
่
วัดหรือไม ในกรณีที่เปนแบบสอบวัดผลสัมฤทธิ์อิงกลุม ผูเชี่ยวชาญตองพิจารณาวาแบบสอบนั้นมีขอสอบ
แตละขอตรงตามเนื้อหาและพฤติกรรมการเรียนรูที่จะวัด ตลอดจนจํานวนขอมีสอดคลองกับตาราง
วิเคราะหหลักสูตร (Table of Specifications) หรือไม
ในกรณีที่เปนแบบสอบวัดผลสัมฤทธิ์อิงเกณฑ ผูเชี่ยวชาญตองพิจารณาวาแบบสอบนั้นมีขอสอบ
แตละขอตรงตรงตามวัตถุประสงคเชิงพฤติกรรมหรือไม
การใหผูเชียวชาญตัดสินความสอดคลองของขอคําถามกับเนื้อหาและพฤติกรรมการเรียนรูจะมี
่
แบบฟอรมใหผูเชี่ยวชาญพิจารณาเปนรายขอคําถาม โดยมีการระบุน้ําหนักคะแนน ดังนี้
ถาขอคําถามมีความสอดคลองกับเนื้อหา ระดับพฤติกรรม และวัตถุประสงคที่ตองการวัดจะได
คะแนน +1
ถาไมแนใจวาขอคําถามมีความสอดคลองกับเนื้อหา ระดับพฤติกรรม และวัตถุประสงคที่ตองการ
วัดจะไดคะแนน 0
ถาขอคําถามไมความสอดคลองกับเนื้อหา ระดับพฤติกรรม และวัตถุประสงคที่ตองการวัดจะได
คะแนน -1
ตัวอยางแบบฟอรมการตัดสินความตรงตามเนื้อหาของแบบสอบอิงกลุมสําหรับผูเชี่ยวชาญ
เนื้อหา
ความหมายของการวัด
ความหมายของการประเมิน
ผลการวิเคราะหขอสอบ
ระดับ
พฤติกรรม
เขาใจ
เขาใจ
วิเคราะห
ขอสอบ
1. ขอใดเปนการวัด
2.ขอใดเปนการประเมิน
3.ถาขอสอบขอหนึ่งมีคา
P = .50 และคา r = .82
ผลสรุปจากการวิเคราะห
ขอสอบคือขอใด
ความเห็นของผูเชี่ยวชาญ
+1
0
-1
ความคิดเห็น
เพิ่มเติม
21. 22. 25
นั้นไปทดสอบกับกลุมตัวอยางดังกลาวแลวพบวาเปนจริงตามทฤษฎี ก็แสดงวาเครื่องมือนั้นก็จะมีความ
ตรงตามโครงสราง
การตรวจสอบความตรงเชิงโครงสรางทฤษฎีทําไดหลายวิธี ไดแก
1) การตรวจหาความสัมพันธกบเครื่องมือที่มโครงสรางเหมือนกัน
ั
ี
เปนการศึกษาความสัมพันธระหวางผลการวัดที่ไดจากเครื่องมือที่สรางขึ้นกับผลของเครื่องมือ
มาตรฐานที่มโครงสรางเหมือนกัน โดยคํานวณหาคาสัมประสิทธิ์สหสัมพันธอยางงาย (Pearson Product
ี
moment Correlation Coefficient) ดังนี้
[N
r
N
X
Y
=
=
=
=
∑
N
r =
∑
X
2
XY − [( ∑ X )( ∑ Y )]
− ( ∑ X ) 2 ][ N
∑Y
2
− (∑ Y ) 2 ]
คาสัมประสิทธิ์สหสัมพันธในที่นี้คือคาความตรง
จํานวนผูสอบ
คะแนนของแบบสอบที่สรางขึ้นที่ตองการหาคาความตรง
คะแนนของแบบสอบมาตรฐานที่มโครงสรางเหมือนกัน
ี
2) การตรวจสอบดวยการวิเคราะหองคประกอบ (Factor Analysis)
การวิเคราะหองคประกอบเปนเทคนิคทางสถิติสําหรับจับกลุมหรือรวมตัวแปรที่มีความสัมพันธ
กันไวในกลุม ทําใหเขาใจลักษณะของขอมูล แบบแผน โครงสราง ความสัมพันธ เชน ทักษะของผูบริหาร
ตามทฤษฎีกลาวไววาวัดจาก 3 ทักษะ ไดแก ทักษะการบริหารจัดการ ทักษะมนุษยและทักษะทางเทคนิค
ดังนั้นเครื่องมือที่สรางขึ้นเพื่อวัดทักษะของผูบริหาร จะตองประกอบดวยขอคําถามที่ประกอบดวย 3
ทักษะดังกลาว การตรวจสอบความตรงตามโครงสรางโดยอาศัยการวิเคราะหองคประกอบ สามารถทําได
โดยใชการวิเคราะหองคประกอบเชิงสํารวจ(Exploratory Factor Analysis) ในกรณีที่ทฤษฎีที่ใชยังไม
แนนอน หรือใชการวิเคราะหองคประกอบเชิงยืนยัน(Confirmatory Factor Analysis)ในกรณีที่เปนทฤษฎี
ที่แนชัด ในที่นี้ขอนําเสนอตัวอยางการวิเคราะหองคประกอบเชิงสํารวจที่สําคัญ เพื่อหาความตรงเชิง
โครงสรางของเครื่องมือ
ตัวอยางการสรางเครื่องมือวัดทักษะของผูบริหารที่ประกอบดวยทักษะการบริหารจัดการ (ขอ1
5) ทักษะมนุษย (ขอ6-10) และทักษะทางเทคนิค (ขอ11-15) ผลการวิเคราะหองคประกอบไดตาราง
วิเคราะหน้ําหนักองคประกอบ ดังนี้
23. 26
a
Component Matrix
Component
1
ขอ1
ขอ2
ขอ3
ขอ4
ขอ5
ขอ6
ขอ7
ขอ8
ขอ9
ขอ10
ขอ11
ขอ12
ขอ13
ขอ14
ขอ15
2
3
.768
.779
.583
.584
.472
.480
.564
.318
.314
.591
.794
.616
.467
.562
.448
Extraction Method: Principal Component Analysis.
a.
3 components extracted.
จากตาราง แสดงใหเห็นวาเครื่องมือที่สรางขึ้นทั้ง15 ขอ สามารถวัดทักษะผูบริหารออกเปน 3
กลุมตามโครงสราง โดยทักษะการบริหารจัดการ วัดจากรายการคําถามในขอ 1-5 ขอที่วัดทักษะนีไดดี
้
ที่สุด ดูจากคาน้ําหนักองคประกอบในตาราง คือ ขอ 2 รองลงมาคือ ขอ 1 สวนทักษะมนุษย วัดจาก
รายการคําถามในขอ 6-10 ขอที่วัดทักษะนีไดดีที่สุด คือ ขอ 10 รองลงมาคือ ขอ 7 สําหรับทักษะทาง
้
เทคนิค (ขอ11-15) ขอที่วัดทักษะนี้ไดดีที่สุด คือ ขอ 11 รองลงมาคือ ขอ 15 สรุปไดวา เครื่องมือที่สรางขึ้น
เพื่อวัดทักษะผูบริหารมีความตรงตามโครงสรางเพราะมีการเกาะกลุมกัน 3 กลุมตามโครงสรางที่สรางไว
3) การตรวจสอบดวยการเทียบกับกลุมทีรชัด (Known-group)
่ ู
เปนวิธีการเปรียบเทียบกับกลุมที่รูชัด (known group) โดยตองทราบกลุมที่มีคุณลักษณะเดียวกับ
สิ่งที่จะวัดกอน เชน ตองการตรวจสอบความตรงเชิงโครงสรางของแบบวัดเจตคติตอการเปนครู ก็ตอง
ทราบวากลุมที่ศึกษามีใครอยูในกลุมที่มีเจตคติทางบวกและลบตอการเปนครู แลวแบงเปน 2 กลุม คือ
กลุมที่มีเจตคติทางบวก และกลุมที่มีเจตคติทางลบ แลวใหทั้ง 2 กลุมทําแบบวัด ตอจากนั้นนําคะแนนเฉลี่ย
ของแตละกลุมมาเปรียบเทียบกัน โดยใชสถิติ t-test (independent) ถาพบวามีความแตกตางกันอยางมี
นัยสําคัญทางสถิติ แสดงวาแบบวัดที่สรางขึ้นมีความตรงตามโครงสราง
24. 27
สูตรสถิติทดสอบ t-test ในกรณีที่ σ12 = σ22
ในกรณีที่ σ12= σ22
t = (X1 - X2) - d0
Sp√1/n1+1/n2
Sp = ( n1-1) S12+ ( n2-1) S22
n1+n2-2
ที่องศาอิสระ n1+n2-2
โดยที่
ในกรณีที่ σ12 ≠ σ22
t =
ที่องศาอิสระ
โดยทีX1
่
X2
S1
S22
(X1-X2)- d0
√S12/ n1+ S22/n2
(S12/ n1+ S22/n2)2
(S12/ n1)2+ (S22/n2)2
n1-1
n2- 2
ในกรณีที่ σ12 ≠ σ22
คือ กลุมที่มีเจตคติทางบวกตอสิ่งที่วัด
คือ กลุมที่มีเจตคติทางลบตอสิ่งที่วัด
คือ ความแปรปรวนของกลุมที่มีเจตคติทางบวกตอสิ่งที่วัด
คือ ความแปรปรวนของกลุมที่มีเจตคติทางลบตอสิ่งที่วัด
4) การตรวจโดยใชเมตริกซลักษณะหลาก-วิธีหลาย ( Multitrait Multimethod : MTMM)
การตรวจสอบความตรงวิธีนี้เปนแนวคิดของแคมพเบลและฟสค (Campbell and Fiske,1959)
เปนการวิเคราะหความสัมพันธระหวางการวัดหลายลักษณะ ( Multitrait) โดยใชการวัดหลายวิธี
(Multimethod) วิธีนี้สามารถใชไดเมื่อมีการวัดอยางนอย 2 คุณลักษณะ โดยมีวธีการวัดอยางนอย 2 วิธี
ิ
เชน การวัดลักษณะที่แตกตางกัน 2 ลักษณะ
ไดแก A และB โดยใชวธีการวัดที่ตางกัน 2 วิธี คือ 1
ิ
และ2 เมื่อนําแบบวัดทั้ง 4 ฉบับ (ฉบับที่ 1 วัดลักษณะ A ดวยวิธีที่ 1 ฉบับที่ 2 วัดลักษณะ A ดวยวิธีที่ 2
25. 28
ฉบับที่ 3 วัดลักษณะ B ดวยวิธีที่ 1และฉบับที่ 4 วัดลักษณะ B ดวยวิธที่ 2) ไปวัดกับกลุมตัวอยางเดียวกัน
ี
แลวนําคะแนนที่ไดมาหาคาสัมประสิทธิ์สหสัมพันธ ทั้ง4 ฉบับ ผลที่ไดแสดงในตาราง ดังนี้
คุณลักษณะ
คุณลักษณะ
A
B
วิธวัด
ี
๑
๒
๑
1
๓
๔
๑
2
B
1
2
A
1
2
1
๔
๓
๒
2
๑
สัมประสิทธิ์สหสัมพันธที่ไดแบงเปน 4 กลุม ไดแก
1. สัมประสิทธิ์ความเทียง เปนสัมประสิทธิ์สหสัมพันธระหวางคะแนนวัดคุณลักษณะเดียวกัน
่
โดยใชวิธวัดเดียวกันหรือแบบสอบเดียวกัน เปรียบเสมือนเปนการวัดซ้ํา นั่นคือ สัมประสิทธิ์ความเที่ยง
ี
(Reliability) จากตาราง อยูในแนวทแยง ใชเครื่องหมาย ๑
2.สัมประสิทธิความตรง เปนสัมประสิทธิ์สหสัมพันธระหวางคะแนนวัดคุณลักษณะเดียวกัน
์
โดยใชวิธวัดตางกันหรือแบบสอบตางชุดกัน นั่นคือ สัมประสิทธิ์ความตรง ที่เรียกวาความตรงลูเขา
ี
(Convergent Validity)จากตาราง ใชเครื่องหมาย ๒
3.สัมประสิทธิสหสัมพันธระหวางคะแนนวัดคุณลักษณะตางกัน โดยใชวิธวัดเดียวกัน หรือแบบ
์
ี
สอบเดียวกัน จากตาราง ใชเครื่องหมาย ๓
4.สัมประสิทธิสหสัมพันธระหวางคะแนนวัดคุณลักษณะตางกัน โดยใชวิธวัดตางกันแบบสอบ
์
ี
ตางชุดกัน ที่เรียกวาความตรงจําแนก (Discriminant Validity)จากตาราง ใชเครื่องหมาย ๔
การแปลความหมาย
การวัดคุณลักษณะเดียวกัน ถึงแมวาจะใชวิธีตางกัน เรียกวา ความตรงลูเขา (convergent validity)
ยอมมีคาสัมประสิทธิ์สหสัมพันธสูงกวาการวัดคุณลักษณะตางกันวัดดวยวิธี เดียวกันหรือวัดดวยวิธี
ตางกัน เรียกวา ความตรงเชิงจําแนก (Discriminant validity) ดังนัน การที่เครื่องมือที่สรางขึ้นจะมีความ
้
26. 29
ตรงเชิงโครงสราง ตามวิธนี้ไดนั้น คาสัมประสิทธิ์สหสัมพันธจากเครื่องหมาย ๒ ตองมีคาสูงกวาคา
ี
สัมประสิทธิ์สหสัมพันธจากเครื่องหมาย ๓ และ ๔
3. ความตรงเชิงเกณฑสัมพันธ (Criterion-Related Validity) เปนความสามารถในการวัดได
สอดคลองกับเกณฑภายนอกซึ่งวัดไดจากเครื่องมือที่เปนอิสระ โดยวัดจากความสัมพันธระหวางเครื่องมือ
ที่สรางกับเกณฑภายนอกบางอยาง เพื่อใชการพยากรณ ความตรงประเภทนี้ แบงเปน 2 ประเภทยอย คือ
3.1 ความตรงตามสภาพ (Concurrent Validity) เปนความสามารถของเครื่องมือที่วัดไดตรงตาม
สมรรถนะของสิ่งนั้น ในสภาพปจจุบัน เชน ถาตองการตรวจสอบความตรงตามสภาพของแบบวัดเชาวน
ปญญาที่สรางขึ้นวามีความตรงตามสภาพหรือไม ก็ตองหาเครื่องมือมาตรฐานหรือเครื่องมือที่ที่มีความ
นาเชื่อถือที่วัดเชาวนปญญาเหมือนกันมาเปนเกณฑเทียบ ถาคะแนนจากแบบทั้ง 2 ชุด มีความสัมประสิทธิ์
สหสัมพันธสูง ก็ถือวาแบบวัดเชาวนปญญาที่สรางขึ้นมีความตรงตามสภาพ
3.2 ความตรงเชิงพยากรณ (Predictive Validity) เปนความสามารถของเครื่องมือที่สามารถวัดได
ตรงตามสมรรถนะของสิ่งนั้น ที่จะเกิดขึ้นในอนาคต หรือสามารถนําผลการวัดไปพยากรณลักษณะหรือ
พฤติกรรมตาง ๆ ได เชน ถาตองการตรวจสอบความตรงเชิงพยากรณ ของแบบสอบคัดเลือกเขา
มหาวิทยาลัย โดยเชื่อวาผูเรียนที่ผานการสอบคัดเลือกดวยคะแนนสูงแลวก็สามารถทํานายไดวา เมื่อเรียน
จบยอมไดคะแนนสูงดวย ดังนั้น คะแนนจากการสอบคัดเลือกและคะแนนผลสัมฤทธิ์ทางการเรียนเมื่อ
เรียนจบยอมมีความความสัมพันธ โดยใชคาสัมประสิทธิ์สหสัมพันธเปนตัวชี้ที่แสดงถึงความตรงเชิง
พยากรณ
การตรวจสอบความตรงเชิงเกณฑสัมพันธ ทําไดดังนี้
1. การหาสัมประสิทธิ์ความตรง (Validity Coefficient) โดยคํานวณคาสัมประสิทธิ์ สหสัมพันธ
แบบ Pearson Product moment ระหวางคะแนนจากแบบสอบหรือแบบวัดที่ตองการตรวจสอบความตรง
ตามสภาพ กับคะแนนจากแบบวัดที่เปนเกณฑ ซึ่งเปนการหาความตรงตามสภาพ (Concurrent Validity)
2. การหาสัมประสิทธิ์ความตรง (Validity Coefficient) โดยคํานวณคาสัมประสิทธิ์สหสัมพันธ
แบบ Pearson Product moment ระหวางคะแนนจากแบบสอบหรือแบบวัดที่ตองการตรวจสอบความตรง
เชิงพยากรณกบคะแนนจากแบบวัดในอนาคต ซึ่งเปนการหาความตรง เชิงพยากรณ (Predictive Validity)
ั
27. 28. 31
Correlations
แบบวัดที่สรางขึ้น
แบบวัดมาตรฐาน
Pearson Correlation
Sig. (2-tailed)
N
Pearson Correlation
Sig. (2-tailed)
N
แบบวัดที่สรางขึ้น
1
.
10
.768
.009
10
แบบวัดมาตรฐาน
.768
.009
10
1
.
10
** Correlation is significant at the 0.01 level (2-tailed).
การแปลผล
คาสัมประสิทธิ์ความตรงตามสภาพที่มีคาเขาใกล 1 แสดงวามีคาความตรงตามสภาพสูง
สัมประสิทธิ์ความตรงตามสภาพจากตัวอยาง = 0.768 แสดงวามีคาความตรงตามสภาพคอนขางสูง
นอกจากการใชคาสัมประสิทธิ์สหสัมพันธแบบ Pearson Product moment หาความตรงเชิงเกณฑ
แลว ยังสามารถใชคาสถิติหาคาความสัมพันธอื่นๆได ในกรณีที่ระดับการวัดเปนนามบัญญัติ หรืออันดับ
เชน สัมประสิทธิ์ ฟ ( Phi correlation) คาสัมประสิทธิ์สหสัมพันธแบบSpearman
ประเภทของสถิติที่ใชในการวิจัย
แบงตามบทบาทและหนาทีไดแกสถิติเชิงบรรยาย (Descriptive Statistics) และสถิติเชิงสรุปอางอิง
่
(Inferential Statistics )
แบงตามขอตกลงเบื้องตน ไดแก วิธการทางสถิตพาราเมตริก(Parametric) และวิธีการทาง
ี
ิ
สถิตินันพาราเมตริก(Non-parametric Statistics )
แบงตามเปาหมายของการวิจัย ไดแก บรรยายลักษณะของตัวแปร ทดสอบความแตกตางระหวาง
กลุม อธิบายความสัมพันธระหวางตัวแปร ทํานายตัวแปร วิเคราะหโครงสรางของกลุมตัวแปร และ
วิเคราะหเชิงสาเหตุ โดยมีรายละเอียดเสนอในตารางดังนี้
29. 32
การบรรยายลักษณะของตัวแปร
เปาหมายของการวิจัย
1. บรรยายลักษณะ
ของตัวแปร
จํานวนตัวแปรที่ศึกษา ระดับการวัด
1
Nominal
หรือ ≥ 2
1
หรือ ≥ 2
1
หรือ ≥ 2
Ordinal
Interval / ratio
ประเภท/เปาหมายของการบรรยาย
1.บรรยายความถี่ของขอมูล
2. เสนอภาพแสดงการ
แจกแจงความถี่
3. คาสถิติที่ใชบรรยาย
การแจกแจงความถี่
4. วัดแนวโนมเขาสูสวนกลาง
1. บรรยายของถีของการจัด
่
อันดับ
2. เสนอภาพแสดงความถี่
ของการจัดลําดับ
3. คาสถิติที่บรรยายแหนงในกลุม
4.วัดแนวโนมเขาสูสวนกลาง
1.บรรยายความถี่ของขอมูล
2. เสนอภาพแสดงการ
แจกแจงความถี่
3. สถิติที่ใชบรรยายการ
แจกแจงความถี่
4. บรรยายตําแหนงในกลุม
5. วัดแนวโนมเขาสูสวนกลาง
6. วัดคาการกระจาย
วิธีนําเสนอขอมูล
1. ตารางแสดงความถี่
2. Bar chart , Pie chart
3. สัดสวน , รอยละ
4. Mode
1. ตารางแสดงความถี่
ของการจัดอันดับ
2. Bar chart ของการจัดอันดับ
3. Percentile , Decile, Quartile.
4. Mode
1.ตารางแสดงความถี่
2.Histogram , Frequency curve
3. คาความเบ ( Skewness )
คาความโดง ( Kurtosis )
4. Percentile , Decile .........
5. Mode , Median , Mean
6. Range , Variance , C.V.
30. 33
การทดสอบความแตกตางระหวางกลุม
เปาหมายของการวิจัย
2. ทดสอบความแตก
ตางระหวางกลุม
ประเภทตัวแปรและระดับการวัด
ตัวแปรอิสระ ตัวแปรตาม
ตัวแปรควบคุม
1
( interval
/ ratio )
1
1
( Nominal ) ( interval
dichotomous / ratio )
1
( Nominal )
Polytomous
1
( interval
/ ratio )
≥2
( Nominal )
1
( interval
/ ratio )
-
เปาหมายของการวิเคราะห
ทดสอบความแตกตางของ
คาเฉลี่ยของประชากรกับคาที่
คาดหวัง
1. ทราบคาความแปรปรวน
ของประชากร
2.ไมทราบคาความแปร
ปรวนของประชากร
- ทดสอบความแตกตางของ
คาเฉลี่ยระหวางประชากร
2 กลุม
1.กลุมตัวอยาง 2 กลุมเปน
อิสระจากกัน
1.1 ถาประชากรมีความแปร
ปรวนเทากัน
1.2 ถาประชากรมีความแปร
ปรวนไมเทากัน
2. กลุมตัวอยาง 2 กุลมไม
เปนอิสระจากกัน
ทดสอบความแตกตางของคา
เฉลี่ยระหวางประชากร > 2 กลุม
1. ถาประชากรมีความแปร
ปรวนเทากัน
2. ถาประชากรมีความแปร
ปรวนไมเทากัน
ทดสอบความแตกตางของคา
เฉลี่ยระหวางประชากร > 2 กลุม
เมื่อมีตัวแปรอิสระหลายตัว
เทคนิคการวิเคราะห
Z - test
t - test
t - test
( pooled variance )
t - test
( separated variance )
t - test
( paired t - test )
one - way ANOVA
/ F - test
F - test
Factorial ANOVA
31. 34
การทดสอบความแตกตางระหวางกลุม ( ตอ )
เปาหมายของการวิจัย
2. ทดสอบความแตก
ตางระหวางกลุม (ตอ)
ประเภทตัวแปรและระดับการวัด
ตัวแปรอิสระ ตัวแปรตาม
ตัวแปร
ควบคุม
1
1
≥1
(Polytomous) ( interval
/ ratio )
≥2
1
≥1
( Nominal )
( interval
/ ratio )
เปาหมายของการวิเคราะห
เทคนิคการวิเคราะห
ทดสอบความแตกตางของคาเฉลีย
่
one - way ANCOVA
ระหวางประชากร > 2 กลุม โดยมี
การควบคุมตัวแปร
ทดสอบความแตกตางของคาเฉลีย
่
Factorial ANCOVA
ระหวางประชากร > 2 กลุม
เมื่อมีตัวแปรอิสระหลายตัวและมี
การควบคุมตัวแปร
ทดสอบความแตกตางของคาเฉลีย
่
one - way MANOVA
Centroids ระหวางประชากร > 2
กลุม
1
Polytomous
≥2
( interval
/ ratio )
-
≥2
( Nominal )
≥2
( interval
/ ratio )
-
1
(Nominal)
Polytomous
≥2
( interval
/ ratio )
≥1
ทดสอบความแตกตางของคาเฉลีย
่
Centroids ระหวางประชากร > 2
กลุม โดยมีการควบคุมตัวแปร
one - way MANCOVA
≥2
( Nominal )
≥2
( interval
/ ratio )
≥1
ทดสอบความแตกตางของคาเฉลีย
่
Centroids ระหวางประชากร > 2
กลุม เมื่อมีตัวแปรอิสระหลายตัว
และมีการควบคุมตัวแปร
- Factorial MANCOVA
- Profile Analysis
ทดสอบความแตกตางของคาเฉลีย
่
- Factorial MANOVA
Centroids ระหวางประชากร > 2 - Profile Analysis
กลุม เมื่อมีตัวแปรอิสระหลายตัว
32. 35
การทดสอบความสัมพันธระหวางตัวแปร
เปาหมายของการวิจัย
3. อธิบายความสัมพันธ
ระหวางตัวแปร
ประเภทตัวแปรและระดับการวัด
จํานวนตัวแปร ตัวแปรอิสระ ตัวแปรตาม
2
( Nominal
กับNominal )
เปาหมายของการวิเคราะห
เทคนิคการวิเคราะห
1. True dichotomous กับ True /
Artificial dichotomous
2. True / Artificial dichotomous
หรือ Polytomous กับPolytomous
3. Artificial dichotomous กับ
Artificial dichotomous
χ 2 – test , Phi
2
( Nominalกับ
ordinal )
2
( Nominalกับ
interval/ratio )
- True / Artificial dichotomous กับ - r rbis
ordinal
2
( interval/ratioกับ
interval / ratio )
2
- Interval / ratio กับ
Interval / ratio
1. True dichotomous กับ
interval / ratio
2. Artificial dichotomous กับ
interval / ratio
1
1
( Nominal ) ( Nominal )
≥3
( Nominal )
≥2
( Nominal )
1
≥4
( Nominal )
≥2
( Nominal )
≥2
- อธิบายผลของตัวแปรอิสระ 1 ตัว
ตอตัวแปรตาม 1 ตัว
- อธิบายผลของตัวแปรอิสระ
หลายตัวตอตัวแปรตาม 1 ตัว
- อธิบายผลของตัวแปรอิสระ
หลายตัวตอตัวแปรตามหลายตัว
- Phi
- χ 2 - test
- r tet
- χ 2 - test
- r pbis
- r bis
- Simple correlation
( pearson ’ s product
moment )
- χ 2 - test
( 1 factor model )
- χ 2 - test
(≥ 2 Factor model )
- χ 2 - test for
general log - linear
model
33. 36
การทดสอบความสัมพันธระหวางตัวแปร ( ตอ )
เปาหมายของการวิจัย
3. อธิบายความสัมพันธ
ระหวางตัวแปร
ประเภทตัวแปรและระดับการวัด
เปาหมายของการวิเคราะห
จํานวนตัวแปร
ตัวแปรอิสระ ตัวแปรตาม
- ความสัมพันธระหวางตัวแปร
≥3
≥2
1
เกณฑ 1 ตัว กับตัวแปรทํานาย
( interval / ratio )
หลายตัว
- ความสัมพันธระหวางตัวแปรเปน
≥3
≥2
1
รายคู ควบคุมอิทธิพลของตัวแปร
( interval / ratio )
อื่น ๆที่มีอิทธิพลตอตัวแปรเกณฑ
มีตัวแปรควบคุม
และตัวแปรทํานาย
- ความสัมพันธระหวางตัวแปรเปน
รายคูควบคุมอิทธิพลของตัวแปร
อื่น ๆ ที่มีผลตอตัวแปรทํานาย
- ความสัมพันธระหวางชุดของ
≥4
≥2
≥2
ตัวแปรเกณฑ กับชุดของตัวแปร
( interval / ratio )
ทํานาย
ไมมีตัวแปรควบคุม
เทคนิคการวิเคราะห
- Multiple correlation
- Partial correlation
- Part correlation
- Canonical correlation
34. 37
การทํานายตัวแปร
เปาหมายของการวิจัย
ประเภทตัวแปรและระดับการวัด
จํานวนตัวแปร
ตัวแปรอิสระ
ตัวแปรตาม
1. การทํานายสมาชิก
≥2
≥1
1
ของกลุม
(ระดับใด ๆ ) ( dichotomous )
≥2
≥1
1
(ระดับใด ๆ ) ( polytomous )
≥3
≥2
1
( nominal หรือ ( dichotomous )
ordinal )
2. การทํานายตัวแปรตาม
2
1
1
( เวลา )
(interval / ratio )
2
1
1
( ระดับใด ๆ ) (interval / ratio )
≥3
≥2
1
(nominal /
(interval / ratio )
ordinal )
≥3
≥2
1
( ระดับใดๆ)
interval / ratio )
≥3
1
≥2
( เวลา )
(interval / ratio )
≥4
≥2
( ระดับใดๆ)
เปาหมายของการวิเคราะห
เทคนิคการวิเคราะห
- การทํานายลักษณะสมาชิกของ
ประชากร 2 กลุม
- การทํานายลักษณะสมาชิกของ
ประชากรหลายกลุม
- การทํานายลักษณะสมาชิกของ
ประชากร 2 กลุม เมื่อมีตัวแปร
อิสระระดับ nominal / ordinal
- การทํานายตัวแปรเกณฑ 1 ตัว
ตามชวงเวลาตาง ๆ
- การทํานายตัวแปรเกณฑ 1 ตัว
จากตัวแปรทํานาย 1 ตัว
- การทํานายตัวแปรเกณฑ 1 ตัว
จากตัวแปรทํานายหลายตัว
- Discriminant analysis
- การทํานายตัวแปรเกณฑ 1 ตัว
จากตัวแปรทํานายหลายตัว
- การทํานายผลรวมเชิงเสนตรง
ของตัวแปรเกณฑหลายตัวตาม
ชวงเวลาตางๆ
- การทํานายผลรวมเชิงเสนตรง
≥2
(interval / ratio ) ของตัวแปรเกณฑหลายตัวจาก
ตัวแปรทํานายหลายตัว
- Discriminant analysis
- Multiple classification
analysis ( MCA )
- Time Series Analysis
- Box - Jenkins Models
- Simple regression
analysis
- Multiple classification
analysis
- Multiple regression
Analysis
- Multivariate Time
Series Analysis
- Multivariate Multiple
Regression Analysis
35. 38
การวิเคราะหโครงสรางของกลุมตัวแปร
เปาหมายของ
การวิจัย
1. วิเคราะห
โครงสรางของ
กลุมตัวแปร
จํานวนตัวแปรหรือ
สิ่งที่ศึกษา
≥2
≥2
ระดับการวัด
ระดับใด ๆ
Nominal
( dichotomous )
≥2
ordinal
interval / ratio
≥2
ระดับใด ๆ
≥2
ระดับใด ๆ
เปาหมายของ
การวิเคราะห
- การวัดระบบจําแนกหรือกลุมของ
ตัวแปร หรือสิ่งที่ศกษาตาม
ึ
ลักษณะของความคลายคลึงกัน
- การหาลําดับขั้นของตัวแปรหรือ
สิ่ง ที่ศึกษาตามลําดับของความ
ซับซอน
- การหาโครงสรางหรือมิติของตัว
แปรหรือสิ่งที่ศึกษาตามความ
คลายคลึงกัน
- ถาความคลายคลึงกันวัดใน
ระดับ ordinal
- ถาความคลายคลึงกันวัดใน
ระดับ interval / ratio
- การหาจํานวนและองคประกอบ
รวม ( factors ) ของตัวแปรตาม
ลักษณะความสัมพันธระหวาง
ตัวแปร
- การทดสอบจํานวนองคประกอบ
และโครงสรางขององคประกอบ
ตามทฤษฎีหรือสมมุติฐาน
เทคนิคการวิเคราะห
- Cluster Analysis
- Factor Analysis
- Guttman Scaling
- Non – metric
Multidimensional Scaling
- Metric
Multidimensional Scaling
- Exploratory Factor
Analysis
-
Confirmatory Factor
Analysis
36. 39
การวิเคราะหเชิงสาเหตุ
เปาหมายของการวิจัย
ประเภทตัวแปรและระดับการวัด
จํานวนตัวแปร ตัวแปรอิสระ
ตัวแปรตาม
1. การวิเคราะหเชิงสาเหตุ
≥2
≥1
≥1
ที่ไมมีการทดลอง
( interval / ratio )
เปาหมายของการวิเคราะห
เทคนิคการวิเคราะห
- การวิเคราะหผลทางตรงและทาง
ออมของตัวแปรอิสระที่มีตอตัว
แปรตามบนพื้นฐานของทฤษฎี
และการออกแบบการวิจัยที่
เหมาะสม
1) เมื่อตัวแปรทุกตัวสามารถสังเกต - Path Analysis
หรือวัดคาไดโดยตรง โดยไมมี
ความคลาดเคลื่อน
2) เมื่อตัวแปรบางตัวไมสามารถ
- Structural Equation
สังเกตหรือวัดคาไดโดยตรง
Modeling
แตอาศัยการวิเคราะห คาจาก
( LISREL)
ตัวแปรที่สังเกตหรือวัดคาได
ประโยชนของสถิติในการวิจย
ั
จากความหมายของสถิติ จะเห็นวาสถิติมประโยชนอยางมากตอการวิจัย ทั้งในดานการเลือกกลุม
ี
ตัวอยาง ขนาดของกลุมตัวอยาง การเก็บรวบรวมขอมูล การนําเสนอขอมูลเบื้องตน โดยใชสถิติบรรยาย
การวิเคราะหขอมูลโดยใชสถิติอางอิง ตลอดจนการนําผลการวิเคราะหมาสรุปเกียวกับลักษณะที่สนใจ
่
และสามารถนําผลนั้นมาชวยในการตัดสินใจในเรื่องที่ศึกษา หรือเปนขอมูลที่สําคัญได
37. 40
1.
1.1
1.2
1.3
1.4
1.5
1.6
แบบฝกหัด
For each of the following ,indicate the scale of measurement
Red ,Blue , Yellow.
Extremely likely ,likely , Indifferent , Unlikely , and Extremely unlikely
Age in years.
Salary in dollars.
Rank of a state in population ; 1 to 50
Temperature.
2.
2.1
2.2
2.3
2.4
For each of the following ,indicate whether it is a quantitative or qualitative variable.
Hair color.
Sex of an individual.
Number of persons unemployed in Thailand.
Price of product.
3. จงยกตัวอยางหัวขอโครงรางวิทยานิพนธ ที่อยูในความสนใจที่จะทํา แลวใหระบุตวแปรและสถิตที่
ั
ิ
จะใชในการวิเคราะห พรอมกับใหเหตุผลในการเลือกใชสถิติตวนั้นๆ
ั
38. บทที่2
สถิติบรรยาย
สถิติบรรยาย (Descriptive statistics) คือ สถิติที่ใชในการศึกษาขอเท็จจริงจากกลุมขอมูลที่
รวบรวมมาได อาจเปนกลุมตัวอยางหรือกลุมประชากรก็ได เพือใหทราบรายละเอียดเกี่ยวกับ
่
ลักษณะของขอมูลกลุมนั้นโดยไมไดสรุปอางอิงผลการศึกษาไปยังกลุมขอมูลกลุมอื่นหรือสรุป
อางอิงไปยังประชากรที่ศึกษา การบรรยายสรุปลักษณะของกลุมขอมูลไดแก การแจกแจงความถี่
การวัดตําแหนงการเปรียบเทียบ การวัดแนวโนมเขาสูสวนกลาง การกระจายขอมูล การแจกแจง
ขอมูล เปนตน ดังนั้นในบทนี้จึงไดนําเสนอของสถิติภาคบรรยาย ดังมีรายละเอียด ดังนี้
1. การแจกแจงความถี่
การแจกแจงความถี่เปนการนําขอมูลที่เปนคาของตัวแปรที่เราสนใจมาจัดเรียงตามลําดับ
ความมากนอย และแบงเปนชวงเทาๆกัน จํานวนขอมูลในแตละชวงคะแนน เรียกวา ความถี่ ในกรณี
ที่ความแตกตางระหวางคะแนนสูงสุดกับคะแนนต่ําสุดไมมาก ไมจําเปนตองแบงชวงคะแนนเปน
กลุม ในแตละชวงมี 1 คะแนนก็ได การแจกแจงความถีมีจุดมุงหมายเพื่อใหทราบภาพรวมของการ
่
แจกแจงขอมูลทั้งหมดอยางเปนระบบ การจัดระบบและนําเสนอขอมูลในเบื้องตน สามารถนําเสนอ
ขอมูลในรูปของตารางและแผนภูมิ ในทีนี้จะขอแยกเปน 2 สวนในการนําเสนอ คือ ตารางแจกแจง
่
ความถี่ และกราฟและแผนภูมิแบบตางๆ
1.1 ตารางการแจกแจงความถี่
การสรางตารางการแจกแจงความถี่ ทําได 2 แบบ คือ
1) การแจกแจงความถี่ของลักษณะที่สนใจที่เปนไปไดทั้งหมด
2) การแจกแจงความถี่สําหรับคาในแตละชวงของลักษณะที่สนใจ
1) การแจกแจงความถี่ของลักษณะที่สนใจที่เปนไปไดทั้งหมด
การแจกแจงความถี่แบบนีใชกับขอมูลที่มีจํานวนลักษณะที่เปนไปไดทั้งหมดไมมากนัก
้
เชน จําแนกตามเพศ คือ ชาย หญิง จําแนกตามระดับการศึกษา จําแนกตามอาชีพหลัก เปนตน
ดังตัวอยางตอไปนี้
ตัวอยาง จากการสํารวจนิสิตที่สอบคัดเลือกเขาคณะครุศาสตร ในปการศึกษา 2544 โดยแจกแจงความถี่ (นิสิต)
ตามเพศ ไดดังนี้
เพศ
จํานวนนิสิต ( คน )
ชาย
155
หญิง
174
รวม
329
39. 42
2) การแจกแจงความถี่สําหรับคาในแตละชวงของลักษณะที่สนใจ
การแจกแจงความถี่แบบนีใชกับขอมูลที่มีจํานวนลักษณะที่เปนไปไดทั้งหมดจํานวนมาก
้
เชน ศึกษารายไดของคนไทยทั้งหมด หรืออายุของคนไทยทั้งหมด เปนตน ดังนั้นในการแจกแจง
ความถี่จึงควรแบงขอมูลทั้งหมดออกเปนชวงๆที่ตอเนื่องกัน
โดยแตละชวงประกอบดวยขอมูล
หลายๆคา ทําใหลดจํานวนคาที่เปนไปไดทงหมดลง ดังตัวอยางตอไปนี้
ั้
ิ
ตัวอยาง ถาเลือกตัวอยางนิสตหญิง มา 100 คน สอบถามความสูงแลวจัดเปนชวง ๆ ได 5 ชั้น ดังนี้
ความสูงของนิสิตหญิง ( เซ็นติเมตร )
135 – 144
145 – 154
155 – 164
165 – 174
175 - 184
รวม
จํานวนนิสิต
5
18
42
27
8
100
การสรางตารางแจกแจงความถี่สําหรับคาในแตละชวงของลักษณะที่สนใจมีขั้นตอนในการ
สราง ดังนี้
ขั้นตอนการสรางตารางแจกแจงความถี่
1. หาคาพิสัยของขอมูล (R)
พิสัย (Range)
= คาสูงสุด – คาต่ําสุด
2. กําหนดจํานวนชัน ( k )
้
k = 1+3.3 log N
3. คํานวณหาความกวางของชั้น (Class interval)
I = ความกวางของชั้น =
พิสัย
= R
จํานวนชัน
้
k
4. คํานวณหาขีดจํากัด (Class limit)
ขีดจํากัดลางของชั้นแรก = คาต่ําสุด - ( I x k – R ) / 2
หรือ ใชคาต่ําสุดเปนขีดจํากัดบน ของชั้นต่ําสุดของการแจกแจง
5. คํานวณจุดกึ่งกลางของแตละชั้น ( Midpoint )
จุดกึ่งกลางชั้น
= (ขีดจํากัดบน + ขีดจํากัดลาง) / 2
6. คํานวณหาขีดจํากัดชันทีแทจริง ( class boundaries )
้ ่
ขีดจํากัดชันทีแทจริง = ( ขีดจํากัดบนของชั้น+ ขีดจํากัดลางของชั้นถัดไป) / 2
้ ่
40. 43
7. นับจํานวนคาของขอมูล ( ความถี่ ) ในแตละชั้น
เมื่อไดจํานวนแลวสามารถหาความถี่สะสม ความถี่สัมพัทธ และรอยละโดย
การหาความถีสะสม จะเริ่มหาผลบวกของความถี่ที่เริ่มจากชั้นแรกบวกไปเรื่อยๆเมือถึงชั้นนั้นๆ
่
่
การหาความถีสัมพัทธ หรือสัดสวน(proportion) ของชั้นใดก็นําความถี่ของชั้นนั้นหารดวยความถี่
่
ทั้งหมดและเมือคูณดวยรอยจะเรียกวาเปอรเซ็นตหรือรอยละ
่
ตัวอยาง ถาคะแนนสอบของนิสิตที่เรียนวิชาสถิติ จํานวน 80 คน เปนดังนี้
68
73
61
96
62
73
81
84
79
65
78
67
57
72
75
88
75
89
97
88
63
82
73
87
61
78
78
76
68
60
74
75
85
62
75
90
93
62
95
76
76
85
พิสัย = 97 –52 = 45
ตองการสรางตารางที่มีจํานวนชัน = 8 ชั้น
้
ความกวางของชั้น = พิสัย / จํานวนชั้น
= 45 / 8 = 5.62
ขีดจํากัดชั้น
51 – 56
57 – 62
63 – 68
69 – 74
75 – 80
81 – 86
87 – 92
93 - 98
รวม
ขีดจํากัดที่แทจริง
50.5 – 56.5
56.5 – 62.5
62.5 – 68.5
68.5 – 74.5
74.5 – 80.5
80.5 – 86.5
86.5 – 92.5
92.5 – 99.5
62
71
95
60
65
52
77
≈
88
59
78
79
71
74
78
76
85
63
83
75
77
93
75
72
71
72
86
54
64
65
70
65
67
6
จุดกึ่งกลางชั้น
53.5
59.5
65.6
71.5
77.5
83.5
89.5
95.5
ความถี่
1
11
11
13
22
9
6
7
80
79
82
94
79
80
73
41. 44
ตาราง แสดงการแจกแจงความถี่สัมพันธของคะแนนสอบ
ชั้นที่
ขีดจํากัด
1
2
3
4
5
6
7
8
51 – 56
57 – 62
63 – 68
69 – 74
75 – 80
81 – 86
87 – 92
93 - 99
รวม
ความถี่
fi
1
11
11
13
22
9
6
7
80
ความถี่สัมพัทธ
(fi / Σ fi )
1/80 = .0125
11/80 = .1375
11/80 = .1375
13/80 = .1625
22/80 = .275
9/80 = .1125
6/80 = .075
7/80 = .0875
1
ความถี่สะสม
Σ fi
1
12
23
36
58
67
73
80
รอยละ
1.25
13.75
13.75
16.25
27.50
11.25
7.50
8.75
100.00
1.2 กราฟและแผนภูมิแบบตางๆ
การบรรยายหรือนําเสนอขอมูลดวยกราฟและแผนภูมแบบตางๆจะทําใหงายตอการ
ิ
เปรียบเทียบ โดยแบงเปน 4 ประเภทใหญ โดยแตละประเภทมีลักษณะยอย ดังนี้ คือ
1) แผนภูมแทง ( Bar chart )
ิ
- แผนภูมแทงเชิงเดียว (Simple Bar chart )
ิ
่
- แผนภูมแทงเชิงซอน (Multiple Bar chart )
ิ
2) แผนภูมิวงกลม( Pie chart )
3) ฮิสโตแกรม (Histogram)
4) กราฟเสน
- กราฟเสนเชิงเดี่ยว ( Simple Line chart )
- กราฟเสนเชิงซอน ( Multiple Line chart )
- รูปหลายเหลี่ยมแหงความถี่ (Frequency polygon)
- กราฟความถี่สะสม(Ogive curve)
- กราฟเสนโคง (Smooth curve)
1) แผนภูมแทง (Bar Chart) ประกอบดวยแทงรูปสี่เหลี่ยมผืนผาที่มีความกวางเทากัน
ิ
ทุกแหง สวนความสูงจะขึ้นอยูกับขนาดของขอมูล ถาเปนการเปรียบเทียบขอมูลเพียงลักษณะเดียว
เรียกวา แผนภูมิแทงเชิงเดี่ยว (Simple Bar Chart) ถาเปนการเปรียบเทียบขอมูลตั้งแต 2 ลักษณะ
ขึ้นไป เรียกวา แผนภูมแทงเชิงซอน (Multiple Bar chart )
ิ
42. 45
ตัวอยาง แผนภูมิแทงเชิงเดี่ยว เปรียบเทียบจํานวนนักเรียน จําแนกตามโรงเรียนตางๆ
600
500
400
Count
300
200
1
2
3
4
SCHOOL
ตัวอยาง แผนภูมิแทงเชิงซอน เปรียบเทียบจํานวนนักเรียนจําแนกตามอายุและเพศ
300
200
100
Count
SEX
1
2
0
แผนภูมิแสดงจํานวนนักเรียนจําแนกตามอายุและเพศ
11
12
13
14
15
16
17
18
19
AGE
2) แผนภาพวงกลม (Pie Chart ) เปนการแสดงขอมูลในรูปวงกลมโดยแบงวงกลมเปน
สวนยอยๆตามลักษณะสัดสวนตางๆโดยใหเนื้อที่ในวงกลม (360 องศา) เปน รอยเปอรเซ็นตแลว
เทียบสัดสวนหรือเปอรเซ็นตเปนองศา
43. 46
ตัวอยาง แผนภาพวงกลม เปรียบเทียบจํานวนนักเรียน จําแนกตามโรงเรียนตางๆ
school4
school1
school3
school2
3) ฮิสโตแกรม (Histogram) เปนการนําขอมูลที่ไดแจกแจงความถี่แลวในตารางแจกแจง
ความถี่มาแสดงเปนภาพ ซึ่งประกอบดวยแทงสี่เหลี่ยมผืนผา โดยแกนนอนแบงออกเปนชวงๆความ
กวางของแตละชวงเทากับความกวางของชั้น จุดกึ่งกลางของแทงสี่เหลี่ยมแตละแทงเปนจุดกึ่งกลาง
ของแตละชั้น ความสูงของแทงสี่เหลี่ยมแตละแทงจะเปนความถี่ของแตละชั้น
ตัวอยาง ฮิสโตแกรม แสดงจํานวนนักเรียนในแตละชวงอายุ
400
300
200
100
Std. Dev = 1.49
Mean = 15.1
N = 1425.00
0
11.0
12.0
13.0
14.0
15.0
16.0
17.0
18.0
19.0
AGE
4) กราฟเสน (Line Chart) เปนการเสนอขอมูลที่ทําใหเห็นการเปลี่ยนแปลงที่ชัดเจน แบงได
หลายลักษณะ คือ
- กราฟเสนเชิงเดี่ยว ( Simple Line chart )
- กราฟเสนเชิงซอน ( Multiple Line chart )
- รูปหลายเหลี่ยมแหงความถี่ (Frequency polygon)
- กราฟความถี่สะสม(Ogive curve)
- กราฟเสนโคง (Smooth curve)
44. 47
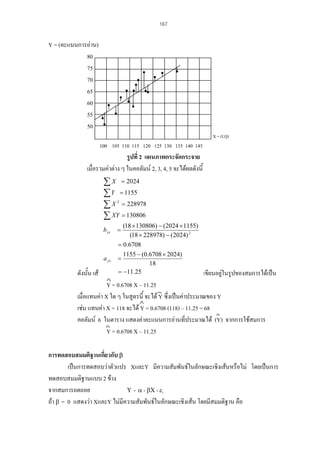
(1) กราฟเสนเชิงเดี่ยว (Simple Line Chart) เปนกราฟทีแสดงการเปรียบเทียบขอมูลโดย
่
พิจารณาลักษณะของขอมูลเพียงลักษณะเดียว เชน จํานวนครอบครัวที่มีรายไดตางๆกัน
70 0
แผนภาพแสดงจํานวนครอบครัวจําแนกตามจํานวนบุตร
(1) แผนภาพเชิงซอน (Multiple Line Chart)
60 0
50 0
40 0
30 0
20 0
un t
10 0
0
1
Iin co me
2
3
4
5
6
7
8
(1 : 1 000 )
กราฟเสนแสดงจํานวนครอบครัวจําแนกตามรายได
2) กราฟเสนเชิงซอน (Multiple Line chart) เปนกราฟที่แสดงการเปรียบเทียบขอมูลโดย
พิจารณาลักษณะของขอมูลตั้งแต 2 ลักษณะขึ้นไป เชน จํานวนครอบครัวจําแนกตามรายไดและ
โรงเรียน
200
100
SCHOOL
1
2
Co
un
t
3
4
0
1
2
3
4
5
6
7
8
iincom e
กราฟเสนเชิงซอนแสดงจํานวนครอบครัวจําแนกตามรายไดและโรงเรียน
(3) รูปหลายเหลี่ยมแหงความถี่ (Frequency polygon) หรือโพลิกอน เปนการเสนอขอมูล
ใหมีความเดนชัดขึ้น ซึ่งแสดงโดยลากเสนตรงเชื่อมตอระหวางคากึ่งกลางชั้นของฮิสโตแกรม แต
ตองเพิ่มในฮิสโตแกรมอีก 2 ชั้น คือ ชั้นต่าสุดและชั้นสูงสุด โดยชั้นทีเ่ พิ่มขึ้นอีก 2 ชั้นมีคาความถี่
ํ
เทากับ ศูนย
45. 48
400
300
200
100
Std. Dev = 1.49
Mean = 15.1
N = 1425.00
0
11.0
12.0
13.0
14.0
15.0
16.0
17.0
18.0
19.0
AGE
โพลิกอนอายุของนักเรียน
(4) กราฟความถี่สะสม (Ogive curve) เปนการนําเสนอขอมูลอีกแบบซึ่งแสดงใหทราบ
ถึงความถี่ที่เกิดขึ้น โดยการหาความถี่สะสม ตองเริ่มหาผลบวกของความถี่โดยเริ่มตั้งแตชั้นแรก
1600
1400
1200
1000
Cumulative Frequency
800
600
400
200
0
11
12
13
14
15
16
17
18
19
AGE
กราฟความถี่สะสมจําแนกตามอายุของนักเรียน
(5) กราฟเสนโคง (Smooth curve) เปนเสนโคงที่เกิดจากการปรับโพลิกอนใหเปนเสนโคง
เรียบ โดยพื้นที่ใตเสนโคงเทากับพื้นที่ในโพลิกอน
400
300
200
100
Std. Dev = 1.49
Mean = 15.1
N = 1425.00
0
11.0
12.0
13.0
14.0
15.0
16.0
17.0
18.0
AGE
กราฟเสนโคงความถี่จําแนกตามอายุของนักเรียน
19.0
46. 49
2. การวัดตําแหนงการเปรียบเทียบ
เปนการบอกใหทราบวาคาทีไดมานั้นมีตําแหนงอยูที่ใด หรือสวนใดของคาทั้งหมด เปน
่
การแสดงใหเห็นความสัมพันธระหวางคาที่ไดกับขอมูลทั้งหมด เชน ครูผูสอนตองการแสดงใหเห็น
วาสวนสูงของนักเรียนก.มีความสัมพันธกบสวนสูงของเพื่อนในชันอยางไร
ั
้
การที่จะบอกวา
นักเรียน ก.สูง 160 ซม. นั้นไมไดสื่อความหมายอยางไร จึงตองใชการวัดตําแหนงการเปรียบเทียบ
ไดแก
1) เปอรเซ็นตไทล ( Percentile )
คาเปอรเซ็นตไทล P หมายถึง คาของขอมูลที่มีจํานวนขอมูลที่มีคาต่ํากวา อยู P % และมี
จํานวนขอมูลที่มีคามากกวาอยู ( 100- P) %
ตําแหนงเปอรเซนไทล P หมายถึง ตําแหนงที่บอกใหทราบวามีขอมูลอยู Pสวนในรอยสวน
ที่มีคาของขอมูลต่ํากวาคาของขอมูล ณ ตําแหนง P
การหาเปอรเซ็นตไทล
การหาเปอรเซ็นตไทลสําหรับขอมูลที่ไมไดจัดกลุม มีขั้นตอน ดังนี้
1. เรียงลําดับขอมูล n คาจากนอยไปมาก
2. คํานวณหาตําแหนง P ( n + 1 ) ถาผลลัพธเปนเลขไมลงตัวใหปดเปนเลขจํานวนเต็มที่มีคาใกลเคียง
มากที่สุด
100
ตัวอยาง จงหาเปอรเซ็นตไทลที่ 68 ของขอมูลตอไปนี้
6.3 6.6 7.6 3.0 9.5 5.9 6.1 5.0 3.6
เรียงลําดับขอมูล 9 คาจากนอยไปมาก ดังนี้
3.0 3.6 5.0 5.9 6.1 6.3 6.6 7.6 9.5
คํานวณหาตําแหนง 68 ( 9 + 1 ) = 6.8 ≈ 7
100
คาเปอรเซ็นตไทลที่ 68 ของขอมูล = 6.6
การหาเปอรเซ็นตไทลสําหรับขอมูลที่แจกแจงความถี่ มีสูตรในการคํานวณ ดังนี้
Pr = L + I [ n x r - Σfi ] / fr
100
เมื่อ L = ขีดจํากัดลางทีแทจริงของอันตรภาคชั้นที่มี Pr อยู
่
I = ความกวางของอันตรภาคชัน
้
r = ตําแหนงเปอรเซ็นตไทลที่ตองการหา
n = จํานวนขอมูลทั้งหมด
Σfi = ความถี่สะสมของอันตรภาคชั้นที่ต่ํากวา L
fr = ความถี่ของชั้น L
47. 50
กอนที่จํานําสูตรนี้ไปหาจะตองทราบกอนวา Pr ควรจะอยูอันตรภาคชันใด โดยเปรียบเทียบ คา n x r
้
กับความถี่สะสม
100
ตัวอยาง การคํานวณหาเปอรเซ็นตไทลสําหรับขอมูลที่แจกแจงความถี่
จงหาเปอรเซ็นตไทลที่ 20 และ 80 ของขอมูลความสูงของนักเรียนที่กําหนดไวในตาราง
แจกแจงความถี่ ดังนี้
ขีดจํากัดที่แทจริงของชั้น
134.5-144.5
144.5-154.5
154.5-164.5
164.5-174.5
174.5-184.5
รวม
ความถี่ ( f )
5
18
42
27
8
100
ความถี่สะสม (Σ f )
5
23
65
92
100
จากความถี่สะสมชั้นที่ 2 มี Σ f = 23 ดังนัน เปอรเซ็นตไทลที่ 20 จะอยูในชั้นที่ 2
้
การหาเปอรเซ็นตไทลที่ 20 ได L = 144.5 I = 10 r = 20 n = 100 Σfi = 5 fr = 18
L + I [ n x 20 - Σfi ] / fr
P20 =
100
=
144.5 + 10 ( 100 x 20 - 5 ] / 18
100
=
144.5+ 8.33
= 152.83
สวนเปอรเซ็นตไทลที่ 80 จากความถี่สะสมชั้นที่ 4 มี Σ f = 92 ดังนั้น เปอรเซ็นตที่ 80 จะ
อยูในชันที่ 4ได L = 164.5 I = 10 r = 80 n = 100 Σfi = 65 fr = 27
้
P 80 =
L + I [ n x 80 - Σfi ] / fr
100
=
164.5 + 10 [ ( 100 x 80 - 65 ] / 27
100
=
164.5+ 5.55
= 170.05
2) ควอไทล (Quartiles )
ควอไทลเปนการแบงขอมูลออกเปน 4 สวนเทาๆกัน สวนละ 25 %โดยเรียงลําดับ
ขอมูลจากนอยไปมาก ดังนัน
้
คาควอไทล1(Q1) หมายถึงคาของขอมูลที่มีจํานวนขอมูลที่มีคาต่ํากวา Q1อยู 25 %
48. 51
คาควอไทล2(Q2) หมายถึงคาของขอมูลที่มีจํานวนขอมูลที่มีคาต่ํากวา Q2อยู 50 %
และมีจํานวนขอมูลที่มีคามากกวา Q2อยู 50 %
คาควอไทล3(Q3) หมายถึงคาของขอมูลที่มีจํานวนขอมูลที่มีคาต่ํากวา Q3อยู 75 %
และมีจํานวนขอมูลที่มีคามากกวา Q3อยู 25 %
ตําแหนงควอไทล หมายถึง ตําแหนงที่บอกใหทราบวามีขอมูลอยู Xสวนในสี่สวน
ที่มีคาของขอมูลต่ํากวาคาของขอมูล ณ ตําแหนง X
การคํานวณหาควอไทลสําหรับขอมูลที่ไมไดจัดกลุม
- เรียงลําดับขอมูล n คา จากนอยไปหามาก
- สําหรับการคํานวณหาคา Q1 ใหคํานวณ (n+1)/4 ถาผลลัพธเปนเลขไมลงตัวให
ปดใหเปนเลขจํานวนเต็มที่มคาใกลเคียงมากที่สุด
ี
สวนการหาคา Q3ใหคํานวณหา 3 (n+1)/4 และปดใหเปนเลขจํานวนเต็มที่ใกลเคียงมากที่สุด
สําหรับการหาควอไทล สําหรับขอมูลที่แจกแจงความถี่ มีสูตรในการคํานวณ ดังนี้
QK = L + I [ n x k - Σfi ] / fk
4
เมื่อ L = ขีดจํากัดลางทีแทจริงของอันตรภาคชั้นที่มี QK อยู
่
I = ความกวางของอันตรภาคชัน
้
k = ตําแหนงควอไทลที่ตองการหา
n = จํานวนขอมูลทั้งหมด
Σfi = ความถี่สะสมของอันตรภาคชั้นที่ต่ํากวา L
fk = ความถี่ของชั้น L
พิสัยควอไทล คือความแตกตางระหวางควอไทลบน (Q3)และควอไทลลาง (Q1)
ตัวอยาง จงหา ควอไทลบน (Q3) คามัธยฐาน และควอไทลลาง (Q1) ของคะแนนเฉลี่ยวิชาภาษาไทย
ของนักเรียน 22 คน ดังนี้
45 50 65 23 55 48 78 89 96 85 74 42 45 75 78 41 56 66 77 88 95 78
เนื่องจาก n = 22 คน เรียงขอมูลจากนอยไปมากไดดังนี้
23 41 42 45 45 48 50 55 56 65 66 74 75 77 78 78 78 85 88 89 95 96
การหา Q3 คํานวณหาคา 3 (n+1)/4 = 17.25 ปดเปน 17
ดังนั้นคาควอไทลบนจะเปนคาของขอมูลตัวที่ 17 ที่เรียงลําดับไวแลว คือ 78
การหาคามัธยฐาน (Q2) คํานวณหาคา 2 (n+1)/4 = 11.5 ปดเปน 12
ดังนั้นคามัธยฐาน จะเปนคาของขอมูลตัวที่ 12 ที่เรียงลําดับไวแลว คือ 74
การหา Q1 คํานวณหาคา (n+1)/4 = 5.75 ปดเปน 6
49. 52
ดังนั้นคาควอไทลลางจะเปนคาของขอมูลตัวที่ 6 ที่เรียงลําดับไวแลว คือ 48
3) เดไซล (Deciles )
เดไซล เปนการแบงขอมูลอออกเปน 10 สวนเทาๆกัน มีจํานวน 9 คา คือ D,
D2…D9 โดยที่ k = 1 ,2, 3, … 9
ตําแหนงเดไซล หมายถึง ตําแหนงที่บอกใหทราบวามีขอมูลอยู X สวนในสิบสวน
ที่มีคาของขอมูลต่ํากวาคาของขอมูล ณ ตําแหนง X
การคํานวณหาเดไซล สําหรับขอมูลที่ไมไดจัดกลุม
- เรียงลําดับขอมูล n คา จากนอยไปหามาก
- สําหรับการคํานวณหาคา Dk ใหคํานวณ k(n+1)/10 ถาผลลัพธเปนเลขไมลงตัวให
ปดใหเปนเลขจํานวนเต็มที่มคาใกลเคียงมากที่สุด
ี
สวนการหา Dk สําหรับขอมูลที่แจกแจงความถี่ มีสูตรในการคํานวณ ดังนี้
Dk = L + I [ n x k - Σfi ] / fk
10
เมื่อ L
I
k
n
Σfi
fk
=
=
=
=
=
=
ขีดจํากัดลางที่แทจริงของอันตรภาคชั้นทีมี Dk อยู
่
ความกวางของอันตรภาคชัน
้
ตําแหนงเดไทลที่ตองการหา
จํานวนขอมูลทั้งหมด
ความถี่สะสมของอันตรภาคชั้นที่ต่ํากวา L
ความถี่ของชั้น L
3. การวัดแนวโนมเขาสูสวนกลาง (Central Tendency)
การวัดแนวโนมเขาสูสวนกลาง เปนการคํานวณคากลางของขอมูลวาอยูที่ใด การศึกษาใน
กรณีที่ตองการคาเพียงคาเดียวเพื่อใชอธิบายขอมูลทั้งชุด
จึงนิยมหาคากลางๆที่เปนตัวแทนของ
ขอมูลทั้งชุด นั่นคือ คาเฉลี่ยเลขคณิต (Mean) มัธยฐาน (Median) และฐานนิยม(Mode) โดยมีวิธการ
ี
หาได ดังนี้
3.1 คาเฉลี่ยเลขคณิตหรือมัชฌิมเลขคณิต (Mean) คือ คาที่ไดจากผลรวมของคะแนนหรือ
คาที่ไดทั้งหมดหารดวยจํานวนนักเรียนหรือจํานวนขอมูล การคํานวณหาคาแบงเปน
50. 53
ก. การหาคาเฉลี่ยเลขคณิตสําหรับขอมูลที่ไมไดจัดกลุม
คาเฉลี่ยเลขคณิตประชากร µ = ΣΧi / Ν = ( Χ1 + Χ2 + … + Χn ) / Ν
คาเฉลี่ยตัวอยาง = Χ = ΣΧi / n = ( Χ1 + Χ2 + … + Χn ) / n
ข. การหาคาเฉลี่ยเลขคณิตสําหรับขอมูลที่จัดกลุม
µ = ΣΧifi / Ν
Χ = ΣΧifi
/n
้
โดยที่ n = ขนาดตัวอยาง , fi = ความถี่ของอันตรภาคชันที่ i
ขอดีของคาเฉลี่ย
1. การเปรียบเทียบขอมูลเชิงปริมาณหลายๆชุดนิยมใชคาเฉลี่ยในการเปรียบเทียบ
2. สะดวกในการคํานวณถึงแมจะเก็บขอมูลไดไมครบ
ขอเสียของคาเฉลี่ย
1. ใชกับขอมูลเชิงปริมาณเทานั้น
2. คาเฉลี่ยจะไมใชคากลางที่ดี ถามีคาผิดปกติไปมาก (คาที่สูงเกินไปมากๆ หรือ
คาที่ต่ําเกินไปมากๆ)
3.2 คามัธยฐาน (Median) คือคาในตําแหนงที่แบงขอมูลออกเปนสองสวนเทาๆกัน คือ
มากกวามัธยฐาน50% นอยกวามัธยฐาน50% หรือคือคาในตําแหนงกึ่งกลางของการแจกแจง ดังนัน
้
คามัธยฐานก็คอ คาของขอมูล ณ ตําแหนงที่ (n+1)/2 เมื่อเรียงลําดับขอมูลแลว
ื
ในกรณีที่จํานวนขอมูลเปนเลขคี่ มัธยฐานคือคาของขอมูลที่อยูกึ่งกลาง แตถาจํานวนขอมูล
เปนเลขคู มัธยฐานจะเทากับคาเฉลี่ยของ 2 จํานวนที่อยูตรงกลาง เชน
10 13 15 16 18 19 20 คามัธยฐานคือ 16
11 12 12 13 15 15 18 19 คามัธยฐานคือ (13+15) / 2 = 14
ในกรณีที่ขอมูลจัดกลุมแลว
Median = L + ( n/2 – CF ) . I
fm
L = ขีดจํากัดลางที่แทจริงของชั้นที่มี Median อยู
n = จํานวนขอมูลทั้งหมด
CF = ความถี่สะสมของชั้นที่ต่ํากวาชันที่มี Median อยู 1 ชั้น
้
51. 54
fm = ความถี่ของชั้นที่มี Median อยู
I = ชวงของอันตรภาคชัน
้
ขอดีของคามัธยฐาน
คามัธยฐานจะไมถูกกระทบกระเทือนเมื่อมีขอมูลที่มีคาสูงหรือต่ําผิดปกติ
ขอเสียของคามัธยฐาน
ไมไดนําคาของขอมูลทุกตัวมาคิดคํานวณ
3.3 ฐานนิยม (Mode) คือคาที่เกิดขึ้นบอยที่สุดในจํานวนชุดของขอมูลทั้งหมด
ุ
สําหรับขอมูลที่ไมไดจดกลุม คาฐานนิยมก็คือคาที่มีความถี่ของคานั้นซ้ํากันมากที่สด
ั
สําหรับขอมูลที่จัดกลุมแลว คาฐานนิยม คํานวณไดจากสูตร
ฐานนิยม = Mode = L + ( fm - f1 ) . I
(fm – f1) + (fm – f2)
L = ขีดจํากัดลางที่แทจริงของชั้นที่มี Mode อยู
fm = ความถี่ของชั้นที่มี Mode อยู
f1 = ความถี่ของชั้นที่ต่ํากวาชั้นที่มี Mode อยู 1 ชั้น
f2 = ความถี่ของชั้นที่สูงกวาชั้นที่มี Mode อยู 1 ชั้น
I = ชวงของอันตรภาคชัน
้
ขอดีของคาฐานนิยม
1. จะไมถูกกระทบกระเทือนเมื่อมีขอมูลที่มีคาสูงหรือต่ําผิดปกติ
2. เปนคากลางที่ใชวัดขอมูลเชิงคุณภาพและเชิงปริมาณ
ขอเสียของคาฐานนิยม
1. ในกรณีที่ไมมีคาของขอมูลที่ซ้ํากัน จะไมมีคาฐานนิยม
2. กรณีที่ขอมูลจัดกลุมแลว ฐานนิยมจะเปลี่ยนไปถาการจําแนกชั้นเปลี่ยนไป
3. ขอมูลบางชุดอาจมีฐานนิยมมากกวา 1 คาโดยที่ฐานนิยมนั้นอาจแตกตางกัน
มาก
ตัวอยาง สําหรับขอมูลที่ไมไดจัดกลุม
จงหาค า เฉลี่ ย เลขคณิ ต ค า มั ธ ยฐาน และค า ฐานนิ ย ม ของน้ํ า หนั ก ของนั ก เรี ย นชั้ น
ประถมศึกษาปที่ 1 จํานวน 10 คนหนวยเปนกิโลกรัม ดังนี้
20 22 23 23 25 26 27 28 29 30
52. 55
คาเฉลี่ยตัวอยาง = ( Χ1 + Χ2 + … + Χn ) / n
= (20+22+23+23+25+26+27+28+29+30 ) / 10
= 25.3
กิโลกรัม
คามัธยฐาน
= 25+26 / 2
= 25.5
คาฐานนิยม
= 23
ตัวอยางสําหรับขอมูลที่จัดกลุมแลว
จงหาค า เฉลี่ ย เลขคณิ ต ค ามั ธ ยฐาน และค า ฐานนิย ม ของความสูง ของนั ก เรี ย นชายชั้ น
มัธยมศึกษาปที่5 ซึ่งอยูในรูปของตารางแจกแจงความถี่
ขอบเขตจํากัดชั้น
ความสูง : ซม.
134.5-144.5
144.5-154.5
154.5-164.5
164.5-174.5
174.5-184.5
รวม
จํานวนนักเรียน
fi
5
18
42
27
8
100
คากึ่งกลางชั้น
Χi
139.5
149.5
159.5
169.5
179.5
Χifi
657.5
2,691.0
6,699.0
4,576.0
1,436.0
16,100.0
หาคาเฉลี่ย
Χ
ความสูงเฉลี่ย
หาคามัธยฐาน
ขีดจํากัดชั้นที่แทจริง
ความสูง : ซม.
134.5-144.5
144.5-154.5
154.5-164.5
164.5-174.5
174.5-184.5
รวม
=
ΣΧifi
/n
= 16,100/100
= 161 ซม.
คากึ่งกลางชั้น
Χi
139.5
149.5
159.5
169.5
179.5
จํานวนนักเรียน
fi
5
18
42
27
8
100
ความถี่สะสม
Σfi
5
23
65
92
100
53. 56
ชั้นที่มีความถีสะสมมากกวา 50 คือ ชั้นที่ 3 ดังนั้นมัธยฐานอยูชั้นที่ 3
่
Median = L + ( n/2 – CF ) . I
fm
= 154.5+(50-23) . 10
42
= 154.5+6.43 = 160.93 ซม.
หาคาฐานนิยม
ฐานนิยม = Mode = L + ( fm - f1 ) . I
(fm – f1) + (fm – f2)
L = 154.5 เนืองจากชั้นที่ 3 มีความถี่สูงสุด คือ 42
่
fm = 42 f1 = 18 f2 = 27
Mode = 154.5 + ( 42 – 1 8) .10
(42-18)+(42-27)
= 154.5+6.15
= 160.65 ซม.
ความสัมพันธระหวางคากลางทั้งสามชนิด
คากลางทั้ง 3 ชนิดมีความสัมพันธกัน ดังนี้
ก. การแจกแจงของขอมูลมีลักษณะสมมาตร ( Symmetry )
ในกรณีที่ขอมูลมีลักษณะสมมาตร คือขอมูลที่เบี่ยงเบนจากคากลางไปในทางบวก
และทางลบพอๆกัน จะมีคาเฉลี่ย คามัธยฐาน และคาฐานนิยมเทากัน
Mean
Median
Mode
54. 57
ข. การแจกแจงของขอมูลมีลักษณะเบขวา ( Skew to the Right )
ขอมูลที่มีลักษณะเบขวา เปนขอมูลที่สวนใหญมีคานอย จะไดความสัมพันธดังนี้
คาเฉลี่ย > มัธยฐาน > ฐานนิยม
Mode
Mean
Median
ค. การแจกแจงของขอมูลมีลักษณะเบซาย ( Skew to the Left )
ขอมูลที่มีลักษณะเบซาย เปนขอมูลที่สวนใหญมีคามาก จะไดความสัมพันธดังนี้
ฐานนิยม > มัธยฐาน > คาเฉลี่ย
Mean Mode
Median
การเลือกคาที่ใชวัดคากลาง
จะพิจารณาจากการกระจายของขอมูล ดังนี้
1. ขอมูลมีลักษณะสมมาตร จะใช คาเฉลี่ย ฐานนิยม มัธยฐาน คาใดคาหนึ่งเปน
ตัววัดคากลาง เนื่องจากคาทั้ง 3 เทากัน
2. ขอมูลมีลักษณะไมสมมาตร กรณีที่ขอมูลเบซายหรือเบขวา จะใชคามัธยฐาน
เปนคาวัดตําแหนงกลาง
4. การวัดการกระจาย (Measure of Variation)
การพิจารณาหรือสรุปลักษณะของขอมูลโดยใชคากลางหรือคาเฉลี่ยเพียงอยางเดียว อาจทํา
ใหไมทราบถึงลักษณะของขอมูลไดชัดเจน เนื่องจากขอมูลที่มีคากลางเทากันแตลักษณะของขอมูล
ตางกัน นั่นคือมีการกระจายของขอมูลไมเหมือนกัน ดังนั้นในการเปรียบเทียบขอมูลหลายๆชุด ควร
จะพิจารณาคาเฉลี่ยและการและการกระจายของขอมูลควบคูไป การวัดการกระจายที่นิยมใชใน
55. 58
การศึกษา ไดแก พิสัย สวนเบี่ยงเบนควอไทล สวนเบี่ยงเบนมาตรฐาน
สัมประสิทธิ์ความแปรผัน
4.1 พิสัย ( Range ) เปนวิธีการวัดการกระจายที่งายที่สุด โดยที่
พิสัย
=
ความแปรปรวน
คาสูงสุด – คาต่ําสุด
ตัวอยาง จงหาคาพิสัยของขอมูล 3 5 8 12 17 19 22
คาพิสัย = 22-3 = 19
4.2 สวนเบี่ยงเบนควอไทล (Quatile Deviation , Q.D ) คือครึ่งหนึ่งของระยะหาง
่
ระหวางควอไทลที่ 3 กับควอไทลท่ี 1 เมื่อขอมูลมีการกระจายนอย สวนเบียงเบนควอไทล มีคา
นอย เมื่อขอมูลมีการกระจายมาก สวนเบี่ยงเบนควอไทล มีคามาก
คํานวณไดจากสูตร
Q.D =
Q3–Q1
2
4.3 คาความแปรปรวน (Variance,σ2) เปนคาที่นิยมใชวัดการกระจายมากที่สุด โดย
พิจารณาจากผลรวมของคาแตกตางระหวางคาของขอมูลแตละคากับคาเฉลี่ยเลขคณิตยกกําลังสอง
แลวหารดวย N
คาความแปรปรวน = σ2 = Σ (
Χi - µ ) 2
Ν
4.4 คาเบี่ยงเบนมาตรฐาน (Standard Deviation : SD) เปนคาที่วัดการกระจายของขอมูล
ที่ทําใหทราบวาคะแนนแตละจํานวนนันมีคาแตกตางจากคาเฉลี่ยมากนอยเพียงใด คาเบี่ยงเบน
้
มาตรฐานจะนอย ถาขอมูลมีคาใกลเคียงกับคาเฉลี่ย และจะมีคามากถาขอมูลมีคาแตกตางไปจาก
คาเฉลี่ยมาก คาเบี่ยงเบนมาตรฐาน คือ รากที่สองของคาความแปรปรวน
σ = √ Σ ( Χi - µ ) 2 / Ν
56. 59
ตัวอยาง จงหาคาความแปรปรวนและสวนเบี่ยงเบนมาตรฐานของความสูงของนักเรียน
134.5-144.5
144.5-154.5
154.5-164.5
164.5-174.5
174.5-184.5
รวม
139.5
149.5
159.5
169.5
179.5
5
18
42
27
8
100
5
23
65
92
100
Xi- µ
(Xi- µ)2
fI(Xi- µ)
fI(Xi- µ)2
-21.5
-11.5
-1.5
8.5
18.5
ขีดจํากัดชั้นแทจริง คากึ่งกลางชั้น จํานวนนักเรียน ความถี่สะสม
fi
ความสูง : ซม.
Σfi
Χi
462.25
132.25
2.25
72.25
342.25
1011.25
-107.5
-207
-63
229.5
148
0
2,311.25
2,380.5
94.5
1950.75
2738
9475
จากขอมูลที่กลาวมาแลว µ
= 161 เซนติเมตร
ความแปรปรวนของความสูงของนักเรียนชาย = Σ f ( Χi - µ ) 2
Ν
=
9475
100
= 94.75 ซม2
สวนเบี่ยงเบนมาตรฐาน
= √ 94.75
= 9.73 ซม.
ในการวัดความแปรปรวน และสวนเบียงเบนมาตรฐาน ของกลุมตัวอยาง สูตรในการคํานวณคาความ
่
แปรปรวนและสวนเบียงเบนมาตรฐานมีความแตกตางจากกลุมประชากรเล็กนอย
่
เนื่องจากคาเฉลี่ยที่ใช
คํานวณของกลุมตัวอยาง เปนคาประมาณพารามิเตอรที่เปนคาเฉลี่ยของประชากร ดังนั้นองศาของความเปน
อิสระ*จะลดลงเทากับจํานวนพารามิเตอรที่ตองประมาณคา ในทีนี้เทากับ 1 สูตรการคํานวณคาความแปร
่
ปรวนและสวนเบี่ยงเบนมาตรฐานของกลุมตัวอยาง คือ
คาความแปรปรวน
S2
= Σ ( Χi - x ) 2
n-1
คาสวนเบี่ยงเบนมาตรฐาน S.D = √
Σ ( Χi - x ) 2 /
n -1
57. 60
*องศาของความเปนอิสระ คือ จํานวนคาของตัวแปรที่สามารถผันแปรไดโดยไมมีขอจํากัด มีคาเทากับจํานวนคาของตัวแปร
ทั้งหมดลบดวยจํานวนพารามิเตอรที่ตองประมาณคา ในการคํานวณหาคาสถิติตัวนั้น
4.5 สัมประสิทธิ์ความแปรผัน (Coefficient of Variation : C.V.) เปนคาที่ใชวดการกระจายของ
ั
ขอมูลที่ไมมีหนวย ซึ่งตางจากคาสถิติตัวอื่นที่ใชวัดการกระจาย ซึงมีหนวยเปนหนวยเดียวกับหนวยของ
่
ขอมูล คาสัมประสิทธิ์ความแปรผัน คือคาเบี่ยงเบนมาตรฐานหารดวยคาเฉลี่ย
CV ของประชากร
=
σ ×100
µ
CV ของตัวอยาง
=
SD×100
x
5. คะแนนมาตรฐาน ( Standard score )
คะแนนมาตรฐานเปนคะแนนที่แปลงรูปมา จากคะแนนดิบ ซึ่งมี 2 ประเภท คือ คะแนน
มาตรฐานเชิงเสน (Linear standard score) กับคะแนนมาตรฐานโคงปกติ (Normalized standard
score )
1) คะแนนมาตรฐานเชิงเสนตรง ไดแก
1.1 คะแนนมาตรฐาน z (Z - score)
ตัวอยาง ทองดีสอบไดคะแนน 32 คะแนน คะแนนเฉลียของผูสอบเทากับคะแนนและสวนเบียงเบน
่
่
มาตรฐานเทากับ จงแปลงคะแนนของทองดีเปนคะแนนมาตรฐาน
(
)
z = x − x / s.d .
z = (32 − 25) / 2
= 2.5
58. 61
1.2 คะแนนมาตรฐาน T (T - score)
เปนคะแนนที่ปรับจากคะแนนมาตรฐาน Z เนื่องจาก คะแนนมาตรฐาน Z มีทั้งคาบวกและ
คาลบ ทําใหแปลความหมายยาก คะแนนมาตรฐาน T จะมีคาเฉลี่ยเปน 50 สวนเบี่ยงเบนมาตรฐาน
เทากับ 10 เขียนเปนสูตรไดดังนี้
T = 10Z + 50
จากตัวอยาง หาคะแนนมาตรฐาน T ไดดงนี้
ั
T = 10Z + 50
= 10 (3.5) + 50
= 85
2) คะแนนมาตรฐานโคงปกติ
คะแนนมาตรฐาน T ปกติ หรือคะแนน T ปกติ (Normalized T -score) เปนคะแนนที่แปลง
จากคะแนนดิบที่มีการแจกแจงความถี่เปนโคงปกติ
วิธีการคํานวณ
2.1 เรียงคะแนนจากมากไปหานอย ( x )
2.2 แจกแจงความถี่ของคะแนนดิบ (f)
2.3 คํานวณหาความถี่สะสม (c f) โดยเอาความถี่ ( f ) บวกสะสมขึ้นไปเรื่อย ๆ
เริ่มตนจากความถี่ของคะแนนที่มีคาต่ําสุด เปนจุดเริ่มตนของชอง cf ในที่นี้คือ
0+2 = 2
ลําดับที่สูงขึ้นมาคือ 2 + 3 = 5
5+4 = 9
9 + 8 = 17
2.4 คํานวณหาคา cf + 1 f ดังนี้
2
ชั้นต่ําสุด
= 0 + 1 (2)
2
= 1.0
สูงขึ้น 1 ระดับ = 2 + 1 (3)
= 3.5
สูงขึ้น 2 ระดับ = 5 + 1 (4)
= 7.0
2
2
59. 62
2.5 คําวณหาคาเปอรเซ็นตไทล
100
(cf + 1
N
2
จากสูตร เปอรเซ็นตไทล=
100
45
f)
(1)
= 2.2
สูงขึ้น 1 ระดับ = 100 (3.5)
=7.78
สูงขึ้น 2 ระดับ = 100 (7)
=15.56
ชั้นต่ําสุด
=
45
45
2.6 หาคา T โดยเปดตาราง (ที่ตารางการเปลี่ยนคะแนนเปอรเซ็นตไทล ใหเปน
คะแนน T ปกติ) ใหหาคาทีใกลเคียงที่สุด
่
เชน เปอรเซ็นตใกล 1 ใกลเคียงกับ 2.22 เทากับ คะแนน T คือ 29
เปอรเซ็นตใกล 5 ใกลเคียงกับ 7.78 เทากับ คะแนน T คือ 35
การวิเคราะหดวยสถิติแบบบรรยายโดยใชโปรแกรม SPSS for Windows
วิธีการวิเคราะหดวยสถิติแบบบรรยาย
การวิเคราะหขอมูลเบื้องตนดวยสถิติแบบบรรยายโดยใชโปรแกรม SPSS for Windows
ประกอบดวย ตารางแสดงความถี่ของขอมูล คากลาง คาการกระจายของขอมูล รวมทั้งกราฟ ที่จะ
นําเสนอขอมูล คําสั่งที่ใชในการหาคาสถิติแบบบรรยาย มี 3 คําสั่ง คือ Frequencies
Descriptives และ Means
60. 63
1. คําสั่ง Frequencies
1.1 การคํานวณสถิติเบื้องตนโดยใชคําสั่ง Frequencies
Analyze
Descriptive Statistics
Frequencies… จะไดหนาจอดังรูปที่ 1
รูปที่ 1 หนาจอการกําหนด Frequencies dialog box
เมื่อเลือกตัวแปรที่ตองการบรรยายลักษณะ และตารางแสดงความถี่ แลว
1.2 เลือก Statistics…. จะไดหนาจอดังรูปที่ 2
รูปที่ 2 หนาจอการกําหนด Frequency : Statistics
61. 64
เลือก เปอรเซ็นตไทล (Percentile Values ) คากลางของขอมูล (Central
Tendency ) สถิติที่วัดการกระจาย ( Dispersion ) และสถิติที่วัดการแจกแจง ( Distribution ) แลว
กลับไปหนาจอเดิม รูปที่ 1 เลือก OK เปดแฟม output จะไดผลลัพธ ดังนี้
ตารางที่ 1 ตัวอยางของผลลัพธของสถิติแบบบรรยาย
Statistics
N
income of
respondent
Valid
Statistic
90
Missing
Statistic
Mean
Statistic
Std.Error
0
19801.00
989.70
Std.
Deviation
Statistic
9389.09
Skewness
Statistic
Std.Error
.467
.254
Kurtosis
Statistic
Std.Error
.146
.503
จาก ผลลัพธ ตารางที่ 1 ไดคาเฉลี่ย ( Mean ) สวนเบียงเบนมาตรฐาน ( SD ) คา
่
ความเบ (sknewness) และ คาความโดง (kurtosis) โดยมีคาความเบมากกวา 0 แสดงวาเสนโคงเบ
ขวา และคาความโดงมากกวา 0 แสดงวาขอมูลมีการแจกแจงคอนขางปาน นอกจากนี้ยังสามารถ
เลือก Charts ในรูปที่ 1 จะไดหนาจอในรูปที่ 3
รูปที่ 3 หนาจอการกําหนด Frequencies Chart
Histogram ( s ) และ 4 With normal curve
- เลือก
- เลือก Continue จะกลับมาที่รูปที่ 1 เลือก OK จะได histogram ซึ่งอยูใน output ดังนี้
จากผลลัพธในตารางที่ 1 สามารถนําเสนอขอมูลในการวิจัย ไดดังนี้
62. 63. 66
รูปที่ 5 หนาจอการกําหนด Descriptive:Option
เลือกคาสถิติแบบบรรยายทีตองการ แลวเลือก continue จะกลับไปหนาจอ ดังรูปที่4
่
เลือก OK จะไดผลลัพธตามตารางที่ 2
ตารางที่ 2 ตัวอยางของผลลัพธ
Descriptive Statistics
N
income of
respondent
Valid N
(listwise )
Minimum
90
3500
Maximum
48900
Mean
19801.00
Std.Deviation
9389.09
Variance
8.8E+07
90
จากตารางที่ 2 จะไดคาต่ําสุด ( Minimum ) คาสูงสุด ( Maximum ) คาเฉลี่ย
(Mean ) คาสวนเบียงเบนมาตรฐาน ( SD ) และคาความแปรปรวน ( variance )
่
3. คําสั่ง Means
- ใชเมื่อตองการหาคาเฉลี่ยและคาเบี่ยงเบนมาตรฐานของตัวแปรเชิงปริมาณแยกตามตัวแปร
คุณภาพ เชน หารายจายแยกตามอาชีพ เปนตน
3.1 ใชคําสั่ง
Analyze
Compare Means
Means….
จะไดหนาจอดังรูปที่ 6
64. 67
รูปที่ 6 หนาจอการกําหนด Means dialog box
เลือกตัวแปรเชิงปริมาณที่ตองการหาคาเฉลี่ยใสในชอง Dependent List : และเลือกตัว
แปรคุณภาพทีตองการแยกกลุมตัวแปรปริมาณใสในชอง Independent List
่
3.2 เลือก Options… จะไดหนาจอดังรูปที่ 7
รูปที่ 7 หนาจอการกําหนด Means options
เลือกสถิติในสวนของ statistics เลือก continue จะกลับไปหนาจอรูปที่ 6 เลือก OK
จะไดผลลัพธแสดงในตารางที่ 3
65. 68
ตารางที่ 3: Total Expense * Occupation of Respondent
Total Expense
government
officer
business
employee
worker
commerce
Total
Mean
Std. Deviation
Mean
Std. Deviation
Mean
Std. Deviation
Mean
Std. Deviation
Mean
Std. Deviation
13415.00
7102.8517
18465.33
6118.8204
6762.6667
3648.8129
16853.91
5698.3560
14868.56
7155.4228
จากตารางที่ 3 แสดงคาเฉลี่ยเบี่ยงเบนมาตรฐาน ของคาใชจาย (ตัวแปรปริมาณ ) จําแนกตาม
อาชีพ ( ตัวแปรคุณภาพ ) ซึ่งนํามาสรางตารางในการนําเสนอขอมูลในการวิจัยไดดังนี้
อาชีพ
รับราชการ
ประกอบธุรกิจ
รับจาง
คาขาย
รวม
คาใชจาย
คาเฉลี่ย
13,415.00
18,465.33
6762.66
16853.91
14868.56
สวนเบี่ยงเบนมาตรฐาน
7102.85
6118.82
3648.81
5698.35
7155.42
สรุป ในบทนี้ไดกลาวถึงสถิติบรรยายสรุปลักษณะของกลุมขอมูล ไดแก การแจกแจง
ความถี่ การวัดตําแหนงการเปรียบเทียบ การวัดแนวโนมเขาสูสวนกลางและการกระจายขอมูล
ประกอบกับการวิเคราะหขอมูล เกี่ยวกับสถิติบรรยายโดยใชโปรแกรมSPSS for Windows สวน
การวิเคราะหโดยใชสถิติอางอิงจะกลาวในบทตอไป
66. 69
แบบฝกหัด
จงคํานวณดวยมือกอนแลวเปรียบเทียบผลการคํานวณดวยโปรแกรมคอมพิวเตอร
1. จงหาคาพิสย คาความแปรปรวน และคาเบี่ยงเบนมาตรฐาน ของขอมูลตอไปนี้
ั
2
1
7
6
5
3
8
5
2
4
5
6
3
4
4
6
9
4
3
4
5
5
7
3
5
2. จากขอมูลตอไปนี้
18
16
16
16
14
18
16
18
14
19
15
19
9
20
10
10
12
14
18
12
14
14
17
12
18
13
15
13
15
19
1) จงหาคาควอไทลลาง มัธยฐาน และควอไทลบน พรอมทั้งอธิบายความหมาย
2) จงหาเปอรเซนตไทลที่ 90
3. จากการสุมตัวอยางยอดขายเพิ่มขึ้นรายปของบริษัทแหงหนึ่งในอดีตมา 8 ป ไดขอมูลดังนี้
13.6 % 25.5 % 43.6 % - 19.8 % - 13.8 %
12.0 % 36.3 % 14.3 %
1) ยอดขายที่เพิ่มขึ้น โดยเฉลี่ยตอปของบริษัทขางตน
2) คาเบี่ยงเบนมาตรฐานของยอดขายที่เพิ่มขึ้น
3) พิสัยควอไทล
4. จากการสุมตัวอยางสถาบันการศึกษาเพือเก็บขอมูลของจํานวนนิสิตตออาจารยของปปจจุบัน ไดคําตอบ
่
ดังนี้
7.2 6.9 6.6 7.3 7.4 6.7 6.8 6.9 7.2 6.4
1) จงหาคาเฉลี่ยตัวอยาง
2) จงหาคามัธยฐานตัวอยาง
5. ถาสมาคมนักกีฬาแหงประเทศไทยไดเก็บรวบรวมขอมูลเกี่ยวกับเงินที่มีผูบริจาคดังนี้
เงินบริจาค ( บาท )
0 – 400
400 – 800
800 – 1,200
1,200 – 1,600
1,600 – 2,000
1) จงเขียนฮิสโตแกรม
3) จงหาความถี่สะสม
5) จงหาคาพิสัยควอไทล
จํานวนคน
2
6
12
6
4
2) จงหาความถี่สัมพันธ
4) จงหาคาเฉลี่ย คาเบี่ยงเบนมาตรฐาน คามัธยฐาน
67. 70
6. จากตารางแจกแจงความถีของคาแรงรายวันของนักการภารโรง 65 คน จงหา
่
คาแรง/วัน
70-79
80-89
90-99
100-109
110-119
120-129
130-139
1)
2)
3)
4)
5)
6)
7)
จํานวนคนงาน
8
10
16
14
10
5
2
คากลางของชั้นที่3 (90-99)
ขีดจํากัดลางของชั้นที่5 และขีดจํากัดบนของชั้นที่ 6
ขอบเขตจํากัดของชั้นที่5
ความกวางของชั้นที่4
ความถี่สัมพัทธของชั้นที่3
เปอรเซ็นตของคนงานที่ไดคาแรงรายวันนอยกวา 80บาท
เปอรเซ็นตของคนงานที่ไดคาแรงรายวันในชวง 60-99.99
7. จากขอมูลคะแนนสอบวิชาภาษาไทยของนักเรียนหองหนึ่งมีดังนี้
77 53 59 85 64 67 59 48 74 78 54 51 53 56 62 61 67
69 75 76 84 87 89 94 95 96 92 93 48 80 55 74 73 70
1) จงสรางตารางแจกแจงความถี่ ความถี่สัมพันธ และความถี่สะสม
2) จงหาคาควอไทลลาง มัธยฐาน และควอไทลบน พรอมอธิบายความหมาย
3) จงหาเปอรเซนตไทลที่ 90 พรอมอธิบายความหมาย
4) จงหาคาเฉลี่ย ความแปรปรวน สวนเบียงเบนมาตรฐาน คาฐานนิยม
่
8. ถานายศักดาตองตัดสินใจเลือกซื้อหุนบริษัทใดบริษัทหนึ่ง จาก 3 บริษัทที่มีอัตราปนผล ดังนี้
บริษัท ก เงินปนผลเฉลี่ยเทากับ 15.6% ตอปและคาเบี่ยงเบนมาตรฐานเปน 3.7%
บริษัท ข เงินปนผลเฉลี่ยเทากับ 13.7% ตอปและคาเบี่ยงเบนมาตรฐานเปน 2.5%
บริษัท ค เงินปนผลเฉลี่ยเทากับ 18.9% ตอปและคาเบี่ยงเบนมาตรฐานเปน 5.8%
ถาทานเปนนายศักดาทานจะตัดสินใจลงทุนซื้อหุนบริษทใด
ั
68. 71
9.จากขอมูลรายไดตอเดือนของครอบครัวนักเรียน ในจังหวัดเชียงใหม มีดังนี้
รายไดตอเดือนของครอบครัว(บาท/เดือน)
ความถี่สัมพันธ
10,000-15,000
.20
15,001-20,000
.18
20,001-25,000
.14
25,001-30,000
.12
30,001-35,000
.14
35,001-40,000
.14
40,001-45,000
.08
จงหา
1) รายไดเฉลี่ยตอเดือนตอครอบครัวนักเรียน ในจังหวัดเชียงใหม
2) คาเบี่ยงเบนมาตรฐานตอเดือนตอครอบครัวนักเรียน ในจังหวัดเชียงใหม
3) คามัธยฐานของรายไดตอเดือนตอครอบครัวนักเรียน ในจังหวัดเชียงใหม
69. บทที่3
สถิติอางอิง
สถิติอางอิง (Inferential statistics) หมายถึง สถิติที่ใชัในการสรุปอางอิงขอมูลที่ไดจากกลุม
ตัวอยางไปยังขอมูลของประชากร โดยใชทฤษฎีความนาจะเปน การประมาณคาพารามิเตอร การ
ทดสอบสมมุติฐาน ดังนั้น เนื้อหาที่สําคัญในบทนี้จะนําเสนอในเรืองที่เกี่ยวของกับสถิติอางอิงกอน
่
ไดแก มโนทัศนเบื้องตนของการแจกแจงความนาจะเปนแบบตางๆ Sampling Distribution ของสถิติ
ทดสอบแบบตางๆ การสุมตัวอยางและขนาดของกลุมตัวอยาง การประมาณคาพารามิเตอร แลวจึง
นําเสนอสถิติอางอิงเบื้องตนที่สําคัญ ไดแก การทดสอบสมมติฐาน การวิเคราะหความแปรปรวน
สวนความสัมพันธระหวางตัวแปรและการทํานายตัวแปร จะกลาวในบทตอไป
มโนทัศนเบื้องตนของการแจกแจงความนาจะเปนแบบตางๆ
ตัวแปรสุม หมายถึง สิ่งที่มีความผันแปรโดยมีโอกาสในการเกิดความผันแปรไดเทาๆกัน
หรือเปนเซ็ตของคาที่ผันแปรได เชน ถาให X เปนตัวแปรสุมของการทอดลูกเตา 1 ครั้ง คาของ X ที่
อาจจะเกิดขึ้นได มีคาตั้งแต 1 – 6 โดยมีคาความนาจะเปนหรือโอกาสในการเกิดคาตางๆไดเทากัน
คือ 1/6 ประเภทของตัวแปรสุมแบงได 2 ชนิด คือ ตัวแปรสุมแบบไมตอเนื่อง (Discrete random
variable) และ ตัวแปรสุมแบบตอเนื่อง (Continuous random variable)
1. ตัวแปรสุมแบบไมตอเนือง (Discrete random variable) คาของตัวแปรสุมแบบไมตอเนื่อง
่
จะมีไดเพียงบางคาและเปนจํานวนนับ ซึ่งอาจมีจํานวนทีจํากัด หรือเปนคาอนันตที่นบได เชน การจับ
่
ั
ใบดํา-แดงในการเกณฑทหาร การโยนเหรียญ การทอดลูกเตา การตรวจสอบคุณภาพของสินคา
ตัวอยางคาที่ไดจากการสุมสินคาที่เสีย X = 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10
2. ตัวแปรสุมแบบตอเนื่อง (Continuous random variable) คาของตัวแปรสุมแบบตอ
เนื่อง จะมีคาจริงในชวงที่ตอเนื่องกัน เชน น้ําหนัก สวนสูง ระยะเวลา ตัวอยางคาของน้ําหนักของ
นักเรียนมัธยมศึกษา จะอยูในชวง 40-90 กิโลกรัม เขียนไดวา 40 < X < 90 กิโลกรัม
การแจกแจงความนาจะเปนของตัวแปรแบบไมตอเนื่อง(Discrete probability distribution)
กรณีที่ตวแปรสุมเปนตัวแปรแบบไมตอเนือง ตัวแปรชนิดนี้จะมีคาบางคาและจะมีการแจก
ั
่
แจงความนาจะเปนแบบตางๆกันขึ้นอยูกับลักษณะของการทดลองสุม ซึ่งการแจกแจงความนาจะเปน
ของตัวแปรแบบไมตอเนื่องที่ควรทราบ มีดังนี้
1. การแจกแจงแบบทวินาม ( Binomial distribution)
เปนการแจกแจงของตัวแปรสุมที่ไมตอเนือง(Discrete random variable) ที่ในการทดลองแต
่
ละครั้งจะเกิดผลลัพธเพียง 2 อยาง คือ สําเร็จ (success) กับผิดหวัง (failure)
การแจกแจงแบบทวินาม เขียนแทนดวย b( x, n, p )
โดยที่ n คือ การทดลองซ้ําๆกันในสภาวะเหมือนๆกัน อยางเปนอิสระ
70. 73
x คือ จํานวนความสําเร็จที่ไดจากการทดลอง n ครั้ง
p คือ ความนาจะเปนที่พบความสําเร็จ
ตัวอยางเหตุการณที่มีการแจกแจงแบบทวินาม เชน การโยนเหรียญ
เลือกตอบ ดังแสดงในตาราง 3.1
ตาราง 3.1 ตัวอยางของตัวแปรทวินาม
การทดลอง
การโยนเหรียญ
สําเร็จ ไมสําเร็จ
p
หัว
กอย
1/2
การมีบุตร
หญิง
การทําขอสอบ
ถูก
เลือกตอบ 4 ตัวเลือก
ชาย
1/2
ผิด
1/4
การมีบุตร การทําขอสอบ
n
x
จํานวนครั้งใน จํานวนครั้งที่ออกหัว
การโยนเหรียญ
จํานวนบุตร
จํานวนบุตรสาวใน
ครอบครัว
จํานวนขอสอบ จํานวนขอที่ตอบถูก
การคํานวณคาการแจกแจงความนาจะเปนแบบทวินาม
สมมติการสอบครั้งหนึ่ง เหลือเวลาอีก 3 วินาที แตยังมีขอสอบ 4 ตัวเลือกอีก 3 ขอที่ยังไมได
ทํา นิสิตจึงตัดสินใจทําขอสอบทั้ง 3 ขอโดยไมอาน จงหาความนาจะเปนในการทําขอสอบไดถูกทั้ง 3
ขอ ถูกเพียง 2 ขอ ถูกเพียง 1 ขอ และไมถูกเลย
ความนาจะเปนในการทําขอสอบถูกในแตละขอ = .25 ความนาจะเปนในการทําขอสอบผิด
ในแตละขอ = .75 (ขอสอบมี 4 ตัวเลือก)
ความนาจะเปนที่จะทําขอสอบถูก 3 ขอ 2 ขอ 1ขอ 0 ขอ สามารถหาได ดังนี้
p (ถูก 3 ขอ) = p(TTT)
= p3 = .25 3 = .02
p (ถูก 2 ขอ) = p(TTF) หรือ ( TFT) หรือ(FTT)
= p(TTF) + p( TFT) + p(FTT)
= (.25×.25×.75) + (.25×.25×.75) +(.25×.25×.75)
= .046+.046+.046
= .14
p (ถูก 1 ขอ) = p(TFF) หรือ ( FTF) หรือ(FFT)
= p(TFF) + p( FTF) + p(FFT)
= (.25×.75×.75) + (.75×.25×.75) +(.75×.75×.25)
= .14+.14+.14
= .42
p (ถูก 0 ขอ) = p(FFF)
= p3 = .75 3 = .42
71. 74
เพื่อความสะดวกนักคณิตศาสตรสถิติไดคิดสูตรสําเร็จเพื่อหาความนาจะเปนแบบทวินาม
ดังนี้
สูตรที่ใชหาคาความนาจะเปนที่จะเกิดความสําเร็จ
b( x, n, p ) = n Cx px q n – x
= n ! px q n – x
x ! (n – x ) !
โดยที่ n = จํานวนครั้งในการทดลอง
x = ความสําเร็จที่เกิดขึ้น
p = ความนาจะเปนทีจะพบความสําเร็จ
่
q = ความนาจะเปนทีจะพบความผิดหวัง
่
ตัวอยาง จากขอมูลการสงแบบสอบถามไปยังสถาบันการศึกษาทัวประเทศ พบวาจะไดรับกลับคืน
่
มา 60% ถาสุมเลือกสถาบันการศึกษา 3 แหง แลวสงแบบสอบถามไปให จงหาความนาจะเปนที่จะ
ไดรับแบบสอบถามกลับคืนมา
กรณีที่ 1 3 ฉบับ
กรณีที่ 2 2 ฉบับ
กรณีที่ 3 นอยกวา 2 ฉบับ
การแจกแจงแบบทวินาม เขียนแทนดวย b( x, n, p )โดยที่
กรณีที่ 1 x = 3 n = 3 p = 0.60
b( x, n, p ) = n Cx px q n – x
=
n ! px q n – x
x ! (n – x ) !
= 0.22
=
3 ! 0.63 0.4 0
3 ! (3 – 3 ) !
กรณีที่ 2 x = 2 n = 3 p = 0.60
b( x, n, p ) =
n ! px q n – x
x ! (n – x ) !
= 3 ! 0.62 0.4 1
2 ! (3 – 2 ) !
= 3× 0.14 = 0.42
72. 75
กรณีที่ 3 x = 1และ 0 n = 3 p = 0.60
b( x, n, p ) =
n ! px q n – x
x ! (n – x ) !
=
3 ! 0.61 0.4 2
1 ! (3 – 1 ) !
และ b( x, n, p )=
3 ! 0.60 0.4 3
0 ! (3 –0) !
=
0.29+.06
= 3×0.096 = 0.29
= 0.06
= 0.35
นอกจากการคํานวณความนาจะเปนแบบทวินามแลว นักสถิติไดสรางตารางการแจกแจง
ความนาจะเปนทวินาม เมื่อตองการหาความนาจะเปนแบบทวินามจากตารางจะตองทราบคา
n , p , x โดยใชตาราง ความนาจะเปนแบบทวินาม ในภาคผนวก
คาเฉลี่ยและความแปรปรวนแบบทวินาม
E(x) = Σ x. p(x) = np
Var (x) = E( X - µ )2 = npq
ตัวอยาง ในระยะ 5 ปที่ผานมา สํานักทะเบียนพบวาในแตละปที่นิสิตลงทะเบียนเรียนวิชาเลือกเสรี ก.
เมื่อตนเทอม จะมีการถอนวิชานี้ถึง 20% ถาปนี้มีนิสิตลงทะเบียนวิชานี้ 100 คน โดยเฉลี่ยจะมีนสิต
ิ
เรียนจบวิชานีกี่คนและมีความแปรปรวนเทากับเทาไร
้
การตัดสินใจของนิสิตคนหนึงก็คือการทดลอง 1 ครั้ง นิสิต 100 คน ก็มีการทดลอง 100 ครั้ง
่
n = 100
้
การตัดสินใจทีเ่ กิดขึ้น คือ ถอน กับไมถอน ความนาจะเปนที่จะเกิดขึนในการถอน(q) = .20
ความนาจะเปนที่จะเรียนจบวิชานี้ (p)= .80
โดยเฉลี่ยแลวจะมีนิสิตเรียนจบวิชานี้ ใชสูตร
E(x) = Σ x. p(x) = np
= 100×0.80
= 80
คน
โดยมีความแปรปรวน
= npq
= 100 × 0.80 × 0.20
= 16
73. 76
ตัวอยาง บารมีเปนนักกีฬาของสถาบัน ความนาจะเปนที่บารมีจะชูตลูกบอลลงตาขาย คือ0.5 ในการ
แขงขันครั้งนี้ บารมีมีโอกาสชูตลูกบอล 6 ครั้ง อยากทราบวาบารมีนาจะชูตลูกบอลลงหวงกี่ครั้ง และ
คาสวนเบี่ยงเบนมาตรฐานเทากับเทาไร
จากโจทย n = 6
p = 0.5 q = 1 - 0.5 = 0.5
E(x) = np
= 6 × 0.5 = 3
บารมีนาจะชูตลูกบอลลงหวง = 3 ครั้ง
Var (x) = E( X - µ )2 = npq
= 6 × 0.5× 0.5 = 1.5
สวนเบี่ยงเบนมาตรฐาน
= 1.22
2. การแจกแจงความนาจะเปนแบบปวซอง (Poisson distribution)
การแจกแจงชนิดนี้มีประโยชนมากชวยแกไขขีดจํากัดของการแจกแจงความนาจะเปนแบบ
ทวินาม เมื่อความนาจะเปนที่จะพบความสําเร็จมีคานอยมาก ( p 0 ) และจํานวนการทดลอง n มี
คามาก (n ∞) การแจกแจงแบบนี้ยังมีประโยชนใชกับจํานวนความสําเร็จหรือเหตุการณที่สนใจ
เกิดขึ้นในชวงเวลาใดเวลาหนึ่ง เชน จํานวนผูปวยที่มาโรงพยาบาลในชวงเวลา 9.00-10.00 น. จํานวน
รถหายในเดือนมกราคม จํานวนคําที่พมพผิดตอหนา เปนตน
ิ
้ ่
การแจกแจงความนาจะเปนแบบปวซองนีจะเกียวของกับการทดลองแบบปวซองที่มี
คุณสมบัติ ดังนี้
1) จํานวนความสําเร็จที่เกิดขึนในชวงเวลาใดเวลาหนึ่ง หรือในสถานการณใดสถานการณ
้
หนึ่งเปนอิสระจากความสําเร็จที่เกิดขึ้นในชวงเวลาอื่นๆหรือสถานการณอื่นๆ
2) ความนาจะเปนที่จะพบความสําเร็จมีคานอยมาก p 0 , q 1 และความนาจะ
เปนนี้จะเปนปฏิภาคกับเวลา
ถา x คือจํานวนความสําเร็จที่ไดจากการทดลองแบบปวซอง และเปนตัวแปรสุมแบบปวซอง
ดังนั้น การแจกแจงความนาจะเปนแบบปวซองก็คือ การแจกแจงความนาจะเปนของตัวแปรสุมปว
ซองที่เปนจํานวนความสําเร็จที่เกิดขึนในชวงเวลาใดเวลาหนึ่ง หรือในสถานการณใดสถานการณ
้
หนึ่ง การแจกแจงนี้เขียนไดดวยสัญลักษณ p( x , λ) แสดงวาการแจกแจงขึ้นอยูกบ λ โดยที่ λคือ
ั
คาเฉลี่ยของความสําเร็จที่เกิดขึ้นในชวงเวลาหนึ่ง หรือสถานการณหนึ่ง ความนาจะเปนที่จะพบ
ความสําเร็จ x ครั้ง ในชวงเวลาหนึ่งหรือสถานการณหนึงคือ
่
= e -λ λ x
เมื่อ x คือ 0,1,2,…
p( x , λ)
x!
λ
= คาเฉลี่ยของความสําเร็จที่เกิดขึ้น
74. 77
e
= 2.71828
ดังนั้นการคํานวณหาความนาจะเปนโดยใชการแจกแจงแบบปวซองจะตองทราบคาเฉลี่ย
ของตัวแปรสุมแบบปวซองกอนเสมอ
เนื่องจาก p
0,q
1 ดังนั้น µ = np = λ และ σ2 = npq = λ
ตัวอยาง ถาสถิติคนตายดวยอุบัติเหตุของเมืองหนึ่งโดยเฉลี่ย วันละ 6.5 คน และเมืองนี้มีประชากร
237,000 คน จงหาความนาจะเปนที่
1) มีคนตาย 5 คน
2) ไมมีคนตายเลย
λ =
6.5
= e -λ λ x
1)
p( x , λ)
x!
p( 5 , 6.5) = (2.71828) – 6. 5 6.5 5
5!
ความนาจะเปนที่จะมีคนตาย 5 คน = 0.1450
= e -λ λ x
2)
p( x , λ)
x!
p( 0 , 6.5) = (2.71828) – 6. 5 6.5 0
0!
ความนาจะเปนที่จะไมมีคนตาย = 0.0015
เพื่อความสะดวกและรวดเร็ว นักคณิตศาสตรจึงไดสรางตารางของการแจกแจงความ
นาจะเปนของการแจกแจงแบบปวซอง โดยจะตองทราบคา x และ λ โดยเปดตารางความนาจะเปน
แบบปวซอง ในภาคผนวก
การแจกแจงของตัวแปรสุมที่ตอเนื่อง (Continuous random variable)
การแจกแจงของตัวแปรสุมที่ตอเนื่องที่สําคัญที่จะกลาวถึงในตอนนี้ ไดแก การแจกแจงแบบ
โคงปกติ การแจกแจงปกติมาตรฐาน การแจกแจงแบบที การแจกแจงแบบไคสแควร และ
การแจกแจงแบบเอฟ
ตัวแปรสุมแบบตอเนื่อง ( Continuous random variable) คาของตัวแปรสุมแบบตอเนื่อง จะมี
คาจริงในชวงที่ตอเนื่องกัน เชน น้ําหนัก สวนสูง ระยะเวลา ตัวอยางคาของน้ําหนักของนักเรียน
มัธยมศึกษา จะอยูในชวง 40-90 กิโลกรัม เขียนไดวา 40< X<90 กิโลกรัม
Sample space ของตัวแปรสุมแบบตอเนื่องจะประกอบดวยปริมาณตาง ๆ ซึ่งเปนคาที่ไดจาก
การวัด เชน คาความเร็วของรถที่วัดได คาน้ําหนักของสัตวที่วัดไดในหองทดลอง คาความสูงของ
75. 78
นักเรียนที่วดได… คาตาง ๆ เหลานี้ที่วดไดมีไดมากมายนับไมถวนจนเราไมสามารถหาคาความนาจะ
ั
ั
เปนที่จะเกิดคาใดคาหนึ่งได ตองหาเปนชวงหรือเปนพืนที่ เชน เราจะหาคาความนาจะเปนที่รถจะวิ่ง
้
ไปที่ใด ๆ ดวยความเร็ว 60 ถึง 70 กม./ชั่วโมง หาคาความนาจะเปนทีสัตวในหองทดลองจะหนัก 6.5
่
ถึง 8.5 ออนซ เปนตน
คาความนาจะเปนที่สัมพันธกับตัวแปรสุมแบบไมตอเนืองถูกกําหนดโดยแทงสี่เหลี่ยมผืนผา
่
กลาวคือสรางเปนรูปฮิสโทแกรมได ในกรณีของตัวแปรสุมแบบตอเนือง จะแทนความนาจะเปนโดย
่
ใชพื้นที่เชนกัน ดังแสดงในรูป 1 แตแทนที่จะแทนดวยแทงสี่เหลี่ยมผืนผาก็จะแทนดวยพื้นทีใตโคง
่
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
รูป1
รูป 1 ทางซายแทนการแจกแจงความนาจะเปนของตัวแปรสุมซึ่งมีคา 0, 1, 2, …, 10 และ
ความนาจะเปนที่จะไดคา 3 แสดงดวยพืนที่สวนที่แรเงา
้
รูป 1 ทางขวาแสดงคาของตัวแปรสุมแบบตอเนื่องซึ่งจะเปนคาใดก็ไดบนชวง 0-10 ความ
นาจะเปนที่จะไดคาระหวาง 3.0 กับ 4.0 แสดงดวยพื้นทีใตโคงที่แรเงาดวยสีทึบซึ่งอยูทางซายของรูป
่
และความนาจะเปนที่จะไดคา 8 ขึ้นไปแสดงดวยพื้นทีใตโคงที่แรเงาดวยสีทึบซึ่งอยูทางขวาของรูป
่
รูปโคงที่แสดงทางขวาของรูป 1 ก็คือกราฟของฟงกชันที่มีชื่อเฉพาะวา Probability density
function
พื้นที่ใตโคงระหวาง 2 คาใด ๆ a และ b (ดังรูป 2) ใชบอกคาความนาจะเปนของตัวแปรสุม
แบบตอเนื่องเปนชวงจาก a ถึง b
a b
รูป 2
คาของ Probability density function จะไมมีทางเปนลบ และพื้นทีใตโคงทั้งหมดมีคาเทากับ
่
1 เสมอ
76. 79
1. การแจกแจงแบบโคงปกติ
การแจกแจงความนาจะเปนของตัวแปรสุมแบบตอเนื่องที่สําคัญที่สุดคือการแจกแจงปกติ
(Normal distribution) กราฟของการแจกแจงปกติเรียกวา โคงปกติ (Normal curve) ซึ่งมีลักษณะ
เหมือนระฆังคว่ํา ดังรูป 3
µ
รูป 3 โคงปกติ
ขอมูลสวนใหญมักจะมีการแจกแจงเปนรูปโคงปกติ ใน ค.ศ. 1733 De Moivre เปนผูสราง
สมการทางคณิตศาสตรของโคงปกติขึ้น การแจกแจงปกตินี้ บางทีเรียกวา Gaussian distribution เพื่อ
เปนเกียรติกับ Karl Gauss (ค.ศ.1777–1855) ผูซึ่งไดสรางสมการสําหรับโคงปกติจากการศึกษา
ความคลาดเคลื่อนที่เกิดขึ้นเมื่อมีการวัดซ้ํา ๆ กัน
ตัวแปรสุม X ที่มีการแจกแจงเปนรูประฆังคว่ําดังแสดงในรูป 3 เรียกวา “ตัวแปรสุมปกติ”
(Normal random variable) สมการทางคณิตศาสตรสําหรับการแจกแจงความนาจะเปนของตัวแปร
สุมแบบตอเนือง ขึ้นอยูกับคาพารามิเตอร 2 ตัว คือ µ (Mean) และ σ (Standard deviation) ดังนั้น
่
Probability density function ของตัวแปรสุม X จึงแสดงดวย n (X ; µ, σ)
ถา X เปนตัวแปรสุมปกติดวยคาเฉลี่ย = µ และความแปรปรวน = σ2 แลว
สมการของโคงปกติคือ (Walpole, 1974 : 102)
โคงปกติ
−1 X −µ ⎞ 2
⎟
σ ⎠ ,−∞ < X < ∞
⎛
⎜
1
n( X; µ, σ) =
e 2⎝
2πσ
เมื่อ π = 3.14159… และ e = 2.71828…
หรือเขียนในอีกรูปหนึ่งคือ
N −( X−µ ) 2 / 2σ 2
e
σ 2π
เปนสวนสูงของโคง (Ordinate) ขึ้นอยูกับคา X แตละคา
เปนตัวคงที่มีคา 3.1416
เปนตัวคงที่อีกตัวหนึงมีคา 2.7183
่
Y=
เมื่อ
Y
π
e
77. 80
จากสมการโคงปกติแสดงวา โคงปกติไมใชมีเพียงรูปเดียว แตมไดหลาย ๆ รูป โดยจะมี
ี
รูปรางโดงมาก(Leptokertic)โดงปานกลาง(Mesokertic) หรือที่รูจักกันทั่วไปวาโคงปกติ (Normal
curve) หรือโคงลาด (platykertic) แตกตางกันออกไปขึนอยูกับคา µ และ σ นั่นคือโคงจะอยูตรง
้
ตําแหนงใดของแกนนอนขึ้นอยูกับคา µ และลักษณะของโคงจะโดงมากนอยเพียงใดหรือลาด
เพียงใดขึ้นอยูกับคาของ σ ถา σ มากโคงจะลาด ถา σ นอยโคงจะโดง ดังแสดงไดดวยรูปตาง ๆ
ดังนี้
σ1
σ2
µ1
µ2
รูป 4 รูปโคงปกติเมื่อ µ1 ≠ µ2
σ 1 = σ2
X
σ1
σ2
µ1 = µ2
รูป 5 รูปโคงปกติเมื่อ µ1 = µ2
σ1 < σ2
X
σ1
σ2
µ1
รูป 6 รูปโคงปกติเมื่อ µ1 ≠ µ2
σ1 < σ2
µ2
X
78. 81
รูป 4 เปนรูปโคงปกติ 2 รูปที่มีความเบี่ยงเบนมาตรฐานเทากัน แตคาเฉลี่ยไมเทากัน รูปโคง
ปกติ 2 รูปนี้มีรูปรางเหมือนกัน แตอยูคนละตําแหนงกันเพราะคาเฉลี่ยไมเทากัน นั่นคือ ถามี σ
เทากัน แต µ ไมเทากัน จะเปนโคงคนละรูป
รูป 5 เปนรูปโคงปกติ 2 รูปที่มีคาเฉลี่ยเทากันแตความเบียงเบนมาตรฐานไมเทากัน โคงปกติ
่
2 รูปนี้มีจุดกึ่งกลางอยูที่ตําแหนงเดียวกันบนแกน X แตโคงปกติที่มีคาความเบี่ยงเบนมาตรฐานสูงจะ
ต่ํากวาและแผกวางกวา นั่นคือ ถามี µ เทากัน แต σ ไมเทากัน จะเปนโคงคนละรูป โปรดจําไววา
พื้นที่ใตโคงปกติจะตองเทากับ 1 เสมอ ดังนั้นถาคาสังเกตยิ่งแตกตางกันมาก โคงก็จะยิ่งต่ําและลาด
รูป 6 แสดงรูปโคงปกติ 2 รูป ที่มีคาเฉลี่ยไมเทากันและความเบียงเบนมาตรฐานไมเทากัน
่
่
รูปโคงปกติทั้ง 2 รูปมีจุดกึ่งกลางอยูตําแหนงตางกันบนแกน X และมีรูปรางตางกันดวย นันคือ ถา µ
และ σ ไมเทากัน โคงจะเปนคนละรูป
ตัวอยางการแจกแจงปกติ 3 รูปที่มีคา µ และ σ ตางกัน
f(X)
σ=1
µ = 40
X
f(X)
σ=5
µ = 10
X
f(X)
σ=2
µ = 50
X
79. 82
สมการของโคงปกติขึ้นอยูกบคาของ µ และ σ จึงทําใหไดโคงปกติรูปรางตาง ๆ กันไปดัง
ั
แสดงในรูป 4, 5, 6 ซึ่งทําใหพื้นที่ใตโคงมีคาตาง ๆ ไปดวย ในทางปฏิบัติจะหาพืนที่ใตโคงโดยใช
้
ตารางสําเร็จในภาคผนวก
เนื่องจากวาเปนไปไมไดและไมจําเปนดวยที่จะสรางตารางหาพื้นที่ใตโคงสําหรับ µ และ σ
ที่เกิดขึ้นทุกคู จึงไดมการสรางตารางแสดงพื้นที่สําหรับการแจกแจงปกติที่มี µ = 0, σ = 1 เทานั้น
ี
ซึ่งมีชื่อเรียกเฉพาะวา Standard normal distribution สําหรับใชกับโคงปกติรูปตาง ๆ แลวหาพืนที่
้
ใตโคงปกติใด ๆ ได โดยเปลี่ยนคาของสเกลเดิมหรือ X-scale (ดังรูป 7) เปนหนวยมาตรฐาน
(Standard units) หรือคะแนนมาตรฐาน (Standard scores) หรือคะแนนซี (Z-scores) โดยใชสูตร
Z =
X −µ
σ
Z-score นี้เปนสเกลใหม ซึ่งคา Z จะบอกใหทราบวามีอยูกี่ความเบี่ยงเบนมาตรฐานที่อยู
เหนือหรือใตคาตัวกลางเลขคณิต
µ-3σ µ-2σ µ-σ
-3
-2
-1
µ
0
µ+σ µ+2σ µ+3σ
X-Scale
1
Z-Scale
2
3
รูป 7
คุณสมบัติที่สําคัญของโคงปกติ (Walpole,1974 : 103)
1. คาของฐานนิยมอยูที่ X = µ ซึ่งเปนจุดบนแกน X ที่เกิดจากการลากเสนตั้งฉากจากจุดที่
โคงสูงที่สุดลงมายังแกนนอน X
2. โคงมีลักษณะสมมาตร ถาแบงโคงนี้ตามเสนแนวตั้งตรงคาของ µ เสนแนวตั้งนี้จะแบง
พื้นที่ออกเปน 2 สวนเทา ๆ กัน
3. เสนโคงจะเขาใกลแกนนอน X ไปเรื่อย ๆ ทั้ง 2 ขาง แตไมจรดแกนนอน
4. พื้นที่ใตโคงทังหมดมีคาเทากับ 1
้
5. พื้นที่ใตโคงเกือบทั้งหมดอยูระหวาง µ - 3σ และ µ + 3σ
80. 83
การหาพื้นที่ใตโคงปกติ
พื้นที่ใตโคงปกติทั้งหมดมีคาเปน 1 หรืออาจจะทําเปนเปอรเซ็นตก็ได โดยคูณดวย 100
ในการหาพื้นที่ใตโคงจะตองหาคะแนนมาตรฐานซี (Z-score) กอน จากสูตร
X −µ
Z=
σ
เมื่อ Z
แทนคาของคะแนนมาตรฐานซี
X
แทนคาของคะแนนดิบใด ๆ ที่ตองการแปลงเปน Z
µ
แทนตัวกลางเลขคณิตของคะแนนชุด X
σ
แทนความเบี่ยงเบนมาตรฐานของคะแนนชุด X
คุณสมบัตของคะแนนมาตรฐาน Z
ิ
1. คาเฉลี่ยของคะแนนมาตรฐาน (Z) = 0
2. คะแนนมาตรฐาน Z มีคาเปนบวกและลบ
3. ความแปรปรวนของคะแนนมาตรฐาน(σ2) = 1
4. ผลบวกของคะแนนมาตรฐาน Z = 0
5. ผลบวกกําลังสองของคะแนนมาตรฐานมีคาเทากับจํานวนขอมูล ΣZ2 = N
6. การแจกแจงของคะแนนมาตรฐานเหมือนการแจกแจงของคะแนนดิบ
การแจกแจงของคะแนนมาตรฐานมีคาเฉลี่ยเลขคณิต เทากับ 0 และสวนเบี่ยงเบนมาตรฐานเทา
กับ 1 จึงทําใหสามารถนําคาคะแนนมาตรฐานมาเปรียบเทียบได
จากสูตรจะเห็นวา Z-score ก็คือคะแนนดิบที่ถูกแปลงใหเปนหนวยของความเบี่ยงเบน
มาตรฐานนั่นเอง
เพื่อจะหาวามีอยูกี่หนวยความเบียงเบนมาตรฐานที่คะแนนดิบอยูเหนือหรือใต
่
ตัวกลางเลขคณิต ถาคะแนนดิบ X อยูเหนือตัวกลางเลขคณิตหนึ่งหนวยความเบียงเบนมาตรฐานก็จะ
่
ั
มีคา Z เปน 1 ถาคะแนนดิบ X อยูใตตวกลางเลขคณิตครึ่งหนวยความเบี่ยงเบนมาตรฐานคะแนนดิบ
X ตัวนี้กจะมีคา Z เปน –0.5 เปนตน
็
ขั้นตอนในการคํานวณคะแนนมาตรฐานซี มีดังนี้
ขั้นที่ 1 หาคาตัวกลางเลขคณิต (µ) และความเบียงเบนมาตรฐาน (σ) ของ
่
คะแนนชุด X
ขั้นที่ 2 เอาคะแนนดิบ X ตั้งลบดวย µ (ตองเอา X เปนตัวตั้งเสมอไมวา X จะมี
คามากหรือนอยกวา µ ก็ตาม)
ขั้นที่ 3 เอา σ หารคาในขั้นที่ 2
81. 84
ตัวอยางที่ 1
จากการวัดความถนัดของนิสิตชั้นปที่ 1 ของมหาวิทยาลัยแหงหนึ่ง พบวาหาตัวกลางเลข
คณิต µ ได 48 และหาความเบี่ยงเบนมาตรฐาน σ ได 8 ถา X เปน 43 จะเทากับ Z เทาใด
Z =
X −µ
σ
43 − 48
8
= −0 . 625
=
นั่นคือ คะแนนดิบ X = 43 อยูใตตวกลางเลขคณิต 0.625 หนวยความเบี่ยงเบนมาตรฐาน
ั
้
่
ขอสังเกต บางครั้งโจทยอาจจะไมบอกคา µ และ σ แตบอกคะแนนทังชุดใหกอนทีจะหา Z
จะตองหา µ และ σ กอน โดยใชสูตรตามที่กลาวมาแลว
จาก Z-score ที่คํานวณได นําไปหาพืนทีใตโคงปกติในลักษณะตาง ๆ ได โดยใชตารางหา
้ ่
พื้นที่ใตโคงปกติ ซึ่งอยูในภาคผนวก
ตัวอยางที่ 2
ผลการสอบวิชาสถิติของนิสิตกลุมหนึ่ง หาตัวกลางเลขคณิต (µ) ได 16 และความเบี่ยงเบน
มาตรฐาน (σ) ได 5 นิสิต ก. สอบได 24.65 คะแนน จงหาพื้นที่ที่อยูระหวางตัวกลางเลขคณิตกับ
คะแนน 24.65
ในการหาพื้นที่ใตโคง จําเปนตองใช Z-score เพราะฉะนั้นจะตองแปลงคะแนนดิบ (X) ที่
กําหนดใหเปน Z-score กอนโดยใชสูตร
X −µ
σ
24.65 − 16
Z=
5
= 1.73
Z=
ที่ Z-score เทากับ 1.73 จากตาราง หาพืนที่ใตโคงได 0.4582 หรือ 45.82% ซึ่งเปนพื้นที่
้
ระหวางตัวกลางเลขคณิตกับคะแนนของนิสิต ก. เนื่องจากพื้นที่ใตโคงทั้งหมด ทางซายของตัวกลาง
เลขคณิตมีคา 50% เพราะฉะนั้นสามารถสรุปไดอีกอยางหนึ่งวมพื้นที่ใตโคงทั้งหมดอยู 95.82% (50%
ี
+ 45.82%) ที่อยูใตคะแนน 24.65 ซึ่งแสดงวานิสิต ก. อยูในตําแหนงเปอรเซ็นตไทล (Percentile rank)
ที่ 95.82 นั่นคือที่ Z = 1.73 แปลไดวามีนิสตที่ไดคะแนนต่ํากวานิสิต ก. อยู 96 คนใน 100 คน
ิ
82. 85
.4582
0
1.73
รูป 8 แสดงการหาพื้นที่ใตโคงระหวางตัวกลางเลขคณิตกับคะแนน X
ถานิสิต ข. สอบไดคะแนน 7.35 แปลงเปน Z-score ไดดังนี้
7.35 − 16
Z=
5
= −1.73
ถา Z ติดลบก็ใช ตาราง เชนเดียวกันกับ Z เปนบวก เพียงแตอยูคนละขางกันเทานั้น ดังนั้น
พื้นที่ใตโคงทีอยูระหวางตัวเลขคณิตกับคะแนน 7.35 จึงมีคาเทากับ 45.82% ถาจะหาพื้นที่ใตโคงทีอยู
่
่
ใตคะแนน 7.35 ทําได 2 วิธีคือ วิธีหนึ่งเปดจาก ตาราง ซึ่งจะไดพนทีใตโคง 0.0418 หรือ 4.18% อีก
ื้ ่
วิธีหนึ่งคือเอา 45.82% ลบออกจาก 50% จะได 4.18% แสดงวานิสิต ข. อยูในตําแหนงเปอรเซ็นตไทล
ที่ 4.18
สําหรับความสัมพันธระหวาง Raw score, Z-score และ Percentile rank ไดแสดงใหเห็นดัง
รูป 9 โดยให
Raw score
Z-score
Percentile rank
20
-3
0.13
30
-2
2.28
40
-1
15.87
50
0
50.00
60
+1
84.13
70
+2
97.72
80
+3
99.87
รูป 9 ความสัมพันธระหวาง Raw score, Z-score และ Percentile rank ของรูปที่มีการแจกแจง
โคงปกติ ซึ่งมี µ = 50 และ σ = 10
เนื่องจากคา Z-SCORE มีคาติดลบและเปนทศนิยม นักการศึกษาจึงนิยมแปลงคะแนนZ ใหมScale
ี
ใหญขึ้น คาติดลบหรือทศนิยมจะไดหมดไป โดยแปลงใหเปนคะแนน T โดยที่
83. 86
T = 10Z + 50
จากตัวอยางที่ 2 ถาตองการหาคาคะแนน T ของนิสิต ก. ซึ่งไดคะแนน Z =1.73 หาได ดังนี้
T = (10 ×1.73) + 50
= 67.3
การใชการแจกแจงปกติมาตรฐานประมาณคาการแจกแจงแบบทวินาม
∞ ) สามารถใชการแจกแจง
เมื่อจํานวนครั้งของการทดลองทวินามมีขนาดใหญ ( n
ปกติมาตรฐานประมาณคาการแจกแจงทวินามได
ตัวอยาง จงหาความนาจะเปนที่จะไดหว 4 ครั้งจากการโยนเหรียญ 8 ครั้ง
ั
n = 8 x = 4 p = 0.5 q = 0.5
เปดตารางความนาจะเปนแบบทวินามในภาคผนวก ได p = 0.2734
np = 4 npq = 2
เปรียบเทียบกับการประมาณคาแบบโคงปกติมาตรฐาน
p ( 4,8,0.5) = p ( 3.5 – 4 < z < 4.5 - 4 )
2
2
=
p ( -.354 < z < .354 ) เปดตารางไดพื้นที่ = .1368+.1368
ความนาจะเปนที่จะไดหว 4 ครั้ง = .2736 ซึ่งใกลเคียงกับการแจกแจงทวินามมาก
ั
2. การแจกแจงแบบ ที (t-distribution)
เมื่อเริ่มแรก ไดมีการใช Z- Distribution หรือ Standard Normal Distribution อยางกวางขวาง
ในประเทศยุโรป จนกระทั่งมีวิศวกร ชาวไอรแลนด คนหนึ่งที่ทํางานในโรงงานผลิตเบียร ได
สังเกตเห็นวา การที่เขาเก็บตัวอยางมาแคจํานวนไมมากนั้น ทําใหเขาได Distribution ที่ไมตรงกับ
Standard normal distribution เสมอ และถาเขาเพิ่มหรือลดจํานวนตัวอยางที่สุมมา Distribution ก็จะ
แปรเปลี่ยนไป ดังนั้น จํานวนตัวอยางจึงมีผลตอ t-Distribution ดวยนอกจาก คากลางและคาสวน
เบี่ยงเบนมาตรฐาน แตเมื่อตองการอธิบายถึงจํานวนตัวอยาง เราจะเรียกวา Degree of freedom แทน
เชนเดียวกับ Z-Score เมื่อเราเก็บตัวอยางมา เราก็จะหา T-Score โดยใชสูตร ดังตอไปนี้
คุณสมบัติของ t-Distribution จะเหมือนกันกับ Standard normal distribution เกือบทุก
ประการ เพียงแตสวนปลาย (Tail) ของ t-Distribution จะมีคา Probability ที่สูงกวา เมื่อเทียบจุดที่
หางจากคากลางที่เทากัน แตเมื่อ degree of freedom เขาหา Infinite นั้น t-Distribution จะมีคุณสมบัติ
เขาใกล Standard normal distribution เชนกัน
84. 87
รูป 10 t -Distribution เพื่อใหมองเห็นภาพ ผลของ degree of freedom และขอแตกตางของปลาย (Tail)
ดังนั้นเมื่อเราทําการศึกษาตัวอยาง คาที่เราจําเปนจะตองรู จึงเปนคา t ไมใช Z อีกตอไป
เชนเดียวกับ Z-Distribution จะมีตาราง T-Table สําหรับ t-Distribution เหมือนกัน เวลาเราเขียน คา t
เราจึงจําเปนตองระบุ α และ degree of freedom ดวยเสมอ โดยแทนดวย ( k ) เชน t α , k
เนื่องจาก t - Distribution จะมีลักษณะสมมาตรรอบๆ ศูนย (0) ดังนั้น คา t1- α จึงเทากับ -t α
t - Distribution ไดถูกนําไปใชเปนเครื่องมือในการ ทดสอบสมมติฐาน ความแตกตางของคา
กลางของตัวอยาง ดวย เราจึงเรียก วิธีที่เรานําไปใชดังกลาวตามชื่อ t-Distribution ดวยเชนกันวา t-test
เปนตนวา 1-Sample t-test หมายถึงการทดสอบคากลางของตัวอยางกลุมเดียวกับคาที่กําหนด หรือ
2-Sample t-test หมายถึง การทดสอบความแตกตางของคากลางของตัวอยางสองกลุม
คุณสมบัติสําคัญของการแจกแจง ที
1) โคงการแจกแจงมีลักษณะสมมาตรและระฆังคว่ํา มีศูนยกลางอยูที่ t =0
2) คา mean = mode = median คือ 0
3) ความนาจะเปนสะสม หรือพื้นที่ใตโคง = 1
4) ความแปรปรวน= df / df –2
5) การแจกแจงที จะมีคาพิสัยตั้งแต - ∞ - +∞
6) การแจกแจง t จะเขาใกลการแจกแจงปกติมาตรฐานเมื่อ df มีคามาก
เนื่องจากการใชคาการแจกแจงปกติมาตรฐานประมาณคาหรือทดสอบสมมติฐานเกียวกับ
่
คาเฉลี่ยเลขคณิต (µ)จําเปนตองทราบความแปรปรวนของประชากรกอนจึงใชสถิติ Z แตในกรณีที่
ไมทราบคาความแปรปรวนของประชากรกลุมตัวอยางจะตองมีขนาดใหญจึงจะใชความแปรปรวน
ของกลุมตัวอยางประมาณคาความแปรปรวนของประชากรได จึงยังสามารถใชสถิติ Z แตในทาง
85. 88
ปฏิบัติมักไมทราบความแปรปรวนของประชากรละกลุมตัวอยางทีใชมขนาดเล็ก จึงตองใชการแจก
่ ี
แจงที นอกจากนี้การแจกแจงทีก็นําไปใชกับกลุมตัวอยางขนาดใหญไดเพราะการแจกแจงที จะเขา
ใกลการแจกแจงปกติมาตรฐานที่มีคาเฉลี่ยเลขคณิต (µ) = 0 ความแปรปรวน = 1 เมื่อองศาอิสระเขา
ใกลคาอนันต
3. การแจกแจงแบบไคสแควร (χ2- distribution)
ไคสแคว (Chi-square) ถือไดวาเปน Sampling distribution ที่ถูกนําไปประยุกตใชในการ
ทดสอบสมมติฐานมากที่สุดอีกชนิดหนึ่ง พื้นฐานของ Chi-square มีสมการดังตอไปนี้
เมื่อ xi คื่อคาใดๆ โดยที่ i = 1,2,3...u และเปนขอมูลที่มีการกระจายแบบ Normal
distribution และคาแตละคาตองเปนอิสระตอกันดวย ซึ่งจากสมการคา Chi-square ก็เทากับ
Z2 นั่นเอง การแจกแจงแบบไคสแควร ไดมาจากการแจกแจงแบบโคงปกติ มีหลายรูปแบบ แตละ
รูปแบบจะกําหนดได ดวยคา df
χ 2 = Z2
χ 2 = Z2 + Z 2
เมื่อ df = 1
เมื่อ df = 2
ได รูปการแจกแจงใหม
ได รูปการแจกแจงใหม
รูป 11 การแจกแจงแบบไคสแควร ตามคาองศาอิสระ(df)
แกน Y คือ คาฟงกชันของ X หรือ f(X) สวนในแกน X คือคา Chi-square
จากรูป11 แสดงใหเห็นถึงความสัมพันธกันระหวาง Degree of freedom กับลักษณะของ
Distribution แตลักษณะของ Chi-square distribution ที่สําคัญคือ กราฟจะตองเบขวาเสมอ แตเมื่อใดก็
86. 89
ตามที่เพิ่มจํานวน Degree of freedom ความเบนี้จะลดลงเรื่อย และจะเขาหา Normal distribution ใน
ที่สุด
การแจกแจงแบบไคสแควรถือวาเปน distribution free เพราะการนําไปใชไมตองมีขอตกลง
เบื้องตนเกี่ยวกับการแจกแจงของประชากร การแจกแจงแบบไคสแควรจึงมีประโยชนมากมาย
ลักษณะพื้นที่ใตกราฟของ Chi-square distribution จะถูกนําไปเปนคาทดสอบ สําหรับขอมูลทางสถิติ
ประเภทที่สามารถจัดเปนหมวดหมูได (Attribute data ) และใชทดสอบคาความแปรปรวนแบบ
ประชากรเดี่ยว (One-variation test) ทดสอบความสัมพันธระหวางตัวแปร หรือทดสอบความเปน
อิสระ (Test of independence) การทดสอบภาวะรูปสนิทดี (Goodness of fit) ทดสอบวาสิ่งที่กําลัง
ศึกษามีการแจกแจงปกติหรือไม ดังนั้นจึงจัดไดวา มีความจําเปนที่เราจะตองเขาใจถึงคุณสมบัติของ
Chi-square อยางดี กอนนําไปใชเปนตัวทดสอบ
คุณสมบัติที่สําคัญของการแจกแจงแบบไคสแควร
1. รูปรางเบไปทางดานบวก ขึนอยูกับdf เมื่อdf เขาใกลอนันต จะสมมาตร
้
2. การแจกแจงไคสแควรไมมคาติดลบ เพราะเปนผลรวมกําลังสอง จึงมีคาพิสัย ตั้งแต 0 ถึง
ี
อนันต
3. พื้นที่ใตโคงมีคาเทากับ 1
4. ความสูงของโคงการแจกแจง( ordinate) จะมีคาใกล 0 เมื่อ χ2 เขาใกล∞
4. การแจกแจงแบบเอฟ (F – distribution)
การแจกแจงแบบเอฟ เปน Sampling distribution อีกชนิดหนึ่งที่มีการประยุกตใช
คอนขางมากในการทดสอบคาความแปรปรวนแบบสองประชากร (Two-variation test) พื้นฐานของ
F-Distribution คือเปนสัดสวนของคาความผันแปรของสองขอมูล โดยมีสมการพื้นฐานดังนี้
โดยที่ s1 > s2
เมื่อสมการพื้นฐานของ F-distribution เกิดจากประชากรสองตัว ดังนันตัวแปรที่สําคัญคือ
้
Degree of freedom จึงตองคิดของทั้งสองประชากร ดังนั้น df1 = n1-1 และ df 2 = n2-1
87. 90
รูป12 การแจกแจงแบบเอฟ
แกน Y คือ คาฟงกชันของ X หรือ f(X) สวนในแกน X คือคา F
จากกราฟลักษณะการกระจายตัวของ F จะเปนกราฟเบขวาตลอด ซึ่งเปนลักษณะเดียวกันกับ
Chi-square distribution และคา Degree of freedom มีผลตอลักษณะการกระจายตัว F
การแจกแจงแบบเอฟ ไดมาจากการแจกแจงโคงปกติ โดยนําความแปรปรวนของ 2 กลุมมา
เปรียบเทียบกัน
σ21 จะไดความสัมพันธ
กลุมที่ 1 µ1
σ12 χ2df1
S 12 =
n1 -1
σ22 จะไดความสัมพันธ
กลุมที่ 2 µ2
σ22 χ2df2
S 22 =
n2 –1
χ2df1/ n1 –1 โดยมี df 1 = n1 –1 และ df 2 = n 2–1
F
=
χ2df2/ n2 -1
ตารางการแจกแจงแบบเอฟถูกนําไปใชประโยชนโดยเปนคาทดสอบในการเปรียบเทียบ
ความแตกตางคาเฉลี่ยเลขคณิตของกลุมตัวอยางมากกวา 2 กลุมขึ้นไป ถาใชวิธีเปรียบเทียบกลุม
ตัวอยาง 2 กลุมจะทําใหเสียเวลาเพราะตองทดสอบทีละคู นอกจากนี้ยังเพิ่มความคลาดเคลื่อนชนิดที่
1 มากกวาที่กาหนดดวย ดังนั้นจึงควรใชเทคนิคที่เรียกวาการวิเคราะหความแปรปรวน (Analysis of
ํ
variance) ซึ่งตองใชสถิติ F ทดสอบนัยสําคัญเพื่อสรุปอางอิง นอกจากนียังสามารถทดสอบและ
้
88. 91
ประมาณคาความแตกตางระหวางความแปรปรวนของประชากร 2 กลุม และการทดสอบ
สัมประสิทธิ์สหสัมพันธพหุคูณ
คุณสมบัติที่สําคัญของการแจกแจงแบบเอฟ
1. การแจกแจงไมสมมาตร เบไปทางบวก เมื่อ df เขาใกลอนันต จะสมมาตร
2. ไมมีคาลบ มีคาพิสัย 0- อนันต
3. พื้นที่ใตโคง มีคา =1
ขอตกลงเบื้องตนของการแจกแจงแบบเอฟ
1. F - distribution กลุมตัวอยางจะตองสุมมาจากประชากรที่มีการแจกแจงปกติ
2. ความแปรปรวนของประชากรในแตละกลุมจะตองเทากัน
3. คาประมาณความแปรปรวน S12 และ S22 จะตองมาจากตัวแปรสุมอิสระ (random variable)
นั่นคือกลุมตัวอยางจะตองไดมาโดยวิธีสุม
การแจกแจงความนาจะเปนของสถิติทดสอบแบบตางๆ(Sampling Distribution of statistics)
การแจกแจงความนาจะเปนของสถิติทดสอบแบบตางๆ หมายถึงการแจกแจงความนาจะเปน
ของคาสถิติไดจากกลุมตัวอยางสุม ซึ่งจะบอกใหทราบวาคาสถิติที่ไดจากกลุมตัวอยางนั้นมีการแปร
ผันไปเชนใดบาง เพราะคาสถิติเปนตัวแปรสุม กลุมตัวอยางกลุมหนึ่งก็จะมีคาคาหนึ่งแตกตางกันไป
การมีความรูความเขาใจเกียวกับรูปรางลักษณะการแจกแจงของคาสถิติของกลุมตัวอยาง มีความจํา
่
เปนมากสําหรับวิชาสถิติ โดยเฉพาะในเรื่องการประมาณคาและการทดสอบสมมติฐาน การแจกแจง
ของคาสถิติที่ควรรูจักไดแก
1. การแจกแจงคาเฉลี่ยเลขคณิตของกลุมตัวอยาง
2. การแจกแจงคาสัดสวนของกลุมตัวอยาง
3. การแจกแจงคาความแปรปรวนของกลุมตัวอยาง
1. การแจกแจงคาเฉลี่ยเลขคณิตของกลุมตัวอยาง (Sample Distribution of Sample mean)
เมื่อมีการสุมตัวอยางจํานวน n จากประชากรที่มีคาเฉลี่ยเลขคณิต = µ ความแปรปรวน
=σ2 ตามทฤษฎี Central limit Theorem การแจกแจงของคาเฉลี่ยเลขคณิตของกลุมตัวอยาง จะมี
คาเฉลี่ย E(X) = µ x = µ
และความแปรปรวน (σ x 2) = σ2/ n เมื่อประชากรมีขนาดใหญเปน infinite population สุมตัวอยาง
ประชากรแบบแทนที่
และความแปรปรวน(σx2) = σ2 ×N-n เมื่อประชากรมีขนาดเล็กเปน finite population สุม
n × N-1
ตัวอยางประชากรแบบไมแทนที่
89. 92
การแจกแจงความนาจะเปนของคาเฉลียเลขคณิตของกลุมตัวอยาง มีคณลักษณะ ดังนี้
่
ุ
1) ถาประชากรมีขนาดใหญ และมีการแจกแจงปกติ จะทําใหการแจกแจงของคาเฉลี่ยของ
กลุมตัวอยางมีการแจกแจงปกติ
2) ถาประชากรมีขนาดใหญ แตไมมีการแจกแจงปกติ จะทําใหการแจกแจงของคาเฉลี่ย
ของกลุมตัวอยางเขาใกลการแจกแจงปกติ เมื่อกลุมตัวอยางมีขนาดใหญ
3) คาเฉลี่ยเลขคณิตของการแจกแจงคาเฉลี่ย จะเทากับ คาเฉลี่ยเลขคณิตของประชากร
µx = µ
4) คาสวนเบี่ยงเบนมาตรฐานของการแจกแจงคาเฉลี่ยหรือคาความคลาดเคลื่อนมาตรฐาน
คือ σ x = σ/ n เมื่อประชากรมีขนาดใหญเปน infinite population สุมตัวอยาง
ประชากรแบบแทนที่
และคาสวนเบียงเบนมาตรฐานของการแจกแจงคาเฉลี่ย คือ σ x = σ N − n
่
n
N −1
เมื่อประชากรมีขนาดเล็กเปน finite population สุมตัวอยางประชากรแบบไมแทนที่
ในการหาความนาจะเปนของประชากรและตัวอยางประชากรที่มีขนาดใหญ สามารถนํา
ตารางNormal Area Table มาใช โดยคาความนาจะเปนก็คอพื้นที่ใตโคงการแจกแจงปกตินั่นเอง
ื
เมื่อมีการแจกแจงปกติ คาเฉลี่ยเลขคณิต = 0 ความแปรปรวน = 1
คา Z = X - µ
σ/ n
แลวนําไปเปดคาความนาจะเปนหรือพื้นทีจากตารางความนาจะเปนแบบปกติ
่
ดังนั้น การคํานวณหาความนาจะเปนที่ X จะมีคานอยกวา a ที่กําหนดใหหรือไมหาไดจากสมการ
P (X< a ) = P (Z < a - µ ) = P( Z < a - µ )
σx
σ/ n
2. การแจกแจงคาสัดสวนของกลุมตัวอยาง
ในบางครั้งประชากรที่สนใจอาจเปนขอความหรือเปนขอมูลเชิงคุณภาพ โดยแบงประชากร
ออกเปน 2 พวกหรือ 2 ลักษณะ เชน นิสิตชาย (n1) และนิสิตหญิง(n2) โดยที่ n อนิสิตทั้งหมด
π คือพารามิเตอรที่แสดงสัดสวนของประชากร เชน สัดสวนของนิสตหญิง = n2/n
ิ
เมื่อตองการจะประมาณคาหรือทดสอบสมมติฐานที่เกี่ยวกับ π จะตองเลือกกลุมตัวอยาง
เพื่อหาคาสัดสวนของกลุมตัวอยาง(P)แลวใชสัดสวนของกลุมตัวอยางเปนตัวประมาณคาหรือ
ทดสอบสมมติฐานเกียวกับ π
่
90. 93
จากคาเฉลี่ยและความแปรปรวนแบบทวินาม
E(X) = Σ X. p(X) = nπ
Var (X) = E( X - µ )2
= nπ(1- π)
โดยที่ X คือความสําเร็จที่เกิดขึ้น
ถา P คือสัดสวนของการเกิดความสําเร็จในกลุมตัวอยาง
P
= X/n
E(P) = E( X / n ) = 1/n . E(X)
= 1/n . n π
= π
VAR (P)
= VAR (X / n)
= 1/n2 n.π (1- π)
กรณี n มีขนาดใหญ
= π (1- π)
n
กรณี n มีขนาดเล็ก
VAR (P)
= π ( 1- π) N-n
n
N-1
เมื่อ Sample proportion มีการแจกแจงปกติหรือเขาใกลการแจกแจงปกติสามารถคํานวณ
ความนาจะเปนที่สัดสวนของกลุมตัวอยางจะเทากับหรือนอยกวาคาที่กาหนดใหได เนื่องจาก
ํ
Z = P- π
σp
σp =
π (1 − π )( N − n)
n( N − 1)
(P < a ) = P ( Z < a - π
)
π (1 − π )( N − n)
n( N − 1)
3. การแจกแจงคาความแปรปรวนของกลุมตัวอยาง
เมื่อมีการสุมตัวอยางประชากร n มาจากประชากรที่มีการแจกแจงปกติ การแจกแจงความ
แปรปรวนของกลุมตัวอยาง(S2) จะเปนการแจกแจงปกติ โดยมี
คาเฉลี่ยของความแปรปรวน
µ s 2 = σ2(n-1)/n
ความแปรปรวนของคาความแปรปรวน σ2 s 2 = σ2√ 2/n
เมื่อ n มีขนาดใหญ
ถา n มีขนาดเล็ก การแจกแจงความแปรปรวนของกลุมตัวอยางไมเปนการแจกแจงปกติ แต
มีการแจกแจงแบบไคสแควร โดยมีองศาอิสระ = n-1
91. 94
ถาองศาอิสระ = 1
ถาองศาอิสระ = n-1
χ2(1)
χ2(n-1)
= Z2
= Σ (n-1) S2
σ2
การคํานวณหาความนาจะเปนที่จะเลือกกลุมตัวอยางซึ่งมี S2 ตามที่กําหนดไว คือการหาพื้นที่
ใตโคงการแจกแจงไคสแควรนั่นเอง จากสมการ
P (S2 > a ) = P (χ2 > ∑ (n-1) a )
σ2
การเลือกกลุมตัวอยางและขนาดของกลุมตัวอยาง
การเลือกกลุมตัวอยางมีความจําเปนอยางยิงในทางสถิติอางอิง ทั้งนี้เนื่องจากการเก็บขอมูล
่
กับประชากรทุกหนวยอาจทําใหเสียเวลาและคาใชจายที่สูงมากและบางครั้งเปนเรื่องที่ตองตัดสินใจ
ภายในเวลาจํากัด การเลือกศึกษาเฉพาะบางสวนของประชากรจึงเปนเรื่องที่มีความจําเปน เรียกวา
กลุมตัวอยาง ดังนั้นกลุมตัวอยาง จึงเปนสวนหนึ่งของประชากรทีนํามาศึกษาซึ่งเปนตัวแทนของ
่
ี
ประชากร การที่กลุมตัวอยางจะเปนตัวแทนที่ดของประชากรเพื่อการอางอิงไปยังประชากรอยาง
นาเชื่อถือไดนน จะตองมีการเลือกตัวอยางและขนาดตัวอยางที่เหมาะสม ซึ่งจะตองอาศัยสถิติเขามา
ั้
ชวยในการสุมตัวอยางและการกําหนดขนาดของกลุมตัวอยาง
ประเภทของการเลือกกลุมตัวอยาง
วิธีการเลือกตัวอยางแบงเปน 2 ประเภทใหญๆ คือ
1. การเลือกตัวอยางโดยไมใชความนาจะเปน ( Nonprobability sampling )
เปนการเลือกตัวอยางโดยไมคํานึงวาตัวอยางแตละหนวยมีโอกาสถูกเลือกมากนอยเทาไร
ทําใหไมทราบความนาจะเปนที่แตละหนวยในประชากรจะถูกเลือก การเลือกกลุมตัวอยางแบบนี้ไม
สามารถนําผลที่ไดอางอิงไปยังประชากรได
แตมความสะดวกและประหยัดเวลาและคาใชจาย
ี
มากกวา ซึ่งสามารถทําไดหลายแบบ ดังนี้
1.1 การเลือกกลุมตัวอยางแบบบังเอิญ (Accidental Sampling) เปนการเลือกกลุมตัวอยาง
เพื่อใหไดจํานวนตามตองการโดยไมมีหลักเกณฑ กลุมตัวอยางจะเปนใครก็ไดที่สามารถใหขอมูลได
1.2 การเลือกกลุมตัวอยางแบบโควตา (Quota Sampling) เปนการเลือกกลุมตัวอยางโดย
คํานึงถึงสัดสวนองคประกอบของประชากร เชนเมื่อตองการกลุมตัวอยาง 100 คน ก็แบงเปนเพศชาย
50 คน หญิง 50 คน แลวก็เลือกแบบบังเอิญ คือเจอใครก็เลือกจนครบตามจํานวนที่ตองการ
1.3 การเลือกกลุมตัวอยางแบบเจาะจง (Purposive Sampling) เปนการเลือกกลุมตัวอยาง
โดยพิจารณาจากการตัดสินใจของผูวิจัยเอง ลักษณะของกลุมที่เลือกเปนไปตามวัตถุประสงคของการ
วิจัย การเลือกกลุมตัวอยางแบบเจาะจงตองอาศัยความรอบรู ความชํานาญและประสบการณในเรือง
่
นั้นๆของผูทําวิจัย การเลือกกลุมตัวอยางแบบนี้มีชื่อเรียกอีกอยางวา Judgement Sampling
92. 95
2. การเลือกตัวอยางโดยใชความนาจะเปน (Probability Sampling)
เปนการเลือกตัวอยางโดยสามารถกําหนดโอกาสที่หนวยตัวอยางแตละหนวยถูกเลือก
ทําใหทราบความนาจะเปนทีแตละหนวยในประชากรจะถูกเลือก
่
การเลือกกลุมตัวอยางแบบนี้
สามารถนําผลที่ไดอางอิงไปยังประชากรได สามารถทําไดหลายแบบ ดังนี้
2.1 การสุมตัวอยางแบบงาย (Simple Random Sampling) เปนการสุมตัวอยางโดยถือวา
ทุกๆหนวยหรือทุกๆสมาชิกในประชากรมีโอกาสจะถูกเลือกเทาๆกัน การสุมวิธีนี้จะตองมีรายชื่อ
ประชากรทั้งหมดและมีการใหเลขกํากับ เทคนิคการสุมตัวอยางแบบงายเปนเทคนิควิธีพื้นฐานของ
การสุมตัวอยางโดยทั่วไป วิธีการอาจใชวิธีการจับสลากโดยทํารายชื่อประชากรทั้งหมด หรือใช
ตารางเลขสุม (Table of random number) แตวิธีการสุมตัวอยางแบบงายนั้น จะใชไมไดหรือไม
เหมาะสมถารายชื่อของสมาชิกทุกหนวยในกลุมประชากรไมมีหรือมีไมครบ
วิธีการจับสลาก โดยทําสลากแบบเดียวกันมีหมายเลขกํากับตามหนวยยอยของประชากร
ตั้งแตเลข 1 ถึงเลขสุดทายซึ่งเทากับจํานวนประชากร แลวทําการสุมจับสลากขึ้นมาทีละใบ จนครบ
ตามขนาดของกลุมตัวอยางทีตองการ
่
วิธีการใชตารางเลขสุม โดยมีบัญชีรายชื่อของทุกหนวยยอยของประชากร กําหนดหมายเลข
ประจําหนวยยอยของประชากร แลวกําหนดกฎเกณฑการใชตารางเลขสุม เชน สุมหลัก (Column)
และสุมแถว(Row) ของตัวเลขเริ่มตน แลวอานจากซายไปขวา เมื่อจบแถวใหขึ้นแถวใหม ถาได
หมายเลขซ้ําตองตัดออก จนไดจํานวนครบตามที่ตองการ หรือใชตารางเลขสุมนี้จะสรางขึ้นจากการ
สุมโดยเครื่องคอมพิวเตอร
2.2 การสุมตัวอยางแบบเปนระบบ (Systematic Sampling) เปนการสุมตัวอยางโดยมีรายชื่อ
ของทุกหนวยประชากรมาเรียงเปนระบบตามบัญชีเรียกชือ การสุมจะแบงประชากรออกเปนชวงๆที่
่
เทากันอาจใชชวงจากสัดสวนของขนาดกลุมตัวอยางและประชากร แลวสุมประชากรหนวยแรก สวน
หนวยตอๆไปนับจากชวงสัดสวนที่คํานวณไว เชน ตองการสุมนิสิต250คน จากนิสิตทั้งหมด 3000
คน ดังนั้นจึงสุมทุกๆ 12 คน เอามา 1 คน สมมติเมื่อสุมผูที่ตกเปนตัวอยางคนแรก ไดหมายเลข 0005
คนที่สองไดแกหมายเลข 0017 คนที่สามไดแกหมายเลข 0029 และคนตอๆไปจะไดหมายเลข 0041
,0053,0065,…2993 จนครบ 250 คน
การสุมตัวอยางแบบเปนระบบนี้ตางจากการสุมแบบงายที่วา สมาชิกแตละหนวยที่ไดรับ
เลือกไมไดเปนอิสระตอกันอยางแทจริงเหมือนกับการสุมแบบงาย หลังจากสมาชิกคนแรกไดรับ
้
เลือกแลว คนตอ ๆ ไปก็เทากับไดรับเลือกโดยอัตโนมัติ การสุมตัวอยางแบบนีจะใชไดผลดีเมื่อ
รายชื่อของสมาชิกไมไดจัดอยูในลักษณะทีเ่ ปนแนวโนมเรียงจากมากไปหานอย หรือนอยไปหามาก
รายชื่อสมาชิกในกลุมประชากรนั้นจะตองจัดเรียงลําดับโดยการสุม
93. 96
2.3 การสุมตัวอยางแบบแบงชั้นภูมิ (Stratified Sampling) คือ การสุมตัวอยางชนิดที่
แบง กลุมประชากรออกเปนชั้นยอย ๆ (Strata) เสียกอนบนพื้นฐานของระดับของตัวแปรที่สําคัญที่
สงผลกระทบตอตัวแปรตาม โดยมีหลักในการจัดแบงชั้นภูมิใหภายในชั้นภูมิแตละชั้นมีความเปน
เอกพันธ (Homogeneous) หรือมีลักษณะที่เหมือนกันใหมากที่สุดเทาที่จะทําได แตระหวางชันภูมให
้ ิ
ิ
มีความเปนวิวธพันธ (Heterogeneous) หรือมีความแตกตางกันใหมากที่สุดเทาที่จะทําได และ
หลังจากที่จดแบงชั้นภูมิเรียบรอยแลวจึงสุมตัวอยางอยางงายจากแตละชันภูมิ ลักษณะการจัดชันภูมิ
ั
้
้
อาจจะแสดงโดยใชแผนภาพประกอบดังนี้
วัตถุประสงคหลักของการสุมตัวอยางแบบแบงเปนชั้นภูมคือ เพื่อใหไดกลุมตัวอยางทีมี
ิ
่
องคประกอบของลักษณะตาง ๆ ใกลเคียงกับกลุมประชากร และใหไดกลุมตัวอยางที่สามารถ
ตอบสนองวัตถุประสงคของการวิจยได
ั
2.4 การสุมตัวอยางแบบกลุม (Cluster Sampling) คือวิธีการสุมตัวอยางที่หนวยของกลุมคือ
กลุมของสมาชิกของกลุมประชากร ไมใชสมาชิกรายหนวยเหมือนกับการสุมทั้ง 3 วิธีดังกลาวขางตน
สวนใหญเปนการสุมตัวอยางประชากรจากพื้นที่ตามจํานวนที่ตองการ แลวศึกษาทุกหนวยประชากร
ในกลุมพื้นทีนนๆ หรือจะทําการสุมตอเปนลําดับขั้นมากกวา 1 ระดับ โดยอาจแบงพืนที่จากภาค เปน
่ ั้
้
จังหวัด จาก จังหวัดเปนอําเภอ และเรื่อยไปจนถึงหมูบาน จุดเดนของการสุมตัวอยางแบบกลุม ก็คือ
ชวยลดคาใชจายในการสุม แตจุดดอยของการสุมแบบกลุม ก็คือ ความคลาดเคลื่อนในการประมาณ
คาพารามิเตอรของกลุมประชากรจะสูงกวาการสุมตัวอยางแบบงาย
และการคํานวณคาความ
แปรปรวนของขอมูลจะยุงยากกวาการสุมตัวอยางแบบงาย การสุมตัวอยางแบบกลุมนั้น เหมาะสมที่
จะใชในกรณีที่คาใชจาย ในการสุมตัวอยางเปนรายหนวยมีคาสูงมากจึงตองใชการสุมแบบกลุมเพื่อ
94. 97
ลดคาใชจายโดยมีหลักการดังนี้
1. ใหสมาชิกภายในกลุมแตละกลุมมีลักษณะของความเปนวิวิธพันธ หรือมีลักษณะ
หลากหลายโดยรวมลักษณะตาง ๆ ที่สําคัญของประชากรไวครบถวนภายในกลุมแตละกลุมถารวม
ลักษณะสําคัญไวไดมากเทาไรจะยิ่งทําใหความคลาดเคลื่อนในการประมาณคาของกลุมประชากรลด
นอยลง
2. ใหระหวางกลุมมีลักษณะเปนเอกพันธ คือ มีลักษณะที่เหมือนกันหรือคลายคลึงกันให
มากที่สุดทุกๆกลุม ลักษณะการจัดกลุมอาจจะแสดงไดโดยใชแผนภาพดังนี้
2.5 การสุมตัวอยางแบบหลายขั้น (Multistage Sampling) เปนการสุมตัวอยางที่
ประกอบดวยหลายขั้นตอน โดยเริ่มจากกลุมประชากรมาจนถึงขั้นของการเลือกสมาชิกเขาสูกลุม
ตัวอยาง เทคนิคการสุมตัวอยางที่ใชในแตละขั้นตอนนันอาจจะเหมือนกันหรือตางกันก็ได แลวแต
้
ความเหมาะสม เชน ตองการสุมนักเรียนชั้นมัธยมศึกษาปที่ 6 จากทัวประเทศใชการสุมแบบหลาย
่
ขั้นตอนดังนี้
ขั้นที่ 1 ใชการสุมแบบแบงเปนชันภูมิผสมกับการสุมแบบกลุม (Stratified cluster sampling)
้
โดยการแบงจังหวัดทั้งหมดออกตามภาคภูมิศาสตรแลวสุมจังหวัดจากแตละภาคในขันนี้ภาคเปนชัน
้
้
ภูมิและจังหวัดเปนกลุม
ขั้นที่ 2 ในแตละจังหวัด ใชการสุมแบบแบงชันภูมิผสมผสานกับการสุมแบบกลุมโดยการ
้
แบงโรงเรียนในแตละจังหวัดเปน 3 ชั้นภูมิ ตามขนาดของโรงเรียนคือ ใหญ กลาง เล็ก แลวสุม
โรงเรียนมาจากแตละชันภูมิ ในขั้นนี้ตัวแปรที่ใชในการแบงเปนชั้นภูมิคือ ขนาดของโรงเรียนและ
้
โรงเรียนคือกลุมของนักเรียน
ขั้นที่ 3 ในแตละโรงเรียนสุมนักเรียนชั้นมัธยมศึกษาป 6 โดยวิธีสุมแบบงาย
95. 96. 99
e คือความคลาดเคลื่อนที่ยอมใหเกิดขึ้นในรูปของสัดสวน
ตัวอยาง ถาประชากรที่ศึกษามี 1,800 คน และตองการใหเกิดความคลาดเคลื่อนในการสุมตัวอยาง
รอยละ 5 ขนาดของกลุมตัวอยางควรเปนเทาไร
สูตรที่ใชในการคํานวณขนาดของกลุมตัวอยาง คือ n = N
1+Ne2
= 1,800
= 327
1+1,800(.05) 2
จะตองเลือกตัวอยาง 327 คน
2. การประมาณคาสัดสวนของประชากร(π) ยอมใหเกิดความคลาดเคลื่อน e % ที่
ระดับความเชือมั่น (1- ∝)%
่
2.1 ในกรณีททราบคา π
ี่
จาก
Z = P- π
σp
σp
=
π (1 − π )
n
= Z 2 π ( 1- π)
e2
ตัวอยาง ถาตองการประมาณคาสัดสวนของคนกทม.ที่มีบานเปนของตนเองในปนี้ใหผิดพลาดไม
เกิน 3 % ดวยระดับความเชือมั่น 90 % ควรสุมตัวอยางคนในกทม.มากี่คน ถาทราบวาเปอรเซ็นตของ
่
คนที่มีบานเปนของตนเองเมื่อ 2 ปที่ผานมา เทากับ 60%
π = .60
1- π = 1-0.6 = 0.4
e = 0.03
Z = 1.645 (ที่ระดับความเชื่อมั่นเทากับ 90 %)
n =
Z2 π ( 1- π)
e2
= (1.645)2 .60 (0.4) = 721.6
(0.03) 2
ดังนันควรสุมตัวอยางคนในกทม.
้
= 721 คน
ในกรณีที่ไมทราบคา π Yamane ไดหาคา π (1- π) ดังนี้
π (1- π)จะมีคามากที่สุดเมื่อ π = ½ คือπ ( 1- π) = 1/4
ดังนั้น
n =
Z2
4 e2
ดังนั้น
n
97. 100
ตัวอยาง
ในการสํารวจความคิดเห็นของนิสิตคณะครุศาสตรที่มีตอวิชาชีพครู ถาตองการใหเกิด
ความผิดพลาด 2% ที่ระดับความเชื่อมั่น 90% ควรสอบถามนิสิตคณะครุศาสตรกี่คน
e = 0.02
Z = 1.645
n = Z2
4 e2
= (1.645) 2
= 1691.265
4(0.02) 2
จะตองสอบถามจากนิสิต
1691
คน
การประมาณคา (Estimation)
การประมาณคา เปนวิธการวิเคราะหทางสถิติที่มีความสําคัญมาก จะพบวาในปจจุบันมีการ
ี
ใชการประมาณคาในทุกๆองคกร เชนประมาณผลสัมฤทธิ์ทางการเรียนของนักเรียน เพื่อวางแผนการ
จัดการเรียนการสอน เปนตน การประมาณคาตางๆ คือ การประมาณคาพารามิเตอรของประชากร
เชน คาเฉลี่ยประชากร(µ) คาสัดสวนประชากร (π) คาความแปรปรวนของประชากร(σ2) โดยใช
ขอมูลจากกลุมตัวอยาง
ประเภทของการประมาณคา แบงเปน 2 ประเภท คือ
1. การประมาณคาแบบจุด (Point Estimation) เปนการประมาณคาพารามิเตอร ดวยเลขตัว
ใดตัวหนึ่งโดยใชขอมูลจากกลุมตัวอยาง เชน ใชคาเฉลี่ยของตัวอยางประมาณคาเฉลี่ยของประชากร
ตัวอยางคือการประมาณคารายไดเฉลี่ยของคนในประเทศดวยรายไดเฉลี่ยของคนในกรุงเทพ เปนตน
คาประมาณแบบจุดนี้อาจจะมีคาเทากับพารามิเตอรหรือไมก็ได และมีโอกาสคลาดเคลื่อนไปจาก
คาพารามิเตอรไดมาก
การประมาณคาพารามิเตอรแบบจุด
ประชากรที่มีการแจกแจงแบบใดๆ
หนึ่งประชากร
คาเฉลี่ยประชากร
คาสัดสวนประชากร
คาความแปรปรวนของประชากร
สองประชากร
ผลตางของคาเฉลี่ยประชากร
ผลตางของคาสัดสวนประชากร
พารามิเตอรที่ตองการประมาณ
µ
π
σ2
µ 1- µ 2
π1 - π2
คาประมาณแบบจุด
x
P
S2
x1–x2
P1 - P2
98. 101
2. การประมาณคาแบบชวง (Interval Estimation) เปนการประมาณคาพารามิเตอรวาอยู
ในชวงใดชวงหนึ่ง โดยใชขอมูลจากกลุมตัวอยาง โดยที่ชวงของการประมาณคาจะบอกคาต่ําสุด
และสูงสุด เชน ใชชวงของคาเฉลี่ยของตัวอยางประมาณคาเฉลี่ยของประชากร ซึ่งมีโอกาส
คลาดเคลื่อนไปจากคาพารามิเตอรไดนอยกวาการประมาณคาแบบจุด
การประมาณคาแบบชวงนี้ คาต่ําสุดและคาสูงสุดจะขึ้นอยูกับระดับความเชื่อมั่น (Level of
่
Confidence) ชวงของการประมาณคาจะกวางหรือแคบขึ้นอยูกับระดับความเชื่อมันและการกระจาย
ของลักษณะประชากรที่สนใจศึกษา ถาระดับความเชื่อมันสูงและลักษณะที่สนใจศึกษามีการกระจาย
่
มาก ชวงของคาประมาณจะกวาง ถาระดับความเชื่อมันต่ําและลักษณะที่สนใจศึกษามีการกระจาย
่
นอย ชวงของคาประมาณจะแคบ
ระดับความเชือมั่น หมายถึง โอกาสที่พารามิเตอรของประชากรจะอยูในชวงของคาที่
่
ประมาณได เชน p ( L< µ< U ) = .95 หมายถึง โอกาสที่ µ จะอยูในชวงของ L และ U เทากับ
95% และ p ( µ < L ) + p ( µ > U ) = .05 หมายถึง โอกาสที่ µ จะนอยกวา L และมากกวา U
เทากับ 5%
การประมาณคาเฉลี่ยของประชากร ( µ ) แบบชวง
พิจารณาจาก 3 กรณี
1. ประชากรที่มีการแจกแจงแบบปกติ ทราบคาความแปรปรวนของประชากร
2. ประชากรที่มีการแจกแจงแบบใดๆ กลุมตัวอยางมีขนาดใหญ ( n ≥ 30)
3. ประชากรที่มีการแจกแจงแบบปกติหรือใกลเคียง ไมทราบคาความแปรปรวนของประชากรและ
กลุมตัวอยางมีขนาดเล็ก ( n ≤ 30)
1. ประชากรที่มีการแจกแจงแบบปกติ ทราบคาความแปรปรวนของประชากร
ตองการประมาณคาเฉลี่ยประชากร (µ ) จากคาเฉลี่ยตัวอยาง (X)
X ∼ normal( µ , σ2 / n )
p ( L< µ< U ) = 1- ∝
แปลง X ใหเปน Z
Z= (x -µ)/ σ
n
1- ∝ = p (-Z 1- ∝ / 2 < Z < Z 1- ∝ / 2)
= p ( -Z 1- ∝ / 2< x - µ / σ < Z1- ∝ / 2)
n
= p ( -Z 1 - ∝ / 2 σ < x - µ< Z 1 - ∝ / 2 σ )
n
n
สมการ 1
99. 102
จากสมการ 1 แยกได 2 สมการยอย
x - µ < Z1- ∝ / 2 σ ) และ
x
- µ > -Z1 - ∝ / 2 σ
n
x
– Z 1- ∝ / 2 σ ) < µ และ
n
x
+Z
n
ดังนัน
้
σ > µ
1- ∝/ 2
n
p ( x - Z1- ∝ / 2 σ < µ < x + Z1 - ∝ / 2 σ )
n
1- ∝
=
n
สรุป คาประมาณคาเฉลี่ยประชากร แบบชวง ที่ระดับความเชื่อมั่น ( 1- ∝) =
x
± Z1- ∝ / 2 σ
n
ในทํานองเดียวกัน ประชากรที่มีการแจกแจงแบบใดๆ กลุมตัวอยางมีขนาดใหญ ( n ≥ 30)
และประชากรที่มีการแจกแจงแบบปกติหรือใกลเคียงแตไมทราบคาความแปรปรวนของประชากร
และกลุมตัวอยางมีขนาดเล็ก ( n < 30) ตลอดจนการประมาณคาสัดสวนประชากร (π) คาความ
แปรปรวนของประชากร(σ2) สรุปคาประมาณแบบชวงจากประชากรกลุมเดียวและสองกลุมไดจาก
ตารางดังตอไปนี้
สรุปคาประมาณแบบชวง
พารามิเตอรที่ตองการประมาณคาของประชากรเดียว
การประมาณคาเฉลี่ยประชากร µ แบบชวง
1. ประชากรมีการแจกแจงแบบปกติและทราบคา σ2
2. ประชากรมีการแจกแจงแบบใดๆตัวอยางมีขนาดใหญ (n≥30)
2.1 ทราบคา σ2
2.2 ไมทราบคา σ2
3. ประชากรมีการแจกแจงแบบปกติแตไมทราบคา σ2
ตัวอยางมีขนาดเล็ก (n < 30 )
คาประมาณแบบชวง
x
± Z 1- ∝ / 2 σ / n
x ± Z 1 - ∝ / 2 σ/
x ± Z 1-∝ / 2 s /
x ±t
1-
n
n
∝ / 2; n-1 s / n
การประมาณคาสัดสวนประชากร πแบบชวง
ประชากรมีการแจกแจงแบบใดๆตัวอยางมีขนาดใหญ (n≥30)
P ± Z 1 - ∝ / 2 √pq/ n
การประมาณคาความแปรปรวนประชากร σ2แบบชวง
ประชากรมีการแจกแจงแบบปกติ
( n-1) s2 , ( n-1) s2
χ 21 - ∝ / 2
χ2 ∝ / 2
100. 103
พารามิเตอรทตองการประมาณคาของสองประชากร
ี่
คาประมาณแบบชวง
การประมาณคาผลตางระหวางคาเฉลียของสองประชากรที่มี
่
การสุมตัวอยางสองชุดอยางเปนอิสระ
1. ประชากรมีการแจกแจงแบบปกติและทราบคาσ12 และ σ22 x 1- x 2 ± Z 1- ∝ / 2 √ σ12/ n1+σ22/n2
2. ประชากรมีการแจกแจงแบบใดๆตัวอยางมีขนาดใหญ
(n1, n2≥30)
2
2
x 1- x 2 ± Z1- ∝ / 2 √ σ1 / n1+σ2 /n2
2.1 ทราบคา σ12 และ σ22
2
2
x 1- x 2 ± Z1- ∝ / 2 √ S1 / n1+S2 /n2
2.2 ไมทราบคา σ12 และ σ22
3. ประชากรมีการแจกแจงแบบปกติแตไมทราบคา σ12 และ
σ22 ตัวอยางมีขนาดเล็ก (n1, n2 < 30 )
x 1- x 2 ± t 1 - ∝ / 2 Sp√1/n1+1/n2
3.1 ไมทราบคา σ12 และ σ22 แตทราบวา σ12 = σ22
t 1 - ∝ / 2 ที่องศาอิสระ n1+n2-2
Sp = ( n1-1) S12+ ( n2-1) S22
n1+n2-2
3.2 ไมทราบคา σ12 และ σ22 แตทราบวา σ12 ≠ σ22
± t 1- ∝ / 2 √S12/ n1+ S22/n2
t 1 - ∝ / 2 ที่องศาอิสระ γ
γ = ( S12/ n1+ S22/n2) 2
(S12/ n1) 2+ (S22/n2) 2
n1-1
n2- 2
x 1- x
2
การประมาณคาผลตางระหวางคาเฉลียของสองประชากรแบบ d ± t 1 - ∝ / 2; n-1 Sd / n
่
จับคู
d i= x 1I – x 2I
ประชากรมีการแจกแจงแบบปกติหรือใกลเคียง n < 30
d = ∑ di / n , Sd2 = ∑( di - d) 2/(n-1)
การประมาณคาผลตางระหวางคาสัดสวนสองประชากร
(n1, n2≥30)
การประมาณคาอัตราสวนระหวางความแปรปรวนของสอง
ประชากร σ12/ σ22
( p1- p2)+ Z1 -∝ / 2 √p1q1/n1+ p2q2/n2
, S12 F 1- ∝ / 2; n2-1,n1-1
S12 1
S22 F 1- ∝ / 2 ; n1-1,n2-1 S22
101. 104
การทดสอบสมมติฐาน (Test of Hypothesis)
สมมติฐาน คือสิ่งที่คาดวาจะเกิดขึ้นหรือคําตอบที่คาดวาจะไดรับจากการศึกษา สมมติฐานจึง
มักเปนขอสมมุติที่สมเหตุสมผลจากแนวคิดทฤษฎีที่เสนอขึ้นมา แลวใชเปนแนวทางในการสืบสวน
คนควา เพื่อทําการตรวจสอบความถูกตองของสมมติฐาน สมมติฐานที่ใชอยูในการวิจัยจําแนกเปน 2
ประเภทใหญๆ คือ
1. สมมติฐานทางการวิจย (Research Hypothesis) หมายถึง ขอความที่เปนความคาดหวังหรือ
ั
เปนคําตอบของการวิจยไวลวงหนาโดยอาศัยประสบการณ หลักการ ทฤษฎีตางๆ ซึ่งอาจจะถูกหรือ
ั
ผิดไปจากผลการวิจัยก็ได
2. สมมติฐานทางสถิติ (Statistical Hypothesis) หมายถึง ขอความที่เกี่ยวของกับ
คาพารามิเตอรที่ยังไมทราบคา การตั้งสมมติฐานทางสถิติเพื่อการทดสอบจะตองประกอบดวย
สมมติฐาน 2 ชนิดทุกครั้ง คือ
1) สมมติฐานวาง (Null Hypothesis) ใชสัญลักษณ Ho คือ สมมติฐานที่ระบุความไมแตกตาง
กันของคาพารามิเตอร จะเห็นวาสมมติฐานวาง จะมีเครืองหมาย เทากับ ปรากฏอยูเสมอ เชน
่
Ho: µ = 10,000 หมายถึง คาเฉลี่ยของกลุมประชากรมีคาเทากับ 10,000
Ho: µ1 = µ2 หมายถึงคาเฉลี่ยของกลุมประชากรกลุมที่ 1เทากับคาเฉลี่ยของกลุมประชากรกลุมที่ 2
2) สมมติฐานแยง (Alternative Hypothesis) ใหสัญลักษณ Ha หรือ H1 หมายถึง ขอความ
ที่ตรงขามกับสมมติฐานวางที่ตองการทดสอบ
ซึ่งเขียนในลักษณะที่แสดงความแตกตางของ
คาพารามิเตอรที่ตองการทดสอบ โดยทีสมมติฐานวางและสมมติฐานแยง จะอยูในทิศทางที่ตรงกัน
่
ขามเสมอ แบงเปน 2 แบบ
2.1 สมมติฐานทางเลือกที่ไมแสดงทิศทางของความแตกตางระหวางคาพารามิเตอรที่ตองการ
ทดสอบ ใชสําหรับการทดสอบ 2 ทาง (Two- tailed Test ) เชน
Ho : µ1 = µ2 ( สมมติฐานวาง )
H1 : µ1 ≠ µ2 ( สมมติฐานแยง )
2.2 สมมติฐานทางเลือกที่แสดงทิศทางของความแตกตางระหวางคาพารามิเตอรที่ตองการ
ทดสอบ เปนการกลาวถึงพารามิเตอรอยางเจาะจงวามีคามากกวาหรือนอยกวา จึงใชสําหรับการ
ทดสอบทางเดียว (One- tailed Test ) เชน
Ho : µ1 = µ 2 ( สมมติฐานวาง )
H1 : µ1 > µ 2 ( สมมติฐานแยง ) หรือ
H1 : µ1 < µ 2
นอกจากนี้ยังสามารถเขียนการเขียนสมมติฐานทางสถิติในรูปของขอความไดดวย เชน
Ho : รายไดเฉลี่ยตอเดือนของคนไทยเปน 10,000 บาท
H1 : รายไดเฉลี่ยตอเดือนของคนไทยไมเทากับ 10,000 บาท
102. 105
ตัวอยาง การเขียนสมมติฐาน
บริษัทผูผลิตหลอดไฟแหงหนึ่งอางวาหลอดไฟของเขาจะมีอายุการใชงานเฉลี่ยนานกวา1,000 ชั่วโมง
และคาดวาคําอางเปนจริง สมมติฐานจะเขียนไดเปน
Ho : µ = 1000
H1 : µ > 1000
ถาคาดวาคะแนนเฉลี่ยของนักเรียนม.1 / a เทากับนักเรียนม.1 / b สมมติฐานจะเขียนไดเปน
Ho : µa = µb
H1 : µa ≠ µb
การทดสอบสมมติฐานทางสถิติ
การทดสอบสมมติฐานทางสถิติ เปนการตัดสินใจผลทีไดจากการเปรียบเทียบระหวางคาสถิติ
่
ที่ไดจากกลุมตัวอยางกับคาพารามิเตอรตามสมมติฐานวางที่กําหนดไวลวงหนา (สมมติคาพารามิเตอร
ของประชากร) โดยอาศัยเกณฑที่ตั้งไว ผลที่ไดจากการทดสอบสมมติฐานทางสถิติ มี 2 ลักษณะ คือ
1) การยอมรับหรือคงสมมติฐาน หมายความวา ความแตกตางของคาสถิติที่คํานวณไดจาก
้
กลุมตัวอยางกับคาพารามิเตอรตามสมมติฐานวาง มีขนาดตางกันเล็กนอยและความแตกตางนันอยู
ภายในขอบเขตที่ยอมรับได
และถือไดวาเปนความแตกตางโดยบังเอิญอันเนื่องมาจากความ
คลาดเคลื่อนจากการสุมตัวอยางหรือลักษณะเฉพาะของกลุมตัวอยางประชากรนั้น
อันมิใชความ
แตกตางทีแทจริง จึงกลาวไดวาการทดสอบไมมีนัยสําคัญ จึงยอมรับหรือคงสมมติฐานวางไว
่
2) การปฏิเสธสมมติฐาน หมายความวา ความแตกตางของคาสถิติที่คํานวณไดจากกลุม
ตัวอยางกับคาพารามิเตอรตามสมมติฐานวาง
มีขนาดตางกันมากและความแตกตางนั้นมากเกิน
ขอบเขตที่ยอมรับได และถือไดวาเปนความแตกตางทีแทจริง ไมใชบงเอิญ จึงกลาวไดวาการทดสอบ
่
ั
มีนัยสําคัญ เปนการปฏิเสธสมมติฐานวางทีตั้งไวและยอมรับสมมติฐานแยง
่
ความผิดพลาดในการทดสอบสมมติฐานทางสถิติ
เนื่องจากการตัดสินใจยอมรับหรือปฏิเสธสมมติฐานวาง ขึ้นอยูกับสถิติที่ใชทดสอบ ซึ่ง
คํานวณไดจากกลุมตัวอยางมิใชจากกลุมประชากร จึงอาจทําใหการตัดสินใจถูกตองหรืออาจเกิดความ
คลาดเคลื่อนได ดังนี้
1. ความผิดพลาดประเภทที่ 1 (Type I Error ) เปนความผิดพลาดเนื่องจากการปฏิเสธ Ho
ั
่
หรือไมยอมรับ Ho เมื่อ Ho เปนจริง ใชสญลักษณ α โดยทีα = P ( ปฏิเสธ Ho โดยที่ Ho เปนจริง )
2. ความผิดพลาดประเภทที่ 2 ( Type II Error ) เปนความผิดพลาดเนื่องจากการยอมรับ Ho
โดยที่ Ho ไมเปนจริง และใชสัญลักษณ β แทนความผิดพลาดประเภทนี้ โดยที่ β = P ( ยอมรับ Ho
โดยที่ Hoไมเปนจริง )
103. 106
แสดงผลการทดสอบและความผิดพลาดในการทดสอบ
ความเปนจริง
ผลการทดสอบ
Ho เปนจริง
Ho ไมเปนจริง
ผลการทดสอบถูกตอง
ยอมรับ Ho
ความผิดพลาดประเภทที่ 2 (β)
ปฏิเสธ Ho
ความผิดพลาดประเภทที่ 1 (α) ผลการทดสอบถูกตอง
ระดับความมีนัยสําคัญ
ระดับความมีนัยสําคัญ หมายถึง ความนาจะเปนในการปฏิเสธสมมติฐานวางที่ถูก จึงเปน
โอกาสของความคลาดเคลื่อนประเภทที่ 1 โดยทั่วไปนิยมใชสัญลักษณ α แทนระดับการมีนัยสําคัญ
เชน α=0.05
ระดับความเชือมั่น
่
ระดับความเชือมั่น หมายถึง ความนาจะเปนในการยอมรับสมมติฐานวางที่ถูก (1-α)
่
โดยทั่วไปนิยมคํานวณเปน คารอยละ เชน ระดับความเชือมั่นเทากับ 95 %
่
บริเวณวิกฤตหรือเขตการปฏิเสธ (Critical Region)
บริเวณวิกฤต (Critical Region) เปนขอบเขตที่กําหนดตามระดับการมีนัยสําคัญ ถาคาสถิติที่
คํานวณไดตกอยูในขอบเขตนี้ ถือวาการทดสอบนั้นมีนยสําคัญ (Significance)
ั
หลักการทดสอบสมมติฐานทางสถิติ
การทดสอบสมมติ ฐ านทางสถิ ติ เป น การตั ด สิ น ใจเชิ ง สถิ ติ เ กี่ ย วกั บ ค า พารามิ เ ตอร ข อง
ประชากรวามีความแตกตางกันหรือไม ดวยการใชขอมูลคาสถิติจากกลุมตัวอยางเพื่อคํานวณคาสถิติ
ทดสอบและตัดสินใจคงสมมติฐานวางหรือปฏิเสธสมมติฐานวางตามหลักเกณฑที่กําหนดทําให
สามารถสรุปผลเกี่ยวกับคาพารามิเตอรของประชากรได
ขั้นตอนของการทดสอบสมมติฐาน
ขั้นที่1 ตั้งสมมติฐานเพื่อการทดสอบ สําหรับการทดสอบแบบทางเดียว หรือ สองทางโดย
ตั้งสมมติฐาน Ho และ H1
ขั้นที่2 กําหนดสถิติเพื่อการทดสอบ
1) การทดสอบเกี่ยวกับคาเฉลี่ยของประชากร 1 กลุม ใชสถิติทดสอบ Z และ t-test
2) การทดสอบเกี่ยวกับคาเฉลี่ยของประชากร 2 กลุม ใชสถิติทดสอบ Z และ t-test
ขั้นที่3 คํานวณคาสถิติทดสอบ โดยนําขอมูลที่ไดมาแทนคาในสูตรคํานวณคาสถิติทดสอบ
ขั้นที่4 กําหนดระดับนัยสําคัญ โดยทั่วไปมักกําหนดใหคา α เทากับ 0.01 หรือ0.05
104. 107
ขั้นที่5 กําหนดบริเวณวิกฤตที่เปนเขตปฏิเสธสมมติฐาน Ho คือการหาคาวิกฤต ซึ่งเปนคาที่
แบงเขตปฏิเสธและเขตยอมรับ Ho คาวิกฤตนี้ขึ้นอยูกับประเภทของการทดสอบ วาเปนการทดสอบ
แบบทางเดียวหรือสองทาง
การกําหนดบริเวณวิกฤตแบบทางเดียว
หรือ
2. H0 : µ ≥ µ o
H0 : µ ≤ µ o
H1 : µ > µ o
H1 : µ < µ o
ชวงความเชื่อมั่น
α
0
α
บริเวณวิกฤต
ชวงความเชื่อมั่น
บริเวณวิกฤต
0
คาวิกฤต
คาวิกฤต
การกําหนดบริเวณวิกฤตแบบสองทาง
H0 : µ = µ o
H1 : µ ≠ µ o
α/ 2
บริเวณวิกฤต
ชวงความเชื่อมัน
่
α/ 2
0
บริเวณวิกฤต
คาวิกฤต
ขั้นที่6 สรุปผลการทดสอบ โดยนําคาสถิติทดสอบที่คํานวณไดจากขั้นที่ 3 มาเปรียบเทียบกับ
คาวิกฤต ในขันที่ 5 ถาคาสถิติทดสอบอยูในเขตปฏิเสธ จะสรุปวาปฏิเสธ Ho แตถาคาสถิติทดสอบอยู
้
ในเขตยอมรับ จะสรุปวายอมรับ Ho
ประเภทของการทดสอบสมมติฐาน
การทดสอบสมมติฐานทางสถิติ ในที่นี้ขอนําเสนอเปน 6 การทดสอบหลักที่สําคัญ ไดแก
1. การทดสอบสมมติฐานเกี่ยวกับคาเฉลี่ยของประชากรเดียว (µ )
2. การทดสอบสมมติฐานเกี่ยวกับคาสัดสวนประชากร (π )
3. การทดสอบสมมติฐานเกี่ยวกับคาแปรปรวนประชากร (σ 2)
105. 108
4. การทดสอบสมมติฐานเกี่ยวกับผลตางระหวางคาเฉลี่ยของสอง ประชากร ( µ 1 - µ2 )
4.1 การทดสอบความแตกตางระหวางคาเฉลี่ยสองประชากรโดยใช Z – test
4.2 การทดสอบความแตกตางระหวางคาเฉลี่ยสองประชากรโดยใช
t – test (Independent)
4.3 การทดสอบความแตกตางระหวางคาเฉลี่ยสองประชากรโดยใช paired t –test
5. การทดสอบความแตกตางระหวางสัดสวนสองประชากร( โดยใช Z – test)
6. การทดสอบความแตกตางระหวางคาความแปรปรวนสองประชากร
1. การทดสอบสมมติฐานเกี่ยวกับคาเฉลี่ยของประชากรเดียว (µ )
1) การทดสอบสมมติฐานเกียวกับคาเฉลี่ยประชากรเมื่อประชากรมีการแจกแจงแบบปกติ
่
และทราบคาแปรปรวนประชากร
สมมติฐาน
H0 : µ ≤ µ o หรือ 2. H0 : µ ≥ µ o หรือ 3. H0 : µ = µ o
H1 : µ > µ o
H1 : µ < µ o
H1 : µ ≠ µ o
สถิติทดสอบ
Z =
x - µo
σ/ n
2) การทดสอบสมมติฐานเกียวกับคาเฉลี่ยประชากร เมือประชากรมีการแจกแจงแบบใด ๆ
่
่
และขนาดตัวอยางใหญ (> 30) เมื่อทราบคาแปรปรวนประชากร
สถิติทดสอบ
Z =
x - µo
σ/ n
เมื่อไมทราบคาแปรปรวนประชากร
Z =
x
- µo
s/ n
106. 109
3) การทดสอบสมมติฐานเกียวกับคาเฉลี่ยประชากร เมื่อไมทราบคาความแปรปรวนของ
่
ประชากรและตัวอยางมีขนาดเล็ก (n < 30 )
t = x - µo
s/ n
สมมติฐานแยง
1. H1 : µ > µ o
2. H1 : µ < µ o
3. H1 : µ ≠ µ o
เขตปฏิเสธ H0
t > t1 - α : n-1
t < - t1 - α : n-1
⏐ t ⏐ > t1 - α / 2 : n-1
ตัวอยาง ผูอํานวยการโรงเรียนแหงหนึ่งคาดวาปริมาณกระดาษทีใชในการถายเอกสารในโรงเรียนจะ
่
ไมต่ํากวา 880 แผนตอวัน จึงเก็บขอมูลปริมาณกระดาษทีใชถายเอกสารตอวันมา 50 วัน คํานวณได
่
ปริมาณเฉลี่ย 871 แผนตอวัน คาสวนเบียงเบนมาตรฐานเปน 21 แผน การคาดคะเนของผูอํานวยการ
่
โรงเรียนถูกตองหรือไมที่ระดับนัยสําคัญ 0.05
H0 :
µ ≥ 880
H1 :
µ < 880
สถิติที่ใช
Z = x - µo
s/ n
= 871- 880
21 / 50
=
- 3.03
การตัดสินใจ จะปฏิเสธ H0 ถา Z ที่คํานวณได นอยกวา -1.67
สรุปผล
คา Z ที่คํานวณได นอยกวา -1.67 จึงปฏิเสธ H0 นั่นคือ การคาดคะเนของ
ผูอํานวยการโรงเรียนไมถูกตอง ซึ่งหมายความวาโรงเรียนแหงนีใชกระดาษเพื่อถายเอกสาร นอยกวา
้
880 แผนตอวันอยางมีนยสําคัญทางสถิติที่ระดับ 0.05
ั
2. การทดสอบสมมติฐานเกียวกับคาสัดสวนประชากร (π )
่
สมมติฐาน
H0 : p ≤ p o หรือ 2. H0 : p ≥ p o หรือ 3. H0 : p = p o
H1 : p > p o
H1 : p < p o
H1 : p ≠ p o
107. 110
สถิติทดสอบ
Z
p − p0
=
สมมติฐานแยง
1. H1 : p > p o
2. H1 : p < p o
3. H1 : p ≠ p o
p0q0 / n
เขตปฏิเสธ H0
Z > Z1 - α
Z < - Z1 - α
⏐Z⏐ > Z1 - α / 2
ตัวอยาง สํานักงานเขตพืนทีการศึกษาแหงหนึ่ง คาดวาในปนี้มีผูเรียนที่ศึกษาในสถานศึกษาที่อยูใน
้ ่
ความรับผิดชอบของสํานักฯ สามารถสอบเขามหาวิทยาลัยอยางนอย 30 % จึงสุมตัวอยางผูเรียน
มัธยมศึกษาปที่ 6 มา 500 คน ปรากฏวามีผูสอบเขามหาวิทยาลัย250 คน อยากทราบวาสิ่งที่
สํานักงานเขตพื้นที่การศึกษาคาดไวเปนจริงหรือไม ที่ระดับนัยสําคัญ .05
สมมติฐาน H0 : p ≥ 0.3
H1 : p < 0.3
p o = 0.3 q0 = (1 - 0.3) = 0.7 p = 250/500 = 0.5
สถิติที่ใช
Z =
=
p − p0
p0q0 / n
0.5- 0.3
0.3 × 0.7 / 500
=
9.76
การตัดสินใจ จะปฏิเสธ H0 ถา Z ที่คํานวณได นอยกวา -1.64
สรุปผล
คา Z ที่คํานวณได มากกวา -1.64 จึงไมอาจปฏิเธสมมติฐาน H0 หรือคงสมมติฐาน
H0 ไว นั่นคือ การคาดคะเนของสํานักงานเขตพื้นที่การศึกษาถูกตอง ซึ่งหมายความวามีผูเรียนที่ศึกษา
ในสถานศึกษาที่อยูในความรับผิดชอบของสํานักฯ สามารถสอบเขามหาวิทยาลัยอยางนอย 30 %
อยางมีนัยสําคัญทางสถิติที่ระดับ 0.05
108. 111
3. การทดสอบสมมติฐานเกี่ยวกับคาแปรปรวนประชากร (σ 2)
สมมติฐาน
หรือ 2. H0 : σ2 = σ20
หรือ 3. H0 : σ2 = σ20
H0 : σ2 = σ20
H1 : σ2< σ20
H1 : σ2 ≠ σ20
H1 : σ2> σ20
สถิติทดสอบ
χ2
( n – 1 ) S2
σ20
ที่องศาอิสระ n – 1
=
ตัวอยาง สถานศึกษาระดับประถมศึกษาแหงหนึ่ง แจกนมสดถุงใหผูเรียนดื่มทุกวันแตละถุงมี
ปริมาตร 250 มิลลิลิตร และจากการตรวจสอบมักพบวาผูเรียนมักดื่มนมไมหมดถุง ครูที่รับผิดชอบ
เชื่อวาปริมาณนมที่ผูเรียนรับประทานไมหมดใน 1 ถุง มีคาสวนเบี่ยงเบนมาตรฐาน 5 มิลลิลิตร ถา
ตองการทดสอบความเชื่อดังกลาวจึงสุมผูเรียนมา 30 คน คํานวณคาสวนเบี่ยงเบนมาตรฐานได 5.5
มิลลิลิตร กําหนด α = 0.05 ถาปริมาณนมสดที่ผูเรียนดื่ม มีการแจกแจงแบบปกติ
ตองการทดสอบ คาสวนเบี่ยงเบนมาตรฐานเทากับ 5 มิลลิลิตร ดังนั้น ความแปรปรวนมีคาเทากับ 25
สมมติฐาน H0 : σ2 = 25
H1 : σ2 ≠ 25
n = 30 df = 30-1 =29 σ20 = (5×5) = 25 S2 = 5.5×5.5 = 30.25
สถิติที่ใช
χ2 = ( n – 1 ) S2
σ20
= (30 - 1) 30.25
25
=
35.09
กําหนดระดับนัยสําคัญ α = 0.05
การทดสอบครั้งนี้เปนแบบ 2 ทาง ดังนั้น α 2 = .025, 1 - α 2 = .975
การตัดสินใจ จะปฏิเสธ H0 ถา χ2 ที่คํานวณไดนอยกวาχ2.025, 30-1 หรือมากกวาχ2.975,30-1
เปดตาราง χ2.025,29 ไดคาเทากับ 16.0 และχ2.975,29 ไดคาเทากับ 45.7
109. 112
สรุปผล
คา χ2 ที่คํานวณได อยูระหวาง 16.0 -45.7 จึงไมอาจปฏิเสธสมมติฐาน H0 หรือคง
่
สมมติฐาน H0ไว นันคือ ปริมาณน้ํานมที่ผเู รียนรับประทานไมหมดใน 1 ถุง มีคาสวนเบี่ยงเบน
มาตรฐาน 5 มิลลิลิตร อยางมีนัยสําคัญทางสถิติที่ระดับ 0.05
4. การทดสอบสมมติฐานเกี่ยวกับผลตางระหวางคาเฉลี่ยของสอง ประชากร ( µ 1 - µ2 )
คาเฉลี่ย
µ1
µ2
ประชากรที่ 1
ประชากรที่ 2
ตัวอยางที่สุมจากประชากรที่ 1
ตัวอยางที่สุมจากประชากรที่ 2
ขนาดตัวอยาง
n1
n2
1. การทดสอบแบบทางเดียว
Η0 : µ1 - µ2 ≤ d0 หรือ Η0
Η1 : µ1 - µ2 > d0
Η1
2. การทดสอบแบบ 2 ทาง
Η0 : µ1 - µ2 = 0 ถา d0 = 0 หรือ
Η1 : µ1 - µ2 ≠ 0
คาแปรปรวน
σ21
σ22
คาเฉลี่ย
Χ1
Χ2
คาแปรปรวน
S21
S22
: µ1 - µ2 ≥ d0
: µ1 - µ2 < d0
Η0 : µ1 = µ2
Η1 : µ1 ≠ µ2
สถิติที่ใชทดสอบ
สามารถใชสถิติ Z – test และ t – test ขึ้นอยูกับขอตกลงเบื้องตนของการใชสถิติแตละตัว
4.1 การทดสอบความแตกตางระหวางคาเฉลี่ยสองประชากร โดยใช Z – test
ขอตกลงเบื้องตนของ Z – test
1. กลุมตัวอยางทัง 2 เปนอิสระตอกัน
้
2. คาของตัวแปรตามในแตละหนวยเปนอิสระกัน
3. กลุมตัวอยางไดมาอยางสุมจากประชากรทีมีการแจกแจงแบบปกติและมีขนาดใหญ(>30)
่
4. ทราบคาความแปรปรวนของแตละประชากร
Η0 : µ1 - µ2 = d0 ถา d0 = คาคงที่ หรือ Η0 : µ1 = µ2
110. 113
สถิติทดสอบ
Z = ( x 1- x 2) - d0
√ σ12/ n1+σ22/n2
ถาไมทราบคา σ12 และ σ22 แทนคาดวย S12 และ S22
4.2 การทดสอบความแตกตางระหวางคาเฉลี่ยสองประชากร โดยใช t – test (Independent)
ขอตกลงเบื้องตนของ t – test (Independent )
1. กลุมตัวอยางทั้ง 2 เปนอิสระตอกัน
2. คาของตัวแปรตามในแตละหนวยเปนอิสระกัน
3. กลุมตัวอยางไดมาอยางสุมจากประชากรที่มีการแจกแจงแบบปกติหรือใกลเคียงและมีขนาดเล็ก
4. ไมทราบคาความแปรปรวนของแตละประชากร
Η0 : µ1 - µ2 = d0 ถา d0 = คาคงที่ หรือ Η0 : µ1 = µ2
มี 2 เงื่อนไข คือ ในกรณีที่ σ12= σ22
สูตรสถิติทดสอบ ในกรณีที่ σ12 = σ22
t = ( x 1Sp
โดยที่
ในกรณีที่ σ12 ≠ σ22
กับ
x 2) - d0
⎛1
1
⎜ +
⎜n n
2
⎝ 1
ในกรณีที่ σ12= σ22
⎞
⎟
⎟
⎠
Sp = ( n1-1) S12+ ( n2-1) S22
n1+n2-2
ที่องศาอิสระ n1+n2-2
สูตรสถิติทดสอบ ในกรณีที่ σ12 ≠ σ22
t = ( x 1- x 2)- d0 ในกรณีที่ σ12 ≠ σ22
√S12/ n1+ S22/n2
ที่องศาอิสระ
(S12/ n1+ S22/n2)2
(S12/ n1)2+ (S22/n2)2
n1-1 n2- 1
111. 114
ตัวอยาง ครูในโรงเรียนแหงหนึ่งตองการทราบวาการสอนแบบการสรางผังความคิดจะเพิ่มคะแนน
เฉลี่ยวิชาชีววิทยาของนักเรียนหรือไม จึงเก็บขอมูลคะแนนสอบวิชาชีววิทยาของนักเรียน 2 หองโดย
หองแรกเรียนตามปกติ มีนักเรียน50 คน หองที่สองเรียนแบบการสรางผังความคิดมีนักเรียน 30 คนได
คะแนนเฉลี่ยของนักเรียนหองแรก 12.55 คะแนน หองที่สอง 13.30 คะแนน คาสวนเบี่ยงเบน
มาตรฐานหองแรก เปน 2.15 คะแนน หองที่สอง 2.38 คะแนน จากขอมูลที่มีอยูจะทําใหครูสรุปได
หรือไมวาการสอนแบบการสรางผังความคิดทําใหคะแนนเฉลี่ยวิชาชีววิทยา เพิ่มขึน โดยกําหนดให
้
α = .05 ทั้ง 2 กลุมมีการแจกแจงแบบปกติ ที่มีคาแปรปรวนไมเทากัน
Η : µ1 = µ2
สมมติฐาน
Η 1 : µ1 > µ2
µ1 คะแนนเฉลี่ยของนักเรียนที่เรียนแบบการสรางผังความคิด
µ2คะแนนเฉลี่ยของนักเรียนที่เรียนตามปกติ
สถิติที่ใช ในกรณีที่ σ12 ≠ σ22
t = ( x 1- x 2)- d0
√S12/ n1+ S22/n2
= (13.30-12.55) - 0
0
⎛ (2.38)2 (2.15)2 ⎞
⎜
⎟
⎜ 30 + 50 ⎟
⎝
⎠
=
0.75
0.528
= 1.42
ที่องศาอิสระ
= (S12/ n1+ S22/n2)2
(S12/ n1)2+ (S22/n2)2
n1-1 n2- 1
=
(0.281)2
(.092) 2/49) +(0.188) 2/29)
=
.078
.00138
≈
57
การตัดสินใจ จะปฏิเสธ H0 ถา t ที่คํานวณได มากกวา t .05,57 = 1.64
สรุปผล
คา t ที่คํานวณไดนอยกวา 1.64 จึงไมอาจปฏิเสธสมมติฐาน H0 หรือคงสมมติฐาน H0
ไวคือ คะแนนเฉลี่ยของนักเรียนที่เรียนแบบการสรางผังความคิดไมแตกตางจากคะแนนเฉลี่ยของ
นักเรียนที่เรียนตามปกติ อยางมีนัยสําคัญทางสถิติที่ระดับ 0.05
112. 115
ตัวอยาง จากการที่มีนิสตรองเรียนอาจารยผูสอนวิชาสถิติวาการอนุญาตใหใชเครืองคิดเลขในการ
ิ
่
สอบจะทําใหเกิดการไดเปรียบเสียเปรียบของคะแนนสอบเกินกวา 15 % เนื่องจากความแตกตางกัน
ของเครื่องคิดเลข อาจารยผูสอนจึงตองการทดสอบขอรองเรียนของนิสิต โดยการสุมตัวอยางนิสิต
มา 45 คน แลวแบงนิสิตออกเปน 2 กลุมอยางสุม กลุมที่ 1 มีนิสิต 23 คน ใหสอบโดยใชเครื่องคิดเลข
กลุมที่ 2 มีนิสิต 22 คน ใหสอบขอเดียวกันโดยไมใหใชเครื่องคิดเลข โดยที่ขอสอบนั้นเปนขอสอบที่
มีการคํานวณมาก ปรากฎวาไดขอมูลดังนี้
ใชเครื่องคิดเลข
ไมใชเครื่องคิดเลข
คะแนนเฉลี่ย
80.7
78.9
คาความแปรปรวน
49.5
60.4
ขนาดตัวอยาง
23
22
จากขอมูลที่ได จงทดสอบวาคะแนนเฉลี่ยของกลุมที่ใชเครื่องคิดเลขจะมากกวาคะแนน
เฉลี่ยของกลุมที่ไมใชเครื่องคิดเลขไมเกิน 15 % ( 15 คะแนน ขอสอบคะแนนเต็ม 100 ) กําหนด
ระดับนัยสําคัญ = .10 และทราบวาคะแนนสอบของทั้ง 2 กลุมมีการแจกแจงแบบปกติ ที่มีคา
แปรปรวนเทา กัน
Η : µ1 - µ2 ≤ 15
สมมติฐาน
Η1 : µ1 - µ2 > 15
สถิติที่ใช
t = ( x 1 - x 2) - d0
0
Sp
โดยที่
⎛1
1 ⎞
⎜ + ⎟
⎜n n ⎟
2 ⎠
⎝ 1
Sp = ( n1-1) S12+ ( n2-1) S22
n1+n2-2
= (23-1)49.5 + (22-1)60.4
23+22-2
= 1089+1268.4
43
=
54.82
t =
(80.7 - 78.9) –15
54.82
=
ที่องศาอิสระ n1+n2-2
1 ⎞
⎛ 1
⎜ + ⎟
⎝ 23 22 ⎠
-13.2
54.82 √0.297
= -0.80
113. 116
การตัดสินใจ จะปฏิเสธ H0 ถา t ที่คํานวณได มากกวา t 43 (.90) = 1.303
สรุปผล
คา t ที่คํานวณไดนอยกวา 1.303 จึงไมอาจปฏิเสธสมมติฐาน H0 หรือคงสมมติฐาน
H0 ไว นั่นคือ คะแนนเฉลี่ยของกลุมที่ใชเครื่องคิดเลขจะมากกวาคะแนนเฉลี่ยของกลุมที่ไมใชเครื่อง
คิดเลขไมเกิน 15 % อยางมีนยสําคัญทางสถิติที่ระดับ 0.10
ั
4.3 การทดสอบความแตกตางระหวางคาเฉลี่ยสองประชากร โดยใช Dependent or paired t – test
ขอตกลงเบื้องตนของ t – test (Dependent or paired t – test )
1. ขอมูล 2 ชุดไดมาจากกลุมตัวอยางเดียวกัน หรือมาจากกลุมตัวอยาง 2 กลุมที่สัมพันธกัน
2. คาของตัวแปรตามในแตละหนวยเปนอิสระกัน
3. กลุมตัวอยางไดมาอยางสุมจากประชากรที่มีการแจกแจงแบบปกติหรือใกลเคียง
4. ไมทราบคาความแปรปรวนของแตละประชากร
Η0 : µ1 - µ2 = d0 ถา d0 = คาคงที่ หรือ Η0 : µd = d0
Η1 : µ1 - µ2 ≠ d0
หรือ Η1 : µd ≠ d0
สถิติทดสอบ
t =
d - d0
Sd / n
ที่องศาอิสระ n-1
2
2
d = ∑ di/ n , Sd = ∑( di - d ) / ( n-1)
di = x 1i – x 2i
ตัวอยาง ในการดสอบคุณภาพของยางรถยนต 2 ยีหอ คือ A และ B จึงสุมตัวอยางยางรถยนตมายี่หอ
่
ละ 5 อัน แลวใสยางรถยนตยี่หอละ 1 อันที่ลอหลังของรถยนตแตละคัน ดังนั้นจึงตองใชรถยนต 5
คัน แลวใหรถยนตทุกคันวิ่งจนกวายางจะเสีย โดยบันทึกระยะทางที่วงไดดังนี้
ิ่
ระยะทางทีวิ่งได ( หนวย : 10,000 กิโลเมตร )
่
รถยนตคนที่
ั
1
2
3
4
5
ยางรถยนต A
10.6
9.8
12.3
9.7
8.8
ยางรถยนต B
10.2
9.4
11.8
9.1
8.3
114. 117
อยากทราบวาคุณภาพของยางรถยนตทั้ง 2 ยี่หอนีแตกตางกันหรือไม กําหนดระดับนัยสําคัญ = .05
้
ถาอายุการใชงานของยางรถยนตมีการแจกแจงแบบปกติ
รถยนตคันที่
1
2
3
4
5
ยางรถยนต A
10.6
9.8
12.3
9.7
8.8
ยางรถยนต B
10.2
9.4
11.8
9.1
8.3
di
0.4
0.4
0.5
0.6
0.5
∑ di = 2.4
d = 0.48
Sd2 =.007 Sd =.0837 n = 5 d0 = 0
: µ1 = µ2
Η 1 : µ1 ≠ µ2
สถิติที่ใช
t =
d - d0
Sd / n
=
0.48-0
.0837/ 5
=
12.8
การตัดสินใจ จะปฏิเสธ H0 ถา t ที่คํานวณได มากกวา t .025, 4 หรือนอยกวา - t .025, 4
เปดตาราง t ไดคา t .025, 4 = 2.78
สรุปผล คา t ที่คํานวณไดมากกวา 2.78 จึงปฏิเสธสมมติฐาน H0 นั่นคือ คุณภาพของยางรถยนต
ทั้ง 2 ยี่หอนีแตกตางกัน อยางมีนัยสําคัญทางสถิติที่ระดับ 0.05
้
สมมติฐาน
Η0
5. การทดสอบความแตกตางระหวางสัดสวนสองประชากร ( โดยใช Z – test)
Η0 : P1 - P2 = P0 ถา P0 = คาคงที่
Η 1 : P 1 - P 2 ≠ P0
หรือ
Η0 : P1 = P2
Η 1 : P 1 ≠ P2
115. 118
สถิติทดสอบ
Z =
( p1- p2) - p0
√(p1q1/n1)+ (p2q2/n2)
ตัวอยาง ถาตองการเปรียบเทียบผลการรักษาโรคมะเร็ง 2 วิธี จึงสุมคนไขที่ไดรับการรักษามาวิธละ
ี
100 คน พิจารณาผลของการรักษาโดยการตรวจสอบอาการ ( เชื้อโรค ) ที่เกิดขึ้นอีก ในชวง 2 ปนบ
ั
จากไดรับการรักษา ไดขอมูลดังนี้
วิธีรักษา
จํานวนคนไข
จํานวนคนไขที่ไมมีอาการของโรคใน 2 ป
1
100
87
2
100
78
จงทดสอบวาการรักษาโรคมะเร็งวิธีที่ 2 ไดผลดีกวาวิธีที่ 1 อยางนอย 15 % กําหนดระดับ
นัยสําคัญ = .10
p1 = 0.87
p2 = 0.78
p0 = 0.15
n1= n2=100
q1 = (1-0.87) =0.13 q2 = (1-0.78)=0.22
สมมติฐาน
Η0 : P1 - P2 ≥ 0.15
Η1 : P1 - P2 < 0.15
สถิติทดสอบ
Z =
( p1- p2) - p0
√(p1q1/n1)+ (p2q2/n2)
=
(0.87-0.78)-0.15
.87 × .13 / 100 ) + .( 78 × .22 100
=
- . 006
. 053
= - 0.113
การตัดสินใจ จะปฏิเสธ H0 ถา Z ที่คํานวณไดนอยกวา Z .05
เปดตาราง Z ไดคา Z .05 = 1.65
่
สรุปผล คา Z ที่คํานวณไดนอยกวา 1.65 จึงปฏิเสธสมมติฐาน H0 นันคือ คุณภาพการรักษา
โรคมะเร็งวิธีที่ 2 ไดผลดีกวาวิธีที่ 1 อยางนอย 15 % อยางมีนัยสําคัญทางสถิติที่ระดับ 0.05
116. 119
6. การทดสอบความแตกตางระหวางคาความแปรปรวนสองประชากร
Η0 : σ1
= σ22
2
2
Η1 : σ1 ≠ σ2
2
สถิติทดสอบ
F = S12
S22
S12 > S22 ที่องศาอิสระ n1 – 1 และ n2 – 2
ตัวอยาง
ถาตองการเปรียบเทียบคาแปรปรวนของ 2 ประชากรวาเทากันหรือไม โดยที่
ประชากรทั้ง 2 มีการแจกแจงแบบปกติ จึงสุมตัวอยางจากประชากรทั้ง 2 อยางเปนอิสระกัน และได
ขอมูลดังนี้
กําหนดระดับนัยสําคัญ = 0.10
n1 = 8 n2 = 12 S1 = 6.35 S2 = 4.85
สมมติฐาน Η0 : σ12 = σ22
2
2
Η1 : σ1 ≠ σ2
สถิติทดสอบ
F = S12
S22
=
6 . 35
2
4 . 85
2
= 1.714
การตัดสินใจ จะปฏิเสธ H0 ถา F ที่คํานวณไดมากกวา F .05 ที่องศาอิสระ n1 – 1 และ n2 – 2
เทากับ (8-1) =7 และ(12-1)=11 ตามลําดับ
เปดตาราง F .05 ที่องศาอิสระ7,11 ไดคา F .05 = 4.89
สรุปผล คา F ที่คํานวณไดนอยกวา 4.89 จึงไมอาจปฏิเสธสมมติฐาน H0 หรือคงสมมติฐาน H0ไว
นั่นคือ คาแปรปรวนของ 2 ประชากรเทากันหรือไมแตกตางกันอยางมีนัยสําคัญทางสถิติที่ระดับ 0.05
117. 120
การทดสอบสมมติฐานโดยใชโปรแกรม SPSS for Windows
การทดสอบสมมติฐานสามารถวิเคราะห โดยใชโปรแกรม SPSS for Windows มีวธีการ ดังนี้
ิ
1. การทดสอบความแตกตางระหวางกลุม
1) ประชากรกลุมเดียว ( ใชสถิติ one sample t - test )
1.1 ใชคําสั่ง
Analyze
Compare Means
จะไดหนาจอดังรูปที่ 1
One - Sample T Test ….
รูปที่ 1
One Sample T Test
เมื่อ click ตามรูปที่ 1 แลวเลือกตัวแปรที่ตองการใสใน box ของ Test variable ใสคาที่เปนเกณฑ
ใน box ของ Test value ดังตัวอยางรูปที่ 2
รูปที่ 2
Test Variables
1.2 เลือก Options จะไดหนาจอดังรูปที่ 3
รูปที่ 3 One Sample T Test :Option
118. 121
ใส confidence interval แลวเลือก continue จะกลับไปหนาจอเดิม รูปที่ 1 แลวคลิก OK จะ
ไดผลลัพธในตารางที่ 1
ตารางที่ 1 ผลลัพธของตัวอยาง
One - Sample Test
Test Value = 30,000
95 % Confidence
Sig
Mean
Interval of the Difference
t
Df (2 –tailed ) Difference
Lower
Upper
Income of
11.17 1399
.0001
11567.14
9536.69
13597.60
respondent
จากตารางที่ 1 คา t = 11.17 sig ( 2-tailed ) = .000 แสดงวารายไดของผูรับผิดชอบ
ครอบครัวเฉลี่ยแตกตางจาก 30,000 ( เปนการทดสอบ 2 ทาง ) ถาทดสอบทางเดียวนําคา Sig หาร 2
จะได Sig = .0001 / 2 = .00005 แสดงวา รายไดของผูรับผิดชอบครอบครัวเฉลี่ยสูงกวา 30,000
บาทที่ระดับนัยสําคัญ .05
2) ประชาการสองกลุมที่เปนอิสระกัน ( ใชสถิติ Independent t –t est )
2.1 ใชคําสั่ง
Analyze
Compare Means
จะไดหนาจอดังรูปที่ 4
Independent –Sample T Test…..
รูปที่ 4 Independent –Sample T Test
119. 122
จากรูปที่ 4 เลือกตัวแปรที่ตองการทดสอบใสใน box ของ Test variable (s) เลือกตัวแปร
ตนที่ใชแบงตัวแปรตามเปน 2 กลุม ใสใน box ของ Grouping variable ดังตัวอยางในรูปที่ 5
รูปที่ 5 Test variables
2.2 เลือก Define Group จะไดหนาจอดังรูปที่ 6
รูปที่ 6 Define Group
ใสคาของกลุมใน Group 1 และ Group 2 แลวเลือก continue จะกลับมาที่หนาจอเดิมรูป 5
2.3 เลือก option จะไดหนาจอ ดังรูปที่ 7
รูปที่ 7 Option
120. 123
เลือก confidence Interval และ Missing values แลวเลือก continue เพื่อกลับไป
หนาจอเดิม แลวเลือก OK จะไดผลลัพธ ในตารางที่ 2 และ 3
ตารางที่ 2 Group Statistics
จํานวนผูหาเลี้ยงครอบครัว
N
513
887
1 คน
2 คน
Mean
30753.28
47821.39
Std.
Deviation
35063.40
39383.34
Std.Error
Mean
1548.09
1322.36
ตารางที่ 3 Independent Sample Test
Levene’s Test for
quality of Variances
income
Equal variances
assumed
Equal variances
not assumed
F
11.773
Sig.
.001
t –test for Equality of Means
T
-8.128
-8.383
Sig
Df
(2-tailed)
1398
.000
1171.3
.000
95% Confidence
Interval of the Mean
Lower
Upper
Mean
Difference
-17068.11
Sts.Error
Difference
2099.94
-21187.48
-12948.74
-17068.11
2035.98
-21062.68
-13073.53
ความหมายของผลลัพธในตารางที่ 3
Levene’s Test for Equality of Variance เปนการทดสอบที่ใชในการทดสอบวาคา
แปรปรวนประชากรจากแตละกลุมเทากันหรือไม เนื่องจากการศึกษานี้เปนการสุมตัวอยางผูหาเลี้ยง
ครอบครัวจํานวน 1 คน มี 513 คนและผูหาเลี้ยงครอบครัว จํานวน 2 คน มี 887 คน อยางเปน
อิสระกัน (ขนาดตัวอยางจากแตละกลุมไมจําเปนตองเทากัน ) และไมทราบคาแปรปรวนประชากร
ของรายไดของแตละกลุม จึงตองตรวจสอบวา คาแปรปรวนประชากรของรายไดของอยางผูหาเลี้ยง
ครอบครัวจํานวน 1 คน เทากับของผูหาเลี้ยงครอบครัวจํานวน 2 คน หรือไม
H0 : σ 21 = σ 22
H1 : σ 21 ≠ σ 22
สถิติทดสอบ F = 11.775
เขตปฏิเสธ จะปฏิเสธสมมติฐาน H0 ถา
1. F > F .975 : 1 , 89 ซึ่งคา F .975 : 1 , 89 จะเปดไดจากตารางการแจกแจงแบบ F หรือ
121. 124
2. คา Significance < α
โดยที่ Significance = P (F > F ที่คํานวณได )
ในที่นี้ P (F > 11.775 ) = Sig = .001 ซึ่งนอยกวาคา α (.05) จึงปฏิเสธสมมติฐาน H0 นั่น
คือ คาแปรปรวนของรายไดของผูหาเลี้ยงครอบครัวจํานวน 1 คน ไมเทากับของผูหาเลี้ยงครอบครัว
จํานวน 2 คน σ 21 ≠ σ 22
วัตถุประสงคของการทดสอบ t – test ตองการทราบวารายไดเฉลี่ยของครอบครัวจากผูหา
เลี้ยงครอบครัวจํานวน 1 คนมากกวาของผูหาเลี้ยงครอบครัวจํานวน 2 คนหรือไม โดยใช α = .05
สมมติฐานเพื่อการทดสอบคือ
H0 : รายไดเฉลี่ยของครอบครัวจากผูหาเลี้ยงครอบครัวจํานวน 1 คนเทากับรายไดเฉลี่ยของ
ครอบครัวจากผูหาเลี้ยงครอบครัวจํานวน 2 คน
H1 : รายไดเฉลี่ยของครอบครัวจากผูหาเลี้ยงครอบครัวจํานวน 2 คนมากกวารายไดเฉลี่ย
ของครอบครัวจากผูหาเลี้ยงครอบครัวจํานวน 1 คน
จากตารางที่ 3 ผลลัพธของ t –test จะใชสวนของ Equal variance not assumed เนื่องจาก
Levene’ s Test สรุปไดวา σ 21 ≠ σ 22
t ในที่นี้ = -8.383 sig (2-tailed ) = .000 แตเนื่องจากสมมติฐานเลือก เปน 1-tailed ดังนั้น
sig (1-tailed ) = .000 / 2 = .000 แสดงวา ปฏิเสธ H0 นั่นคือ: รายไดเฉลี่ยของครอบครัวจากผูหาเลี้ยง
ครอบครัวจํานวน 2 คนมากกวารายไดเฉลี่ยของครอบครัวจากผูหาเลี้ยงครอบครัวจํานวน 1 คนอยาง
มีนัยสําคัญที่ระดับ 0.05
การนําเสนอผลการวิจัย ควรสรางตารางนําเสนอใหม ซึงสามารถนําเสนอผลการวิเคราะห
่
ไดในตารางตอไปนี้
กลุม
ผูหาเลี้ยงครอบครัว
จํานวน 1 คน
ผูหาเลี้ยงครอบครัว
จํานวน 2 คน
คาเฉลี่ย
30753.28
เงินเดือน
สวนเบี่ยงเบนมาตรฐาน
35063.40
47821.39
39383.34
t – test
p –value
-8.383
.000
122. 125
3) ประชากรสองกลุมไมเปนอิสระกัน ( ใชสถิติ dependent t-test )
3.1 ใชคําสั่ง
Analyze
Compare Means
จะไดหนาจอรูปดังรูปที่ 8
Paired - Samples T Test….
รูปที่ 8 Paired – Samples T-Test
จากรูปที่ 8 เลือกตัวแปรที่จะทดสอบ โดยเลือกครั้งละ 1 ตัว โดยตัวแปรแรกจะเขาไปอยู
variable 1 ตัวแปรตัวที่ 2 จะเขาไปอยู variable 2 คลิกเลือกเครื่องหมาย 4 จะปรากฏตัวแปร
ทั้ง 2 ใน box ของ Paired variables ดังรูปที่ 9
รูปที่ 9 Paired – variables
3.2 เลือก options ใส confidence interval
เลือก Exclude analysis by analysis เลือก continue และเลือก OK จะไดผลลัพธในตารางที่ 4-6
ตารางที่ 4 Paired Samples Statistics
Pair 1 EDUFA
EDUMA
Mean
12.05
10.91
N
1406
1406
Std. Deviation
4.81
5.17
Std.Error Mean
.13
.14
123. 126
จากตารางที่ 4 หมายความวา จํานวนปของการศึกษาเฉลียของบิดา (mean ของ EDUFA ) =
่
12.05 สวนเบียงมาตรฐานเทากับ 4.81 สวนจํานวนปของการศึกษาเฉลี่ยของมารดา(mean ของ
่
EDUMA) =10.91 สวนเบี่ยงมาตรฐานเทากับ (SD) = 5.17
ตารางที่ 5 Paired Sample correlation
N
1406
Pair 1 EDUFA & EDUMA
Correlation
.716
Sig.
.000
จากตารางที่ 5 หมายความวา จํานวนปของการศึกษาเฉลียของบิดา และมารดามี
่
ความสัมพันธกันในทิศทางบวก = 0.716 อยางมีนัยสําคัญทางสถิติที่ระดับ 0.05
ตารางที่ 6 Paired Samples Test
Paired Differences
Mean
Pair 1 EDUFA EDUMA
1.14
Std.
Std.Error
Deviation Mean
3.78
.10
95% Confidence
Interval of the
Difference
Lower
Upper
t
df
.94
1.33
11.29
1405
จากตารางที่ 6 หมายความวา จํานวนปของการศึกษาเฉลียของบิดา และมารดาแตกตางกัน
่
อยางมีนัยสําคัญที่ระดับ 0.05 ( t = 11.29 , sig = .000 )
การนําเสนอผลในการวิจัย ไมจําเปนตองนําตารางจากการวิเคราะหดวย SPSS for
Windows ทุกตารางไปใส ควรสรางตารางใหมและนําคาที่สําคัญไปนําเสนอ เชน การนําเสนอผล
การวิเคราะหในเรื่องนี้ สามารถเสนอได ดังนี้
กลุม
บิดา
มารดา
จํานวนปของการศึกษา
คาเฉลี่ย
สวนเบี่ยงเบนมาตรฐาน
12.05
4.81
10.91
5.17
t - test
11.291
p -value
.000
Sig.
(2-tailed)
.000
124. 127
การวิเคราะหความแปรปรวน (Analysis of Variance)
หลักการของการวิเคราะหความแปรปรวน
การวิเคราะหความแปรปรวน ใชอักษรยอทีเ่ รารูจักกันคือ ANOVA ซึ่งเปนระเบียบวิธ(ไมใช
ี
สถิติทดสอบ) ที่สามารถนํามาวิเคราะหโดยมีหลักเกณฑที่ใชในการทดสอบสมมติฐาน คือ การแยก
ความแปรปรวนทั้งหมดของขอมูลออกตามสาเหตุที่ทําใหขอมูลแตกตางกัน
นั่นคือแยกความ
แปรปรวน/ความผันแปรทั้งหมดของขอมูลออกเปน
1. ความผันแปรระหวางประชากร ( Sum of Square Between Groups ( SSB ) )
2. ความผันแปรภายในประชากรเดียวกัน ( Sum of Square Within Groups ( SSW ) )
ความผันแปรทั้งหมด = ความผันแปรระหวางประชากร + ความผันแปรภายในประชากรเดียวกัน
Sum of Square Total (SST) = Sum of Square Between Groups+ Sum of Square Within Groups
Mean Squares Between Groups ( MSB ) =
SSB
= SSB
dfB
K- 1
Mean Squares Within Groups ( MSW) =
SSW
= SSW
dfw
n-K
สถิติทดสอบ F = MSB
ซึ่งมีการแจกแจงแบบ F ดวยองศาอิสระ K – 1, n - K
MSW
ซึ่งเปนอัตราสวนระหวางคาผันแปรระหวางประชากรกับคาผันแปรภายในประชากร
โดยที่ K คือ จํานวนกลุมประชากร
n คือ จํานวนหนวยตัวอยาง
ถาความผันแปรระหวางประชากรมีคามากเมื่อเทียบกับความผันแปรภายในประชากร
เดียวกัน แสดงวาความแตกตางระหวางคาเฉลี่ยประชากรมากกวาความแตกตางภายในประชากร
่
เดียวกัน ในกรณีนี้จะปฏิเสธสมมติฐาน Ho ที่คาเฉลี่ยของประชากรเทากัน นันคือจะสรุปไดวามี
คาเฉลี่ยประชากรอยางนอย 1 ประชากรที่แตกตางจากประชากรอื่นๆ ความผันแปรภายในประชากร
เดียวกันมีคามากกวาความผันแปรระหวางประชากร จะทําใหสรุปไดวาคาเฉลี่ยประชากรที่ตองการ
ทดสอบนั้นไมแตกตางกัน
ขอตกลงเบื้องตนของ การวิเคราะหความแปรปรวน
1. Independent : การสุมตัวอยางแตละหนวยจากแตละประชากรจะตองเปนอิสระจากกัน
2. Normality : ประชากรทั้ง Kกลุมมีการแจกแจงแบบโคงปกติ
3. Homogeneity of variances : คาความแปรปรวนของแตละประชากรมีคาเทากัน
การวิเคราะหความแปรปรวน
ในที่นี้จะขอกลาวถึง ONE way ANOVA ( ตัวแปรอิสระ 1 ตัว )และ N - way ANOVA
( ตัวแปรอิสระ 2 ตัว ขึ้นไป )
125. 128
ONE way ANOVA เปนการวิเคราะหความแปรปรวนที่มีตัวแปรอิสระ 1 ตัว ที่มีมาตรการ
วัดแบบนามบัญญัติหรืออันดับ โดยแบงกลุมมากกวา 2 กลุมตัวอยาง สวนตัวแปรตามมี 1 ตัวโดยมี
มาตรการวัดแบบอันตรภาคหรืออัตราสวน
N - way ANOVA เปนการวิเคราะหความแปรปรวนที่มีตัวแปรอิสระ มากกวา1 ตัว ที่มี
มาตรการวัดแบบนามบัญญัติหรืออันดับ สวนตัวแปรตามมี 1 ตัวโดยมีมาตรการวัดแบบอันตรภาค
หรืออัตราสวน
การวิเคราะหความแปรปรวน แบบ ONE way ANOVA
สรุปการวิเคราะหความแปรปรวนแบบมีปจจัยเดียว เพื่อทดสอบความแตกตางระหวาง คาเฉลี่ย k ประชากร
สมมติฐาน Η0 : µ1 = µ2 = µ3=… = µk
Η1 : มี µi ≠ µj อยางนอย 1 คู ; i ≠ j
สถิติทดสอบ F = MSTrt
MSE
เขตปฏิเสธ จะปฏิเสธ Η0 ถา F > F 1-α;k-1,n-k
ตารางการคํานวณของ ANOVA
แหลงแปรปรวน
ระหวางทรีทเมนต
( Treatment )
ภายในทรีทเมนต
(ความคลาดเคลื่อน )
ผลรวม ( Total )
องศาอิสระ
DF
k-1
ผลบวกกําลัง
สอง SS
SSTrt
คาเฉลี่ยกําลังสอง
MS = SS/DF
MSTrt
n-k
SSE
MSE
n-1
SST
ตัวอยาง เปรียบเทียบผลการประเมินการปฏิบัติของสวนงาน 3 แหง
ตัวแปรอิสระ (X) : สวนงาน 3 แหง
ตัวแปรตาม (Y) : คะแนนประเมินผล
F
MSTrt
MSE
126. 129
สวนงาน ก.
สวนงาน ข.
สวนงาน ค.
10
6
5
9
4
6
10
7
5
8
3
2
8
5
2
รวม
45
25
20
Ho : µ 1 = µ 2 = µ3
H1 : µ i ≠ µ j อยางนอย 1 คู
คาสถิติที่ตองหา
1 ) คาความแตกตางทั้งหมด (The total variation) คํานวณไดจากการเปรียบเทียบคาจริงกับ
คาเฉลี่ยทั้งหมด ( Grand mean ) Y
สูตร Sum of Square Total ( SST )
n
SST = ∑ (Yi - Y ) 2
i=1
2 ) คาความแตกตางระหวางกลุม ( The between group variation ) คํานวณไดจากการ
เปรียบเทียบคาเฉลี่ยของแตละกลุม(Yj) กับคาเฉลี่ยทั้งหมด (Y)
สูตร Sum of Square Between Groups ( SSB )
K
SSB = ∑ n ( Yj -Y ) 2
j=1
3 ) คาความแตกตางภายในกลุม ( The within group variation ) คํานวณไดโดยการ
เปรียบเทียบคาจริงของหนวยตัวอยางที่เกิดขึ้นของแตละกลุม( Yi j)กับคาเฉลี่ยของกลุมนั้น(Yj)
สูตร Sum of Square Within Groups ( SSW )
K n
SSW = ∑ ∑ ( Yi j - Yj ) 2
j = 1 i=1
SST = SSB + SSW
MST = SST
= SST
dfT
n–1
127. 130
MSB
MSW
F
η2
= SSB
dfB
= SSW
dfw
=
MSB
MSW
=
SSB
SST
= SSB
K-1
= SSW
n–K
แทนคาจากตัวอยาง
คาเฉลี่ยของแตละกลุม
Y1
=
Y2
=
Y3
=
45 =
5
25 =
5
20 =
5
9
5
4
คาเฉลี่ยทั้งหมด (Grand mean)
Y
= 45+25+20 = 6
15
คา Sum of Square ทั้ง 3 สามารถคํานวณได ดังนี้
SST = (10 - 6)2+ (9 - 6)2+ (10 - 6)2 + (8 - 6)2+(8 - 6)2 +(6 - 6)2+(4 - 6)2+
(7 - 6 )2+(3 - 6 )2+ (5 - 6)2+ (5 - 6)2+ (6 - 6)2+ (5 - 6)2+ (2 - 6)2+ (2 - 6) 2
= 98
SSB = 5 (9 - 6) 2 + 5 (5 - 6) 2 + 5 (4 - 6) 2
= 70
SSW = (10 - 9)2 + (9 - 9)2 + (10 - 9)2 + (8 - 9)2 + (8 - 9)2 + (6 - 5)2 + (4 - 5)2 +
(7 - 5)2+ (3 - 5)2+ (5 - 5)2+ (5 - 4)2+ (6 - 4)2+ (5 - 4)2+ (2 - 4)2+ (2 -4)2
= 28
F
=
MSB
MSW
=
SSB / ( K - 1 )
SSW / ( n - K )
128. 131
=
70 / ( 3 - 1 )
28 / ( 15 - 3 )
=
=
70 x 12
2 28
ผลการวิเคราะหความแปรปรวนทางเดียว
15.02
แหลงความแปรปรวน df
SS
MS
F
ระหวางกลุม
2
70
35
15.02
ภายในกลุม
12
28
2.33
รวม
14
98
เปดตาราง Critical value ของ F จากตาราง ∝ = 0.01 และ องศาอิสระของ F คือ 2 และ 12 คือ
6.93
ปฏิเสธ Ho สรุปไดวาคะแนนประเมินผลเฉลี่ยของ สวน
F คํานวณ > F เปดตาราง
งานมีความแตกตางกันอยางนอย 1 คู อยางมีนัยสําคัญทางสถิติที่ระดับ 0.01
การที่จะทราบวากลุมใดบางที่แตกตางกัน ตองทําการทดสอบตอไป เรียกวา Post hoc
analysis โดยใชวิธีการวิเคราะหที่เรียกวาวิธีเปรียบเทียบพหุ (Multiple comparison procedure) ซึ่งมี
หลายวิธี ดังตอไปนี้
วิธีการเปรียบเทียบซึ่งโปรแกรม SPSS แบงออกเปน 2 กลุมคือ
1. วิธีการเปรียบเทียบเชิงซอนที่มีเงื่อนไขวา คาแปรปรวนของขอมูลทุกชุดตองเทากัน
ประกอบดวย
1.Least-Significant Different(LSD)
2.Bonferroni
3.Sidak
4.Scheffe
5.RE-G-WF
6.R-E-G-WQ
7.S-N-K(Student-Newman-Keuls)
8.Tukey
9.Tukey’s – b
10.Duncan
11.Hochberg’s GT2
12.Gabriel
13.Waller – Duncan
14.Dunnett’s C
2. วิธีการเปรียบเทียบเชิงซอนที่ไมมีเงื่อนไขเกี่ยวกับการเทากันของคาแปรปรวน
1.Tamhane’s T2
2.Dunnett’s T3
3.Games-Howell
4.Dunnett’s C
129. 132
ในที่นี้จะอธิบายวิธีการเปรียบเทียบเชิงซอนบางวิธีดังนี้
1. Least-Significant Different(LSD)
LSD หรือ Fisher’s Least-Significant Difference เปนเทคนิคที่ R.A. Fisher ได
พัฒนาขึ้นเพื่อเปรียบเทียบคาเฉลี่ยประชากรไดครั้งละหลายคู โดยมีขั้นตอนดังนี้
LSD = t
MSE
α
1− ;n − k
2
1
1
+
ni n j
1) คํานวณคา LSD โดยที่
ถา ni = nj จะทําให
LSD = t
X Max
α
1− ;n − k
2
2 MSE
ni
คํานวณความแตกตางระหวางคาเฉลี่ย X i − X j
2) นํา | X i − X j | เปรียบเทียบกับคา LSD
3.1 ถา | X i − X j | > LSD แสดงวา µ i ≠ µ j
3.2 ถา | X i − X j | ≤ LSD แสดงวา µ i ไมแตกตางจาก
หมายเหตุ สวนใหญผูวเิ คราะหมักจะคํานวณหา
− X Min |, | X ÃͧMax − X ÃͧMin |,... แลวนํามาเปรียบเทียบกับคา LSD
µj
2. Student-Newman-Keuls (SNK) Multiple Range Test
เปนวิธีการเปรียบเทียบคาเฉลี่ยประชากรโดยใชคาเฉลี่ยตัวอยางมีคามากที่สุดและนอย
ที่สุดกับคา Studentized range statistic
ี้
เงื่อนไข วิธีนจะใชไดเมื่อขนาดตัวอยางแตละชุดเทากัน คือ n 1 = n 2 = n 3 = ... = n k = r
SNK (v , α ) = q α .v .n −k
MSE
r
โดยที่คา q เปดไดจากตาราง และ v = จํานวนคาเฉลี่ยที่อยูในชวงที่เปรียบเทียบ โดย
พิจารณาจากคาเฉลี่ยตัวอยางแตละชุดที่เรียงลําดับจากนอยไปมาก จํานวน t คาดังนี้
X Min ≤ X ≤ ... ≤ X Max
X [1 ] ≤ X [ 2 ] ≤ ... ≤ X [ k ]
X
(1 )
= min( X [1 ] , X [ 2 ] ,..., X [ k ] )
X [ k ] = max( X 1 , X 2 ,..., X k )
130. 133
ขั้นตอนในการใช SNK ในการเปรียบเทียบคาเฉลี่ย 2 ประชากรหลาย ๆ คูพรอมกัน มีดังนี้
1. คํานวณคา SNK
2. คํานวณคาเฉลี่ยตัวอยาง X 1 , X 2 ,..., X k แลวนํามาเรียงลําดับจากนอยไปหามาก
3. คํานวณคา | X i − X j |
4. นําคา | X i − X j | เปรียบเทียบกับ SNK(v,α)
4.1 ถา | X i − X j | > SNK(v,α) จะปฏิเสธ H0 นั่นคือ µ1 ≠ µ 2 โดยที่ X i และ
X j หางกัน v อันดับ
4.2 ถา | X i − X j | ≤ SNK(v,α) จะสรุปวา µ i ไมแตกตางจาก µ j
3.Tukey’s Honesty Significant Difference (HSD)
เปนวิธีการเปรียบเทียบคาเฉลี่ยประชากร ที่มีเงื่อนไขเหมือนวิธี SNK คือ ตัวอยางแตละชุดมี
ขนาดเทากัน = r
HSD = q α .v .n −k
MSE
r
โดยที่ v = จํานวนกลุม/ประชากรที่ตองการเปรียบเทียบ คา q เปดไดจากตาราง ขั้นตอนมี
ดังนี้
1. คํานวณ HSD
2. คํานวณคา | X i − X j |
3. เปรียบเทียบคา | X i − X j | กับ HSD
3.1 ถา | X i − X j | > HSD แสดงวา µ1 ≠ µ 2
3.2 ถา | X i − X j | ≤ HSD จะสรุปวา µ i ไมแตกตางจาก µ j
หมายเหตุ สําหรับวิธีอื่น ๆ คือ Duncan , Tukey’s และ Scheffe มีหลักเกณฑคลาย ๆ กัน โดยที่
Scheffe จะใชสถิติ F
131. 134
การวิเคราะหความแปรปรวน แบบ N- way ANOVA
ในที่นี้จะขอยกตัวอยาง Two- way ANOVA
ตัวอยางเชน ผลการเรียนซึ่งขึ้นอยูกับปจจัย 2 ปจจัยคือ
ปจจัยที่ 1 : ครูผูสอนซึ่งมี 3 คน ( a = 3 )
ปจจัยที่ 2 : วิธการสอนซึ่งมี 4 วิธี ( b = 4 )
ี
ซึ่งทําใหมีจํานวนทรีทเมนต = ab 3(4) = 12 ทรีทเมนต โดยที่ทรีทเมนตที่ 1 คือ ครูผูสอนคนที่ 1 ใช
วิธีการสอนแบบที่ 1 ,….., และทรีทเมนตที่ 12 คือ ครูผูสอนคนที่ 3 ใชวิธีการสอนแบบที่ 4
และ m คือจํานวนขอมูลในแตละทรีทเมนต
สําหรับเงื่อนไขของการวิเคราะหความแปรปรวนแบบมี 2 ปจจัย มีดังนี้
1. แตละประชากรมีการแจกแจงแบบปกติ
2. แตละประชากรมีคาแปรปรวนเทากัน
SST = SSA + SSB + SSAB + SSE
SST = ผลบวกของความผันแปรทั้งหมดที่มีองศาอิสระ abm – 1
= n-1
SSA = ผลบวกของความผันแปรที่เกิดจากปจจัย A ที่มีองศาอิสระ ( a-1 )
SSB = ผลบวกของความผันแปรที่เกิดจากปจจัย B ที่มีองศาอิสระ ( b-1 )
SSAB = ผลบวกของความผันแปรที่เกิดจากอิทธิพลรวมของปจจัย A และ B ที่มีองศา
อิสระ( a-1 ) ( b-1 )
SSE = ผลบวกของความคลาดเคลื่อนยกกําลังสอง ที่มีองศาอิสระ ab(m-1)
SST = ΣΣΣ( Χi j k - x ) 2
a
SSA = Σ bm ( Ai -
x
)2
i=1
b
SSB = Σ bm ( Bj - x ) 2
j=1
SSE = ΣΣΣ( Χi j k -( AB )i j) 2
และ SSAB = SST – SSA – SSB – SSE
132. 135
ตารางการวิเคราะหความแปรปรวนแบบมี 2 ปจจัย
F
องศาอิสระ
SS
ปจจัย A
a-1
SSA
ปจจัย B
b-1
SSB
AB
(a-1)(b-1) SSAB
ความคลาดเคลื่อน
ab(m-1)
SSE
ผลรวม
abm-1
SST
MS = SS/df
F
MSA MSA/ MSE
MSB MSB/ MSE
MSAB MSAB/ MSE
MSE
สมมติฐานของการทดสอบเมื่อมีปจจัย 2 ปจจัย มีดังนี้
1. การทดสอบอิทธิพลของระดับตาง ๆ ของปจจัยที่ 1 ( ปจจัย A )
Η0 : ไมมีความแตกตางระหวางระดับตาง ๆ ของปจจัย A ( ปจจัยที่ 1 )
Η1 : มีอยางนอย 1 ระดับที่แตกตางจากระดับอื่น ๆ ของปจจัย A
สถิติทดสอบ F = MSA
MSE
เขตปฏิเสธ จะปฏิเสธ Η0 ถา F > F1- α ; ที่องศาอิสระ ( a-1) และ ab(m-1)
2. การทดสอบอิทธิพลของระดับตาง ๆ ของปจจัยที่ 2 ( ปจจัย B )
Η0 : ไมมีความแตกตางระหวางระดับตาง ๆ ของปจจัย B ( ปจจัยที่ 2 )
Η1 : มีอยางนอย 1 ระดับที่แตกตางจากระดับอื่น ๆ ของปจจัย B
สถิติทดสอบ F = MSB
MSE
เขตปฏิเสธ จะปฏิเสธ Η0 ถา F > F1- α ; ที่องศาอิสระ ( b-1) และ ab(m-1)
3. การทดสอบอิทธิพลของระดับตาง ๆ ของปจจัยที่ 1 และ ปจจัยที่ 2
Η0 : ไมมีความแตกตางระหวางระดับตาง ๆ ของปจจัย A และ B
Η1 : มีอยางนอย 1 ระดับที่แตกตางจากระดับอื่น ๆ ของปจจัย A และB ที่ตางจากทรีทเมนตอื่นๆ
สถิติทดสอบ F = MSAB
MSE
เขตปฏิเสธ จะปฏิเสธ Η0 ถา F > F1- α ; ที่องศาอิสระ ( a-1)(b-1) และ ab(m-1)
133. 136
ตัวอยาง ระดับคานิยมเกียวกับการประหยัดของประชาชนจําแนกตามการศึกษาและอาชีพ
่
ตัวแปรอิสระ (X1) : อาชีพ 3 อยาง
(X2) : การศึกษา 4 ระดับ
ตัวแปรตาม (Y) : ระดับคานิยมเกี่ยวกับการประหยัดของประชาชน
ป4
รวม
จบมัธยมตอนตน
รวม
จบมัธยมตอนปลาย
รวม
จบอุดมศึกษา
รวม
รวมทั้งหมด
ขาราชการ
X1 X21
2
4
3
9
1
1
4
16
10
30
5
4
3
2
14
3
2
3
1
9
3
2
4
1
10
43
25
16
9
4
54
9
4
9
1
23
9
4
16
1
30
137
คาขาย
X1 X21
3
9
4
16
2
4
3
9
12
38
เกษตรกร
X1 X21
4
16
3
9
4
16
2
4
13
45
4
3
2
1
10
3
4
4
3
14
4
4
1
4
12
48
5
2
3
3
13
4
3
5
3
15
5
3
3
4
14
55
การคํานวณ ANOVA สองทางก็คลายกับทางเดียว
SST =
SSx1 + SS x2 + SSx1 x2 + SS error
η2 =
SSx1 + SS x2 + SSx1 x2
16
9
4
1
30
9
16
16
9
50
16
16
1
16
42
160
25
4
9
9
47
16
9
25
9
59
25
9
9
16
54
205
รวม
35
37
38
36
146
134. 137
จากตัวอยาง จะตองหาคา ∑ X t , ∑ X2 t และ nt ดังนี้
∑ Xt
=
43 + 48 + 55
= 146
∑ X2 t
=
137 + 160 + 206 = 502
nt
=
16 + 16 + 16
= 48
จากนั้นหาผลรวมความเบียงเบนกําลังสอง ซึ่งการวิเคราะหแบบสองทางจะตองหาร SS รวม
่
( SSt ) ตามแนวตั้ง ( SSc) ตามแนวนอน ( SSr ) ระหวางกลุม ( SSb ) ปฏิสัมพันธรวม ( SSi )และ
ความคลาดเคลื่อน ( SSe )
SSt
SSc
SSr
SSb
SSi
SSe
= ∑ X2 t - ( ∑ X t ) 2
nt
2
= 502 - ( 146 ) = 57.92
48
= ( ∑ Xc 1 ) 2 + ( ∑ Xc 2 ) 2 + ( ∑ Xc 3 ) 2 - ( ∑ Xt ) 2
nc1 nc2
nc3
nct
2
2
2
2
= ( 43 ) + ( 48 ) + ( 55 ) - ( 146 )
16
16
16
48
= 4.54
= ( ∑ Xr 1 ) 2 + ( ∑ Xr 2 ) 2 + ( ∑ Xr 3 ) 2 + ( ∑ Xr4 - (∑ Xt ) 2
nr1
nr2
nr3
nr4
nt
2
2
2
2
2
= ( 35 ) + ( 37 ) + ( 38 ) + ( 36 ) - ( 146 )
12
12
12
12
48
= 0.42
= ( ∑ Xc 1r1 ) 2 + ( ∑ Xc 2r2 ) 2 ++ ......... - ( ∑ Xt ) 2
nc1r1
nc2r2
nt
= ( 10 ) 2 + ( 12 ) 2 + ( 13 ) 2 ++...+ ( 14 ) 2 - ( 146 ) 2
4
4
4
4
48
= 10.92
= SSb - SSc - SSr
= 10.92 - 4.54 - 0.42 = 5.96
= SSt - SSb
= 57.92 - 10.92 = 47.00
จากนั้นทําตารางวิเคราะหความแปรปรวน ดังนี้
135. 138
ผลการวิเคราะหความแปรปรวนสองทาง
แหลงความแปรปรวน
ตามแนวตั้ง ( c )
ตามแนวนอน ( r )
ปฏิสัมพันธรวม ( i )
ความคลาดเคลื่อน ( e )
รวม
df
2
3
6
36
SS
4.54
0.42
5.96
47.00
47
MS
2.27
0.14
0.99
1.30
57.92
F
1.75
0.11
0.76
-
P
> .05
> .05
> .05
-
คา df ของ SSe = c - 1 ของ SSr = r - 1 ของ SSi = ( c - 1 ) ( r - 1 ) และ SSe = nt - cr
ของ SSt =
nt - 1 สวน MS หาไดดวยการเอา df หาร SS ของแตละแหลง F นั้น จะมีคา 3 คา
ดวยการเอา MSe หาร MSc , Msr และ MSi
การแปลผลจะตองดูคา F ของปฏิสัมพันธรวมกอน โดยนําไปเทียบกับ F ในตารางที่ df =
6,36 และ α = 0.05 มีคา 2.42 แสดงวานอยกวาคาในตาราง แปลวา อิทธิพลจากปฎิสัมพันธ
ระหวางการศึกษากับอาชีพไมมีผลตอคานิยมเกียวกับการประหยัด จากนั้นจึงแปลผลตามแนวตั้งและ
่
แนวนอนตอไป เชนเดียวกันคือ พบวานอยกวาคา F ในตาราง แสดงวาทั้งการศึกษาและอาชีพไมมผล
ี
ที่จะทําใหคานิยมเรื่องนี้ตางกัน ถาตางกันจะตองวิเคราะหรายคูตอไปเชนเดียวกับการวิเคราะหทาง
เดียว สวนถาพบวาปฏิสัมพันธรวมมีนัยสําคัญ ( Significance ) จะแปลผลตามแนวตั้งและแนวนอน
ตอไปไมได เพราะจะทําใหเขาใจผิดได ดังนั้นจึงตองควบคุมตัวแปรตามแนวนอนและแนวตั้งทีละตัว
และวิเคราะหตอไป
การวิเคราะห ANOVA โดยใชโปรแกรม SPSS for Windows
มีวิธีการ ดังนี้
1. การทดสอบความแตกตางระหวางกลุมทีมีประชากรมากกวาสองกลุม ตัวแปรอิสระ 1
่
ตัว ( ใชสถิติ one way ANOVA)
1.1 ใชคําสั่ง
Analyze
Compare Means
One - Way ANOVA
จะไดหนาจอดังรูปที่ 1
รูปที่ 1 One way ANOVA
136. 139
จากรูป 1 - เลือกตัวแปรตามที่มีระดับการวัด interval ขึ้นไป ใสใน Dependent List
เชน รายไดของครอบครัว(income)
- เลือกตัวแปรตนที่มีระดับการวัดเปน Nominal หรือ Ordinal ที่มีการแบงกลุม
เพื่อเปรียบเทียบคาเฉลี่ยระหวางกลุม เชน ชื่อโรงเรียน ทั้งนี้เพื่อคํานวณรายไดเฉลี่ยจําแนกตาม
โรงเรียน ใสใน Factor
1.2 เลือก Post Hoc… จะไดหนาจอดังรูปที่ 2
รูปที่ 2 Post Hoc Multiple Comparisons
จากรูปที่ 2 จะแสดงถึงวิธีการเปรียบเทียบเชิงซอน เพื่อตองการทดสอบวาคาเฉลี่ยของกลุม
ใดบางที่แตกตางกัน ซึ่งมี 2 เงื่อนไข คือ
1. Equal Variances Assumed หมายถึง ขอมูลทุกชุดตองมีคาความแปรปรวนเทากัน
จึงใชสถิติทดสอบคูที่แตกตางใน BOX แรกรูป 8 ตัวใดตัวหนึ่งหรือหลายตัวก็ได
2. Equal Variances Not Assumed หมายถึง ขอมูลทุกชุดไมมีเงื่อนไขของการเทากันเลือก
สถิติทดสอบแลวเลือก continue จะกลับมาที่หนาจอรูป 1
1.3 เลือก Options… จะไดหนาจอดังรูป 3
รูปที่ 3 : Options
137. 140
สามารถเลือก - Descriptive สถิติแบบบรรยาย ( X , SD , SE , MAX , MIN )
- Homogeneity of variance จะหาคาสถิติทดสอบ Levene ของการ
ทดสอบความเทากันของคาแปรปรวน แลวเลือก continue จะกลับมาหนาจอดังรูปที่ 1
แลว เลือก OK จะไดผลลัพธในตารางที่ 1 – 3
ตารางที่ 1 Test of Homogeneity of Variances
Levene
Statistic
income
df1
18.942
df2
3
Sig
1396
.000
จากตารางที่ 1 หมายความวา ความแปรปรวนของรายไดครอบครัวนักเรียนของแตละ
โรงเรียนไมเทากัน (Sig = .000)
ตารางที่ 2 ANOVA
Sum of
Squares
Income of Between Groups
Within Groups
Total
df
168497230601.3
1929890669186
2098387899787
3
1396
1399
Mean
Square
56165743533.772
1382443172.769
F
40.628
Sig.
.000
จากตารางที่ 2 หมายความวา รายไดเฉลี่ยมีความแตกตางกันในแตละโรงเรียนอยางนอย 1
คู อยางมีนัยสําคัญทางสถิติ จึงตองทดสอบตอไปวาโรงเรียนใดบางทีมีรายไดเฉลี่ยตางกัน โดยใชวิธี
่
LSD ดังแสดงในผลลัพธ ตารางที่ 3
138. 141
ตารางที่ 3 Multiple Comparisons
Dependent Variable : income of respondent
LSD
Mean
(I )
(J)
Difference
School
School
Std. Error
( I-J )
2674.17
24938.28*
1
2
2968.12
23621.64*
3
3023.31
5566.56
4
2674.17
-24938.28*
2
1
2710.65
-1316.64
3
2770.97
-19371.72*
4
2968.12
-23621.64*
3
1
2710.65
1316.64
3
3055.62
-18055.08
4
3023.31
-5566.56
4
1
2770.97
19371.72*
2
3055.62
18055.08*
3
95 % Confidence Interval
Lower Bound Upper Bound
Sig.
30184.11
19692.45
0.000
29444.10
17799.18
0.000
11497.27
-364.16
0.066
-19692.45
-30184.11
0.000
4000.74
.6634.02
0.627
-13936.02
.24807.43
0.000
-17799.18
-29444.10
0.000
6634.02
-4000.74
0.627
-12060.99
-24049.18
0.000
364.16
-11497.27
0.066
24807.43
13936.02
0.000
24049.18
12060.99
0.000
• The mean difference is significant at the .05 level.
จากตารางที่ 3 หมายความวา เมื่อเปรียบเทียบรายไดของครอบครัวนักเรียนแตละโรงเรียน
พบวาคูที่มีรายไดของครอบครัวนักเรียนทีแตกตางกัน 4 คู ไดแก
่
1. โรงเรียน 1 และ 2
2. โรงเรียน 1 และ 3
3. โรงเรียน 2 และ 4
4. โรงเรียน 3 และ 4
ซึ่งสามารถนําเสนอผลการวิเคราะหในตาราง ดังตอไปนี้
โรงเรียน
รายไดของครอบครัวนักเรียน
F -test P-value
คาเฉลี่ย
สวนเบี่ยงเบนมาตรฐาน
1
56541.35
48285.67
40.628
0.000
2
31603.07
23386.18
3
32919.71
23205.95
4
50974.79
51427.68
139. 142
เปรียบเทียบรายคู
โรงเรียน 1 2
1 3
1 4
2 3
2 4
3 4
ความแตกตางของคาเฉลี่ย( Mean Difference )
24938.28*
23621.64*
5566.56
-1316.64
-19371.72*
-18055.08*
P - value
0.000
0.000
0.066
0.627
0.000
0.000
2. ประชากรมากกวาสองกลุมที่มีตัวแปรอิสระ 2 ตัวขึ้นไป ( ใชสถิติ factorial ANOVA )
2.1ใชคําสั่ง
Analyze
General Linear Model
Univariate…
จะไดหนาจอแสดงดังรูปที่ 4
รูปที่ 4 : Univariate
จากรูปที่ 4 - เลือกตัวแปรตามที่มีระดับการวัด interval ขึ้นไป ใสใน dependent เชน income
- เลือกตัวแปรตนที่มีระดับการวัดเปน nominal หรือ ordinal ที่เปนการจัดประเภทใสใน
Fixed Factor (s)
2.2 เลือก Models จะไดหนาจอ ดังรูปที่ 5
รูปที่ 5 : Univariate: Model
140. 143
จากรูปที่ 5 เลือก Full factorial จะไดอิทธิพลของและปจจัยและปจจัยรวมของปจจัยตางๆ
แลวเลือก continue จะกลับมาหนาจอดังรูปที่ 4
2.3 เลือก Contrasts จะไดหนาจอ ดังรูปที่ 6
รูปที่ 6 : Univariate: Contrasts
การใชคําสั่ง Contrast เมื่อตองการทดสอบความแตกตางของแตละระดับของปจจัย
สามารถเลือกชนิดของ Contrast ใน box ของContrasts ตอจากนั้นจึงเลือก continue จะกลับมา
หนาจอดังรูปที่ 4
2.4 เลือก Plots จะไดหนาจอ ดังรูปที่ 7
รูปที่ 7 Plots
การใชคําสั่ง Plots จะไดกราฟเสนตรงที่แตละจุดประมาณคา เฉลี่ยของตัวแปรตามทีแตละ
่
ระดับของปจจัย เมื่อเลือกแลว ตามดวย continue จะกลับมาหนาจอดังรูปที่ 4
2.5 เลือก Post Hoc จะไดหนาจอ ดังรูปที่ 8
รูปที่8 Post Hoc Multiple Comparison
141. 144
การใชคําสั่ง Post Hoc เพื่อเปรียบเทียบเชิงซอนของคาเฉลี่ยแตละคู เมื่อเลือกแลว ตามดวย
continue จะกลับมาหนาจอดังรูปที่ 4
2.6 เลือก Options… จะไดหนาจอรูปที่ 9
รูปที่ 9 : Options
จากรูปที่ 9 ผูวิจัยสามารถเลือก Estimated Marginal Means , Display , Significance Level
แลวเลือก continue จะกลับมาที่หนาจอรูปที่ 4 แลวเลือก OK จะไดผลลัพธแสดงในรูปตารางที่ 4
ตารางที่ 4 ผลลัพธของตัวอยาง ANOVA
Sum of
Squares
Income
Model
school
status
2 - Way Interactions sschool*status
Error
Total
Corrected Total
df
2.6E+12
1.0E+10
2.8E+10
1.0E+10
1.8E+12
4.5E+12
2.0E+12
16
3
3
9
1384
1400
1399
Mean
Square
1.6E+11
3.4E+09
9.5E+09
1.1E+09
1.3E+09
F
Sig.
120.56
2.51
7.00
0.87
.000
0.57
0.00
0.54
R Squared = .582 (Adjusted R Squared = .577)
จากตารางที่ 4 หมายความวา ตัวแปรตนหรือ Main Effects มี 2 ตัว ไดแก โรงเรียนของ
นักเรียน( school ) และสถานภาพสมรสของผูรับผิดชอบครอบครัว ( status ) ตัวแปรตามไดแก
รายไดของผูรับผิดชอบครอบครัว ( income of respondent ) กอนอื่นตองดูผลของปฏิสัมพันธ
ระหวางตัวแปรตน ( 2- way interactions ) ถา interaction มีผลตอรายไดของผูรับผิดชอบครอบครัว
ไมจําเปนตองอานผลตอ แตถา interaction ไมมีผลตอรายได ฯ( sig > 0.05) จึงกลับไปดู Main
Effects แตละตัว วามีผลตอรายได ฯ หรือไม ซึ่งจากตารางพบวาโรงเรียน ไมมีผลตอรายไดของ
ครอบครัว แตสถานภาพสมรสมีผลตอรายไดของครอบครัว
(sig <0.05 ) ซึ่งสามารถนําเสนอผลการวิเคราะหไดดังนี้
142. 145
ปจจัยที่มีผลตอรายได
ของผูรับผิดชอบครอบครัว
- โรงเรียน
- สถานภาพสมรส
- ปฏิสัมพันธระหวาง
โรงเรียนและสถานภาพสมรส
F
P-value
2.51
7.00
0.87
0.57
.000
0.54
แบบฝกหัด
(ใชโปรแกรมสําเร็จรูป)
1. อธิการบดีของสถานบันการศึกษาแหงหนึ่งเชื่อวามีนสิตที่พนสภาพการเปนนักศึกษาโดยเฉลี่ย ไม
ิ
เกิน 13% ของนักศึกษาทั้งหมด จึงสุมตัวอยาง จากคณะ ก. เพียงคณะเดียว แลวเก็บขอมูลรอยละของ
นักศึกษาที่พนสภาพในปที่ผานมา ยอนหลัง 12 ป ไดขอมูลดังนี้
13.4 13.3 14.5 11.7 14.0 12.0 15.4 12.3 12.9 12.6 14.9 13.1
จงทดสอบความเชื่อของอธิการบดีของสถานบันการศึกษาแหงนี้ที่ระดับนัยสําคัญ .05
2. โรงงานแหงหนึ่งมีคนงาน 2 ชุด ( 2 กะ ) ทางโรงงานเชื่อวาคนงานกะกลางวันผลิตสินคาเฉลี่ยตอวัน
ไดมากกวาคนงานกะกลางคืน จึงเลือกตัวอยางคนงานกะกลางวันมา 6 คน กะกลางคืน 9 คน และ
ตรวจสอบจํานวนชิ้นที่ผลิตไดตอวันไดขอมูลดังนี้
กลางวัน
41
20
19
36
38
26
กลางคืน
9
26
16
10
31
28
35
15
10
กําหนด α = .01 และถาทราบวาความสามารถในการทํางานของคนงานทั้ง 2 กะมีความแปรปรวนไม
แตกตางกัน
3. ในการวัดประสิทธิภาพการสอนวิชาสถิติการศึกษา จึงสุมนิสิตมา 10 คน กอนที่นสิตจะไดเรียนวิชา
ิ
นี้ แลวใหทดสอบความรูทางสถิติ แลวจึงใหเขาเรียนวิชาสถิติการศึกษา เปนเวลา 4 เดือน หลังจากเรียน
จบแลวจึงใหสอบใหมแลวตรวจสอบคะแนนของนิสิตทัง 10 คนขางตน ไดดังนี้
้
นิสิต
1
2
3
4
5
6
7
8
9
10
กอนเรียน
50
62
51
41
63
56
49
67
42
57
หลังเรียน
65
68
52
43
60
70
48
69
53
61
อยากทราบวา การสอนวิชาสถิติการศึกษา มีประสิทธิภาพหรือไม α = .025
143. 146
4. โรงเรียนแหงหนึ่งตองการทดสอบวาการเขาโครงการฝกปฏิบัติธรรมจะชวยใหนกเรียนมีผลสัมฤทธิ์
ั
ในการทํางานกลุมสูงขึ้นหรือไม จึงทําการทดสอบกับนักเรียน 10 คน เก็บคะแนนการทํางานกลุมของ
ทุกคน แลวจึงจัดใหเขาโครงการฝกปฏิบัติธรรมนาน 1 เดือน เมื่อสิ้นสุดโครงการแลววัดการทํางานกลุม
ของนักเรียนอีกครั้ง ปรากฏวาไดคะแนน ดังนี้
คะแนนการทํางานกลุม
นักเรียน
1
2
3
4
5
6
7
8
9
10
กอนเขาโครงการ 63
93
84
72
65
72
91
84
71
80
หลังเขาโครงการ 78
92
91
80
69
85
99
82
81
87
อยากทราบวาโครงการฝกปฏิบัติธรรมทําใหคะแนนการทํางานกลุมสูงขึ้นหรือไม กําหนดให α = .01
5. บริษัทซึ่งผลิตสบูออกจําหนายตองการทดสอบตลาดของสบูชนิดใหม 3 ชนิด ( A,B,C ) จึงนําสบู
ออกวางจําหนายในปที่ผานมา โดยเก็บยอดขายของสบูตามภาคตาง ๆ ที่วางขายไดขอมูลดังนี้
หนวย : 1000 บาท
ภาค
ภาคกลาง
ภาคเหนือ
ภาคใต
ภาคอีสาน
A
47
63
79
52
ชนิดของสบู
B
57
63
67
50
C
65
76
54
49
อยากทราบวายอดขายเฉลียของสบูใหมทั้ง 3 ชนิดและแตละภาคแตกตางกันหรือไมที่ระดับความเชื่อมั่น
่
95 %
6. ในหองปฏิบัติการการทอผาแหงหนึ่งตองการศึกษาผลของสีพิมพผา 4 ชนิด ( A,B,C,D ) เพื่อทําให
สีคงทน ไมซีดงาย แตเนื่องจากอาจารยผูสอนคิดวาชนิดของผาที่มีผลตอคุณภาพของสีดวย จึงสุมตัวอยาง
ผามา 3 ชนิด ๆ ละผืน แลวแบงผาแตละผืนเปน 4 สวน เทา ๆ กัน กําหนดสีผาพิมพแตละชนิดใหผาแตละ
สวนอยางสุม แลวทําการทดสอบความคงทนของสีไดดงนี้
ั
144. 147
1
C
9.9
A
10.1
B
11.4
D
12.1
ชนิดของผา
2
D
13.4
B
12.9
A
12.2
C
12.3
3
B
12.7
D
12.9
C
11.4
A
11.9
ก. จากขอมูลสรุปไดหรือไมวาคุณภาพของสีพิมพผาทั้ง 4 ชนิด แตกตางกันที่ระดับนัยสําคัญ .10
ข. อยากทราบวาชนิดของผามีผลทําใหคุณภาพของสีแตกตางกันหรือไม ที่ระดับนัยสําคัญ .05
7. ถาตองการเปรียบเทียบประสิทธิภาพของปุย 3 ชนิด ( ก , ข , ค ) จึงทดลองโดยการสุมพื้นที่มา 4 แหง
แลวแบงพื้นทีแตละแหงเปน 3 สวน ในแตละพื้นที่จะกําหนดชนิดของปุยแตละชนิดใหแตละสวนอยาง
่
สุม ไดขอมูลผลผลิต ดังนี้
พื้นที่
1
2
3
4
ก
11
13
16
10
ชนิดของปุย
ข
ค
15
10
17
15
20
13
12
10
จากขอมูลขางตนสรุปไดหรือไมวาปุยทั้ง 3 ชนิดมีประสิทธิภาพไมแตกตางกันที่ระดับนัยสําคัญ 0.05
7. ถาตองการศึกษาความแตกตางของวัตถุดิบที่ใชทํายางรถยนต 3 ชนิด ขนาดของยางรถยนต 3
ขนาด วามีอิทธิพลตออายุการใชงานของยางรถยนตหรือไม จึงสุมรถยนตมา 36 คัน แลวสุมให
ใชยางรถยนตและขนาดของยางรถยนตกลุมละ 4 คัน ไดขอมูล ดังนี้
145. 148
ชนิดของวัตถุดิบ
ขนาดของยางรถยนต
เล็ก
กลาง
ใหญ
1
78,62,72,68
82,78,70,75
92,85,87,90
2
65,70,75,69
72,68,73,76
85,79,84,80
3
81,78,75,85
87,83,82,85
94,90,89,95
ก. อยากทราบวามีอิทธิพลรวมของขนาดของยางรถยนต และชนิดของวัตถุดิบที่มีตอระยะทางทีวิ่ง
่
หรือไม
ข. อยากทราบวาขนาดของยางรถยนต มีอิทธิพลตอระยะทางที่วิ่งหรือไม
ค. อยากทราบวาชนิดของวัตถุดิบมีอิทธิพลตอระยะทางทีวงหรือไม
่ ิ่
กําหนดระดับนัยสําคัญ = 0.05
146. บทที่4
ความสัมพันธระหวางตัวแปรและการทํานายตัวแปร
ความสัมพันธระหวางตัวแปร
การศึกษาความสัมพันธระหวางตัวแปรเปนเปาหมายของขอสรุปงานวิจัยเพื่อใหเกิดความรู
ความเขาใจทีจะสามารถบรรยาย อธิบาย ตลอดจนควบคุมสิ่งตางๆได คาสถิติที่นํามาใชบอยมาก คือ คา
่
ั
สัมประสิทธิ์สหสัมพันธ (rxy) ซึ่งใชไดกบตัวแปร x และ y ที่มีมาตรการวัดแบบอันตรภาคขึ้นไป แตยังมี
คาสถิติอีกหลายตัวทีใชหาความสัมพันธระหวางตัวแปรที่อยูในเงื่อนไขที่ตางออกไป กอนที่จะอธิบาย
่
รายละเอียดของสถิติที่ใชหาความสัมพันธระหวางตัวแปรนั้น เพื่อใหเกิดความเขาใจในการเลือกใชสถิติ
เพื่อศึกษาความสัมพันธระหวางตัวแปรที่ชดเจนขึ้น จึงมีความจําเปนตองเขาใจในเรื่องมาตรการวัดของ
ั
ตัวแปร ซึ่งสรุปได ดังนี้
การแบงประเภทของขอมูลตามมาตรการวัด
แบงเปน
1 มาตรการวัดแบบนามบัญญัติ (Nominal data) เปนการจําแนกลักษณะของขอมูลที่ได
ออกเปนประเภทตางๆหรือเปนพวกๆ โดยจัดลักษณะทีเ่ หมือนกันไวดวยกัน เชน ตัวแปร เพศ เชือชาติ
้
สถานภาพสมรส เปนตน การจําแนกลักษณะของขอมูลของตัวแปรเปน 2 ลักษณะ เรียกวาตัวแปรทวิ
ิ
วิภาค (Dichotomous Variable) มีรูปแบบในการจําแนกทีแตกตางกันได 2 ลักษณะ คือ ตัวแปรทวิวภาค
่
แท (True dichotomous Variable) และตัวแปรทวิวภาคจําแนกตามเกณฑ (Artificially dichotomous
ิ
Variable) โดยพิจารณาจากเกณฑการจําแนกที่มีอยูแลว กับเกณฑที่ตองสรางขึ้น ถาเกณฑในการ
แบงตัวแปรออกเปน 2 ลักษณะ เปนเกณฑที่มีอยูแลว เชน ตัวแปรเพศ แบงเปน หญิงและชาย ก็จัดวา
ิ
เปนทวิวิภาคแท แตถาเปนเกณฑที่ตองสรางขึ้นเชนการสอบได - ตกของนักเรียนก็จัดวาเปนทวิวภาค
จําแนกตามเกณฑ
2 มาตรการวัดแบบอันดับ (Ordinal data) เปนการกําหนดลักษณะของขอมูลที่ได ออกเปน
อันดับที่บอกความมากนอยระหวางกันได เชนลําดับที่ของนักเรียนมารยาทดี คาลําดับที่ 1 , 2 , 3
สามารถบอกไดวาใครมารยาทดีกวาใคร แตไมสามารถบอกไดวาคนที่ไดมารยาทดีลําดับที่ 1 ดีกวา
ลําดับที่ 2 อยูเทาไร และไมสามารถบอกไดวาความแตกตางระหวางคนที่ไดมารยาทดีลําดับที่ 1 และ 2
จะเทากับความแตกตางระหวางคนที่ไดมารยาทดีลําดับที่ 2 และ 3 หรือชวงความหางของคาตัวแปรแต
ละคาไมเทากัน
3 มาตรการวัดแบบอันตรภาค (Interval data) เปนการกําหนดตัวเลขใหกับลักษณะของขอมูล
ตามความมากนอยโดยตัวเลขที่กําหนดสามารถบอกความมากนอยระหวางกันแลวยังมีชวงหางระหวาง
คาที่เทากันดวย แตคาศูนยทกําหนดตามมาตรการวัดนีไมใชศูนยแท ตัวอยาง เชน คะแนน อุณหภูมิ
ี่
้
เปนตน คาของอุณหภูมิ 80°C สูงกวาอุณหภูมิ 50°C อยู 30°C แตอุณหภูมิ 0°C มิไดแปลวาไมมความ
ี
รอน ความจริงมีความรอนระดับหนึ่งแตถูกสมมุติใหเปน 0°C
147. 150
4. มาตราการวัดแบบอัตราสวน (Ratio data) เปนการกําหนดตัวเลขใหกับลักษณะของขอมูล
เดียวกับมาตรการวัดแบบอันตรภาค แตมาตรการวัดระดับนีจะมีคา 0 ที่แทจริงดวย เชน อายุ รายได
้
น้ําหนัก สวนสูง เปนตน สวนสูง 0 เซนติเมตรก็แปลวาไมมีความสูงเลย
เพื่อใหเห็นภาพรวมของสถิติที่ใชในการหาความสัมพันธ จึงขอเสนอตารางสรุประเบียบวิธีวด
ั
ความสัมพันธจําแนกตามมาตรวัดตัวแปรกอนแลวตามดวยรายละเอียดของแตละวิธีตอไป
สรุประเบียบวิธีวัดความสัมพันธจําแนกตามมาตรวัดตัวแปร
มาตรวัดตัวแปร
มาตรวัดตัวแปร
ทวิวิภาคแท
ทวิวภาคแท
ิ
ทวิวภาคจําแนกตามเกณฑ
ิ
อันดับ
อันตรภาค/อัตราสวน
ทวิวิภาคจําแนก
ตามเกณฑ
Ø
Ø
rrb
rpb
rt e t
rrb
rbis
อันดับ
อันตรภาค/
อัตราสวน
rsr ,τ
rxy
1. Phi coefficient
เมื่อตองการหาความสัมพันธระหวางตัวแปรที่มีมาตรการวัดเปนทวิวิภาคแททั้งคู หรือตัวหนึ่ง
เปนทวิวิภาคแท อีกตัวหนึ่งเปนทวิวิภาคจําแนกตามเกณฑ จะตองใชสมประสิทธิ์ฟ (Ø) โดยมีลักษณะ
ั
ั
เปนตาราง 2 × 2 สัมประสิทธิ์ที่คํานวณไดเปนขนาดความสัมพันธวาตัวแปรทั้ง 2 ตัวมีความสัมพันธกน
มากนอยเพียงใด เชน การหาความสัมพันธระหวางฐานะเศรษฐกิจกับการไปเลือกตั้ง โดยมีสูตรใน
การคํานวณ ดังนี้
∧
bc − ad
สูตร
φ =
( a + b )( b + d )( a + c )( c + d )
คา a, b, c, d เปนคาความถี่ของตัวแปรไขวของ 2 ตัวแปร ดังตัวอยางในตาราง
ความขยัน
ขยัน
ไมขยัน
เพศ
ชาย
a
b
a+b
รวม
หญิง
c
d
c+d
a+c
b+d
a+b+c+d
148. 151
หลังจากการคํานวณคาสัมประสิทธิ์สหสัมพันธิ์แลว จึงทดสอบนัยสําคัญโดยใชสถิติ χ2 หรือ t – test
โดยมีสูตรคํานวณ ดังนี้
χ
t −
=
test
N φ
=
2
r
2
N
− 2
1 − r 2
ตัวอยาง การหาความสัมพันธระหวางเพศกับการไปโรงเรียน
การไปโรงเรียน
เพศ
ชาย
10 (a)
40 (b)
50
สาย
ไมสาย
30
82
112
bc − ad
∧
φ =
หญิง
20 (c)
42 (d)
62
รวม
( a + b )( b + d )( a + c )( c + d )
=
(40 20) - (10 42)
50 × 82 × 30 × 62
=
=
380
2761.52
0.1376
การทดสอบความมีนยสําคัญโดยใช χ2 หรือ t-test
ั
χ
2
= Nφ 2
= 112 × 0.13762
=
0.29
เปดตาราง χ 2 ที่องศาอิสระ n-1 = 112-1 = 111 α = .05 ไดคา 124
คา χ 2 ที่คํานวณไดนอยกวาคาทีไดจากการเปดตาราง แสดงวาไมอาจปฏิเสธสมมติฐานวางได
่
สรุปไดวาเพศกับการไปโรงเรียนไมมีความสัมพันธกันอยางมีนัยสําคัญทางสถิติที่ระดับ0.05
149. 152
2. The Tetracholic coefficient
เมื่อตองการหาความสัมพันธระหวางตัวแปรที่มีมาตรการวัดเปนทวิวิภาคโดยจําแนกตาม
เกณฑ ทังคู
้
r tet =
สูตร
โดยที่ Ux
Uy
n
bc − ad
u xu yn 2
= คาความสูงของการแจกแจงปกติมาตรฐาน(ordinate) ณ จุดตัด(สัดสวน)
จากตัวแปร x
= คาความสูงของการแจกแจงปกติมาตรฐาน(ordinate) ณ จุดตัด(สัดสวน)
จากตัวแปร y
= ขนาดของกลุมตัวอยาง
ตัวอยาง การหาความสัมพันธระหวางความชอบของหวาน กับความชอบผลไม
ความชอบ
ผลไม(y)
ชอบ
12(a)
32(b)
44
.55
ชอบ
ไมชอบ
รวม
สัดสวน
r tet =
ความชอบของหวาน (x)
ไมชอบ
รวม
สัดสวน
21(c)
33
.42
15(d)
47
.58
36
80
.45
Ux =.3958
bc − ad
u xu yn 2
= (32 21) - (12 15)
(.3958)(.3910) 802
= 492
990.44
= 0.4967
Uy =.3910
150. 153
3. The Rank-biserial correlation coefficient
เมื่อตองการหาความสัมพันธระหวางตัวแปรที่มีมาตรการวัดเปนทวิวิภาคและอันดับ
สูตร
โดยที่
y1
y0
(y
2
n
r rb =
− y
1
0
)
= คาเฉลี่ยอันดับของตัวแปรy จากกลุมตัวแปร x= 1
= คาเฉลี่ยอันดับของตัวแปรy จากกลุมตัวแปร x= 0
ตัวอยาง การหาความสัมพันธระหวางการทํางานบานกับอันดับที่ของคะแนน
การทํางานบาน (x)
อันดับที่ของคะแนน (y)
r rb
1
1
=
2
n
(y
0 1 1 1 0 0 1 1 1
2 3 4 5 6 7 8 9 10
− y
1
0
)
=
2 ( 5.71 - 5 )
10
= 0.142
4. The Spearman Rank correlation
เปนวิธีหาความสัมพันธระหวางตัวแปร 2 ตัวที่มีมาตรการวัดเปนอันดับทั้งคู มีสูตรในการ
คํานวณ คือ
สูตร
r sr = 1 −
6
∑
n (n
2
d
2
− 1)
โดยที่ d = ความแตกตางระหวางอันดับของ 2 ตัวแปร
n = จํานวนกลุมตัวอยาง
สถิติทดสอบนัยสําคัญ
t=
r N− 2
1− r 2
df = n-2
151. 154
ตัวอยาง การหาความสัมพันธระหวาง การใหคะแนนสอบวิชาสถิติ ของอาจารย 2 คน
นักเรียน
ครู
d
d2
คนที่1
คะแนน อันดับที่
19
17
16
18
15
1
2
3
4
5
สูตร
คนที่2
คะแนน อันดับที่
1
3
4
2
5
r sr
18
16
14
20
15
= 1 −
1
0
1
-1
-1
2
3
5
1
4
6
∑
n (n
d
2
1
0
1
1
1
2
− 1)
= 1- 6 4
5 (25-1)
=
0.8
แสดงวาการใหคะแนนของครู 2 คนมีความสัมพันธกันในระดับสูง
การทดสอบนัยสําคัญ
H0 : ρ = 0
Η1 : ρ > 0
r N− 2
t =
1− r2
=
0 .8 5 − 2
1− r2
= 0.8 (1.732)
0.6
= + 2.30
α 0.10
0
1.63 t (df =5-2 = 3)
t คํานวณมากกวาคาวิกฤต แสดงวาปฏิเสธสมมติฐาน H0 นั่นคือ การใหคะแนนของครู 2 คนมี
ความสัมพันธกันอยางมีนัยสําคัญทางสถิติที่ระดับ 0.10
152. 155
5. Kendall’s Tau
เมื่อตองการหาความสัมพันธระหวางตัวแปรที่มีมาตรการวัดเปนอันดับทั้งคู
คํานวณ คือ
สูตร
τ =
มีสูตรในการ
P − Q
n (n − 1) / 2
โดยที่ จํานวนความสอดคลอง คือ จํานวนอันดับที่ที่เหลือที่สูงกวาอันดับที่จัดเรียงจาก
ตัวแปรY เทียบตามอันดับทีจากนอยไปมากของตัวแปรX
่
จํานวนความผกผัน คือ จํานวนอันดับที่ที่เหลือต่ํากวาอันดับที่จัดเรียงจากตัว
แปรY เทียบตามอันดับที่จากนอยไปมากของตัวแปรX
p = ผลรวมของจํานวนความสอดคลอง
q = ผลรวมของจํานวนความผกผัน
n = ขนาดของตัวอยาง
ตัวอยาง ความสัมพันธระหวางอันดับที่ของจํานวนสส.และอันดับที่ของบัญชีรายชื่อ
ชื่อพรรค
ไทยรักไทย
ประชาธิปปตย
ชาติไทย
ชาติพัฒนา
ความหวังใหม
ประชากรไทย
เสรีธรรม
ถิ่นไทย
อันดับที่ของ อันดับที่ของ จํานวนความ
จํานวนสส.(x) บัญชีรายชื่อ(y) สอดคลอง
1
3
5
2
1
6
3
2
5
4
4
4
5
7
1
6
8
0
7
5
1
8
6
0
P=22
Q=6
τ =
=
=
P − Q
n (n − 1) / 2
22 - 6
8(8 -1)/2
16
=
28
0.57
จํานวนความ
ผกผัน
2
0
0
0
2
2
0
0
153. 156
6. The Point Biserial Correlation
เมื่อตองการหาความสัมพันธระหวางตัวแปรที่มีมาตรการวัดเปนทวิวิภาคแทและอันตรภาค/
อัตราสวน มีสูตรในการคํานวณ คือ
สูตร
y1 − y
sy
r pb =
n1n 0
(n − 1)n
0
โดยที่ y = คาเฉลี่ยของขอมูลระหวางตัวแปรy จากกลุมตัวแปร x= 1
y = คาเฉลี่ยของขอมูลระหวางตัวแปรy จากกลุมตัวแปร x= 2
1
0
SY = สวนเบี่ยงเบนมาตรฐานของขอมูลจากตัวแปร y ทั้งหมด
ตัวอยาง การหาความสัมพันธระหวางเพศกับคะแนนสถิติ
เพศ
ช
ช
ช
ช ช
ญ
ญ
ญ
ญ
ญ
คะแนนสถิติ
15
19
12
9 18
11
16
19
13
7
y = (15+19+12+9+18)/5 = 14.6
1
y = (11+16+19+13+7)/5 = 13.2
0
SY = 4.2
=
r pb
=
y
− y
1
s
n 1n 0
(n − 1)n
0
y
14.6 − 13.2
4.2
5× 5
(10 − 1)10
= 0.33 .52
= 0.17
7. The Biserial Correlation
เมื่อตองการหาความสัมพันธระหวางตัวแปรที่มีมาตรการวัดเปนทวิวิภาคตามเกณฑและ
อันตรภาค/อัตราสวน
สูตร
r bi
=
(y
1
− y
s
y
0
)
.
pq
u
โดยที่ y1 = คาเฉลี่ยของขอมูลระหวางตัวแปรy จากกลุมตัวแปร x= 1
y0 = คาเฉลี่ยของขอมูลระหวางตัวแปรy จากกลุมตัวแปร x= 0
p = สัดสวนของคนทีอยูในกลุมตัวแปร x= 1
่
154. 157
q = สัดสวนของคนทีอยูในกลุมตัวแปร x= 0
่
u = คาความสูงของการแจกแจงปกติมาตรฐาน(ordinate)ณ จุดตัด(สัดสวน)
SY = สวนเบี่ยงเบนมาตรฐานของขอมูลจากตัวแปร y ทั้งหมด
ตัวอยาง การหาความสัมพันธระหวางการตอบขอ 3 กับคะแนนรวม
การตอบขอ3
1
1
1
1
1
1
1
1
คะแนนรวม
21
35
37
32
22
28
39
40
การตอบขอ3
1
1
0
0
0
0
0
0
r bi
=
y
คะแนนรวม
38
36
31
28
21
22
27
33
− y
1
s
y
0
.
การตอบขอ3
0
0
0
0
0
0
0
0
0
คะแนนรวม
26
35
36
21
23
25
27
26
25
pq
u
= (32.8 - 27.06) ( 0.4 0.6)
6.28
0.3863
= 0.91 0 .621
= 0.565
8. Correlation coefficient
สหสัมพันธอยางงาย (Correlation) เปนการหาความสัมพันธระหวางตัวแปรตั้งแต 2 ตัวขึ้นไป
วามีความสัมพันธเกี่ยวของกันหรือไมลักษณะใดและความสัมพันธกนมากนอยเพียงใด สหสัมพันธมี
ั
หลายชนิด ทีรูจักกันทัวไปไดแก สหสัมพันธเชิงเดียว (Simple Correlation) สหสัมพันธพหุคณ
่
่
ุ
( Multiple Correlation) นอกจากนันจากสหพันธนยังวิเคราะหตอไปไดอีกเชนการวิเคราะหถดถอย
้
ี้
(Regression Analysis)
สหสัมพันธเชิงเดี่ยวเปนการหาความสัมพันธระหวางตัวแปร 2 ตัว และสมมติวามี
ความสัมพันธกันในลักษณะเสนตรง ความสัมพันธของตัวแปรของทังสองอาจจะสัมพันธกันใน 4
้
ลักษณะ คือ
155. 158
ลักษณะที่ 1 เปนการสัมพันธกันเชิงบวกอยางสมบูรณ มีลักษณะแปรผันตามกัน เมื่อ X
เพิ่ม Y ก็จะเพิมขึ้นดวย ถา X ลดลง Y ก็จะลดลงดวย และเพิ่มขึ้นหรือลดลงในอัตราสวนที่คงที่ ดัง
่
ลักษณะ 1
ลักษณะที่ 2 เปนการสัมพันธกันเชิงลบอยางสมบูรณ ในลักษณะผกผันกัน เมื่อ X เพิม Y ก็
่
จะลดลงดังลักษณะ 2
ลักษณะที่ 3 เปนการสัมพันธกันแบบไมสมบูรณ ซึ่งจะเปนลักษณะแปรผันตามกันหรือ
ผกผันกันได แตมีลักษณะสัมพันธต่ํา การสัมพันธจะกระจายกัน แตก็ยังเกาะกลุมกันทําใหเห็นวาเปน
เสนตรง ดังลักษณะ 3
ลักษณะที่ 4 เปนลักษณะที่ไมสัมพันธกันเปนเสนตรง คาของ X และ Y ที่ตัดกันกระจัด
กระจายทั่วไป และมีลักษณะคลายจะเปนวงกลม ไมสามารถบอกความสัมพันธของ X และ Y ไดวาเปน
ทิศทางใด ดังลักษณะ 4
12
10
10
8
8
6
6
4
4
2
2
0
0
2
4
6
8
10
Y
Y
12
12
X
0
0
2
4
6
8
10
12
4
6
8
10
12
X
ลักษณะ 1
ลักษณะ 2
12
7
6
10
5
8
4
3
6
2
1
2
0
2
4
6
8
10
Y
Y
4
12
0
0
X
2
X
ลักษณะ 3
ลักษณะ 4
ขนาดของความสัมพันธ ขนาดของความสัมพันธมีคาจาก 0 ถึง 1.00 สามารถจัดระดับความสัมพันธได
โดยประมาณ ดังนี้
ความสัมพันธทางลบอยางสมบูรณ
ลบระดับสูง
-1.00
ไมมีความสัมพันธ
ลบระดับกลาง ลบระดับต่ํา
-0.50
ความสัมพันธทางบวกอยางสมบูรณ
บวกระดับต่ํา บวกระดับกลาง บวกระดับสูง
0
+0.50
+1.00
156. 159
สูตรที่ใชในการคํานวณ คา r
r เรียกวา Pearson correlation coefficiient , Simple correlation , Correlation coefficient
r =
r =
r =
∑
− X )( Y
(X
NS
X
S
−Y )
=
∑
Y
∑ XY − [( ∑ X )( ∑Y ) / N
[( ∑ X ) − ( ∑ X ) / N ][ ∑Y ) − ( ∑Y )
2
2
2
∑
X .Y
2
X
2
∑
Y
2
/ N]
N ∑ XY − [( ∑ X )( ∑Y )]
[N ∑ X − ( ∑ X ) 2 ][N ∑Y − ( ∑Y ) 2 ]
2
2
ตัวอยาง จากการศึกษาความสัมพันธระหวางความรูกบความคิดเห็นของนักศึกษา 5 คน ไดคะแนน
ั
ความรูและความคิดเห็น ดังตาราง อยากทราบวา ความรูกับความคิดเห็นสัมพันธกันหรือไม ถาสัมพันธ
สัมพันธกันในทิศทางใด
การคํานวณ สมมติให X = คะแนนความรู และ Y = คะแนนความคิดเห็น จัดระเบียบเตรียมการ
วิเคราะห ดังนี้
ตาราง การจัดระเบียบเตรียมการวิเคราะหสหพันธแบบ Pearson
คนที่
1
2
3
4
5
รวม
X
5
5
4
3
3
20
X2
25
25
16
9
9
84
Y
8
9
8
6
7
38
Y2
64
81
64
36
49
294
การคํานวณคา r
N
r =
[N
=
=
=
∑
X
∑
2
XY − [(
∑
X )(
− ( ∑ X ) ][ N
2
∑Y
∑Y
2
)]
− (∑ Y ) 2 ]
5 (156)-(20)(38)
√(5(84)-400) (5(294)-(1444)
20
√ (20)(26)
0.877
XY
40
45
32
18
21
156
157. 160
สัมประสิทธิ์สหสัมพันธ เทากับ 0.877 แสดงวาความสัมพันธระหวางความรูกบความคิดเห็นของ
ั
นักศึกษา มีความสัมพันธในทางบวกระดับสูง
การทดสอบนัยสําคัญของคา r
ในการวิจัยนั้น หลังจากทีคํานวณคาสัมประสิทธิ์สหสัมพันธไดแลว และตองการที่จะ
่
สรุปวาตัวแปรคูนั้นมีความสัมพันธกันจริงหรือไม จะไมพิจารณาเฉพาะคาสัมประสิทธิ์สหสัมพันธที่
คํานวณได กลาวคือถึงแมวาจะคํานวณคาสัมประสิทธิ์สหสัมพันธไดคาหนึ่งซึ่งคอนขางสูง เชน .70 ขึ้น
ไป ก็จะยังไมสรุปวาตัวแปร 2 ตัวนั้นมีความสัมพันธกันจนกวาจะมีการทดสอบนัยสําคัญกอน (Test of
significance) ซึ่งตั้ง H0 และ H1 ดังนี้ H0 : ρ = 0, H1 : ρ ≠ 0 (Welkowitz. 1971 : 158)
วิธีทําสอบมี 2 วิธี คือใชตารางสําเร็จที่มีชื่อวาคาวิกฤตของสหสัมพันธแบบเพียรสัน หรือ
ใชการทดสอบคาที (t-test) จากสูตร
r N− 2
1− r 2
r แทน คาสัมประสิทธิ์สหสัมพันธที่คํานวณได
N แทน จํานวนขอมูลหรือจํานวนคน
วิธีการทดสอบมีขั้นตอนดังนี้
(1) คํานวณคา t จากสูตร
(2) เปด Table หาคา t ที่ df = N-2 ณ ระดับนัยสําคัญทางสถิติที่ตั้งไว
(3) เปรียบเทียบคา t ที่คํานวณไดกับคา t ที่เปดจากตาราง
ี
ถา t คํานวณ > t ตาราง แสดวาคา r ที่คํานวณไดมนัยสําคัญทางสถิติ แปลความหมายไดวา
ตัวแปร 2 ตัวนันมีความสัมพันธกันอยางมีนัยสําคัญทางสถิติที่ระดับ…
้
ถา t คํานวณ < t ตาราง แสดงวาคา r ที่คํานวณไดไมมนยสําคัญทางสถิติ แปลความไดวา
ี ั
ตัวแปร 2 ตัวนันมีความสัมพันธกันอยางไมมีนัยสําคัญทางสถิติ
้
ตัวอยางการทดสอบนัยสําคัญ
ตัวอยางที….จงทดสอบนัยสําคัญของคา r เมื่อ r = .877
่
t=
สูตร
t=
r N− 2
1− r 2
r = .877 , N = 5
t
=
=
. 877
5 − 2
1 − (. 877
1 . 519
. 480
)
2
= 3 . 164
158. 161
จากตาราง t ที่ α .10, df = 5-2 = 3, ได t = 2.353
t คํานวณ > t ตาราง แสดงวา r = .877 ที่คํานวณไดมนัยสําคัญทางสถิติ นั่นคือ มีความสัมพันธ
ี
ระหวางความรูกับความคิดเห็นของนักศึกษา อยางมีนยสําคัญทางสถิติที่ระดับ 0.10
ั
การทดสอบความสัมพันธระหวางตัวแปร 2 ตัว โดยใชโปรแกรม SPSS for Windows
การทดสอบความสัมพันธระหวางตัวแปร 2 ตัว สามารถการวิเคราะห โดยใชโปรแกรม
SPSS for Windows ไดดังนี้
1. ความสัมพันธระหวางตัวแปร 2 ตัว ที่มีระดับการวัดเปน ordinal (ใชสถิติ Spearman Rank
correlation )
2. ความสัมพันธระหวางตัวแปร 2 ตัว ที่มีระดับการวัดเปน interval หรือ ratio ( ใชสถิติ
Pearson product moment correlation )
1.1 ใชคําสั่ง
Statistics
Correlate
Bivariate
จะไดหนาจอ ดังรูปที่1
รูปที่ 1
เลือก ตัวแปรที่ตองการหาความสัมพันธใสใน box ของ variables แลวเลือก Spearman ใน
กรณีที่ตองการหาความสัมพันธของ 2 ตัวแปรที่มีระดับการวัดแบบ ordinal หรือเลือก Pearson ใน
กรณีที่ตองการหาความสัมพันธของ 2 ตัวแปรที่มีระดับการวัดแบบ interval หรือ ratio แลวเลือก
OK จะไดผลลัพธแสดงในตารางที่ 1-2
159. 162
ตารางที่ 1
Spearman's rho
EDUFA
EDUMA
Spearman's rho EDUFA
Correlation Coefficient
1.000
.729
Sig. (2-tailed)
.
.000
N
1408
1406
EDUMA Correlation Coefficient
.729
1.000
Sig. (2-tailed)
.000
.
N
1406
1421
** Correlation is significant at the .01 level (2-tailed).
จากตารางที่ 1 หมายความวา การศึกษาของบิดา ( Edufa ) มีความสัมพันธกับการศึกษาของ
มารดา (Eduma) อยางมีนยสําคัญทางสถิติที่ระดับ .01
ั
ซึ่งสามารถนําเสนอผลการวิเคราะหขอมูล ไดตามตารางตอไปนี้
ตัวแปร
Spearman's rho
การศึกษาของบิดา
การศึกษาของมารดา
.729
p - value
0.000
ตารางที่ 2 Pearson correlation
Pearson
Correlation
Sig.
( 1- tailed )
N
Total Expense
income of respondent
Total Expense
income of respondent
Total Expense
income of respondent
Total Expense income of respondent
1.000
.956
.956
1.000
.
.000
.000
.
90
90
90
90
จากตารางที่ 2 หมายความวา คาใชจาย ( Expense ) มีความสัมพันธกับ รายไดของ
ผูรับผิดชอบครอบครัว ( income of respondent ) อยางมีนัยสําคัญทางสถิติที่ระดับ .01
ซึ่งสามารถนําเสนอผลการวิเคราะหขอมูล ไดตามตารางตอไปนี้
ตัวแปร
r
p - value
คาใชจาย –รายได
.956
0.000
160. 163
การทํานายตัวแปร : การวิเคราะหถดถอย (Regression Analysis )
การวิเคราะหการถดถอย เปนสถิติที่ใชในการทํานายตัวแปรวิธีหนึ่ง เมื่อมีตัวแปรตนหรือตัว
แปรอิสระเพียงตัวเดียว และตองการทดสอบวาตัวแปรตนนั้นมีความสัมพันธกับตัวแปรตามอยางไร ใน
กรณีที่มีตวแปรเพียง 2 ตัวเชนนี้การวิเคราะหการถดถอยนี้เรียกวา Bivariate regression หรือ Simple
ั
regression ถา plot จุด โดยใหแกน X เปนจํานวนครั้งของการไปซื้อสินคา และแกน Y เปนทัศนคติของ
ผูบริโภคที่มีตอหางสรรพสินคา จะไดรูป Scatter diagram ดังนี้
การ Plot ขอมูลทัศนคติที่มีตอหางสรรพสินคาและจํานวนครั้งที่ผูบริโภคไปซื้อสินคา
Y ( ทัศนคติ )
X
X
X
X
X
X
X
X
X
X จํานวนครั้งที่ไปซื้อสินคา
การพิจารณา Scatter diagram จะทําใหสามารถมองเห็น “ รูปราง ” ของความสัมพันธระหวางตัว
แปรทั้ง 2 ตัวได จะสังเกตไดวาเมื่อตัวแปร X เพิ่มขึ้น ตัวแปร Y ก็มีแนวโนมเปนความสัมพันธเชิงเสนตรง
(Linear relationship )เทคนิคในการ Fit ตัวแบบจําลอง ( Model ) ใหสามารถอธิบายขอมูล (Data) ไดนั้น
เรียกวาเทคนิค Least - square เทคนิคนี้จะกําหนดเสนตรงที่ดีที่สุด โดยที่เมื่อลากเสนตรงเสนนี้ระหวาง
Plot บน Scatter diagram แลว ผลรวมของความแตกตางระหวางจุดทุกจุดที่หางจากเสนตรงรวมกันจะตองมี
คานอยที่สุด เสนตรงเสนที่ดีที่สุดนี้เรียกวา เสน Regression line หรือ เสนสมการถดถอย ระยะตั้งฉาก
ระหวางจุดที่ polt กับเสนตรง เรียกวา Error ระยะหางจากจุดทุกจุดที่ Plot กับเสนตรงเมื่อยกกําลัง 2 และ
นํามาบวกรวมกันเรียกวาผลรวมของความคลาดเคลื่อนยกกําลังสอง(Sum of squared errors) ∑ ei2 จะตองมี
สมการ
คานอยที่สุด เสน Regression line ที่ดีที่สุดจึงถูกเรียกวา The regression line of Y on X
Bivariate regression ของเสนตรง regression line สามารถเขียนไดดังนี้
Υ = α + βΧ + εi
โดยที่
Υ
Χ
=
=
ตัวแปรตาม ( Dependent or criterion variable ) หรือยอดขาย
ตัวแปรอิสระ ( Independent or predictor variable ) ตัวที่ 1
161. 164
= คาคงที่ ( Intercept of the line )
β =
คาความชันของเสน ( Slope of the line )
εI = ความคลาดเคลื่อนที่เกิดขึ้นเนื่องจาก Y แตกตางจาก Y
การประมาณคา α และ β ดวย a และ b โดยใชวิธีกําลังสองนอยที่สุด ซึ่งเปนวีธีหาคา a และb ที่ทํา
ใหผลบวกของคาความคลาดเคลื่อนยกกําลังสองมีคานอยที่สุด
จากสมการ
Υ = α + βΧ + εI
และ
Υ = a + bΧ
ทําใหสามารถคํานวณหาคา ของ a และ b คือ
b = n ∑ xi yi - ( ∑ xi ) (∑ yi )
n ∑ xi2 - ( ∑ xi ) 2
=
SSxy
SSxx
a = Y-bX
Y = ∑ yI/n
โดยที่ X = ∑ xI /n
α
ตัวอยางที่1 การวิเคราะหสมการถดถอยอยางงาย : สมมติใหผูประกอบการแหงหนึ่งตองการตรวจสอบ
ดูวาการใชความถี่ของโฆษณาในทางโทรทัศนตอเดือน มีความสัมพันธอยางไรกับยอดขายของกิจการ
จึงเก็บตัวอยางยอดขายและจํานวนความถี่ของโฆษณาในทางโทรทัศนตอเดือนไดขอมูลดังนี้
ยอดขาย (Υ )
( หนวย : พันบาท )
260.3
286.1
279.4
410.8
438.2
315.3
656.1
570.0
426.1
315.0
จํานวนครั้ง / เดือนของการโฆษณาทางโทรทัศน (Χ )
5
7
6
9
12
8
11
16
13
7
162. 165
10
∑ Υi = ( 260.3 + 286.1 + .... + 315.0 ) =
3,866.3
i=1
10
∑ Χi = ( 5+7+ ... +7 )
=
94
i=1
10
∑ ΧIΥi
= 5(260.3)+7(286.1)+...+7(315.0) =
39,539
i=1
10
2
∑Χ
= 52+72+...+72
=
= 260.3+286.1+...+315.0
10
=
994
i=1
Y
X
∴
= 5+7+...+7/10
b
∴a
3,866.3
10
= 386.63
= 94 /10
= 9.4
n
n
n
= n ∑ ΧiΥi - (∑ Χi ) ( ∑Υi )
i=1
i=1
i=1
n
n
2
n ∑ Χi - (∑ Χi )2
i=1
i=1
= 10(39,539)-(94)(3866.3)
10(994)-(94)2
= 395,390-363,432.2
9940 – 8836
= 31,957.8
= 28.947
1104
=
Y - b X
=
386.63 - 28.95(9.4)
=
386.63-272.13
= 114.5
163. 166
ดังนั้นสมการถดถอยจะเขียนไดดังนี้
=
114.5 + 28.95 (Χi )
ถาแทนคา Χi ใดๆ ลงในสมการก็จะคํานวณหาคา Υ ( ยอดขายโดยเฉลี่ย ) ไดจากสมการ
ถดถอยขางตนสามารถอธิบายไดวายอดขายจะเพิ่มขึ้น 28,950 บาท สําหรับการเพิ่มความถี่ของโฆษณา
ทางโทรทัศนขึ้นจากเดิม 1 ครั้ง (b = 28.95) ถาไมมีการโฆษณาทางโทรทัศนเลยยอดขายจะเทากับ
114,500 บาท (a = 114.5 )
Υ
ตัวอยางที่ 2 คอลัมนที่ 2 และ 3 ในตารางแสดงคาคะแนน I.Q. (X) และคะแนนการอานที่ไดจากการ
สอบ (Y) ของนักเรียน 18 คน คอลัมน 4 แสดงคา X2 และคอลัมน 5 แสดงคาของผลคูณ XY
(1)
นักเรียนคนที่
(2)
คะแนน IQ (X)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
ผลรวม
118
99
118
121
123
98
131
121
108
111
118
112
113
111
106
102
113
101
2,024
(3)
คะแนนการอาน
(Y)
66
50
73
69
72
54
74
70
65
62
65
63
67
59
60
59
70
57
1,155
(4)
X2
13,924
9,801
13,924
14,641
15,129
9,604
17,161
14,641
11,664
12,321
13,924
12,544
12,769
12,321
11,236
10,404
12,769
10,201
228,978
(5)
XY
(6)
คาที่พยากรณได Y
7,788
4,950
8,614
8,349
8,856
5,292
9,694
8,470
7,020
6,882
7,670
7,056
7,571
6,549
6,360
6,018
7,910
5,757
130,806
68
55
68
70
71
54
77
70
61
63
68
64
65
63
60
57
65
57
164. 167
Y = (คะแนนการอาน)
80
75
70
65
60
55
50
X = (I.Q)
100 105 110 115 120 125 130 135 140 145
รูปที่ 2 แผนภาพกระจัดกระจาย
เมื่อรวมคาตาง ๆ ในคอลัมน 2, 3, 4, 5 จะไดผลดังนี้
∑ X = 2024
∑ Y = 1155
∑ X = 228978
∑ XY = 130806
2
(18 × 130806) − (2024 × 1155)
(18 × 228978) − (2024) 2
= 0.6708
1155 − (0.6708 × 2024)
a yx =
18
= หรั . พยากรณคา Y เมื่อทราบคา X เขียนอยูในรูปของสมการไดเปน
ดังนั้น เสนถดถอยสํา−11บ25
b yx
=
Y = 0.6708 X – 11.25
เมื่อแทนคา X ใด ๆ ในสูตรนี้ จะได Y ซึ่งเปนคาประมาณของ Y
เชน แทนคา X = 118 จะได Y = 0.6708 (118) – 11.25 = 68
คอลัมน 6 ในตาราง แสดงคาคะแนนการอานที่ประมาณได (Y) จากการใชสมการ
Y = 0.6708 X – 11.25
การทดสอบสมมติฐานเกี่ยวกับ β
เปนการทดสอบวาตัวแปร XและY มีความสัมพันธในลักษณะเชิงเสนหรือไม โดยเปนการ
ทดสอบสมมติฐานแบบ 2 ขาง
จากสมการถดถอย
Υ = α + βΧ + εI
ถา β = 0 แสดงวา XและY ไมมีความสัมพันธในลักษณะเชิงเสน โดยมีสมมติฐาน คือ
165. 168
H0 : β = 0 หรือ XและY ไมมีความสัมพันธในลักษณะเชิงเสน
H1 : β ≠ 0 หรือ XและY มีความสัมพันธในลักษณะเชิงเสน
สถิติทดสอบ t = b - 0
=
b
sb
syx / √ ssxx
โดยที่ Syx =
√Σ (Y-Ý )2 / n – 2
SSxx = ΣX2 - (ΣX)2/ n
การทดสอบสมมติฐานเกี่ยวกับ α
เปนการทดสอบวาตัวแปร X=0แลว Yจะเทากับ 0 หรือไม โดยเปนการทดสอบสมมติฐาน
H0 : α = 0
H1 : α ≠ 0
สถิติทดสอบ t = a - 0
sa
sa = s2 yx (1/n + x 2 / ssxx )
ความคลาดเคลื่อนมาตรฐานในการพยากรณ (Standard error of estimate)
ถาขอมูล 2 ชุดที่มาหาความสัมพันธกันนั้นคลอยตามกันไมเปนเสนตรง (rxy ≠ 1) ในการ
พยากรณคาตัวแปรตัวหนึ่งจากตัวแปรอีกตัวหนึ่งจะมีความคลาดเคลื่อนเกิดขึ้น
ถาสัมประสิทธิ์
สหสัมพัน (rxy) ที่คํานวณไดมีคาสูง ความคลาดเคลื่อนก็จะนอย ถาสัมประสิทธิ์สหสัมพันธ (rxy) ที่
คํานวณไดมีคาต่ํา ความคลาดเคลื่อนก็จะมาก ความคลาดเคลื่อนมาตรฐานในการพยากรณจะมีคามาก
นอยเทาใด คํานวณไดจากสูตรนี้
(1) กรณีพยากรณคา Y เมื่อทราบคา X
สูตร
S yx = S y 1 − r 2
(2) กรณีพยากรณคา X เมื่อทราบคา Y
สูตร
เมื่อ
S xy = S x 1 − r 2
Syx
Sy
Sxy
แทนความคลาดเคลื่อนมาตรฐานในการพยากรณคา Y เมื่อทราบคา X
แทนความเบี่ยงเบนมาตรฐานของคะแนนชุด Y
แทนความคลาดเคลื่อนมาตรฐานในการพยากรณคา X เมื่อทราบคา Y
166. 169
Sx
แทนความเบี่ยงเบนมาตรฐานของคะแนนชุด X
R
แทนสัมประสิทธิ์สหสัมพันธที่คํานวณได
ขอสังเกต ถา rxy มีคาเปน 1 ความคลาดเคลื่อนมาตรฐานในการพยากรณจะมีคาเปน0
การวิเคราะหถดถอยเชิงซอน ( Multiple regression )
สมการการถดถอยเชิงซอน ( Multiple regression equation ) มีรูปแบบคลายคลึงกับสมการการ
ถดถอยอยางงาย ( Simple regression equation ) เพียงแตวาสมการถดถอยเชิงซอนจะมีตัวแปรอิสระ Χ
มากกวา1 ตัวขึ้นไป สมมติใหนกวิจัยสนใจตัวแปรอิสระ Χ 3 ตัว ( Χ1 , Χ2 และ Χ3 ) วาจะมี
ั
ผลกระทบโดยตรงตอยอดขาย (Υ) สมการถดถอยเชิงซอนในรูปแบบความสัมพันธเชิงเสนตรง
สามารถเขียนไดแบบงายๆ ดังนี้
Υ
=
α + β1Χ1 + β2Χ2 + β3Χ3 + ε
ถาหากตองการเขียนสมการขางตนดังกลาวอยางถูกตองอาจจะเขียนใหมไดดังนี้
Υ123
=
α123 + βΥ1.23 Χ1 + βΥ2.13 Χ2 + βΥ3.12 Χ3 + ε(123)
โดยที่ Υ123 คือ คาของ Υ ที่คาดคะเนไดจากสมการถดถอยเชิงซอน
Υ คือ ตัวแปรตาม และ Χ1 , Χ2 และ Χ3 คือตัวแปรอิสระ
α123 คือ คา Intercept ของสมการถดถอยเชิงซอน
βΥ1.23 คือ คา Coefficient คา Χ1 ในสมการถดถอยเชิงซอน คา βΥ1.23 นี้มีชื่อ
เรียกอีก ชื่อหนึ่งอยางเปนทางการวา Coefficient of partial regression
βΥ1.23 เปนคาที่แสดงถึงการเปลี่ยนแปลงของตัวแปรตาม Υ เมื่อตัวแปรอิสระ Χ1 เปลี่ยนแปลง
ไป 1 หนวย เลข 1 หลัง Υ หมายถึงตัวแปรอิสระ Χ1 ( Predictor variable ตัวที่ 1 ) สวนเลข 2 และ3 หลัง
จุดทศนิยมนั้น บอกใหทราบวายังมีตวแปรตน หรือ Predictor variable อีก 2 ตัว คือ Χ2 และ Χ3
ั
ที่มีคาคงที่ ดังนั้น βΥ2.13 และ βΥ3.12 จะมีความหมายในทํานองเดียวกัน
่
ε(123) คือ คาความผิดพลาดที่เกียวของกับการพยากรณคา Υ โดยที่มี Χ1 , Χ2 และ Χ3
เปนตัวแปรอิสระ
คาประมาณของY คือ y = a+ b1 x1+b2x2 +b3x3+….+e
โดยที่ a คือ ระยะตัดแกน Y กับX เมื่อกําหนดให x1 = x2 = x3 = 0
b1, b2, b3 เปนคาซึ่งแสดงความสัมพันธระหวาง Y กับX และมีความหมาย ดังนี้
b1 หมายถึง ถา x1 เพิ่มขึ้น 1 หนวยจะทําให Y เปลี่ยนแปลงไป b1 หนวย โดยที่ตวแปรอิสระ
ั
อื่นๆ (x2 , x3) มีคาคงที่ สวน b2 และ b3 จะมีความหมายในทํานองเดียวกัน
ในกรณีที่แปลงสัมประสิทธิ์การถดถอย (b) ใหเปนสัมประสิทธิ์การถดถอยมาตรฐาน(β) จะ
เขียนสมการไดเปน
Zy = β1zx1 +β2zx2 +β3zx3 +…+ ε
167. 170
ขอตกลงเบื้องตนของ Multiple regression
1. ตัวทํานายแตละตัวและตัวแปรเกณฑมีความสัมพันธเชิงเสนตรง
2. ตัวแปรเกณฑตองมีลักษณะตอเนื่อง และอยางนอยควรอยูในมาตราอันตรภาค
3. ความแปรปรวนของความคลาดเคลื่อน ในทุก ๆ คาของตัวแปร x จะมีคาเทากัน
4. ตัวทํานายจะตองไมสัมพันธกันเองสูง ( ไมเกิด multicollinearity )
5. การแปรคาของตัวแปรตามแตละคาตองเปนอิสระจากกัน
6. การแจกแจงของความคลาดเคลื่อนจะตองเปนNormality
การทดสอบสมมติฐานเกี่ยวกับสัมประสิทธิ์ความถดถอย (β)
เปนการทดสอบวาตัวแปร X อยางนอย 1 ตัว Y มีความสัมพันธกับY โดยมีสมมติฐาน คือ
H0 : βi = 0
H1 : β i ≠ 0 ; i = 1,2 ,…,k
สถิติทดสอบ t = bi - 0
sbi
สัมประสิทธิ์การทํานาย ( Coefficient of determination ,R2)
สัมประสิทธิ์การทํานาย เปนสัดสวนที่ตวแปรอิสระสามารถอธิบายความผันแปรของตัวแปร
ั
Y ได ใชสัญลักษณ R2 y.123…k
โดยที่ R2 = ความผันแปรเนื่องจากอิทธิพลของX1, X2, … Xk
ความผันแปรทั้งหมด
= SSR/SST = (SST –SSE) / SST
R2 เขาใกล 1 มากเทาไรแสดงวาความผันแปรของตัวแปร y ถูกอธิบายไดดวยตัวแปรอิสระมากเทานัน
้
สัมประสิทธพหุคูณ (Multiple correlation , R )
สัมประสิทธพหุคูณ ไดจากการถอดรากที่สองของสัมประสิทธิ์การทํานาย โดยที่สัมประ
สิทธพหุคูณแสดงถึงความสัมพันธระหวาง Y กับ X1, X2, … Xk ถามีคาเขาใกลศูนยแสดงวา Y กับ X1,
X2, … Xk มีความสัมพันธนอยมาก ถามีคาเทากับ 0 แสดงวา Y กับ X1, X2, … Xk ไมมีความสัมพันธกน
ั
ถา มีคาเขาใกล 1 แสดงวา Y กับ X1, X2, … Xk มีความสัมพันธกันมาก
168. 171
การทดสอบการทํานายตัวแปรโดยใชโปรแกรม SPSS for Windows
1. การทํานายตัวแปรเกณฑ 1 ตัว จากตัวแปรทํานาย 1 ตัว ใชสถิติ Simple regression
analysis
ตัวอยาง ถาตองการศึกษาวารายไดของครอบครัวเปนตัวทํานายรายจายของครอบครัวไดหรือไม
แสดงวามีแปรเกณฑ 1 ตัวไดแก รายจายของครอบครัว ตัวแปรทํานาย 1 ตัว ไดแก รายไดของ
ครอบครัว
สามารถใชโปรแกรม SPSS for Windows ไดดังนี้
1ใชคําสั่ง
Analyze
Regression
Linear
จะไดหนาจอดังแสดงในรูปที่ 3
รูปที่ 3 Linear Regression
จากรูปที่ 3 เลือกตัวแปรเกณฑ 1 ตัว คือ รายจายของครอบครัว ใสใน box ของ dependent
และเลือกตัวแปรทํานาย คือ รายไดของครอบครัว ใสใน box ของ independent เลือก method
2 เลือก statistics จะไดหนาจอดังรูปที่ 4
รูปที่ 4 Linear Regression : Statistics
169. 172
3. เลือกสถิติที่ตองการแลวเลือก continue จะกลับมาหนาจอเดิมรูปที่ 4 เลือก OK
จะไดผลลัพธในตารางที่ 3-5
ตารางที่ 3 Model Summaryb
Model
R
R Square
Adjusted R Std.Error of the
Square
Estimate
Durbin-Wastson
1
.956b
.914
.913
2105.6496
2.000
Predictors(Constant),income of respondent
จากตารางที่ 3 หมายความวา รายไดของครอบครัวสามารถอธิบายความผันแปรของรายจายได
91.4%(R a =.914)
ตารางที่ 4 ANOVAb
Model
Sum of Squares
df
Mean Square
F
Sig.
1
Regression
4166635796.39
1
416635796 939.752
.000
Residual
390170915.834
88
4433760.407
Total
4556806712.22
89
a . Predictors : ( Constant ) , income of respondent
ตารางที่ 4 ANOVA แสดงถึงตารางวิเคราะหความแปรปรวนของสมการ
Expense = α + β Income + e สําหรับการทดสอบสมมติฐาน
H0 : Expense ≠ α + β Income + e หรือ H0 : β = 0
H1 : Expense = α + β Income + e หรือ H1 : β ≠0
สถิติทดสอบ F = MSRegression = 4166635796 = 939.572
MS Residual
4433760.407
จะปฏิเสธสมมติฐาน H0 ถา F > F 1., 88,:.95 = 3.84 เนื่องจาก F = 939.572 จึงปฏิเสธ H0 หรือตัวแปร
expense สัมพันธกับตัวแปร income ในรูปเชิงเสน
ตารางที่ 5 Coefficients
Unstandardizes
Standardized
Coefficients
Coefficients
B
Std. Error
Beta
Model
1 ( Constant)
income of
respondent
438.720
.024
.843
520.416
.729
t
.956
30.7
95 % Confidence
Interval for B
Sig
Lower
Upper
Bound
Bound
.402 -595.498 1472.938
.000
.682
.776
170. 173
ตารางที่ 5 Coefficients จะแสดงสัมประสิทธิ์ความถดถอย
a = 438.72 บาท SE. (a ) = 520.416 บาท
b = .729 บาท SE (b) = .024 บาท
ฺBeta = b S x = .956
Sy
ก. สมมติฐาน H0 : β = 0 เปนการทดสอบวารายไดและรายจายสัมพันธกันในรูปเชิงเสนหรือไม
H1 : β ≠0
สถิติทดสอบ : t = 30.7 Sig. ของสถิติทดสอบ t = .000 จึงปฏิเสธ H0 หรือ β≠0 นั่นเอง เมื่อมี
ตัวแปรอิสระเพียงตัวเดียว สถิติทดสอบ t2 = F และผลสรุปจะเหมือนกัน
ข. สมมติฐาน H0 : α = 0 เปนการทดสอบเกี่ยวกับสวนการตัดแกน Y
H1 : α ≠0
สถิติทดสอบ t = .843 Sig ของ t = .402 > .05 จึงยอมรับ H0 หรือ β = 0
ดังนั้นผลการทดสอบโดยสถิตทดสอบ F และ t สรุปไดวาสมการความถดถอยซึ่งแสดง
ความสัมพันธระหวาง รายไดและรายจายเปน
Exp^ense = 0.729 Income
2. การทํานายตัวแปรเกณฑ 1 ตัว จากตัวแปรทํานายมากกวา 1 ตัว ใชสถิติ Multiple
regression analysis
ตัวอยาง ถาตองการศึกษาวารายไดของครอบครัว และเกียรติภูมในอาชีพของบิดาเปนตัว
ิ
ทํานายเงินที่บตรไดไปโรงเรียนตอวัน ไดหรือไม แสดงวามีแปรเกณฑ 1 ตัวไดแก เงินที่บุตรไดไป
ุ
โรงเรียน ตัวแปรทํานาย 2 ตัว ไดแก รายไดของครอบครัว และเกียรติภูมิในอาชีพของบิดา สามารถ
ใชโปรแกรม SPSS for Windows ไดดังนี้
1ใชคําสั่ง
Analyze
Regression
Linear
จะไดหนาจอดังแสดงในรูปที่ 5
171. 174
รูปที่ 5 Linear Regression
จากรูปที่ 6 เลือกตัวแปรเกณฑ 1 ตัว คือ เงินที่บุตรไดไปโรงเรียน (pocketm) ใสใน box ของ
dependent และเลือกตัวแปรทํานาย คือ รายไดของครอบครัว(income) และเกียรติภูมในอาชีพของบิดา
ิ
(occupafa) ใสใน box ของ independent สวนของ method เลือกenter
2 เลือก statistics จะไดหนาจอดังรูปที่ 6
รูปที่ 6 Linear Regression : Statistics
3. รูปที่ 7 ในสวนของ Regression Coefficient เลือก Estimates และ Confidence interval
ในสวนของ Residuals เลือก Durbin-Watson เลือก Model fit , R square change , Part and partial
correlation และ Collinearity Diagostics แลวเลือก continue จะกลับมาหนาจอเดิมรูปที่ 6
เลือก OK จะไดผลลัพธในตารางที่ 6-10
ตารางที่ 6
b
Variables Entered/Removed
Model
1
Variables Entered
OCCUPAFA,
a
INCOME
a.
All requested variables entered.
b.
Dependent Variable: POCKETM
Variables
Removed
Method
.
Enter
172. 175
ตารางที่6 เปนตารางที่อธิบายถึงการเลือกตัวแปรอิสระเขาสมการโดยวิธี enter โดยมีเงินที่บุตรไดไป
โรงเรียน (pocketm) เปนตัวแปรตาม และตัวแปรอิสระที่นําเขา คือ รายไดของครอบครัว(income) และ
เกียรติภูมิในอาชีพของบิดา (occupafa)
ตารางที่ 7
Model Summary
Model
1
R
R Square
.253a
.064
b
Adjusted R Square
.063
Std. Error of
the Estimate
20.94
Durbin-Watson
1.877
a. Predictors: (Constant), OCCUPAFA, INCOME
b. Dependent Variable: POCKETM
ตารางที่ 7 สรุปไดดังนี้
R Square = .064 คือคาสัมประสิทธิ์การทํานาย เปนสัดสวนที่ตวแปรอิสระสามารถอธิบาย
ั
ความผันแปรของตัวแปรไดมากนอยเทาไร ในที่นี้แสดงวารายไดของครอบครัว(income) และ
เกียรติภูมิในอาชีพของบิดา (occupafa) สามารถอธิบายความผันแปรของเงินที่บุตรไดไปโรงเรียน
(pocketm) รอยละ 6.4 ที่เหลืออธิบายไดดวยตัวแปรอื่น
สําหรับคา Adjusted R Square เปนคาที่มีการปรับใหคาสัมประสิทธิ์การทํานายมีความ
่
้
ถูกตองมากขึ้น เนื่องจากตัวแปรอิสระที่เพิมมากขึ้นในสมการถดถอย จะทําใหคา R Square เพิ่มขึน
ทั้งๆที่ตัวแปรอิสระที่เพิ่มมานั้นอาจไมมีความสัมพันธกบตัวแปรตาม ดังนั้น จึงตองมีการปรับสูตร R
ั
Square เพื่อลดปญหาดังกลาว
R เปนคาสัมประสิทธพหุคูณ ที่แสดงถึงความสัมพันธระหวางตัวแปรตามและชุดของตัวแปร
อิสระ ในที่นมีคาเทากับ .253 แสดงวา เงินที่บุตรไดไปโรงเรียน (pocketm) กับ รายไดของครอบครัว
ี้
(income) และเกียรติภูมิในอาชีพของบิดา (occupafa) มีความสัมพันธกนไมมากนัก
ั
Std Error of estimate เปนคาความคลาดเคลื่อนมาตรฐานของการประมาณคาซึ่งเทากับ 20.94
บาท มีหนวยเดียวกับตัวแปรตาม
Durbin-Watson เปนคาสถิติที่ทดสอบความเปนอิสระของความคลาดเคลื่อน ซึ่งเปนเงื่อนไข
หนึ่งของการวิเคราะหถดถอย ในทีนี้ มีคาเทากับ 1.877 ซึ่งมีคาใกล 2 แสดงวาคาความคลาดเคลื่อน
่
เปนอิสระจากกัน
173. 176
ตารางที่ 8
ANOVA b
Model
1
Sum of Squares
Regressio
n
df
Mean Square
F
Sig.
a
41655.907
2
20827.954
Residual
608436.309
1387
438.671
Total
650092.217
47.480
.000
1389
a. Predictors: (Constant), OCCUPAFA, INCOME
b. Dependent Variable: POCKETM
ตารางที่ 8 เปนตารางวิเคราะหความแปรปรวนทางเดียว ซึ่งใชในการทดสอบสมมติฐาน
H0 : β 1 = β 2 = 0
H1 : β i ≠0 อยางนอย 1 ตัว ; i = 1,2
ในที่นี้ ไดคาF = 47.480 Sig = .000 แสดงวาปฏิเสธสมมติฐาน H0 สรุปไดวามีตวแปรอิสระอยางนอย
ั
1 ตัวที่มีความสัมพันธเชิงทํานายตัวแปรตาม อยางมีนัยสําคัญ จึงตองทําการทดสอบตอไปวาตัวแปร
อิสระใดบางทีมีความสัมพันธเชิงทํานาย เงินที่บุตรไดไปโรงเรียน (pocketm) ในตารางที่ 9
่
ตารางที่ 9
Unstandardizes
Standardized
Coefficients
Coefficients
B
Std. Error
Beta
Model
1 (Constant)
income
t
2.842
.000
.139
14.678
4.962
.165
5.877
41.711
7.768 E-05
.054
.317
occupafa
Dependent Variable : POCKETM
95 % Confidence
Correations
Collinearity
Interval for B
Statistics
Sig Lower Upper Zero Par part toler VIF
Bound Bound order tial
ance
.000 36.137 47.286
.000 .202 .132 .129 .856 1.168
.000
.000
.000
.211
.422
.218 .156 .153 .856 1.168
ตารางที่ 9 เปนตารางที่แสดงการทดสอบความสัมพันธเชิงทํานายระหวางตัวแปรตามกับตัว
แปรอิสระที่ละตัว สรุปได ดังนี้
ใน Column Unstandardized Coefficient มีคา B ซึ่งแสดงถึงคาคงที่(a) และคาสัมประสิทธิ์
ถดถอย(b) สวน Std Error คือคาความคลาดเคลื่อนมาตรฐานของคา a และb ในที่นี้ไดคาดังนี้
คาคงที่ a = 41.711 บาท SE(a) = 2.842
คาสัมประสิทธิ์ถดถอยของตัวแปรรายไดของครอบครัว(income)(b1)=.000077 บาท
174. 177
SE(b1) =0
คาสัมประสิทธิ์ถดถอยของตัวแปรเกียรติภูมิในอาชีพของบิดา (occupafa) b2 = .317 บาท
SE (b2 ) = .054 บาท
ฺสมการถดถอยที่คาดไวจะเปน
^
POCKETM = 41.711 + .000077 income + .317 occupafa
จะตองทดสอบตอวาเปนจริงหรือไม
ใน Column Standardized Coefficient แสดงคาสัมประสิทธิ์ถดถอยมาตรฐาน ซึ่งไมมีหนวย อยูในรูป
ของคะแนนมาตรฐาน (Z Score)
คาสัมประสิทธิ์ถดถอยมาตรฐาน ของตัวแปรรายไดของครอบครัว (income) = .139
คาสัมประสิทธิ์ถดถอยมาตรฐาน ของตัวแปรเกียรติภูมในอาชีพของบิดา (occupafa) = .165
ิ
แสดงวามีความสัมพันธเชิงทํานายตัวแปรตาม คือ เงินที่บุตรไดไปโรงเรียน
มากกวารายไดของครอบครัว
โดยใชคา t ทดสอบสมมติฐานเกี่ยวกับคาคงที่และสัมประสิทธิ์ถดถอย α , β1 และ β2
ก. สมมติฐาน H0 : α = 0 เปนการทดสอบเกี่ยวกับคาคงที่
H1 : α ≠0
สถิติทดสอบ t = .14.678 Sig ของ t = ..000 < .05 จึงปฏิเสธ H0 หรือ α ≠0
ข. สมมติฐาน H0 : β1 / β2 = 0
H1 : β1 / β2 ≠ 0 หรือ
H0 : รายไดของครอบครัว ไมมีความสัมพันธเชิงทํานายเงินที่บุตรไดไปโรงเรียนเมื่อกําหนดให
เกียรติภูมิในอาชีพของบิดาคงที่
H1 : รายไดของครอบครัว มีความสัมพันธเชิงทํานายเงินที่บุตรไดไปโรงเรียนเมื่อกําหนดใหเกียรติภูมิ
ในอาชีพของบิดาคงที่
สถิติทดสอบ : t = 4.962 Sig. ของสถิติทดสอบ t = .000 จึงปฏิเสธ H0 หรือ β1 / β2 ≠ 0 นั่น
คือ รายไดของครอบครัว มีความสัมพันธเชิงทํานายเงินที่บุตรไดไปโรงเรียนเมื่อกําหนดใหเกียรติภูมิ
ในอาชีพของบิดาคงที่
ค . สมมติฐาน H0 : β2 / β1 = 0
H1 : β2 / β1 ≠ 0 หรือ
H0 : เกียรติภูมในอาชีพของบิดาไมมีความสัมพันธเชิงทํานายเงินที่บตรไดไปโรงเรียน เมื่อกําหนดให
ิ
ุ
รายไดของครอบครัว คงที่
175. 178
H1 : เกียรติภูมในอาชีพของบิดามีความสัมพันธเชิงทํานายเงินที่บุตรไดไปโรงเรียนเมื่อกําหนดให
ิ
รายไดของครอบครัว คงที่
สถิติทดสอบ : t = 5.877 Sig. ของสถิติทดสอบ t = .000 จึงปฏิเสธ H0 หรือ β2 / β1 ≠ 0 นั่นคือ
เกียรติภูมิในอาชีพของบิดามีความสัมพันธเชิงทํานายเงินที่บุตรไดไปโรงเรียน เมื่อกําหนดใหรายได
ของครอบครัว คงที่
สรุป จากการทดสอบทั้งหมด สรุปไดวาตัวแปรอิสระทั้ง 2 ตัว คือรายไดของครอบครัว และเกียรติภมิ
ู
ในอาชีพของบิดามีความสัมพันธเชิงทํานายตัวแปรตาม คือเงินที่บุตรไดไปโรงเรียนอยางมีนัยสําคัญ
ทางสถิติที่ระดับ 0.05
ใน column 95 % Confidence Interval for B หมายถึง คาประมาณแบบชวงของสัมประสิทธิ์ถดถอย
ที่ระดับความเชื่อมั่น 95 %
ใน column Correlation มีคาสัมประสิทธิ์สหสัมพันธแบงเปน 3 สวน คือ
1. Zero –Order หมายถึง คาสัมประสิทธิ์สหสัมพันธระหวางตัวแปรตามกับตัวแปรอิสระแต
ละตัวโดยไมไดควบคุมตัวแปรอิสระตัวอื่นๆ ในที่นี้ไดคาดังนี้
คาสัมประสิทธิ์สหสัมพันธระหวางตัวแปร pocketm กับ income =.202
คาสัมประสิทธิ์สหสัมพันธระหวางตัวแปร pocketm กับ occupafa = .218
แสดงวาความสัมพันธระหวางเงินที่บุตรไดไปโรงเรียนกับเกียรติภูมิในอาชีพของบิดามีมากกวา
ความสัมพันธระหวางเงินทีบุตรไดไปโรงเรียนกับรายไดของครอบครัว
่
2. Partial หมายถึง คาสัมประสิทธิ์สหสัมพันธบางสวนระหวางตัวแปรตาม(y) กับตัวแปร
อิสระแตละตัว(เชน x1 )โดยไดควบคุมตัวแปรอิสระตัวอื่นๆ (เชน x2)ที่อาจจะสัมพันธกับตัวแปรตาม
(y) กับตัวแปรอิสระแตละตัว(x1 ) ในที่นี้ไดคาดังนี้
คาสัมประสิทธิ์สหสัมพันธระหวางตัวแปร pocketm กับ income โดยควบคุมตัวแปร
occupafaที่อาจจะสัมพันธกบ pocketm กับ income มีคา = .132
ั
คาสัมประสิทธิ์สหสัมพันธระหวางตัวแปร pocketm กับ occupafa โดยควบคุมตัวแปร
incomeที่อาจจะสัมพันธกับ pocketm กับ occupafa มีคา = .156
3. Part หมายถึง คาสัมประสิทธิ์สหสัมพันธบางสวนระหวางตัวแปรตาม(y) กับตัวแปรอิสระ
แตละตัว(เชน x1 )โดยไดควบคุมตัวแปรอิสระตัวอื่นๆ (เชน x2)ที่อาจจะสัมพันธกับตัวแปรอิสระแตละ
ตัว (x1 ) ในทีนี้ไดคาดังนี้
่
คาสัมประสิทธิ์สหสัมพันธระหวางตัวแปร pocketm กับ income โดยควบคุมตัวแปร
occupafa ที่อาจจะสัมพันธ กับ income มีคา = .129
คาสัมประสิทธิ์สหสัมพันธระหวางตัวแปร pocketm กับ occupafa โดยควบคุมตัวแปร
incomeที่อาจจะสัมพันธกับ occupafa มีคา = .153
ใน column Collinearity Statistics หมายถึง คาสถิติที่วัดความสัมพันธของตัวแปรอิสระ
176. 179
Tolerance = 1-R2
ถามีคาต่ําแสดงวาตัวแปรอิสระตัวนันมีความสัมพันธกับตัวแปรอิสระตัวอื่นๆมาก
้
2
VIF
= 1/ 1-R
ถามีคามากแสดงวาตัวแปรอิสระตัวนั้นมีความสัมพันธกบตัวแปรอิสระตัวอืนๆมาก
ั
่
ในที่นี้ไดคาดังนี้
Tolerance ของ income และ occupafa = .856 VIF = 1.168
ตารางที่ 10
Residuals Statistics a
Predicted Value
Minimum Maximum
49.33
99.70
Mean
62.38
Std. Deviation
5.48
N
1390
Residual
-49.70
87.58
-2.24E-14
20.93
1390
Std. Predicted
Value
-2.382
6.816
.000
1.000
1390
Std. Residual
-2.373
4.182
.000
.999
1390
a. Dependent Variable: POCKETM
ตารางที่ 10 เปนตารางที่ใหคาสถิติของคาความคลาดเคลื่อน
Predicted Value หมายถึง คาประมาณของตัวแปรตาม ในที่นี้คือคาประมาณของเงินที่บุตรได
ไปโรงเรียน หรือ Pock^etm ที่มีคาสูงสุด = 99.70 ต่ําสุด = 49.33
Residual หมายถึง คาความคลาดเคลื่อนที่เกิดจากการประมาณคา Pocketm ดวย Pock^etm
โดยที่
Residual = Pocketm - Pock^etm
Std. Predicted Value หมายถึง คาประมาณของตัวแปรตามในที่นี้คือคาประมาณของเงินที่
บุตรไดไปโรงเรียน ในรูปคะแนนมาตรฐาน = Z poc^ketm
โดยที่
Z poc^ketm = Pock^etm - mean (Pock^etm )
SD(Pock^etm )
Std. Residual หมายถึง ถึง คาความคลาดเคลื่อนมาตรฐาน หรือ Z Residual
Z Residual = Residual - mean (Residual)
SD( Residual)
สรุป จากการวิเคราะหสมการถดถอยของตัวแปรเงินที่บตรไดไปโรงเรียน กับรายไดของ
ุ
ครอบครัวและเกียรติภูมิในอาชีพบิดานั้น พบวาตัวแปรอิสระทั้ง 2 ตัว มีความสัมพันธเชิงทํานายกับตัว
แปรตามอยางมีนัยสําคัญทางสถิติ และสามารถเขียนสมการในรูปของคะแนนดิบและในรูปของ
คะแนนมาตรฐานได ดังนี้
177. 180
สมการในรูปของคะแนนดิบ
^
POCKETM = 41.711 + .000077 income + .317 occupafa
สมการในรูปของคะแนนมาตรฐาน
^
Zpocketm = .139 Z income + .165 Zoccupafa
……………………………………………………
แบบฝกหัด
1. จงระบุสถิติที่ใชในการหาความสัมพันธของตัวแปรตอไปนี้
1.1 การหาความสัมพันธระหวางอันดับที่ของภาพวาดจากกรรมการ 2 ทาน
1.2 การหาความสัมพันธระหวางคะแนนภาวะผูนํากับการเปนที่ยอมรับของผูใตบังคับบัญชา
1.3 การหาความสัมพันธระหวางการไปเลือกตั้งกับระดับการศึกษา
1.4 การหาความสัมพันธระหวางการชอบเลนฟุตบอลกับการชอบดูฟุตบอล
1.5 การหาความสัมพันธระหวางเพศกับการเรียนตอตางประเทศ
2. จงหาความสัมพันธระหวางสวนสูงกับน้ําหนักของนิสิต 5 คนจากขอมูลตอไปนี้ พรอมแปล
ความหมายและทดสอบนัยสําคัญของคาสหสัมพันธดังกลาว ที่ระดับนัยสําคัญที่0.05
นิสิต
สวนสูง
น้ําหนัก
1
160
49
2
170
60
3
165
55
4
148
40
5
155
50
3. จงหาความสัมพันธระหวางการกวดวิชากับคะแนนสอบเขามหาวิทยาลัยของนิสิต
ขอมูลที่กําหนดพรอมทั้งแปลความหมาย
นิสิตคนที่ 1
2
3
4
5
6
7
8
9
กวดวิชา 1
1
1
1
1
0
0
0
0
คะแนน 300 250 275 190 400 200 150 210 305
10 คน จาก
10
0
175
178. 181
4. นักวิจัยตองการศึกษาวาทัศนคติตอวิชาสถิติจะทํานายคะแนนวิชาสถิติไดหรือไม จึงสุมตัวอยางนิสิต
มา 10 คน เก็บขอมูลทัศนคติตอวิชาสถิติและคะแนนสถิติ ไดดังนี้
นิสิตคนที่ 1 2 3 4 5 6 7 8 9 10
ทัศนคติ
10 8 8 3 4 5 7 8 9 4
คะแนน
7 8 7 5 6 3 9 5 6 3
จงสรางสมการทํานายทั้งคะแนนดิบและคะแนนมาตรฐานพรอมทดสอบนัยสําคัญของ
สัมประสิทธิ์การถดถอย
5.นักการศึกษาตองการศึกษาวาผลสัมฤทธิ์ทางการเรียนของนิสิตมีความสัมพันธกับแรงจูงใจ
ใฝสัมฤทธิ์ของนิสิตและอายุของนิสิตหรือไม จึงเก็บขอมูลกับนิสิต 15 คน ไดขอมูล ดังนี้
นิสิต
แรงจูงใจ
อายุ
คะแนน
1
8
20
70
2
10
22
82
3
12
24
83
4
15
26
85
5
18
28
84
6
20
30
90
7
18
28
87
8
16
26
84
9
14
22
81
10
12
24
82
11
10
22
79
12
18
25
81
13
17
25
84
14
16
24
82
15
15
26
86
5.1จงเขียนสมการถดถอยแสดงความสัมพันธระหวางผลสัมฤทธิ์ทางการเรียน แรงจูงใจใฝสัมฤทธิ์
ของนิสิตและอายุของนิสิต
5.2 จงทดสอบความสัมพันธในขอ5.1 ที่ระดับนัยสําคัญที่ 0.05
5.3 จงหาคาสัมประสิทธิ์การทํานายพรอมทั้งอธิบายความหมาย
179. บทที่ 5
การทดสอบไคสแควร
ไคสแควร (χ2) เปนสถิติที่ถูกนํามาใชเพือในการวิเคราะหขอมูลจําแนกประเภท หรือนับความถี่
่
ของแตละระดับหรือของแตละกลุม การทดสอบไคสแควรมีหลายรูปแบบแตในทีนี้จะจําแนกเปนดังนี้
่
1. การทดสอบสมมติฐานสําหรับขอมูลที่จําแนกทางเดียว แบงเปน
1.1 การทดสอบความแตกตางระหวางความถี่
1.2 การทดสอบสัดสวนประชากรวาเทากับทีคาดหวังหรือไม
่
1.3 การทดสอบการแจกแจงของประชากรวาเปนไปตามที่คาดหวังหรือไม(Goodness of fit)
2. การทดสอบสมมติฐานสําหรับขอมูลที่จําแนกสองทาง
2.1 การทดสอบความเปนอิสระกันระหวางลักษณะ 2 ลักษณะ(ความสัมพันธระหวาง 2 ตัว)
1. การทดสอบสมมติฐานสําหรับขอมูลที่จําแนกทางเดียว ลักษณะของขอมูลที่จําแนกทางเดียว
คือเปนขอมูลที่จําแนกตามลักษณะใดลักษณะหนึ่งเพียงลักษณะเดียว เชน จําแนกคนตามระดับการศึกษา
สูงสุด เชน ต่ํากวามัธยมศึกษาตอนปลาย มัธยมศึกษาตอนปลาย ปริญญาตรีหรืออนุปริญญา สูงกวา
ปริญญาตรี การทดสอบสมมติฐานสําหรับขอมูลที่จําแนกทางเดียวดังกลาว สามารถทดสอบสมมติฐาน
โดยใชสถิติไคสแควร (χ2) โดยมีขอตกลงเบื้องตน ดังนี้
ขอตกลงเบื้องตนของ χ2 - test
1. ขอมูลแตละคาจะตองอยูที่ cell ใด cell หนึง เทานั้น
่
2. ขอมูลแตละคาจะเปนอิสระจากขอมูลอื่น
3. ขอมูลที่นํามาวิเคราะหจะเปนคาความถี่
4. คาความถี่คาดหวังในแตละ Cell จะตองไมนอยกวา 5 สําหรับ กรณีที่ df ≥ 2 และไมนอย
กวา 10 ถา df = 1
ทดสอบสมมติฐานโดยใชสถิติไคสแควร (χ2)ในที่นี้จะสรุปเปน 3 ลักษณะ คือการทดสอบความแตกตาง
ระหวางความถี่ การทดสอบสัดสวนประชากรวาเทากับที่คาดหวังหรือไม และการทดสอบการแจกแจง
ของประชากรวาเทากับที่คาดหวังหรือไม (Goodness of fit) โดยมีรายละเอียดดังนี้
1.1 การทดสอบความแตกตางระหวางความถี่ การทดสอบแบบนี้จะมีตัวแปรที่ตองการวิเคราะห
มีเพียงตัวเดียว แตแบงเปนหลายประเภท และทดสอบวา ความถี่ที่เกิดขึ้นในแตละประเภทเทากันหรือไม
หรือทดสอบวาความถี่ที่เกิดขึ้นเทากับความถี่ที่กําหนดหรือไม โดยมีสมมติฐาน คือ
Η 0 : ¶1 = ¶2 =… ¶k = 1/k
Η 1 : ¶i : ≠ 1/k อยางนอย 1 คา I = 1 , 2 ,… k
180. 183
โดยมีสถิติที่ใชในการทดสอบ คือ
n
χ = ∑ ( Οi− Ε i ) 2
i=1 Ε i
2
เมื่อ
χ2 =
สัญลักษณของไคสแควร
Ο = ความถีที่แจงนับได
่
Ε = ความถี่ที่คาดหวังหรือที่กําหนด
n = จํานวนตัวอยางทั้งหมด
เขตปฏิเสธ จะปฏิเสธ Η 0 เมื่อ χ 2 > χ 2(1 - α ) : k-1
ตัวอยาง ในโรงเรียนแหงหนึ่งไดใหนกเรียน100 คน เลือกครูภาษาไทยดีเดนในโรงเรียน ซึงมี ครู
ั
่
ภาษาไทยอยู 5 คน คือครู ก ครู ข ครู ค ครู ง และครู จ โดยที่ผูอํานวยการโรงเรียนตองการทราบวาครู
จ ซึ่งเปนครูใหม จะไดรับการเลือกจากนักเรียนแตกตางจากครูเกาหรือไม
การคํานวณ ถาครู ไดรับการเลือกจากนักเรียนเทาๆกัน จะตองไดรับการคัดเลือก คนละ 20 เสียง
สามารถคํานวณหาคา χ 2 ไดดังนี้
Ο
ครู
ก
ข
ค
ง
จ
รวม
Ε
17
27
22
15
19
100
(Ο- Ε)2
Ο- Ε
20
20
20
20
20
100
-3
7
2
-5
-1
0
9
49
4
25
1
(Ο- Ε)2/Ε
.45
2.45
.20
1.25
.05
4.40
Η 0 : ¶1 = ¶2 = ¶3 = ¶4 = ¶5 = 1/5
Η1 :
¶i :
≠
1/5 อยางนอย 1 คา i = 1 , 2 ,… k
n
χ = ∑ ( Οi− Ε i ) 2
i=1 Ε i
= 4.40
2
เขตปฏิเสธ จะปฏิเสธ Η 0 เมื่อ χ 2 > χ 2 α : k-1 ที่องศาอิสระ 5-1 = 4 จากการเปดตาราง χ 2 ไดχ 2(0.95: 4)
=9.49 ซึ่งมากกวา 4.4 จึงไมสามารถปฏิเสธ Η 0 นั่นคือยอมรับ Η 0 คือ ครูไดรับการเลือกจากนักเรียนไม
แตกตางกันอยางมีนัยสําคัญทางสถิติที่ระดับ 0.05
181. 184
1.2 การทดสอบสัดสวนประชากรวาเทากับที่คาดหวังหรือไม การทดสอบแบบนี้จะมีตัวแปรที่
ตองการวิเคราะหมีเพียงตัวเดียว แตแบงเปนหลายประเภท และทดสอบวาสัดสวนที่เกิดขึ้นเทากับสัดสวน
ที่กําหนดหรือไม โดยมีสมมติฐาน คือ
Η 0 : ¶1 : ¶2 … : ¶k = ¶10 : ¶20 … : ¶k0
Η 1 : ¶i ≠ ¶i0 อยางนอย 1 คา ; i = 1, 2 ,…k
โดยที่ ¶i0 = สัดสวนที่คาดวาจะเปน ซึ่งเปนคาคงที่ อยูระหวาง 0 – 1
สถิติที่ใชทดสอบคือ n
χ 2 = ∑ ( Οi− Ε i ) 2
i=1 Ε i
เมื่อ
χ2 =
สัญลักษณของไคสแควร
Ο = ความถีที่แจงนับได
่
Ε = ความถี่ที่คาดหวังหรือที่กําหนด
n = จํานวน
สูตรคํานวณ Ε = n pi0
เขตปฏิเสธ จะปฏิเสธ Η 0 เมื่อ χ 2 > χ 2 α : k-1
ตัวอยาง ยาแกปวดศรีษะชนิดหนึ่ง บริษัทอางวารักษาผูปวยหายภายใน 3 ชั่วโมง รอยละ 90 เพื่อ
ทดสอบสรรพคุณของยาชนิดนี้ จึงเลือกผูปวยมา 400 คน และใหกินยาดังกลาวพบวาหายภายใน 3
ชั่วโมง 320 คนยาชนิดนี้สรรพคุณตามที่อางหรือไม
การคํานวน ถายานี้มีสรรพคุณที่อางผูปวย 100 คน จะตองหาย 90 ฉะนั้นถาทดลองกับผูปวย
400 คน จะตองหาย 360 คน และไมหาย 40 คน จากหลักการนี้สามารถคํานวนหาคาไคสแควร ดังนี้
สมมติฐาน สัดสวนการหายปวด : ไมหายปวด = 90 : 10
หรือ Η 0 : ¶1 : ¶2 = 90 : 10
Η 1 : ¶1 : ¶2 ≠ 90 : 10
Ε = n p
ตารางการวิเคราะหไคสแควร
ผลการทดลอง
หาย
ไมหาย
รวม
Ο
Ε
Ο −Ε
320
80
400
360
40
400
- 40
40
0
( Ο −Ε ) 2 ( Ο −Ε ) 2 / Ε
1600
1600
4.44
40.00
44.44
182. 185
ฉะนั้น χ 2 = 44.44 นําไปเปรียบเทียบกับคา χ 2 ในตาราง df = 2-1 = 1 และ α =0.05 =3.84
แสดงวาคา χ 2 ที่คํานวณไดมากกวาคาในตาราง หมายความวา ยานี้ใหผลตางจากรอยละ 90 นั้น คือ ไมมี
สรรพคุณตามที่อางไว
อนึ่ง ในการคํานวณคา χ 2 ถา df = 1หรือ คา Ε นอยกวา 5 ควรปรับสูตรดวยการเอา
0.5 ลบออกจากผลที่ไดไมตดเครื่องหมายกอนแลวจึงยกกําลังสองจึงจะทําใหคา χ 2 ที่ไดตรงกับความ
ิ
เปนจริงมากขึน สูตรก็เปน
้
χ 2 = ∑ (⎟ Ο −Ε⎮− 0.5) 2
Ε
1.3 การทดสอบการแจกแจงของประชากรวาเปนไปตามที่คาดหวังหรือไม การทดสอบแบบนี้
จะมีตวแปรทีตองการวิเคราะหมีเพียงตัวเดียว แตแบงเปนหลายประเภท และทดสอบวาสัดสวนที่เกิดขึ้น
ั
่
เทากับสัดสวนตามการแจกแจงตามที่คาดหวังหรือไม
ยังคงเรียกวาการทดสอบภาวะรูปสนิทดี
(Goodness of fit) การแจกแจงที่คาดไวอาจเปนการแจกแจงแบบตอเนื่อง เชนการแจกแจงแบบปกติ
หรือการแจกแจงแบบไมตอเนื่อง เชนการแจกแจงแบบทวินามหรือการแจกแจงแบบปวซอง โดยมี
สมมติฐาน คือ
Η 0 : ประชากรมีการแจกแจงแบบ Y
Η 1 : ประชากรไมไดมการแจกแจงแบบ Y
ี
โดยที่ Y อาจเปนแบบปกติ ทวินามหรือปวซอง
สถิติที่ใชทดสอบคือ
n
χ 2 = ∑ ( Οi− Ε i ) 2
i=1 Ε i
เมื่อ
χ2 =
สัญลักษณของไคสแควร
Ο = ความถีที่แจงนับได
่
Ε = ความถี่ที่คาดหวังหรือที่กําหนด
n = จํานวน
สูตรคํานวณ Ε = n × ความนาจะเปนที่จะเกิดขึนในลักษณะที่ i ของการแจกแจงที่คาดไว
้
โดยที่ χ 2 มีการแจกแจงแบบไคสแควรที่องศาอิสระ (k-1)-m
m คือจํานวนพารามิเตอรที่ตองประมาณคา จะมีคาเทาไรขึ้นอยูกับการแจกแจงที่คาดไว
ที่ตองการทดสอบ เชน ถาสมมติฐาน คือ Η 0 : ประชากรมีการแจกแจงแบบปกติ
m = 2 เนื่องจากตองประมาณคาเฉลี่ยและคาความแปรปรวน χ 2 ~ χ 2(k-1-2)
ถาสมมติฐาน คือ Η 0 : ประชากรมีการแจกแจงแบบปกติดวยคาเฉลี่ย = 5 คาความแปรปรวน = 6
m = 0 เนื่องจากไมตองประมาณคาเฉลี่ย (µ)และคาความแปรปรวน(σ2) χ 2 ~ χ 2(k-1)
183. 186
ตัวอยาง จากการถามคนไทยในเขตหนองจอก จํานวน 83 คน ถึงรายไดตอเดือน ปรากฏวาไดขอมูล ดังนี้
รายไดตอเดือน(หนวย:100,000 บาท
นอยกวา .1
.1แตนอยกวา .15
.15 แตนอยกวา .20
.20 แตนอยกวา .25
ตั้งแต .25 ขึ้นไป
รวม
จํานวน (คน)
12
20
23
15
13
83
จงทดสอบวารายไดของคนในเขตหนองจอก มีการแจกแจงปกติดวยรายไดเฉลี่ย 20,000บาทตอเดือน คา
เบี่ยงเบนมาตรฐาน 5,000 บาทตอเดือนที่ระดับความเชื่อมัน 99%
่
สมมติฐานเพื่อการทดสอบ คือ
Η 0 : รายไดของคนหนองจอกมีการแจกแจงแบบปกติดวยรายไดเฉลี่ย 20,000 บาท สวนเบี่ยงเบน
มาตรฐาน 5,000 บาท
Η 1 : รายไดของคนหนองจอกไมมีการแจกแจงแบบปกติดวยรายไดเฉลี่ย 20,000 บาท สวนเบี่ยง
เบนมาตรฐาน 5,000 บาท
สถิติที่ใชทดสอบคือ
n
χ = ∑ ( Οi− Ε i ) 2
i=1 Ε i
2
เมื่อ Ο1 = 12 , Ο2 = 20 , Ο3 = 23 , Ο4 = 15 , Ο5 = 13
ให x = รายไดตอเดือนของคนในเขตหนองจอก
คํานวณหาคา E ไดดังนี้
เมื่อ Η 0 จริง E = np
โดยที่ p = ความนาจะเปนทีคนในเขตหนอกจอกมีรายไดในชวงที่ i ; i =1,2,3,4,5
่
นั่นคือคํานวณคา p เมื่อ x ~ normal ((µ= .2 ,σ= .05) ดังแสดงในรูป
.05
-3
.1
-2
.15
.2
.25
.3
.35
-1
0
1
2
3
X-Scale
Z-Scale
184. 187
เปลี่ยน x เปน z โดยที่ z = x - µ /σ = x - .2 / .05 ไดคา z และหาคา E ไดดงตาราง ดังนี้
ั
ชวงที่
1
2
3
4
5
รายได(x)
x < .1
.1< x < .15
.15 < x < .2
.2 < x < .25
x ≥ .25
z = x - .2 / .05
.1 - .2 / .05 = - 2
.15 - .2 / .05 = - 1
.2 - .2 / .05 = 0
.25 - .2 / .05 = 1
p
.0228
.1359
.3413
.3413
.1587
E= 83p
1.89
11.28
28.33
28.33
13.17
O
12
20
23
15
13
เนื่องจากE1 = 1.89 นอยกวา 5 จึงรวมรายไดชวงที่ 1 และชวงที2 เขาดวยกัน ดังนั้นจํานวนชวงจึง
่
เหลือ 4 และ O1 = 12+20 =32 E1= 1.89+11.28 = 13.17
χ 2 = ∑ ( Ο− Ε ) 2
Ε
= (32-13.17)2 +(23-28.33)2 +(15-28.33)2 +(13-13.17)2
13.17
28.33
28.33
13.17
= 34.20
เขตปฏิเสธ จะปฏิเสธ Η 0 เมื่อ χ 2 > χ 2.01 : 4-1 จากการเปดตาราง χ 2 ไดχ 2.01 : 3 = 11.34 ดังนั้นจึงปฏิเสธ
Η 0 นั่นคือ รายไดตอเดือนของคนในเขตหนองจอกไมไดมีการแจกแจงแบบปกติ ที่มีคาเฉลี่ย = 20,000
บาท คาเบี่ยงเบนมาตรฐาน = 5,000 บาทอยางมีนัยสําคัญทางสถิติที่ระดับ 0.01
สําหรับการทดสอบการแจกแจงลักษณะอืนๆก็มีวิธีการหาเชนเดียวกัน
่
2. การทดสอบสมมติฐานสําหรับขอมูลที่จําแนกสองทาง
2.1 การทดสอบความเปนอิสระกันระหวางลักษณะ 2 ลักษณะ (ความสัมพันธระหวาง 2 ตัวแปร)
กรณีนี้จะมีตวแปร 2 ตัว ระดับการวัดเปนนามบัญญัติ ( Nominal scale ) ทั้งคู โดยใชตารางจําแนกแบบ
ั
2 ทาง คือแนวตั้งและแนวนอน ตัวอยาง เชน เพศกับผลการเรียนเปนอิสระกันหรือไม โดยที่เพศ แบงเปน
2 กลุม คือ ชาย และหญิง สวนผลการเรียนแบงเปน ดี ปานกลาง ออน เปนตน
สถิติที่ใชคงเปน χ 2 โดยมีสมมติฐาน คือ
Η 0 : ลักษณะหรือตัวแปรทังสองเปนอิสระกัน
้
Η 1 : ลักษณะหรือตัวแปรทังสองไมเปนอิสระกัน
้
สถิติที่ใชทดสอบคือ
χ 2 = ∑ ( Ο− Ε ) 2
Ε
185. 188
โดยที่
= R ×C
N
เมื่อ R = ผลรวมของความถี่ในแถวนอน
C = ผลรวมของความถี่ในแนวตั้ง
N = ผลรวมของความถี่ทั้งหมด
เขตปฏิเสธ จะปฏิเสธ Η 0 เมื่อ χ 2 > χ 2α : ( r- 1 ) ( c - 1) ดวยองศาอิสระ (r-1)(c-1)
ตัวอยาง จากการศึกษาจํานวนนักศึกษาทีมีความเชื่อโชคลาง จําแนกตามประเภทนักศึกษา
่
ประเภทนักศึกษา เชื่อ
ไมแนใจ
ไมเชื่อ
รวม
วิทยาศาสตร
5
45
50
100
แพทยศาสตร
25
55
20
100
รัฐศาสตร
40
40
20
100
อักษรศาสตร
45
25
30
100
สังคมศาสตร
35
35
30
100
รวม
150
200
150
500
จากตาราง หาความถี่ที่คาดหวัง ( Ε ) ของแตละประเภทไดดวยสูตร
Ε = R ×C
N
เมื่อ R = ผลรวมของความถี่ในแถวนอน
C = ผลรวมของความถี่ในแนวตั้ง
N = ผลรวมของความถี่ทั้งหมด
เชน แถวนอน เมื่อ O = 5 , E = 100 X150 = 30
500
ทํานองเดียวกันจะคํานวณคา E ของทุกประเภทได ซึ่งจะไดตาราง
ตาราง จํานวนนักศึกษาที่คาดวาจะเชื่อโชคลาง จําแนกตามประเภทของนักศึกษา
เชื่อ
ไมแนใจ
ไมเชื่อ
O
E
O
E
O E
วิทยาศาสตร
5 30
45 40
50 30
แพทยศาสตร
25 30
55 40
20 30
รัฐศาสตร
40 30
40 40
20 30
อักษรศาสตร
45 30
25 40
30 30
สังคมศาสตร
35 30
35 40
30 30
Ε
186. 189
จากตาราง ก็จะหาคา χ 2 ไดดวยการแทนคาในสูตรดังนี้
χ 2 = ( 5 - 30 ) 2 + ( 25 - 30 ) 2 + ( 40 - 30 ) 2 + ( 45 - 30 ) 2 + ( 35 - 30 ) 2
30
30
30
30
30
= 65.83
การแปลความหมายจะตองนําคา χ 2 ที่คํานวณไดไปเปรียบเทียบกับ คา χ 2 ในตาราง
df = ( r - 1 ) ( c -1 ) = ( 3 - 1 ) ( 5 - 1 ) = 8 และ∝ ที่กําหนด คือ 0.05 หรือ 0.01 หรือ 0.001 ถากําหนด =
0.05 คา χ 2ในตารางจะได 15.51 ซึ่งคาที่คํานวณไดมากกวา แสดงวาการเชื่อโชคลางไมเปนอิสระจาก
ประเภทของนักศึกษา หรือการเชื่อโชคลางมีความสัมพันธกับประเภทของนักศึกษา แตยังไมทราบวา
ประเภทใดกับประเภทใดสัมพันธกันบางจะตองวิเคราะหรายคูตอไป ดวยการจับนักศึกษาแตละประเภท
ั
เปรียบเทียบกันทีละคู ๆ หาคา Ε ใหม และแทนคาในสูตรเดิม เชน คูวิทยาศาสตรกบแพทยศาสตร ก็จะ
ไดดังตาราง
ตาราง จํานวนนักศึกษาที่เชื่อและคาดวาจะเชื่อโชคลางจําแนกตามประเภทของนักศึกษา
เชื่อ
ไมแนใจ
ไมเชื่อ
O E
O E
O
E
วิทยาศาสตร
5 15
45 50
50 35
แพทยศาสตร
25 15
55 50
20
35
สําหรับการทดสอบสมมติฐาน χ 2 ที่ทดสอบความสัมพันธของตัวแปรหรือทดสอบความเปนอิสระ
ของตัวแปร โดยใชโปรแกรม SPSS for Windows มีรายละเอียด ดังนี้
การทดสอบ χ 2 โดยใชโปรแกรม SPSS for Windows
การทดสอบχ 2 สามารถการวิเคราะห โดยใชโปรแกรม SPSS for Windows มีวิธีการ ดังนี้
1 ) อธิบายความสัมพันธระหวางตัวแปร
1 . ความสัมพันธระหวางตัวแปร 2 ตัว ที่มีระดับการวัดเปน nominal ( ใชสถิติ χ 2)
1.1ใชคําสั่ง
Analyze
Descriptive Statistics
จะไดหนาจอดังรูปที่ 1
Crosstabs
187. 190
รูปที่ 1
จากรูปที่ 1 - เลือกตัวแปรทีมีการวัดระดับ nominal ที่ตองการใสใน Box ของ Row และ Column
่
1.2 เลือก statistics จะไดหนาจอดังรูปที่ 2
รูปที่ 2
จากรูปที่ 2 เลือก chi - square แลวเลือก continue จะกลับไปหนาจอรูปที่ 1
1.3 เลือก cells จะไดหนาจอดังรูปที่ 3
รูปที่ 3
จากรูปที่ 3 สามารถเลือก counts , percentages และ Residuals เมื่อ เลือกแลวเลือก continue จะ
กลับไปหนาจอรูปที่ 1
188. 191
1.4 เลือก Format….. จะไดหนาจอ ดังรูปที่ 4
รูปที่ 4
จาก รูปที่ 4 เลือก Row Order
- Ascending แสดงตัวแปร row ตามคาที่เรียงจากนอยไปมาก
- Descending แสดงตัวแปร row ตามคาที่เรียงจากมากไปนอย
เลือก continue จะกลับมาหนาจอรูปที่ 1 เลือก OK จะไดผลลัพธแสดงในตารางที่ 1-2
ตารางที่ 1 School * Status of parent Crosstabulation
School
1
School
2
School
3
School
4
4
School
total
Count
% within school
% within status
% of Total
Count
% within school
% within status
% of Total
Count
% within school
% within status
% of Total
Count
% within school
% within status
% of Total
Count
% within school
% within status
% of Total
status of parent
1 (คู)
2 (หมาย) 3(หยา)
5
5
306
1.6%
1.6%
95.3 %
9.1%
8.9%
24.3%
0.4%
0.4%
21.5%
20
17
431
4.1 %
3.5 %
88.1 %
36.4%
30.4%
34.2%
1.4%
1.2%
30.2%
13
22
265
4.1 %
7.0 %
84.1 %
23.6%
39.3%
21.0%
0.9%
1.5%
18.6%
17
12
288
5.7%
4.0%
86 %
30.9%
21.4%
20.5%
1.2%
0.8%
18.1%
55
56
1260
3.9 %
3.9 %
88.4 %
100%
100%
100%
3.9%
3.9%
88.4%
4 (แยก)
5
1.6%
9.3%
0.4%
21
4.3 %
38.9%
1.5%
15
4.8 %
27.8%
1.1%
13
4.3%
24.1%
0.9%
54
3.8 %
100%
3.8%
Total
321
100.0%
22.5%
22.5%
489
100.0 %
34.3%
34.3%
315
100.0 %
22.1%
22.1%
300
100%
21.1%
21.1%
1425
100 %
100%
100%
189. 192
ตารางที่ 2 Chi -Square Tests
Value
df
Asymp Sig ( 2-sided )
Pearson Chi-Square
27.565a
9
.001
Likelihood Ratio
29.612
9
.001
Linear – by – Linear Association
12.104
1
.001
N of Vaild Cases
1425
a. 0 cells ( 0% ) have expected count less than 5. The minimum expected count is 11.37
ความหมายของผลลัพธในตารางที่ 1
1
2
3
4
5
แสดง label ของตัวแปรทางดาน row คือ school ซึ่งแบงเปน 4ประเภท คือ 1 2 3 และ 4
แสดง label ของตัวแปรทางดาน column คือ status ซึ่งแบงเปน 4 ประเภท คือ 1 (คู)
2 (หมาย) 3 (หยา) และ4 (แยก)
แสดงจํานวน และเปอรเซ็นตของสถานภาพสมรสคู ดังนี้
- ผูปกครองมีสถานภาพสมรสคู 306 คน ( Observed)
- มีผูปกครองของนักเรียนที่เรียนอยูในโรงเรียน ประเภท1 มีสถานภาพสมรสคู 95.3 % ของ
จํานวนนักเรียนที่เรียนอยูในโรงเรียนประเภท 1 ทั้งหมด ( 306/321 :Row Percent )
- มีผูปกครองของนักเรียนที่เรียนอยูในโรงเรียน ประเภท1 มีสถานภาพสมรสคู 24.3 % ของ
ผูปกครองที่มีสถานภาพสมรสคูทั้งหมด ( 306/1260 %:column percent )
- มีผูปกครองของนักเรียนที่เรียนอยูในโรงเรียน ประเภท1 มีสถานภาพสมรสคู 21.5 % ของ
ตัวอยางทั้งหมด ( 306/1425 : Total percent ) - ใน cell อื่น ๆ ก็มีความหมายในลักษณะ
เดียวกัน
แสดงความถี่และเปอรเซ็นตรวมของแตละสถานภาพสมรส เชน
- มีผูปกครองมีสถานภาพสมรสคู 1260 ครอบครัว จากตัวอยางทั้งหมด 1425 ครอบครัว
หรือคิดเปน 84.1 % ของตัวอยางทั้งหมด
- มีผูปกครองมีสถานภาพสมรสหยา 55 ครอบครัว จากตัวอยางทั้งหมด 1425 ครอบครัว
หรือคิดเปน3.9 % ของตัวอยางทั้งหมด
แสดงความถี่และเปอรเซ็นตรวมของแตละเพศ เชน
- มีนักเรียนจากโรงเรียนประเภท 1 321 คน จากตัวอยางทั้งหมด 1425 คน หรือคิดเปน 22.5
% ของตัวอยางทั้งหมด
- มีนักเรียนจากโรงเรียนประเภท 2 489 คน จากตัวอยางทั้งหมด 1425 คน หรือคิดเปน 34.3
% ของตัวอยางทั้งหมด
190. 193
ความหมายของผลลัพธในตารางที่ 2
6
7
8
9
H0 : ประเภทของโรงเรียน และสถานภาพสมรสของผูปกครองเปนอิสระกัน
H1 : ประเภทของโรงเรียน และสถานภาพสมรสของผูปกครองมีความสัมพันธกัน
กําหนดระดับนั้นสําคัญ = .05 สถิติทดสอบ Pearson Chi - Square = 27.565 ที่องศาอิสระ 9 และ ไดคา
Significance ของการทดสอบ = .001 ซึ่งนอยกวากวาระดับนัยสําคัญที่กําหนด ( .05 ) จึงปฏิเสธ H0 นั้นคือ
ประเภทของโรงเรียน และสถานภาพสมรสของผูปกครองมีความสัมพันธกัน
สถิติทดสอบ Likelihood Ratio Chi-Square =29.612 องศาอิสระ = 9 Singnificance = .001 จึงสรุปวา
ประเภทของโรงเรียน และสถานภาพสมรสของผูปกครองมีความสัมพันธกัน
สถิติทดสอบ Linear - by - Lienar Association Chi-Square ที่ใชทดสอบสมมติฐาน
H0 : ประเภทของโรงเรียน และสถานภาพสมรสของผูปกครองไมมีความสัมพันธกันในรูปเชิงเสน
H1 : ประเภทของโรงเรียน และสถานภาพสมรสของผูปกครองมีความสัมพันธกันในรูปเชิงเสน
ไดคาสถิติทดสอบ =.12.104 ที่องศาอิสระ = 1และคา Significance = .001 จึงสรุปไดวาประเภทของ
โรงเรียน และสถานภาพสมรสของผูปกครองมีความสัมพันธกันในรูปเชิงเสน
ระบุจํานวน cell ที่มีความถี่ที่คาดไว < 5 ในที่นี้ไมมีcell ที่มีความถี่ที่คาดไวต่ํากวา5 เลย ความถี่ที่ต่ําสุด
ใน cell =11.37
แบบฝกหัด
1. ทางฝายการศึกษาของสถาบันการศึกษาแหงหนึ่งตองการทดสอบความสัมพันธระหวางเพศของ
อาจารยกับสถานศึกษาที่อาจารยจบ ที่ระดับนัยสําคัญ .05 จึงสุมอาจารยในสถาบันมา 84 คน แยก
ตามเพศและสถานศึกษาที่อาจารยจบ ดังนี้
เพศ
สถานศึกษาทีอาจารยจบ
่
ในประเทศ
ตางประเทศ
ทั้งในและตางประเทศ
ชาย
12
6
13
หญิง
19
16
18
2. บริษัทขายคอมพิวเตอรแหงหนึ่งไดเก็บขอมูลของลูกคาในปที่ผานมา ดังนี้
บริษัทเอกชน 69 % รัฐบาล 21 % ฝายการศึกษา 7 % บานอยูอาศัย 3 %
ทางบริษัทตองการตรวจสอบวาลักษณะของลูกคาในปนี้เหมือนปที่ผานมาหรือไม จึงสุมจากลูกคา
มา 50 ราย พบวา เปนบริษัทเอกชน 20 ราย รัฐบาล 12 ราย ฝายการศึกษา 12 ราย บานอยูอาศัย 4
ราย จงทดสอบที่ระดับนัยสําคัญ .10
191. 194
3. ผูสมัครเปนนายกสโมสรของนิสิตในสถาบันการศึกษาแหงหนึ่ง มี 5 คน คือหมายเลข 1 – 5 ถา
ผูสมัครตองการทราบวาสัดสวนของนิสิตทีมีสิทธิ์เลือกตั้งจะเลือกนายกสโมสรแตละคนเทากัน
่
หรือไม กอนการเลือกตั้งจึงสุมนิสิตที่มีสิทธิ์เลือกตั้ง จํานวน 30 คน สอบถามวาจะเลือกหมายเลขใด
ไดขอมูล ดังนี้
ผูสมัครหมายเลข
1
2
3
4
5
จงทดสอบที่ระดับนัยสําคัญ .01
จํานวนผูเลือก
3
9
6
5
7
4. นักจิตวิทยาเชือวาลูกชายมักจะมีอาชีพเดียวกับพอ จึงสุมลูกชายมา 60 คน สอบถามอาชีพของเขา
่
และอาชีพของพอ ไดขอมูล ดังนี้
อาชีพพอ
นักธุรกิจ
ขาราชการ/วิสาหกิจ
เกษตรกร
นักธุรกิจ
5
8
6
อาชีพลูกชาย
ขาราชการ/วิสาหกิจ
8
7
5
จงทดสอบความเชื่อของนักจิตวิทยา ที่ระดับนัยสําคัญ .05
เกษตรกร
6
5
10
192. 193. 196
จงหาผลลัพธจากโจทยที่กําหนดใหโดยวิเคราะหขอมูลดวยโปรแกรม SPSS
1. ใหบรรยายลักษณะของผูเรียนที่เปนกลุมตัวอยางโดยใชสถิติบรรยาย
ตัวแปรที่มมาตรวัดเปน nominal และ ordinal ใหเสนอตารางแจกแจงความถี่
ี
ตัวแปรที่มมาตรวัดเปน interval และ ratio ใหเสนอคาการวัดแนวโนมเขาสูสวนกลาง การกระจาย
ี
2. ตรวจสอบวาคาเฉลี่ยของรายไดรวมของครอบครัวเทากับ10,000 บาทหรือไม
ตรวจสอบวาคาเฉลี่ยของคะแนนเชาวนปญญาของนักเรียน เทากับ 100 คะแนนหรือไม
3. เปรียบเทียบเกรดเฉลี่ยสะสมระหวางนักเรียนที่มีเพศตางกัน จํานวนผูหาเลี้ยงครอบครัวตางกัน
การศึกษาของบิดาตางกัน
4. เปรียบเทียบจํานวนปเฉลี่ยของการศึกษาของบิดาและมารดา
5. เปรียบเทียบเกรดเฉลี่ยสะสมจําแนกตามโรงเรียน 3 แหง และสถานภาพสมรสของบิดามารดา
6. เปรียบเทียบคะแนนเชาวนปญญาจําแนกตามโรงเรียน 3 แหง และสถานภาพสมรสของบิดามารดา
7. ศึกษาความสัมพันธของรายไดรวมของครอบครัวและเงินที่บุตรไดไปโรงเรียนตอวัน
8. ศึกษาความสัมพันธของเกรดวิชาภาษาไทย วิทยาศาสตร คณิตศาสตร ภาษาอังกฤษ
9. ศึกษาปจจัย(คะแนนเชาวนปญญา คะแนนความคาดหวังของบิดามารดา รายไดรวมของครอบครัว
แรงจูงใจใฝสัมฤทธิ์ ที่มีความสัมพันธเชิงสาเหตุของเกรดเฉลี่ยสะสม
10. สรางสมการพยากรณเกรดเฉลี่ยสะสม
194. บรรณานุกรม
กัลยา วานิชยบัญชา.(2542). การวิเคราะหสถิติ : สถิติเพื่อการตัดสินใจ. พิมพครั้งที่ 4. กรุงเทพฯ :
โรงพิมพแหงจุฬาลงกรณวิทยาลัย.
กัลยา วานิชยบัญชา.(2541).การวิเคราะหขอมูลดวย SPSS for Windows. กรุงเทพ ฯ :
โรงพิมพแหงจุฬาลงกรณมหาวิทยาลัย.
ชูศรี วงศรัตนะ (2541). เทคนิคการใชสถิติเพื่อการวิจัย.พิมพครั้งที่ 7. กรุงเทพ ฯ :
ศูนยหนังสือจุฬาลงกรณมหาวิทยาลัย.
นงนุช ภัทราคร. (2538). สถิติการศึกษา. กรุงเทพ ฯ : สุวีริยาสาสน.
บุญธรรม กิจปรีดาบริสุทธิ์.(2540). ระเบียบวิธีการวิจัยทางสังคมศาสตร.พิมพครั้งที่7. กรุงเทพฯ :
โรงพิมพและปกเจริญผล.
บุญเรียง ขจรศิลป.(2536). สถิติวิจัย I. กรุงเทพมหานคร: พิชาญเพรส.
ลวน สายยศ และ อังคณา สายยศ. (2540). สถิติวิทยาทางการวิจัย. กรุงเทพมหานคร: สุวีริยาสาสน
ศิริชัย กาญจนวาสี, ดิเรก ศรีสุโข และทวีวัฒน ปตยานนท.( 2535) การเลือกใชสถิติที่เหมาะสม
สําหรับการวิจัยทางสังคมศาสตร. กรุงเทพมหานคร : จุฬาลงกรณมหาวิทยาลัย.
ศิริชัย กาญจนวาสี.(2545).สถิติประยุกตสําหรับการวิจัย.พิมพครั้งที่ 3.กรุงเทพฯ: โรงพิมพแหง
จุฬาลงกรณมหาวิทยาลัย.
Bryman, A. and Cramer, D. (2001). Quantitative Data Analysis with SPSS Release 10 for
Windows. London : Taylor&Francis Group.
Freund,J.E.and Simon,G.A. (1997). Modern Elementary Statistics.New Jersey : Prentice-Hall,Inc.
Heiman,G.W. (1996).Basic Statistics for the Behavioral Sciences. 2nd Edition. Boston : Houghton
Mifflin Company.
Howell,D.C. (1989).Fundamental Statistics for the Behavioral Sciences. 2nd Edition. Boston : PWSKENT Publishing Company.
Kanji, G.K. (1993). 100 Statistical Tests. 3nd Edition. London : SAGE Publications Inc.
195. ภาคผนวก
การประมวลผลขอมูล
ขอมูลที่ไดจาการวิจัย ที่รวบรวมไดจากแบบสอบถามหรือการสังเกต หรือการทดลอง
อาจจะอยูในรูปของขอความหรือตัวเลข จึงเปนหนาที่ของผูวิจัยทีจะตองทําการประมวลผลขอมูล
่
หรือทําการวิเคราะหเพื่อใหไดผลลัพธที่สามารถตอบวัตถุประสงคที่กําหนดไวได
• ความหมายของการประมวลผลขอมูล
การประมวลผลขอมูล คือการจัดเก็บขอมูลอยางเปนระบบ เพื่อใหขอมูลที่ไดรับการ
ประมวลผลแลวอยูในรูปแบบที่สามารถนําไปใชงานไดอยางมีประสิทธิภาพ
• วัตถุประสงคของการประมวลผลขอมูล
1. จัดเตรียมขอมูลใหอยูในสภาพพรอมที่จะนําเขาสูกระบวนการวิเคราะหตอไป
2. วิเคราะหขอมูลเพื่อใหไดผลลัพธที่สามารถตอบวัตถุประสงคที่กําหนดไว
• ขั้นตอนการประมวลผลขอมูล
การประมวลผลขอมูล 3 ขั้นตอนใหญ ๆ ดังนี้
1. การเตรียมขอมูลเพื่อการประมวลผล ( Input Data )
2. การประมวลผลขอมูล ( Processing )
3. การนําเสนอหรือแสดงผลลัพธ ( Output )
• วิธีการประมวลผลขอมูล
การประมวลผลขอมูล มีวิธีการตามขั้นตอนการประมวลผลขอมูล ดังนี้
1. วิธีการเตรียมขอมูลเพื่อการประมวลผล
2. วิธีการวิเคราะหขอมูลเพื่อการประมวลผลขอมูล
3. วิธีการแสดงผลลัพธ
โดยจะนําเสนอเนื้อหาเปน 2 สวน คือ สวนแรก คือ วิธการเตรียมขอมูลเพื่อการ
ี
ประมวลผล ซึ่งจะมีรายละเอียดของเนื้อหาในบทนี้ สวนที่สอง คือ วิธีการวิเคราะหขอมูล และ
วิธีการแสดงผลลัพธ ซึ่งจะมีรายละเอียดของเนื้อหาในบทที่ 8 ดังนี้
1. วิธีการเตรียมขอมูลเพื่อการประมวลผล ประกอบดวย
1.1 การเก็บรวบรวมขอมูล ขอมูลที่เก็บรวบรวมอาจไดจากเอกสารตาง ๆ ซึ่งเปนขอมูล
ทุติยภูมิ และ / หรือ เปนขอมูลปฐมภูมิ ซึ่งเก็บรวบรวมจากหนวยใหขอมูลโดยตรง สวนมากมักจะ
ใชแบบสอบถามเปนเครื่องมือในการเก็บขอมูล
196. 148
1.2 การตรวจสอบขอมูล เปนการตรวจสอบความถูกตองของขอมูลจากเครื่องมือที่ไดรับ
คืนมาโดยสามารถตรวจสอบ ขณะอยูระหวางการเก็บขอมูล ( Field edit ) และตรวจสอบเมื่อได
ขอมูลจากทุกสวนแลว ( Central office edit )
1.3 การเปลี่ยนสภาพขอมูล เปนการเปลี่ยนสภาพของขอมูลที่รวบรวมไดใหอยูในรูปแบบ
ที่สะดวกตอการนําไปประมวลผล หรือ วิเคราะห การเปลี่ยนสภาพขอมูล มีวิธีการ ดังนี้
1.3.1 การสรางรหัสสําหรับขอมูล
1.3.2 การจัดทําคูมือลงรหัส
1.3.3 การลงรหัส
1.3.1 การสรางรหัสสําหรับขอมูล
หลังจากที่ไดขอมูลมาแลว ควรมีการกําหนดตัวแปร และกําหนดรหัส หรือให
คาตัวแปร การกําหนดคาของตัวแปรและการใหความหมายของคา มักจะใชกับขอมูลเชิงคุณภาพ
เปนสวนใหญ เชน เพศ อาชีพ ระดับการศึกษา ความคิดเห็นตาง ๆ สวนขอมูลเชิงปริมาณมี
การกําหนดคาของตัวแปร ซึ่งมีคาตามคาปริมาณจริง ไมจําเปนตองใหความหมายของคา
ในการกําหนดรหัส หรือใหคาตัวแปรมักทําควบคูไปกับการออกแบบสอบถาม
นั่นคือ จะตองพิจารณาถึงตัวแปร ซึ่งคําถาม 1 ขอ จะสรางตัวแปรไดอยางนอย 1 ตัว และคาของ
ตัวแปรคือ ขอมูล โดยทั่วไปแบบสอบถามจะกําหนด หรือมีชองใหใสรหัสไวทางดานขวามือของ
แบบสอบถาม ดังแสดงไวในรูปที่ 1
รูปที่ 1 ตัวอยางบางสวนของแบบสอบถาม
เลขที่แบบสอบถาม………
สถานภาพสวนบุคคล
1. เพศ
( ) 1.ชาย
( ) 2. หญิง
SEX
2. อายุ ………ป
AGE
3. การศึกษาสูงสุด
EDUC
( ) 1. มัธยมตน
( ) 4. ปริญญาตรี
( ) 2. มัธยมปลาย / ปวช. ( ) 5. สูงกวาปริญญาตรี
( ) 3. อนุปริญญา / ปวส.
( ) 6. อื่น ๆ (ระบุ)…..
4. รายไดตอเดือน
INCOME
( ) 1. ไมมีรายได
( ) 5. 30,000-49,990
( ) 2. ต่ํากวา 5,000 บ.
( ) 6. 50,000-100,000
( ) 3. 5,000 -9,999 บ.
( ) 7. มากกวา 100,000 บ.
( ) 4. 10,000-29,999 บ.
197. 149
จะพบวาชองสี่เหลี่ยมทางดานขวาใหใสรหัสหรือคาตัวแปรของแตละขอ ทั้งนี้ผูวิจยควร
ั
ทําสมุดคูมือการกําหนดรหัสของตัวแปร โดยจะกลาวในหัวขอตอไป สวนการสรางรหัส มีวิธีการ
ดังนี้
1 ) การกําหนดขนาดของตัวแปร
ขนาดของตัวแปร แสดงถึงความยาวของตัวแปร ซึ่งขึนอยูกับชนิดของตัวแปร
้
หรือ ขอมูล ดังนี้
ตัวแปรเชิงปริมาณ เปนตัวแปรที่มีคาเปนตัวเลขที่ระบุไดวามากหรือนอยกวากัน
เทาไร เชน ยอดขาย รายได น้ําหนัก สวนสูง ความยาว อายุ จํานวนคน สัตว สิ่งของ ฯลฯ
จากรูปที่ 1 ตัวแปรที่เปนปริมาณ ไดแก อายุ การกําหนดขนาดของตัวแปร ถาคิดวา อายุคน
สูงสุดไมเกิน 99 ป ก็กําหนดใหมจํานวนหลัก 2 หลัก จึงมีชองสี่เหลี่ยมไว 2 ชอง
ี
ตัวแปรเชิงคุณภาพ เปนตัวแปรที่เปนขอความ เมื่อแปลงรหัสเปนตัวเลข จํานวน
หลักของตัวเลขควรเทากับจํานวนหลักของตัวเลือกที่มีคาสูงสุด เชน จาก รูปที่ 1 ระดับการศึกษา
หรือ ตัวแปร EDUC จะมีคา 1 , 2 , ……., 6 จึงเปนหลักเลข 1 หลัก จึงใหชองสี่เหลียมไว 1 ชอง
่
การสรางรหัสของตัวแปรจะขึ้นอยูกับชนิดของคําถามในแบบสอบถาม ดังนั้น
ในที่นี้จะกลาวถึงวิธีการกําหนดรหัสโดยแบงตามชนิดของคําถาม ดังนี้
1. การกําหนดรหัสโดยแบงตามชนิดของคําถาม
การกําหนดรหัสของขอมูลจะตองคํานึงชนิดของคําถาม โดยที่ชนิดของคําถามแบงเปน
1. คําถามปลายปด ( closed - end question )
ก. คําถามที่มีเพียงคําตอบใหเลือกเพียง 2 คําตอบ ( Dichotomous question ) เชน
คําถามขอ 1 ในรูปที่ 1 ซึ่งถามเกี่ยวกับเพศของผูตอบจะมี 1 ตัวแปร คือ SEX ซึ่งเปนตัวแปรเชิง
คุณภาพ หมายถึง คําตอบเปนขอความ คือ ชาย หรือ หญิง ผูตอบเลือกไดเพียงคําตอบเดียว ในที่นี้
จะกําหนดวาตัวแปร SEX มีขนาด 1 หลัก และมีคาเพียงคาใดคาหนึ่ง จาก 2 คา คือ
1
หมายถึง ชาย
SEX =
2
หมายถึง หญิง
คาตัวเลขที่กําหนดแทนชายและหญิง เปนรหัสที่แสดงถึงชายหรือหญิงเทานั้น ไมได
หมายความวาหญิงมีคามากกวาชาย ในการใชรหัสจะใชเลข 0 แทนชาย เลข 1 แทนหญิงหรือใช
0 และ 1 แทนหญิงและชาย ตามลําดับก็ได แตถาใชแบบใดก็ตองใชแบบนั้นตลอดสําหรับ
แบบสอบถามทุกชุด
ข. คําถามที่มคําตอบใหเลือกหลายคําตอบ ( Multiple choice questions )
ี
เปนคําถามที่มีใหเลือกหลายคําตอบ ผูตอบจะตองเลือกคําตอบใดคําตอบหนึ่งเพียง
คําตอบเดียวจากรูปที่ 1 คําถาม ขอ 3 การศึกษาสูงสุด และขอ 4 รายไดตอเดือน ตัวแปร
198. 150
การศึกษาสูงสุด ( EDUC ) เปนตัวแปรเชิงคุณภาพ สวนตัวแปร รายไดตอเดือน ( INCOME )
จะถือวาเปนตัวแปรเชิงคุณภาพ ( Category Variable ) เชนเดียวกัน เพราะถึงแมรายไดจะเปน
ตัวเลข แตเมื่อกําหนดใหเลือกเปนชวง ถาผูตอบมีรายได 25,000 บาท ตอเดือน จะเลือกทางเลือก
ที่
( ) 4. 10,000-29,999 บาท ซึ่งถือวาเลือกชวงนีหรือกลุมนี้ จึงถือวาเปนตัวแปรเชิงคุณภาพ
้
ดังนั้นตัวแปร INCOME จึงเปนตัวเลขที่แสดงถึงกลุม และมีคา 1 หลัก คือ เลข 1 , 2 , …….., 7
ค. คําถามที่สามรถเลือกคําตอบไดหลายคําตอบ ( Checklist questions )
กรณีที่คําถามมีคําตอบใหเลือกหลาย ๆ คําตอบ และผูตอบสามารถตอบไดหลาย ๆ
คําตอบ เชน คําถามเกี่ยวกับการใชสายการบิน ดังนี้
สําหรับทานที่เดินทางไปตางประเทศใน 6 เดือนที่ผานมา ทานใชสายการบินใดบาง
( ตอบไดมากกวา 1 ขอ )
( ) 1. Thai Airline
( ) 2. Singapore Airline
( ) 3. Japan Airline
( ) 4. TWA
( ) 5. สายการบินอื่น ๆ
การกําหนดตัวแปรหรือกําหนดรหัสสําหรับคําถามประเภทนี้ อาจทําไดหลาย
แบบ แตที่นยม คือ Multiple dichotomy method
ิ
เปนการกําหนดใหคําตอบแตละทางเลือกเปน 1 ตัวแปร จากตัวอยางมีทางเลือก
5 ขอ จึงมี 5 ตัวแปร โดยที่แตละตัวแปรเปน dichotomous คือมีได 2 คา ถากําหนดตัวแปร 5
ตัวแปร คือ V1 , V2 ……., V5
1
ถาผูตอบเลือก Thai Airline
V1 =
0
ถาผูตอบไมเลือก Thai Airline
1
ถาผูตอบเลือก Singapore Airline
0
ถาผูตอบไมเลือก Singapore Airline
V2 =
199. 151
1
ถาผูตอบเลือกสายการบินอืน ๆ
่
V5 =
0
ถาผูตอบไมเลือกสายการบินอื่น ๆ
ถาใน 6 เดือนที่ผานมา นาย ก. ใชการบินไทย และ TWA ตัวแปร V1 และ
V4 เปน 1 V2 , V3 และ V5 จะเปน 0 ดังนั้น ขอมูลที่ตองบันทึก คือ
1 0 0 1 0
V1 V2 V3 V4 V5
สําหรับการวิเคราะห เชนการหาจํานวนผูใชสายการบินตาง ๆ และสัดสวน
หรือเปอรเซ็นตจะสามารถแยกทําครั้งละตัวแปรหรือครั้งละสายการบิน เชน ถาเก็บขอมูลมา 100
คน เปอรเซ็นตของผูใชสายการบินตางๆ มีดังนี้
ใช
ไมใช
รวม
การใช Thai Airline
รหัส ความถี่ เปอรเซ็นต
1
67
67.0
0
33
33.0
100
100.0
ใช
ไมใช
รวม
การใช Japan Airline
รหัส ความถี่ เปอรเซ็นต
1
54
54.0
0
46
46.0
100
100.0
ใช
ไมใช
ใช
ไมใช
การใช Singapore Airline
รหัส ความถี่ เปอรเซ็นต
1
25
25.0
0
75
75.0
100
100.00
การใช TWA
รหัส ความถี่
1
41
0
59
100
เปอรเซ็นต
41.0
59.0
100.00
ง. คําถามที่ใหคําตอบใสลําดับที่ ( Rank question )
เปนคําถามที่มีรายการใหเลือก โดยใหผูตอบเปรียบเทียบรายการทีกาหนดให และใส
่ํ
หมายเลขเมื่อเรียงลําดับความสําคัญ อาจเรียงจากนอยสุดไปมากสุด หรือมากสุดไปนอยสุด
ตัวอยาง
200. 152
กรุณาเรียงลําดับความสําคัญของปจจัยที่ทําใหทานเลือกเรียนพยาบาล 3 ลําดับแรก
โดยใหปจจัยทีสําคัญที่สุดเปนลําดับที่ 1 รองลงมาเปนปจจัยที่ 2 และ 3 โดยใหใสลําดับในวงเล็บ
่
หนาขอ
( ) 1. เปนอาชีพที่ความมีเกียรติ
( ) 2. หางานงาย
( ) 3. รายไดดี
( ) 4. เปนประโยชนตอครอบครัวและสังคม
ถาน.ส.ราตรี เลือก เปนประโยชนตอครอบครัวและสังคม ตามดวย เปนอาชีพที่
ความมีเกียรติ และหางานงาย เรียงลําดับตามความสําคัญจากมากไปนอย 3 ลําดับ จะไดคา
E1 = 4 , E2 = 1 , E3 = 2 ดังแสดงในรูปที่ 2
รูปที่ 2
(2)
(3)
( )
(1)
1. เปนอาชีพที่ความมีเกียรติ
2. หางานงาย
4
3. รายไดดี
E1
4. เปนประโยชนตอครอบครัวและสังคม
1
E2
2
E3
จ. คําถามทีใหแสดงระดับความมากนอย ( Scale Questions )
คําถามประเภทนี้สวนใหญจะถามความคิดเห็น ความชอบ ความพอใจวามีมาก /
นอย เห็นดวยหรือไมเห็นดวย สเกลที่แสดงระดับความคิดเห็นจะเรียงจากดานหนึ่งไปยังอีกดาน
หนึ่ง เชน จากไมเห็นดวยอยางยิ่ง จนถึง เห็นดวยอยางยิ่ง จํานวนระดับของสเกลสวนใหญมักจะ
เปนเลขคี่ เชน 3, 5 , 7 หรือ 9 สวนใหญจะนิยมใช 5 หรือ 7 ระดับ โดยมีสเกลตรงกลาง
การกําหนดรหัสในกรณีที่เรียงจากไมเห็นดวยอยางยิงจนถึงเห็นดวยอยางยิ่ง หรือ ไม
่
ชอบมากที่สุดจนถึงชอบมากที่สุด จะใหคาจากต่ําสุดไปหาสูงสุด เชน ในสเกล 5 ระดับ ไมเห็น
ดวยอยางยิ่งจะมีรหัสเปน 1 จนถึงเห็นดวยอยางยิ่ง จะมีรหัสเปน 5 นั่นคือ
ความคิดเห็น
ไมเห็นดวยอยางยิ่ง
ไมเห็นดวย
เฉย ๆ
เห็นดวย
รหัส
1
2
3
4
201. 153
เห็นดวยอยางยิ่ง
5
2 ) คําถามปลายเปด ( Open -ended Question )
สําหรับคําถามใหแสดงความคิดเห็นซึ่งเวนทีใหผูตอบเขียนนัน ในการให
่
้
รหัสผูวิจัยจะตองพิจารณคําตอบเดียวกันหรือคลายกันเปนรหัสเดียวกัน เชนถาอานจากคําตอบแลว
พบวามีความคิดเห็นทีแตกตางกัน 13 แบบ อาจใหรหัสเปน 01,02 ,…….,13
่
1.3.2 การจัดทําคูมือลงรหัส
ในกรณีที่มีจํานวนคําถามในแบบสอบถามมากๆ ผูใสรหัสอาจจะจํารหัสไดไม
ครบจึงจําเปนตองจัดทําคูมือลงรหัส อันประกอบดวย
ก. เลขที่แบบสอบถาม หมายถึงเลขที่ของแบบสอบถามที่ไดรับคืนกลับมา
การใสเลขที่แบบสอบถาม จะทําใหสามารถตรวจสอบขอมูลจากแบบสอบถามไดงาย ใน
กรณีที่มีการพิมพขอมูล เชน ถาพบวาอายุของผูตอบจากแบบสอบถามชุดที่ 150 เปน 99 ป ทําให
สามารถตรวจสอบวาพิมพผดหรือไม โดยตรวจสอบจากแบบสอบถามชุดที่ 150
ิ
ข. เลขที่คําถาม ( Question Number )
เปนเลขที่คําถามในแบบสอบถาม ผูวิจัยจะกําหนดรหัสใหตรงกับเลขที่ขอใน
แบบสอบถาม
ค. ชื่อตัวแปร ( Variable Name )
สวนใหญมกจะกําหนดใหชอตัวแปรสอดคลองกับความหมายของขอมูล เชน เพศ มักจะ
ั
ื่
ใช SEX รายได เปน INCOME เปนตน
ง. รายการของขอมูล
เปนสวนที่ระบุถึงคําถามในแตละขอ
จ. ขนาดของตัวแปร
เปนการกําหนดความกวางของตัวแปร ถาเปนตัวแปรเชิงปริมาณ เชน กําไร ( PROFIT)
ตัวแปรอาจจะมีจุดทศนิยม ตองกําหนดจํานวนหลักหลังจุดทศนิยมดวย เชน ถาความกวางของตัว
แปร PROFIT เปน 8.2 หมายถึงมีจํานวนจุดหนาจุดทศนิยม 5 หลัก และจํานวนหลักหลังจุด
ทศนิยม 2 หลัก ( เลข 8 รวมหมายถึงจํานวนหลักหนาจุดทศนิยม จุดทศนิยมและจํานวนหลัก
หลังจุดทศนิยม )
ฉ. คาที่เปนไปไดพรอมคําอธิบายความหมาย ( Possible Values or Label )
202. 154
หมายถึงสวนที่จะระบุคาที่เปนไปไดของตัวแปร เชน ตัวแปร SEX มีคา “ 0 ” หมายถึง
ชาย และคา “ 1 ” หมายถึงหญิง สวนเลข 9 หมายถึง ผูตอบไมตอบคําถามนี้ ( missing
values )
ตัวอยางการจัดทําคูมือการกําหนดรหัสของแบบสอบถามเรื่องความพึงพอใจของการ
ใหบริการของบริษัทดีทัวร ซึ่งจะสอบถามจากลูกคาที่เคยใชบริการของบริษัท ฯ
ตัวอยางบางสวนของแบบสอบถาม
แบบสอบถามของการสํารวจ “ ความพึงพอใจของบริษทดีทัวร ”
ั
ชื่อพนักงานสัมภาษณ………………………
วัน เดือน ป ที่สัมภาษณ…………………..
I สถานภาพสวนบุคคล
1. เพศ
( ) 1. ชาย
( ) 2. หญิง
2. อายุ ……ป
3. การศึกษาสูงสุด
( ) 1. มัธยมตน
( ) 2. มัธยมปลาย / ปวช.
( ) 3. อนุปริญญา / ปวส.
4. สถานภาพสมรส
( ) 1. โสด
( ) 2. แตงงานแลว
( ) 4. ปริญญาตรี
( ) 5. สูงกวาปริญญาตรี
( ) 6. อื่น ๆ (ระบุ)…..
( ) 3. หยา
( ) 4. เปนหมาย
5. รายไดตอเดือน
( ) 1. ไมมีรายได
( ) 4. 10,000-29,990 บาท
( ) 2. ต่ํากวา 5,000 บาท ( ) 5. 30,000-49,999 บาท
( ) 3. 5,000 -9,999 บาท ( ) 6. 50,000 บาทขึ้นไป
6. อาชีพขอทานในปจจุบน
ั
203. 155
( ) 1. ขาราชการ / พนักงานรัฐวิสาหกิจ ( ) 5. นักเรียน / นักศึกษา
( ) 2. พนักงานธุรกิจเอกชน
( ) 6. กิจการสวนตัว
( ) 3. แมบาน
( ) 7. อื่น ๆ ระบุ
( ) 4. เกษตรกร
II การเดินทาง
1. ทานเดินทางไปตางประเทศปละ …… ครั้ง
( ) 1. 0 - 1 ครั้ง
( ) 3. 6 - 9 ครั้ง
( ) 2. 2 - 5 ครั้ง
( ) 4 . ตั้งแต 10 ครั้งขึ้นไป
2. จุดประสงคของการเดินทางไปตางประเทศ
( ) 1. ธุรกิจ / ธุระอื่น ๆ
( ) 2. พักผอน
( ) 3. ทั้งพักผอนและธุรกิจ / ธุระอื่น ๆ
3. สวนใหญแลวทานเดินทางไปตางประเทศกับใครบาง
( ) 1. ไปคนเดียว
( ) 2. ไปกับครอบครัว
( ) 3. ไปกับเพื่อนสนิท
4. ปจจัยที่ทานเลือกใชบริการของบริษัทดีทัวร โดยใหเรียงลําดับความสําคัญ ปจจัยที่
สําคัญที่สุดเปนลําดับที่ 1 ปจจัยที่สําคัญนอยที่สุดเปนลําดับที่ 4 โ ดยใหใสลําดับที่ไวในวงเล็บ
( ) 1. ชื่อเสียงของบริษัท
( ) 2. ราคา
( ) 3. ชวงเวลาที่เหมาะสม ( ชวงเวลาที่วางตรงกับที่บริษัทดีทัวรจัด )
( ) 4. สายการบินที่บริษัทใช
5. ทานรูจักบริษทแสนดีทัวรจากแหลงใดบาง ( เลือกไดหลายคําตอบ )
ั
( ) 1. ทางทีวี
( ) 2. ทางสื่อสิ่งพิมพ เชน หนังสือพิมพ นิตยสาร ใบปลิว
( ) 3. เพื่อน / ญาติ แนะนํา
( ) 4. สมุดโทรศัพท
III ความพึงพอใจในการบริการของบริษัทดีทัวร
ทานมีความรูสึกอยางไรเกียวกับบริการดานตาง ๆ ของบริษัทดีทัวร ดังนี้
่
พอใจอยางยิ่ง
1. การบริการดานการจอง คําแนะนํา การติดตอ
2. คุณภาพและรสชาดของอาหาร
พอใจ
เฉยๆ ไมพอใจ ไมพอใจอยางยิ่ง
204. 156
3. การบริการของไกด
4. ความรู ความสามารถของไกดในการนําเที่ยว
5. บริการดานพาหนะ
ตัวอยางการจัดทําคูมือการลงรหัส
จากตัวอยาง ซึ่งเปนตัวอยางบางสวนของแบบสอบถามเพื่อสํารวจความพอใจของลูกคาที่มี
ตอบริการของบริษัทดีทัวร
เนื่องจากในทีนี้ใชโปรแกรม SPSS for Windows จึงไมตองกําหนดเลขที่แบบสอบถาม
่
สวนที่ I สถานภาพสวนบุคคล
คําถามที่ ชื่อตัวแปร รายการขอมูล ขนาดตัวแปร(จํานวนหลัก ) คาที่เปนไปไดและความหมาย
1.
SEX
เพศ
1
1. ชาย
2. หญิง
9. ไมตอบ
2.
AGE
อายุ
2
15- 80 ( 99 ไมตอบ )
3.
EDUCA
การศึกษา
1
4.
INCOME รายไดตอ
เดือน
1
5.
OCCUPA อาชีพ
1
1. มัธยมตน
2. มัธยมปลาย / ปวช.
3. อนุปริญญา / ปวส.
4. ปริญญาตรี
5. สูงกวาปริญญาตรี
6. อื่น ๆ 9. ไมตอบ
1. ไมมีรายได
2. ต่ํากวา 5,000 บาท
3. 5 ,000 - 9,999 บาท
4. 10 ,000 - 29,999 บาท
5. 30,000 - 49,999 บาท
6. 50,000 บาทขึ้นไป
9. ไมตอบ
1. ขาราชการ/ รัฐวิสาหกิจ
2. พนักงานธุรกิจเอกชน
3. แมบาน
ขอสังเกตุ
เลือกได
คําตอบเดียว
ระบุอายุจริง
เลือกได
คําตอบเดียว
เลือกได
คําตอบเดียว
เลือกได
คําตอบเดียว
205. 157
4. เกษตรกร
5. นักเรียน / นักศึกษา
6. กิจการสวนตัว
9. ไมตอบ
สวนที่ II การเดินทาง
คําถามที่ ชื่อตัวแปร รายการขอมูล
1.
V1
2.
V2
3.
V3
4
V4
4
V5
4
V6
ขนาดตัวแปร คาที่เปนไปไดและความหมาย
(จํานวนหลัก/ชอง)
จํานวนครั้งที่
1
1. 0 -1 ครั้ง
เดินทางตอป
2. 2 - 5 ครั้ง
3. 6 - 9 ครั้ง
4. ตั้งแต 10 ครั้งขึ้นไป
9. ไมตอบ
จุดประสงค
1
1. ธุรกิจ / ธุระกิจ
ของการ
2. พักผอน
เดินทาง
3. ทั้งพักผอนแลธุรกิจ/ธุรกิจอืน ๆ
่
ผูที่เดินทางไป
1
1. ไปคนเดียว
ดวย
2. ไปกับครอบครัว
3. ไปกับเพื่อนสนิท
4. ไมตอบ
ปจจัยในการเลือกบริษัททัวร
ชื่อเสียง
1
1. เลือกเปนลําดับ 1
2. เลือกเปนลําดับ 2
3. เลือกเปนลําดับ 3
4. เลือกเปนลําดับ 4
9. ไมตอบ
ราคา
1
1. เลือกเปนลําดับ 1
2. เลือกเปนลําดับ 2
3. เลือกเปนลําดับ 3
4. เลือกเปนลําดับ 4
9. ไมตอบ
ชวงเวลาที่
1
1. เลือกเปนลําดับ 1
ขอสังเกตุ
เลือกได
คําตอบเดียว
เลือกได
คําตอบเดียว
เลือกได
คําตอบเดียว
การใหลําดับที่
กําหนจํานวน
ตัวแปรเทากับ
จํานวน
ทางเลือก
206. 158
เหมาะสม
2. เลือกเปนลําดับ 2
3. เลือกเปนลําดับ 3
4. เลือกเปนลําดับ 4
9. ไมตอบ
คําถามที่ ชื่อตัวแปร รายการขอมูล
4
V7
ขนาดตัวแปร คาที่เปนไปไดและความหมาย
(จํานวนหลัก/ชอง)
สายการบินที่
1
1. เลือกเปนลําดับ 1
บริษัทใช
2. เลือกเปนลําดับ 2
3. เลือกเปนลําดับ 3
4. เลือกเปนลําดับ 4
9. ไมตอบ
ขอสังเกตุ
แหลงที่รูจักบริษัท
คําถามที่ ชื่อตัวแปร รายการขอมูล
ขนาดตัวแปร คาที่เปนไปไดและความหมาย
(จํานวนหลัก/ชอง)
1
0 : ไมเลือก
1 : เลือก
5.
V8
ทีวี
5.
V9
สื่อสิ่งพิมพ
1
0 : ไมเลือก
1 : เลือก
5.
V10
เพื่อน / ญาติ
1
5.
V11
สมุดโทรศัพท
1
0:
1:
0:
1:
ไมเลือก
เลือก
ไมเลือก
เลือก
ขอสังเกตุ
เลือกไดหลาย
คําตอบโดย
กําหนด
จํานวน
ตัวแปรเทากับ
จํานวน
ทางเลือก
207. 159
สวนที่ III ความพึงพอใจในการบริการ
คําถาม ชื่อตัวแปร รายการขอมูล
ขนาดตัวแปร คาที่เปนไปไดและความหมาย
ที่
(จํานวนหลัก/ชอง)
1.
U1
การจองแนะนํา
1
-2.ไมพอใจอยางยิ่ง
ฯลฯ
-1.ไมพอใจ 0. เฉย ๆ 1. พอใจ
2. พอใจอยางยิ่ง
9. ไมตอบ
2.
U2
อาหาร
1
-2.ไมพอใจอยางยิ่ง
-1.ไมพอใจ 0. เฉย ๆ 1. พอใจ
2. พอใจอยางยิ่ง
9. ไมตอบ
3.
U3
บริการของไกด
1
-2.ไมพอใจอยางยิ่ง
-1.ไมพอใจ 0. เฉย ๆ 1. พอใจ
2. พอใจอยางยิ่ง
9. ไมตอบ
4.
U4
ความสามารถ
1
-2.ไมพอใจอยางยิ่ง
ของไกด
-1.ไมพอใจ 0. เฉย ๆ 1. พอใจ
2. พอใจอยางยิ่ง
9. ไมตอบ
5.
U5
พาหนะ
1
-2.ไมพอใจอยางยิ่ง
-1.ไมพอใจ 0. เฉย ๆ 1. พอใจ
2. พอใจอยางยิ่ง
9. ไมตอบ
ขอสังเกตุ
1.3.3 การลงรหัส
วิธีการลงรหัสโดยใชโปรแกรม SPSS for Windows จะตองสรางแฟมขอมูล และ
สิ่งที่ควรทราบกอนสรางแฟมขอมูลโดยใช Data Editor จะตองกําหนด ดังนี้
1) กําหนดชือตัวแปร ( Variable Name )
่
2) กําหนดชนิดของตัวแปร
3) กําหนด label ของตัวแปร ( โดยเฉพาะตัวแปรที่เปนคุณภาพ )
4) กําหนดรหัสสําหรับคาสูญหาย ( missing value )
5) กําหนดความกวางของ column ( width )
1) การตังชื่อตัวแปร ( Variable Name )
้
สเกลแสดง
ลําดับความ
พอใจ
208. 160
SPSS จะตั้งตัวแปรเปน var 00001 , var00002 …… เปน default
สําหรับตัวแปรใหม การเปลี่ยนชื่อตัวแปรทําโดยการพิมพชื่อใหมแทนที่ ผูใชควรจะตั้งชื่อตัวแปร
ใหสอดคลองกับความหมายของคาของตัวแปร เชน อายุ ควรตั้งเปน age สวนรายได ควรตั้งชื่อ
ตัวแปร income เปนตน
กฏการตั้งชื่อตัวแปรของ SPSS
1.1 ความยาวของชื่อตัวแปรตองไมเกิน 8 ตัว
1.2 ชื่อตัวแปรตองเริ่มตนดวยอักษรเทานั้น สวนตัวอื่น ๆ อาจเปนตัวอักษร
ตัวเลข จุด หรือสัญลักษณพิเศษ เชน @ ,# , - หรือ $ ก็ได
1.3 ชื่อตัวแปรตองไมจบดวยจุด และควรหลีกเลี่ยงเครื่องหมาย “ _” ( ขีดลาง )
เปนตัวสุดทาย
1.4 หามใชสัญลักษณพิเศษตอไปนี้ในการตั้งชื่อตัวแปร ! ? ’ *
1.5 ชื่อตัวแปรในแฟมขอมูลเดียวกันตองไมซ้ํากัน
1.6 ตัวอักษรใหญหรือเล็ก จะถือเปนตัวแปรเดียวกัน เชน
INCOME income inCOME ถือเปนอยางเดียวกัน
1.7 หามตั้งชื่อตอไปนี้เปนชื่อตัวแปร
ALL
NE EQ TO LE LT
BY
OR
GT AND NOT GE WITH
ตัวอยางชื่อตัวแปรที่ถูกตอง INCOME satis _1 locate#1 Y.1
ตัวอยางชื่อตัวแปรที่ไมถูกตอง 1 INCOME WITH and satis 1_
2) ชนิดของตัวแปร ( Variable Type )
นอกจากจะตองตั้งชื่อตัวแปรแลว จะตองมีการกําหนดชนิดของตัวแปร ตัวแปร
หนึ่ง ๆ จะตองเปนชนิดใดชนิดหนึ่งเทานัน SPSS แบงตัวตัวแปรออกเปน 8 ชนิด แตที่ใชทวไป
้
ั่
เปน Numeric ซึ่งมีรายละเอียด ดังนี้
Numeric
เปนตัวแปรชนิดตัวเลข ซึ่งรวมทั้งเครื่องหมายบวกหรือลบที่นําหนาตัวเลข และรวมถึงจุด
ทศนิยม ถาเลือก Numeric จะตองกําหนดความกวาง ( Width ) และจํานวนหลักของตัวเลขหลัง
จุดทศนิยม ( Decimal Places ) ดวย เชน ถากําหนด
Decimal Places
=
2
Width
=
8
209. 161
ความกวาง 8 นี้ไดรวมจุดและจํานวนหลักจุดทศนิยมดวย จึงเหลือจํานวนหลักของเลข
หนาจุดทศนิยมเปน 5 หลัก หรือหลักหมืนนั่นเอง ผูวิเคราะหจะตองพิจารณาคาของขอมูลตัวแปร
่
วาสูงสุดมีกี่หลัก และกําหนดจํานวนหลักสูงสุดไว
เราสามารถกําหนดความกวางไดสูงสุด 40 หลักและจํานวนหลักหลังจุดทศนิยมสูงสุดเปน
10
3) การกําหนด Labels
กรณีที่ขอมูลที่ไดเปนตัวแปรเชิงคุณภาพ ไมวาจะเปนชนิดสเกลนามกําหนด หรือสเกล
อันดับก็ตาม เมื่อนําขอมูลใสแฟมขอมูลจะพิจารณาแปรเหลานี้ในลักษณะของ category variable
โดยที่ใน SPSS จะตองกําหนดคาตัวเลขใหแตละกลุมแลวใส label เพื่ออธิบายความหมายที่
แทจริงของคาตัวแปรไว
เชน คําถามเกี่ยวกับอาชีพ ซึ่งมีคําตอบใหเลือกดังนี้
1. นิสิต / นักศึกษา
2. ขาราชการ / พนักงานรัฐวิสาหกิจ
3. พนักงานธุรกิจเอกชน
4. เจาของกิจการสวนตัว
5. อื่น ๆ
ถาตอบเปนขาราชการจะตอบ “2” แตจะใสใน label วา “ 2 ” หมายถึง ขาราชการหรือ
พนักงานรัฐวิสาหากิจ
4) การกําหนดคาขอมูลสูญหาย ( Missing Value )
ในการวิจัยครังหนึ่ง ๆ มักจะเกิดการสูญหายของขอมูลบาสวน เชน แตละ case ควรมี 20
้
ตัวแปร แตมคาของบางตัวแปรหายไป จึงเรียกวา missing ซึ่งอาจเกิดจาการที่ผูตอบคําถมบางขอ
ี
หรือผูใสขอมูลเขาลืมใสขอมูลบางคําตอบ
อยางไรก็ตาม SPSS ไดแบง missing values ออกเปน 2 ชนิด คือ
1. System - missing values
ถา cell ใดในแฟมขอมูลไมมีขอมูลอยู หรือเปน cell วาง โปรกรมจะใหคาเปน
จุด (.) ซึ่งหมายถึง system-missing values
2. User - missing values
ผูวิเคราะหสามารถกําหนดคาของ missing value ตามความหมายได
210. 162
5) การกําหนดความกวางของ Column Format
SPSS จะกําหนดใหความกวางของ column เทากับความกวางของตัวแปรที่
กําหนดไว อยางไรก็ตาม บางครั้งชื่อตัวแปรจะยาวกวาคาของขอมูล เชน อายุ (AGE ) เราอาจ
กําหนดเปนชนิด Numeric เปนตัวเลขจํานวนเต็ม 2 ตําแหนง ความกวางของ column จะเปน 2
อัตโนมัติ จะทําใหชื่อตัวแปรเหลือเพียง 2 ตัว คือ AG จึงควรกําหนดความกวางของ column
เปน 3 โดยการเปลี่ยนแปลงคาความกวางจาก 2 เปน 3
การสรางแฟมขอมูลโดยใช Data Editor ของ SPSS
การสรางแฟมขอมูลจะตองเลือกคําสั่งตอไปนี้จาก Menu bar
File
New
Data
หลังจากนันจะตองคลิกที่หว column แรก ตรงที่มีคําวา var แลวเลือกคําสั่งตอไปนี้จาก
้
ั
เมนูบาร
Data
Define Variable
1) การตังชื่อตัวแปร ( Variable Name )
้
ถาตัวแปรที่ตองการกําหนดเปน sex จะตองเปลี่ยนชื่อตัวแปรจากรูปที่ 1
Variable Name : VAR00001 ใหเปลี่ยนชื่อ VAR00001 เปน SEX
รูปที่ 1
รูปหนา 54
2) กําหนดชนิดตัวแปร ( Type )
เลือก Type จากหนาจอในรูปที่ 1 จะไดหนาจอดัง รูปที่ 2 ดังนี้
211. 163
รูปที่ 2 หนาจอกําหนดชนิดตัวแปร
รูป 5.2 หนา 56
ในที่นี้จะกําหนดเปนชนิด Numeric จึงคลิกเลือก Numeric และกําหนดความกวางเปน
1 หลัก ซึ่งเปนเลขจํานวนเต็ม จึงไมมีเลขหลังจุดทศนิยม นั่นคือจํานวนหลักของเลขหลังจุด
ทศนิยมเปน 0 จึงใสคา และ 0 ใน Text box ดังนี้
Width
=
1
Decimal
=
0
แลวคลิกปุม Continue จะกลับไปที่หนาจอในรูปที่ 1
3) กําหนดฉลากตัวแปร ( Labels )
ในรูปที่ 1 คลิกที่ปุม Labels จะไดหนาจอดังนี้
รูปที่ 3 : หนาจอการกําหนด label
รูป 5.3 หนา 56
Variable Label : เปนการระบุความหมายของตัวแปร ผูใชควรจุระบุความหมายของตัว
แปร โดยเฉพาะอยางยิ่งกรณีที่ในแฟมขอมูลมีจํานวนตัวแปรมาก ๆ และชื่อตัวแปรเปนชื่อยอ ผูใช
อาจจะไมสามารถจําความหมายของตัวแปรไดหมด จึงควรระบุความหมายไว
นอกจากนั้น เมื่อกําหนดความหมายของตัวแปรแลว ผลลัพธของการวิเคราะหขอมูลจะ
แสดงความหมายของตัวแปรดวย ทําใหสามารถนําผลการวิเคราะหไปใชไดสะดวก
ในสวนของ Value Labels จะตองกําหนดคาของตัวแปร โดยเฉพาะขอมูลเชิงคุณภาพ
212. 164
4) กําหนดคาขอมูลสูญหาย ( Missing Value )
ถา cell ใดไมมีขอมูล SPSS จะถือวาเปน missing Values ใน SPSS จะ
ประกอบดวย missing value 2 ชนิด
ขั้นตอนการกําหนด User - missing values มีดังนี้
ในรูปที่ 1 เลือก Missing Values… จะเห็นหนาจอดังรูปที่ 4 ดังนี้
รูปที่ 4 : หนาจอการกําหนด User -missing values
รูป5.5 หนา58
จากรูปที่ 4 ผูใชตองคลิกเลือกทางไดเพียงทางเลือกเดียว โดยมีทางเลือก ดังนี้
0 No missing values หมายถึง การไมกําหนดคา missing กรณีนี้ถาในแฟมขอมูลมี
Cell วาง จะมีจุดอยูใน Cell วางเทานั้น
0 Discrete missing values หมายถึง ผูใชสามารถกําหนดคา missing ของแตละตัว
แปรได โดยกําหนดคาสูงสุดไมเกิน 3 คา
0 Range of missing values กรณีนี้ผูใชสามารถกําหนดคา missing values ใหมีคา
ในชวงทีกําหนดคาก็ได โดยกําหนดคาต่ําสุด ( Low) และคาสูงสุด ( High)
่
0 Rang of plus one discrete missing value คาทุกคาที่ใชกําหนดเปนชวงที่อยูในชวง
และรวมคาต่ําสุด และคาสูงสุด รวมทั้งอีก 1 คา ( Discrete Value ) ที่ไมมีอยูในชวงที่
กําหนดจะเปนคา missing values เชนกําหนดคา missing value เปน 10-19 และ
อีก 1 คาเปน 99
5) การกําหนด Column Format
เปนการกําหนดความกวางของ column ซึ่งสวนใหญจะกวางกวาความกวางของตัวแปร
โดยมีขั้นตอน ดังนี้
1. ในรูปที่ 1 เลือก Column Format จะไดหนาจอ Define Column Format ดัง
แสดงในรูปที่ 5
2. ใสความกวางของ column ใน text box ของ Column Width สวนใหญมักจะมี
การกําหนดความกวางของ column ใหยาวกวาความกวางของตัวแปร และจะตองพิจารณาชื่อตัว
213. 165
แปรดวย ในทีนี้ความกําหนดความกวางของ column แรกเปน 3 เนื่องจากชื่อตัวแปร sex ยาว 3
่
ตัว ดังแสดงในรูปที่ 5
3. ที่ Text Alignment เปนการกําหนดลักษณะการวางขอมูล วาจะวางชิด ( Left ) ตรง
กลาง ( Center) หรือชิดขวา ( Right) ของ column นั้น ๆ ในที่นี้จะพิมพขอมูลตรงกลาง column
จึงคลิกเลือก Center
รูปที่ 5 หนาจอการกําหนด Column Format
รูป 5.6 หนา 59
1.4 การบรรณาธิกร ( Editing ) เปนการตรวจสอบความถูกตองของขอมูล รวมทั้งขอมูลที่
ไดแปลงใหอยูในรูปรหัสแลว นอกจากนันควรจะตรวจสอบความสมบูรณครบถวนของขอมูล และ
้
ความสอดคลองของขอมูลดวย เชน ถามีผูตอบวา อายุ 19 ป แตมีประสบการณในการทํางาน 25
ป แสดงวาเปนไปไมได ผูตรวจจะตองพิจารณาวาควรจะแกไขอยางไร อาจพิจารณาจากคําถามอื่น
ๆ เชน ระดับการศึกษา ถาผูตอบตอบวาจนการศึกษาระดับปริญญาโท แสดงวาอายุไมถูกตอง
1.5 การแปรสภาพขอมูล ( Transforming ) เปนการเปลียนรูปแบบของขอมูลเพื่อให
่
สะดวกในการวิเคราะห โดยมีการเปลี่ยนแปลงรูปแบบขอมูล การแปรสภาพขอมูลที่ใชบอย คือ
การสั่งคํานวณ ( compute ) และการสั่งเปลี่ยนคาของขอมูล ( recode ) โดยมีวิธีการเปลี่ยนแปลง
โดยใชโปรแกรม SPSS for Windows ได ดังนี้
1 ) คําสัง Compute
่
ใชคํานวณคาของตัวแปรชนิดตัวเลข โดยเมื่อใชคําสั่ง Transform - Compute จะ
ไดหนาจอแสดงในรูปที่ 6
รูปที่ 6 : หนาจอการกําหนด Compute Variable Dialog box
รูปที่ 6.12 หนา 86
214. 166
Target Variable : ผูใชจะตองระบุชื่อตัวแปรใหม ซึ่งเปนตัวแปรที่ปรับคาที่ไดจากการคํานวณ
โดยใชคําสั่ง Compute
Numeric Expression : เปนคําสั่งที่กําหนดคาให Target Variable ซึ่งอาจจะประกอบดวยชื่อ
ตัวแปร คาคงที่ เครื่องหมายคํานวณ และฟงกชันตาง ๆ โดยผูใชสามารถพิมพหรือเลือกฟงกชัน
และเครื่องหมายคํานวณ
Calculator Pad : ประกอบดวยตัวเลข เครื่องหมายทางคณิตศาสตร ( Arithmetic Operators )
เครื่องหมายแสดงความสัมพันธ ( Relational Operators ) และเครื่องหมายทางตรรก ( Logical
Operators ) ผูใชสามารถคลิกเลือกใชได
การกําหนดเงือนไข
่
บางครั้งผูใชอาจตองการคํานวณเฉพาะบางกรณี เชนหารายจายมาเฉพาะขาราชการที่มีอายุ
ตั้งแต 40 ปขึ้นไป ( age > 40 & occupa = 1 ) ผูใชสามารถกําหนดเงื่อนไขโดยเลือก IF…..
ในรูปที่ 8 ซึ่งจะได Compute Variable : if Case Window ดังแสดงรูปที่ 7
รูปที่ 7 : หนาจอการกําหนด Compute Variable : if Case
รูปที่ 6.13 หนา 92
จากรูปที่ 7 ผูใชจะตองเลือกทางเลือกใดทางเลือกหนึ่งจาก 2 ทาง ดังนี้
0 Include all cases หมายถึง ใหคํานวณทุก case ถาเลือกทางเลือกนี้ SPSS จะไมสนใจ
เงื่อนไขใน if เลย
0 Include if case satisfies condition เมื่อเลือกทางเลือกนี้จะตองกําหนดเงื่อนไขใน text box
และ SPSS จะทํางานเฉพาะ case ที่มีคุณสมบัติเปนไปตามเงื่อนไขใน if ถาผูใชตองการใช
คําสั่ง if ตองเลือกทางเลือกนี้ เชนตัวอยางจะคํานวณผลบวกคาใชจายเฉพาะของผูที่มีอายุ 40
ป ขึ้นไปทานัน
้
215. 167
2 ) คําสัง Recode
่
เปนคําสั่งที่ใชในการเปลี่ยนคาของขอมูล เชน ตองการหารายไดเฉลี่ยของผูที่จบการศึกษา
ตั้งแตปริญญาตรีขึ้นไป จะตองกําหนดรหัสหรือคาของตัวแปร edlevel ใหม นั่นคือผูที่จบ
ปริญญาตรี โท และเอก ตองมี Code หรือคาเดียวกัน เชนให = 5
ก. Recode into Same Variables
เปนการเปลี่ยนคาของตัวแปรเดิม ใชคําสั่ง
1. Transform
Recode
Into Same Variables ….
จะไดหนาจอดังรูปที่ 8
รูปที่ 8 หนาจอการกําหนด Recode into Same Variables
รูปที่6.20 หนา 96
2. จากรูปที่ 8 จะตองเลือกตัวแปรที่จะเปลี่ยนคา นอกจากนั้นยังสมารถกําหนด
เงื่อนไขได แลวเลือก Old and New Values…
จะไดหนาจอดังรูปที่ 9
รูปที่ 9 หนาจอการกําหนด Old and New Values
รูปที่6.21 หนา 96
3. ระบุคาเดิมใน Old Value และคาใหมใน New Value ในรูปที่ 9
- เนื่องจากจะรวมผูที่จบตั้งแตปริญญาตรีขึ้นไปไวดวยกัน หรือใหมีรหัส
เดียวกันคือ 5 ในที่นี้เดิมปริญญาตรีคา edllevel = 5 สวนปริญญาโทและเอกมีคา edlevel เปน 6
216. 168
และ 7 ตามลําดับ จึงตองแกไขรหัสของตัวแปร edlevel จาก 6 และ 7 เปนคา ในรูปที่ 9 สวน
ของ Old Value จึงเลือก Range ระบุคา 6 through 7
สวน New Value ระบุคาเปน 5
เลือก Add จะไดขอความ 6 thru 7 = 5 ใน box ของ Old - > New
เลือก Continue จะกลับไปที่หนาจอในรูปที่ 10
4. ในรูปที่ 8 เลือก OK จะทําใหคาตัวแปร edlevel ในแฟมขอมูล มีคา 1 – 5
ข. Recode into Different Variables
เปนการสรางตัวแปรใหมเพือเก็บคา ของตัวแปรที่เปลี่ยนไป โดยตัวแปรเดิมยังมี
่
คาคงเดิม มีขั้นตอนดังนี้
1. ใชคําสั่ง Transform
Recode
Into Different Variables… จะไดหนาจอดังรูปที่ 10
รูปที่ 10 หนาจอการกําหนด Recode into Different Variables
รูป6.22หนา 97
2. เลือกตัวแปรเดิมและใสชื่อตัวแปรใหม และ label ของตัวแปรใหมในสวน
ของ Output Variable
3. เลือก Change
4. เลือก Old and New Values จะไดหนาจอดังรูปที่ 11
รูปที่ 11 หนาจอการกําหนด Recode into Different Variables Old and New Values
รูป 6.23 หนา 97
217. 169
5. ในรูป 11 กําหนดคาเดิมใน old value และคาใหมใน New value
6. เลือก continue
7. เลือก OK จะไดตัวแปรใหมในแฟมขอมูล
……………………………………………………………………………………………
218. 219. 199
ภาคผนวก ก
การประมวลผลขอมูล
ขอมูลที่ไดจาการวิจัย ที่รวบรวมไดจากแบบสอบถามหรือการสังเกต หรือการทดลอง
อาจจะอยูในรูปของขอความหรือตัวเลข จึงเปนหนาที่ของผูวิจัยทีจะตองทําการประมวลผลขอมูล
่
หรือทําการวิเคราะหเพื่อใหไดผลลัพธที่สามารถตอบวัตถุประสงคที่กําหนดไวได
• ความหมายของการประมวลผลขอมูล
การประมวลผลขอมูล คือการจัดเก็บขอมูลอยางเปนระบบ เพื่อใหขอมูลที่ไดรับการ
ประมวลผลแลวอยูในรูปแบบที่สามารถนําไปใชงานไดอยางมีประสิทธิภาพ
• วัตถุประสงคของการประมวลผลขอมูล
1. จัดเตรียมขอมูลใหอยูในสภาพพรอมทีจะนําเขาสูกระบวนการวิเคราะหตอไป
่
2. วิเคราะหขอมูลเพื่อใหไดผลลัพธที่สามารถตอบวัตถุประสงคที่กําหนดไว
• ขั้นตอนการประมวลผลขอมูล
การประมวลผลขอมูล 3 ขั้นตอนใหญ ๆ ดังนี้
1. การเตรียมขอมูลเพื่อการประมวลผล ( Input Data )
2. การประมวลผลขอมูล ( Processing )
3. การนําเสนอหรือแสดงผลลัพธ ( Output )
• วิธีการประมวลผลขอมูล
การประมวลผลขอมูล มีวิธีการตามขั้นตอนการประมวลผลขอมูล ดังนี้
1.วิธีการเตรียมขอมูลเพื่อการประมวลผล
2.วิธีการวิเคราะหขอมูลเพื่อการประมวลผลขอมูล
3.วิธีการแสดงผลลัพธ
1.วิธีการเตรียมขอมูลเพื่อการประมวลผล ประกอบดวย
1.1 การเก็บรวบรวมขอมูล ขอมูลที่เก็บรวบรวมอาจไดจากเอกสารตาง ๆ ซึ่งเปนขอมูล
ทุติยภูมิ และ / หรือ เปนขอมูลปฐมภูมิ ซึ่งเก็บรวบรวมจากหนวยใหขอมูลโดยตรง สวนมากมักจะ
ใชแบบสอบถามเปนเครื่องมือในการเก็บขอมูล
1.2 การตรวจสอบขอมูล เปนการตรวจสอบความถูกตองของขอมูลจากเครื่องมือที่ไดรับ
คืนมาโดยสามารถตรวจสอบ ขณะอยูระหวางการเก็บขอมูล ( Field edit ) และตรวจสอบเมื่อได
ขอมูลจากทุกสวนแลว (Central office edit )
1.3 การเปลี่ยนสภาพขอมูล เปนการเปลี่ยนสภาพของขอมูลที่รวบรวมไดใหอยูในรูปแบบ
ที่สะดวกตอการนําไปประมวลผล หรือ วิเคราะห การเปลี่ยนสภาพขอมูล มีวธีการ ดังนี้
ิ
220. 200
1.3.1 การสรางรหัสสําหรับขอมูล
1.3.2 การจัดทําคูมือลงรหัส
1.3.3 การลงรหัส
1.3.1 การสรางรหัสสําหรับขอมูล
หลังจากที่ไดขอมูลมาแลว ควรมีการกําหนดตัวแปร และกําหนดรหัส หรือให
คาตัวแปร การกําหนดคาของตัวแปรและการใหความหมายของคา มักจะใชกับขอมูลเชิงคุณภาพ
เปนสวนใหญ เชน เพศ อาชีพ ระดับการศึกษา ความคิดเห็นตาง ๆ สวนขอมูลเชิงปริมาณมี
การกําหนดคาของตัวแปร ซึ่งมีคาตามคาปริมาณจริง ไมจําเปนตองใหความหมายของคา
ในการกําหนดรหัส หรือใหคาตัวแปรมักทําควบคูไปกับการออกแบบสอบถาม
นั่นคือ จะตองพิจารณาถึงตัวแปร ซึ่งคําถาม 1 ขอ จะสรางตัวแปรไดอยางนอย 1 ตัว และคาของ
ตัวแปรคือ ขอมูล โดยทั่วไปแบบสอบถามจะกําหนด หรือมีชองใหใสรหัสไวทางดานขวามือของ
แบบสอบถาม ดังแสดงไวในรูปที่ 1
รูปที่ 1 ตัวอยางบางสวนของแบบสอบถาม
เลขที่แบบสอบถาม………
สถานภาพสวนบุคคล
1.เพศ
( ) 1.ชาย
2.อายุ ………ป
3.การศึกษาสูงสุด
( ) 1. มัธยมตน
( ) 2. มัธยมปลาย / ปวช.
( ) 3. อนุปริญญา / ปวส.
4.รายไดตอเดือน
( ) 1. ไมมีรายได
( ) 2. ต่ํากวา 5,000 บ.
( ) 3. 5,000 -9,999 บ.
( ) 4. 10,000-29,999 บ.
( ) 2. หญิง
SEX
AGE
EDUC
( ) 4. ปริญญาตรี
( ) 5. สูงกวาปริญญาตรี
( ) 6. อื่น ๆ (ระบุ)…..
INCOME
( ) 5. 30,000-49,990
( ) 6. 50,000-100,000
( ) 7. มากกวา 100,000 บ.
221. 201
จะพบวาชองสี่เหลี่ยมทางดานขวาใหใสรหัสหรือคาตัวแปรของแตละขอ ทั้งนี้ผูวิจยควร
ั
ทําสมุดคูมือการกําหนดรหัสของตัวแปร โดยจะกลาวในหัวขอตอไป สวนการสรางรหัส มีวิธีการ
ดังนี้
1 ) การกําหนดขนาดของตัวแปร
ขนาดของตัวแปร แสดงถึงความยาวของตัวแปร ซึ่งขึนอยูกับชนิดของตัวแปร
้
หรือ ขอมูล ดังนี้
ตัวแปรเชิงปริมาณ เปนตัวแปรที่มีคาเปนตัวเลขที่ระบุไดวามากหรือนอยกวากัน
เทาไร เชน ยอดขาย รายได น้ําหนัก สวนสูง ความยาว อายุ จํานวนคน สัตว สิ่งของ ฯลฯ
จากรูปที่ 1 ตัวแปรที่เปนปริมาณ ไดแก อายุ การกําหนดขนาดของตัวแปร ถาคิดวา อายุคน
สูงสุดไมเกิน 99 ป ก็กําหนดใหมจํานวนหลัก 2 หลัก จึงมีชองสี่เหลี่ยมไว 2 ชอง
ี
ตัวแปรเชิงคุณภาพ เปนตัวแปรที่เปนขอความ เมื่อแปลงรหัสเปนตัวเลข จํานวน
หลักของตัวเลขควรเทากับจํานวนหลักของตัวเลือกที่มีคาสูงสุด เชน จาก รูปที่ 1 ระดับการศึกษา
หรือ ตัวแปร EDUC จะมีคา 1 , 2 , ……., 6 จึงเปนหลักเลข 1 หลัก จึงใหชองสี่เหลียมไว 1 ชอง
่
การสรางรหัสของตัวแปรจะขึ้นอยูกับชนิดของคําถามในแบบสอบถาม ดังนั้น
ในที่นี้จะกลาวถึงวิธีการกําหนดรหัสโดยแบงตามชนิดของคําถาม ดังนี้
1. การกําหนดรหัสโดยแบงตามชนิดของคําถาม
การกําหนดรหัสของขอมูลจะตองคํานึงชนิดของคําถาม โดยที่ชนิดของคําถามแบงเปน
1) คําถามปลายปด ( closed - end question )
ก. คําถามที่มีเพียงคําตอบใหเลือกเพียง 2 คําตอบ ( Dichotomous question ) เชน
คําถามขอ 1 ในรูปที่ 1 ซึ่งถามเกี่ยวกับเพศของผูตอบจะมี 1 ตัวแปร คือ SEX ซึ่งเปนตัวแปรเชิง
คุณภาพ หมายถึง คําตอบเปนขอความ คือ ชาย หรือ หญิง ผูตอบเลือกไดเพียงคําตอบเดียว ในที่นี้
จะกําหนดวาตัวแปร SEX มีขนาด 1 หลัก และมีคาเพียงคาใดคาหนึ่ง จาก 2 คา คือ
1
หมายถึง ชาย
SEX =
2
หมายถึง หญิง
คาตัวเลขที่กําหนดแทนชายและหญิง เปนรหัสที่แสดงถึงชายหรือหญิงเทานั้น ไมได
หมายความวาหญิงมีคามากกวาชาย ในการใชรหัสจะใชเลข 0 แทนชาย เลข 1 แทนหญิงหรือใช
0 และ 1 แทนหญิงและชาย ตามลําดับก็ได แตถาใชแบบใดก็ตองใชแบบนั้นตลอดสําหรับ
แบบสอบถามทุกชุด
222. 202
ข. คําถามที่มคําตอบใหเลือกหลายคําตอบ ( Multiple choice questions )
ี
เปนคําถามที่มีใหเลือกหลายคําตอบ ผูตอบจะตองเลือกคําตอบใดคําตอบหนึงเพียง
่
คําตอบเดียวจากรูปที่ 1 คําถาม ขอ 3 การศึกษาสูงสุด และขอ 4 รายไดตอเดือน ตัวแปร
การศึกษาสูงสุด (EDUC) เปนตัวแปรเชิงคุณภาพ สวนตัวแปร รายไดตอเดือน ( INCOME )
จะถือวาเปนตัวแปรเชิงคุณภาพ (Category Variable) เชนเดียวกัน เพราะถึงแมรายไดจะเปน
ตัวเลข แตเมื่อกําหนดใหเลือกเปนชวง ถาผูตอบมีรายได 25,000 บาท ตอเดือน จะเลือกทางเลือก
ที่ ( ) 4. 10,000-29,999 บาท ซึ่งถือวาเลือกชวงนีหรือกลุมนี้ จึงถือวาเปนตัวแปรเชิงคุณภาพ
้
ดังนั้นตัวแปร INCOME จึงเปนตัวเลขที่แสดงถึงกลุม และมีคา 1 หลัก คือ เลข 1 , 2 , …….., 7
ค. คําถามที่สามารถเลือกคําตอบไดหลายคําตอบ ( Checklist questions )
กรณีที่คําถามมีคําตอบใหเลือกหลาย ๆ คําตอบ และผูตอบสามารถตอบไดหลาย ๆ
คําตอบ เชน คําถามเกี่ยวกับการใชสายการบิน ดังนี้
สําหรับทานที่เดินทางไปตางประเทศใน 6 เดือนที่ผานมา ทานใชสายการบินใดบาง
( ตอบไดมากกวา 1 ขอ )
(
(
(
(
(
)
)
)
)
)
1. Thai Airline
2. Singapore Airline
3. Japan Airline
4. TWA
5. สายการบินอื่น ๆ
การกําหนดตัวแปรหรือกําหนดรหัสสําหรับคําถามประเภทนี้ อาจทําไดหลาย
แบบ แตที่นยม คือ Multiple dichotomy method
ิ
เปนการกําหนดใหคําตอบแตละทางเลือกเปน 1 ตัวแปร จากตัวอยางมีทางเลือก
5 ขอ จึงมี 5 ตัวแปร โดยที่แตละตัวแปรเปน dichotomous คือมีได 2 คา ถากําหนดตัวแปร 5
ตัวแปร คือ V1 , V2 ……., V5
1
ถาผูตอบเลือก Thai Airline
V1 =
0
ถาผูตอบไมเลือก Thai Airline
1
ถาผูตอบเลือก Singapore Airline
0
ถาผูตอบไมเลือก Singapore Airline
V2 =
223. 203
1
ถาผูตอบเลือกสายการบินอืน ๆ
่
V5 =
0
ถาผูตอบไมเลือกสายการบินอื่น ๆ
ถาใน 6 เดือนที่ผานมา นาย ก. ใชการบินไทย และ TWA ตัวแปร V1 และ
V4 เปน 1 V2 , V3 และ V5 จะเปน 0 ดังนั้น ขอมูลที่ตองบันทึก คือ
1 0 0 1 0
V1 V2 V3 V4 V5
สําหรับการวิเคราะห เชนการหาจํานวนผูใชสายการบินตาง ๆ และสัดสวน
หรือเปอรเซ็นตจะสามารถแยกทําครั้งละตัวแปรหรือครั้งละสายการบิน เชน ถาเก็บขอมูลมา 100
คน เปอรเซ็นตของผูใชสายการบินตางๆ มีดังนี้
ใช
ไมใช
รวม
การใช Thai Airline
รหัส ความถี่ เปอรเซ็นต
1
67
67.0
0
33
33.0
100
100.0
ใช
ไมใช
รวม
การใช Japan Airline
รหัส ความถี่ เปอรเซ็นต
1
54
54.0
0
46
46.0
100
100.0
ใช
ไมใช
ใช
ไมใช
การใช Singapore Airline
รหัส ความถี่ เปอรเซ็นต
1
25
25.0
0
75
75.0
100
100.00
การใช TWA
รหัส ความถี่
1
41
0
59
100
เปอรเซ็นต
41.0
59.0
100.00
ง. คําถามที่ใหคําตอบใสลําดับที่ ( Rank question )
เปนคําถามที่มีรายการใหเลือก โดยใหผูตอบเปรียบเทียบรายการทีกาหนดให และใส
่ํ
หมายเลขเมื่อเรียงลําดับความสําคัญ อาจเรียงจากนอยสุดไปมากสุด หรือมากสุดไปนอยสุด
ตัวอยาง
กรุณาเรียงลําดับความสําคัญของปจจัยที่ทําใหทานเลือกเรียนคณะศึกษาศาสตร 3
ลําดับแรกโดยใหปจจัยที่สําคัญที่สุดเปนลําดับที่ 1 รองลงมาเปนปจจัยที่ 2 และ 3 โดยใหใสลําดับ
ในวงเล็บหนาขอ
224. 204
( ) 1. เปนอาชีพที่มีเกียรติ
( ) 2. หางานงาย
( ) 3. รายไดดี
( ) 4. เปนประโยชนตอสังคม
ถาน.ส.ราตรี เลือก เปนประโยชนตอสังคม ตามดวย เปนอาชีพที่มีเกียรติ และ
หางานงาย เรียงลําดับตามความสําคัญจากมากไปนอย 3 ลําดับ จะไดคา E1 = 4 , E2 = 1 ,
E3 = 2 ดังแสดงในรูปที่ 2
รูปที่ 2
(2)
(3)
( )
(1)
1. เปนอาชีพที่ความมีเกียรติ
2. หางานงาย
3. รายไดดี
4. เปนประโยชนตอสังคม
4
E1
1
E2
2
E3
จ. คําถามทีใหแสดงระดับความมากนอย ( Scale Questions )
คําถามประเภทนี้สวนใหญจะถามความคิดเห็น ความชอบ ความพอใจวามีมาก /
นอย เห็นดวยหรือไมเห็นดวย สเกลที่แสดงระดับความคิดเห็นจะเรียงจากดานหนึ่งไปยังอีกดาน
หนึ่ง เชน จากไมเห็นดวยอยางยิ่ง จนถึง เห็นดวยอยางยิ่ง จํานวนระดับของสเกลสวนใหญมักจะ
เปนเลขคี่ เชน 3, 5 , 7 หรือ 9 สวนใหญจะนิยมใช 5 หรือ 7 ระดับ โดยมีสเกลตรงกลาง
การกําหนดรหัสในกรณีที่เรียงจากไมเห็นดวยอยางยิงจนถึงเห็นดวยอยางยิ่ง หรือ ไม
่
ชอบมากที่สุดจนถึงชอบมากที่สุด จะใหคาจากต่ําสุดไปหาสูงสุด เชน ในสเกล 5 ระดับ ไมเห็น
ดวยอยางยิ่งจะมีรหัสเปน 1 จนถึงเห็นดวยอยางยิ่ง จะมีรหัสเปน 5 นั่นคือ
ความคิดเห็น
ไมเห็นดวยอยางยิ่ง
ไมเห็นดวย
เฉย ๆ
เห็นดวย
เห็นดวยอยางยิ่ง
รหัส
1
2
3
4
5
225. 205
2 ) คําถามปลายเปด ( Open -ended Question )
สําหรับคําถามใหแสดงความคิดเห็นซึ่งเวนที่ใหผูตอบเขียนนั้น ในการใหรหัส
ผูวิจัยจะตองพิจารณคําตอบเดียวกันหรือคลายกันเปนรหัสเดียวกัน เชนถาอานจากคําตอบแลว
พบวามีความคิดเห็นทีแตกตางกัน 13 แบบ อาจใหรหัสเปน 01, 02 ,…….,13
่
1.3.2 การจัดทําคูมือลงรหัส
ในกรณีที่มีจํานวนคําถามในแบบสอบถามมากๆ ผูใสรหัสอาจจะจํารหัสไดไม
ครบจึงจําเปนตองจัดทําคูมือลงรหัส อันประกอบดวย
ก. เลขที่แบบสอบถาม หมายถึงเลขที่ของแบบสอบถามที่ไดรับคืนกลับมา
การใสเลขที่แบบสอบถาม จะทําใหสามารถตรวจสอบขอมูลจากแบบสอบถามไดงาย ใน
กรณีที่มีการพิมพขอมูล เชน ถาพบวาอายุของผูตอบจากแบบสอบถามชุดที่ 150 เปน 99 ป ทําให
สามารถตรวจสอบวาพิมพผดหรือไม โดยตรวจสอบจากแบบสอบถามชุดที่ 150
ิ
ข. เลขที่คําถาม ( Question Number )
เปนเลขที่คําถามในแบบสอบถาม ผูวิจัยจะกําหนดรหัสใหตรงกับเลขที่ขอในแบบสอบถาม
ค. ชื่อตัวแปร ( Variable Name )
สวนใหญมกจะกําหนดใหชอตัวแปรสอดคลองกับความหมายของขอมูล เชน เพศ มักจะ
ั
ื่
ใช SEX รายได เปน INCOME เปนตน
ง. รายการของขอมูล
เปนสวนที่ระบุถึงคําถามในแตละขอ
จ. ขนาดของตัวแปร
เปนการกําหนดความกวางของตัวแปร ถาเปนตัวแปรเชิงปริมาณ เชน คะแนนสอบ ตัวแปร
อาจจะมีจุดทศนิยม ตองกําหนดจํานวนหลักหลังจุดทศนิยมดวย เชน ถาความกวางของตัวแปร
คะแนนสอบ เปน 8.2 หมายถึงมีจํานวนจุดหนาจุดทศนิยม 5 หลัก และจํานวนหลักหลังจุด
ทศนิยม 2 หลัก (เลข 8 รวมหมายถึงจํานวนหลักหนาจุดทศนิยม จุดทศนิยมและจํานวนหลัก
หลังจุดทศนิยม)
ฉ. คาที่เปนไปไดพรอมคําอธิบายความหมาย ( Possible Values or Label)
หมายถึงสวนที่จะระบุคาที่เปนไปไดของตัวแปร เชน ตัวแปร SEX มีคา “ 0 ” หมายถึง
ชาย และคา “ 1 ” หมายถึงหญิง สวนเลข 9 หมายถึง ผูตอบไมตอบคําถามนี้ ( missing
values )
ตัวอยางการจัดทําคูมือการกําหนดรหัสของแบบสอบถามเรื่องความพึงพอใจของการ
ใหบริการของบริษัทดีทัวร ซึ่งจะสอบถามจากลูกคาที่เคยใชบริการของบริษัท ฯ
226. 206
ตัวอยางบางสวนของแบบสอบถาม
แบบสอบถามของการสํารวจ “ ความพึงพอใจของบริษทแสนดีทัวร ”
ั
ชื่อพนักงานสัมภาษณ………………………
วัน เดือน ป ที่สัมภาษณ…………………..
I สถานภาพสวนบุคคล
1.เพศ
( ) 1. ชาย
( ) 2. หญิง
2. อายุ ……ป
3.การศึกษาสูงสุด
( ) 1. มัธยมตน
( ) 4. ปริญญาตรี
( ) 2. มัธยมปลาย / ปวช. ( ) 5. สูงกวาปริญญาตรี
( ) 3. อนุปริญญา / ปวส.
( ) 6. อื่น ๆ (ระบุ)…..
4.สถานภาพสมรส
( ) 1. โสด
( ) 3. หยา
( ) 2. แตงงานแลว
( ) 4. เปนหมาย
5. รายไดตอเดือน
( ) 1. ไมมีรายได
( ) 4. 10,000-29,990 บาท
( ) 2. ต่ํากวา 5,000 บาท ( ) 5. 30,000-49,999 บาท
( ) 3. 5,000 -9,999 บาท ( ) 6. 50,000 บาทขึ้นไป
6.อาชีพขอทานในปจจุบัน
( ) 1. ขาราชการ / พนักงานรัฐวิสาหกิจ ( ) 5. นักเรียน / นักศึกษา
( ) 2. พนักงานธุรกิจเอกชน
( ) 6. กิจการสวนตัว
( ) 3. แมบาน
( ) 7. อื่น ๆ ระบุ
( ) 4. เกษตรกร
II การเดินทาง
1. ทานเดินทางไปตางประเทศปละ …… ครั้ง
2. จุดประสงคของการเดินทางไปตางประเทศ
( ) 1. ธุรกิจ / ธุระอื่น ๆ
( ) 2. พักผอน
( ) 3. ทั้งพักผอนและธุรกิจ / ธุระอื่น ๆ
227. 207
3.สวนใหญแลวทานเดินทางไปตางประเทศกับใครบาง
( ) 1. ไปคนเดียว
( ) 2. ไปกับครอบครัว
( ) 3. ไปกับเพื่อนสนิท
4. ปจจัยที่ทานเลือกใชบริการของบริษัทแสนดีทัวร โดยใหเรียงลําดับความสําคัญ ปจจัยที่
สําคัญที่สุดเปนลําดับที่ 1 ปจจัยที่สําคัญนอยที่สุดเปนลําดับที่ 4 โ ดยใหใสลําดับที่ไวใน
วงเล็บ
( ) 1. ชื่อเสียงของบริษัท
( ) 2. ราคา
( ) 3. ชวงเวลาที่เหมาะสม ( ชวงเวลาที่วางตรงกับที่บริษัทแสนดีทัวรจัด )
( ) 4. สายการบินที่บริษัทใช
5. ทานรูจักบริษทแสนดีทัวรจากแหลงใดบาง ( เลือกไดหลายคําตอบ )
ั
( ) 1. ทางทีวี
( ) 2. ทางสื่อสิ่งพิมพ เชน หนังสือพิมพ นิตยสาร ใบปลิว
( ) 3. เพื่อน / ญาติ แนะนํา
( ) 4. สมุดโทรศัพท
III ความพึงพอใจในการบริการของบริษัทแสนดีทัวร
ทานมีความรูสึกอยางไรเกียวกับบริการดานตาง ๆ ของบริษัทแสนดีทวร ดังนี้
่
ั
พอใจอยางยิ่ง พอใจ
เฉยๆ ไมพอใจ ไมพอใจอยางยิง
่
1. การบริการดานการจอง คําแนะนํา การติดตอ
2. คุณภาพและรสชาดของอาหาร
3. การบริการของไกด
4. ความรู ความสามารถของไกดในการนํา
เที่ยว
5. บริการดานพาหนะ
ตัวอยางการจัดทําคูมือการลงรหัส
จากตัวอยาง ซึ่งเปนตัวอยางบางสวนของแบบสอบถามเพื่อสํารวจความพอใจของลูกคาที่มี
ตอบริการของบริษัทแสนดีทวร
ั
เนื่องจากในทีนี้ใชโปรแกรม SPSS for Windows จึงไมตองกําหนดเลขที่แบบสอบถาม
่
228. 208
สวนที่ I สถานภาพสวนบุคคล
คําถามที่ ชื่อตัวแปร รายการขอมูล ขนาดตัวแปร(จํานวนหลัก ) คาที่เปนไปไดและความหมาย
1.
SEX
เพศ
1
1.ชาย
2.หญิง
9. ไมตอบ
2.
AGE
อายุ
2
15-80 ( 99 ไมตอบ )
3.
EDUCA
การศึกษา
1
4.
INCOME รายไดตอ
เดือน
1
5.
OCCUPA อาชีพ
1
1.มัธยมตน
2.มัธยมปลาย / ปวช.
3.อนุปริญญา / ปวส.
4.ปริญญาตรี
5.สูงกวาปริญญาตรี
6. อื่น ๆ 9. ไมตอบ
1.ไมมีรายได
2.ต่ํากวา 5,000 บาท
3. 5 ,000 - 9,999 บาท
4. 10 ,000 - 29,999 บาท
5. 30,000 - 49,999 บาท
6. 50,000 บาทขึ้นไป
9. ไมตอบ
1. ขาราชการ/ รัฐวิสาหกิจ
2.พนักงานธุรกิจเอกชน
3.แมบาน
4.เกษตรกร
5.นักเรียน / นักศึกษา
6.กิจการสวนตัว
9. ไมตอบ
ขอสังเกตุ
เลือกได
คําตอบเดียว
ระบุอายุจริง
เลือกได
คําตอบเดียว
เลือกได
คําตอบเดียว
เลือกได
คําตอบเดียว
229. 209
สวนที่ II การเดินทาง
คําถามที่ ชื่อตัวแปร รายการขอมูล
1.
V1
2.
V2
3.
V3
4
V4
4
V5
4
V6
ขนาดตัวแปร คาที่เปนไปไดและความหมาย
(จํานวนหลัก/ชอง)
จํานวนครั้งที่
1
1. 1 ครั้ง
เดินทางตอป
2. 2 - 5 ครั้ง
3. 6 - 9 ครั้ง
4. ตั้งแต 10 ครั้งขึ้นไป
9. ไมตอบ
จุดประสงค
1
1. ธุรกิจ / ธุระกิจ
ของการ
2. พักผอน
เดินทาง
3. ทั้งพักผอนแลธุรกิจ/ธุรกิจอืน ๆ
่
ผูที่เดินทางไป
1
1. ไปคนเดียว
ดวย
2.ไปกับครอบครัว
3.ไปกับเพื่อนสนิท
9. ไมตอบ
ปจจัยในการเลือกบริษัททัวร
ชื่อเสียง
1
1. เลือกเปนลําดับ 1
2. เลือกเปนลําดับ 2
3. เลือกเปนลําดับ 3
4. เลือกเปนลําดับ 4
9. ไมตอบ
ราคา
1
1.เลือกเปนลําดับ 1
2.เลือกเปนลําดับ 2
3.เลือกเปนลําดับ 3
4.เลือกเปนลําดับ 4
9. ไมตอบ
ชวงเวลาที่
1
1.เลือกเปนลําดับ 1
เหมาะสม
2.เลือกเปนลําดับ 2
3.เลือกเปนลําดับ 3
4.เลือกเปนลําดับ 4
9. ไมตอบ
ขอสังเกตุ
เลือกได
คําตอบเดียว
เลือกได
คําตอบเดียว
เลือกได
คําตอบเดียว
การใหลําดับที่
กําหนจํานวน
ตัวแปรเทากับ
จํานวน
ทางเลือก
230. 210
คําถามที่ ชื่อตัวแปร รายการขอมูล
4
V7
ขนาดตัวแปร คาที่เปนไปไดและความหมาย
(จํานวนหลัก/ชอง)
สายการบินที่
1
1.เลือกเปนลําดับ 1
บริษัทใช
2.เลือกเปนลําดับ 2
3.เลือกเปนลําดับ 3
4.เลือกเปนลําดับ 4
9. ไมตอบ
ขอสังเกตุ
แหลงที่รูจักบริษัท
คําถามที่ ชื่อตัวแปร รายการขอมูล
ขนาดตัวแปร คาที่เปนไปไดและความหมาย
(จํานวนหลัก/ชอง)
1
0 : ไมเลือก
1 : เลือก
5.
V8
ทีวี
5.
V9
สื่อสิ่งพิมพ
1
0 : ไมเลือก
1 : เลือก
5.
V10
เพื่อน / ญาติ
1
5.
V11
สมุดโทรศัพท
1
0:
1:
0:
1:
ไมเลือก
เลือก
ไมเลือก
เลือก
ขอสังเกตุ
เลือกไดหลาย
คําตอบโดย
กําหนด
จํานวน
ตัวแปรเทากับ
จํานวน
ทางเลือก
231. 211
สวนที่ III ความพึงพอใจในการบริการ
คําถาม ชื่อตัวแปร รายการขอมูล
ขนาดตัวแปร คาที่เปนไปไดและความหมาย
ขอสังเกตุ
ที่
(จํานวนหลัก/ชอง)
1.
U1
การจองแนะนํา
1
1ไมพอใจอยางยิ่ง
สเกลแสดง
ฯลฯ
2ไมพอใจ 3 เฉย ๆ 4 พอใจ
ลําดับความ
5 พอใจอยางยิง
่
9. ไมตอบ
พอใจ
2.
U2
อาหาร
1
1ไมพอใจอยางยิ่ง
2ไมพอใจ 3 เฉย ๆ 4 พอใจ
5 พอใจอยางยิง
่
9. ไมตอบ
3.
U3
บริการของไกด
1
1ไมพอใจอยางยิ่ง
2ไมพอใจ 3 เฉย ๆ 4 พอใจ
5 พอใจอยางยิง
่
9. ไมตอบ
4.
U4
ความสามารถ
1
1ไมพอใจอยางยิ่ง
ของไกด
2ไมพอใจ 3 เฉย ๆ 4 พอใจ
5 พอใจอยางยิง
่
9. ไมตอบ
5.
U5
พาหนะ
1
1ไมพอใจอยางยิ่ง
2ไมพอใจ 3 เฉย ๆ 4 พอใจ
5 พอใจอยางยิง
่
9. ไมตอบ
1.3.3 การลงรหัส
วิธีการลงรหัสโดยใชโปรแกรม SPSS for Windows จะตองสรางแฟมขอมูล และ
สิ่งที่ควรทราบกอนสรางแฟมขอมูลโดยใช Data Editor จะตองกําหนด ดังนี้
1) กําหนดชือตัวแปร ( Variable Name )
่
2) กําหนดชนิดของตัวแปร
3) กําหนด label ของตัวแปร ( โดยเฉพาะตัวแปรที่เปนคุณภาพ )
4) กําหนดรหัสสําหรับคาสูญหาย ( missing value )
5) กําหนดความกวางของ column ( width )
1) การตังชื่อตัวแปร ( Variable Name )
้
SPSS จะตั้งตัวแปรเปน var 00001 , var00002 …… เปน default สําหรับตัว
แปรใหม การเปลี่ยนชื่อตัวแปรทําโดยการพิมพชื่อใหมแทนที่ ผูใชควรจะตั้งชื่อตัวแปรให
232. 212
สอดคลองกับความหมายของคาของตัวแปร เชน อายุ ควรตั้งเปน age สวนรายได ควรตั้งชื่อตัว
แปร income เปนตน
กฏการตั้งชื่อตัวแปรของ SPSS
1.1 ความยาวของชื่อตัวแปรตองไมเกิน 8 ตัว
1.2 ชื่อตัวแปรตองเริ่มตนดวยอักษรเทานั้น สวนตัวอืน ๆ อาจเปนตัวอักษร
่
ตัวเลข จุด หรือสัญลักษณพิเศษ เชน @ ,# , - หรือ $ ก็ได
1.3 ชื่อตัวแปรตองไมจบดวยจุด และควรหลีกเลี่ยงเครื่องหมาย “ _” ( ขีดลาง )
เปนตัวสุดทาย
1.4 หามใชสัญลักษณพเิ ศษตอไปนี้ในการตังชื่อตัวแปร ! ? ’ *
้
1.5 ชื่อตัวแปรในแฟมขอมูลเดียวกันตองไมซ้ํากัน
1.6 ตัวอักษรใหญหรือเล็ก จะถือเปนตัวแปรเดียวกัน เชน
INCOME income inCOME ถือเปนอยางเดียวกัน
1.7 หามตั้งชื่อตอไปนี้เปนชื่อตัวแปร
ALL
NE EQ TO LE LT
BY
OR
GT AND NOT GE WITH
ตัวอยางชื่อตัวแปรที่ถูกตอง INCOME satis _1 locate#1 Y.1
ตัวอยางชื่อตัวแปรที่ไมถูกตอง 1 INCOME WITH and satis 1_
2) ชนิดของตัวแปร ( Variable Type )
นอกจากจะตองตั้งชื่อตัวแปรแลว จะตองมีการกําหนดชนิดของตัวแปร ตัวแปร
หนึ่ง ๆ จะตองเปนชนิดใดชนิดหนึ่งเทานัน SPSS แบงตัวตัวแปรออกเปน 8 ชนิด แตที่ใชทวไป
้
ั่
เปน Numeric ซึ่งมีรายละเอียด ดังนี้
Numeric
เปนตัวแปรชนิดตัวเลข ซึ่งรวมทั้งเครื่องหมายบวกหรือลบที่นําหนาตัวเลข และรวมถึงจุด
ทศนิยม ถาเลือก Numeric จะตองกําหนดความกวาง ( Width ) และจํานวนหลักของตัวเลขหลัง
จุดทศนิยม ( Decimal Places ) ดวย เชน ถากําหนด
Decimal Places
=
2
Width
=
8
ความกวาง 8 นี้ไดรวมจุดและจํานวนหลักจุดทศนิยมดวย จึงเหลือจํานวนหลักของเลข
หนาจุดทศนิยมเปน 5 หลัก หรือหลักหมืนนั่นเอง ผูวิเคราะหจะตองพิจารณาคาของขอมูลตัวแปร
่
วาสูงสุดมีกี่หลัก และกําหนดจํานวนหลักสูงสุดไว
เราสามารถกําหนดความกวางไดสูงสุด 40 หลักและจํานวนหลักหลังจุดทศนิยมสูงสุดเปน
10
233. 213
3) การกําหนด Labels
กรณีที่ขอมูลที่ไดเปนตัวแปรเชิงคุณภาพ ไมวาจะเปนชนิดสเกลนามกําหนด หรือสเกล
อันดับก็ตาม เมื่อนําขอมูลใสแฟมขอมูลจะพิจารณาแปรเหลานี้ในลักษณะของ category variable
โดยที่ใน SPSS จะตองกําหนดคาตัวเลขใหแตละกลุมแลวใส label เพื่ออธิบายความหมายที่
แทจริงของคาตัวแปรไว
เชน คําถามเกี่ยวกับอาชีพ ซึ่งมีคําตอบใหเลือกดังนี้
1. นิสิต / นักศึกษา
2. ขาราชการ / พนักงานรัฐวิสาหกิจ
3.พนักงานธุรกิจเอกชน
4.เจาของกิจการสวนตัว
5. อื่น ๆ
ถาตอบเปนขาราชการจะตอบ “2” แตจะใสใน label วา “ 2 ” หมายถึง ขาราชการหรือ
พนักงานรัฐวิสาหากิจ
4) การกําหนดคาขอมูลสูญหาย ( Missing Value )
ในการวิจัยครังหนึ่ง ๆ มักจะเกิดการสูญหายของขอมูลบาสวน เชน แตละ case ควรมี 20
้
ตัวแปร แตมีคาของบางตัวแปรหายไป จึงเรียกวา missing ซึ่งอาจเกิดจาการที่ผูตอบคําถมบางขอ
หรือผูใสขอมูลเขาลืมใสขอมูลบางคําตอบ
อยางไรก็ตาม SPSS ไดแบง missing values ออกเปน 2 ชนิด คือ
1. System - missing values
ถา cell ใดในแฟมขอมูลไมมีขอมูลอยู หรือเปน cell วาง โปรแกรมจะใหคา
เปนจุด (. ) ซึ่งหมายถึง system-missing values
2.User - missing values
ผูวิเคราะหสามารถกําหนดคาของ missing value ตามความหมายได
5) การกําหนดความกวางของ Column Format
SPSS จะกําหนดใหความกวางของ column เทากับความกวางของตัวแปรที่
กําหนดไว อยางไรก็ตาม บางครั้งชื่อตัวแปรจะยาวกวาคาของขอมูล เชน อายุ (AGE ) เราอาจ
กําหนดเปนชนิด Numeric เปนตัวเลขจํานวนเต็ม 2 ตําแหนง ความกวางของ column จะเปน 2
อัตโนมัติ จะทําใหชื่อตัวแปรเหลือเพียง 2 ตัว คือ AG จึงควรกําหนดความกวางของ column
เปน 3 โดยการเปลี่ยนแปลงคาความกวางจาก 2 เปน 3
…………………………………………………………
234. 235. 236. 237. 217
Normal Distribution
Area between 0 and z
0.00
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.0 0.0000 0.0040 0.0080 0.0120 0.0160 0.0199 0.0239 0.0279 0.0319 0.0359
0.1 0.0398 0.0438 0.0478 0.0517 0.0557 0.0596 0.0636 0.0675 0.0714 0.0753
0.2 0.0793 0.0832 0.0871 0.0910 0.0948 0.0987 0.1026 0.1064 0.1103 0.1141
0.3 0.1179 0.1217 0.1255 0.1293 0.1331 0.1368 0.1406 0.1443 0.1480 0.1517
0.4 0.1554 0.1591 0.1628 0.1664 0.1700 0.1736 0.1772 0.1808 0.1844 0.1879
0.5 0.1915 0.1950 0.1985 0.2019 0.2054 0.2088 0.2123 0.2157 0.2190 0.2224
0.6 0.2257 0.2291 0.2324 0.2357 0.2389 0.2422 0.2454 0.2486 0.2517 0.2549
0.7 0.2580 0.2611 0.2642 0.2673 0.2704 0.2734 0.2764 0.2794 0.2823 0.2852
0.8 0.2881 0.2910 0.2939 0.2967 0.2995 0.3023 0.3051 0.3078 0.3106 0.3133
0.9 0.3159 0.3186 0.3212 0.3238 0.3264 0.3289 0.3315 0.3340 0.3365 0.3389
1.0 0.3413 0.3438 0.3461 0.3485 0.3508 0.3531 0.3554 0.3577 0.3599 0.3621
1.1 0.3643 0.3665 0.3686 0.3708 0.3729 0.3749 0.3770 0.3790 0.3810 0.3830
1.2 0.3849 0.3869 0.3888 0.3907 0.3925 0.3944 0.3962 0.3980 0.3997 0.4015
1.3 0.4032 0.4049 0.4066 0.4082 0.4099 0.4115 0.4131 0.4147 0.4162 0.4177
1.4 0.4192 0.4207 0.4222 0.4236 0.4251 0.4265 0.4279 0.4292 0.4306 0.4319
1.5 0.4332 0.4345 0.4357 0.4370 0.4382 0.4394 0.4406 0.4418 0.4429 0.4441
1.6 0.4452 0.4463 0.4474 0.4484 0.4495 0.4505 0.4515 0.4525 0.4535 0.4545
1.7 0.4554 0.4564 0.4573 0.4582 0.4591 0.4599 0.4608 0.4616 0.4625 0.4633
1.8 0.4641 0.4649 0.4656 0.4664 0.4671 0.4678 0.4686 0.4693 0.4699 0.4706
1.9 0.4713 0.4719 0.4726 0.4732 0.4738 0.4744 0.4750 0.4756 0.4761 0.4767
2.0 0.4772 0.4778 0.4783 0.4788 0.4793 0.4798 0.4803 0.4808 0.4812 0.4817
2.1 0.4821 0.4826 0.4830 0.4834 0.4838 0.4842 0.4846 0.4850 0.4854 0.4857
2.2 0.4861 0.4864 0.4868 0.4871 0.4875 0.4878 0.4881 0.4884 0.4887 0.4890
2.3 0.4893 0.4896 0.4898 0.4901 0.4904 0.4906 0.4909 0.4911 0.4913 0.4916
2.4 0.4918 0.4920 0.4922 0.4925 0.4927 0.4929 0.4931 0.4932 0.4934 0.4936
2.5 0.4938 0.4940 0.4941 0.4943 0.4945 0.4946 0.4948 0.4949 0.4951 0.4952
2.6 0.4953 0.4955 0.4956 0.4957 0.4959 0.4960 0.4961 0.4962 0.4963 0.4964
2.7 0.4965 0.4966 0.4967 0.4968 0.4969 0.4970 0.4971 0.4972 0.4973 0.4974
2.8 0.4974 0.4975 0.4976 0.4977 0.4977 0.4978 0.4979 0.4979 0.4980 0.4981
2.9 0.4981 0.4982 0.4982 0.4983 0.4984 0.4984 0.4985 0.4985 0.4986 0.4986
3.0 0.4987 0.4987 0.4987 0.4988 0.4988 0.4989 0.4989 0.4989 0.4990 0.4990
To index
238. 218
Student's t Table t table with right tail probabilities
dfp
0.40
0.25
0.10
0.05
0.025
0.01
0.005
0.0005
1
0.324920
1.000000
3.077684
6.313752
12.70620
31.82052
63.65674
636.6192
2
0.288675
0.816497
1.885618
2.919986
4.30265
6.96456
9.92484
31.5991
3
0.276671
0.764892
1.637744
2.353363
3.18245
4.54070
5.84091
12.9240
4
0.270722
0.740697
1.533206
2.131847
2.77645
3.74695
4.60409
8.6103
5
0.267181
0.726687
1.475884
2.015048
2.57058
3.36493
4.03214
6.8688
6
0.264835
0.717558
1.439756
1.943180
2.44691
3.14267
3.70743
5.9588
7
0.263167
0.711142
1.414924
1.894579
2.36462
2.99795
3.49948
5.4079
8
0.261921
0.706387
1.396815
1.859548
2.30600
2.89646
3.35539
5.0413
9
0.260955
0.702722
1.383029
1.833113
2.26216
2.82144
3.24984
4.7809
10
0.260185
0.699812
1.372184
1.812461
2.22814
2.76377
3.16927
4.5869
11
0.259556
0.697445
1.363430
1.795885
2.20099
2.71808
3.10581
4.4370
12
0.259033
0.695483
1.356217
1.782288
2.17881
2.68100
3.05454
4.3178
13
0.258591
0.693829
1.350171
1.770933
2.16037
2.65031
3.01228
4.2208
14
0.258213
0.692417
1.345030
1.761310
2.14479
2.62449
2.97684
4.1405
15
0.257885
0.691197
1.340606
1.753050
2.13145
2.60248
2.94671
4.0728
16
0.257599
0.690132
1.336757
1.745884
2.11991
2.58349
2.92078
4.0150
17
0.257347
0.689195
1.333379
1.739607
2.10982
2.56693
2.89823
3.9651
18
0.257123
0.688364
1.330391
1.734064
2.10092
2.55238
2.87844
3.9216
19
0.256923
0.687621
1.327728
1.729133
2.09302
2.53948
2.86093
3.8834
20
0.256743
0.686954
1.325341
1.724718
2.08596
2.52798
2.84534
3.8495
21
0.256580
0.686352
1.323188
1.720743
2.07961
2.51765
2.83136
3.8193
22
0.256432
0.685805
1.321237
1.717144
2.07387
2.50832
2.81876
3.7921
23
0.256297
0.685306
1.319460
1.713872
2.06866
2.49987
2.80734
3.7676
24
0.256173
0.684850
1.317836
1.710882
2.06390
2.49216
2.79694
3.7454
25
0.256060
0.684430
1.316345
1.708141
2.05954
2.48511
2.78744
3.7251
26
0.255955
0.684043
1.314972
1.705618
2.05553
2.47863
2.77871
3.7066
27
0.255858
0.683685
1.313703
1.703288
2.05183
2.47266
2.77068
3.6896
28
0.255768
0.683353
1.312527
1.701131
2.04841
2.46714
2.76326
3.6739
29
0.255684
0.683044
1.311434
1.699127
2.04523
2.46202
2.75639
3.6594
30
0.255605
0.682756
1.310415
1.697261
2.04227
2.45726
2.75000
3.6460
inf
0.253347
0.674490
1.281552
1.644854
1.95996
2.32635
2.57583
3.2905
239. 240. 220
Chi-Square Table
Right tail areas for the Chi-square Distribution
dfa
rea
.995
.990
.975
.950
.900
.750
.500
.250
.100
.050
.025
.010
.005
1
0.000
04
0.000
16
0.000
98
0.003
93
0.015
79
0.101
53
0.454
94
1.323
30
2.705
54
3.841
46
5.023
89
6.634
90
7.879
44
2
0.010
03
0.020
10
0.050
64
0.102
59
0.210
72
0.575
36
1.386
29
2.772
59
4.605
17
5.991
46
7.377
76
9.210
34
10.59
663
3
0.071
72
0.114
83
0.215
80
0.351
85
0.584
37
1.212
53
2.365
97
4.108
34
6.251
39
7.814
73
9.348
40
11.34
487
12.83
816
4
0.206
99
0.297
11
0.484
42
0.710
72
1.063
62
1.922
56
3.356
69
5.385
27
7.779
44
9.487
73
11.14
329
13.27
670
14.86
026
5
0.411
74
0.554
30
0.831
21
1.145
48
1.610
31
2.674
60
4.351
46
6.625
68
9.236
36
11.07
050
12.83
250
15.08
627
16.74
960
6
0.675
73
0.872
09
1.237
34
1.635
38
2.204
13
3.454
60
5.348
12
7.840
80
10.64
464
12.59
159
14.44
938
16.81
189
18.54
758
7
0.989
26
1.239
04
1.689
87
2.167
35
2.833
11
4.254
85
6.345
81
9.037
15
12.01
704
14.06
714
16.01
276
18.47
531
20.27
774
8
1.344
41
1.646
50
2.179
73
2.732
64
3.489
54
5.070
64
7.344
12
10.21
885
13.36
157
15.50
731
17.53
455
20.09
024
21.95
495
9
1.734
93
2.087
90
2.700
39
3.325
11
4.168
16
5.898
83
8.342
83
11.38
875
14.68
366
16.91
898
19.02
277
21.66
599
23.58
935
10
2.155
86
2.558
21
3.246
97
3.940
30
4.865
18
6.737
20
9.341
82
12.54
886
15.98
718
18.30
704
20.48
318
23.20
925
25.18
818
11
2.603
22
3.053
48
3.815
75
4.574
81
5.577
78
7.584
14
10.34
100
13.70
069
17.27
501
19.67
514
21.92
005
24.72
497
26.75
685
12
3.073
82
3.570
57
4.403
79
5.226
03
6.303
80
8.438
42
11.34
032
14.84
540
18.54
935
21.02
607
23.33
666
26.21
697
28.29
952
13
3.565
03
4.106
92
5.008
75
5.891
86
7.041
50
9.299
07
12.33
976
15.98
391
19.81
193
22.36
203
24.73
560
27.68
825
29.81
947
14
4.074
67
4.660
43
5.628
73
6.570
63
7.789
53
10.16
531
13.33
927
17.11
693
21.06
414
23.68
479
26.11
895
29.14
124
31.31
935
15
4.600
92
5.229
35
6.262
14
7.260
94
8.546
76
11.03
654
14.33
886
18.24
509
22.30
713
24.99
579
27.48
839
30.57
791
32.80
132
16
5.142
21
5.812
21
6.907
66
7.961
65
9.312
24
11.91
222
15.33
850
19.36
886
23.54
183
26.29
623
28.84
535
31.99
993
34.26
719
17
5.697
22
6.407
76
7.564
19
8.671
76
10.08
519
12.79
193
16.33
818
20.48
868
24.76
904
27.58
711
30.19
101
33.40
866
35.71
847
18
6.264
80
7.014
91
8.230
75
9.390
46
10.86
494
13.67
529
17.33
790
21.60
489
25.98
942
28.86
930
31.52
638
34.80
531
37.15
645
19
6.843
97
7.632
73
8.906
52
10.11
701
11.65
091
14.56
200
18.33
765
22.71
781
27.20
357
30.14
353
32.85
233
36.19
087
38.58
226
241. 242. 222
F Distribution Tables
F Table for alpha=.10 .
df2
/
df1
1
2
3
4
5
6
7
8
9
10
12
15
20
24
30
40
60
120
INF
1
39.863
46
49.500
00
53.593
24
55.832
96
57.240
08
58.204
42
58.905
95
59.438
98
59.857
59
60.194
98
60.705
21
61.220
34
61.740
29
62.002
05
62.264
97
62.529
05
62.794
28
63.060
64
63.328
12
2
8.5263
2
9.0000
0
9.1617
9
9.2434
2
9.2926
3
9.3255
3
9.3490
8
9.3667
7
9.3805
4
9.3915
7
9.4081
3
9.4247
1
9.4413
1
9.4496
2
9.4579
3
9.4662
4
9.4745
6
9.4828
9
9.4912
2
3
5.5383
2
5.4623
8
5.3907
7
5.3426
4
5.3091
6
5.2847
3
5.2661
9
5.2516
7
5.2400
0
5.2304
1
5.2156
2
5.2003
1
5.1844
8
5.1763
6
5.1681
1
5.1597
2
5.1511
9
5.1425
1
5.1337
0
4
4.5447
7
4.3245
6
4.1908
6
4.1072
5
4.0505
8
4.0097
5
3.9789
7
3.9549
4
3.9356
7
3.9198
8
3.8955
3
3.8703
6
3.8443
4
3.8309
9
3.8174
2
3.8036
1
3.7895
7
3.7752
7
3.7607
3
5
4.0604
2
3.7797
2
3.6194
8
3.5202
0
3.4529
8
3.4045
1
3.3679
0
3.3392
8
3.3162
8
3.2974
0
3.2682
4
3.2380
1
3.2066
5
3.1905
2
3.1740
8
3.1573
2
3.1402
3
3.1227
9
3.1050
0
6
3.7759
5
3.4633
0
3.2887
6
3.1807
6
3.1075
1
3.0545
5
3.0144
6
2.9830
4
2.9577
4
2.9369
3
2.9047
2
2.8712
2
2.8363
4
2.8183
4
2.7999
6
2.7811
7
2.7619
5
2.7422
9
2.7221
6
7
3.5894
3
3.2574
4
3.0740
7
2.9605
3
2.8833
4
2.8273
9
2.7849
3
2.7515
8
2.7246
8
2.7025
1
2.6681
1
2.6322
3
2.5947
3
2.5753
3
2.5554
6
2.5351
0
2.5142
2
2.4927
9
2.4707
9
8
3.4579
2
3.1131
2
2.9238
0
2.8064
3
2.7264
5
2.6683
3
2.6241
3
2.5893
5
2.5612
4
2.5380
4
2.5019
6
2.4642
2
2.4246
4
2.4041
0
2.3830
2
2.3613
6
2.3391
0
2.3161
8
2.2925
7
243. 244. 245. 225
F Table for alpha=.05 .
To index
df2
/
df1
1
2
3
4
5
6
7
8
9
10
12
15
20
24
30
40
60
120
INF
1
161.44
76
199.50
00
215.70
73
224.58
32
230.16
19
233.98
60
236.76
84
238.88
27
240.54
33
241.88
17
243.90
60
245.94
99
248.01
31
249.05
18
250.09
51
251.14
32
252.19
57
253.25
29
254.31
44
2
18.512
19.000
19.164
19.246
19.296
19.329
19.353
19.371
19.384
19.395
19.412
19.429
19.445
19.454
19.462
19.470
19.479
19.487
19.495
3
10.128
9.5521
9.2766
9.1172
9.0135
8.9406
8.8867
8.8452
8.8123
8.7855
8.7446
8.7029
8.6602
8.6385
8.6166
8.5944
8.5720
8.5494
8.5264
4
7.7086
6.9443
6.5914
6.3882
6.2561
6.1631
6.0942
6.0410
5.9988
5.9644
5.9117
5.8578
5.8025
5.7744
5.7459
5.7170
5.6877
5.6581
5.6281
5
6.6079
5.7861
5.4095
5.1922
5.0503
4.9503
4.8759
4.8183
4.7725
4.7351
4.6777
4.6188
4.5581
4.5272
4.4957
4.4638
4.4314
4.3985
4.3650
6
5.9874
5.1433
4.7571
4.5337
4.3874
4.2839
4.2067
4.1468
4.0990
4.0600
3.9999
3.9381
3.8742
3.8415
3.8082
3.7743
3.7398
3.7047
3.6689
7
5.5914
4.7374
4.3468
4.1203
3.9715
3.8660
3.7870
3.7257
3.6767
3.6365
3.5747
3.5107
3.4445
3.4105
3.3758
3.3404
3.3043
3.2674
3.2298
8
5.3177
4.4590
4.0662
3.8379
3.6875
3.5806
3.5005
3.4381
3.3881
3.3472
3.2839
3.2184
3.1503
3.1152
3.0794
3.0428
3.0053
2.9669
2.9276
9
5.1174
4.2565
3.8625
3.6331
3.4817
3.3738
3.2927
3.2296
3.1789
3.1373
3.0729
3.0061
2.9365
2.9005
2.8637
2.8259
2.7872
2.7475
2.7067
10
4.9646
4.1028
3.7083
3.4780
3.3258
3.2172
3.1355
3.0717
3.0204
2.9782
2.9130
2.8450
2.7740
2.7372
2.6996
2.6609
2.6211
2.5801
2.5379
11
4.8443
3.9823
3.5874
3.3567
3.2039
3.0946
3.0123
2.9480
2.8962
2.8536
2.7876
2.7186
2.6464
2.6090
2.5705
2.5309
2.4901
2.4480
2.4045
12
4.7472
3.8853
3.4903
3.2592
3.1059
2.9961
2.9134
2.8486
2.7964
2.7534
2.6866
2.6169
2.5436
2.5055
2.4663
2.4259
2.3842
2.3410
2.2962
13
4.6672
3.8056
3.4105
3.1791
3.0254
2.9153
2.8321
2.7669
2.7144
2.6710
2.6037
2.5331
2.4589
2.4202
2.3803
2.3392
2.2966
2.2524
2.2064
14
4.6001
3.7389
3.3439
3.1122
2.9582
2.8477
2.7642
2.6987
2.6458
2.6022
2.5342
2.4630
2.3879
2.3487
2.3082
2.2664
2.2229
2.1778
2.1307
246. 247. 227
F Table for alpha=.025 .
To index
df2/d
f1
1
2
3
4
5
6
7
8
9
10
12
15
20
24
30
40
60
120
INF
1
647.78
90
799.50
00
864.16
30
899.58
33
921.84
79
937.11
11
948.21
69
956.65
62
963.28
46
968.62
74
976.70
79
984.86
68
993.10
28
997.24
92
1001.4
14
1005.5
98
1009.8
00
1014.0
20
1018.2
58
2
38.506
3
39.000
0
39.165
5
39.248
4
39.298
2
39.331
5
39.355
2
39.373
0
39.386
9
39.398
0
39.414
6
39.431
3
39.447
9
39.456
2
39.465
39.473
39.481
39.490
39.498
3
17.443
16.044
15.439
15.101
14.884
14.734
14.624
14.539
14.473
14.418
14.336
14.252
14.167
14.124
14.081
14.037
13.992
13.947
13.902
4
12.217
10.649
9.9792
9.6045
9.3645
9.1973
9.0741
8.9796
8.9047
8.8439
8.7512
8.6565
8.5599
8.5109
8.461
8.411
8.360
8.309
8.257
5
10.007
8.4336
7.7636
7.3879
7.1464
6.9777
6.8531
6.7572
6.6811
6.6192
6.5245
6.4277
6.3286
6.2780
6.227
6.175
6.123
6.069
6.015
6
8.8131
7.2599
6.5988
6.2272
5.9876
5.8198
5.6955
5.5996
5.5234
5.4613
5.3662
5.2687
5.1684
5.1172
5.065
5.012
4.959
4.904
4.849
7
8.0727
6.5415
5.8898
5.5226
5.2852
5.1186
4.9949
4.8993
4.8232
4.7611
4.6658
4.5678
4.4667
4.4150
4.362
4.309
4.254
4.199
4.142
8
7.5709
6.0595
5.4160
5.0526
4.8173
4.6517
4.5286
4.4333
4.3572
4.2951
4.1997
4.1012
3.9995
3.9472
3.894
3.840
3.784
3.728
3.670
9
7.2093
5.7147
5.0781
4.7181
4.4844
4.3197
4.1970
4.1020
4.0260
3.9639
3.8682
3.7694
3.6669
3.6142
3.560
3.505
3.449
3.392
3.333
10
6.9367
5.4564
4.8256
4.4683
4.2361
4.0721
3.9498
3.8549
3.7790
3.7168
3.6209
3.5217
3.4185
3.3654
3.311
3.255
3.198
3.140
3.080
11
6.7241
5.2559
4.6300
4.2751
4.0440
3.8807
3.7586
3.6638
3.5879
3.5257
3.4296
3.3299
3.2261
3.1725
3.118
3.061
3.004
2.944
2.883
12
6.5538
5.0959
4.4742
4.1212
3.8911
3.7283
3.6065
3.5118
3.4358
3.3736
3.2773
3.1772
3.0728
3.0187
2.963
2.906
2.848
2.787
2.725
13
6.4143
4.9653
4.3472
3.9959
3.7667
3.6043
3.4827
3.3880
3.3120
3.2497
3.1532
3.0527
2.9477
2.8932
2.837
2.780
2.720
2.659
2.595
14
6.2979
4.8567
4.2417
3.8919
3.6634
3.5014
3.3799
3.2853
3.2093
3.1469
3.0502
2.9493
2.8437
2.7888
2.732
2.674
2.614
2.552
2.487
248. 249. 229
F Table for alpha=.01 .
To index
df2/d
f1
1
2
3
4
5
6
7
8
9
10
12
15
20
24
30
40
60
120
INF
1
4052.1
81
4999.5
00
5403.3
52
5624.5
83
5763.6
50
5858.9
86
5928.3
56
5981.0
70
6022.4
73
6055.8
47
6106.3
21
6157.2
85
6208.7
30
6234.6
31
6260.6
49
6286.7
82
6313.0
30
6339.3
91
6365.8
64
2
98.503
99.000
99.166
99.249
99.299
99.333
99.356
99.374
99.388
99.399
99.416
99.433
99.449
99.458
99.466
99.474
99.482
99.491
99.499
3
34.116
30.817
29.457
28.710
28.237
27.911
27.672
27.489
27.345
27.229
27.052
26.872
26.690
26.598
26.505
26.411
26.316
26.221
26.125
4
21.198
18.000
16.694
15.977
15.522
15.207
14.976
14.799
14.659
14.546
14.374
14.198
14.020
13.929
13.838
13.745
13.652
13.558
13.463
5
16.258
13.274
12.060
11.392
10.967
10.672
10.456
10.289
10.158
10.051
9.888
9.722
9.553
9.466
9.379
9.291
9.202
9.112
9.020
6
13.745
10.925
9.780
9.148
8.746
8.466
8.260
8.102
7.976
7.874
7.718
7.559
7.396
7.313
7.229
7.143
7.057
6.969
6.880
7
12.246
9.547
8.451
7.847
7.460
7.191
6.993
6.840
6.719
6.620
6.469
6.314
6.155
6.074
5.992
5.908
5.824
5.737
5.650
8
11.259
8.649
7.591
7.006
6.632
6.371
6.178
6.029
5.911
5.814
5.667
5.515
5.359
5.279
5.198
5.116
5.032
4.946
4.859
9
10.561
8.022
6.992
6.422
6.057
5.802
5.613
5.467
5.351
5.257
5.111
4.962
4.808
4.729
4.649
4.567
4.483
4.398
4.311
10
10.044
7.559
6.552
5.994
5.636
5.386
5.200
5.057
4.942
4.849
4.706
4.558
4.405
4.327
4.247
4.165
4.082
3.996
3.909
11
9.646
7.206
6.217
5.668
5.316
5.069
4.886
4.744
4.632
4.539
4.397
4.251
4.099
4.021
3.941
3.860
3.776
3.690
3.602
12
9.330
6.927
5.953
5.412
5.064
4.821
4.640
4.499
4.388
4.296
4.155
4.010
3.858
3.780
3.701
3.619
3.535
3.449
3.361
13
9.074
6.701
5.739
5.205
4.862
4.620
4.441
4.302
4.191
4.100
3.960
3.815
3.665
3.587
3.507
3.425
3.341
3.255
3.165
14
8.862
6.515
5.564
5.035
4.695
4.456
4.278
4.140
4.030
3.939
3.800
3.656
3.505
3.427
3.348
3.266
3.181
3.094
3.004
15
8.683
6.359
5.417
4.893
4.556
4.318
4.142
4.004
3.895
3.805
3.666
3.522
3.372
3.294
3.214
3.132
3.047
2.959
2.868
250. 251.












![16
เครืองมือและคุณภาพของเครืองมือที่ใชในการเก็บขอมูล
่
่
การสรางเครื่องมือเพื่อใชในการเก็บขอมูลขึ้นอยูกับวิธการที่ใชในการเก็บขอมูล เครื่องมือที่ใช
ี
ไดแก แบบสอบถาม (Questionnaire ) แบบสอบ (Test ) แบบสัมภาษณ (Interview form) แบบสังเกต
(Observation form ) ตลอดจนเครื่องมือตางๆที่สรางขึ้นเพื่อเก็บขอมูลโดยการทดลอง
สําหรับคุณภาพของเครื่องมือที่ใชในการเก็บขอมูล จะตองตรวจสอบคุณภาพรายขอและคุณภาพ
ของเครื่องมือทั้งฉบับ โดยการตรวจสอบคุณภาพรายขอ ตองดูความสอดคลองกับตัวแปรที่มุงวัด ความ
เปนปรนัย ความยากงาย และอํานาจจําแนก สวนการตรวจสอบคุณภาพของเครื่องมือทั้งฉบับตองดูความ
ตรงและความเที่ยงของเครื่องมือ โดยความตรง ตองตรวจสอบ ความตรงตามเนือหา ความตรงตาม
้
โครงสราง ความตรงตามเกณฑ สวนความเที่ยง ตองตรวจสอบความเที่ยงแบบความคงที่ ความเที่ยงแบบ
ความทัดเทียมกัน ความเที่ยงแบบความสอดคลองภายใน โดยมีรายละเอียดของการตรวจสอบคุณภาพของ
เครื่องมือ ดังนี้
ความเที่ยง (Reliability)
ความเที่ยง หมายถึง ความคงเสนคงวาของผลการวัดจากเครื่องมือชนิดเดียวกันที่ทําการวัดซ้ํา
หรือ คือ อัตราสวนระหวางความแปรปรวนของคะแนนจริงกับความแปรปรวนของคะแนนที่สังเกตได
สวนความหมายของความเที่ยงในทางปฏิบัติ คือ คาสัมประสิทธิ์สหสัมพันธระหวางคะแนนจากแบบสอบ
คูขนาน 2 ชุด ซึ่งสอบโดยกลุมผูสอบกลุมเดียวกัน
วิธการตรวจสอบความเที่ยง
ี
1. การหาความเที่ยงเชิงความคงที่ (Stability) ทําไดโดยใชวิธีวัดซ้ํา คือใหผูตอบกลุมเดียวทําแบบ
วัดชุดเดียวกันสองครั้งในเวลาหางกันพอสมควร (test-retest method )แลวนําคะแนนทั้งสองชุดมาหา
ความสัมพันธกัน ถาคาสัมประสิทธิ์สหสัมพันธมีคาสูง แสดงวามีความเที่ยงสูง การวัดความคงที่โดยการ
วัดซ้ําสามารถใชไดกับเครื่องมือวัดที่เปนแบบสอบ แบบสอบถามหรือแบบวัดเจตคติชนิดมาตราสวน
ประมาณคา โดยคํานวณหาคาสัมประสิทธิ์สหสัมพันธอยางงาย (Pearson Product moment Correlation
Coefficient) มีสูตร ดังนี้
[N
r
∑
N
r =
∑
X
2
XY − [( ∑ X )( ∑ Y )]
− ( ∑ X ) 2 ][ N
∑Y
2
− (∑ Y ) 2 ]
= คาสัมประสิทธิ์สหสัมพันธในที่นี้คือคาความเที่ยง
= จํานวนผูสอบ](https://image.slidesharecdn.com/random-131014013121-phpapp01/85/statistics-13-320.jpg)
![17
= ผลบวกของผลคูณคะแนนครั้งแรกและครั้งที่สองเปนคู ๆ
= ผลบวกของคะแนนการสอบครั้งแรก
= ผลบวกของคะแนนการสอบครั้งที่สอง
= กําลังสองของคะแนนครั้งแรก
= กําลังสองของคะแนนครั้งที่สอง
2. การหาความเที่ยงเชิงความเทาเทียมกัน (Equivalence) ทําไดโดยวิธีใชแบบทดสอบสมมูลกัน
(Equivalent -form) หรือ เปนแบบสอบคูขนาน (Parallel-form) ไปทดสอบพรอมกันหรือเวลาใกลเคียงกัน
สองฉบับกับกลุมเดียวกันแลวนําคะแนนทั้งสองชุดมาหาความสัมพันธกัน ถาคาสัมประสิทธิ์สหสัมพันธมี
คาสูง แสดงวามีความเที่ยงสูง คํานวณ โดยหาคาสัมประสิทธิ์สหสัมพันธอยางงาย (Pearson Product
moment Correlation Coefficient) มีสูตรคํานวณ ดังนี้
∑
N
r =
[N
∑
X
2
XY − [( ∑ X )( ∑ Y )]
− ( ∑ X ) 2 ][ N
∑Y
2
− (∑ Y ) 2 ]
r = คาสัมประสิทธิ์สหสัมพันธในที่นี้คือคาความเที่ยง
= จํานวนผูสอบ
ในที่นี้ X และ Y เปนแบบสอบที่คูขนานกัน
3. การหาความเที่ยงเชิงความสอดคลองภายใน (Internal Consistency)
เปนวิธีที่ใชการวัดครั้งเดียวและมีวิธประมาณคาความเทียงไดหลายวิธีคือ
ี
่
3.1 วิธแบงครึ่ง (Split-Half Method) วิธีนใชแบบวัดเพียงฉบับเดียวทําการวัดครั้งเดียว แตแบง
ี
ี้
้
ตรวจเปนสองสวนที่เทาเทียมกัน เชน แบงเปนชุดขอคูกับขอคี่ หรือแบงครึ่งแรกกับครึ่งหลัง ทังนี้ตอง
วางแผนสรางใหสองสวนคูขนานกันกอน วิธวิเคราะหคาความเที่ยงโดยหาคาสัมประสิทธิ์สัมพันธอยาง
ี
งายระหวางคะแนนทั้งสองครึ่งกอนดังนี้
N
r =
[N
∑
X
∑
2
XY − [( ∑ X )( ∑ Y )]
− ( ∑ X ) 2 ][ N
∑Y
2
− (∑ Y ) 2 ]](https://image.slidesharecdn.com/random-131014013121-phpapp01/85/statistics-14-320.jpg)
![18
r = คาสัมประสิทธิ์สหสัมพันธในที่นี้คือคาความเที่ยง
N = จํานวนผูสอบ
ในที่นี้กําหนดให X เปนคะแนนขอคูหรือครึ่งแรกแลวแตกรณี
Y เปนคะแนนขอคีหรือครึ่งหลังแลวแตกรณี
่
r ที่ไดเปน r hh คือ สหสัมพันธระหวางคะแนนครึ่งฉบับกับอีกครึงฉบับแลวปรับขยายเปน
่
สหสัมพันธทั้งฉบับ (r tt ) ดวยสูตรของ Spearman Brown ดังนี้
=
2rhh
1 + rhh
การประมาณคาความเที่ยงดวยวิธีนี้มจุดออนคือผลที่ไดไมคงที่ขึ้นอยูกบวิธีทใชแบงครึ่งขอสอบ
ี
ั
ี่
ตัวอยาง การหาความเที่ยงของแบบสอบเลือกตอบ 20 ขอ โดยใชวิธแบงครึ่ง (Split-Half
ี
Method)แบงแบบสอบเลือกตอบ 20 ขอ เปน 2 ชุด คือ ชุดขอคู (X) 10 ขอ และชุดขอคี่(y ) 10 ขอ ทําการ
ทดสอบกับผูเรียน 5 คน ไดคะแนน ดังตาราง
คนที่
1
2
3
4
5
รวม
การคํานวณคา rhh
X
5
5
4
3
3
20
rhh =
N
=
=
rhh
X2
25
25
16
9
9
84
Y
8
9
8
6
7
38
=
[N
∑
X
∑
2
Y2
64
81
64
36
49
294
XY − [( ∑ X )( ∑ Y )]
− ( ∑ X ) 2 ][ N
∑Y
2
− (∑ Y ) 2 ]
5(156) − (20)(38)
(5(84) − 400))((5(294) − (1444))
20
(20)(26)
0.877
XY
40
45
32
18
21
156](https://image.slidesharecdn.com/random-131014013121-phpapp01/85/statistics-15-320.jpg)


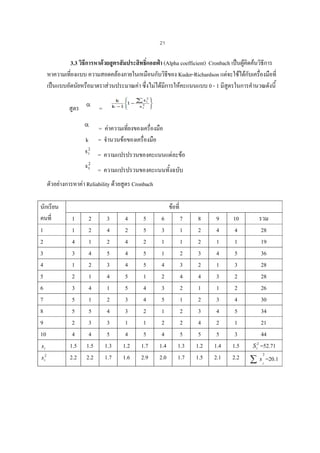


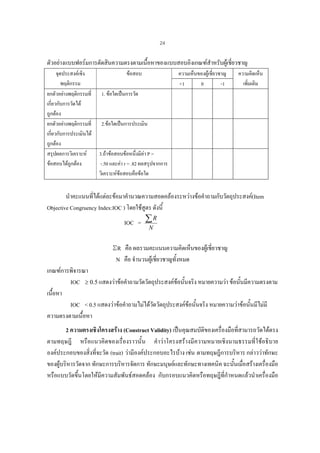
![25
นั้นไปทดสอบกับกลุมตัวอยางดังกลาวแลวพบวาเปนจริงตามทฤษฎี ก็แสดงวาเครื่องมือนั้นก็จะมีความ
ตรงตามโครงสราง
การตรวจสอบความตรงเชิงโครงสรางทฤษฎีทําไดหลายวิธี ไดแก
1) การตรวจหาความสัมพันธกบเครื่องมือที่มโครงสรางเหมือนกัน
ั
ี
เปนการศึกษาความสัมพันธระหวางผลการวัดที่ไดจากเครื่องมือที่สรางขึ้นกับผลของเครื่องมือ
มาตรฐานที่มโครงสรางเหมือนกัน โดยคํานวณหาคาสัมประสิทธิ์สหสัมพันธอยางงาย (Pearson Product
ี
moment Correlation Coefficient) ดังนี้
[N
r
N
X
Y
=
=
=
=
∑
N
r =
∑
X
2
XY − [( ∑ X )( ∑ Y )]
− ( ∑ X ) 2 ][ N
∑Y
2
− (∑ Y ) 2 ]
คาสัมประสิทธิ์สหสัมพันธในที่นี้คือคาความตรง
จํานวนผูสอบ
คะแนนของแบบสอบที่สรางขึ้นที่ตองการหาคาความตรง
คะแนนของแบบสอบมาตรฐานที่มโครงสรางเหมือนกัน
ี
2) การตรวจสอบดวยการวิเคราะหองคประกอบ (Factor Analysis)
การวิเคราะหองคประกอบเปนเทคนิคทางสถิติสําหรับจับกลุมหรือรวมตัวแปรที่มีความสัมพันธ
กันไวในกลุม ทําใหเขาใจลักษณะของขอมูล แบบแผน โครงสราง ความสัมพันธ เชน ทักษะของผูบริหาร
ตามทฤษฎีกลาวไววาวัดจาก 3 ทักษะ ไดแก ทักษะการบริหารจัดการ ทักษะมนุษยและทักษะทางเทคนิค
ดังนั้นเครื่องมือที่สรางขึ้นเพื่อวัดทักษะของผูบริหาร จะตองประกอบดวยขอคําถามที่ประกอบดวย 3
ทักษะดังกลาว การตรวจสอบความตรงตามโครงสรางโดยอาศัยการวิเคราะหองคประกอบ สามารถทําได
โดยใชการวิเคราะหองคประกอบเชิงสํารวจ(Exploratory Factor Analysis) ในกรณีที่ทฤษฎีที่ใชยังไม
แนนอน หรือใชการวิเคราะหองคประกอบเชิงยืนยัน(Confirmatory Factor Analysis)ในกรณีที่เปนทฤษฎี
ที่แนชัด ในที่นี้ขอนําเสนอตัวอยางการวิเคราะหองคประกอบเชิงสํารวจที่สําคัญ เพื่อหาความตรงเชิง
โครงสรางของเครื่องมือ
ตัวอยางการสรางเครื่องมือวัดทักษะของผูบริหารที่ประกอบดวยทักษะการบริหารจัดการ (ขอ1
5) ทักษะมนุษย (ขอ6-10) และทักษะทางเทคนิค (ขอ11-15) ผลการวิเคราะหองคประกอบไดตาราง
วิเคราะหน้ําหนักองคประกอบ ดังนี้](https://image.slidesharecdn.com/random-131014013121-phpapp01/85/statistics-22-320.jpg)




![30
ตัวอยาง การหาความตรงตามสภาพของแบบวัดเชาวนปญญา จากขอมูลในตาราง
ผูเรียน
คะแนนจากแบบวัด
เชาวนปญญาที่สรางขึ้น
(X)
คะแนนจากแบบวัด
เชาวนปญญาที่เปน
มาตรฐาน(y)
X2
Y2
XY
1
10
9
100
81
90
2
9
10
81
100
90
3
10
8
100
64
80
4
6
5
36
25
30
5
9
9
81
81
81
6
8
8
64
64
64
7
8
7
64
49
56
8
7
8
49
64
56
9
9
7
81
49
63
10
6
5
36
25
30
ΣX = 82
ΣY = 76
ΣX2= 692
ΣY2=602
ΣXY=640
การหาความตรงตามสภาพคํานวณได จากสูตร Pearson Product moment โดยกําหนดให
X คือ คะแนนจากแบบวัดเชาวนปญญาทีสรางขึ้น
่
Y คือ คะแนนจากแบบวัดเชาวนปญญาที่เปนมาตรฐาน
∑
N
r =
[N
=
=
∑
X
2
XY
− [(
− (∑ X )
∑
2
X )(
][ N
∑
∑
Y
Y )]
2
− (∑ Y )
2
]
10(640) − (82 × 76)
(10(692) − (82 × 82))(10(602) − (76 × 76) )
.768
หรือคํานวณโดยใช โปรแกรม SPSS ผลทีไดแสดงในตาราง
่](https://image.slidesharecdn.com/random-131014013121-phpapp01/85/statistics-27-320.jpg)
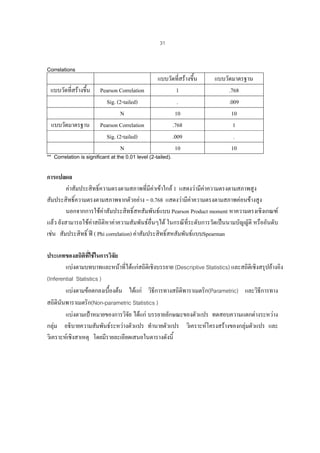
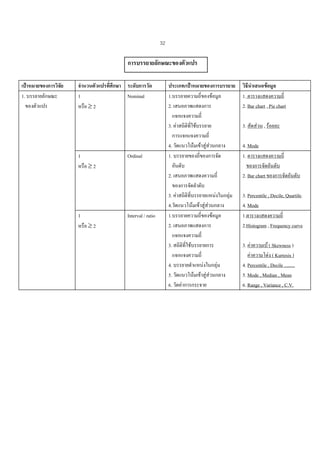
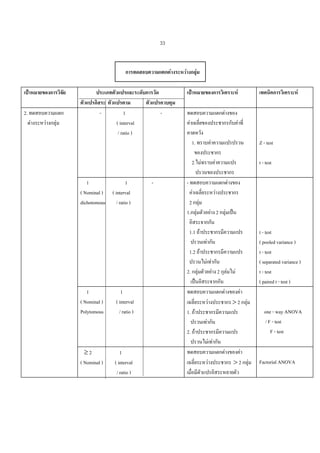
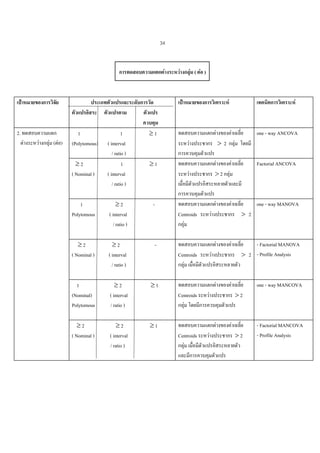
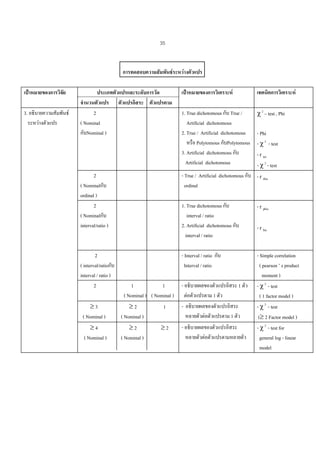
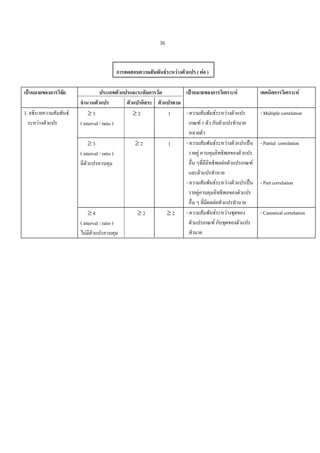
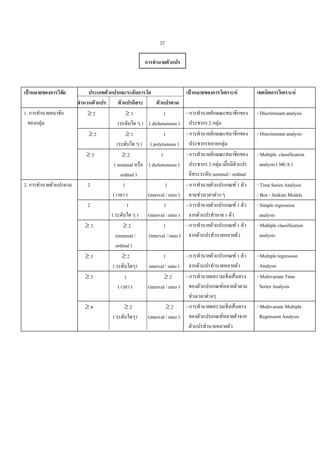
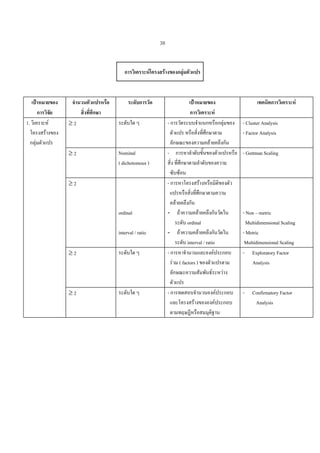
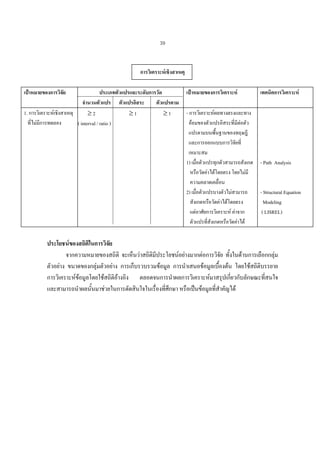




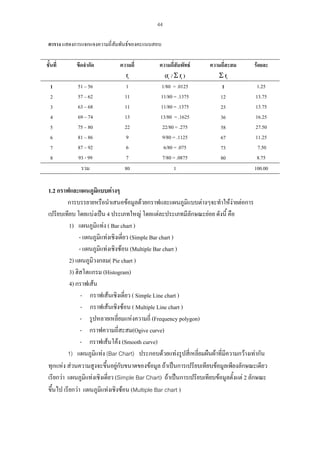
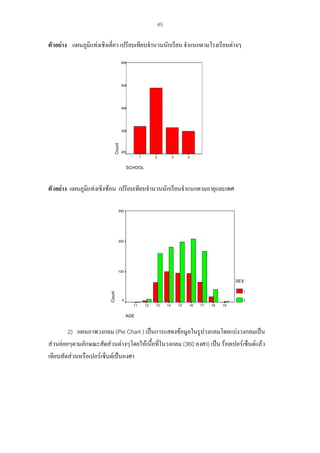
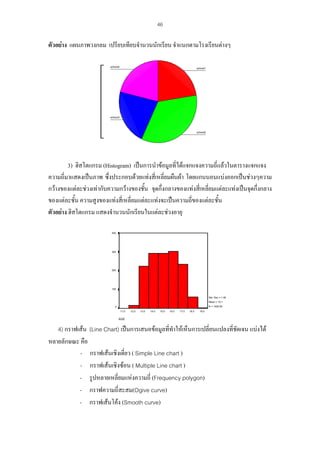
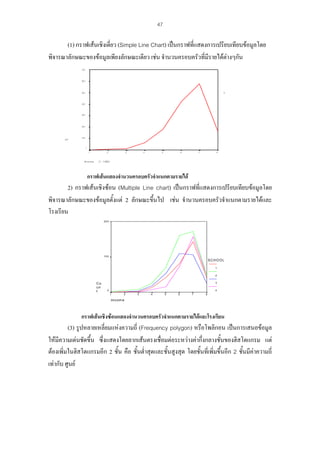
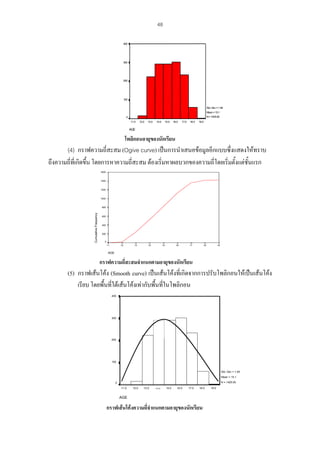
![49
2. การวัดตําแหนงการเปรียบเทียบ
เปนการบอกใหทราบวาคาทีไดมานั้นมีตําแหนงอยูที่ใด หรือสวนใดของคาทั้งหมด เปน
่
การแสดงใหเห็นความสัมพันธระหวางคาที่ไดกับขอมูลทั้งหมด เชน ครูผูสอนตองการแสดงใหเห็น
วาสวนสูงของนักเรียนก.มีความสัมพันธกบสวนสูงของเพื่อนในชันอยางไร
ั
้
การที่จะบอกวา
นักเรียน ก.สูง 160 ซม. นั้นไมไดสื่อความหมายอยางไร จึงตองใชการวัดตําแหนงการเปรียบเทียบ
ไดแก
1) เปอรเซ็นตไทล ( Percentile )
คาเปอรเซ็นตไทล P หมายถึง คาของขอมูลที่มีจํานวนขอมูลที่มีคาต่ํากวา อยู P % และมี
จํานวนขอมูลที่มีคามากกวาอยู ( 100- P) %
ตําแหนงเปอรเซนไทล P หมายถึง ตําแหนงที่บอกใหทราบวามีขอมูลอยู Pสวนในรอยสวน
ที่มีคาของขอมูลต่ํากวาคาของขอมูล ณ ตําแหนง P
การหาเปอรเซ็นตไทล
การหาเปอรเซ็นตไทลสําหรับขอมูลที่ไมไดจัดกลุม มีขั้นตอน ดังนี้
1. เรียงลําดับขอมูล n คาจากนอยไปมาก
2. คํานวณหาตําแหนง P ( n + 1 ) ถาผลลัพธเปนเลขไมลงตัวใหปดเปนเลขจํานวนเต็มที่มีคาใกลเคียง
มากที่สุด
100
ตัวอยาง จงหาเปอรเซ็นตไทลที่ 68 ของขอมูลตอไปนี้
6.3 6.6 7.6 3.0 9.5 5.9 6.1 5.0 3.6
เรียงลําดับขอมูล 9 คาจากนอยไปมาก ดังนี้
3.0 3.6 5.0 5.9 6.1 6.3 6.6 7.6 9.5
คํานวณหาตําแหนง 68 ( 9 + 1 ) = 6.8 ≈ 7
100
คาเปอรเซ็นตไทลที่ 68 ของขอมูล = 6.6
การหาเปอรเซ็นตไทลสําหรับขอมูลที่แจกแจงความถี่ มีสูตรในการคํานวณ ดังนี้
Pr = L + I [ n x r - Σfi ] / fr
100
เมื่อ L = ขีดจํากัดลางทีแทจริงของอันตรภาคชั้นที่มี Pr อยู
่
I = ความกวางของอันตรภาคชัน
้
r = ตําแหนงเปอรเซ็นตไทลที่ตองการหา
n = จํานวนขอมูลทั้งหมด
Σfi = ความถี่สะสมของอันตรภาคชั้นที่ต่ํากวา L
fr = ความถี่ของชั้น L](https://image.slidesharecdn.com/random-131014013121-phpapp01/85/statistics-46-320.jpg)
![50
กอนที่จํานําสูตรนี้ไปหาจะตองทราบกอนวา Pr ควรจะอยูอันตรภาคชันใด โดยเปรียบเทียบ คา n x r
้
กับความถี่สะสม
100
ตัวอยาง การคํานวณหาเปอรเซ็นตไทลสําหรับขอมูลที่แจกแจงความถี่
จงหาเปอรเซ็นตไทลที่ 20 และ 80 ของขอมูลความสูงของนักเรียนที่กําหนดไวในตาราง
แจกแจงความถี่ ดังนี้
ขีดจํากัดที่แทจริงของชั้น
134.5-144.5
144.5-154.5
154.5-164.5
164.5-174.5
174.5-184.5
รวม
ความถี่ ( f )
5
18
42
27
8
100
ความถี่สะสม (Σ f )
5
23
65
92
100
จากความถี่สะสมชั้นที่ 2 มี Σ f = 23 ดังนัน เปอรเซ็นตไทลที่ 20 จะอยูในชั้นที่ 2
้
การหาเปอรเซ็นตไทลที่ 20 ได L = 144.5 I = 10 r = 20 n = 100 Σfi = 5 fr = 18
L + I [ n x 20 - Σfi ] / fr
P20 =
100
=
144.5 + 10 ( 100 x 20 - 5 ] / 18
100
=
144.5+ 8.33
= 152.83
สวนเปอรเซ็นตไทลที่ 80 จากความถี่สะสมชั้นที่ 4 มี Σ f = 92 ดังนั้น เปอรเซ็นตที่ 80 จะ
อยูในชันที่ 4ได L = 164.5 I = 10 r = 80 n = 100 Σfi = 65 fr = 27
้
P 80 =
L + I [ n x 80 - Σfi ] / fr
100
=
164.5 + 10 [ ( 100 x 80 - 65 ] / 27
100
=
164.5+ 5.55
= 170.05
2) ควอไทล (Quartiles )
ควอไทลเปนการแบงขอมูลออกเปน 4 สวนเทาๆกัน สวนละ 25 %โดยเรียงลําดับ
ขอมูลจากนอยไปมาก ดังนัน
้
คาควอไทล1(Q1) หมายถึงคาของขอมูลที่มีจํานวนขอมูลที่มีคาต่ํากวา Q1อยู 25 %](https://image.slidesharecdn.com/random-131014013121-phpapp01/85/statistics-47-320.jpg)
![51
คาควอไทล2(Q2) หมายถึงคาของขอมูลที่มีจํานวนขอมูลที่มีคาต่ํากวา Q2อยู 50 %
และมีจํานวนขอมูลที่มีคามากกวา Q2อยู 50 %
คาควอไทล3(Q3) หมายถึงคาของขอมูลที่มีจํานวนขอมูลที่มีคาต่ํากวา Q3อยู 75 %
และมีจํานวนขอมูลที่มีคามากกวา Q3อยู 25 %
ตําแหนงควอไทล หมายถึง ตําแหนงที่บอกใหทราบวามีขอมูลอยู Xสวนในสี่สวน
ที่มีคาของขอมูลต่ํากวาคาของขอมูล ณ ตําแหนง X
การคํานวณหาควอไทลสําหรับขอมูลที่ไมไดจัดกลุม
- เรียงลําดับขอมูล n คา จากนอยไปหามาก
- สําหรับการคํานวณหาคา Q1 ใหคํานวณ (n+1)/4 ถาผลลัพธเปนเลขไมลงตัวให
ปดใหเปนเลขจํานวนเต็มที่มคาใกลเคียงมากที่สุด
ี
สวนการหาคา Q3ใหคํานวณหา 3 (n+1)/4 และปดใหเปนเลขจํานวนเต็มที่ใกลเคียงมากที่สุด
สําหรับการหาควอไทล สําหรับขอมูลที่แจกแจงความถี่ มีสูตรในการคํานวณ ดังนี้
QK = L + I [ n x k - Σfi ] / fk
4
เมื่อ L = ขีดจํากัดลางทีแทจริงของอันตรภาคชั้นที่มี QK อยู
่
I = ความกวางของอันตรภาคชัน
้
k = ตําแหนงควอไทลที่ตองการหา
n = จํานวนขอมูลทั้งหมด
Σfi = ความถี่สะสมของอันตรภาคชั้นที่ต่ํากวา L
fk = ความถี่ของชั้น L
พิสัยควอไทล คือความแตกตางระหวางควอไทลบน (Q3)และควอไทลลาง (Q1)
ตัวอยาง จงหา ควอไทลบน (Q3) คามัธยฐาน และควอไทลลาง (Q1) ของคะแนนเฉลี่ยวิชาภาษาไทย
ของนักเรียน 22 คน ดังนี้
45 50 65 23 55 48 78 89 96 85 74 42 45 75 78 41 56 66 77 88 95 78
เนื่องจาก n = 22 คน เรียงขอมูลจากนอยไปมากไดดังนี้
23 41 42 45 45 48 50 55 56 65 66 74 75 77 78 78 78 85 88 89 95 96
การหา Q3 คํานวณหาคา 3 (n+1)/4 = 17.25 ปดเปน 17
ดังนั้นคาควอไทลบนจะเปนคาของขอมูลตัวที่ 17 ที่เรียงลําดับไวแลว คือ 78
การหาคามัธยฐาน (Q2) คํานวณหาคา 2 (n+1)/4 = 11.5 ปดเปน 12
ดังนั้นคามัธยฐาน จะเปนคาของขอมูลตัวที่ 12 ที่เรียงลําดับไวแลว คือ 74
การหา Q1 คํานวณหาคา (n+1)/4 = 5.75 ปดเปน 6](https://image.slidesharecdn.com/random-131014013121-phpapp01/85/statistics-48-320.jpg)
![52
ดังนั้นคาควอไทลลางจะเปนคาของขอมูลตัวที่ 6 ที่เรียงลําดับไวแลว คือ 48
3) เดไซล (Deciles )
เดไซล เปนการแบงขอมูลอออกเปน 10 สวนเทาๆกัน มีจํานวน 9 คา คือ D,
D2…D9 โดยที่ k = 1 ,2, 3, … 9
ตําแหนงเดไซล หมายถึง ตําแหนงที่บอกใหทราบวามีขอมูลอยู X สวนในสิบสวน
ที่มีคาของขอมูลต่ํากวาคาของขอมูล ณ ตําแหนง X
การคํานวณหาเดไซล สําหรับขอมูลที่ไมไดจัดกลุม
- เรียงลําดับขอมูล n คา จากนอยไปหามาก
- สําหรับการคํานวณหาคา Dk ใหคํานวณ k(n+1)/10 ถาผลลัพธเปนเลขไมลงตัวให
ปดใหเปนเลขจํานวนเต็มที่มคาใกลเคียงมากที่สุด
ี
สวนการหา Dk สําหรับขอมูลที่แจกแจงความถี่ มีสูตรในการคํานวณ ดังนี้
Dk = L + I [ n x k - Σfi ] / fk
10
เมื่อ L
I
k
n
Σfi
fk
=
=
=
=
=
=
ขีดจํากัดลางที่แทจริงของอันตรภาคชั้นทีมี Dk อยู
่
ความกวางของอันตรภาคชัน
้
ตําแหนงเดไทลที่ตองการหา
จํานวนขอมูลทั้งหมด
ความถี่สะสมของอันตรภาคชั้นที่ต่ํากวา L
ความถี่ของชั้น L
3. การวัดแนวโนมเขาสูสวนกลาง (Central Tendency)
การวัดแนวโนมเขาสูสวนกลาง เปนการคํานวณคากลางของขอมูลวาอยูที่ใด การศึกษาใน
กรณีที่ตองการคาเพียงคาเดียวเพื่อใชอธิบายขอมูลทั้งชุด
จึงนิยมหาคากลางๆที่เปนตัวแทนของ
ขอมูลทั้งชุด นั่นคือ คาเฉลี่ยเลขคณิต (Mean) มัธยฐาน (Median) และฐานนิยม(Mode) โดยมีวิธการ
ี
หาได ดังนี้
3.1 คาเฉลี่ยเลขคณิตหรือมัชฌิมเลขคณิต (Mean) คือ คาที่ไดจากผลรวมของคะแนนหรือ
คาที่ไดทั้งหมดหารดวยจํานวนนักเรียนหรือจํานวนขอมูล การคํานวณหาคาแบงเปน](https://image.slidesharecdn.com/random-131014013121-phpapp01/85/statistics-49-320.jpg)


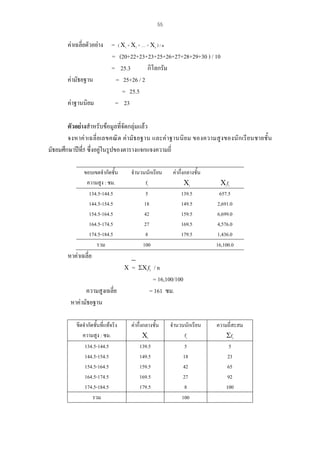
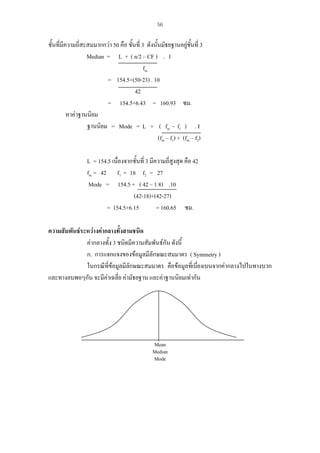
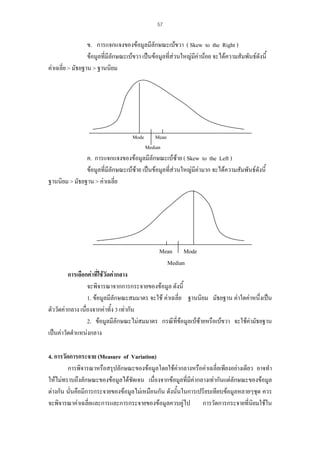

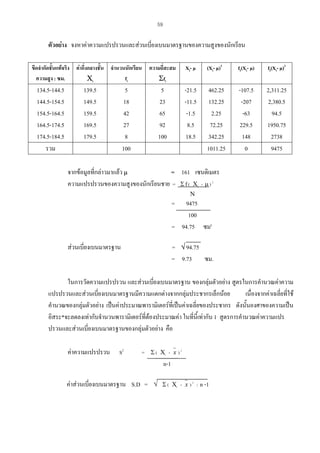








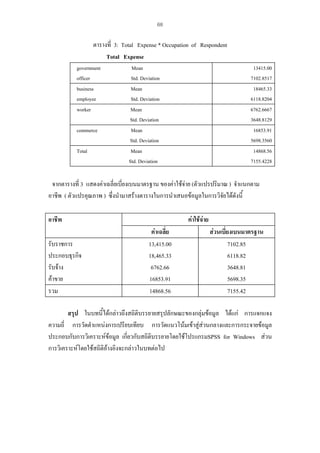




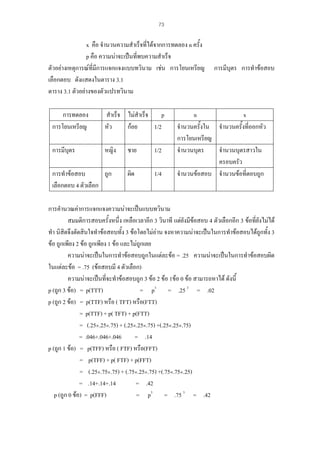




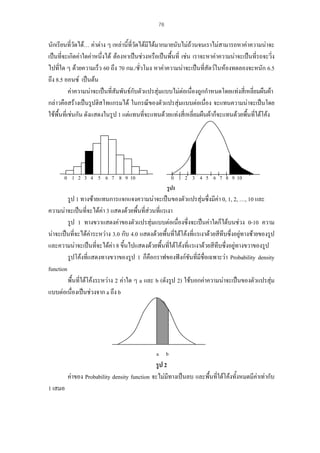

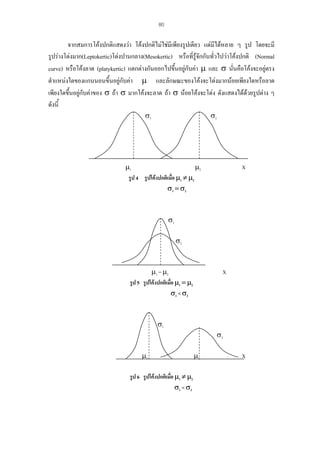
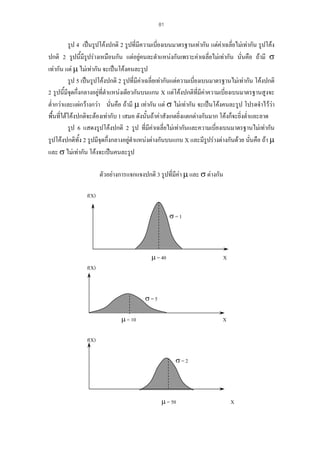





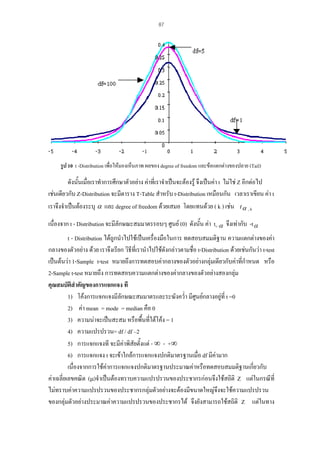
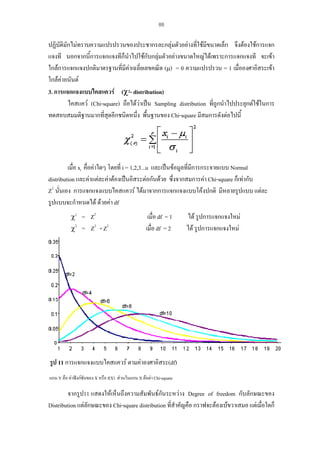

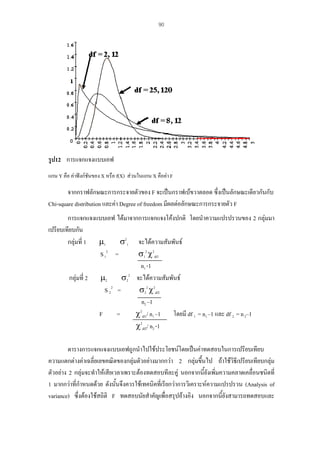





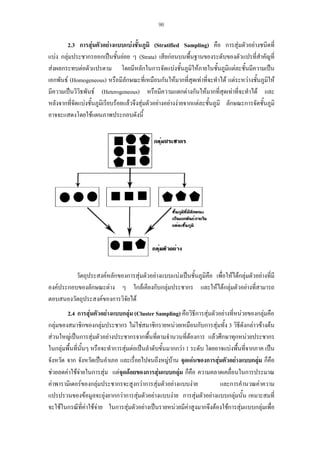










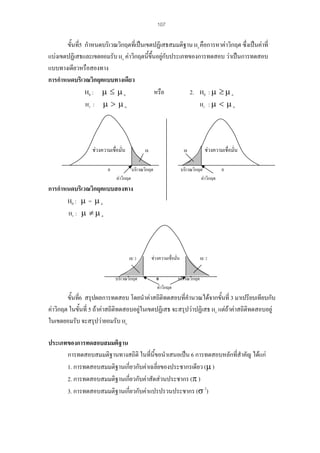













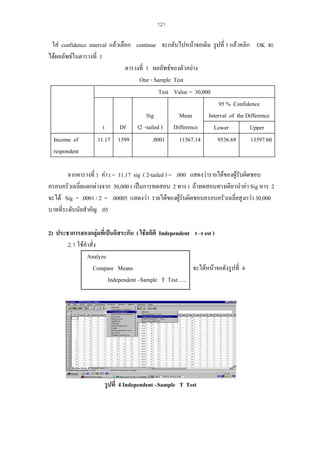

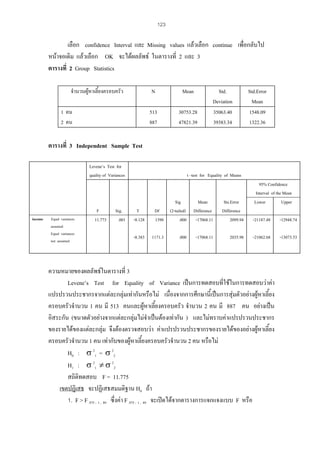








![132
ในที่นี้จะอธิบายวิธีการเปรียบเทียบเชิงซอนบางวิธีดังนี้
1. Least-Significant Different(LSD)
LSD หรือ Fisher’s Least-Significant Difference เปนเทคนิคที่ R.A. Fisher ได
พัฒนาขึ้นเพื่อเปรียบเทียบคาเฉลี่ยประชากรไดครั้งละหลายคู โดยมีขั้นตอนดังนี้
LSD = t
MSE
α
1− ;n − k
2
1
1
+
ni n j
1) คํานวณคา LSD โดยที่
ถา ni = nj จะทําให
LSD = t
X Max
α
1− ;n − k
2
2 MSE
ni
คํานวณความแตกตางระหวางคาเฉลี่ย X i − X j
2) นํา | X i − X j | เปรียบเทียบกับคา LSD
3.1 ถา | X i − X j | > LSD แสดงวา µ i ≠ µ j
3.2 ถา | X i − X j | ≤ LSD แสดงวา µ i ไมแตกตางจาก
หมายเหตุ สวนใหญผูวเิ คราะหมักจะคํานวณหา
− X Min |, | X ÃͧMax − X ÃͧMin |,... แลวนํามาเปรียบเทียบกับคา LSD
µj
2. Student-Newman-Keuls (SNK) Multiple Range Test
เปนวิธีการเปรียบเทียบคาเฉลี่ยประชากรโดยใชคาเฉลี่ยตัวอยางมีคามากที่สุดและนอย
ที่สุดกับคา Studentized range statistic
ี้
เงื่อนไข วิธีนจะใชไดเมื่อขนาดตัวอยางแตละชุดเทากัน คือ n 1 = n 2 = n 3 = ... = n k = r
SNK (v , α ) = q α .v .n −k
MSE
r
โดยที่คา q เปดไดจากตาราง และ v = จํานวนคาเฉลี่ยที่อยูในชวงที่เปรียบเทียบ โดย
พิจารณาจากคาเฉลี่ยตัวอยางแตละชุดที่เรียงลําดับจากนอยไปมาก จํานวน t คาดังนี้
X Min ≤ X ≤ ... ≤ X Max
X [1 ] ≤ X [ 2 ] ≤ ... ≤ X [ k ]
X
(1 )
= min( X [1 ] , X [ 2 ] ,..., X [ k ] )
X [ k ] = max( X 1 , X 2 ,..., X k )](https://image.slidesharecdn.com/random-131014013121-phpapp01/85/statistics-129-320.jpg)








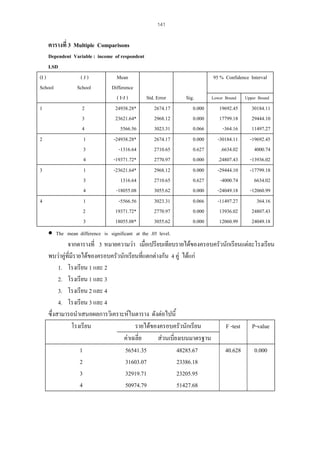



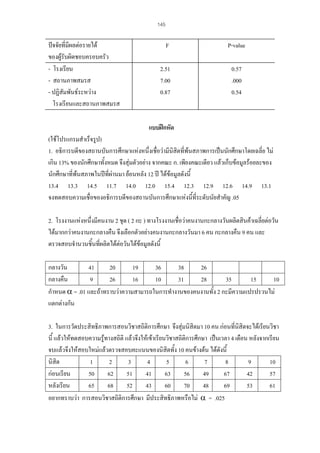








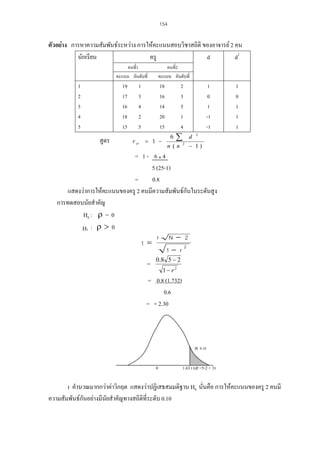


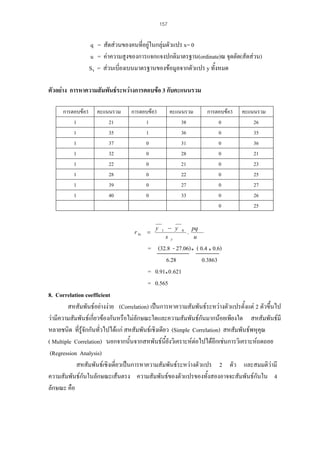
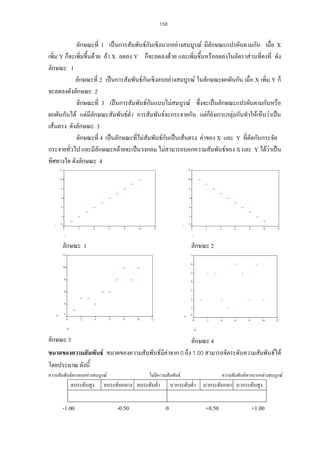
![159
สูตรที่ใชในการคํานวณ คา r
r เรียกวา Pearson correlation coefficiient , Simple correlation , Correlation coefficient
r =
r =
r =
∑
− X )( Y
(X
NS
X
S
−Y )
=
∑
Y
∑ XY − [( ∑ X )( ∑Y ) / N
[( ∑ X ) − ( ∑ X ) / N ][ ∑Y ) − ( ∑Y )
2
2
2
∑
X .Y
2
X
2
∑
Y
2
/ N]
N ∑ XY − [( ∑ X )( ∑Y )]
[N ∑ X − ( ∑ X ) 2 ][N ∑Y − ( ∑Y ) 2 ]
2
2
ตัวอยาง จากการศึกษาความสัมพันธระหวางความรูกบความคิดเห็นของนักศึกษา 5 คน ไดคะแนน
ั
ความรูและความคิดเห็น ดังตาราง อยากทราบวา ความรูกับความคิดเห็นสัมพันธกันหรือไม ถาสัมพันธ
สัมพันธกันในทิศทางใด
การคํานวณ สมมติให X = คะแนนความรู และ Y = คะแนนความคิดเห็น จัดระเบียบเตรียมการ
วิเคราะห ดังนี้
ตาราง การจัดระเบียบเตรียมการวิเคราะหสหพันธแบบ Pearson
คนที่
1
2
3
4
5
รวม
X
5
5
4
3
3
20
X2
25
25
16
9
9
84
Y
8
9
8
6
7
38
Y2
64
81
64
36
49
294
การคํานวณคา r
N
r =
[N
=
=
=
∑
X
∑
2
XY − [(
∑
X )(
− ( ∑ X ) ][ N
2
∑Y
∑Y
2
)]
− (∑ Y ) 2 ]
5 (156)-(20)(38)
√(5(84)-400) (5(294)-(1444)
20
√ (20)(26)
0.877
XY
40
45
32
18
21
156](https://image.slidesharecdn.com/random-131014013121-phpapp01/85/statistics-156-320.jpg)