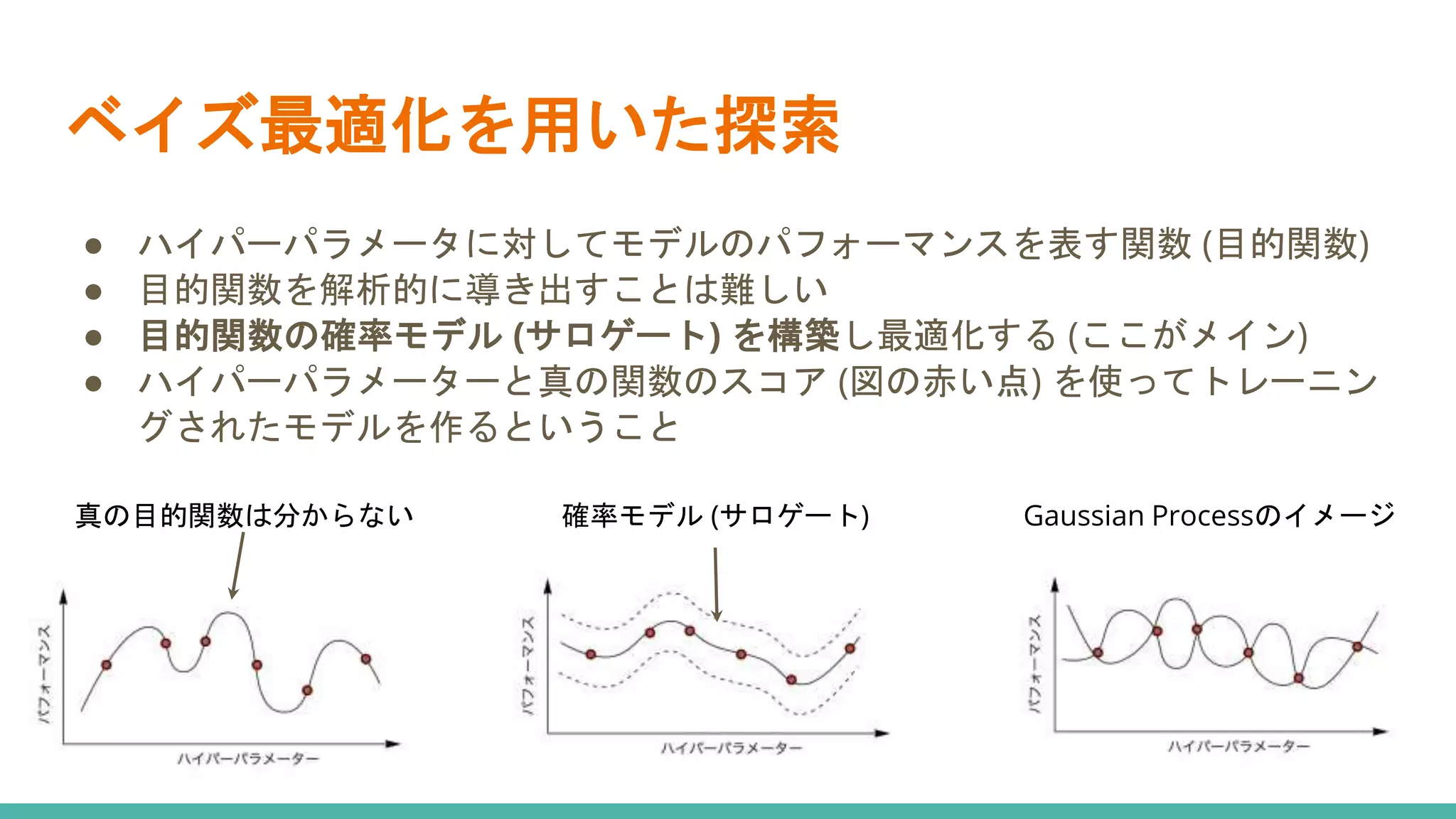
ベイズ最適化によるハイパーパラメータ探索についてざっくりと解説しました。 今回紹介する内容の元となった論文 Bergstra, James, et al. "Algorithms for hyper-parameter optimization." 25th annual conference on neural information processing systems (NIPS 2011). Vol. 24. Neural Information Processing Systems Foundation, 2011. https://hal.inria.fr/hal-00642998/

1. ベイズ最適化を用いた
ハイパーパラメータ探索
機械学習秘伝のタレを自動化

2. 今回紹介する内容
● Algorithms for Hyper-Parameter Optimization
○ 著者: James Bergstra, R. Bardenet, Yoshua Bengio, Balazs Kegl
○ 投稿: Neural Information and Processing Systems, 2011
○ 引用: 2571件 (2021/05/28 時点)
● 論文の内容
○ アルゴリズムを用いたハイパーパラメータの探索
○ MLPとDBNを用いてrandom searchとベイズ最適化手法の性能比較
○ 少ない計算量でgird searchやrandom searchと同等またはそれ以上の結果を出す

3. ハイパーパラメータとは
● モデルのパラメータのうち、人が決めるものモデルの設定のようなもの
● モデルの性能に関わる
● 探索が大変

4. 代表的な探索手法
● 代表的な手法
○ Grid Search (例: sklearn.model_selection.RandomizedSearchCV)
■ 候補点を全て探索
○ Random Search (例: sklearn.model_selection.RandomizedSearchCV)
■ 指定した探索回数でランダムに選択
● データ数が多くない場合は許容できる時間内で十分な結果を出す
● 計算時間は探索パラメータ数の指数オーダーであり、データ数が多いと探索
は困難に

5. ベイズ最適化を用いた探索
● 2つの手法
○ Gaussian Process Approach (GP)
○ Tree-Structured Parzen Estimator Approach (TPE)
● 探索方法は、SMBO(Sequential Model-Based Optimization) とも
呼ばれる
○ SMBO: 反復的に関数評価と代理モデルの更新をしていく
● 今回は、各手法の細かい内容までは触れない。

6. ベイズ最適化を用いた探索
● H: 観測点とその評価値の集合
● T: イテレーション数
● x: パラメータベクトル
● M: サロゲート(パラメータの分布を推定)
● S: 獲得関数(Mの元であるxを使用した時のloss
の期待値計算)
● f(x): モデルにパラメータx 使用した際のloss
[アルゴリズム]
1. 各パラメータに対する評価値を入れる集合H を用
意
2. T回イテレーション↓
3. あるパラメータベクトルxと代理関数Mを用いて
loss を最も小さくするパラメータを選択
4. そのパラメータを評価しサンプル(x, f(x))を得る
5. Hを更新
6. 代理関数Mの更新

7. ベイズ最適化を用いた探索
● ハイパーパラメータに対してモデルのパフォーマンスを表す関数 (目的関数)
● 目的関数を解析的に導き出すことは難しい
● 目的関数の確率モデル (サロゲート) を構築し最適化する (ここがメイン)
● ハイパーパラメーターと真の関数のスコア (図の赤い点) を使ってトレーニン
グされたモデルを作るということ
確率モデル (サロゲート) Gaussian Processのイメージ
真の目的関数は分からない

8. 実験結果
● アルゴリズムはMLPとDBNを使用
● GP, TPE どちらもイテレーションを増やすとlossが下がっていく
● 最終的にはgrid search, random searchよりも良いパラメータを見つ
けている
● 詳しくは論文を参照 (https://hal.inria.fr/hal-00642998/)

9. 実際に使ってみたい人は
● ライブラリなどを使うと数十行で簡単に最適化ができる
● 実行環境によってどれを使うか考えると良い
● 環境
○ 自前のマシンでやるとき便利なライブラリを使う
■ Hyperopt: https://github.com/hyperopt/hyperopt
■ Optuna: https://github.com/optuna/optuna
■ scikit-optimize: https://github.com/scikit-optimize/scikit-optimize
○ Cloud上のツール
■ Amazon Sage Makerなど

10. まとめ
● 機械学習の精度向上を目指すとき、ハイパーパラメータのチューニングは必
須
● ベイズ最適化ではサロゲートを用いてハイパーパラメータとパフォーマンス
の関係を確率分布で表し最適化を行う
● DBNのハイパーパラメータ探索において、GPとTPEはともにrandom search
よりも良い性能を示した
● Hyperoptなどを利用することで簡単にベイズ最適化を組み込むことができる

11. チャンネル紹介
● チャンネル名: 【経営xデータサイエンスx開発】西岡 賢一郎のチャンネル
● URL: https://www.youtube.com/channel/UCpiskjqLv1AJg64jFCQIyBg
● チャンネルの内容
○ 経営・データサイエンス・開発に関する情報を発信しています。
○ 例: アジャイル開発、データパイプライン構築、AIで使われるアルゴリズム4種類など
● noteでも情報発信しています → https://note.com/kenichiro

12. ベイズ最適化を用いた探索
● Gaussian Process Approach (GP)
○ 代理関数にガウス過程回帰
○ 獲得関数に以下を用いる(EI: Expected Improvement)
■ ある閾値y*よりyがどれほど改善するかをみる → 直感的
■ p_M: xを観測した後のyの事後分布

13. ベイズ最適化を用いた探索
● Tree-Structured Parzen Estimator Approach (TPE)
○ optunaで使われているアルゴリズム
○ GPと異なり、p(x|y), p(y) をモデル化する(ノンパラメトリック)
■ p(y|x) = p(x|y)p(y)/p(x)
○ 獲得関数はGPと同じEIを用いる

14. 性能の比較
● MLPを用いた実験
○ データセット: Boston Housing dataset (506レコード, 13の特徴) → 回帰問題
○ ハイパーパラメータ10個
■ 学習率、正則化の種類、中間層の数、イテレーション数
● 5イテレーションごとに最も低くな
たloss (1σのエラーバー含む)
● 赤: GP
● 青: Random search
● 探索空間に比べデータ数は少ないが、
GPの方が良いパラメータのくみを
見つけている

15. 性能の比較
● DBNを用いた実験
○ データセット: convex, MRBI(MNIST rotated backgroud images) → 分類問題
○ ハイパーパラメータ: 32個

16. 性能の比較
● DBNを用いた実験
● 各ドット: SMBOアルゴリズムによってサンプリングさ
れたパラメータの評価値
● 太線(赤or青): イテレーションごとのベストなバリデー
ションloss
● 実線: grid search & manual search(先行研究)
● 点線: random search(イテレーションごとのlossの
99.5%点: それぞれ457, 361回のイテレーション)
● GP, TPE どちらもイテレーション
を増やすとlossが下がっている
● 最終的にはgrid search, random
searchよりも良いパラメータを見
つけている
● どちらも計算時間は24時間以内
(5つのGPU)