Downloaded 11 times
![モンテカルロ法
独立な確率分布からランダムな数値を与え、シミュ
レーションを行う手法。
土井さんの資料「モンテカルロ法解説資料」参照
(SVN>勉強会>アルゴリズム解説資料)
例)
独立に一様分布に従う 𝑥, 𝑦 ∈ 0,1 × [0,1]を多数生
成し、𝑥2 + 𝑦2 < 1を満たす個数の割合が円周率の
1/4に近似できる。
10
l = 10000000
x= runif(l)
y= runif(l)
p = x^2+y^2
pi = 4*sum(p<1)/l
print(pi)
3.141686
四角の面積は1
扇型の面積はπ/4
試行回数が多いと近
似がよくなる](https://image.slidesharecdn.com/04-181210034534/75/MCMC-10-2048.jpg)
![24
𝐿 𝜆 ~𝑁(0,1)としてメトロポリス法を実装し、実行した結果が以下
MCMC法-メトロポリス法-実験
λ
試行回数n 確率
平均 E[λ]：-0.097
分散Var[λ]：1.016](https://image.slidesharecdn.com/04-181210034534/75/MCMC-24-2048.jpg)
MCMC法
- 1. MCMC法 2018/12/10 東京工業大学 工学院 経営工学系3年 松井諒生 1
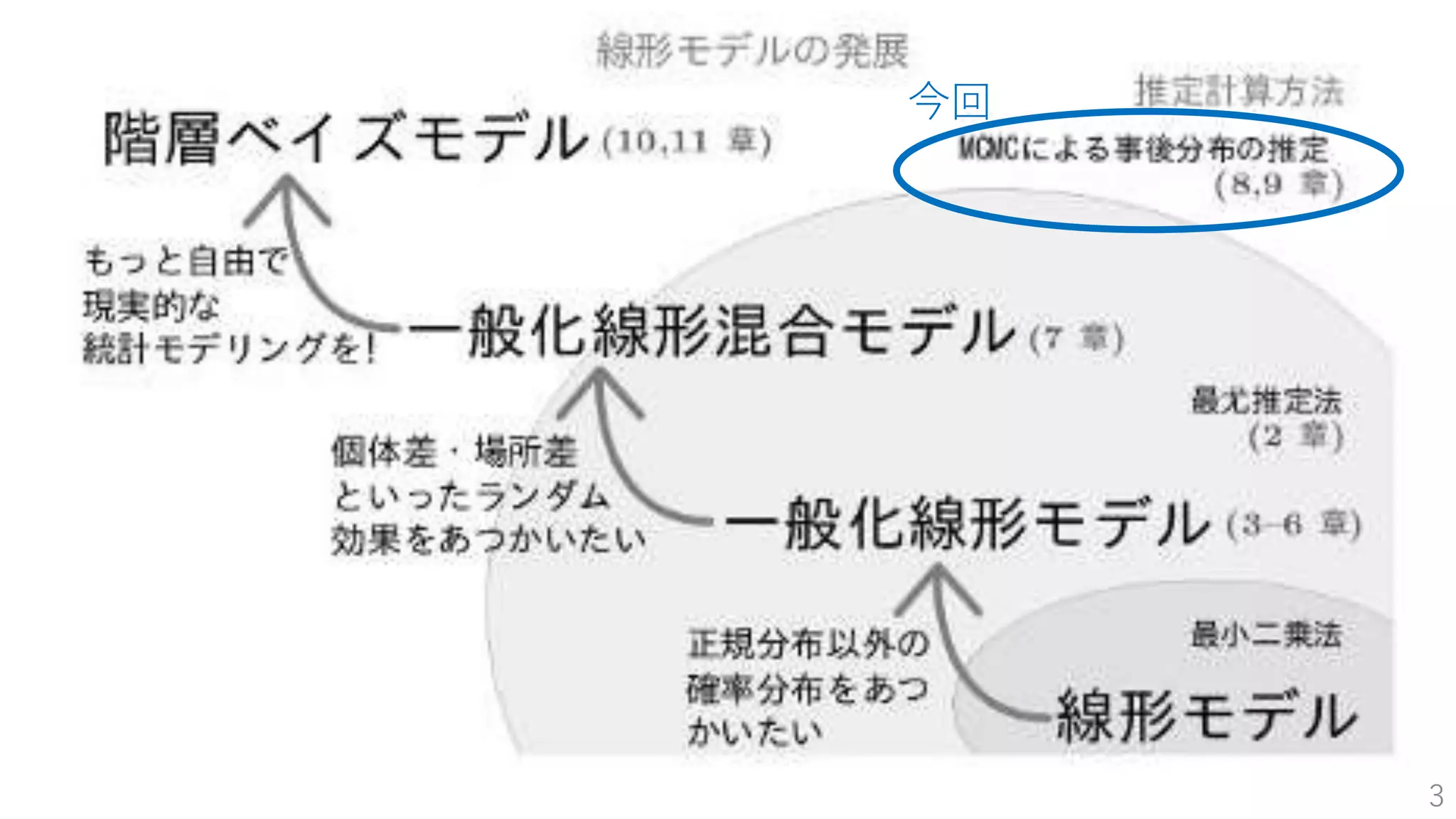
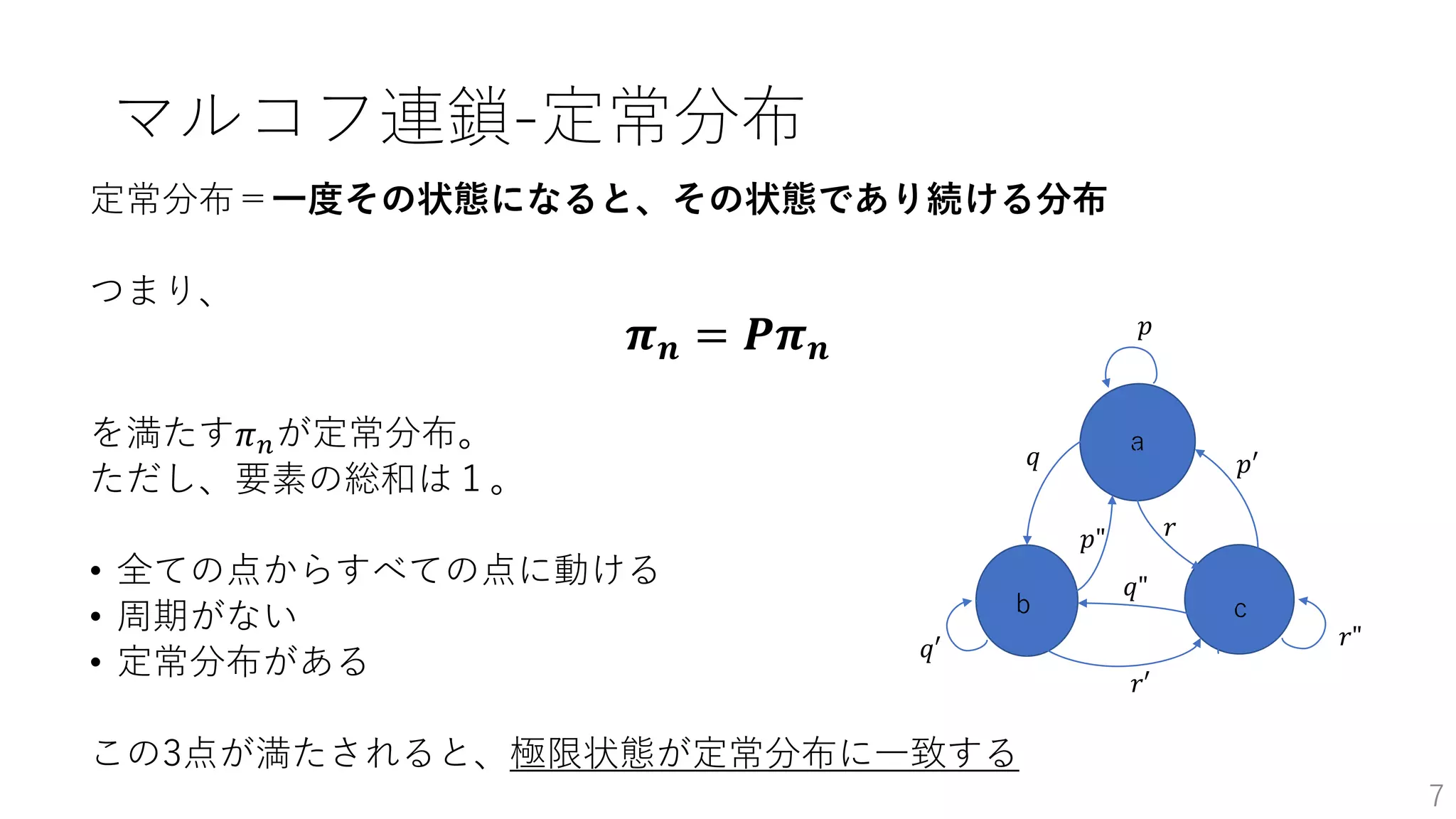
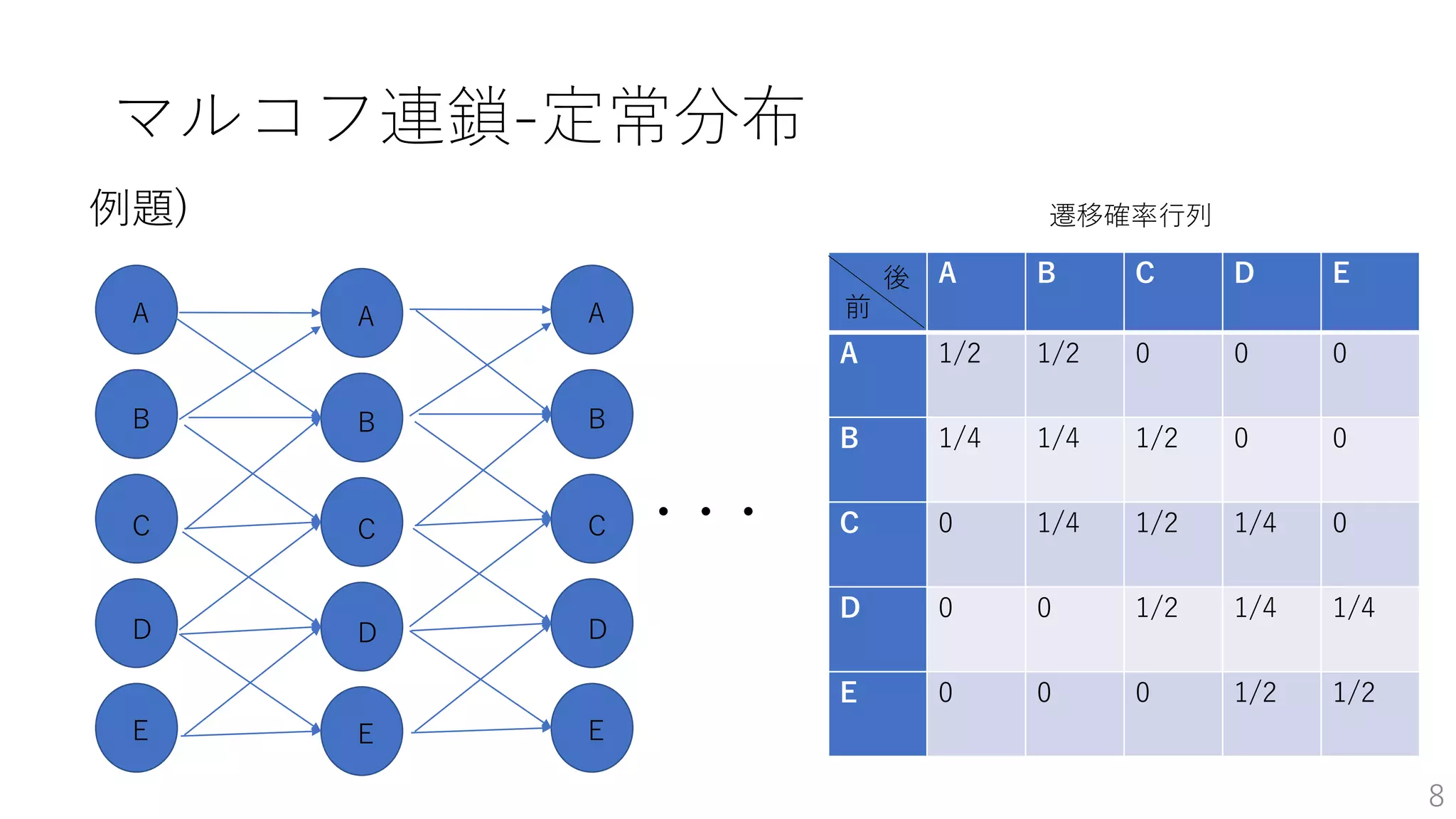
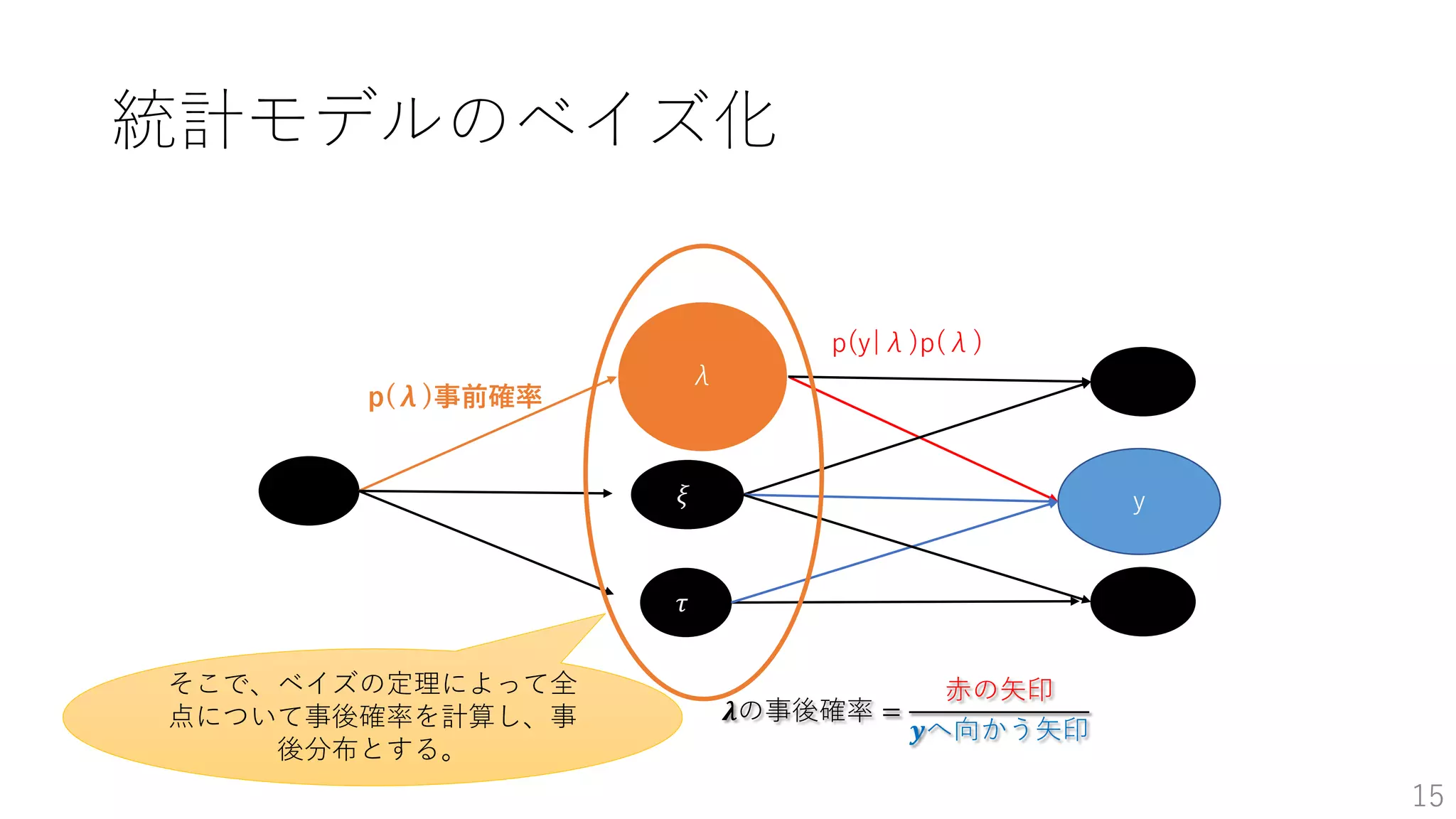
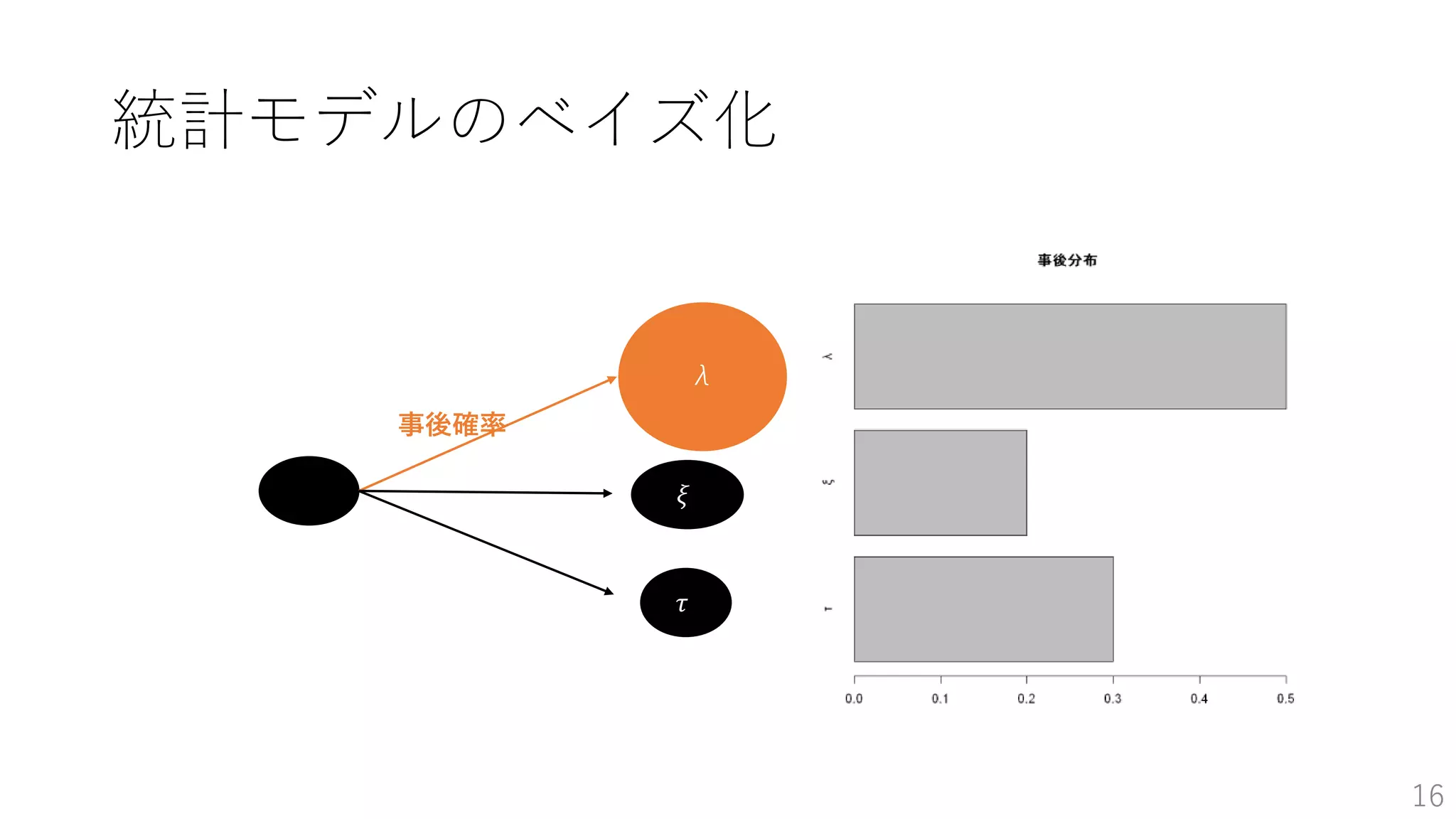
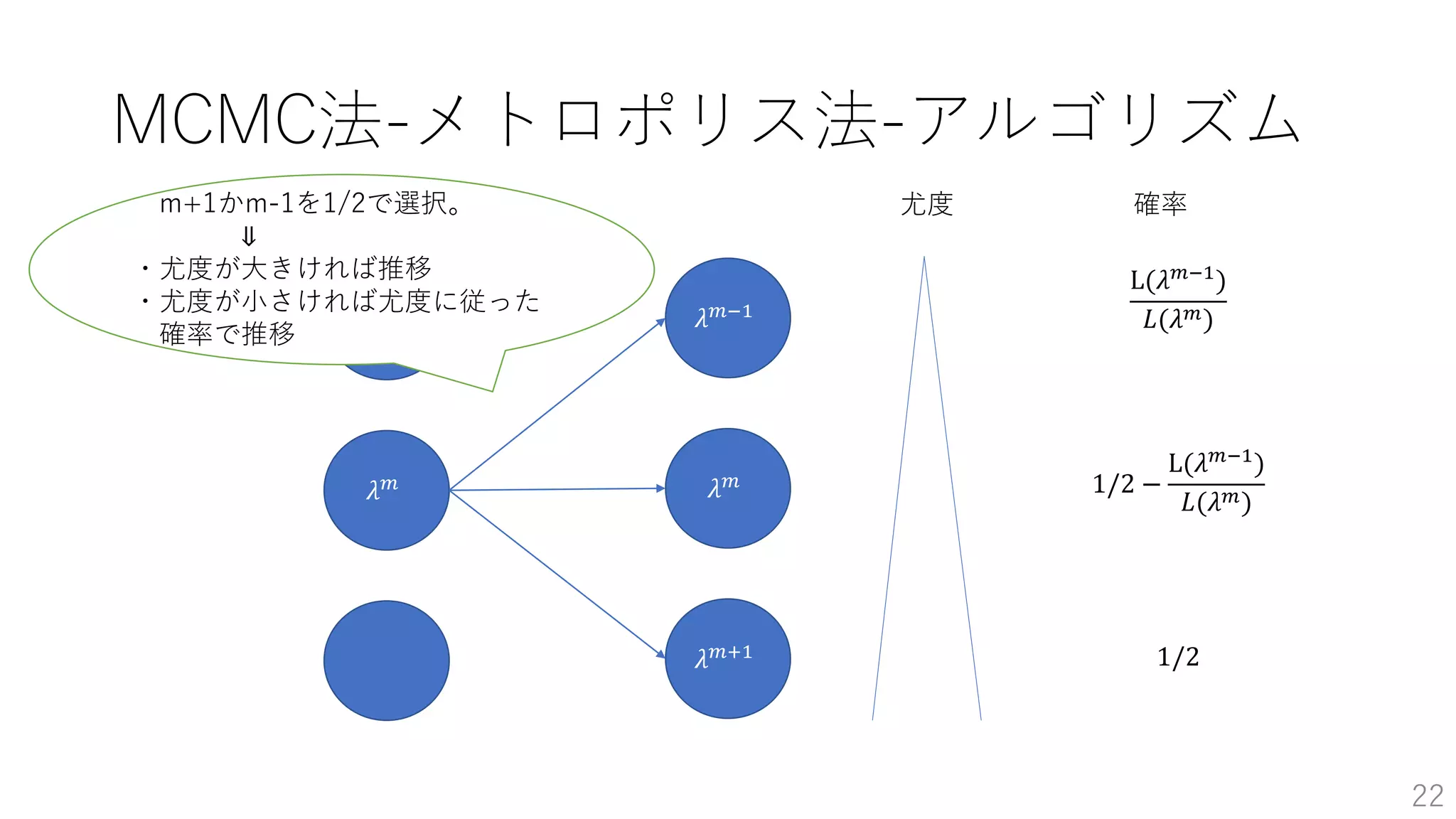
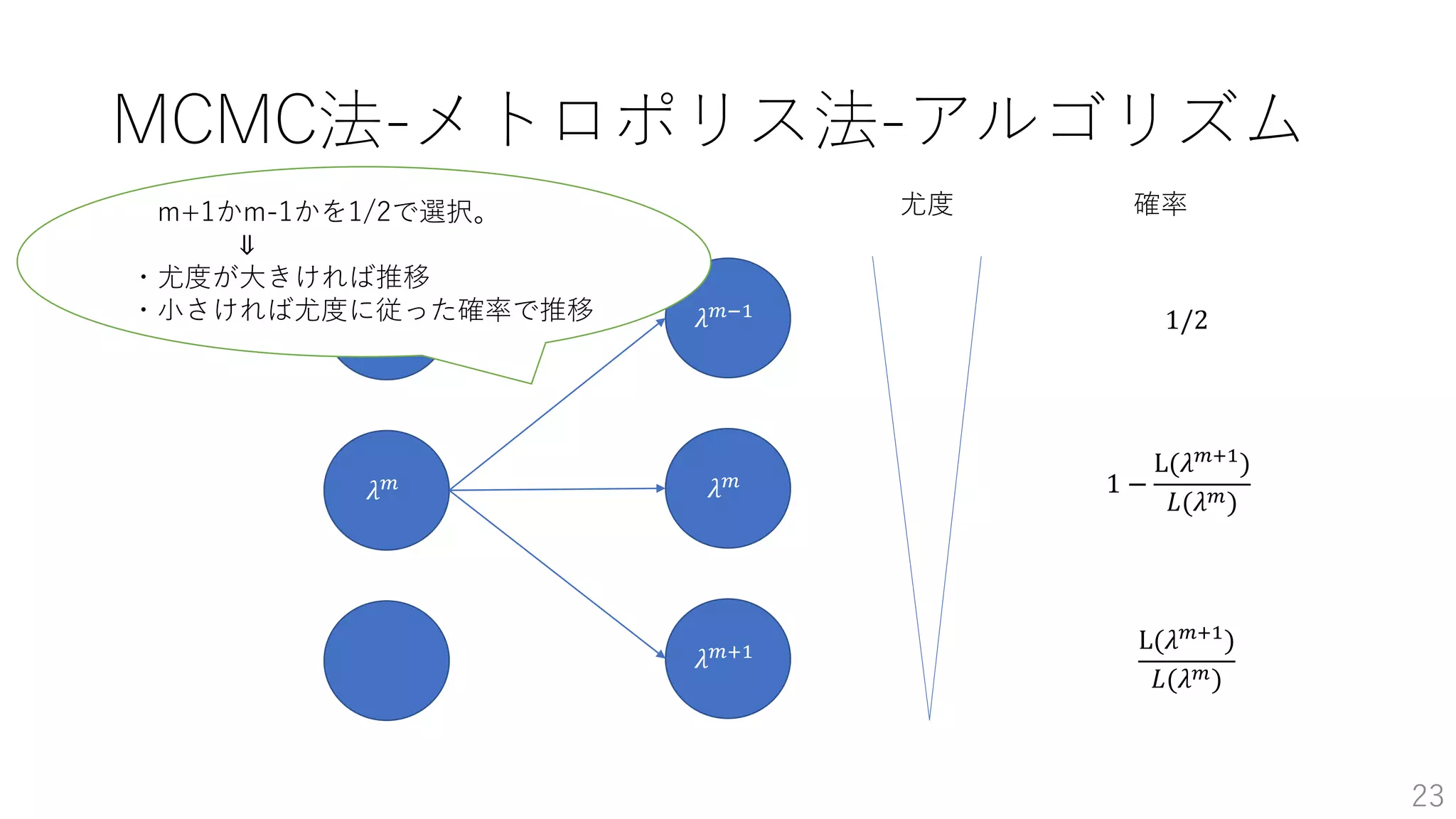
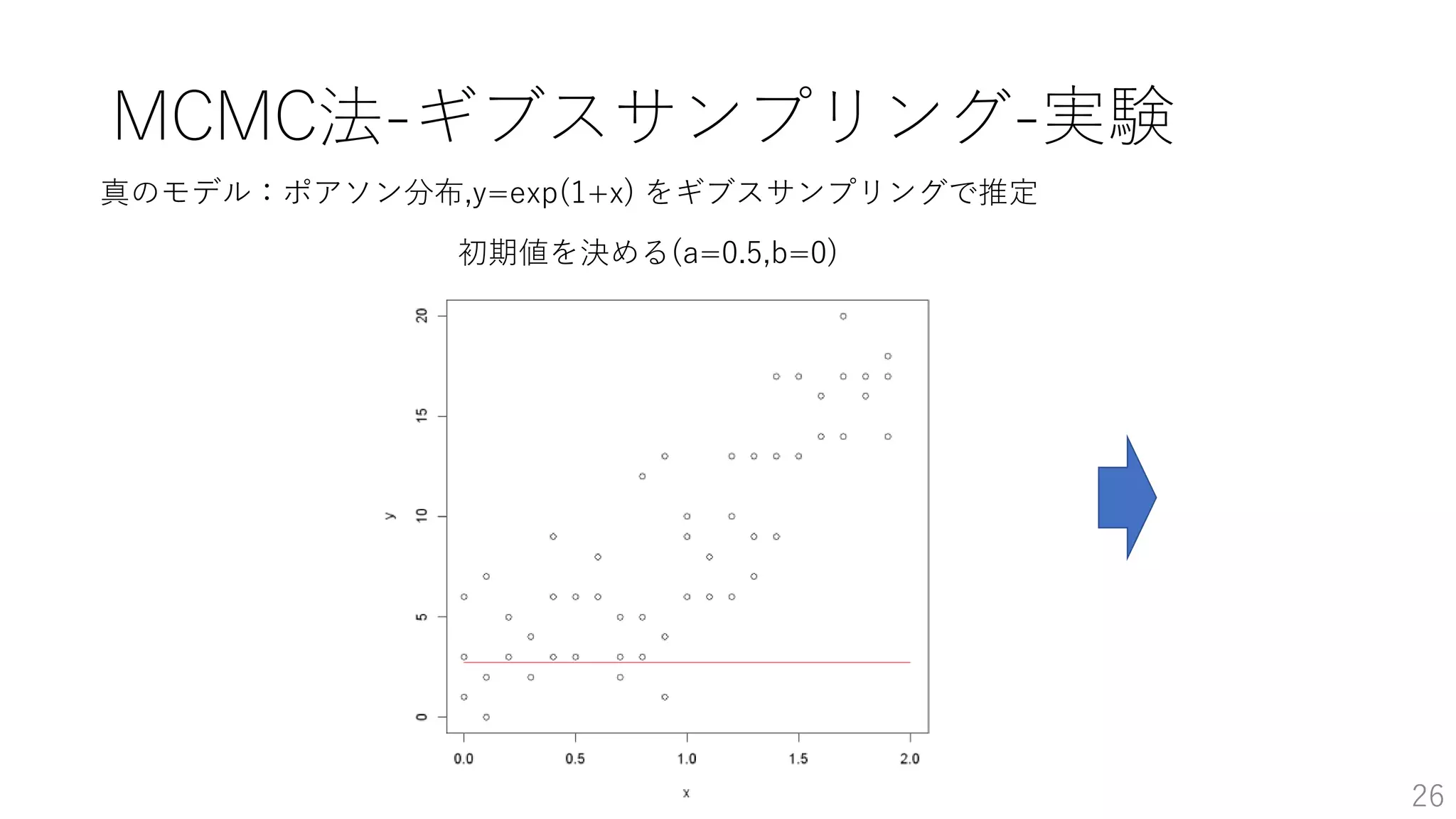
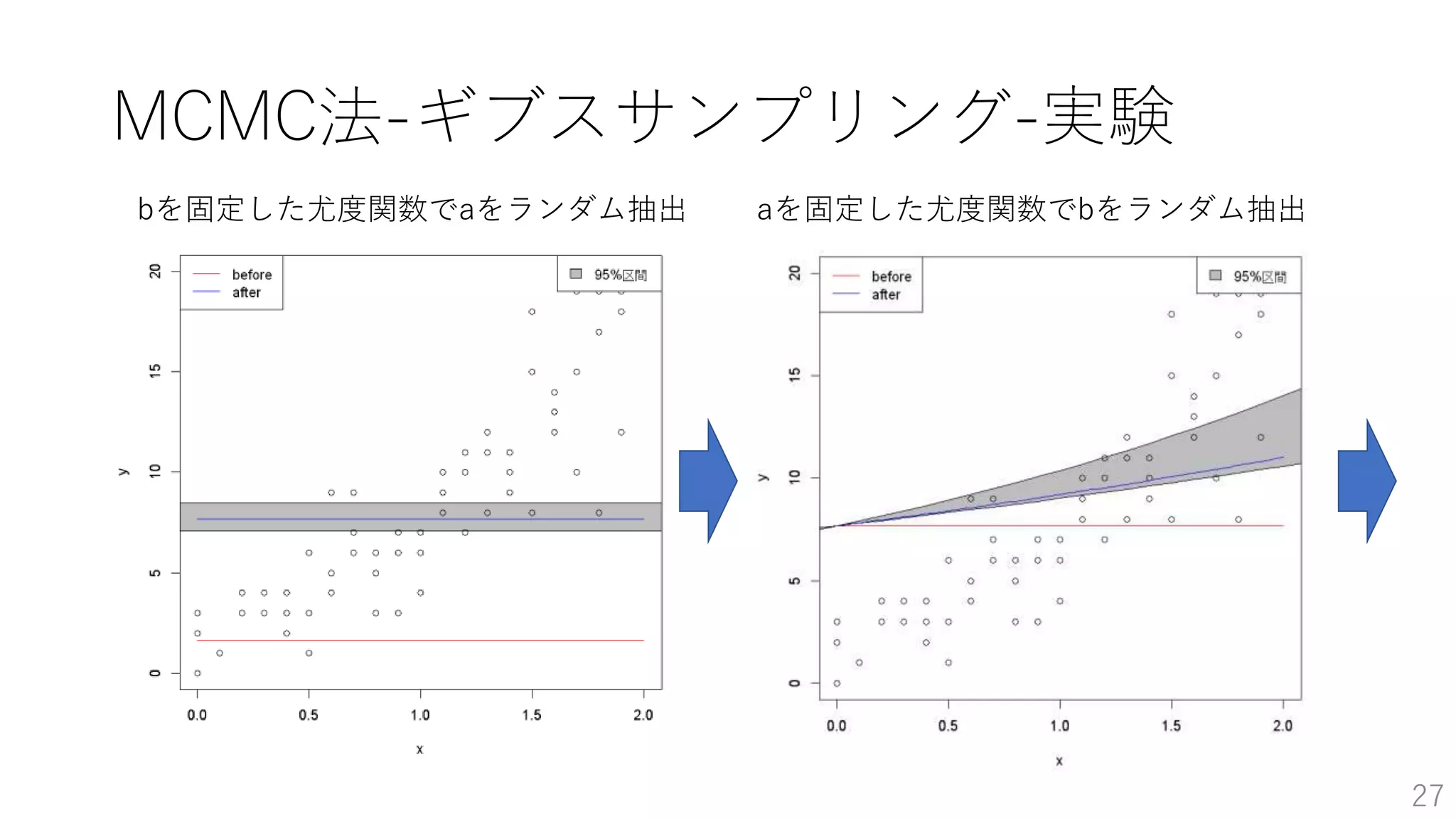
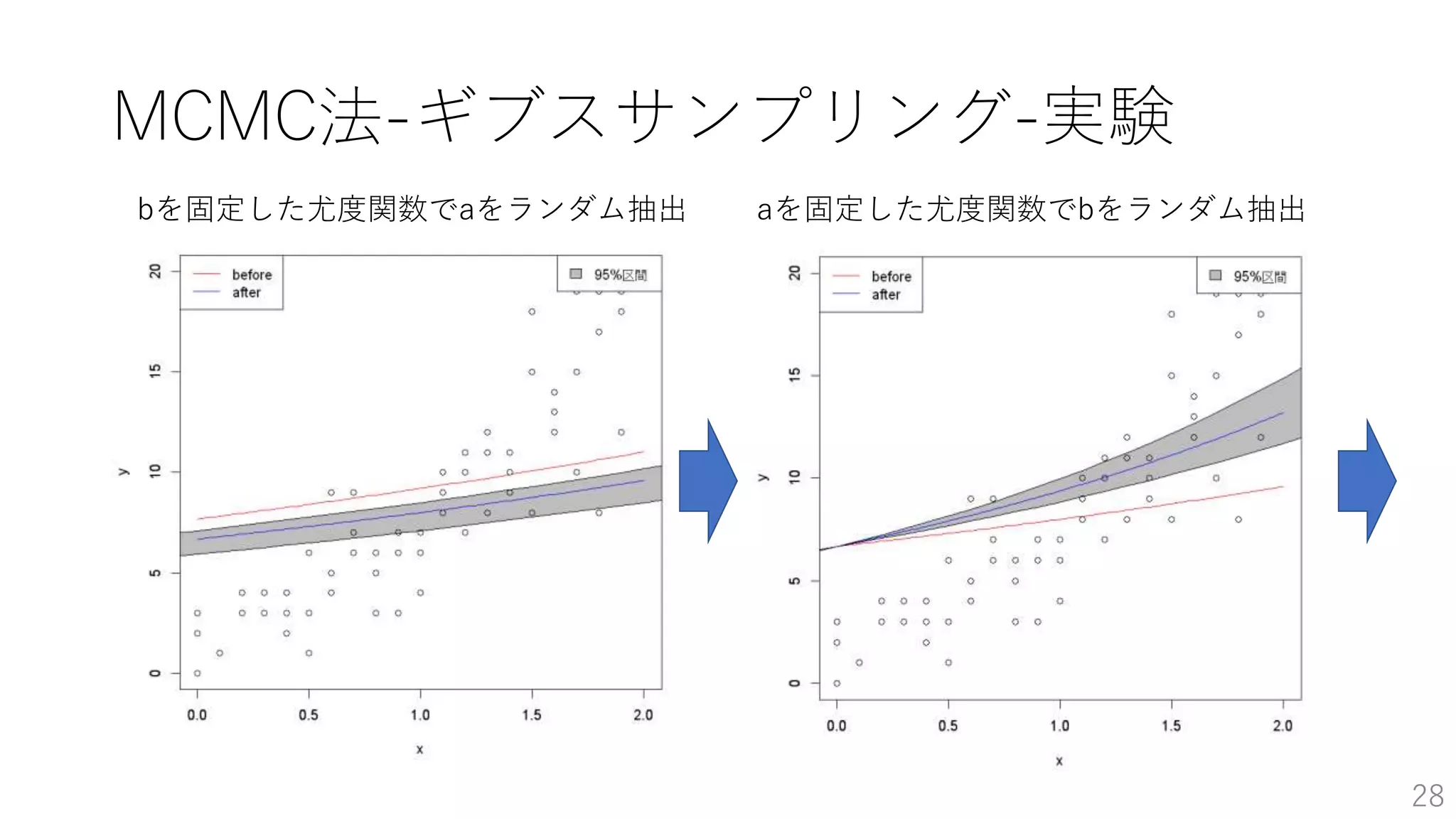
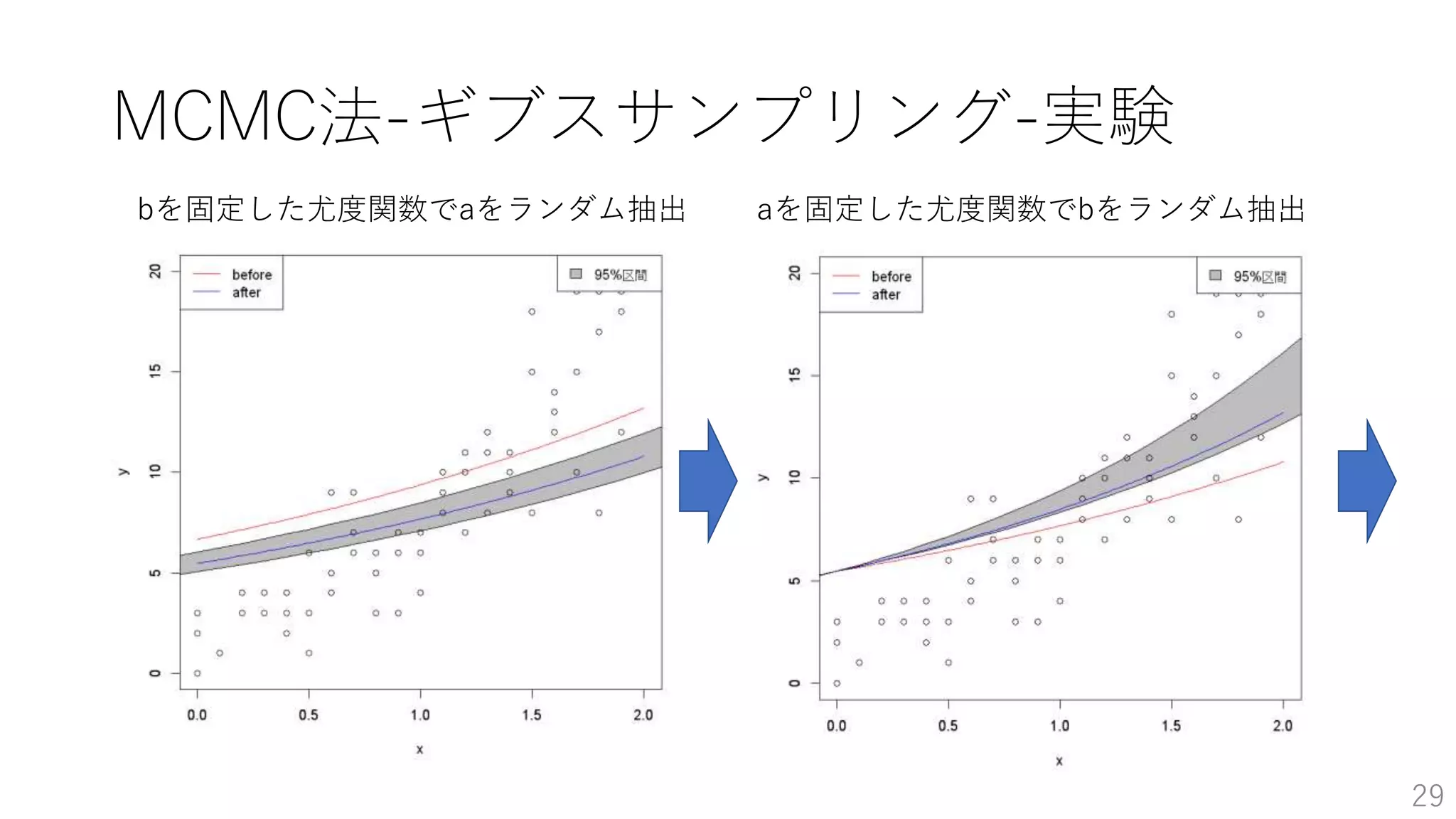
- 2. 目次 • 統計モデル俯瞰図 …p3 •MCMC法 …p4 • マルコフ連鎖 …p5~ • マルコフ連鎖-定常分布 …p7~ • モンテカルロ法 …p10 • 統計モデルのベイズ化 …p11~ • 統計モデルのベイズ化-事後分布 …p17~ • MCMC法-メトロポリス法 …p20 • MCMC法-メトロポリス法-アルゴリズム …p21~ • MCMC法-メトロポリス法-実験 …p24 • MCMC法-ギブスサンプリング …p25 • MCMC法-ギブスサンプリング-実験 …p26~ • MCMC法-まとめ …p32 2
- 3.
- 4. MCMC＝Marcov chain MonteCarlo method マルコフ連鎖モンテカルロ法 • 解析的に特定できない関数の近似曲線を求める方法の一つ。 • マルコフ連鎖とモンテカルロ法を組み合わせたモデル。 • 統計モデルにおいては尤度関数を求め、パラメータの事後分布 とする際に用いる。 具体的な手法の前にまずはそれぞれの概要について。 4
- 5. マルコフ連鎖 • ひとつ前の状態にのみ依存し、一定の確率で状態変化を繰り返 すモデル。確率漸化式であらわされる。 5 n=kn=k-1 n=k+1 𝑎𝑛 = 𝑝𝑎 𝑛−1 + 𝑞𝑏 𝑛−1 + 𝑟𝑐 𝑛−1 𝑏 𝑛 = 𝑝′𝑎 𝑛−1 + 𝑞′𝑏 𝑛−1 + 𝑟′𝑐 𝑛−1 𝑐 𝑛 = 𝑝"𝑎 𝑛−1 + 𝑞"𝑏 𝑛−1 + 𝑟"𝑐 𝑛−1 𝑐 𝑛 𝑎 𝑘−1 𝑎 𝑘+1 𝑏 𝑘𝑏 𝑘−1 𝑏 𝑘+1 𝑎 𝑘 𝑐 𝑘−1 𝑐 𝑘+1
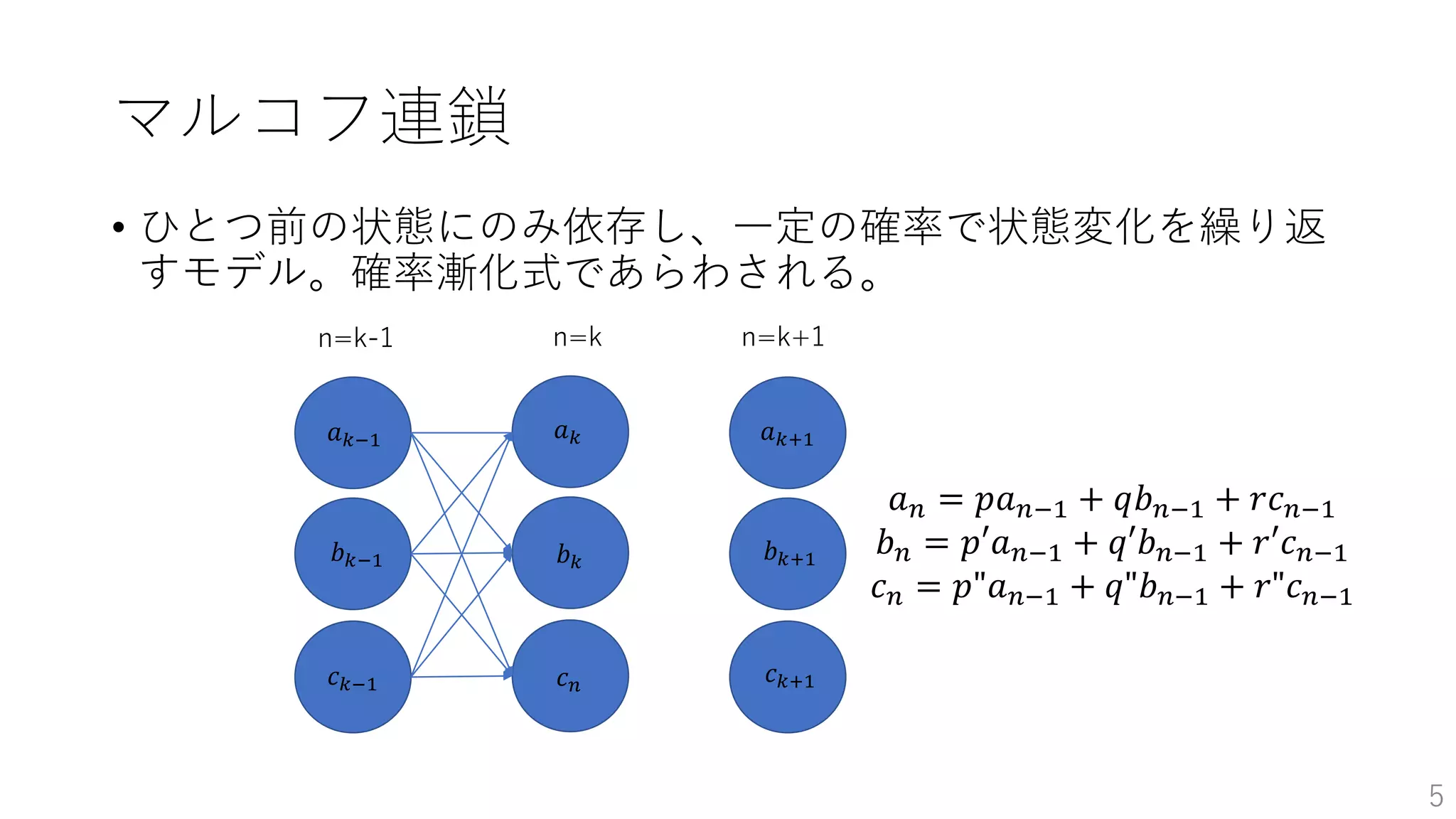
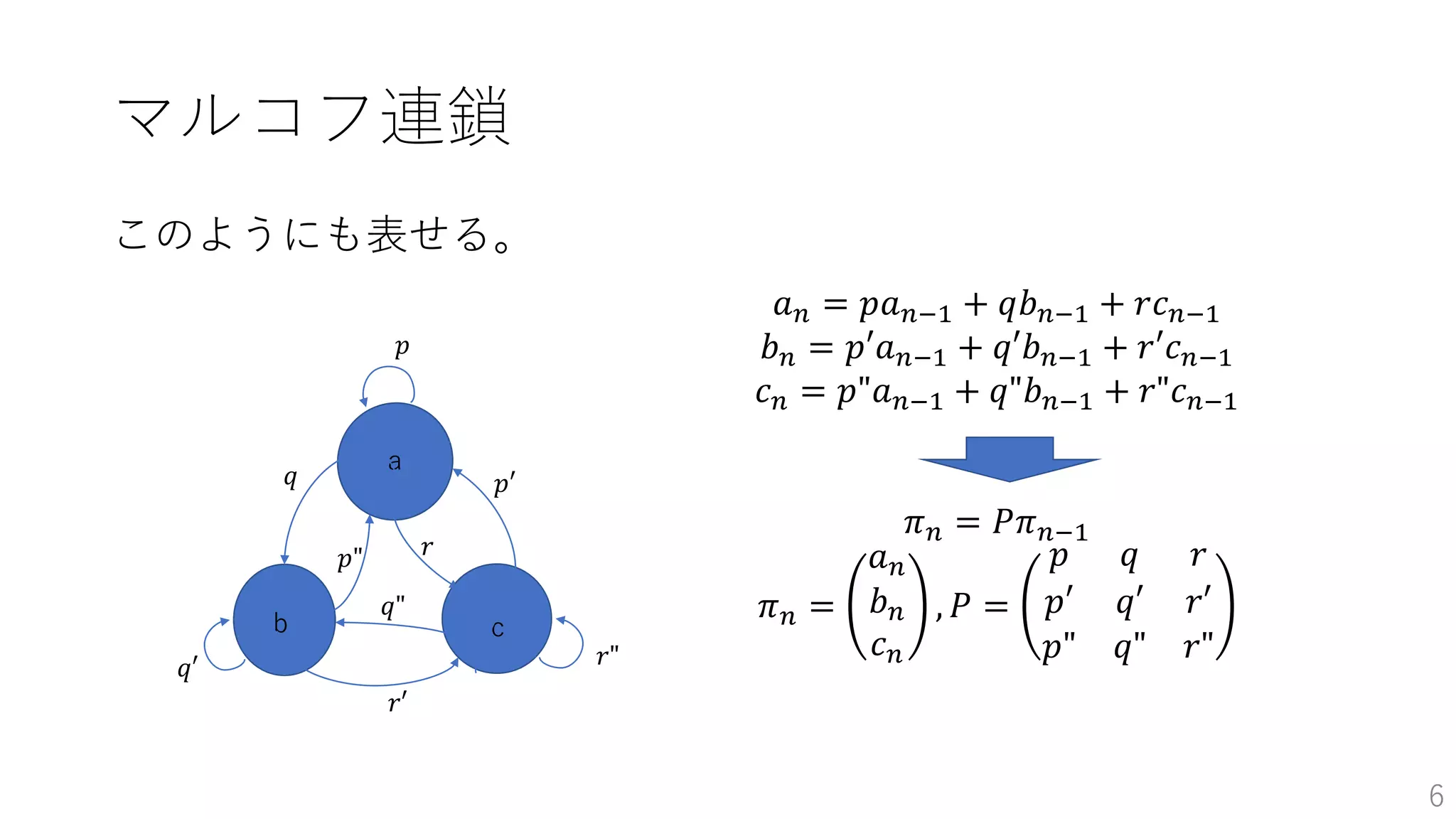
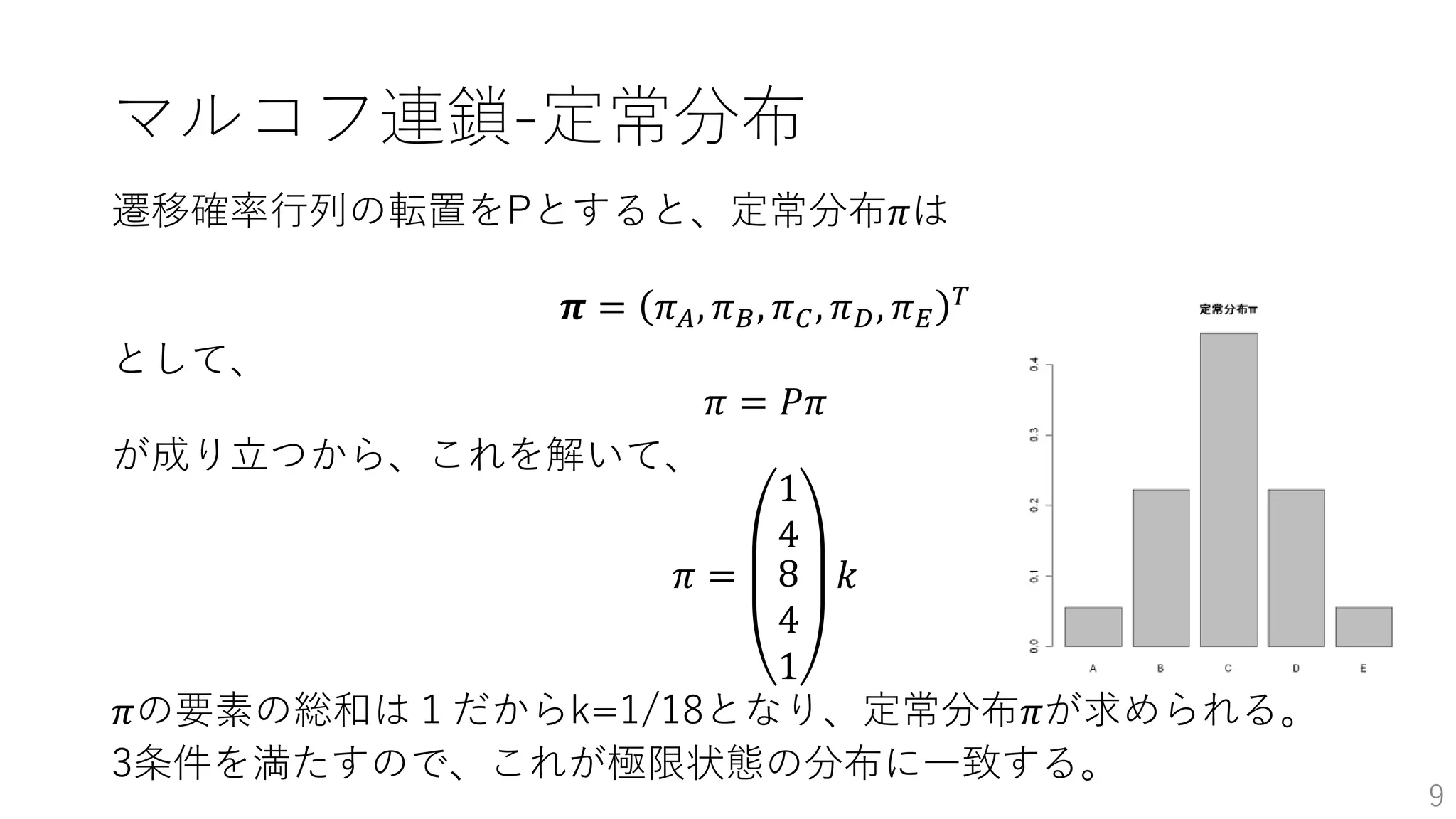
- 6. マルコフ連鎖 このようにも表せる。 6 𝑎 𝑛 =𝑝𝑎 𝑛−1 + 𝑞𝑏 𝑛−1 + 𝑟𝑐 𝑛−1 𝑏 𝑛 = 𝑝′𝑎 𝑛−1 + 𝑞′𝑏 𝑛−1 + 𝑟′𝑐 𝑛−1 𝑐 𝑛 = 𝑝"𝑎 𝑛−1 + 𝑞"𝑏 𝑛−1 + 𝑟"𝑐 𝑛−1 𝜋 𝑛 = 𝑃𝜋 𝑛−1 𝜋 𝑛 = 𝑎 𝑛 𝑏 𝑛 𝑐 𝑛 , 𝑃 = 𝑝 𝑞 𝑟 𝑝′ 𝑞′ 𝑟′ 𝑝" 𝑞" 𝑟" cb a 𝑝 𝑝′ 𝑝" 𝑞 𝑞′ 𝑞" 𝑟 𝑟′ 𝑟"
- 7. マルコフ連鎖-定常分布 定常分布＝一度その状態になると、その状態であり続ける分布 つまり、 𝝅 𝒏 =𝑷𝝅 𝒏 を満たす𝜋 𝑛が定常分布。 ただし、要素の総和は１。 • 全ての点からすべての点に動ける • 周期がない • 定常分布がある この3点が満たされると、極限状態が定常分布に一致する 7 cb a 𝑝 𝑝′ 𝑝" 𝑞 𝑞′ 𝑞" 𝑟 𝑟′ 𝑟"
- 8. マルコフ連鎖-定常分布 例題) 8 A B C D E A B C D E A B C D E A B CD E A 1/2 1/2 0 0 0 B 1/4 1/4 1/2 0 0 C 0 1/4 1/2 1/4 0 D 0 0 1/2 1/4 1/4 E 0 0 0 1/2 1/2 前 後 ・・・ 遷移確率行列
- 9. マルコフ連鎖-定常分布 遷移確率行列の転置をPとすると、定常分布𝜋は 𝝅 = 𝜋𝐴, 𝜋 𝐵, 𝜋 𝐶, 𝜋 𝐷, 𝜋 𝐸 𝑇 として、 𝜋 = 𝑃𝜋 が成り立つから、これを解いて、 𝜋 = 1 4 8 4 1 𝑘 𝜋の要素の総和は１だからk=1/18となり、定常分布𝜋が求められる。 3条件を満たすので、これが極限状態の分布に一致する。 9
- 10. モンテカルロ法 独立な確率分布からランダムな数値を与え、シミュ レーションを行う手法。 土井さんの資料「モンテカルロ法解説資料」参照 (SVN>勉強会>アルゴリズム解説資料) 例) 独立に一様分布に従う 𝑥, 𝑦∈ 0,1 × [0,1]を多数生 成し、𝑥2 + 𝑦2 < 1を満たす個数の割合が円周率の 1/4に近似できる。 10 l = 10000000 x= runif(l) y= runif(l) p = x^2+y^2 pi = 4*sum(p<1)/l print(pi) 3.141686 四角の面積は1 扇型の面積はπ/4 試行回数が多いと近 似がよくなる
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17. 統計モデルのベイズ化-事後分布 17 Q.事後分布はどのように求めるか? A.事後分布は事前分布と尤度関数によって決まる。 𝑝 𝜆 𝑦= 𝑝 𝑦 𝜆 𝑝(𝜆) 𝑝 𝑦 𝜆 𝑝( 𝜆) ∝ 𝑝 𝑦 𝜆 𝑝 𝜆 Q.事前分布はどのように決まるのか? A.無情報事前分布： ベイズ統計学において、事前分布は人の知見や経験を反映さ せるように設定するが、それらの情報がないとき、パラメー タλは(-∞,∞)のどの値も自由に取りうるものとみなす。 事前分布尤度 定数(yへ向かう矢印) 事後分布 (赤の矢印)
- 18. 18 つまり、λの事前分布は(-∞,∞)の一様分布とする。 (十分大きい値kをとって(-k,k)とする。) よって、事前分布は定数をとるから、 𝑝 𝜆 𝑦= 𝑝 𝑦 𝜆 𝑝(𝜆) 𝑝 𝑦 𝜆 𝑝( 𝜆) ∝ 𝑝 𝑦 𝜆 𝑝 𝜆 ∝ 𝑝(𝑦|𝜆) 尤度 となって、事後分布は尤度に比例することがわかる。 事後分布 統計モデルのベイズ化-事後分布
- 19.
- 20.
- 21. MCMC法-メトロポリス法-アルゴリズム 21 簡単のため、まずは１変数でのアルゴリズム パラメータλを適度な範囲でk個の数に離散化して𝜆1, 𝜆2, ⋯, 𝜆 𝑘と し、それらをノードとするマルコフ過程を考える。 1. λの初期値(n=1におけるノード)を選ぶ 2. λを以下の確率で推移させる ・確率𝑝+(𝑚) = 1 2 min 1, 𝐿 𝜆 𝑚+1 𝐿 𝜆 𝑚 で𝑘 = 𝑚 + 1に推移 ・確率𝑝−(𝑚) = 1 2 min 1, 𝐿 𝜆 𝑚−1 𝐿 𝜆 𝑚 で𝑘 = 𝑚 − 1に推移 ・確率𝑝0(𝑚) = 1 − 𝑝+(𝑚) − 𝑝−(𝑚)でk=mに推移 𝜆 𝑘 𝜆3 𝜆2 𝜆1 ⋮ 𝜆 𝑘 𝜆3 𝜆2 𝜆1 ⋮ 𝜆 𝑘 𝜆3 𝜆2 𝜆1 ⋮
- 22. MCMC法-メトロポリス法-アルゴリズム 22 𝜆 𝑚 𝜆𝑚 𝜆 𝑚−1 𝜆 𝑚+1 尤度 確率 1/2 L(𝜆 𝑚−1 ) 𝐿(𝜆 𝑚) 1/2 − L(𝜆 𝑚−1 ) 𝐿(𝜆 𝑚) m+1かm-1を1/2で選択。 ⇓ ・尤度が大きければ推移 ・尤度が小さければ尤度に従った 確率で推移
- 23. MCMC法-メトロポリス法-アルゴリズム 23 𝜆 𝑚 𝜆𝑚 𝜆 𝑚−1 𝜆 𝑚+1 尤度 確率 1/2 L(𝜆 𝑚+1) 𝐿(𝜆 𝑚) 1 − L(𝜆 𝑚+1 ) 𝐿(𝜆 𝑚) m+1かm-1かを1/2で選択。 ⇓ ・尤度が大きければ推移 ・小さければ尤度に従った確率で推移
- 24. 24 𝐿 𝜆 ~𝑁(0,1)としてメトロポリス法を実装し、実行した結果が以下 MCMC法-メトロポリス法-実験 λ 試行回数n確率 平均 E[λ]：-0.097 分散Var[λ]：1.016
- 25. MCMC法-ギブスサンプリング • 一般化線形モデルで回帰を行う際は多変数になるが、多変数だとこのままでは推定できない • そこで用いるのがギブスサンプリング 1.実現値yとパラメータβからなる尤度関数L(𝛽1,𝛽2, ⋯ 𝛽 𝑛)が得られる。 2.初期値𝛽 = (𝛽1 𝛽2 ⋯ 𝛽 𝑛)を決める。 3-1. 𝛽1以外を初期値に固定した尤度関数を𝛽1の確率分布として、それに従う𝛽1 ′ を新たにランダム発生させる。 3-2. 𝛽2以外を𝛽1 ′ , 𝛽3, ⋯ 𝛽 𝑛に固定した関数を𝛽2の確率分布として、それに従う𝛽2 ′ を新たにランダム発生させる。 ⋮ 3-n. 𝛽 𝑛以外を𝛽1 ′ , 𝛽2 ′ , ⋯ 𝛽 𝑛−1 ′ に固定した関数を𝛽 𝑛の確率分布として、それに従う𝛽 𝑛 ′ を新たにランダム発生させる。 4. 3の操作を十分な回数繰り返す。 25
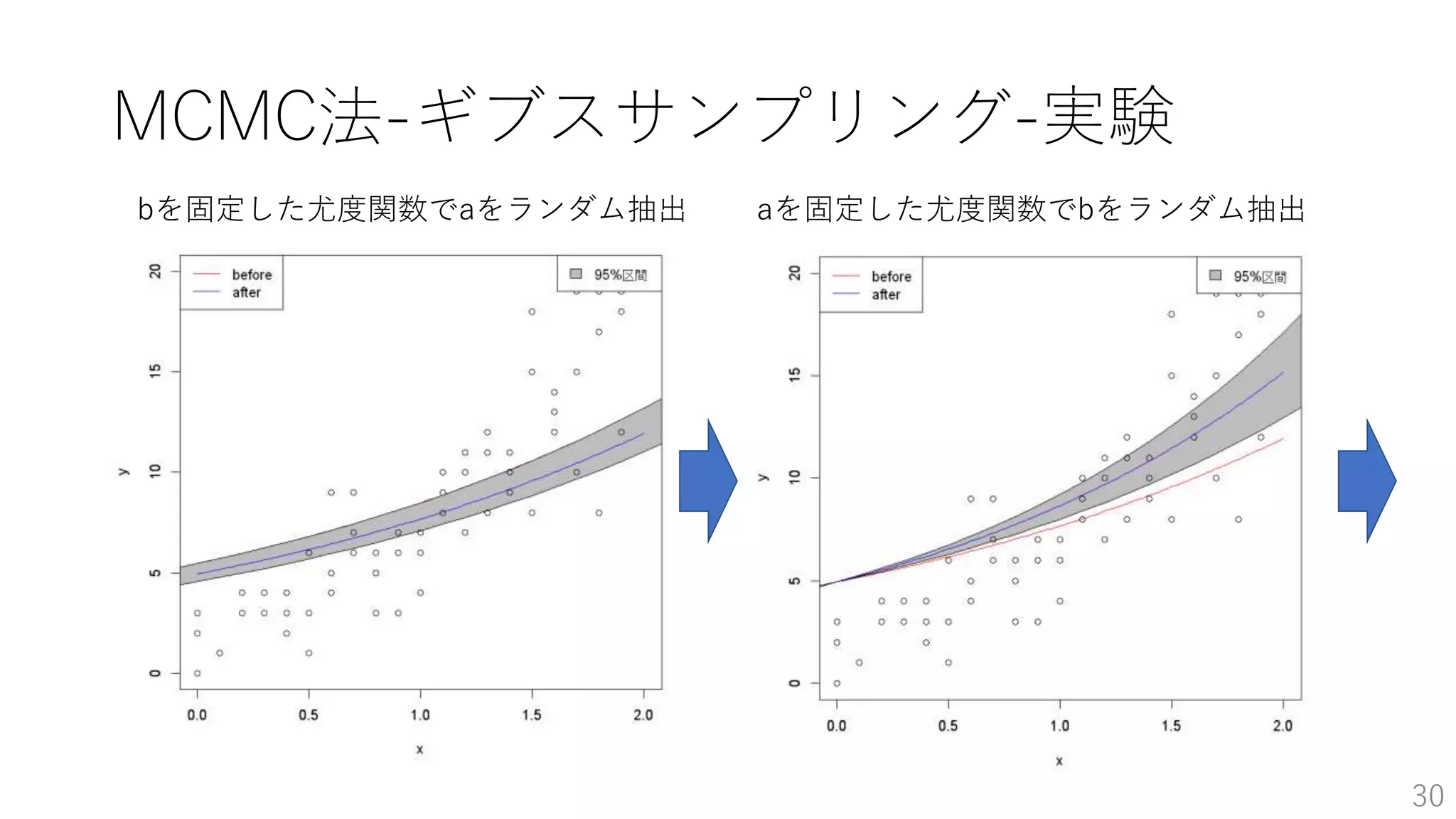
- 26.
- 27.
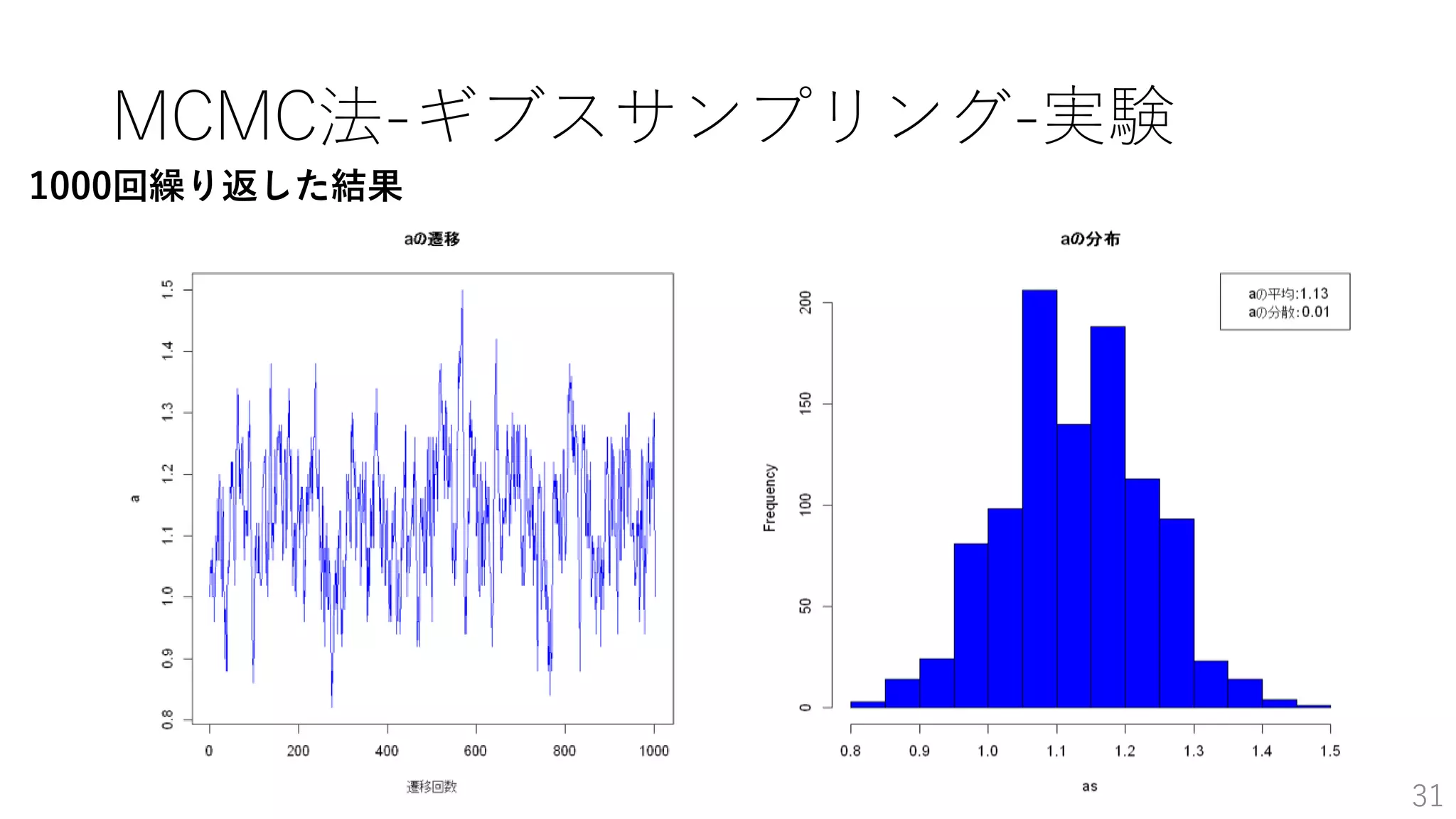
- 28.
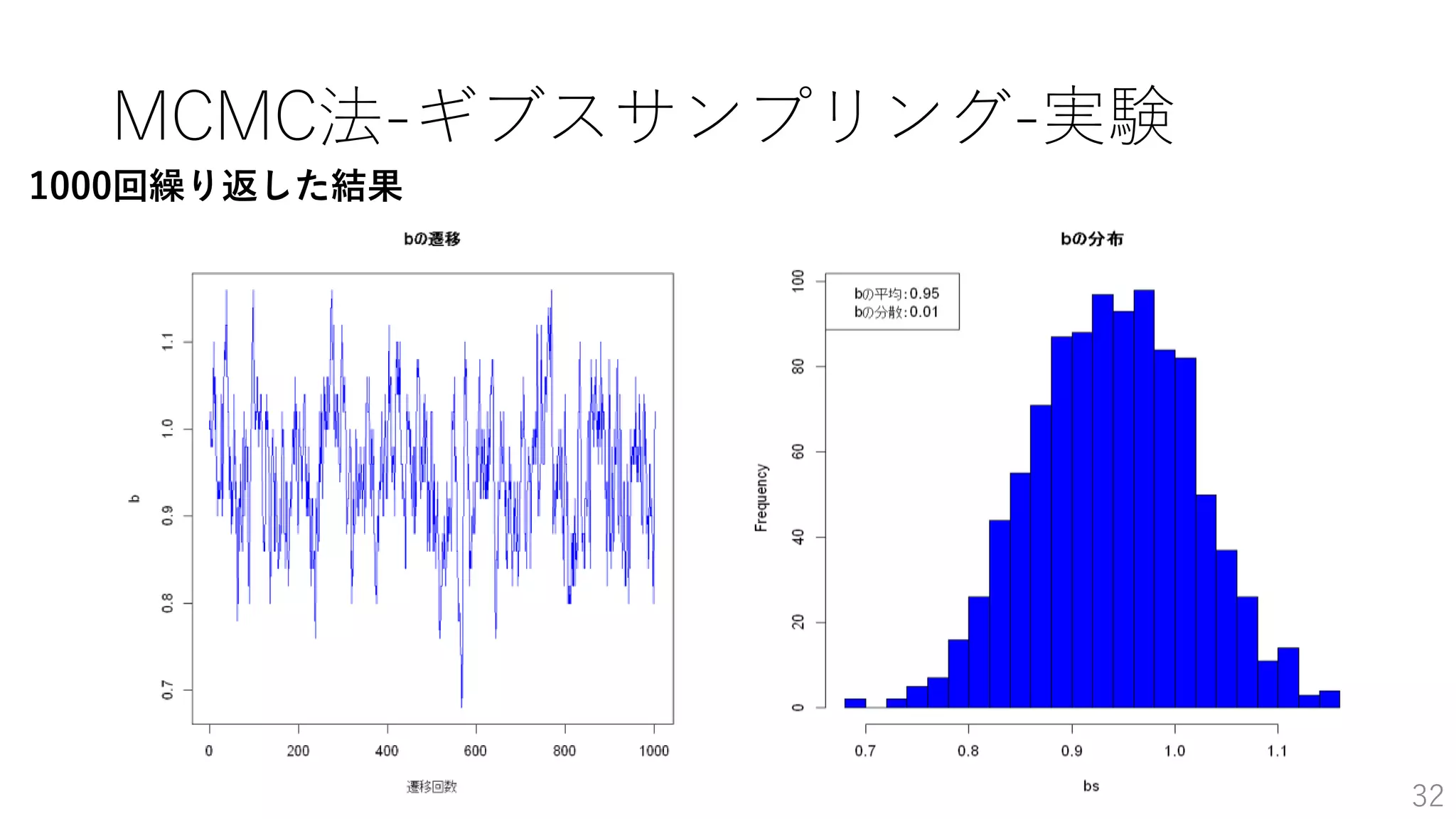
- 29.
- 30.
- 31.
- 32.
- 33.
- 34. 参考文献 データ解析のための統計モデリング入門: 一般化線形モデル・階 層ベイズモデル・MCMC • 著者:久保拓弥 • 出版社: 岩波書店, シリーズ「確率と情報の科学」 • 編集: 甘利俊一，麻生英樹，伊庭幸人 34