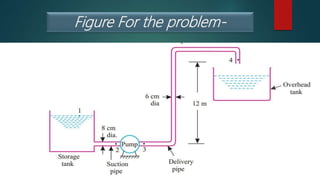
The document presents a fluid dynamics problem involving a pump drawing a solution through pipes with specific parameters. It calculates the pump's power rating and pressure developed using Bernoulli's and continuity equations. Key values include the pump efficiency at 65% and friction losses of 5.5 m.

1. -
WELCOME TO OUR PRESENTATION
PRESENTED BY GROUP G
Mohammad Naimul
Hossain
200212046

2. Solving A problem
of Fluid Dynamics

3. Figure For the problem-

4. Detaile of figure
Above drawn figure showing that-
A pump drawing a solution (specific gravity =1.8) from a
storage tank through an 8 cm steel pipe in which the flow
velocity is 0.9 m/s. The pump discharges through a 6 cm steel
pipe to an overhead tank, the end of discharge is 12 m above
the level of the solution in the feed tank. If the friction losses
in the entire piping system are 5.5 m and pump efficiency is 65
%

5. What we determine ?
POWER RATING OF THE PUMP.
PRESSURE DEVELOPED BY THE PUMP .

6. Lets Solve the problem!
Given:
 d2 = 8 cm or 0.08 m;
 d3 = 6 cm or 0.06 m;
 V2 = 0.9 m/s,
 ηpump = 65%

7. Necessary Equation
 Bernoulli’s Equation
 Continuity Equation
 Power Rating Equation

8. Bernoulli’s Equation
“In an ideal incompressible fluid when the flow is
steady and continuous, the sum of pressure energy,
kinetic energy and potential (or datum) energy is
constant along a stream line.”

9. Bernoulli’s Equation
Mathematically-
𝒑
𝒘
+
𝒗𝟐
𝟐𝒈
+z = Constant Where-
𝒑
𝒘
=Pressure Energy,
𝒗𝟐
𝟐𝒈
= Kinetic Energy, And
z= Datumn or (Elevation) Energy

10. Continuity Equation

11. Power Rating Equation

12. Power rating Determination
From the Continuity equation we know,
𝑨𝟐𝒗𝟐=𝑨𝟑𝒗𝟑
Or , 𝒗𝟑= (𝒗𝟒)=
𝑨𝟐𝒗𝟐
𝑨𝟑
=
𝝅
𝟒
𝟎.𝟎𝟖 𝟐𝑿𝟎.𝟗
𝝅
𝟒
𝟎.𝟎𝟔 𝟐
=1.6 𝒎𝟑
/s

13. Power rating Determination
Applying Bernoulli’s equation at point 1 and 4 we get
𝒑𝟏
𝒘
+
𝒗𝟏
𝟐
𝟐𝒈
+𝒛𝟏+ 𝑯𝒑=
𝒑𝟒
𝒘
+
𝒗𝟒
𝟐
𝟐𝒈
+𝒛𝟒+Losses
(Where, HP =Energy added by the pump per unit weight of liquid in
Nm/N or m of the liquid pumped)
or, 0 + 0 + 0 + Hp = 0 +
(1.6)2
2 × 9.81
+ 12 + 5.5

14. Power rating Determination

15. Determining Pressure developed by the pump
Applying Bernoulli's equation between point 2 and 3, we get:
P2
w
+
V2
2
2g
+ Z2 + Hp =
P3
w
+
V3
2
2g
+ Z3
(
𝑃3 − 𝑃2
w
) = (
V2
2
− V3
2
2g
) + Hp
or,
0.9 2
− 1.6 2
2 × 9.81
+ 17.63 = 17.54 m
or, 𝑃3 − 𝑃2 = 17.54 × (9.81 × 1.8)
2