This document discusses soil-structure interaction and foundation vibrations. It begins with an introduction to soil-structure interaction, noting that the response of the soil influences the motion of the structure and vice versa. It then discusses how soil-structure interaction can alter the natural frequency and add damping to a structural system. The document outlines different effects of soil-structure interaction and how it is an important consideration in seismic analysis and design. It also discusses impedance functions, compliance functions, and modeling of machine foundation vibrations.

1. SOIL-STRUCTURE INTERACTION
AND FOUNDATION VIBRATIONS
BY :
AHMAD HALLAK, M.Sc, P.Eng
29/02/2012 1

2. AGENDA
 12:00 – 12:05 Safety Moment
 12:05 – 12:50 Presentation
 12:50 – 1:00 Questions and Answers
29/02/2012 2

3. SOIL STRUCTURE INTERACTION (SSI):
Definition:
The process in which the response of the soil influences the motion of the structure
and the motion of the structure influences the response of the soil is termed as SSI.
In this case neither the structural displacements nor the ground displacements are
independent from each other.
 Traditional Structural Engineering methods disregard SSI effects, which is
acceptable only for Light structures on relatively stiff soil (low rise structures
and simple rigid retaining walls).
 SSI effects become prominent and must be regarded for structures where P-δ
effects play a significant role,structures with massive or deep seated
foundations,slender tall structures and structures supported on a very soft
soils with average shear velocity less than 100 m/s.[Euro Code 8].
 Modern Seismic Design Codes such as Standard Specifications for Concrete
Structures: Seismic Performance Verification JSCE 2005 (Japan Society of Civil
Engineers) highlight that the response analysis should take into account the whole
structural system ( superstructure + foundation + soil ).
29/02/2012 3

4.  SSI Effects
 Alter the Natural Frequency of the Structure :
 Considering soil-structure interaction makes a structure more flexible and thus
increases the natural period of the structure as compared to the corresponding
rigidly supported structure.
 Add Damping :
 Considering the SSI effect increases the effective damping ratio of the system
( Superstructure + Foundation + Soil ).
 Based on these assumptions, SSI reduces the dynamic response of the
structure and improves the safety margins.
 With this assumption, it has traditionally been considered that SSI can
conveniently be neglected for conservative design. In addition, neglecting SSI
tremendously reduces the complication in the analysis of the structures.
 This conservative simplification is valid for certain classes of structures and soil
conditions, such as light structures in relatively stiff soil.
 However SSI can have a detrimental effect on the structural response, and
neglecting SSI in the analysis may lead to unsafe design for both the
superstructure and the foundation .
29/02/2012 4

5. Detrimental effects of SSI
Mylonakis,G and Gazetas,G. (2000a):
 An Increase in the natural period of a structure due to SSI is not always beneficial
as suggested by the simplified design spectrums.
Example :
 Soft Soil Sediments can significantly elongate the period of seismic waves. The
increase in the natural period of a structure (due to SSI) may lead to resonance
with this long period ground vibration.
 The ductility demand can increase significantly with the increase in the natural
period of the structure due to SSI effect. The permanent deformation and failure of
soil may further aggravate the seismic response of the structure.
29/02/2012 5

6.  SSI – Problem Definition
 Soil-structure interaction can be broadly divided into two phenomena:
A. Kinematic interaction.
B. Inertial interaction.
Examples:
- An Embedded Foundation into soil does not follow the free field motion
( Earthquake ground motion causes soil displacement known as free-filed
motion), this instability of the foundation to match the free field motion causes
the kinematic interaction.
- The mass of the super-structure transmits the inertial force to the soil causing
further deformation in the soil, which is termed as inertial interaction .
 At low level of ground shaking, kinematic effect is more dominant causing the
lengthening of period and increase in radiation damping(dissipation of energy
behaves like a damper for the structure even if the soil is considered as elastic
medium without material damping) .
 With the onset of stronger shaking, near-field soil modulus degradation and soil-
pile gapping limit radiation damping, and inertial interaction becomes predominant,
causing excessive displacements and bending strains concentrated near the
ground surface, resulting in pile damage near the ground level .
29/02/2012 6

7. SSI – Problem Definition
Machine Foundation Seismic Excitation
Inertial Interaction Kinematic Interaction
Inertial forces in structure are Stiffer foundation can not conform to
transmitted to flexible soil the distortions of soil
29/02/2012 7

8. FOUNDATIONS VIBRATIONS
 OBJECTIVE :
 Calculation of the vibrations of the massive foundations of heavy machines i.e.
evaluate the movements of the foundation under the action of external loads.
 consequently anticipate the displacements of the machine taking into account the
characteristics of the foundation and the properties of the soil.
 the analyses of dynamic soil-structure interaction have also been long used for
seismic calculations. Whereas in the first case the machine (or the rail or road
traffic) is the source of the vibrations, in the second case the soil is the source .
29/02/2012 8

9.  GENERAL DESCRIPTION OF IMPEDANCE FUNCTIONS
 Impedance functions (Dynamic Stiffness):
The Dynamic Stiffness K is :
K u(t) = P(t)
P(t) : Harmonic external force (or moment).
u(t) : Harmonic response (rotation, displacement)
 P(t) and u(t) are not in phase therefore K is a Complex expression.
 K is the dynamic Stiffness (Impedance) consists of the two Impedances: the
Super-Structure , Foundation and the Soil :
K1 =Superstructures, Foundation.
K2 = Soil (Subgrade).
 The major difference between both is that the superstructure has finite
dimensions ( Mass can be calculated ),the sub-grade extends to infinity
and the impedance of the sub-grade is defined for the interface between
the structure and the soil (Mass-less structure-foundation interface) .
29/02/2012 9

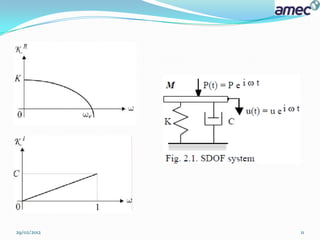
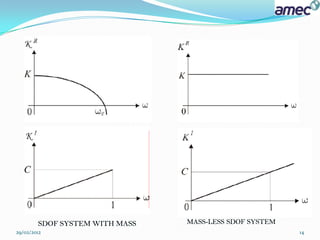
10.  SDOF with mass(Sup-structure & Foundation ):
 M ü +C ù +K u = P(t)
 K1 = KR + iKI
= [(K –Mω2)] +iC ω
 KSTR = - Mω2
 KFDN = K +iC ω.
29/02/2012 10

11. 29/02/2012 11

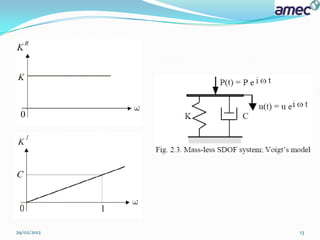
12.  Mass-less SDOF system (SOIL):
 K2 = K+ iC ω .
 KR = K .
 KI = C ω.
 It is important to note that Impedance functions for the soil are always
derived from the massless foundation model.
 K2 : can be obtained by setting M=0 in K1.
 The impedance function of the soil is equal to Foundation impedance
component for SDOF system with mass [ KFDN ].
29/02/2012 12

13. 29/02/2012 13

14. 29/02/2012 14

15.  Compliance Function(Dynamic Flexibility):
 Dynamic Flexibility is also called Transfer Function because it transfers the inputs
(loads) to the output (Displacements).
 U = F * P(t)
 F = K-1
 F (ω) = F R + iF I
 FR=
 FI=
29/02/2012 15

16. IMPORTANT DEFINITIONS
 Natural (Eigen) Frequency( ): only for un-damped systems.
 Natural (Eigen) Frequency( ): only for damped systems.
 Circular Frequency of loading (The excitation Frequency):
 Frequency ratio η =
 Only for systems with Mass.
 =
 Critical Damping:
 Damping Ratio: Not Possible for Massless system.
29/02/2012 16

17.  Vibrations of the mass foundations of heavy machines
 The footing must have two planes of symmetry which are vertical and orthogonal.
 The coordinate system x, y, z coincides with these planes.
 DOF are:
 Vertical displacement along z axis (index “v”).
 Two horizontal displacements (Sliding) along
x axis and along the y axis ( hx and hy )
respectively.
 Rotation (Torsion) around the vertical z-axis
(index “ t ”).
 Two rotations (rocking) around the horizontal
x axis and y axis (index “rx” and “ry” )
respectively.
29/02/2012 17

18. In the case of footings presenting two vertical planes of symmetry the vertical displacements
and torsion movements are uncoupled, whereas the horizontal displacements along x
(respectively -y) and the rocking movements about y-axis (respectively-x) are coupled.
 General Notations for 3-D Footing:
 Mass of Foundation (M).
 Moment of inertia and
 , Applied Forces at C.O.G in directions (x),(z).
 , Applied moments at C.O.G in directions (y),(z).
 , Displacements of C.O.G along (x) and (z) axes.
 , Rotations about (y) and (z) axes.
 , The reactions of displacements at the soil -footing
interface in directions (x), (z).
29/02/2012 18

19.  The reactions of rotations at the soil – footing interface
around the (y),(z) axes and
 Equations of the movements of footing (at C.O.G of
the foundation).
 Two more equations concerning the horizontal
displacement along Y and the rocking about X are
obtained by permuting of indexes X and Y in third and
fourth equations.
29/02/2012 19

20.  General Solutions
 Assume that the external loads are harmonic loads
: could be force or a moment which can be complex.
 The displacement is harmonic and given by the following:
 : Could be rotation or displacement and is generally complex.
Calculate the vertical displacement:
By solving the equation :
After substituting
29/02/2012 20

21. Calculate the Torsion (Rotation around Z axis):
Calculate the Horizontal displacement and rotation about y -axis:
Calculate the amplitudes of the movements and the phases:
29/02/2012 21

22. Applying Complete impedance functions
 Impedance functions in dimensionless forms :
Or :
 Dimensionless circular frequency defined by :
 B : is the half of the width for a rectangular footing or the radius for circular
footing.
 : Shear wave velocity in the Soil.
 The relations between the values with and without dimensions are given in the
following table :
29/02/2012 22

23.  Dimensionless Impedance functions
MODE 2- D 3-D
TRANSLATIONS
ROTATIONS
COUPLED
TRANSL- ROT
29/02/2012 23

24.  Numerical example :
 Objective: illustrate the use of
impedance functions. - G = 45 MPa
 Request : - B=1m
Calculate the movements of two - H= 2m
dimensional structure and loaded by
linear horizontal harmonic force.
 The calculation will be done for one
-
frequency f = 16.71 HZ.
 Data Given:
- M = 6000 kg/m
- a = 1.5 m .
-
-
-
-
-
-
29/02/2012 24

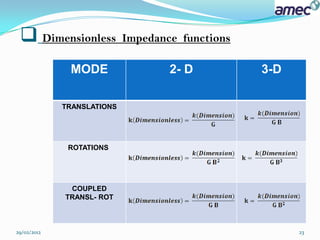
25. Step One :
 Dimensionless Circular frequency is given by the following equation:
= (2*PI*16.71*1)/[SQR(45000/2)] = 0.7
 Comments:
- In 2D structures only three DOF are considered:
1- Vertical displacement along Z-axis.
2- Horizontal displacement along X- axis.
3- Rotation around horizontal Y- axis.
 For our example, we do not have vertical Oscillation of the center of gravity,
therefore the following Displacement functions developed by HUH (1986) [ for strip
foundation without embedment resting on horizontal layer, , ,
H/B=2 ] will not include the vertical displacement functions.
 For foundations that are not embedded, the rotation around Y-axis and the
translation along X-axis are uncoupled. In General Cases these two modes are
always coupled.
29/02/2012 25

26. 29/02/2012 26

27. Step Two :
 Unloaded soil layer with limited thickness (H) has a circular frequency given by the
following :
 In dimensionless form :
 Based on the displacement functions figure ( HUH 1986) we calculate :
 To calculate the horizontal displacement and the rotation around Y-axis we need to
calculate the impedance functions. To transform the displacement functions to
impedance functions we apply the following relations:
29/02/2012 27

28.  The values above represent the dimensionless impedances.
29/02/2012 28

29. Step Three :
 Calculating the dimensional values of the components of the impedance functions by
applying the relations included in the table mentioned above :
 Since the load is not applied at the center of the gravity (G), we have to transfer the load
to the center of gravity (G) and adding a rocking moment:
29/02/2012 29

30. Step Four:
 Calculate , ,
 The term is equal to zero for not embedded
foundation. The numerical values of these terms are :
29/02/2012 30

31. Step Five :
 Calculate the horizontal displacement along X-axis and the rotation around Y-axis:
 Calculate the amplitudes of the movements and the phases :
29/02/2012 31

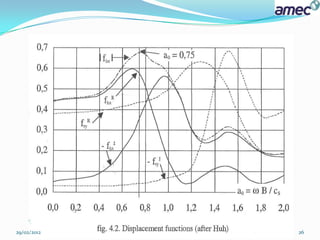
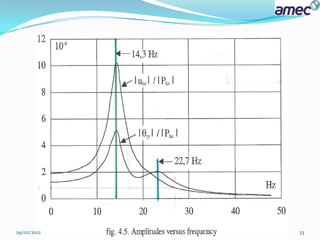
32.  The complete curves are given on the following figures. From these curves we find
that the maximum amplitudes of the displacement and the rotation are obtained for
14.3 HZ [ first mode ].
 the natural (Eigen) frequency of the soil layer without footing which is 18.7 HZ :
The dynamic effect of the soil structure interaction is clear.
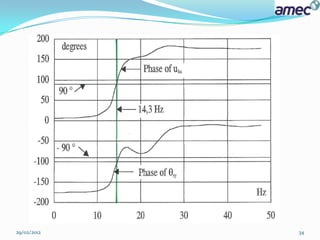
 From the second figure we see that the phases are close to (+/-)90 degrees at the
first maximum of the amplitude.
29/02/2012 32

33. 29/02/2012 33

34. 29/02/2012 34

35.  Questions & Answers
29/02/2012 35