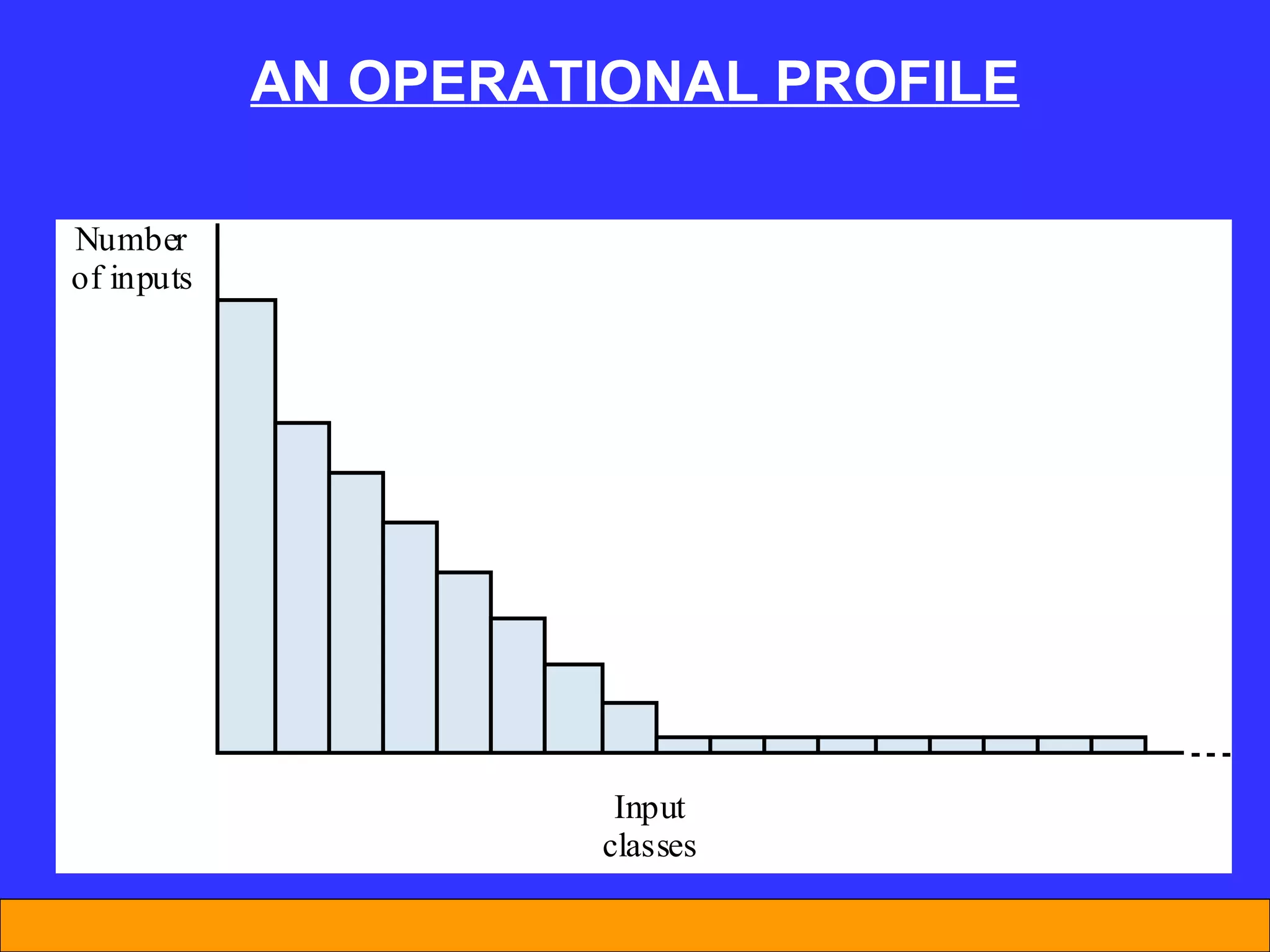
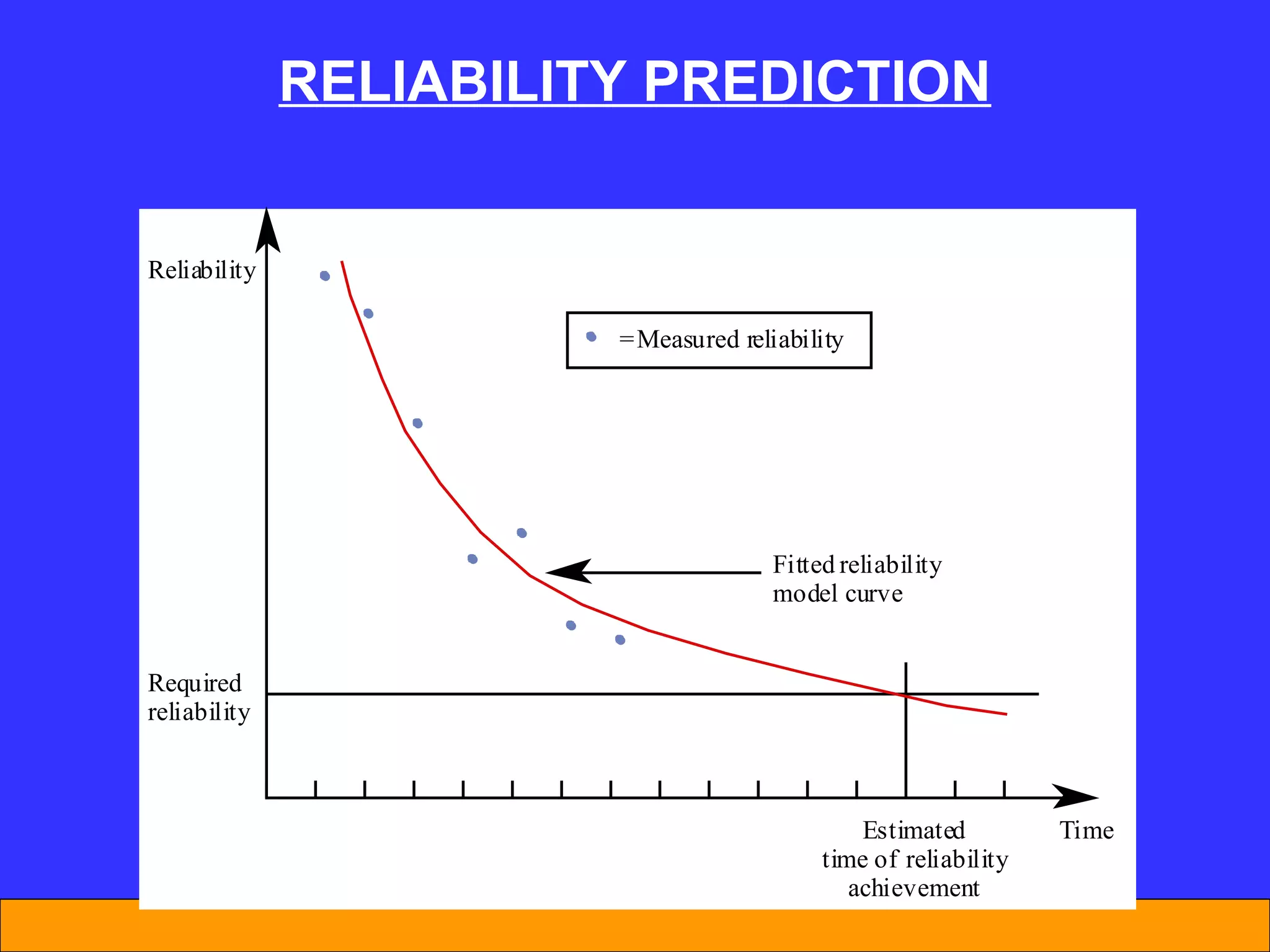
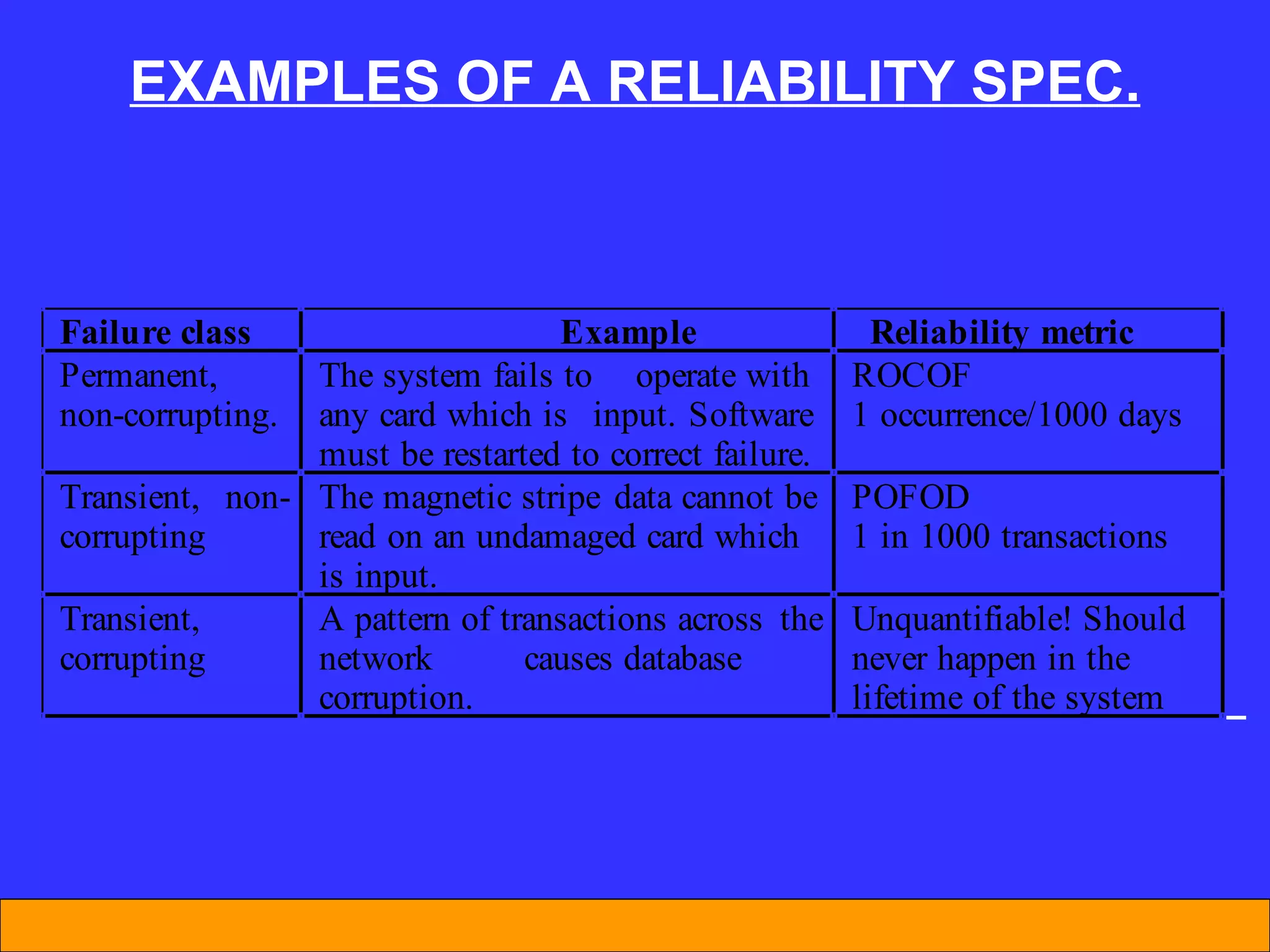
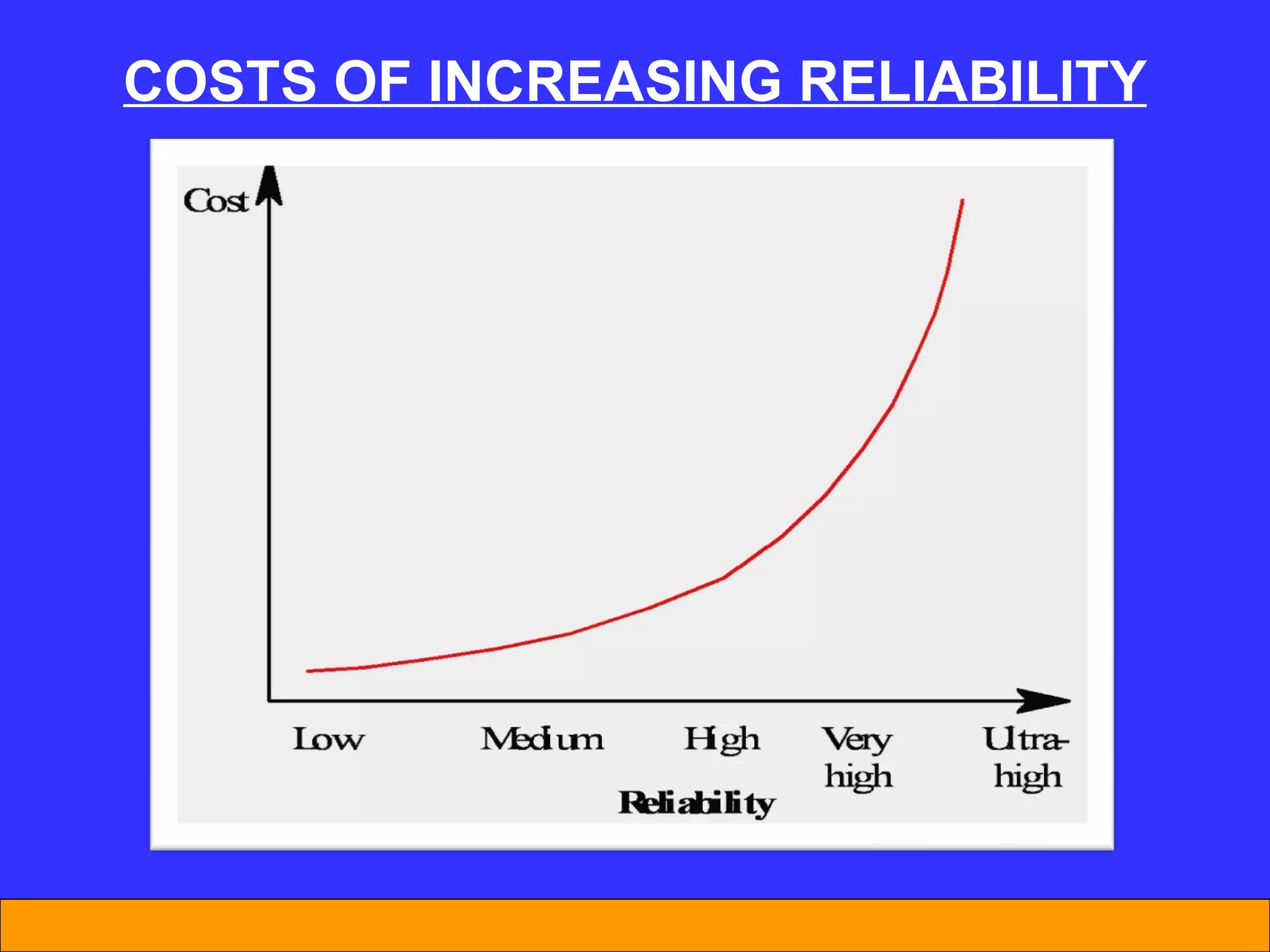
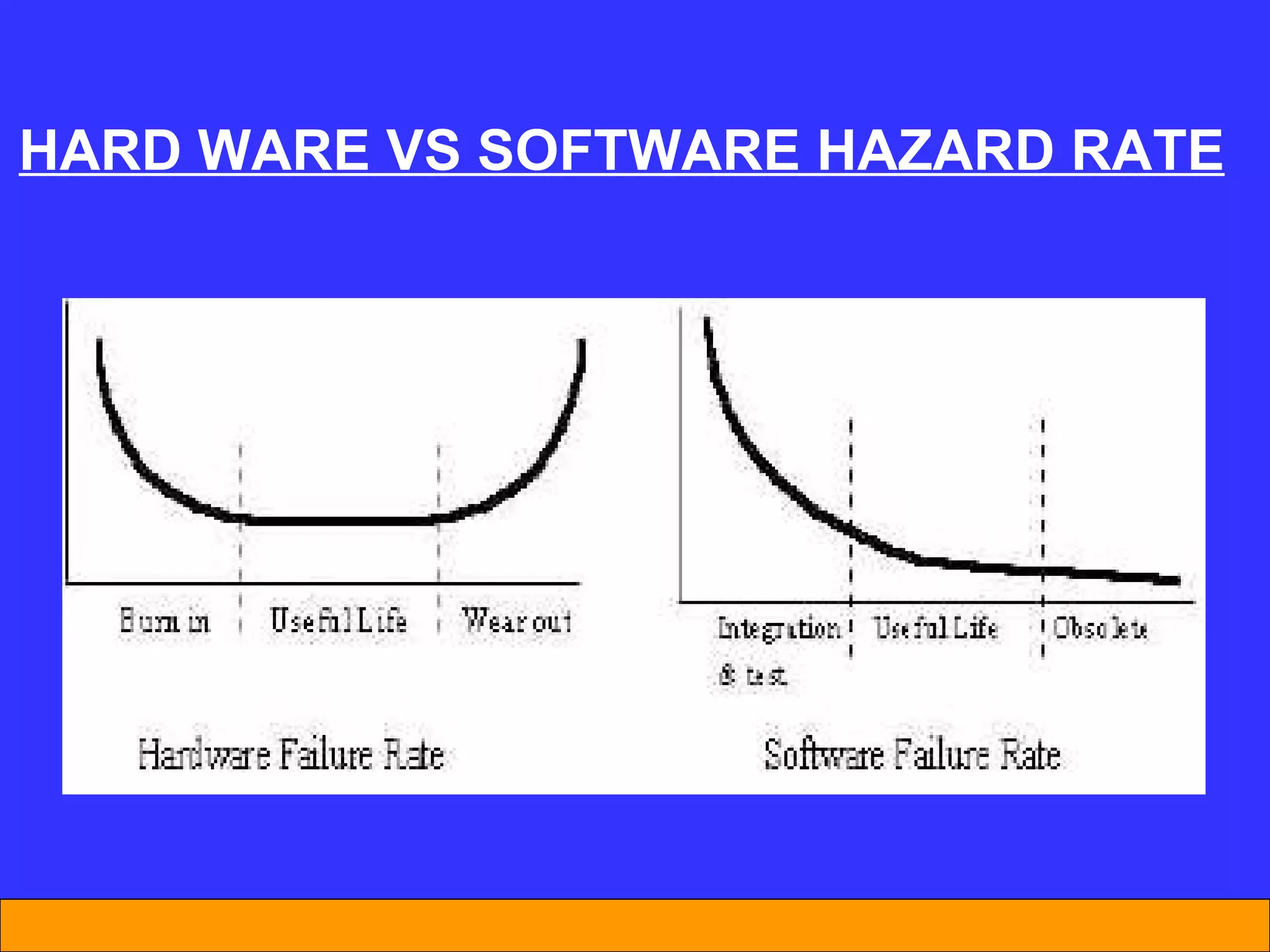
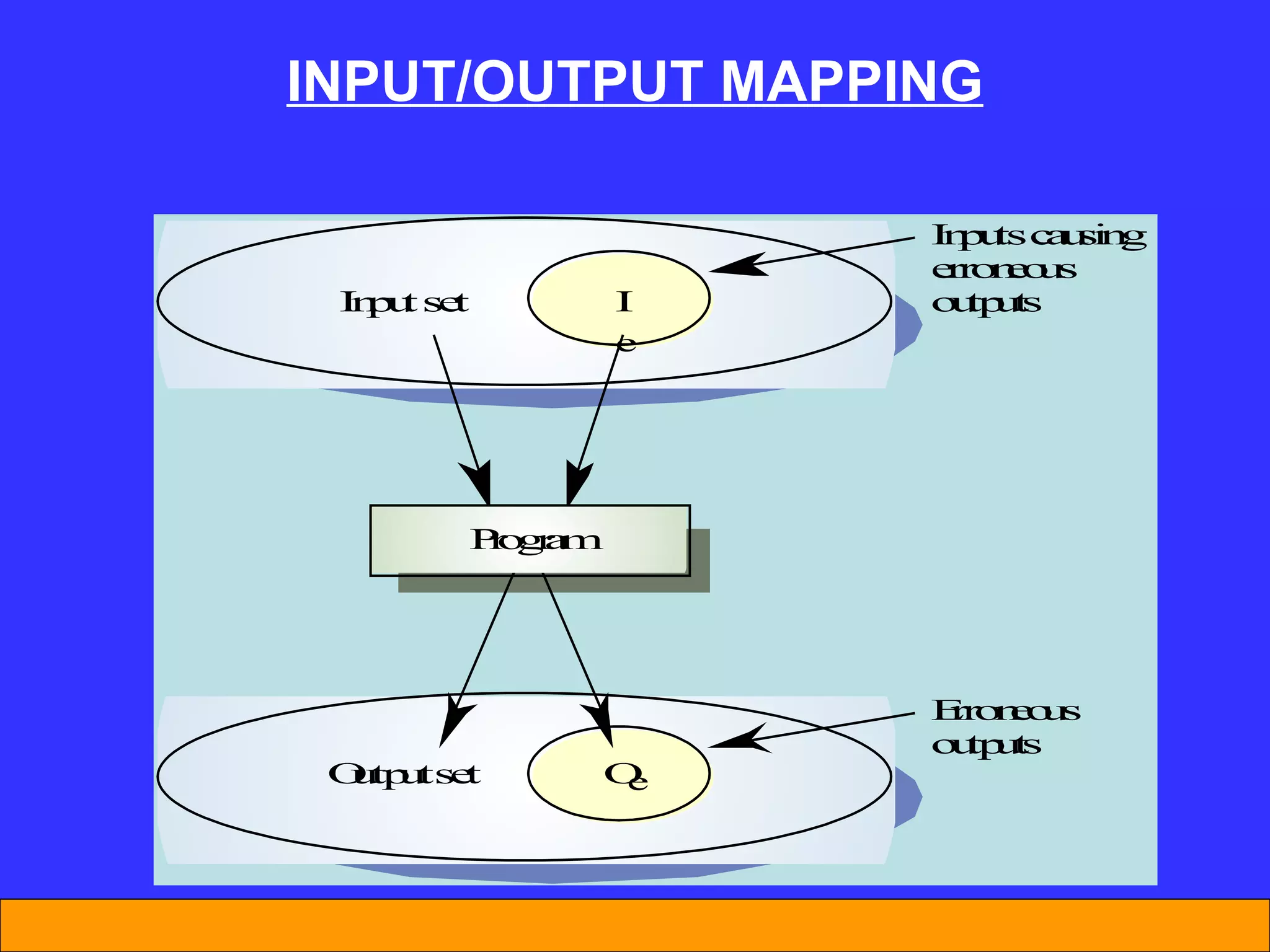
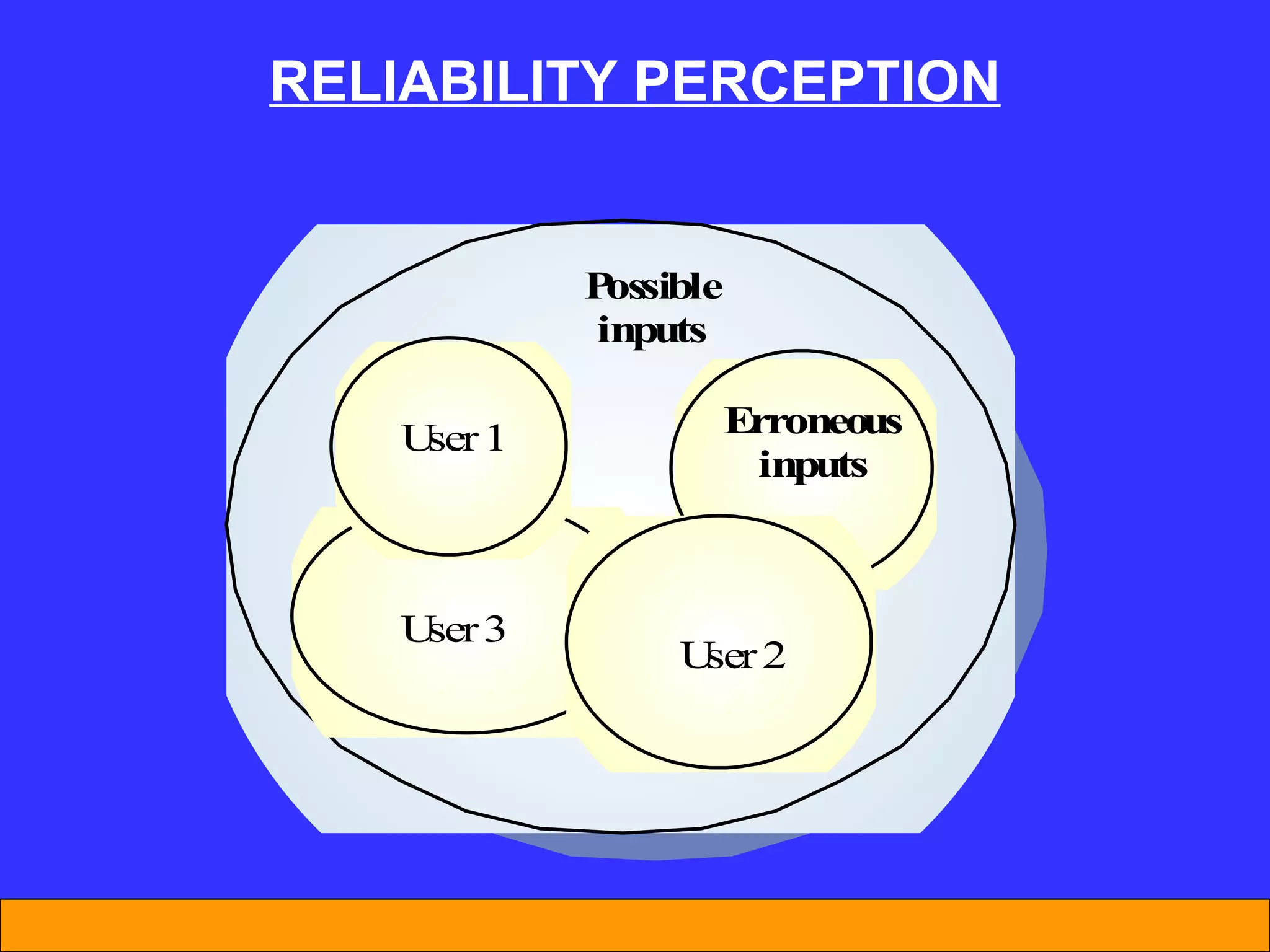
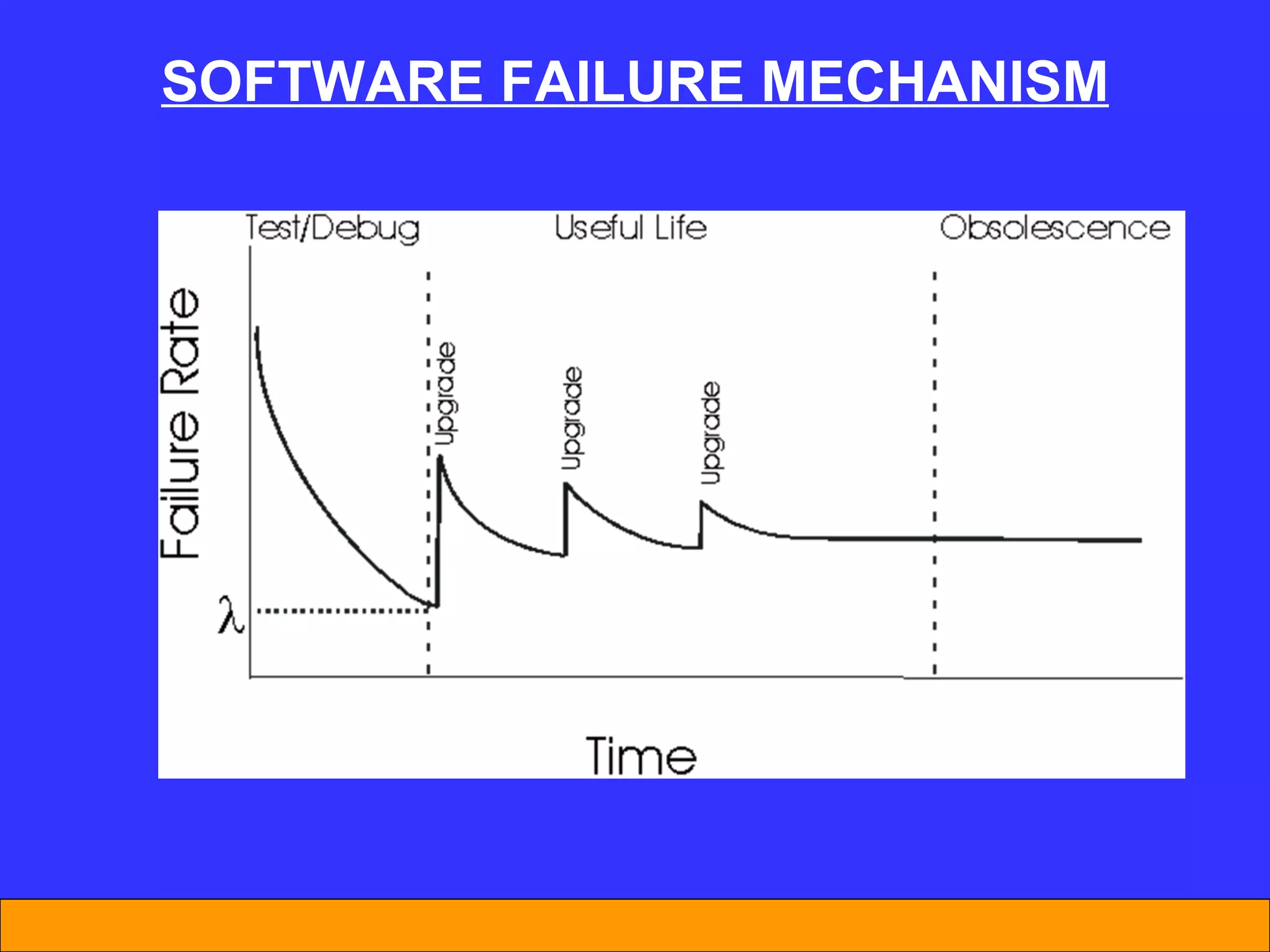
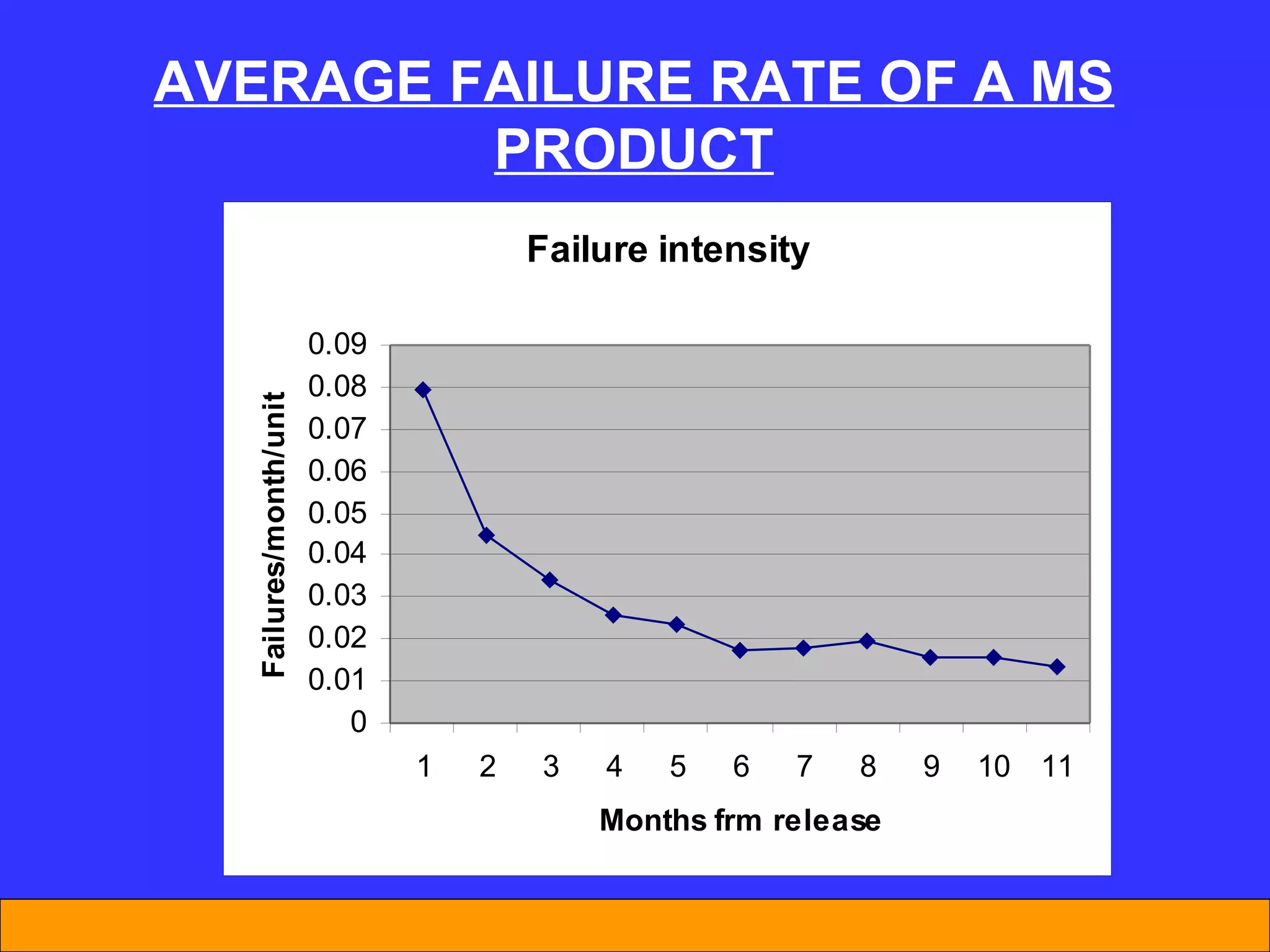
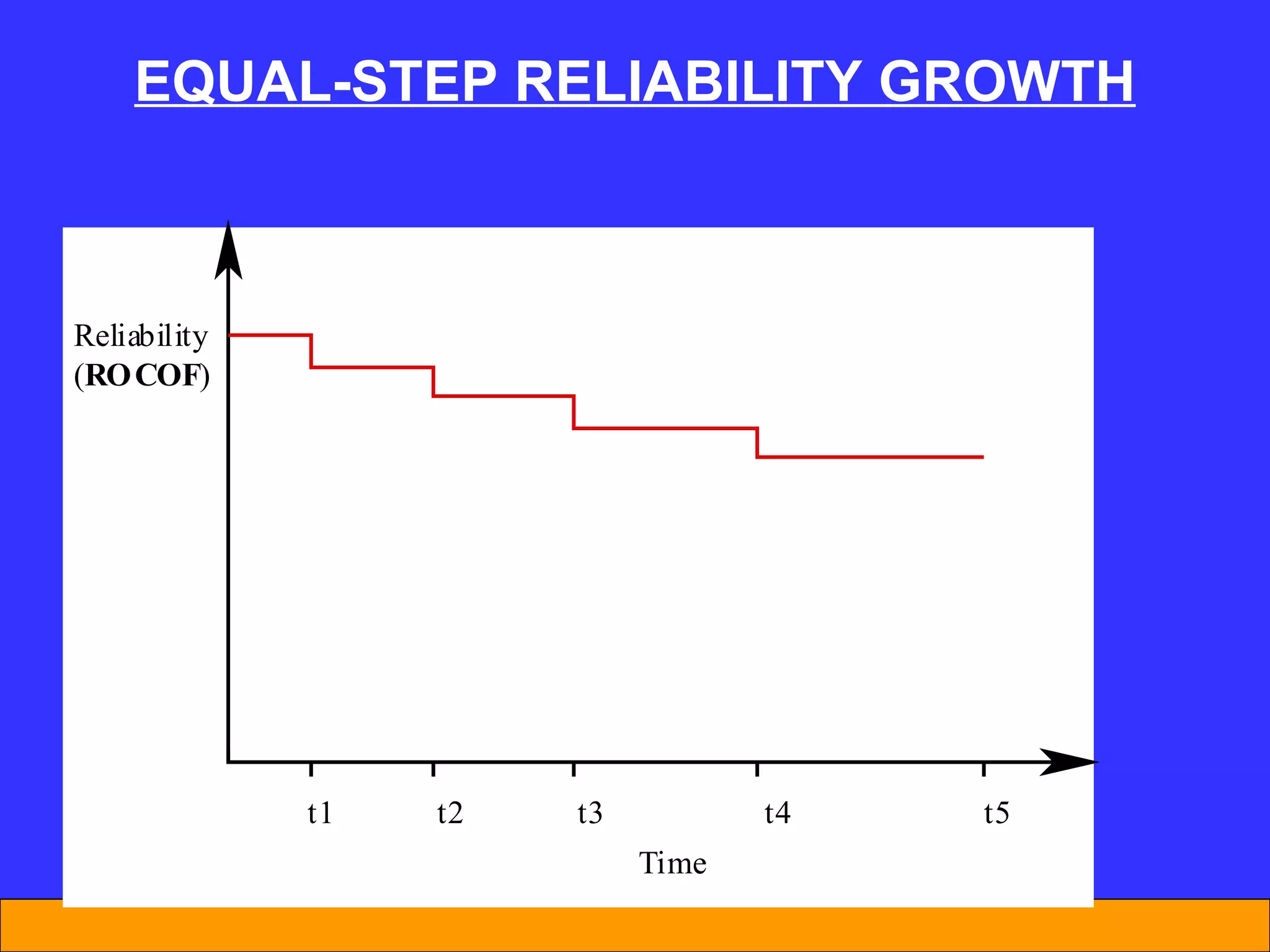
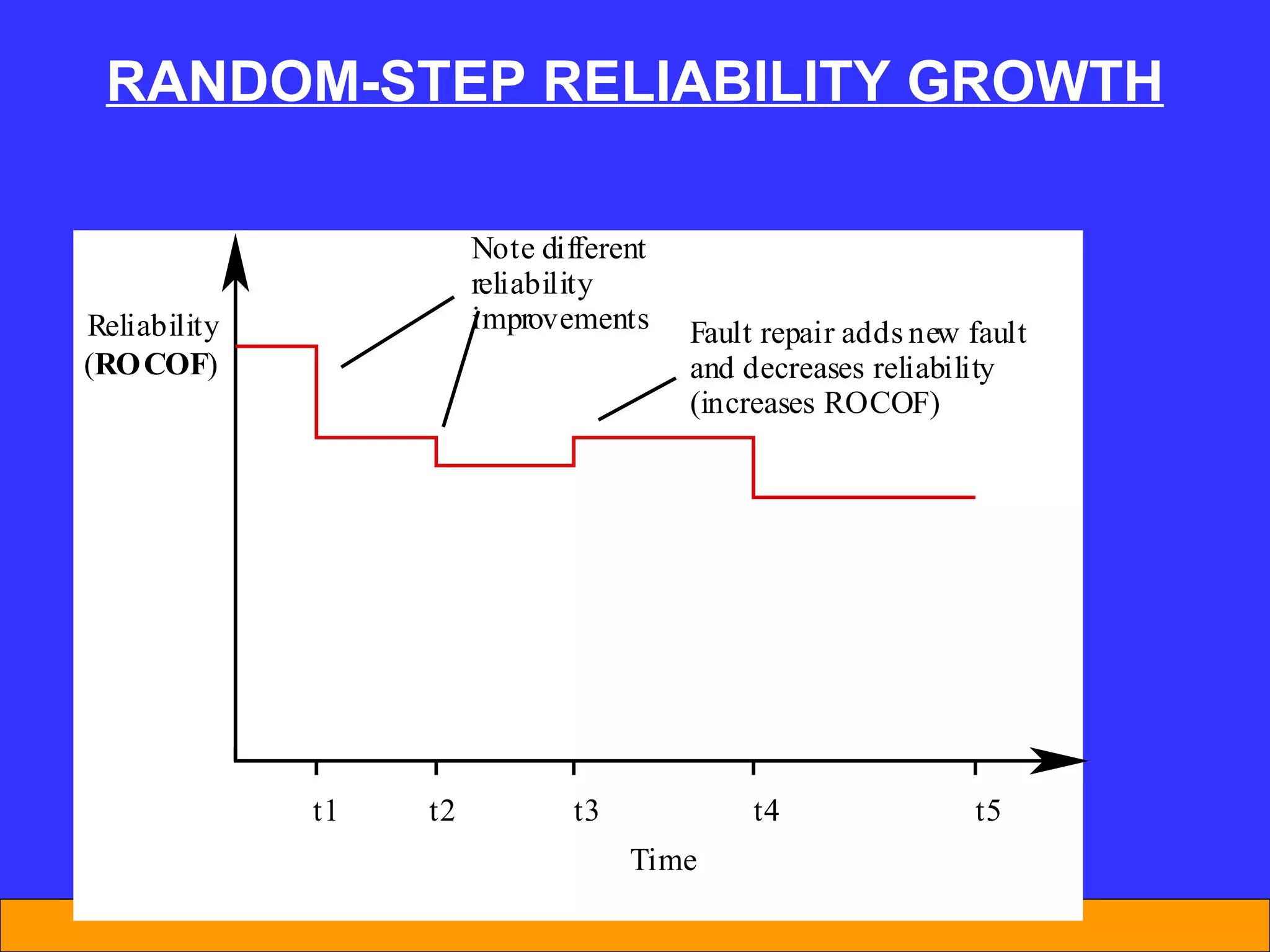
The document discusses software reliability and reliability growth models. It defines software reliability and differentiates it from hardware reliability. It also describes some commonly used software reliability growth models like Musa's basic and logarithmic models. These models make assumptions about fault removal over time to predict how failure rates will change as testing progresses. The key challenges with models are uncertainty and accurately estimating their parameters.

1. LT CDR PABITRA KUMAR PANDA M TECH (RE), IIT KGP 11 AUG 2010 SOFTWARE RELIABILITY

2. INTRODUCTION RELIABILITY HARDWARE VS SOFTWARE RELIABILITY SOFTWARE RELIABILITY GROWTH MODELS STATISTICAL TESTING CONCLUSION SCOPE OF PRESENTATION

3. SOFTWARE RELIABILITY Reliability is usually defined in terms of a statistical measure for the operation of a software system without a failure occurring Software reliability is a measure for the probability of a software failure occurring Two terms related to software reliability Fault : a defect in the software, e.g. a bug in the code which may cause a failure Failure : a derivation of the programs observed behavior from the required behavior

4. SOFTWARE REL I AB I L I TY CONTD . Software Reliability is an important attribute of software quality, together with functionality, usability, performance, serviceability, capability, installability, maintainability, documentation.

5. What is Software Reliability Software Reliability is hard to achieve, because the complexity of software tends to be high. While the complexity of software is inversely related to software reliability, it is directly related to other important factors in software quality, especially functionality, capability.

6. Cannot be defined objectively Reliability measurements which are quoted out of context are not meaningful Requires operational profile for its definition The operational profile defines the expected pattern of software usage Must consider fault consequences Not all faults are equally serious. System is perceived as more unreliable if there are more serious faults Software reliability

7. HARD WARE VS SOFTWARE HAZARD RATE

8. SOFTWARE FA I LURE MECHAN I SM Failure cause : D esign D efects. Repairable system concept : Periodic restarts may fix software problems. Time dependency and life cycle : Not a function of operational time. Environmental factors : Do not affect Reliability prediction : Software reliability can not be predicted from any physical basis, since it depends completely on human factors in design.

9. A failure corresponds to unexpected run-time behaviour observed by a user of the software. A fault is a static software characteristic which causes a failure to occur. Faults need not necessarily cause failures. They only do so if the faulty part of the software is used. FAILURES AND FAULTS

10. INPUT/OUTPUT MAPPING

11. RELIABILITY PERCEPTION

12. FAILURE CLASSIFICATION Transient: failures occur only for certain inputs. Permanent: failures occur for all input values. Recoverable: when failures occur the system recovers with or without operator intervention. Unrecoverable: the system may have to be restarted. Cosmetic:May cause minor irritations. Do not lead to incorrect results. .

13. Measuring Software Reliability Errors do not cause failures at the same frequency and severity. measuring latent errors alone not enough The failure rate is observer-dependent No simple relationship observed between system reliability and the number of latent software defects. Removing errors from parts of software which are rarely used makes little difference to the perceived reliability. removing 60% defects from least used parts would lead to only about 3% improvement to product reliability. Reliability improvements from correction of a single error depends on whether the error belongs to the core or the non-core part of the program. The perceived reliability depends to a large extent upon how the product is used . In technical terms on its operation profile.

14. SOFTWARE FA I LURE MECHAN I SM

15. AVERAGE FAILURE RATE OF A MS PRODUCT

16. REASONS FOR THIS PHENOMENON Users learn with time and avoid failure causing situation. Users start with exploring more, then limit to some part of the product Most users use a few product features Configuration related failures are much more in the start. These failures reduce with time

17. Measuring Software Reliability Don’t define what you won’t collect.. Don’t collect what you won’t analyse.. Don’t analyse what you won’t use..

18. MEASUR I NG SOFTWARE REL I AB I L I TY Measuring software reliability remains a difficult problem because we don't have a good understanding of the nature of software Even the most obvious product metrics such as software size have not uniform definition. Level of reliability required for a software product should be specified in the SRS document .

19. SOFTWARE RELIABILITY MODELING

20. SOFTWARE REL I AB I L I TY MODELS Models have emerged as people try to understand the characteristics of how and why software fails, and try to quantify software reliability Over 200 models have been developed since the early 1970s, but how to quantify software reliability still remains largely unsolved No single model completely represent software reliability . Assumption : reliability is a function of the defect level and as defects are removed, reliability improves .

21. SOFTWARE REL I AB I L I TY MODELS Software modeling techniques can be divided into two subcategories: prediction modeling estimation modeling. Both kinds of modeling techniques are based on observing and accumulating failure data and analyzing with statistical inference.

22. SOFTWARE REL I AB I L I TY MODELS ISSUES PREDICTION MODELS ESTIMATION MODELS DATA REFERENCE Uses historical data Uses data from the current software development effort WHEN USED IN DEVELOPMENT CYCLE Usually made prior to development or test phases; can be used as early as concept phase Usually made later in life cycle(after some data have been collected); not typically used in concept or development phases TIME FRAME Predict reliability at some future time Estimate reliability at either present or some future time

23. SOFTWARE REL I AB I L I TY MODELS Two main types of uncertainty renders any reliability measurement inaccurate: Type 1 uncertainty: our lack of knowledge about how the system will be used Type 2 uncertainty: reflects our lack of knowledge about the effect of fault removal.

24. SOFTWARE REL I AB I L I TY MODELS Most software models contain the following parts: assumptions, factors, a mathematical function relates the reliability with the factors. is usually higher order exponential or logarithmic.

25. SOFTWARE REL I AB I L I TY MODELS Jelinski and Moranda Model Realizes each time an error is repaired reliability does not increase by a constant amount. Reliability improvement due to fixing of an error is assumed to be proportional to the number of errors present in the system at that time.

26. SOFTWARE REL I AB I L I TY MODELS Littlewood and Verall’s Model Assumes different fault have different sizes, thereby contributing unequally to failures. Large sized faults tends to be detected and fixed earlier As number of errors is driven down with the progress in test, so is the average error size, causing a law of diminishing return in debugging

27. EQUAL-STEP RELIABILITY GROWTH

28. RANDOM-STEP RELIABILITY GROWTH

29. MUSA’S MODEL Assumptions:- - Faults are independent and distributed with constant rate of encounter. - Well mixed types of instructions, execution time between failures is large compared to instruction execution time. Set of inputs for each run selected randomly. All failures are observed, implied by definition. - Fault causing failure is corrected immediately, otherwise reoccurrence of that failure is not counted.

30. MUSA’S BASIC MODEL Assumption : Decrement in failure intensity function is constant. Result : Failure intensity is function of average number of failures experienced at any given point in time (= failure probability).  (  ): failure intensity.  0 : initial failure intensity at start of execution.  : average total number of failures at a given point in time. v 0 : total number of failures over infinite time.

31. EXAMPLE Assume that we are at some point of time t time units in the life cycle of a software system after it has been deployed. Assume the program will experience 100 failures over infinite execution time. During the last t time unit interval 50 failures have been observed (and counted). The initially failure intensity was 10 failures per CPU hour. Compute the current (at t ) failure intensity:

32. MUSA/OKUMOTO LOGARITHMIC MODEL Decrement per encountered failure decreases:  : failure intensity decay parameter. Example 2  0 = 10 failures per CPU hour.  = 0.02/failure. 50 failures have been experienced (  = 50). Current failure intensity:

33. Model Extension (1) Average total number of counted experienced failures (  ) as a function of the elapsed execution time (  ). For basic model For logarithmic model

34. Example 3 (Basic Model)  0 = 10 [failures/CPU hour]. v 0 = 100 (number of failures over infinite execution time).  = 10 CPU hours:  = 100 CPU hours:

35. Example 4 (Logarithmic Model)  0 = 10 [failures/CPU hour].  = 0.02 / failure.  = 10 CPU hours:  = 100 CPU hours: (63 in basic model) (100 in basic model)

36. Model Extension (2) Failure intensity as a function of execution time. For basic model: For logarithmic model

37. Example 5 (Basic Model)  0 = 10 [failures/CPU hour]. v 0 = 100 (number of failures over infinite execution time).  = 10 CPU hours:  = 100 CPU hours:

38. Example 6 (Logarithmic Model)  0 = 10 [failures/CPU hour].  = 0.02 / failure.  = 10 CPU hours:  = 100 CPU hours: (3.68 in basic model) (0.000454 in basic model)

39. MODEL DISCUSSION Comparison of basic and logarithmic model: Basic model assumes that there is a 0 failure intensity, logarithmic model assumes convergence to 0 failure intensity. Basic model assumes a finite number of failures in the system, logarithmic model assumes infinite number. Parameter estimation is major problem:  0 ,  , and v 0 . Usually obtained from: system test, observation of operational system, by comparison with values from similar projects.

40. APPL I CAB I L I TY OF SOFTWARE REL I AB I L I TY MODELS There is no universally applicable reliability growth model. Reliability growth is not independent of application. Fit observed data to several growth models. Take the one that best fits the data.

41. STATISTICAL TESTING

42. Testing for reliability rather than fault detection Test data selection should follow the predicted usage profile for the software Measuring the number of errors allows the reliability of the software to be predicted An acceptable level of reliability should be specified and the software tested and amended until that level of reliability is reached STATISTICAL TESTING

43. STAT I ST I CAL TEST I NG Different users have different operational profile: i.e. they use the system in different ways formally, operational profile: probability distribution of input Divide the input data into a number of input classes: e.g. create, edit, print, file operations, etc. Assign a probability value to each input class: a probability for an input value from that class to be selected.

44. Determine operational profile of the software Generate a set of test data corresponding to this profile Apply tests, measuring amount of execution time between each failure After a statistically valid number of tests have been executed, reliability can be measured STATISTICAL TESTING PROCEDURE

45. STATISTICAL TESTING DIFFICULTIES Uncertainty in the operational profile particular problem for new systems with no operational history. High costs of generating the operational profile Costs dependent on what usage information is collected by the organisation which requires the profile Statistical uncertainty when high reliability is specified Usage pattern of software may change with time

46. AN OPERATIONAL PROFILE

47. RELIABILITY PREDICTION

48. CASE STUDY

49. BANK AUTO-TELLER SYSTEM Each machine in a network is used 300 times a day Bank has 1000 machines Lifetime of software release is 2 years Each machine handles about 200, 000 transactions About 300, 000 database transactions in total per day

50. EXAMPLES OF A RELIABILITY SPEC.

51. SPECIFICATION VALIDATION It is impossible to empirically validate very high reliability specifications No database corruptions means POFOD of less than 1 in 200 million If a transaction takes 1 second, then simulating one day’s transactions takes 3.5 days It would take longer than the system’s lifetime to test it for reliability

52. COSTS OF INCREASING RELIABILITY

53. CONCLUS I ONS Software reliability is a key part in software quality Software reliability improvement is hard There are no generic models. Measurement is very important for finding the correct model. Statistical testing should be used but it is not easy again… Software Reliability Modelling is not as simple as it looks.

54. REFERENCES Musa, JD, Iannino, A. and Okumoto, K., “ Software Reliability: Measurement, Prediction, Application” , McGraw-Hill Book Company, NY, 1987. A. V. Aho, R. Sethi, and J. Ullman, " Compilers: Principles,Techniques, and Tools ", Addison-Wesley, Reading, MA, 1986. Reliability Engineering Hand Book, by Bryan Dodson and Dennis Nolan. Software Reliability Prediction Model, White Paper, By M Thangarajan Software Reliability Engineering – A Roadmap by Michael R Lyu

55. THANK YOU!