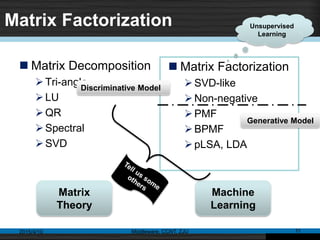
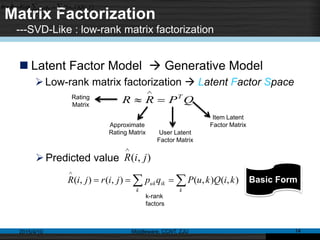
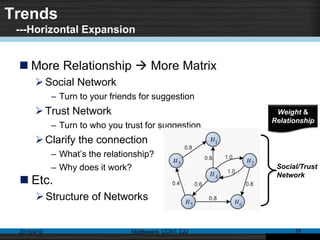
This document discusses social recommender systems. It begins by noting the large size of major social media sites and how recommender systems can help with information overload on these sites. It then discusses how recommender systems are based on principles of word-of-mouth recommendations and collaborate filtering. Several fundamental recommendation approaches are described, including collaborative filtering, content-based filtering, and hybrid methods. Matrix factorization techniques like singular value decomposition (SVD) are also covered. The document concludes by discussing trends in expanding recommender systems to incorporate more relationship data and higher-dimensional tensor models.

1. Social Recommender System
2015/4/10 1Middleware, CCNT, ZJU
Yueshen Xu
Middleware, CCNT, ZJU
xyshzjucs@zju.edu.cn
xyshzjucs@gmail.com
Knowledge
Engineering
&
E-Commerce

2. Outline
2015/4/10 2Middleware, CCNT, ZJU
 Where from?
 How to recommend?
 What to recommend?
 What’s the problem?
 ML & DM
 Related Topics
 Trends
What’s your
perspective?
Basic, Generalized, Comprehensible

3. Introduction
 Social Overload
Facebook  largest social network site
– 600,000,000 users
YouTube  largest video sharing site
– 2,000,000,000
Twitter  largest microblogging site
– 65,000,000 tweets per day
Sina microblog  largest microblogging site in
China
– 400,000,000 users
2015/4/10 Middleware, CCNT, ZJU 3

4. Introduction
 The Recommender Systems is an augmentation
of the social process
 Any CF system has social characteristics
 Social Media and Recommender Systems can
mutually benefit each other
2015/4/10 Middleware, CCNT, ZJU 4

5. Introduction
2015/4/10 Middleware, CCNT, ZJU 5
Real-world examples
Why?
Different man,
Different news
Pioneer
‘....based on
recommendatio
n algorithms....’
Multi-Media

6. Fundamental Recommendation Approaches
 Collaborative filtering based Recommendation
Aggregate ratings of objects from users and generate
recommendation based on inter-user/inter-item
similarity
 Demographic Recommendation
Age,gender,income…
 Content-based Recommendation
Music gene
 Hybrid Methods
Mixed
2015/4/10 Middleware, CCNT, ZJU 6
Your imagination

7. Fundamental Recommendation Approaches
 In the real world, we seek advices from our
trusted people
 CF automate the process of ‘word-of-mouth’
Select a subset of the users(neighbors) to use as
recommenders
2015/4/10 Middleware, CCNT, ZJU 7
Collaborative Filtering

8. Fundamental Recommendation Approaches
 Shall we recommend Superman for John?
Jon’s taste is similar to both Chris and Alice tastes 
Do not recommend Superman to him
2015/4/10 Middleware, CCNT, ZJU 8
User based CF algorithm

9. Fundamental Recommendation Approaches
2015/4/10 Middleware, CCNT, ZJU 9
User based CF algorithm
vi - the mean vote for user i
k - a normalization factor
pij – the predicitive vote
w(i,j ) – the similarity between ui and uk !
Cose based similarity Pearson Based similarity

10. Fundamental Recommendation Approaches
 The transpose of the user-based algorithms
Bob dislike Snow-white(which is similar to Shrek) 
Do not recommend
2015/4/10 Middleware, CCNT, ZJU 10
Item based CF algorithm
W(k,j) is a measure of item similarity – usually the cosine measure

11. Matrix Factorization
 Matrix Decomposition
Tri-angle
LU
QR
Spectral
SVD
2015/4/10 Middleware, CCNT, ZJU 11
 Matrix Factorization
SVD-like
Non-negative
PMF
BPMF
pLSA, LDA
Matrix
Theory
Machine
Learning
Discriminative Model
Generative Model
Unsupervised
Learning

12. Matrix Factorization
---SVD : the ancestor
 Rudiment---Singular Value Decomposition
For an arbitrary matrix A there exists a factorization
named SVD, as follows:
2015/4/10 Middleware, CCNT, ZJU 12

13. Matrix Factorization
---Latent Semantic Analysis  PTM  LDA
 Low-rank matrix factorization
Why factorizing?
– One is about the interpretation
– You prefer Lost in Thailand ‘cause it’s a drama, and X, and
Y, and Z, and ......
– X, Y & Z are named as latent factors
So matrix factorization can be come across as
another type of LSA(Latent Semantic Analysis)
2015/4/10 Middleware, CCNT, ZJU 13
Share us
sth
corssing
your mind
Probabilistic
Topic Model !

14. Matrix Factorization
---SVD-Like : low-rank matrix factorization
 Latent Factor Model  Generative Model
Low-rank matrix factorization  Latent Factor Space
2015/4/10 Middleware, CCNT, ZJU 14
QPRR T


QPRR T


QPRR T


QPRR T


QPRR T


QPRR T


Rating
Matrix
Approximate
Rating Matrix User Latent
Factor Matrix
Item Latent
Factor Matrix
 

ff
ifufui fiQfuPqpriuR ),(),(),(
Predicted value ),( jiR

 

kk
ikuk kiQkuPqpjirjiR ),(),(),(),(
k-rank
factors
Basic Form

15. Matrix Factorization
---SVD-Like : low-rank matrix factorization
 Minimize the sum-squared errors
2015/4/10 Middleware, CCNT, ZJU 15
Skip
Details
 

m
i
n
j
j
T
iij
QP
QPR
1 1
2
, 2
1
min  

m
i
n
j
j
T
iijij
QP
QPRI
1 1
2
,
)(
2
1
min
Frobenius Form
Just like Quadratic regression
I : the indicator function
 Regularization
Avoid overfitting  Why?  Sparsity/Sample
Shortage
2221
1 1
2
, 22
)(
2
1
min FF
m
i
n
j
j
T
iijij
QP
QPQPRI

 
 Solution
Stochastic Gradient Descent

16. Matrix Factorization
---PMF : the production of Bayesian Theory
 SVD-Like is not perfect  Why?
Subject & Object  the victim of formalism
 Maximum Posterior Probability(MAP) 
2015/4/10 Middleware, CCNT, ZJU 16
)()(),|()|,( VpUpVURpRVUp 
   

m
i
n
j
I
Rj
T
iij
R
ij
VUrNVURp
1 1
2
,|),|( 


m
i
UiU IUNUp
1
22
),0|()|(  

n
j
ViV IVNVp
1
22
),0|()|( 
Gaussian
Noise
     

n
j
Vi
m
i
Ui
m
i
n
j
I
Rj
T
iij IVNIUNVUrNRVUp
R
ij
1
2
1
2
1 1
2
),0|(),0|(,|)|,( 
Zero-mean spherical Gaussian prior

17. Surroundings
 Topics related
Non-negative Matrix Factorization
– Deng Cai etc.
Boltzmann Machines
– Discarded
Heterogeneous networks
– Prof. Han
– Link Prediction & Community Discovery
Transfer Learning & Online Learning
– Qiang Yang etc.
2015/4/10 Middleware, CCNT, ZJU 17
Excavate
Structures
Neural
Network
‘Graph
Regularized
NMF for.....’
Different
Certain
Networks
Online
Algorithms
Others 
• Semantic
Web
• Ranking
• Computing
Ads
• Network
Marketing
• Clustering
• NLP
• TM
• Sociology
• Etc.

18. Trends
---Horizontal Expansion
 More Relationship  More Matrix
Social Network
– Turn to your friends for suggestion
Trust Network
– Turn to who you trust for suggestion
Clarify the connection
– What’s the relationship?
– Why does it work?
2015/4/10 Middleware, CCNT, ZJU 18
Weight &
Relationship
Social/Trust
Network
 Etc.
Structure of Networks

19. Trends
---Vertical Expansion
 3-4-5- Dimensions  Tensor
A tensor can be represented as a multi-dimensional
array of numerical values.
– 1-dimensional tensor : Vector
– 2-dimensional tensor : Matrix
Tensor Decomposition & Tensor Factorization
2015/4/10 Middleware, CCNT, ZJU 19
observed
value
3th, Latent factor,
Time or Tag
1th Latent factor
one, User
2thLatent factor ,
Item


20. 2015/4/10 20Middleware, CCNT, ZJU
Social Recommender System