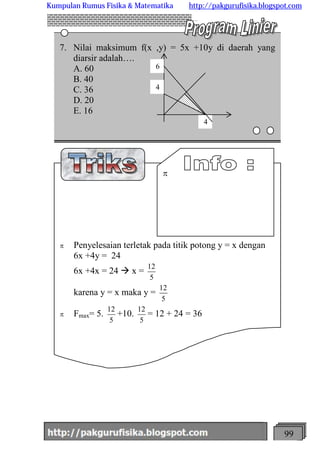
Sistem pertidaksamaan yang mendefinisikan daerah yang diarsir adalah 4x + y ≥ 8, 3x + 4y ≤ 24, dan x + 6y ≥ 12. Dokumen ini berisi penjelasan tentang cara menentukan sistem pertidaksamaan yang mendefinisikan suatu daerah berdasarkan arah panah pada garis-garis yang membatasi daerah tersebut.