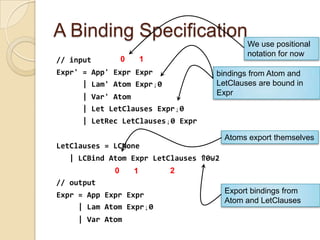
This document summarizes Mitchell Wand's presentation on providing static guarantees for macro bindings. It discusses the motivation for studying macros and desire for static reasoning about hygiene. While previous work addressed related problems dynamically, the goal here is to provide static guarantees. The presentation outlines previous work and the starting points being built upon, including Ott specification language and Herman's thesis. It describes progress made in adapting Pottier's Functional Fresh ML to use plain s-expressions while keeping binding information in types. Next steps include interfacing with an SMT prover and implementing example macros in the system.

1. Static Guarantees for Macro
Bindings
Mitchell Wand
Presentation for Gnosys site visit
12/14/12

2. Why study macros?
 macros are a facility for lightweight
compilers
 translate DSL into host language (Racket),
then let Racket compiler work
 easy interoperation with host language, etc.
 most translation is on a per-s-expression
basis
 Racket macro system has features that
permit interaction between macros,
optimizations, fancier syntax, etc.

3. Want: static reasoning about
hygiene
 Does the expansion of a macro obey its
intended scoping rules?
 Does my-let act like let?
◦ Is id0 bound in body?
(define-syntax my-let
(syntax-rules ()
[(_ ((id0 val0) (id val) ...) body)
((lambda (id ...) body)
val ...)]))
Answer: No

4. Didn't Dybvig solve this in 1993?
 No notion of "intended scoping rules"
 Dybvig's algorithm works out binding
relationships dynamically.
 We want static guarantees.

5. Didn't the nominal logic guys
solve this?
 Nominal logic: Pitts, et al. 2000 or so, et seq.
 Logic for reasoning about names
 Much work about representing terms with
binding. BUT:
 Aimed at theorem proving, not
programming
 Generally involves data representations that
carry their scoping rules with them:
◦ lambda-terms, not s-expressions.
◦ Macros must translate from s-expressions (or
something like them) to lambda-terms (or
something like them)

6. Our Starting Points (I)
 Ott: a specification language for binding
patterns, like Ott (ICFP 2007, JFP 2010)
p ::= // patterns
A primitive binder
| x binders = x
| { l1=p1,...,ln=pn } binders = binders(p1 ... pn)
A composite binder
t ::= // terms
| let p = t in t’ bind binders(p) in t’
Bind these variables in t

7. This doesn't solve the problem
 Ott has back-ends for
◦ Latex
◦ several theorem provers
 But it's not a general-purpose tool

8. Our Starting Points (II)
 Dave Herman's thesis (2010)
◦ took Ott-like specification language
◦ static checking for syntax-rules style macros
 Would reject my-let from slide 1.
 Goal: extend this to procedurally-defined
macros (e.g. syntax-case)

9. Our Starting Points (III)
 Pottier's Functional Fresh ML (LICS 2007)
 A programming language based on
nominal logic.
 His goal: programming with binders.
◦ functions map alpha-equivalent objects to
alpha-equivalent objects
 Attractive semantics
◦ no hidden gensym (!)

10. Pottier's Result
 Theorem 1: Any function in Fresh ML
either preserves alpha-equivalence or
else faults Dynamic! 
◦ careful language design, any bound variable
that escapes its scope triggers a fault.
 Theorem 2: From any program in Fresh
ML, we can derive a formula G s.t. if G is
true, then the program never faults.
Static!  Can use SMT prover

11. Does this solve the problem?
 No: his data still carries around its own
binding information dynamically
 We need to manipulate plain old s-
expressions (or something like them)

12. Our plan
 Adapt Pottier's system to use plain old s-
expressions.
 Keep the binding information in types
(static) rather than in the data (dynamic)

13. Progress [Work by Paul
Stansifer]
 Core language defined
 Static checks defined (extension of
Pottier's)
 Now working on proofs of theorems

14. A Binding Specification
We use positional
notation for now
// input 0 1
Expr' = App' Expr Expr bindings from Atom and
| Lam' Atom Expr↓0 LetClauses are bound in
Expr
| Var' Atom
| Let LetClauses Expr↓0
| LetRec LetClauses↓0 Expr
Atoms export themselves
LetClauses = LCNone
| LCBind Atom Expr LetClauses ⇑0⊎2
0 1 2
// output
Expr = App Expr Expr Export bindings from
Atom and LetClauses
| Lam Atom Expr↓0
| Var Atom

15. Next Steps
 Interface to SMT prover (w/ Fabian
Muehlenboeck)
 What adaptations are necessary to make
these obligations acceptable to an SMT-
style prover?
 Actually write some macros in this
system.