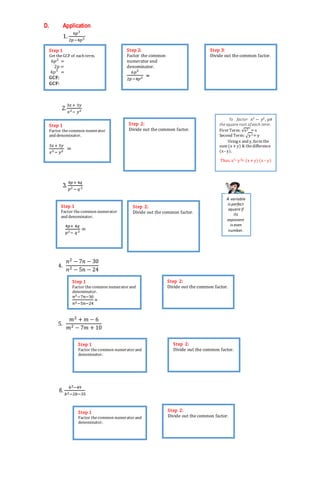
This document contains a lesson plan for teaching simplifying rational expressions in Math 8 at Quiot National High School. The lesson plan outlines the intended learning outcomes, learning content including reference materials, learning activities and experiences, and an evaluation section containing practice problems for students. The lesson aims to teach students how to define, simplify, and apply rational expressions in real-life contexts. Learning activities include defining rational expressions, simplifying examples by factoring and cancelling common factors, and applying the process to additional practice problems. The evaluation section contains 4 practice problems for students to simplify rational expressions.

1. Republic of the Philippines
Department of Education
Region VII Central Visayas
Division of Cebu City
Quiot National High School
Bogo, Quiot, Cebu City
A Semi-Detailed Lesson Plan
In Math 8
___________________
Date of Teaching
____________________
Time of Teaching
Quiot National High School- Afternoon Session
Venue of Teaching
Prepared by:
LORIE JANE L. LETADA
Teacher 1
Observed by:
ELEANOR D. GALLARDO
ASSISTANT PRINCIPAL

2. I. Intended Learning Outcomes
Through varied learning activities, the grade 8 students with at least80 % ofaccuracy shall able to:
1. Define rational expressions
2. Simplify rational expressions
3. Relate simplifying rational expressions in real life situation
II. Learning Content
A. Subject Matter
Simplifying Rational Expressions
B. Reference
Diaz, Z., Mojica M. (2013) . Next Century Mathematics 8; Quezon City ; Phoenix
Publishing House , Inc; Mathematics 8 Learner’s Module K-12; DepEd K-12
Modified Curriculum Guide and Teacher’s Guide for Mathematics 8
https://www.mathsisfun.com/simplifying-fractions.html
C. Materials
Learners’ Module; Google Classroom; powerpointpresentation; google forms
III. Learning Experiences
A. Activity

3. B. Analysis
1. What is the total area of each figure?
2. Using the sides ofthe tiles, write all the dimensions ofthe rectangles.
3. How did you getthe dimensions ofthe rectangles?
4. Did you find difficulty in getting the dimensions?
C. Abstraction
A Rational Expressions is reduced to its simplest form if the numerator and denominator have
no common factors. Putting a rational expression in its simplest form is important as this will
make operations easier.
Simplify the following in its simplest form.
1.
4𝑎
12𝑏
2.
4𝑤2
6𝑤−8𝑤2
3 .
2𝑥−2𝑦
2− 𝑥2
Step 1
Factor thenumerator and denominator and
get theGCF.
4a = (2) (2) a
12b= (3) (2) (2) b
GCF: (2) (2)
GCF: 4
Thus, the common factor is 4.
Step 2:
Divideout thecommon factor.
4𝑎
12𝑏
=
4 ( 𝑎 )
4 (3𝑏)
=
𝑎
3𝑏
Thus, the simplify is
𝑎
3𝑏
.
Step 1
Get theGCF of each term.
4𝑤2
= (2) (2) (w) (w)
6w = (3) (2) (w)
8𝑤2
= (2)(2) (2)(w)
GCF: (2) (w)
GCF: 2w
Thus, the common factor is 2w.
Step 2:
Factor the common
numerator and
denominator.
4𝑤2
6𝑤−8𝑤2 =
2𝑤 ( 2)
2𝑤 (3−4𝑤 )
Step 3:
Divide out the common
factor.
4𝑤2
6𝑤−8𝑤2 =
2𝑤 ( 2)
2𝑤 (3−4𝑤 )
=
2
3−4𝑤
Thus, the simplify is
2
3−4𝑤
.
Step 1
Factor thecommon numerator
and denominator.
2𝑥−2𝑦
𝑦2 − 𝑥2 =
2 (𝑦−𝑥)
( 𝑦−𝑥 )(𝑦+ 𝑥)
Step 2:
Divide out the common factor.
2𝑥−2𝑦
𝑦2 − 𝑥2 =
2 (𝑦−𝑥)
( 𝑦−𝑥 )(𝑦+ 𝑥)
=
2
(𝑥+ 𝑦)
You can only apply the
difference of two squares if:
*The two terms are both
perfect squares.
*The operation is subtraction.
Example:
𝑦2
− 𝑥2
= (y – x ) ( y + x )

4. D. Application
1.
6𝑝2
2𝑝−4𝑝3
DI.
DII.
DIII.
DIV.
2.
3𝑥+ 3𝑦
𝑥2− 𝑦2
3.
4𝑝+ 4𝑞
𝑝2 − 𝑞2
4.
𝑛2 − 7𝑛 − 30
𝑛2 − 5𝑛 − 24
5.
𝑚2 + 𝑚 − 6
𝑚2 − 7𝑚 + 10
6.
𝑏2−49
𝑏2−2𝑏−35
Step 1
Get theGCF of each term.
6𝑝2
=
2p =
4𝑝3
=
GCF:
GCF:
Step 2:
Factor the common
numerator and
denominator.
6𝑝2
2𝑝−4𝑝3 =
Step 3:
Divide out the common factor.
Step 1
Factor thecommon numerator
and denominator.
3𝑥+ 3𝑦
𝑥2 − 𝑦2 =
Step 2:
Divide out the common factor.
To factor 𝑥2
− 𝑦2
, get
the square root of each term.
First Term: √x2 = x
Second Term: √y2= y
Usingx and y, form the
sum (x + y) & thedifference
(x - y).
Thus, x2
- y2
= (x + y) (x – y).
Step 1
Factor thecommon numerator
and denominator.
4𝑝+ 4𝑞
𝑝2− 𝑞2 =
Step 2:
Divide out the common factor.
A variable
is perfect
square if
its
exponent
is even
number.
Step 1
Factor thecommon numeratorand
denominator.
𝑛2−7𝑛−30
𝑛2−5𝑛−24
=
Step 2:
Divide out the common factor.
Step 1
Factor the common numeratorand
denominator.
Step 2:
Divide out the common factor.
Step 1
Factor thecommon numeratorand
denominator.
Step 2:
Divide out the common factor.

5. IV. Evaluation
Simplify each rational expression.
1.
5𝑎𝑏2
20𝑎𝑏
= 5.
𝑥−1
5𝑥−5
=
2.
5𝑔ℎ
10𝑔
= 6.
𝑛2+2𝑛−15
𝑛2−𝑛−6
=
3.
15𝑎𝑐2
45𝑎𝑏3 𝑐
= 7.
𝑐2+7𝑐+10
𝑐2+5𝑐
=
4.
𝑥2−9
𝑥2−𝑥−6
= 8.
𝑞2+8𝑞+12
𝑞2+3𝑞−18
=
V. Assignment
Skill Booster!