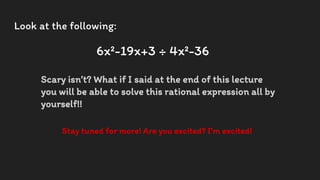
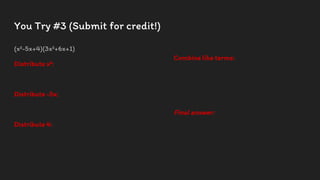
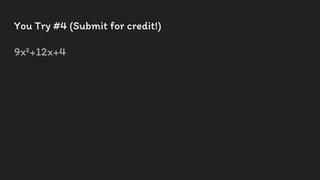
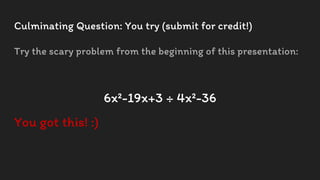
This document provides an overview of simplifying polynomials and rational expressions. It begins by stating the learning objectives and California content standards, which include applying binary operations like addition, subtraction, and multiplication to simplify polynomials and factoring polynomials to simplify rational expressions. Examples are then provided step-by-step for adding, subtracting, multiplying polynomials and factoring polynomials. An example is also worked through for simplifying a rational expression. Interactive examples are included for students to try on their own.

1. Simplifying Polynomials &
Rational Expressions
Let’s have some fun! :)
8th grade Algebra: Ms. Webb

2. Learning Objectives & CA Content Standards
● Lecture Objectives:
○ To apply binary operations such as addition, subtraction, & multiplication to
simplifying polynomials
○ Addressing the different methods to factoring & how that helps with simplifying
rational expressions
○ Defining polynomials & rational expressions
● CA Content Standard:
○ Understand that polynomials form a system analogous to the integers, namely, they
are closed under the operations of addition, subtraction, and multiplication; add,
subtract, and multiply polynomials.

3. Look at the following:
6x²-19x+3 ÷ 4x²-36
Scary isn’t? What if I said at the end of this lecture
you will be able to solve this rational expression all by
yourself!!
Stay tuned for more! Are you excited? I’m excited!

4. Steps for each concept…
Adding
Polynomials
Subtracting
Polynomials
Multiplying
Polynomials
Rational
Expressions
Directions: Write down 4 steps/facts for each
of the provided categories. We will come back
to this table after we review each concept.
Hint: Think
of the ways
we simplify
these
polynomials

5. Definitions: Very Important!
● Definition: A polynomial is an expression consisting of variables (usually
of the same type) and operations such as addition, subtraction, &
multiplication
● Definition: A rational expression is a ratio of two polynomials where the
bottom polynomial (denominator) cannot be 0.

6. Ex. #1: Adding Polynomials
(4x²+6x-7) + (2x²-5x-3)
Combine like terms:
4x² + 2x² = 6x²
6x + (-5x) = 1x
(-7) + (-3) = -10
Put it all together:
6x²+x-10
Final answer: (4x²+6x-7) + (2x²-5x-3) = 6x²+x-10

7. You try #1 (Submit for credit!)
(3x²+5x+10) + (8x²-7x-1)
Combine like terms:
Put it all together:
Final answer:

8. Ex. #2: Subtracting Polynomials
(9x²-2x+4) - (10x²+8x-2)
Distribute the minus sign:
-(10x²+8x-2) = -10x²-8x+2
Combine like terms:
9x² + (-10x²) = -1x²
(-2x) + (-8x) = -10x
4 + 2 = 6
Put it all together:
-x²-10x+6
Final answer: (9x²-2x+4) - (10x²+8x-2) = -x²-10x+6

9. You try #2 (Submit for credit!)
(2x²-7x+3) - (-8x²+x-9)
Distribute the minus sign:
Combine like terms:
Put it all together:
Final answer:

10. Ex. #3: Multiplying Polynomials
(x²-8x+2)(2x²+6x+5)
Distribute x²:
x²(2x²+6x+5) = 2x^4+6x^3+5x²
Distribute: -8x:
-8x(2x²+6x+5) = -16x^3-48x²-40x
Distribute 2:
2(2x²+6x+5) = 4x²+12x+10
Combine like terms:
2x^4+6x^3+5x²-16x^3-48x²-40x+4x²+12x+10
=2x^4-10x^3-39x²-28x+10
Final answer:
(x²-8x+2)(2x²+6x+5) = 2x^4-10x^3-39x²-28x+10

11. You Try #3 (Submit for credit!)
(x²-5x+4)(3x²+6x+1)
Distribute x²:
Distribute -5x:
Distribute 4:
Combine like terms:
Final answer:

12. Ex. #4: Factoring
Watch & take
notes from 9-
14:05 mins

13. You Try #4 (Submit for credit!)
9x²+12x+4

14. Ex. #5: Rational Expressions
(x²-9) ÷ (x²+x-6) = x²-9
x²+x-6
Simplify the numerator x²-9:
x²-9 = (x+3)(x-3)
Simplify the denominator x²+x-6:
-6
1
-2 3
x²+x-6 = (x-2)(x+3)
Rewrite:
(x+3)(x-3)
Simplify the expression:
(x+3)(x-3)
(x-2)(x+3)
(x-2)(x+3)
Final Answer:
(x²-9) ÷ (x²+x-6) = (x-3)
(x-2)

15. You Try #5 (Submit for credit!)
(x²-4) ÷ (x²+4x+4) =
Simplify the numerator x²-4:
Simplify the denominator x²+4x+4:
Rewrite:
Simplify the expression:
Final Answer:

16. Culminating Question: You try (submit for credit!)
Try the scary problem from the beginning of this presentation:
6x²-19x+3 ÷ 4x²-36
You got this! :)