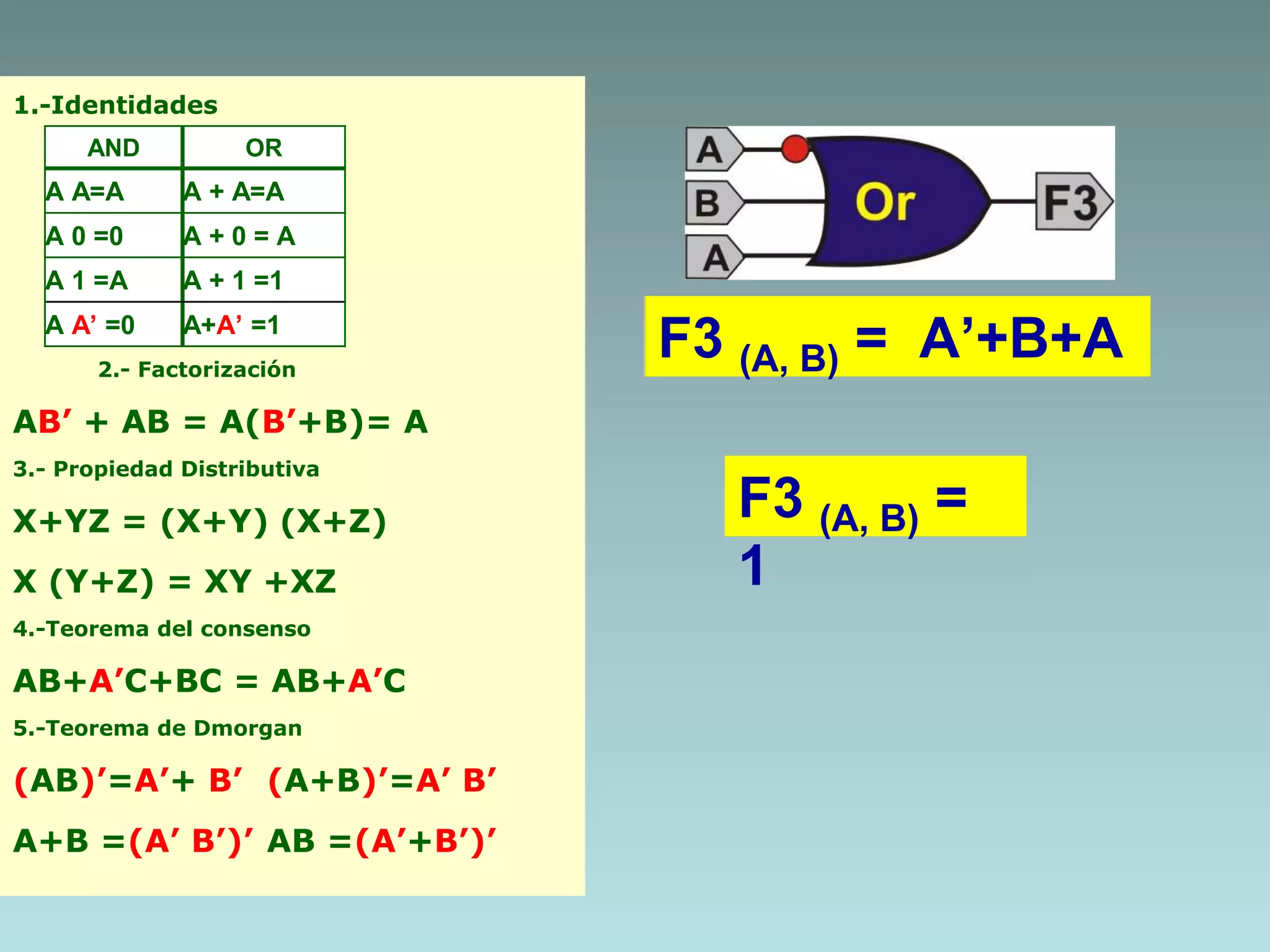
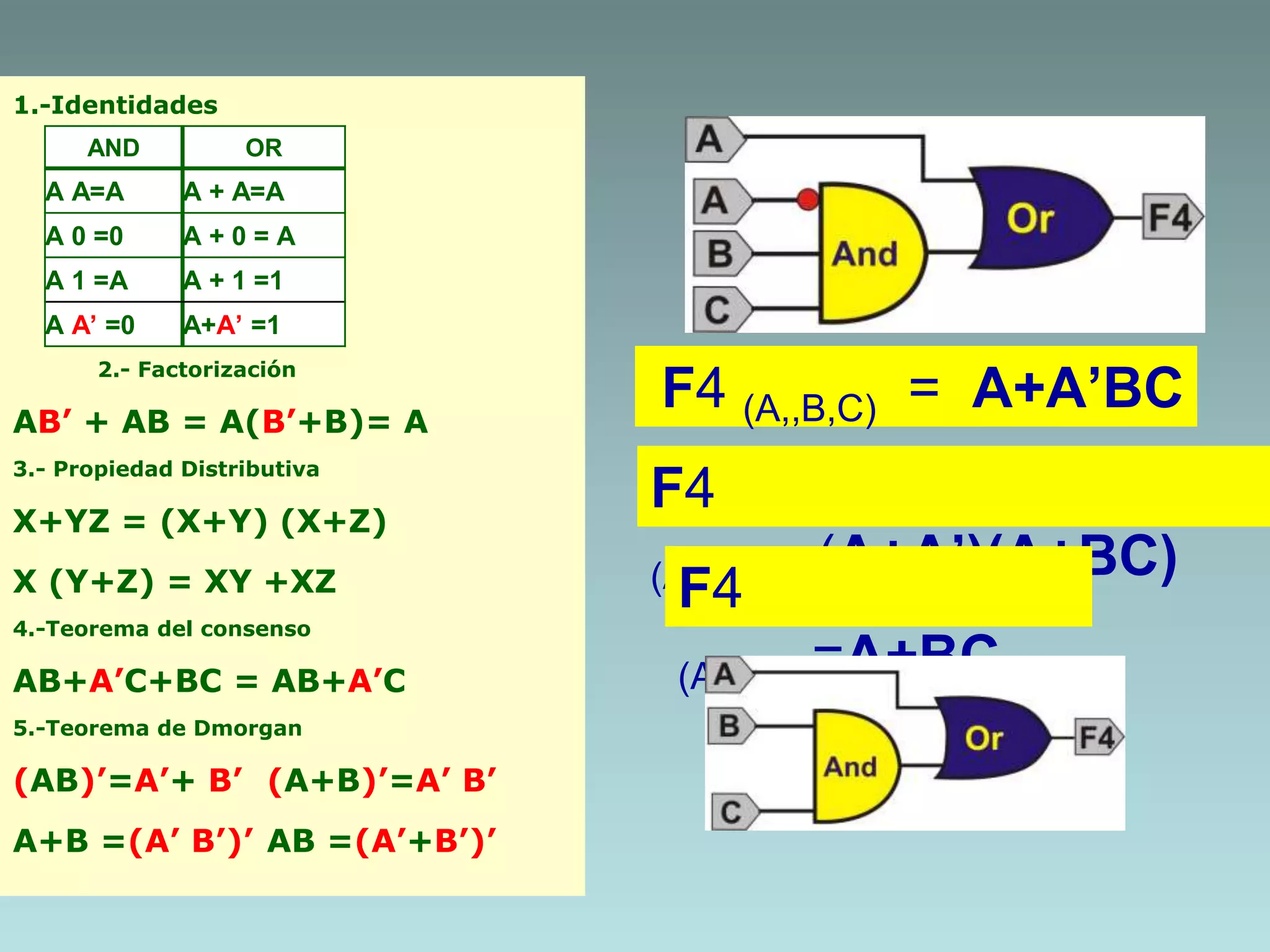
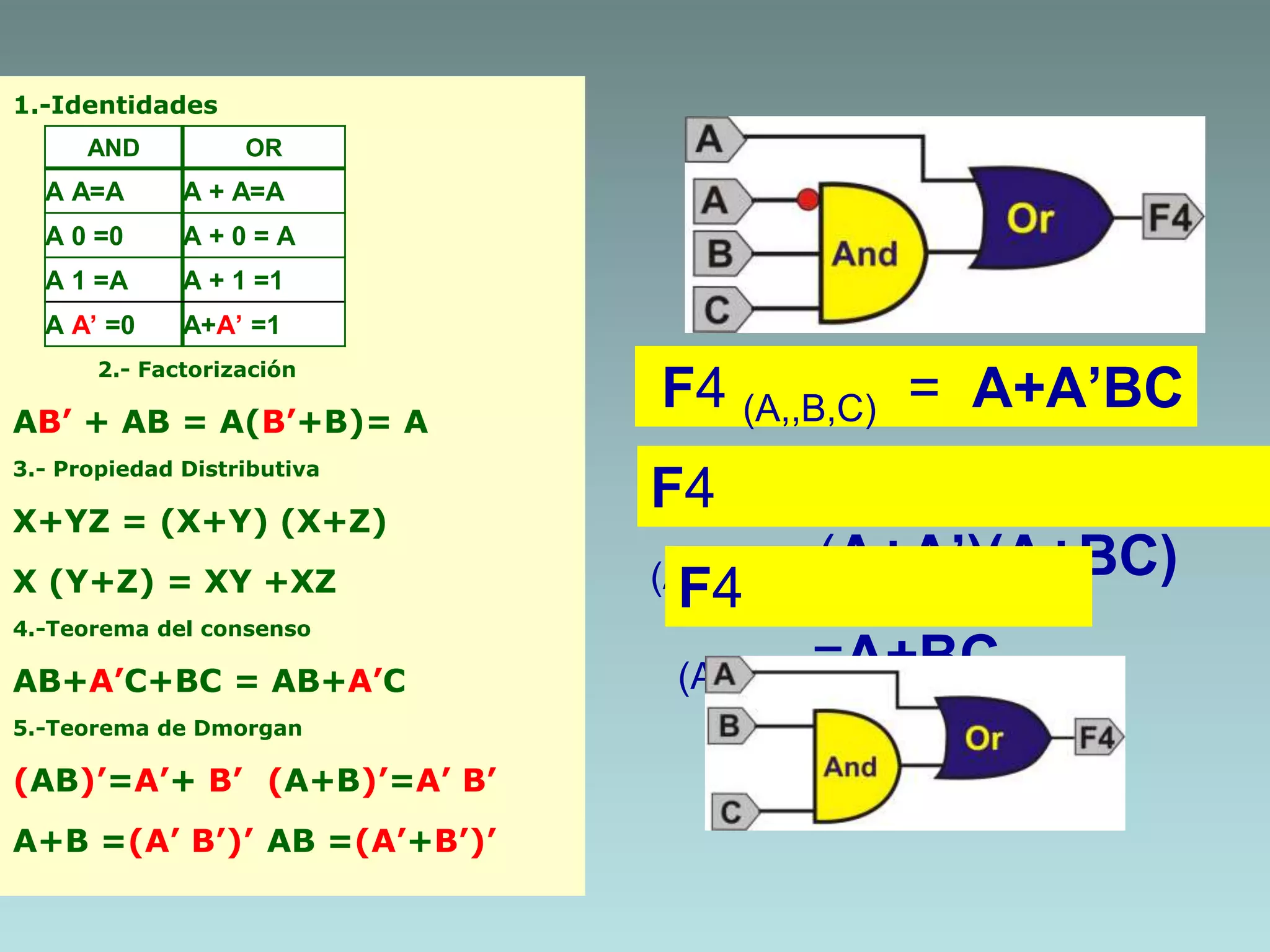
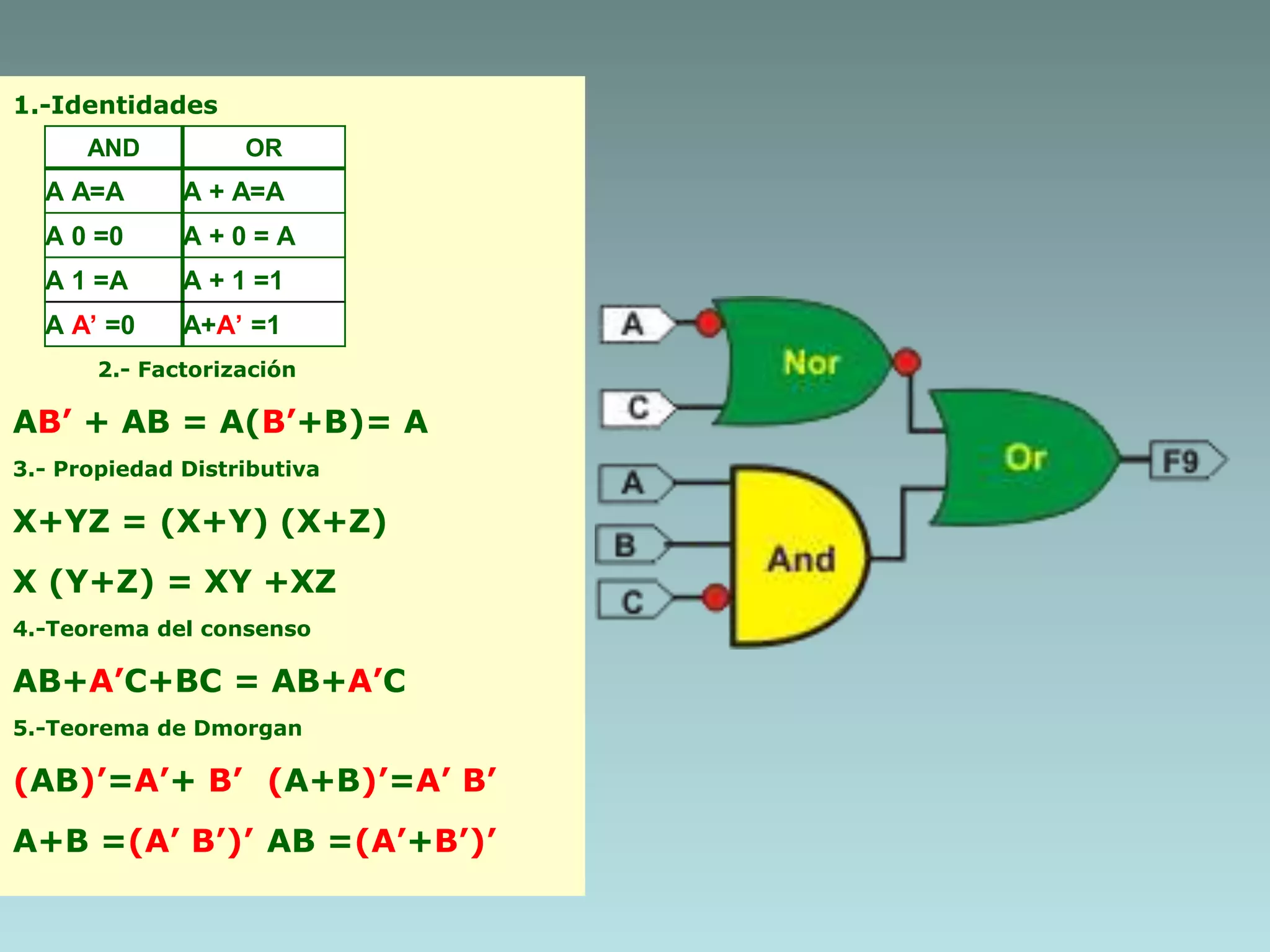
The document discusses methods for minimizing Boolean functions including algebraic methods. It defines four Boolean functions - F1(B,C), F2(D,C), F3(A,B), and F4(A,B,C) - and simplifies each using identities, factorization, distribution, consensus theorem, and De Morgan's laws. It also defines the truth tables for the AND and OR operations.

1. Minimización de funciones
Booleanas
• Métodos algebraicos

2. F1 (B,C)= 1+B’+C
F1 (B,C)=
1
1.-Identidades
2.- Factorización
AB’ + AB = A(B’+B)= A
3.- Propiedad Distributiva
X+YZ = (X+Y) (X+Z)
X (Y+Z) = XY +XZ
4.-Teorema del consenso
AB+A’C+BC = AB+A’C
5.-Teorema de Dmorgan
(AB)’=A’+ B’ (A+B)’=A’ B’
A+B =(A’ B’)’ AB =(A’+B’)’
AND OR
A A=A A + A=A
A 0 =0 A + 0 = A
A 1 =A A + 1 =1
A A’ =0 A+A’ =1

3. F2 (D,C)= DC’(0)
F2 (D,C)= 0
1.-Identidades
2.- Factorización
AB’ + AB = A(B’+B)= A
3.- Propiedad Distributiva
X+YZ = (X+Y) (X+Z)
X (Y+Z) = XY +XZ
4.-Teorema del consenso
AB+A’C+BC = AB+A’C
5.-Teorema de Dmorgan
(AB)’=A’+ B’ (A+B)’=A’ B’
A+B =(A’ B’)’ AB =(A’+B’)’
AND OR
A A=A A + A=A
A 0 =0 A + 0 = A
A 1 =A A + 1 =1
A A’ =0 A+A’ =1

4. F3 (A, B) = A’+B+A
F3 (A, B) =
1
1.-Identidades
2.- Factorización
AB’ + AB = A(B’+B)= A
3.- Propiedad Distributiva
X+YZ = (X+Y) (X+Z)
X (Y+Z) = XY +XZ
4.-Teorema del consenso
AB+A’C+BC = AB+A’C
5.-Teorema de Dmorgan
(AB)’=A’+ B’ (A+B)’=A’ B’
A+B =(A’ B’)’ AB =(A’+B’)’
AND OR
A A=A A + A=A
A 0 =0 A + 0 = A
A 1 =A A + 1 =1
A A’ =0 A+A’ =1

5. F4 (A,,B,C) = A+A’BC
F4
(A,,B,C)=(A+A’)(A+BC)
F4
(A,,B,C)=A+BC
1.-Identidades
2.- Factorización
AB’ + AB = A(B’+B)= A
3.- Propiedad Distributiva
X+YZ = (X+Y) (X+Z)
X (Y+Z) = XY +XZ
4.-Teorema del consenso
AB+A’C+BC = AB+A’C
5.-Teorema de Dmorgan
(AB)’=A’+ B’ (A+B)’=A’ B’
A+B =(A’ B’)’ AB =(A’+B’)’
AND OR
A A=A A + A=A
A 0 =0 A + 0 = A
A 1 =A A + 1 =1
A A’ =0 A+A’ =1

6. F4 (A,,B,C) = A+A’BC
F4
(A,,B,C)=(A+A’)(A+BC)
F4
(A,,B,C)=A+BC
1.-Identidades
2.- Factorización
AB’ + AB = A(B’+B)= A
3.- Propiedad Distributiva
X+YZ = (X+Y) (X+Z)
X (Y+Z) = XY +XZ
4.-Teorema del consenso
AB+A’C+BC = AB+A’C
5.-Teorema de Dmorgan
(AB)’=A’+ B’ (A+B)’=A’ B’
A+B =(A’ B’)’ AB =(A’+B’)’
AND OR
A A=A A + A=A
A 0 =0 A + 0 = A
A 1 =A A + 1 =1
A A’ =0 A+A’ =1

7. 1.-Identidades
2.- Factorización
AB’ + AB = A(B’+B)= A
3.- Propiedad Distributiva
X+YZ = (X+Y) (X+Z)
X (Y+Z) = XY +XZ
4.-Teorema del consenso
AB+A’C+BC = AB+A’C
5.-Teorema de Dmorgan
(AB)’=A’+ B’ (A+B)’=A’ B’
A+B =(A’ B’)’ AB =(A’+B’)’
AND OR
A A=A A + A=A
A 0 =0 A + 0 = A
A 1 =A A + 1 =1
A A’ =0 A+A’ =1