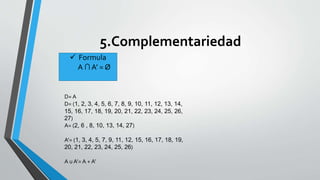
This document discusses set theory concepts like union, intersection, properties of sets, and complementarity. It provides examples of applying properties like idempotence, commutativity, associativity, and distribution to sets A, B, and C. It shows calculations of the union and intersection of sets A, B, and C to verify that they satisfy the properties. Finally, it demonstrates that set A satisfies complementarity by calculating the union of set A with its complement A'.

1. Teoría de Conjuntos
Bachiller:
Hurtado Valentina
C.I: 23.997.291
Republica Bolivariana de Venezuela
Ministerio del Poder Popular para la Educación Superior
I.U.P “Santiago Mariño”
Escuela de Ing. de Sistemas.
Sede Barcelona.

2. Para empezar se debe tener claro que…
Un conjunto es la reunión de
objetos bien definidos y
diferenciables entre si, que se
encuentran en un momento dado.

3. A continuación los siguientes conceptos:
• Unión: Se llama unión de dos conjuntos A y B al conjunto formado por
objetos que son elementos de A o de B, es decir:
A u B
• Intersección: Se llama intersección de dos conjuntos A y B al conjunto
formado por objetos que son elementos de A y de B, es decir:
A ∩ B
Es el conjunto que contiene a todos los elementos de A que al mismo tiempo
están en B.

4. Utilizaremos las siguientes leyes de Conjuntos:
Propiedades Unión Intersección
Idempotencia A u A= A A ∩ A= A
Conmutativa A u B= B uA A ∩ B= B ∩A
Asociativa A u (B u C)= (A u B) u C A ∩ (B ∩ C) = (A ∩ B) ∩ C
Distributiva A u (B ∩ C)= (A u B) ∩ (A u C) A ∩ (B u C) = (A ∩ B) u (A ∩ C)
Complementariedad A u A’ = U A ∩ A’ = Ø

5. Utilizaremos los conjuntos:
A= (2, 6 , 8, 10, 13, 14, 27)
B= (1, 6, 11, 14, 20, 27, 30)
C= (4, 6, 8, 11, 17, 19, 22, 27, 35, 40, 41)
D= ( A, B, C)

6. Ejercicios

7. 1.Idempotencia
 Formula:
A uA= A
A u A= (2, 6 , 8, 10, 13, 14, 27) u (2, 6 , 8, 10, 13, 14, 27)
= (2, 6 , 8, 10, 13, 14, 27)

8. 2. Conmutativa
 Formula
A u B= B u A
A u B= A + B – A ∩ B
A u B= (2, 6 , 8, 10, 13, 14, 27) +(1, 6, 11, 14, 20, 27, 30) – (6, 14, 27)
A u B= (1, 2,8, 10, 11, 13, 20, 27, 30)
Esto es igual a:
B u A= B + A – B ∩ A
B u A= (1, 6, 11, 14, 20, 27, 30) + (2, 6 , 8, 10, 13, 14, 27) - (6, 14, 27)
B u A= (1, 2,8, 10, 11, 13, 20, 27, 30)

9. 3. Asociativa
 Formula
A u (B u C)= (A u B) u C
(B u C)= B + C – B ∩ C
(B u C)= (1, 6, 11, 14, 20, 27, 30) + (4, 6, 8, 11, 17, 19, 22, 27, 35, 40, 41)
– (6, 11, 27)
B u C= (1, 6, 11, 14, 20, 27, 30, 4, 8, 17, 19, 22, 35, 40, 41)
A u (B u C)= (2, 6 , 8, 10, 13, 14, 27) + (1, 6, 11, 14, 20, 27, 30, 4, 8, 17, 19,
22, 35, 40, 41) – (6, 8, 14, 27)
A u ( B u C)= (1, 2, 4, 6, 8, 10, 11, 13, 14, 17, 19, 20, 22, 27, 30,35, 40, 41)

10. 4. Distributiva
 Formula
A u (B ∩ C)= (A u B) ∩ (A u C)
Como A u B es conmutativa
(B ∩ C)= (1, 6, 11, 14, 20, 27, 30) ∩ (4, 6, 8, 11, 17, 19, 22, 27, 35, 40, 41)
(B ∩ C)= ( 6, 11,27)
A u (B ∩ C)= {A+ ( B ∩ C) } – A ∩ (B ∩ C)
A u (B ∩ C)= (2, 6 , 8, 10, 13, 14, 27) + ( 6, 11,27)
A u (B ∩ C)= (2, 6, 8, 10, 11, 13, 14, 27)

11. 4.1 Distributiva A u (B ∩ C)= (A u B) ∩ (A u C) si la
formula es cumplida es distributiva.
A u B= (2, 6 , 8, 10, 13, 14, 27) + (1, 6, 11, 14, 20, 27, 30) - (6, 14, 27)
A u B= (1, 2,8, 10, 11, 13, 20, 27, 30)
A u C= A + C- A ∩ C
A u C= (2, 6 , 8, 10, 13, 14, 27) + (4, 6, 8, 11, 17, 19, 22, 27, 35, 40, 41) –
(6, 8, 27)
A u C= (2, 4, 6, 8, 10, 11, 13, 14, 17, 19, 22, 27, 35, 40, 41)
(A u B) ∩ (A u C)= (1, 2,8, 10, 11, 13, 20, 27, 30) ∩ (2, 4, 6, 8, 10, 11, 13, 14,
17, 19, 22, 27, 35, 40, 41)
(A u B) ∩ (A u C)= (2, 8, 10, 11, 13, 27)

12. 5.Complementariedad
 Formula
A ∩ A’ = Ø
D= A
D= (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14,
15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26,
27)
A= (2, 6 , 8, 10, 13, 14, 27)
A’= (1, 3, 4, 5, 7, 9, 11, 12, 15, 16, 17, 18, 19,
20, 21, 22, 23, 24, 25, 26)
A u A’= A + A’

13. 5.1 Complementariedad
Si A u A’ = Ø
el conjunto es de
complementariedad.
A u A’= A + A’
A u A’= (2, 6 , 8, 10, 13, 14, 27) + (1, 3, 4, 5,
7, 9, 11, 12, 15, 16, 17, 18, 19, 20, 21, 22,
23, 24, 25, 26)
A u A’= (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13,
14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25,
26, 27)