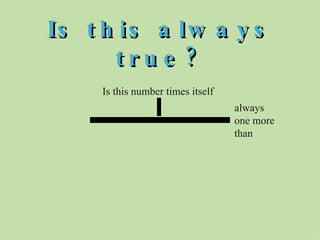
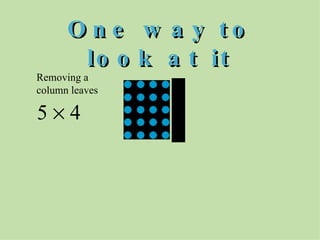
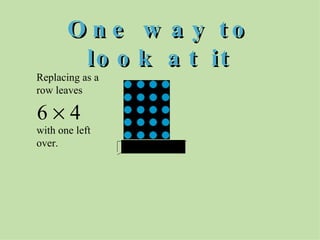
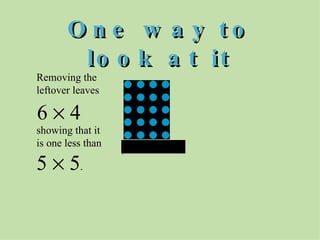
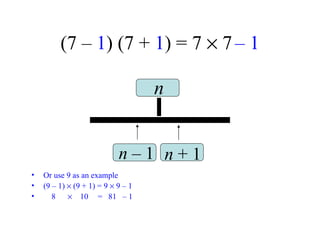
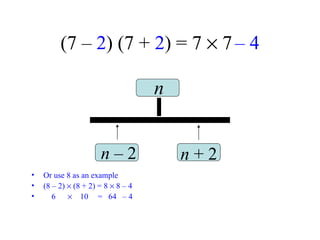
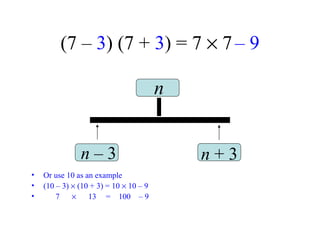
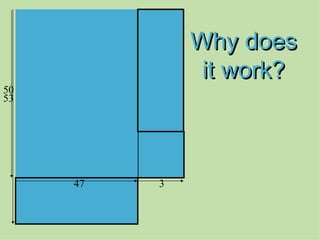
The document discusses methods for helping students memorize multiplication facts. It suggests starting with knowing basic facts like 4 x 4 and using those to derive other facts. Students are quizzed on facts to make the process more engaging. The document then explores patterns in multiplication, like the rule that a number times itself is always one more than the product of that number minus one times itself plus one. These patterns provide shortcuts to derive new facts and build understanding of multiplication relationships.

1. … what could be less sexy than memorizing 4th grade multiplication facts?

2. Just the facts Start by knowing 4  4, 5  5, 6  6, 7  7, … Have most others and easily work out what they don’t have memorized. Goal now is to consolidate!

3. What helps kids memorize multiplication facts? Something memorable!

4. Surprise What is 6  6?

5. Surprise What is 6  6? What is 5  7?

6. Surprise What is 6  6? What is 5  7? 36 35

7. Surprise What is 7  7?

8. Surprise What is 7  7? What is 6  8? 49 48

9. Surprise What is 8  8?

10. Surprise What is 8  8? What is 7  9? 64 63

11. Surprise What is 9  9?

12. Surprise What is 9  9? What is 8 x 10?

13. Surprise What is 9  9? What is 8  10? 81 80

14. Is this always true?

15. Is this always true? always one more than Is this number times itself

16. Is this always true? always one more than Is this number times itself the product of these two numbers?

17. But why does it work?!

18. One way to look at it 5  5

19. One way to look at it 5  4 Removing a column leaves

20. One way to look at it 6  4 Replacing as a row leaves with one left over.

21. One way to look at it 6  4 Removing the leftover leaves showing that it is one less than 5  5 .

22. A second look Removing a column leaves it narrower by 1.

23. A second look Replacing as a row leaves it narrower by 1 and taller by 1 (with 1 left over).

24. What’s the gain? An aid for remembering 6  8 or 7  9 7  7 = 49 6  8 = 48 (6  8) = (7  7) - 1 Direct benefit!

25. What’s the gain? An aid for remembering 6  8 or 7  9 7  7 = 49 6  8 = 48 (6  8) = (7  7) – 1 A practical tool for (some) calculations A hint at a BIG IDEA lurking Investment in the future!

26. Further Investigation In the process of taking this idea further, the children get more multiplication practice. Is there a pattern that lets us use 7  7…

27. Further Investigation In the process of taking this idea further, the children get more multiplication practice. Is there a pattern that lets us use 7  7 to derive 5  9?

28. Experiment a moment Find a pattern that shows how 7  7 relates to 5  9…

29. Experiment a moment … or how 8  8 relates to 6  10…

30. Experiment a moment … or how 9  9 relates to 7  11…

31. (7 – 1 ) (7 + 1 ) = 7  7 – 1 Or use 9 as an example (9 – 1)  (9 + 1) = 9  9 – 1 8  10 = 81 – 1 n n – 1 n + 1

32. (7 – 2 ) (7 + 2 ) = 7  7 – 4 Or use 8 as an example (8 – 2)  (8 + 2) = 8  8 – 4 6  10 = 64 – 4 n n – 2 n + 2

33. (7 – 3 ) (7 + 3 ) = 7  7 – 9 Or use 10 as an example (10 – 3)  (10 + 3) = 10  10 – 9 7  13 = 100 – 9 n n – 3 n + 3

34. Where does this lead?

35. Where does this lead? To do… 53  47

36. Where does this lead? To do… …I think… 53 3 more than 50  47

37. Where does this lead? To do… …I think… 53 3 more than 50  47 3 less than 50 50  50 (well, 5  5 and …) … 2500 Minus 3  3 – 9

38. Where does this lead? To do… …I think… 53 3 more than 50  47 3 less than 50 50  50 (well, 5  5 and …) … 2500 Minus 3  3 – 9 2491

39. Why does it work? 47 3 50 53

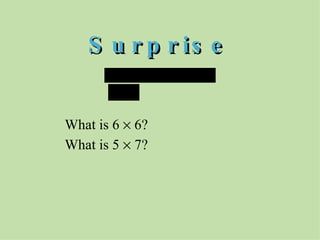
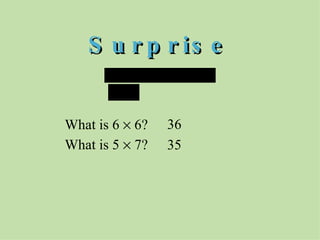
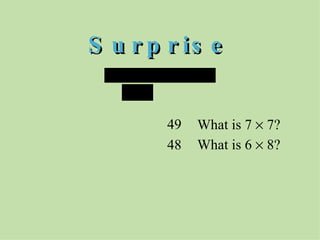
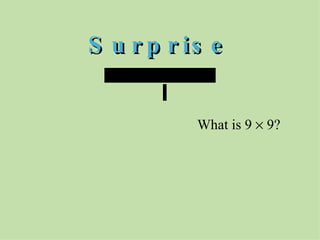
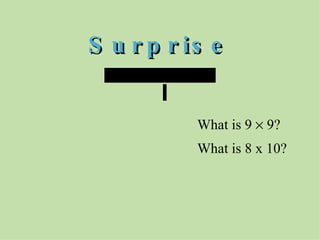
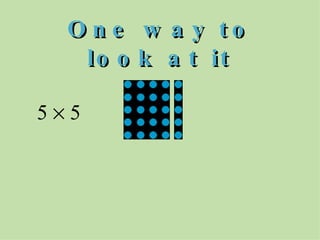
40. www 2 .edc.org/mathworkshop Thanks! E. Paul Goldenberg [email_address] Contact Information

41. www 2 .edc.org/mathworkshop Bye! Thanks! E. Paul Goldenberg [email_address] Contact Information