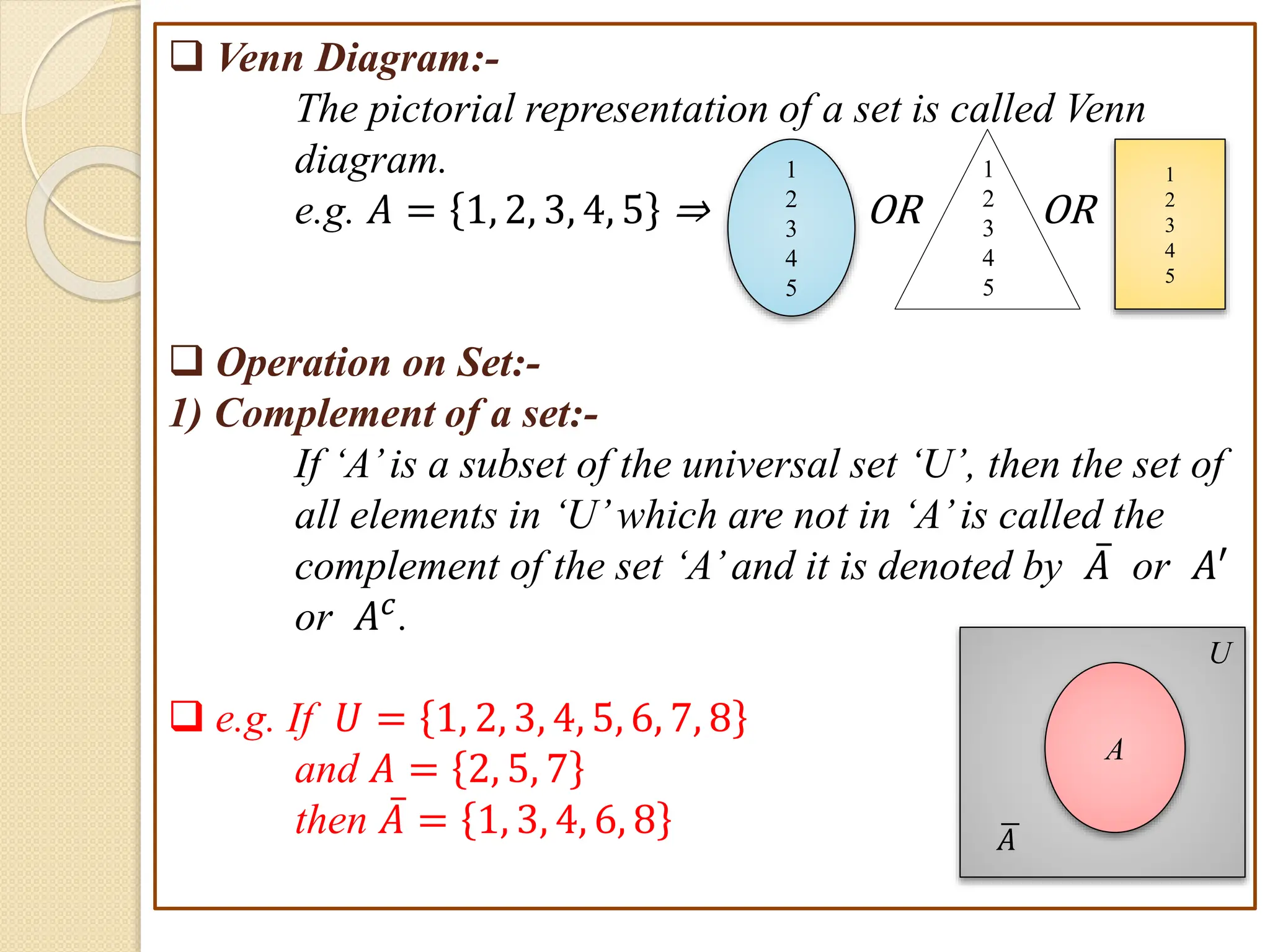
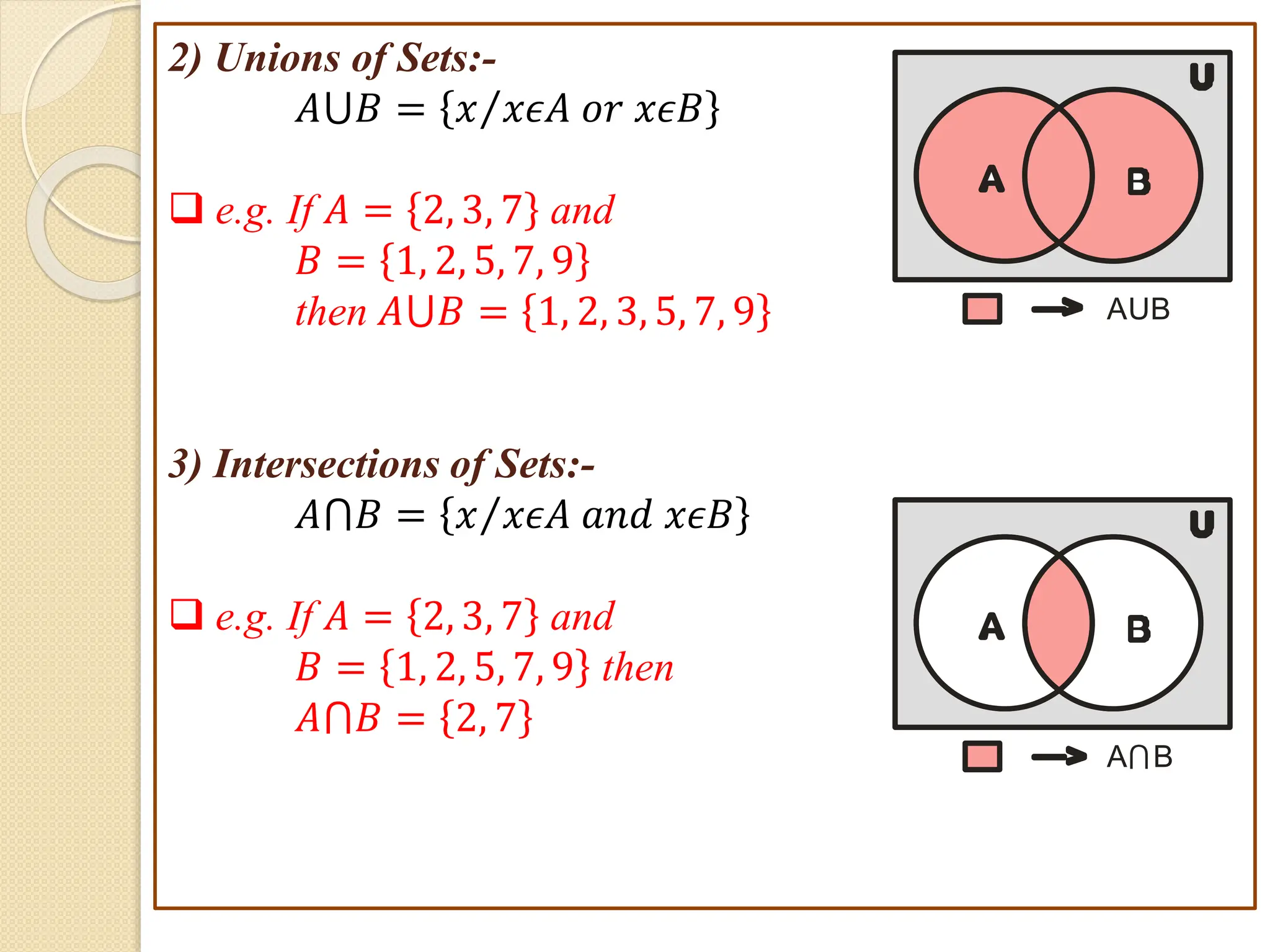
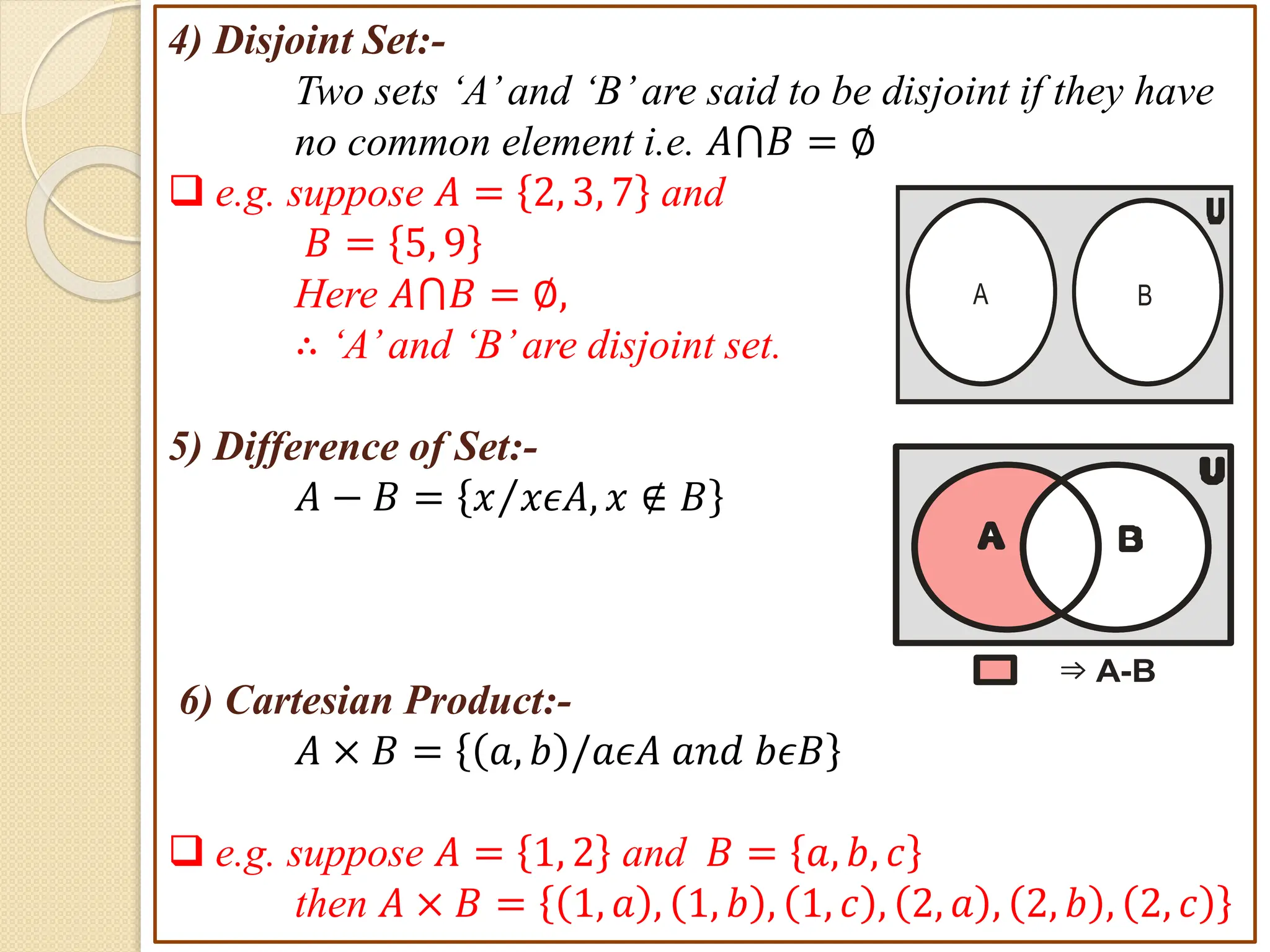
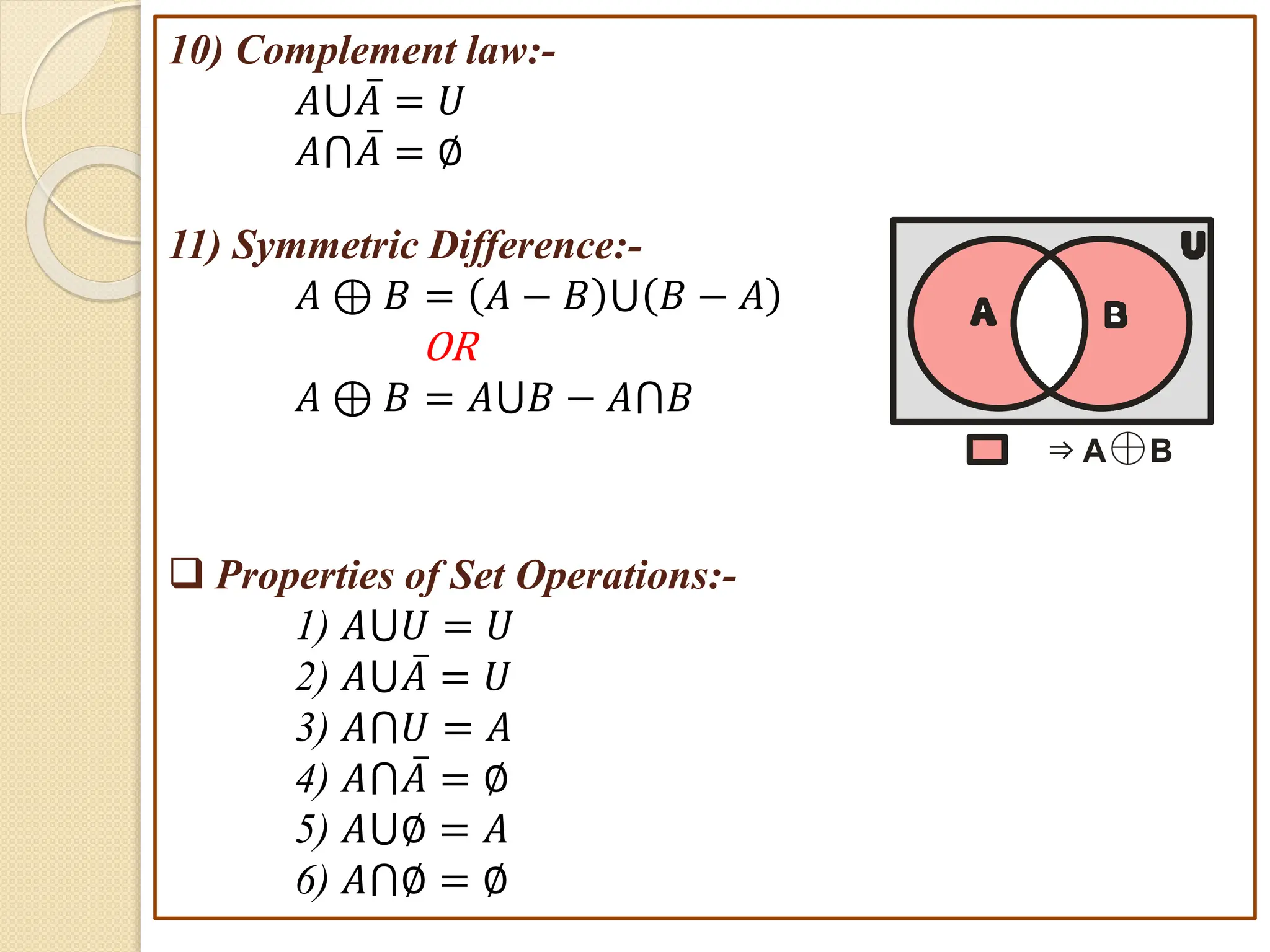
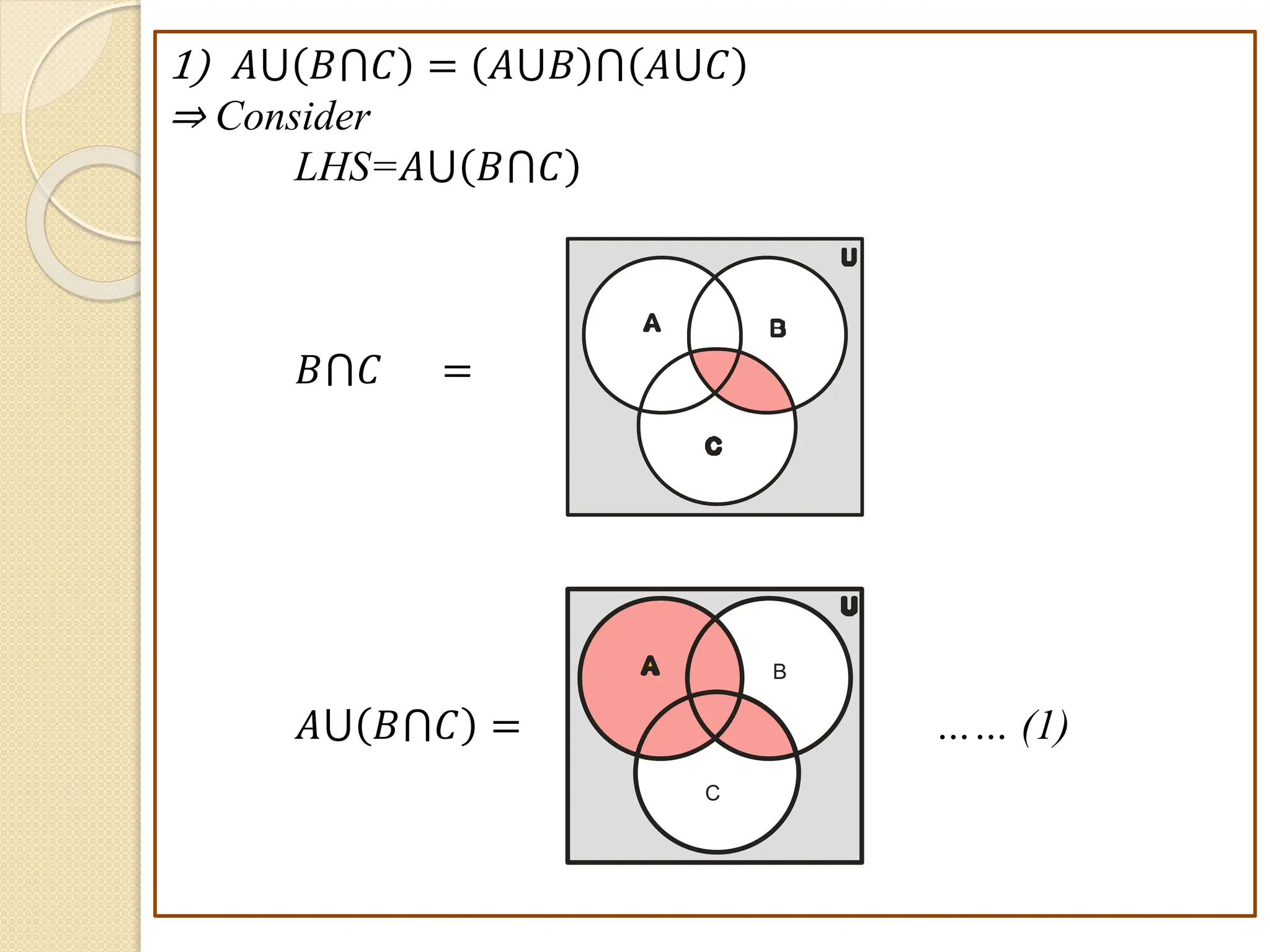
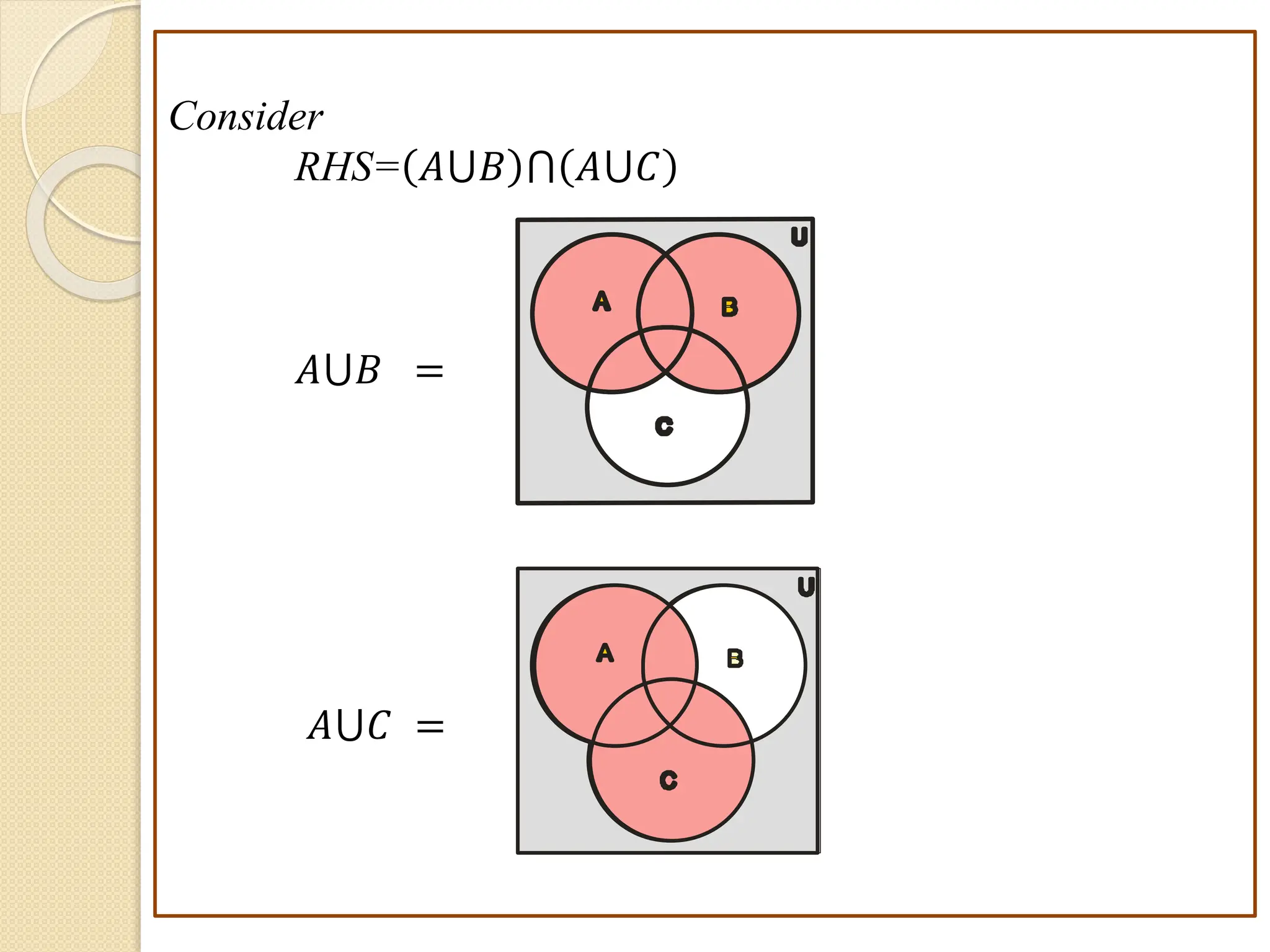
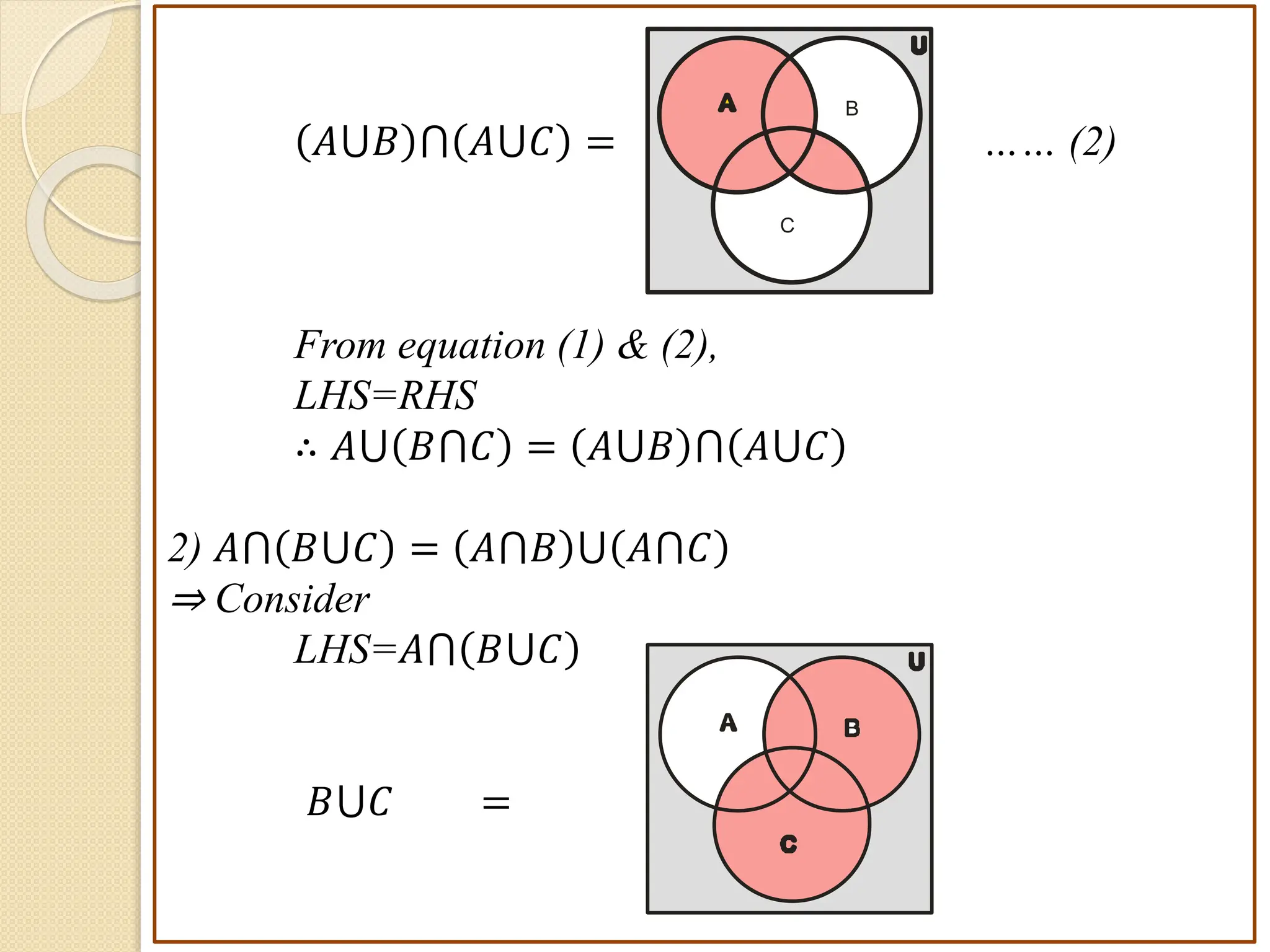
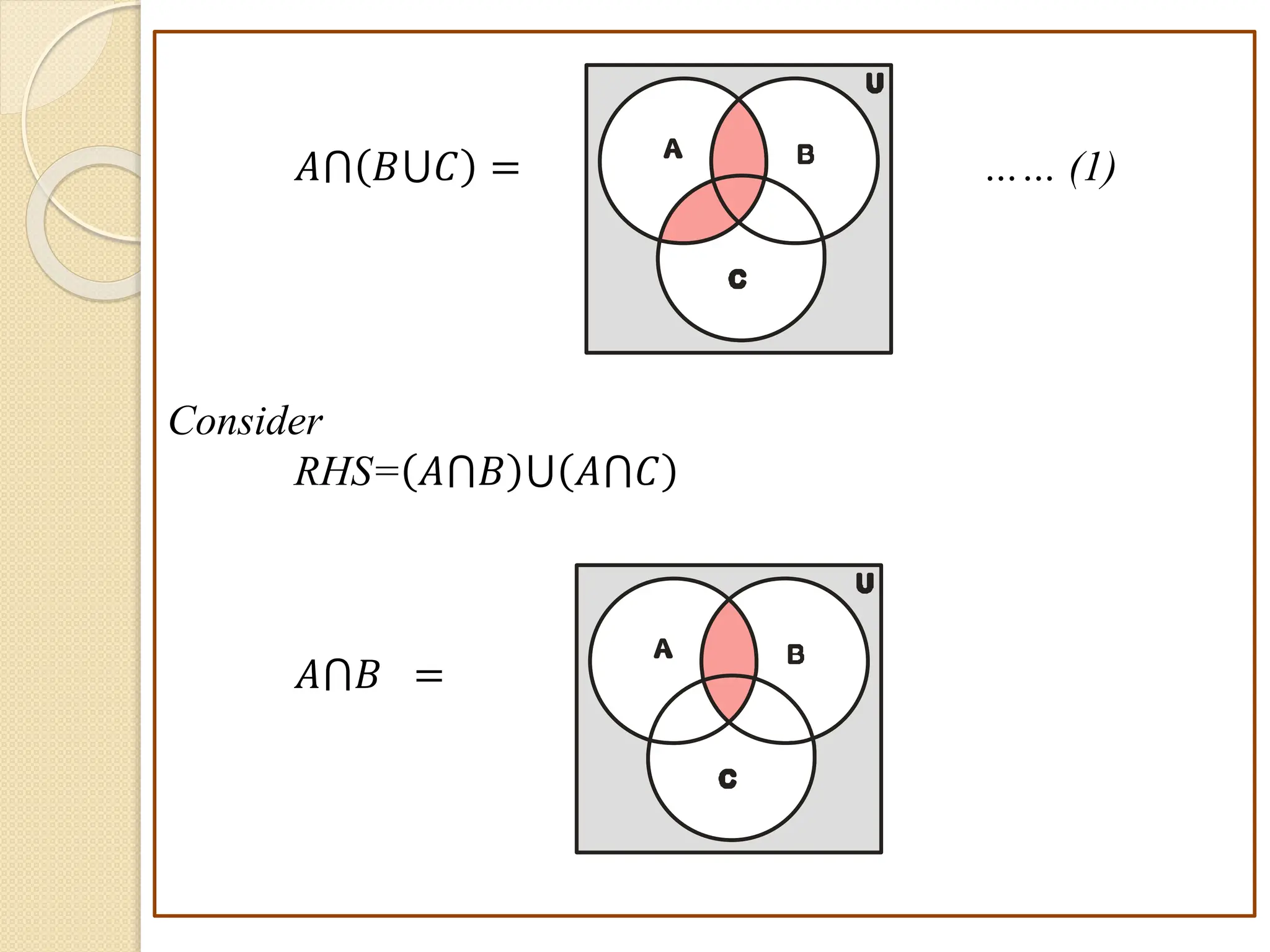
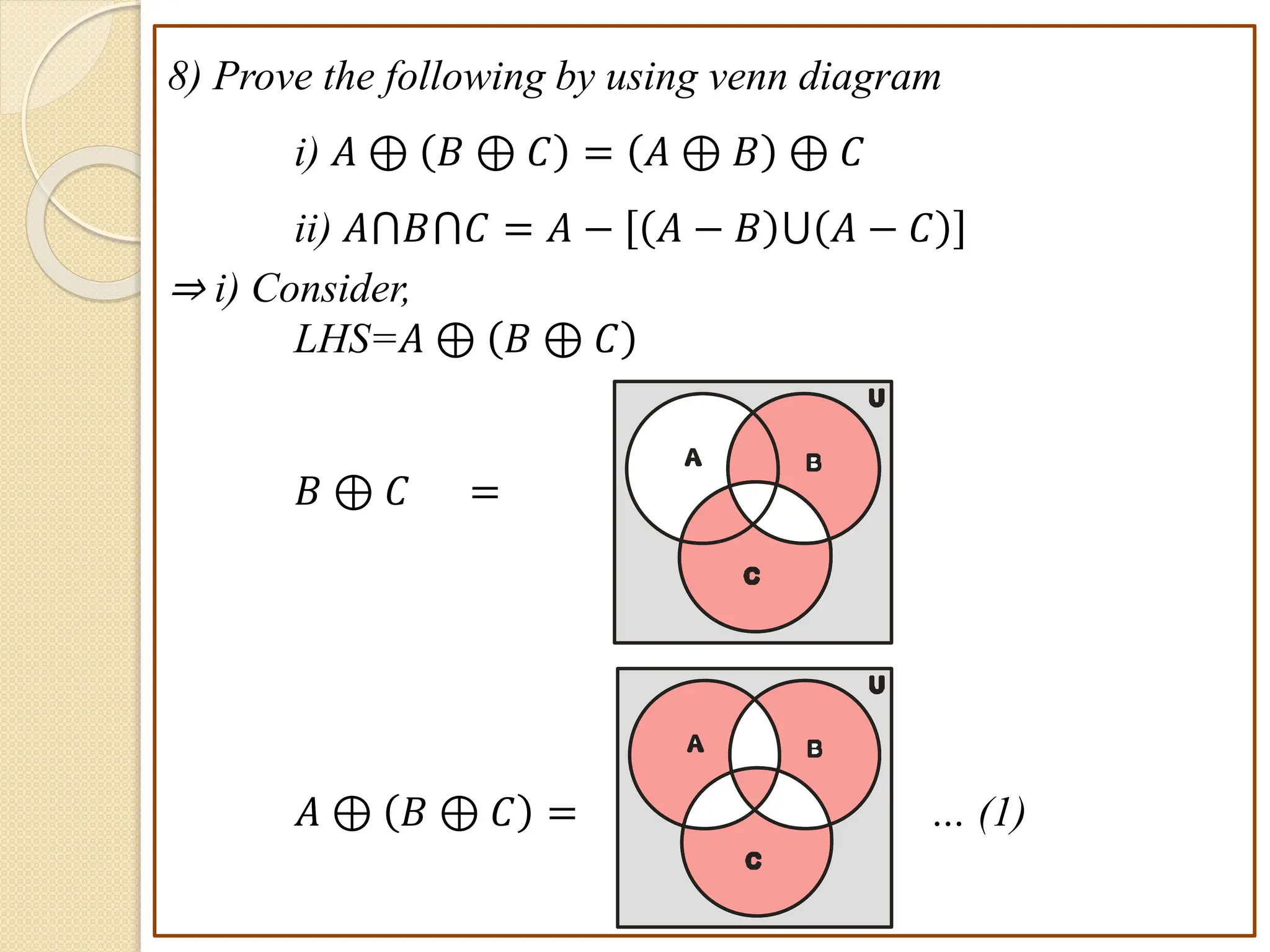
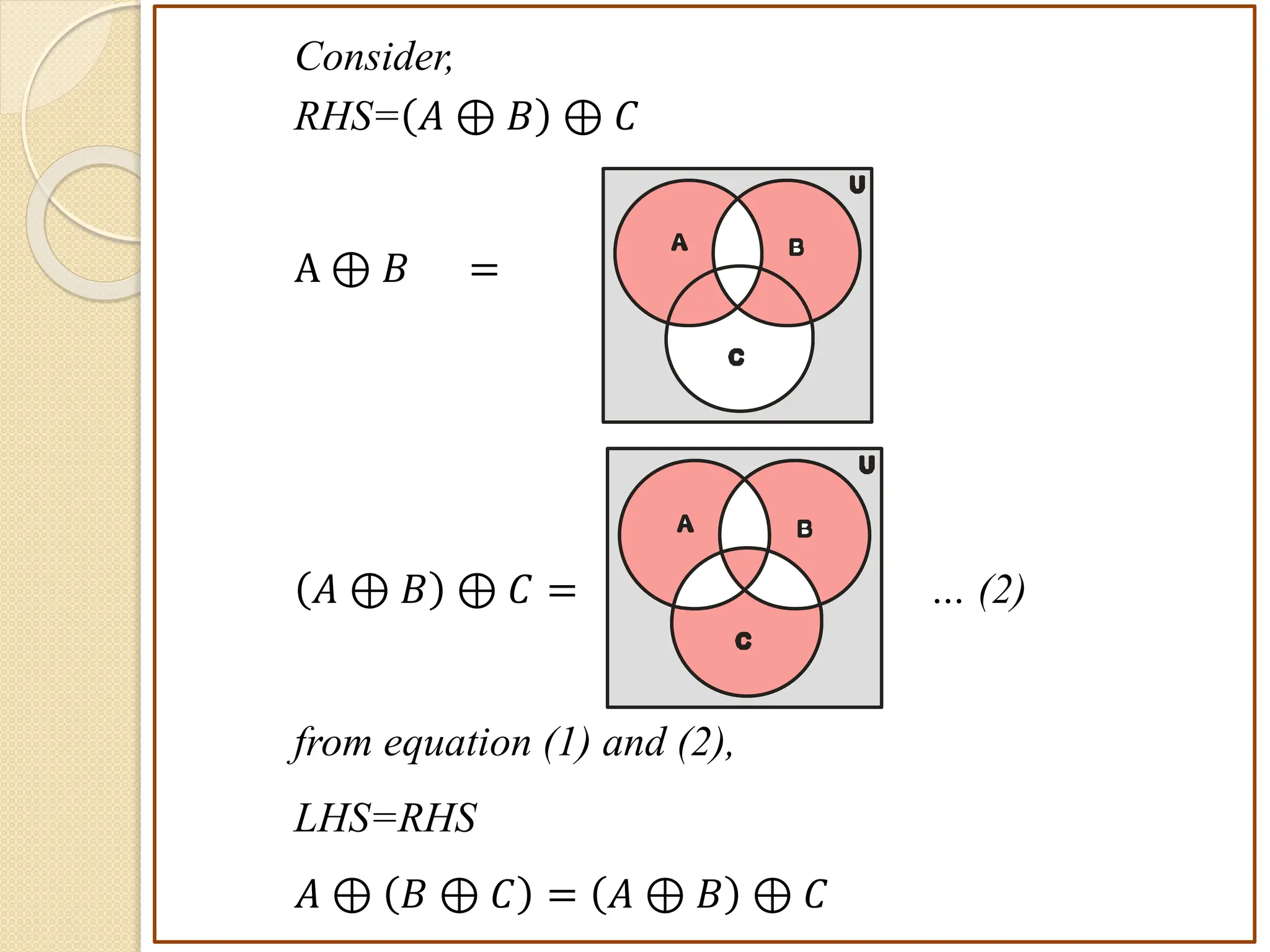
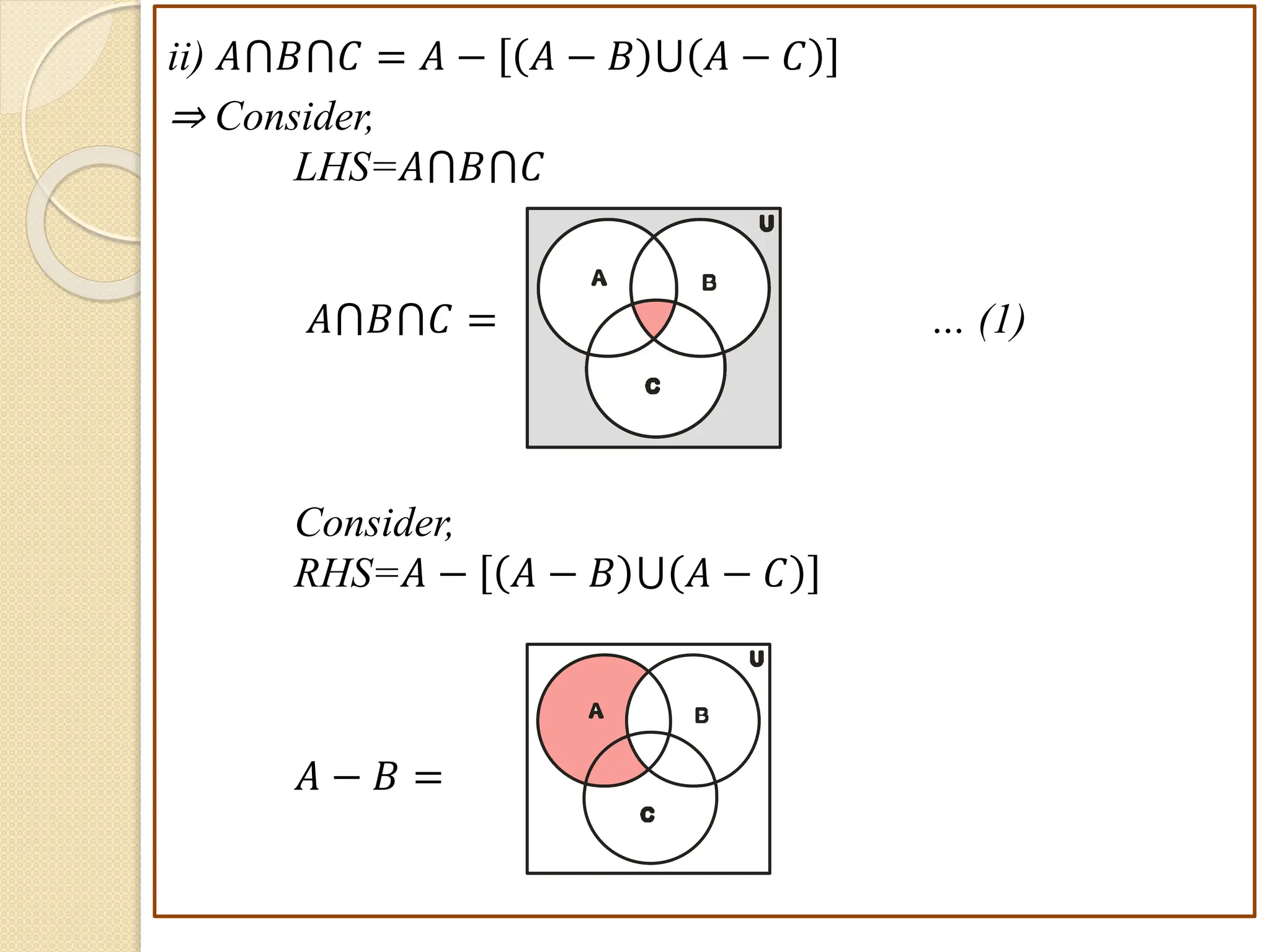
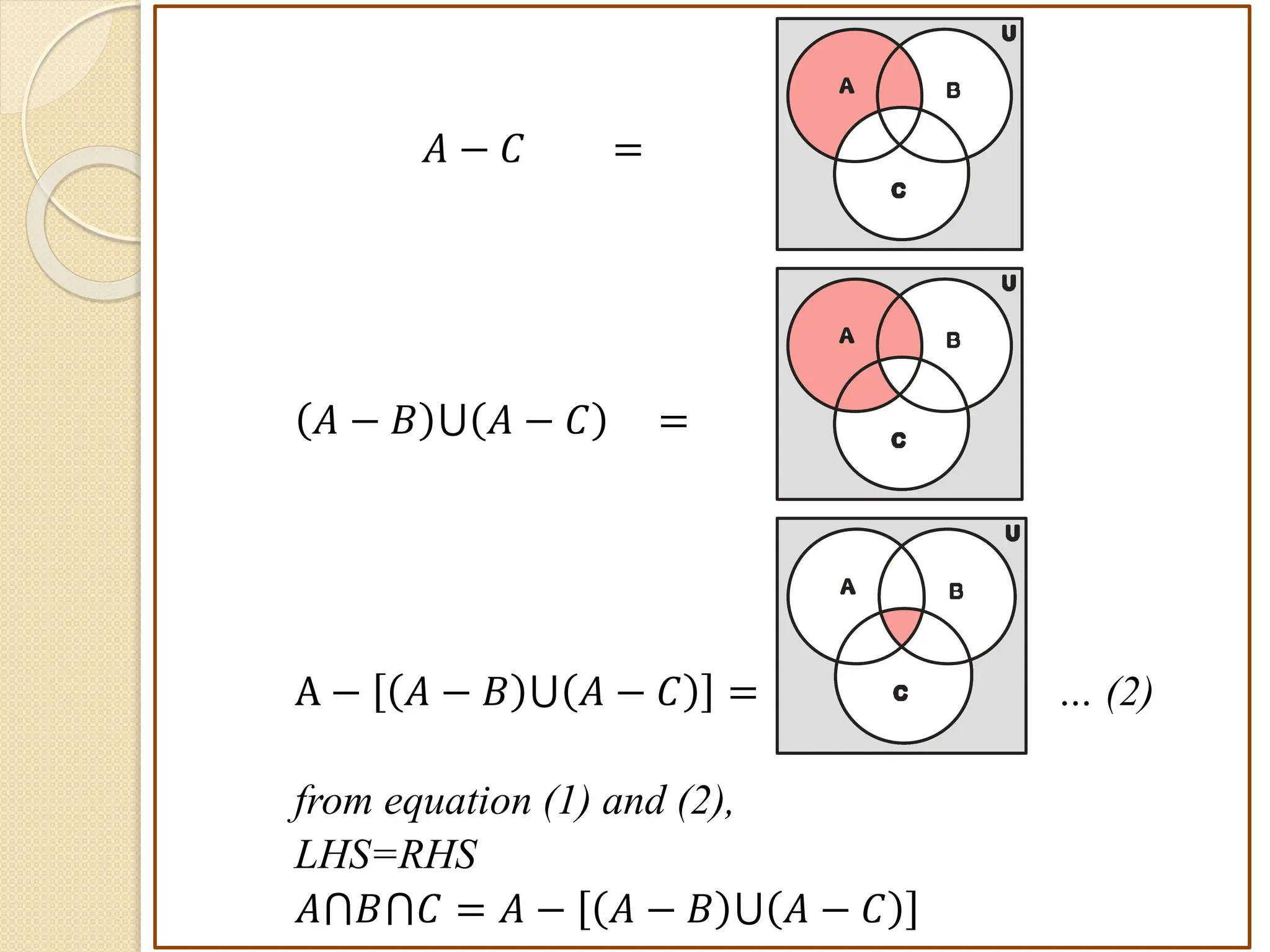
1. This document discusses concepts from set theory and logic that are covered in the Discrete Mathematics course taught by Prof. V. A. Kshirsagar at JSPM's Imperial College of Engineering & Research. 2. Key concepts covered include sets and their elements, operations on sets like union and intersection, different types of sets such as finite and infinite sets, and properties of sets and set operations. 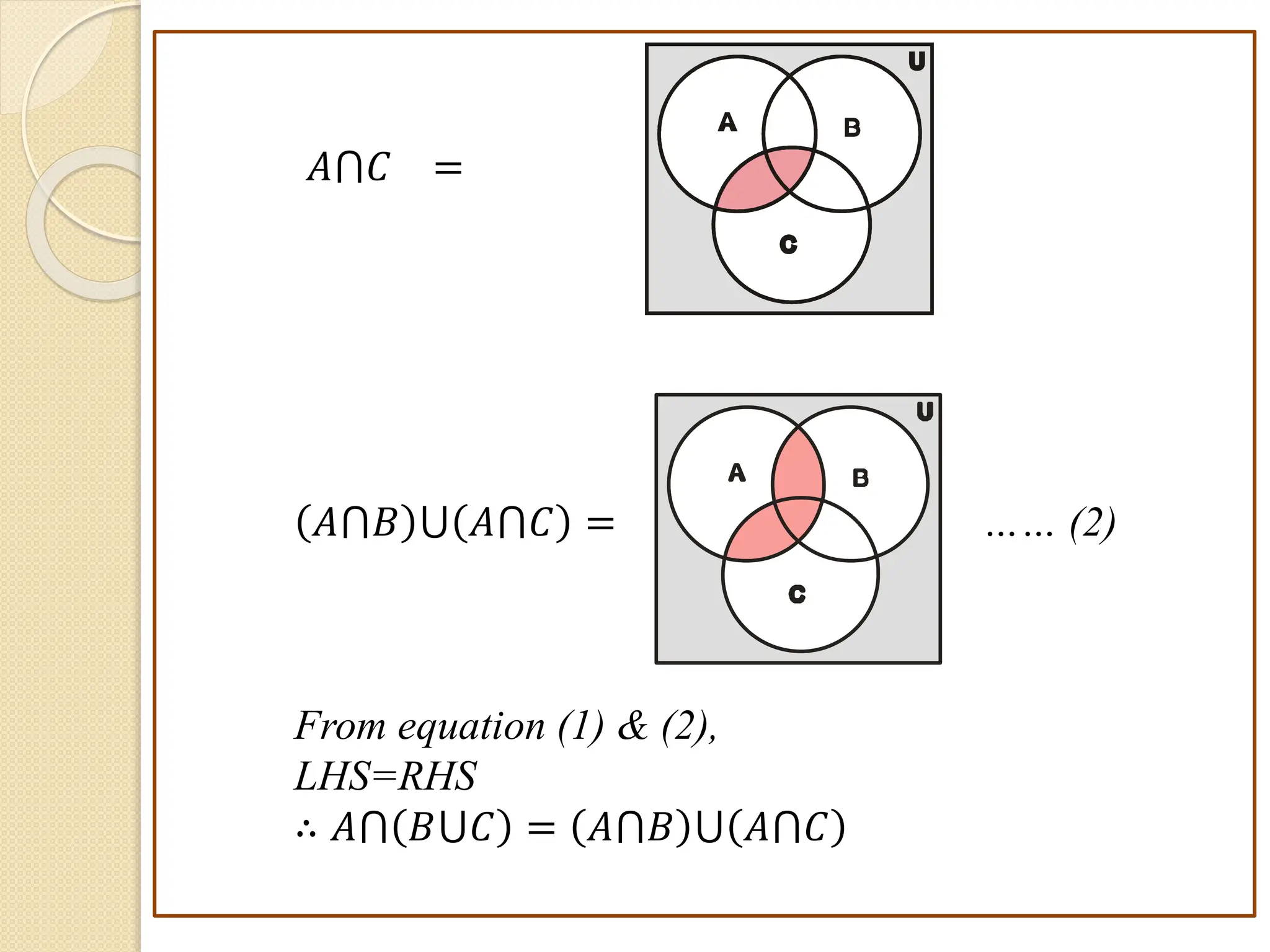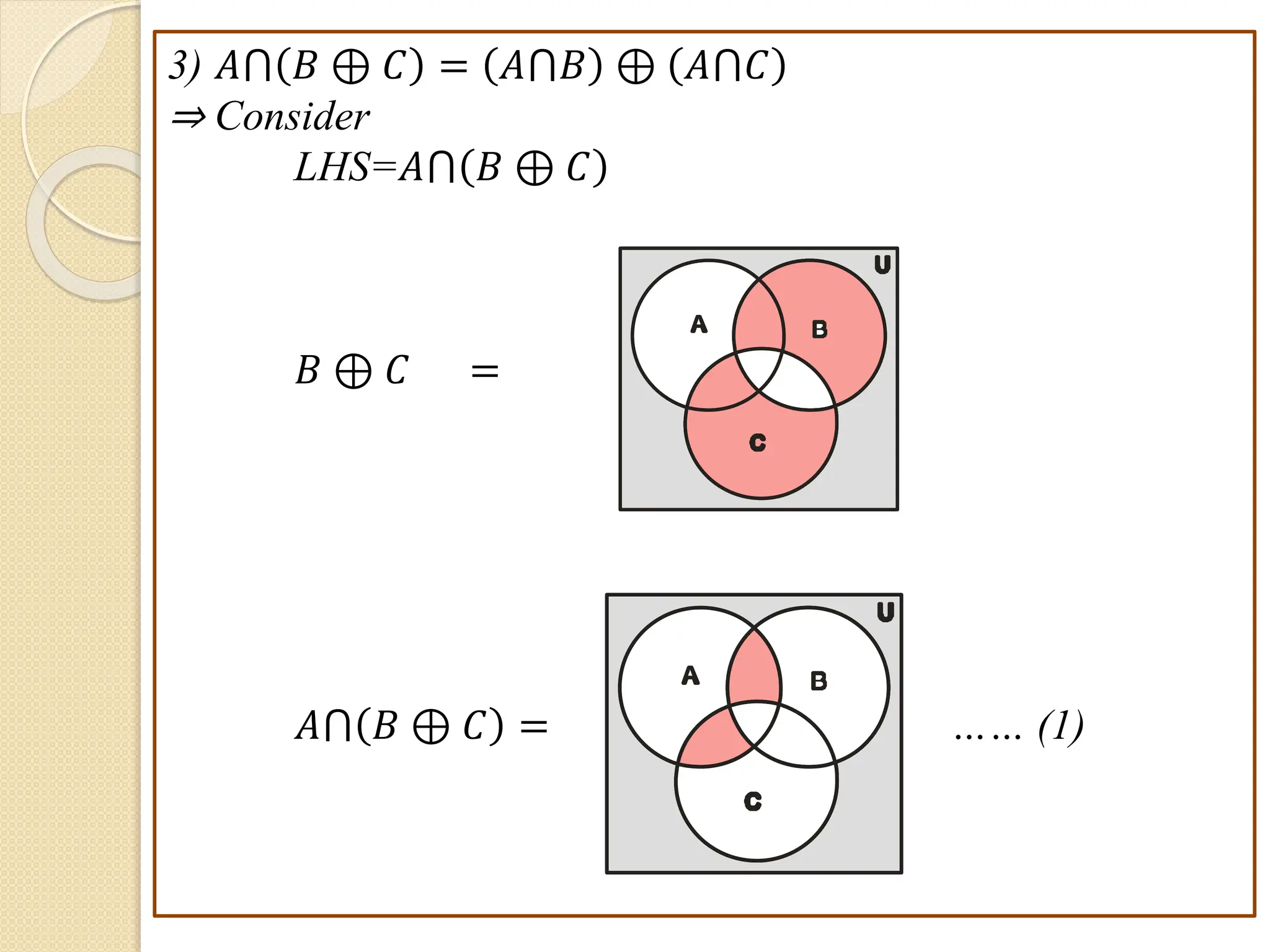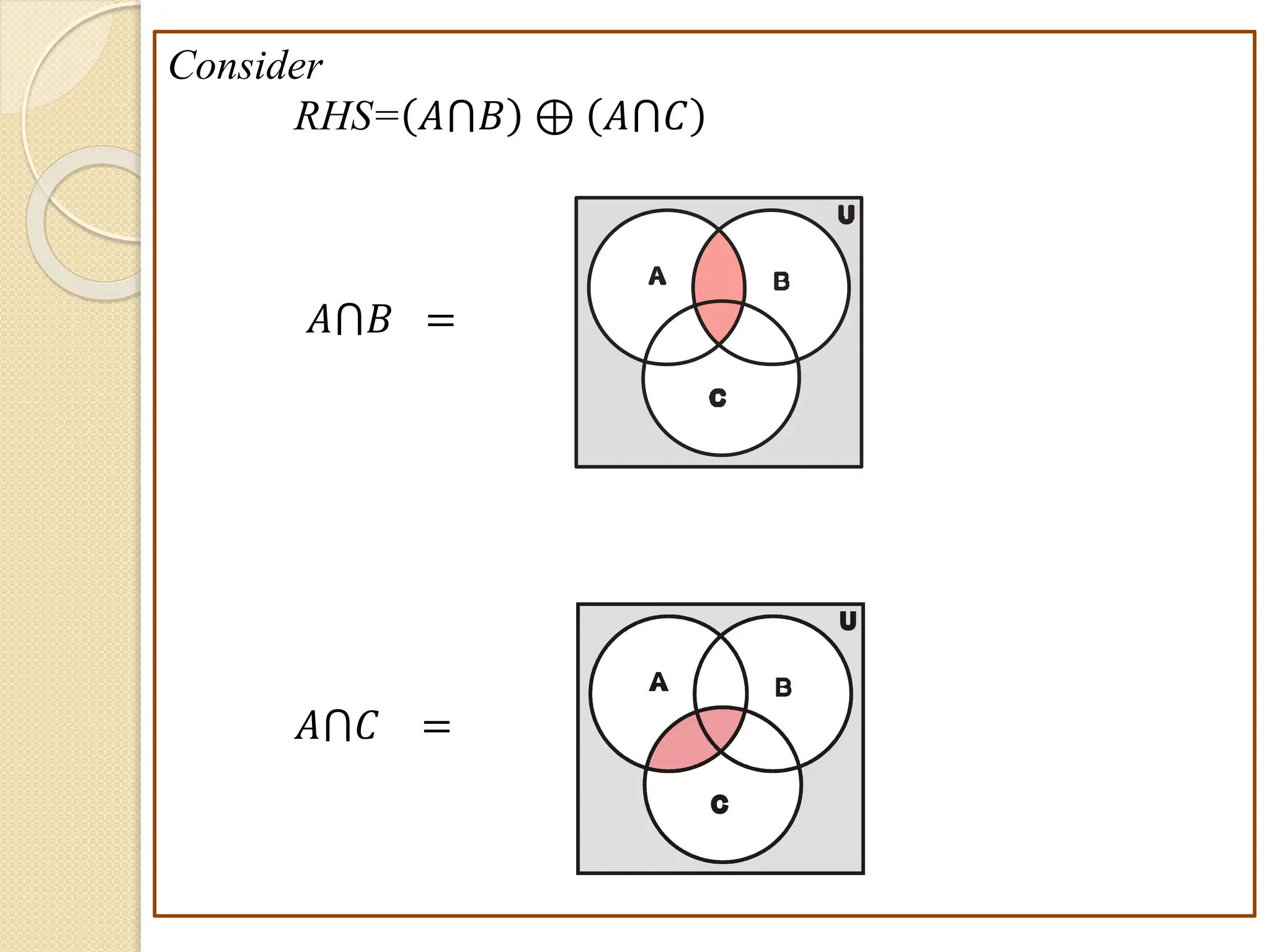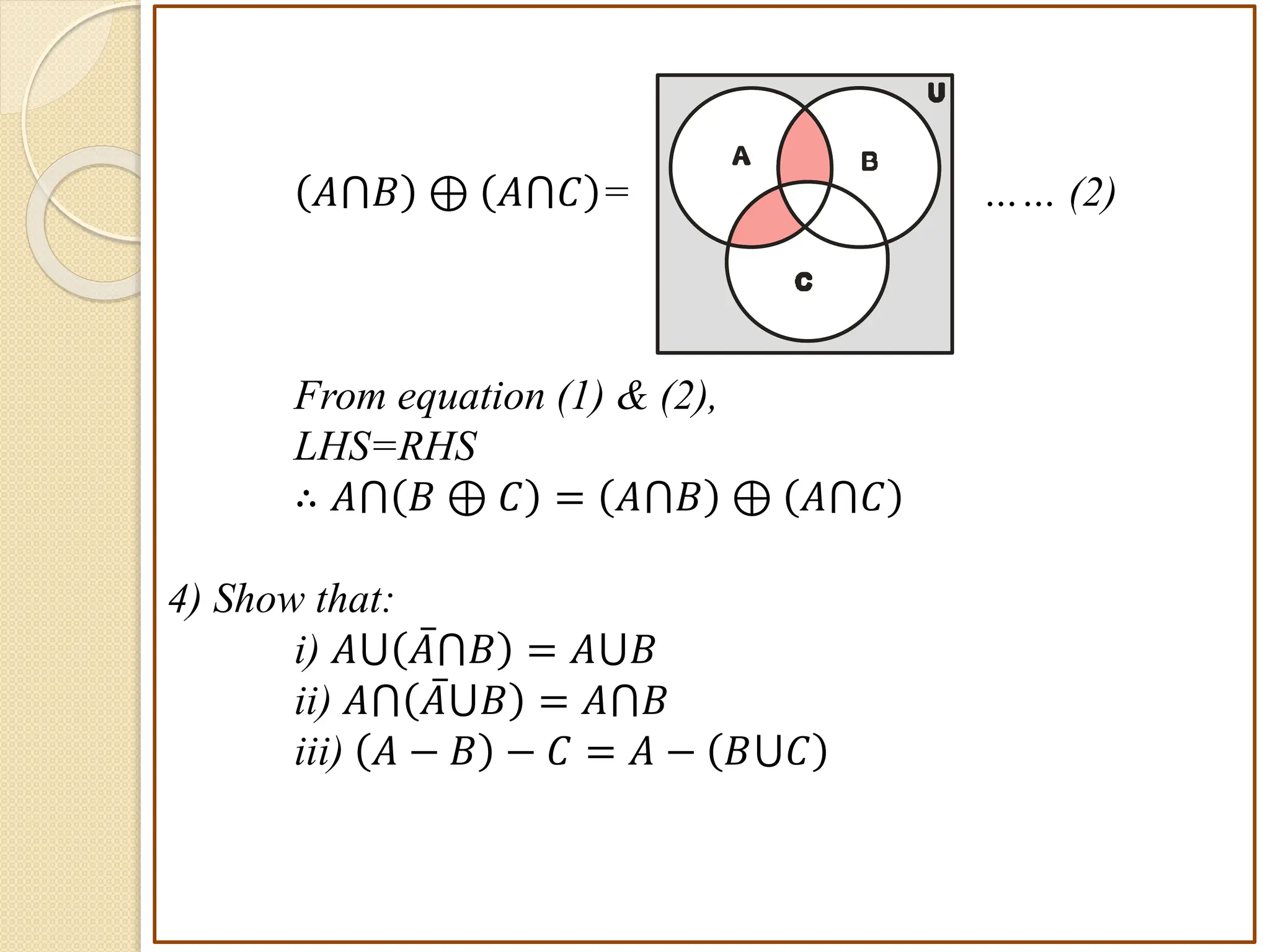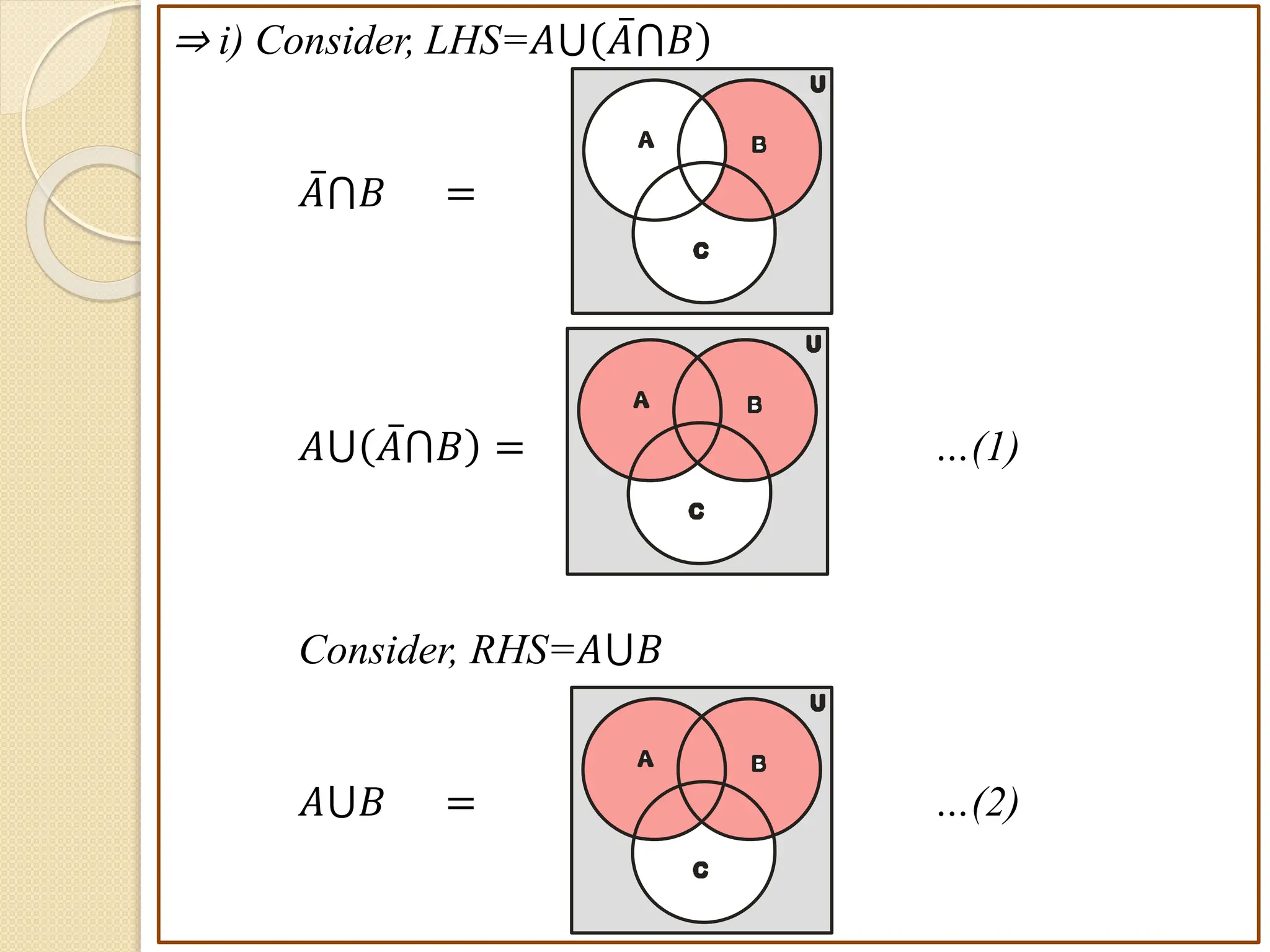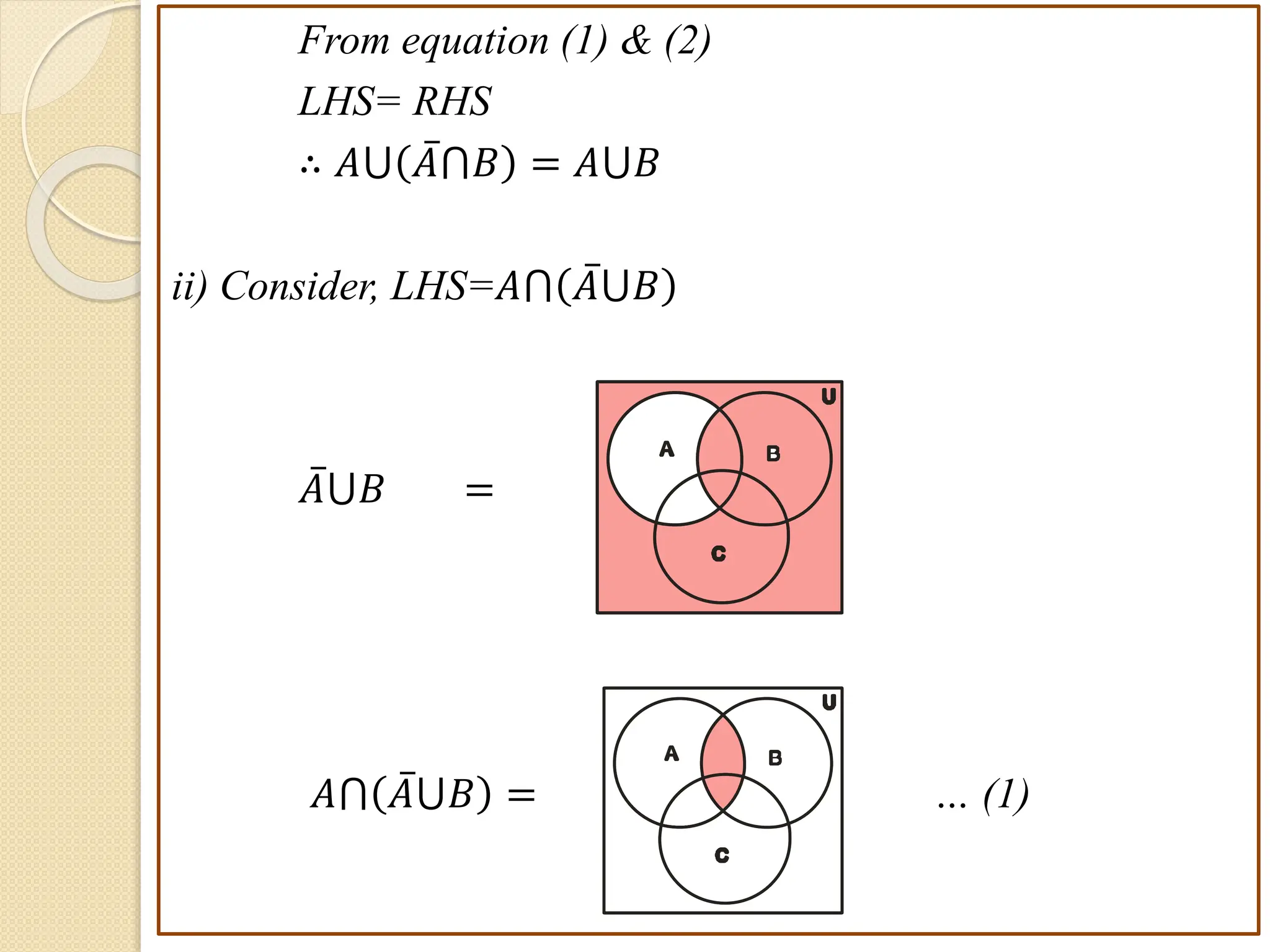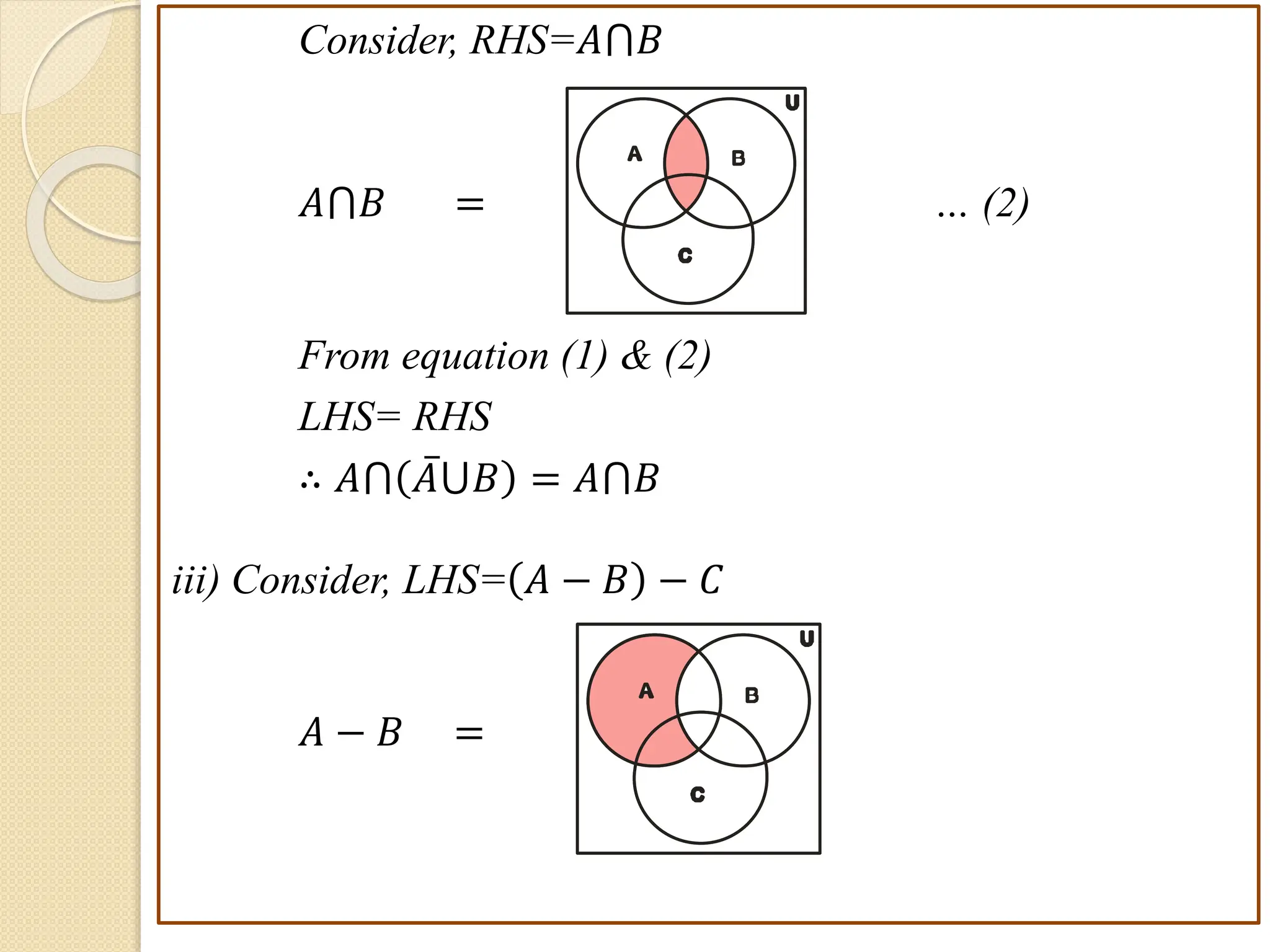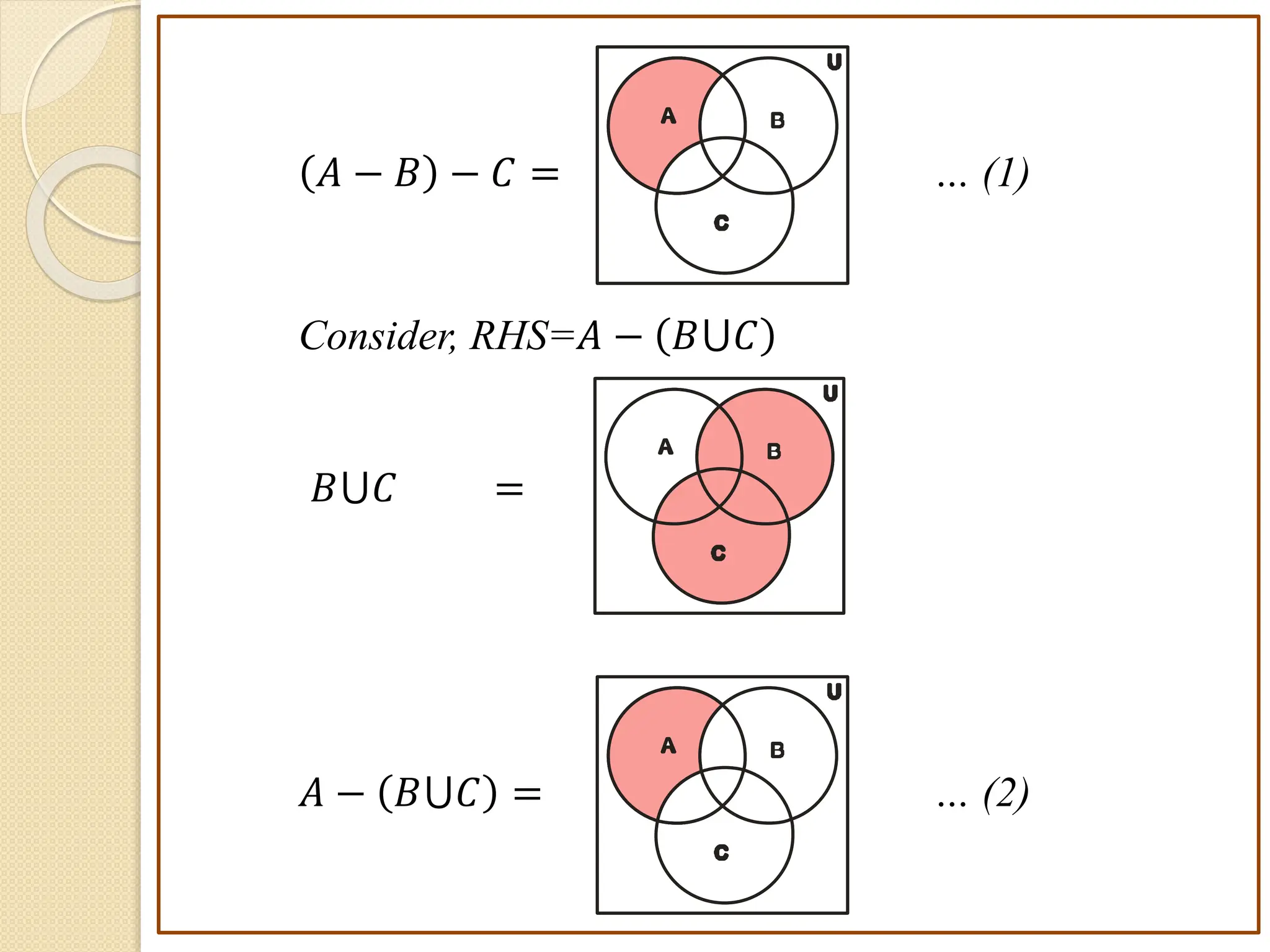3. Examples are provided to illustrate set notation, representation of sets, subset and superset relationships between sets, and operations on sets.

1. Discrete Mathematics
Prof. V. A. Kshirsagar
Contact-7387904685
JSPM’s
Imperial College of Engineering &
Research, Wagholi, Pune.
Department of Computer Engineering

2. Unit-I: Set Theory and Logics
Set Theory :-
The concept of Set is developed by German
mathematician ‘George Cantor’in 1879.
Set:-
Collection of well defining objects is said to be
Set.
* well defining objects means element or
members of Set.
* set is denoted by capital letters A, B, C,
etc.
* elements of set are denoted by small letters
a, b, c, etc.

3. e.g.
1) Successful person in your City.
⇒ not set
2) Clever Students in your class.
⇒ not set
3) Happy people in your town.
⇒ not set
4) Number of days in a week.
⇒ set
𝐴 = 𝑀𝑜𝑛, 𝑇𝑢𝑒𝑠, 𝑊𝑒𝑑, 𝑇ℎ𝑢𝑟𝑠, 𝐹𝑟𝑖, 𝑆𝑎𝑡𝑢𝑟, 𝑆𝑢𝑛
5) First five natural numbers.
⇒ set
𝐵 = 1, 2, 3, 4, 5

4. e.g
 Example:
1) Set of vowels.
⇒ V = 𝑎, 𝑒, 𝑖, 𝑜, 𝑢 = Set of vowels
* here ‘a’is element of set ‘V’, i.e. a ϵ V
*lly e, i, o, u are elements of ‘V’, i.e. e, i, o, u ϵ V
*here ‘b’is not element of set ‘V’, i.e. b ∉ V
2) Set of odd positive integer less than 11.
⇒ C = 1, 3, 5, 7, 9
3) Set of positive integer less than 1000.
⇒ D = 1, 2, 3, … … , 999
4) Set of even positive integer less than 10.
⇒ E = 2, 4, 6, 8

5.  Set can be represented by using three methods.
1. Listing Method
2. Statement Method
3. Set-Builder Method
 e.g.
1. Set of natural numbers less than or equal to 10
⇒ F = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
* Listing Method ⇒ F = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
* Statement Method ⇒ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 are
elements of set ‘F’
*Set-Builder Method ⇒ F = 𝑥 𝑥𝜖ℕ, 0 < 𝑥 ≤ 10
2. Set of negative integer grether than or equal to -5
⇒ G = −5, −4, −3, −2, −1
* Listing Method ⇒ G = −5, −4, −3, −2, −1
* Statement Method ⇒ −5, −4, −3, −2, −1 are
elements of set ‘G’
*Set-Builder Method ⇒ G = 𝑥 𝑥𝜖ℤ−
, −5 ≤ 𝑥 < 0

6.  Some important Sets:-
1. Set of Natural numbers.
⇒ ℕ = 1, 2, 3, … … …
2. Set of whole numbers.
⇒ 𝑊 = 0, 1, 2, 3, … … …
3. Set of Integers.
⇒ ℤ = 0, ±1, ±2, ±3, … … …
4. Set of positive Integers.
⇒ ℤ+
= 1, 2, 3, … … …
5. Set of negative Integers.
⇒ ℤ− = −1, −2, −3, … … …
6. Set of rational numbers.
⇒ ℚ =
𝑝
𝑞
𝑝, 𝑞 ϵ ℤ & 𝑞 ≠ 0

7. 7. Transcendental numbers.
⇒ π , e
8. Imaginary number.
⇒ 𝑖 = −1
 Subset:-
If every element of set ‘A’is also an element of set ‘B’
then we say ‘A’is subset of ‘B’and we write 𝐴 ⊆ 𝐵.
e.g. Suppose 𝐴 = 1, 2, 3 𝑎𝑛𝑑 𝐵 = 1, 2, 3, 4, 5
Here all elements of set ‘A’are in ‘B’.
i.e. 𝐴 ⊆ 𝐵.
 Superset:-
If 𝐴 ⊆ 𝐵, then ‘B’is called a superset of ‘A’and we
write 𝐵 ⊇ 𝐴.
e.g. Suppose 𝐴 = 1, 2, 3 𝑎𝑛𝑑 𝐵 = 1, 2, 3, 4, 5
Here 𝐴 ⊆ 𝐵. i.e. 𝐵 ⊇ 𝐴.

8.  Proper Subset:-
If 𝐴 ⊆ 𝐵 and 𝐴 ≠ 𝐵 then ‘A’is called a proper subset of
‘B’and we write 𝐴 ⊂ 𝐵.
 Types of set:-
 Universal Set:-
If in a particular discussion all sets under consideration
are subsets of set is called universal set for that
discussion and it is denoted by ‘U’.
 Empty Set / Null set (ϕ):-
A set containing no element is called as Empty set or
Null set and it is denoted by ‘ϕ’or { }.
e.g. 𝐴 = 𝑥 𝑥𝜖ℕ, 1 < 𝑥 < 2
 Singleton Set:-
A set containing only one element is called as Singleton
set.
e.g. Set of capital of India ⇒ 𝐴 = 𝐷𝑒𝑙ℎ𝑖

9.  Equal Set:-
Two sets are equal if and only if they have same
elements irrespective of order of element.
e.g. Suppose 𝐴 = 5, 2, 8 𝑎𝑛𝑑 𝐵 = 8, 2, 5
Here 𝐴 ⊆ 𝐵and 𝐵 ⊆ 𝐴, i.e. 𝐴 = 𝐵
 Finite Set:-
A set in which the process of counting of elements
comes to an end is called as Finite set.
 Infinite Set:-
A set which is not finite is called as Infinite set.
 Cardinality of Set:-
If there are exactly ‘n’distinct element in set ‘A’where
‘n’is non-negative integer, we say that set ‘A’is finite &
that ‘n’is cardinality of set ‘A’and it is denoted by 𝐴 .
e.g. 𝐴 = 1, 2, 3, 4, 5 Here 5 elements are present in Set
‘A’, i.e. 𝐴 = 5.

10. Power of Set:-
The set of all subset of a given set ‘A’ is called the
Power set of ‘A’ and it is denoted by P(A).
 Power of Set:-
The set of all subset of a given set ‘A’is called the
Power set of ‘A’and it is denoted by P(A).
 e.g. let 𝐴 = 𝑎, 𝑏, 𝑐
⇒𝑃(𝐴) = ∅, 𝑎 , 𝑏 , 𝑐 , 𝑎, 𝑏 , 𝑏, 𝑐 , 𝑎, 𝑐 , 𝑎, 𝑏, 𝑐
Here Cardinality of set ‘A’= 𝐴 = 3
∴ 𝐶𝑎𝑟𝑑𝑖𝑛𝑎𝑙𝑖𝑡𝑦 𝑜𝑓 𝑃 𝐴 = 𝑃(𝐴) = 23 = 8
 Note:-
1) If there exists even a single element in ‘A’which is
not in ‘B’then ‘A’is not subset of ‘B’and we write
𝐴 ⊈ 𝐵.
2) If 𝐴 = 𝐵 then 𝐴 ⊆ 𝐵 and 𝐵 ⊆ 𝐴.
3) Every elements of power set ‘A’is a set.
4) In general, if 𝐴 = 𝑚 then 𝑃(𝐴) = 2𝑚.

11.  Venn Diagram:-
The pictorial representation of a set is called Venn
diagram.
e.g. 𝐴 = 1, 2, 3, 4, 5 ⇒ OR OR
 Operation on Set:-
1) Complement of a set:-
If ‘A’is a subset of the universal set ‘U’, then the set of
all elements in ‘U’which are not in ‘A’is called the
complement of the set ‘A’and it is denoted by 𝐴 or 𝐴′
or 𝐴𝑐.
 e.g. If 𝑈 = 1, 2, 3, 4, 5, 6, 7, 8
and 𝐴 = 2, 5, 7
then 𝐴 = 1, 3, 4, 6, 8
A
U
𝐴
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5

12. 2) Unions of Sets:-
𝐴⋃𝐵 = 𝑥 𝑥𝜖𝐴 𝑜𝑟 𝑥𝜖𝐵
 e.g. If 𝐴 = 2, 3, 7 and
𝐵 = 1, 2, 5, 7, 9
then 𝐴⋃𝐵 = 1, 2, 3, 5, 7, 9
3) Intersections of Sets:-
𝐴⋂𝐵 = 𝑥 𝑥𝜖𝐴 𝑎𝑛𝑑 𝑥𝜖𝐵
 e.g. If 𝐴 = 2, 3, 7 and
𝐵 = 1, 2, 5, 7, 9 then
𝐴⋂𝐵 = 2, 7
U
A B
AUB
U
A B
A B
⋂

13. 4) Disjoint Set:-
Two sets ‘A’and ‘B’are said to be disjoint if they have
no common element i.e. 𝐴⋂𝐵 = ∅
 e.g. suppose 𝐴 = 2, 3, 7 and
𝐵 = 5, 9
Here 𝐴⋂𝐵 = ∅,
∴ ‘A’and ‘B’are disjoint set.
5) Difference of Set:-
𝐴 − 𝐵 = 𝑥 𝑥𝜖𝐴, 𝑥 ∉ 𝐵
6) Cartesian Product:-
𝐴 × 𝐵 = 𝑎, 𝑏 /𝑎𝜖𝐴 𝑎𝑛𝑑 𝑏𝜖𝐵
 e.g. suppose 𝐴 = 1, 2 and 𝐵 = 𝑎, 𝑏, 𝑐
then 𝐴 × 𝐵 = 1, 𝑎 , 1, 𝑏 , 1, 𝑐 , 2, 𝑎 , 2, 𝑏 , 2, 𝑐
U
A B
⇒ A-B
B
A
U
A B

14.  Note:-
A×B and B×A are not equal unless A=ϕ or B=ϕ or
A=B
7) Equivalent set:-
Two finite set ‘A’and ‘B’are said to be equivalent if
𝐴 = 𝐵
 e.g. suppose 𝐴 = 2, 3, 7 and 𝐵 = 5, 7, 9
Here 𝐴 = 𝐵 = 3 ∴ Set ‘A’and ‘B’are equivalent set.
 Note:- Equal set are equivalent but equivalent set need not
be equal.
 e.g. suppose 𝐴 = 𝑎, 𝑏, 𝑐 and 𝐵 = 𝑑, 𝑒, 𝑓
Here 𝐴 = 𝐵 = 3 ∴ Set ‘A’and ‘B’are equivalent set
but set ‘A’and ‘B’are not equal

15.  Properties of set:-
1) Identity law:-
𝐴⋃∅ = 𝐴
𝐴⋂𝑈 = 𝐴
2) Domination law:-
𝐴⋃𝑈 = 𝑈
𝐴⋂∅ = ∅
3) Idempotent law:-
𝐴⋃𝐴 = 𝐴
𝐴⋂𝐴 = 𝐴
4) Commutative law:-
𝐴⋃𝐵 = 𝐵⋃𝐴
𝐴⋂𝐵 = 𝐵⋂𝐴

16. 5) Complement law:-
𝐴 = 𝐴
6) Associative law:-
𝐴⋃ 𝐵⋃𝐶 = 𝐴⋃𝐵 ⋃𝐶
𝐴⋂ 𝐵⋂𝐶 = 𝐴⋂𝐵 ⋂𝐶
7) Distributive law:-
𝐴⋃ 𝐵⋂𝐶 = 𝐴⋃𝐵 ⋂ 𝐴⋃𝐶
𝐴⋂ 𝐵⋃𝐶 = 𝐴⋂𝐵 ⋃ 𝐴⋂𝐶
8) De morgans law:-
𝐴⋃𝐵 = 𝐴⋂𝐵
𝐴⋂𝐵 = 𝐴⋃𝐵
9) Absorption law:-
𝐴⋃ 𝐴⋂𝐵 = 𝐴
𝐴⋂ 𝐴⋃𝐵 = 𝐴

17. 10) Complement law:-
𝐴⋃𝐴 = 𝑈
𝐴⋂𝐴 = ∅
11) Symmetric Difference:-
𝐴 ⊕ 𝐵 = 𝐴 − 𝐵 ⋃ 𝐵 − 𝐴
OR
𝐴 ⊕ 𝐵 = 𝐴⋃𝐵 − 𝐴⋂𝐵
 Properties of Set Operations:-
1) 𝐴⋃𝑈 = 𝑈
2) 𝐴⋃𝐴 = 𝑈
3) 𝐴⋂𝑈 = 𝐴
4) 𝐴⋂𝐴 = ∅
5) 𝐴⋃∅ = 𝐴
6) 𝐴⋂∅ = ∅
U
A B
⇒ A B
⊕

18. 7) 𝐴⋃∅ = 𝐴
8) 𝐴⋂∅ = ∅
9) 𝑈 = ∅
10) ∅ = 𝑈
11) 𝐴 = 𝑈 − 𝐴
12) 𝐴 = 𝐴
13) 𝐴 − 𝐴 = ∅
14) 𝐴 − 𝐴 = 𝐴
15) ∅ − 𝐴 = ∅
16) 𝐴 − ∅ = 𝐴
17) 𝐴 − 𝐵 = 𝐴⋂𝐵
18) 𝐴 ⊕ 𝐴 = ∅ = 𝐴 − 𝐴 ∪ 𝐴 − 𝐴
19) 𝐴 ⊕ ∅ = 𝐴 = 𝐴 − ∅ ∪ ∅ − 𝐴
 Example
Prove the following expressions by using the Venn diagram.
1) 𝐴⋃ 𝐵⋂𝐶 = 𝐴⋃𝐵 ⋂ 𝐴⋃𝐶
2) 𝐴⋂ 𝐵⋃𝐶 = 𝐴⋂𝐵 ⋃ 𝐴⋂𝐶
3) 𝐴⋂ 𝐵 ⊕ 𝐶 = 𝐴⋂𝐵 ⊕ 𝐴⋂𝐶

19. 1) 𝐴⋃ 𝐵⋂𝐶 = 𝐴⋃𝐵 ⋂ 𝐴⋃𝐶
⇒ Consider
LHS=𝐴⋃ 𝐵⋂𝐶
𝐵⋂𝐶 =
𝐴⋃ 𝐵⋂𝐶 = …… (1)
B
A
C
U
B
A
C
U

20. Consider
RHS= 𝐴⋃𝐵 ⋂ 𝐴⋃𝐶
𝐴⋃𝐵 =
𝐴⋃𝐶 =
B
A
C
U
B
A
C
U

21. 𝐴⋃𝐵 ⋂ 𝐴⋃𝐶 = …… (2)
From equation (1) & (2),
LHS=RHS
∴ 𝐴⋃ 𝐵⋂𝐶 = 𝐴⋃𝐵 ⋂ 𝐴⋃𝐶
2) 𝐴⋂ 𝐵⋃𝐶 = 𝐴⋂𝐵 ⋃ 𝐴⋂𝐶
⇒ Consider
LHS=𝐴⋂ 𝐵⋃𝐶
𝐵⋃𝐶 =
B
A
C
U
B
A
C
U

22. 𝐴⋂ 𝐵⋃𝐶 = …… (1)
Consider
RHS= 𝐴⋂𝐵 ⋃ 𝐴⋂𝐶
𝐴⋂𝐵 =
B
A
C
U
B
A
C
U

23. 𝐴⋂𝐶 =
𝐴⋂𝐵 ⋃ 𝐴⋂𝐶 = …… (2)
From equation (1) & (2),
LHS=RHS
∴ 𝐴⋂ 𝐵⋃𝐶 = 𝐴⋂𝐵 ⋃ 𝐴⋂𝐶
B
A
C
U
B
A
C
U

24. 3) 𝐴⋂ 𝐵 ⊕ 𝐶 = 𝐴⋂𝐵 ⊕ 𝐴⋂𝐶
⇒ Consider
LHS=𝐴⋂ 𝐵 ⊕ 𝐶
𝐵 ⊕ 𝐶 =
𝐴⋂ 𝐵 ⊕ 𝐶 = …… (1)
B
A
C
U
B
A
C
U

25. Consider
RHS= 𝐴⋂𝐵 ⊕ 𝐴⋂𝐶
𝐴⋂𝐵 =
𝐴⋂𝐶 =
B
A
C
U
B
A
C
U

26. 𝐴⋂𝐵 ⊕ 𝐴⋂𝐶 = …… (2)
From equation (1) & (2),
LHS=RHS
∴ 𝐴⋂ 𝐵 ⊕ 𝐶 = 𝐴⋂𝐵 ⊕ 𝐴⋂𝐶
4) Show that:
i) 𝐴⋃ 𝐴⋂𝐵 = 𝐴⋃𝐵
ii) 𝐴⋂ 𝐴⋃𝐵 = 𝐴⋂𝐵
iii) 𝐴 − 𝐵 − 𝐶 = 𝐴 − 𝐵⋃𝐶
B
A
C
U

27. ⇒ i) Consider, LHS=𝐴⋃ 𝐴⋂𝐵
𝐴⋂𝐵 =
𝐴⋃ 𝐴⋂𝐵 = …(1)
Consider, RHS=𝐴⋃𝐵
𝐴⋃𝐵 = …(2)
B
A
C
U
B
A
C
U
B
A
C
U

28. From equation (1) & (2)
LHS= RHS
∴ 𝐴⋃ 𝐴⋂𝐵 = 𝐴⋃𝐵
ii) Consider, LHS=𝐴⋂ 𝐴⋃𝐵
𝐴⋃𝐵 =
𝐴⋂ 𝐴⋃𝐵 = … (1)
B
A
C
U
B
A
C
U

29. Consider, RHS=𝐴⋂𝐵
𝐴⋂𝐵 = … (2)
From equation (1) & (2)
LHS= RHS
∴ 𝐴⋂ 𝐴⋃𝐵 = 𝐴⋂𝐵
iii) Consider, LHS= 𝐴 − 𝐵 − 𝐶
𝐴 − 𝐵 =
B
A
C
U
B
A
C
U

30. 𝐴 − 𝐵 − 𝐶 = … (1)
Consider, RHS=𝐴 − 𝐵⋃𝐶
𝐵⋃𝐶 =
𝐴 − 𝐵⋃𝐶 = … (2)
B
A
C
U
B
A
C
U
B
A
C
U

31. From equation (1) & (2)
LHS= RHS
∴ 𝐴 − 𝐵 − 𝐶 = 𝐴 − 𝐵⋃𝐶

32. 4) Show that:
i) 𝐴⋃ 𝐴⋂𝐵 = 𝐴⋃𝐵
ii) 𝐴⋂ 𝐴⋃𝐵 = 𝐴⋂𝐵
iii) 𝐴 − 𝐵 − 𝐶 = 𝐴 − 𝐵⋃𝐶
⇒ i) Consider
LHS=𝐴⋃ 𝐴⋂𝐵
= 𝐴⋃𝐴 ⋂ 𝐴⋃𝐵 Distributive law
=𝑈⋂ 𝐴⋃𝐵 ∵𝐴⋃𝐴 = 𝐴⋃𝐴 = 𝑈
=𝐴⋃𝐵 ∵𝑈⋂𝐴 = 𝐴⋂𝑈 = 𝐴
LHS= RHS

33. ii) Consider
LHS=𝐴⋂ 𝐴⋃𝐵
= 𝐴⋂𝐴 ⋃ 𝐴⋂𝐵 Distributive law
=∅⋃ 𝐴⋂𝐵 ∵𝐴⋂𝐴 = 𝐴⋂𝐴 = ∅
=𝐴⋂𝐵 ∵∅⋃𝐴 = 𝐴⋃∅ = 𝐴
LHS= RHS
iii) Consider
LHS= 𝐴 − 𝐵 − 𝐶
= 𝐴⋂𝐵 − 𝐶 ∵𝐴 − 𝐵 = 𝐴⋂𝐵
= 𝐴⋂𝐵 ⋂𝐶
=𝐴⋂ 𝐵⋂𝐶 Commutative Property
=𝐴⋂ 𝐵⋃𝐶 Demorgans law
=𝐴 − 𝐵⋃𝐶 ∵𝐴⋂𝐵 = 𝐴 − 𝐵
LHS= RHS

34. 5) Show that
𝐴⋂𝐵 ⋃ 𝐴⋂𝐵 ⋃ 𝐴⋂𝐵 = 𝐴⋃𝐵
⇒ Consider
LHS= 𝐴⋂𝐵 ⋃ 𝐴⋂𝐵 ⋃ 𝐴⋂𝐵
= 𝐴⋂𝐵 ⋃ 𝐴⋂ 𝐵⋃𝐵 Distributive law
= 𝐴⋂𝐵 ⋃ 𝐴⋂𝑈 ∵𝐵⋃𝐵 = 𝐵⋃𝐵 = 𝑈
= 𝐴⋂𝐵 ⋃𝐴 ∵𝐴⋂𝑈 = 𝑈⋂𝐴 = 𝐴
= 𝐴⋃ 𝐴⋂𝐵 ∵𝐴⋃𝐵 = 𝐵⋃𝐴
= 𝐴⋃𝐴 ⋂ 𝐴⋃𝐵 Distributive law
=U⋂ 𝐴⋃𝐵 ∵𝐴⋃𝐴 = 𝐴⋃𝐴 = 𝑈
=𝐴⋃𝐵
LHS= RHS

35. 6) If 𝐴 = 1, 4, 7, 10 , B= 1, 2, 3, 4, 5 , C= 2, 4, 6, 8 ,
U= 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 then find
i) 𝐴⋃𝐵 ii) 𝐵⋂𝐶 iii) 𝐴 − 𝐵 iv) 𝐵 − 𝐴
v) 𝐴 vi) 𝑈 − 𝐶 vii) 𝐶 viii) 𝑈
ix) 𝐴⋂𝐵 − 𝐶 x) 𝐴⋂𝐵⋂𝐶 xi) 𝐴⋃𝐵 − 𝐶
xii) 𝐴⋂𝐵⋂𝐶
⇒ i) 𝐴⋃𝐵 = 1, 2, 3, 4, 5, 7, 10
ii) 𝐵⋂𝐶 = 2, 4
iii) 𝐴 − 𝐵 = 7, 10
iv) 𝐵 − 𝐴 = 2, 3, 5
v) 𝐴 = 2, 3, 5, 6, 8, 9
vi) 𝑈 − 𝐶 = 1, 3, 5, 7, 9, 10
vii) 𝐶 = 1, 3, 5, 7, 9, 10

36. viii) 𝑈 = ∅
ix) 𝐴⋂𝐵 = 1, 4
∴ 𝐴⋂𝐵 − 𝐶 = 1
x) 𝐴⋂𝐵⋂𝐶 = 4
xi) 𝐴⋃𝐵 = 1, 2, 3, 4, 5, 7, 10
𝐶 = 1, 3, 5, 7, 9, 10
∴ 𝐴⋃𝐵 − 𝐶 = 2, 4
xii) 𝐴 = 2, 3, 5, 6, 8, 9 , 𝐵 = 6, 7, 8, 9, 10
𝐶 = 1, 3, 5, 7, 9, 10
∴ 𝐴⋂𝐵⋂𝐶 = 9

37. 7) If 𝐴 = 𝑎, 𝑏, 𝑎, 𝑐 , ∅ then find
i) 𝑃(𝐴) ii) 𝐴 − 𝑎, 𝑐 iii) 𝑎, 𝑐 − 𝐴
iv) 𝐴 − 𝑎, 𝑏 v) 𝑎, 𝑐 − 𝐴 vi) 𝐴 − 𝑎, 𝑏
⇒ i) Cardnality of 𝑃 𝐴 = 𝑃(𝐴) = 24
= 16
𝑃 𝐴 =
∅, 𝑎 , 𝑏 , 𝑎, 𝑐 , ∅ , 𝑎, 𝑏 , 𝑎, 𝑎, 𝑐 ,
𝑎, ∅ , 𝑏, 𝑎, 𝑐 , 𝑏, ∅ , 𝑎, 𝑐 , ∅ ,
𝑎, 𝑏, 𝑎, 𝑐 , 𝑎, 𝑏, ∅ , 𝑎, 𝑎, 𝑐 , ∅ ,
𝑏, 𝑎, 𝑐 , ∅ , 𝑎, 𝑏, 𝑎, 𝑐 , ∅
ii) 𝐴 − 𝑎, 𝑐 = 𝑏, 𝑎, 𝑐 , ∅
iii) 𝑎, 𝑐 − 𝐴 = ∅
iv) 𝐴 − 𝑎, 𝑏 = 𝑎, 𝑏, 𝑎, 𝑐 , ∅ = 𝐴
v) 𝑎, 𝑐 − 𝐴 = 𝑐
vi) 𝐴 − 𝑎, 𝑏 = 𝑎, 𝑐 , ∅

38. 8) Prove the following by using venn diagram
i) 𝐴 ⊕ 𝐵 ⊕ 𝐶 = 𝐴 ⊕ 𝐵 ⊕ 𝐶
ii) 𝐴⋂𝐵⋂𝐶 = 𝐴 − 𝐴 − 𝐵 ⋃ 𝐴 − 𝐶
⇒ i) Consider,
LHS=𝐴 ⊕ 𝐵 ⊕ 𝐶
𝐵 ⊕ 𝐶 =
𝐴 ⊕ 𝐵 ⊕ 𝐶 = … (1)
B
A
C
U
B
A
C
U

39. Consider,
RHS= 𝐴 ⊕ 𝐵 ⊕ 𝐶
A ⊕ 𝐵 =
𝐴 ⊕ 𝐵 ⊕ 𝐶 = … (2)
from equation (1) and (2),
LHS=RHS
𝐴 ⊕ 𝐵 ⊕ 𝐶 = 𝐴 ⊕ 𝐵 ⊕ 𝐶
B
A
C
U
B
A
C
U

40. ii) 𝐴⋂𝐵⋂𝐶 = 𝐴 − 𝐴 − 𝐵 ⋃ 𝐴 − 𝐶
⇒ Consider,
LHS=𝐴⋂𝐵⋂𝐶
𝐴⋂𝐵⋂𝐶 = … (1)
Consider,
RHS=𝐴 − 𝐴 − 𝐵 ⋃ 𝐴 − 𝐶
𝐴 − 𝐵 =
B
A
C
U
B
A
C
U

41. 𝐴 − 𝐶 =
𝐴 − 𝐵 ⋃ 𝐴 − 𝐶 =
A − 𝐴 − 𝐵 ⋃ 𝐴 − 𝐶 = … (2)
from equation (1) and (2),
LHS=RHS
𝐴⋂𝐵⋂𝐶 = 𝐴 − 𝐴 − 𝐵 ⋃ 𝐴 − 𝐶
B
A
C
U
B
A
C
U
B
A
C
U

42. 9) Check the following sets are equal
i) 𝐴 = 𝑥 𝑥2 + 𝑥 = 2 , 𝐵 = 1, −2
ii) 𝑃 = 𝑥 5 < 𝑥2 < 36 , 𝑄 = 1, 2, 4, 8
⇒ i) Here given,
𝐴 = 𝑥 𝑥2
+ 𝑥 = 2 and 𝐵 = 1, −2
now, 𝑥2
+ 𝑥 = 2
𝑥2 + 𝑥 − 2 = 0
𝑥2 + 2𝑥 − 𝑥 − 2 = 0
𝑥 𝑥 + 2 − 1 𝑥 + 2 = 0
𝑥 + 2 𝑥 − 1 = 0
𝑥 + 2 = 0 , 𝑥 − 1 = 0
𝑥 = −2 , 𝑥 = 1
𝐴 = 1, −2 and 𝐵 = 1, −2
Here 𝐴 ⊆ 𝐵 and 𝐵 ⊆ 𝐴
∴ 𝐴 = 𝐵

43. ⇒ ii) Here given,
𝑃 = 𝑥 5 < 𝑥2
< 36 and 𝑄 = 1, 2, 4, 8
now, 5 < 𝑥2 < 36
5 < 12 = 1 < 36 not satishfy
5 < 22
= 4 < 36 not satishfy
5 < 42 = 16 < 36 satishfy
5 < 82
= 64 < 36 not satishfy
Here 𝑃 ⊈ 𝑄 and 𝑄 ⊈ 𝑃
∴ 𝑃 ≠ 𝑄

44. 10) Let A: Set of all vehicles manufacture in india
B: Set of all imported vehicles
C: Set of all vehicles designed before 2000
D: Set of all with current cost <20,000
& E: Set of all vehicles owned by students of SE computer
Express following sentences in terms of set theoretical
notation.
i) Vehicles owned by students of SE computer are either
in india or are imported
ii) All indian vehicles designed before 2000 have
market value <20,000
iii) All imported vehicles designed after 2000 have
market value more than rupees 20,000
⇒ i) 𝐸 ⊆ 𝐴⋃𝐵
ii) 𝐴⋂𝐶⋂𝐷 𝑜𝑟 𝐴⋂𝐶 ⊆ 𝐷
iii) B⋂𝐶⋂𝐷 𝑜𝑟 (B⋂𝐶) ⊆ 𝐷