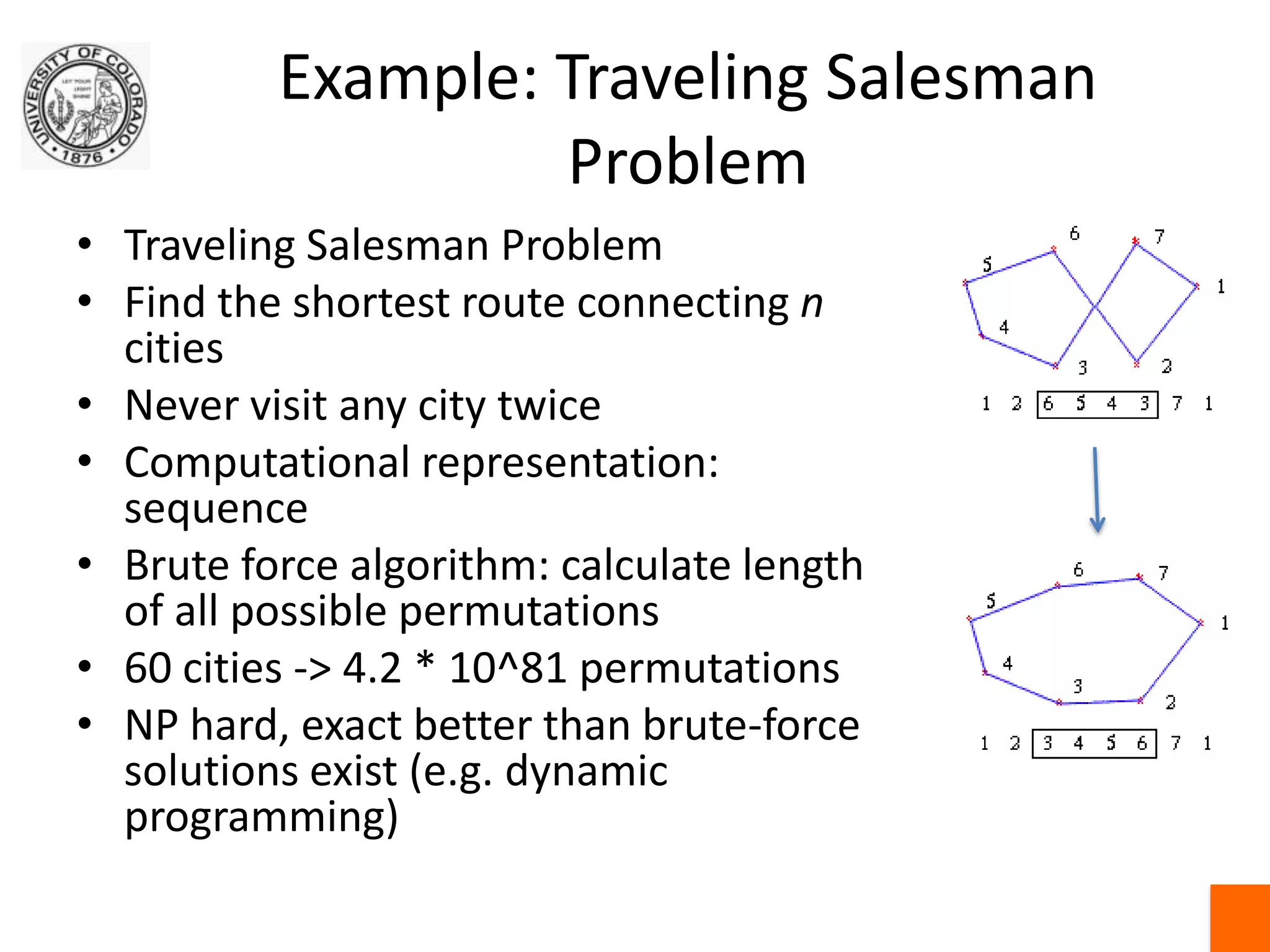
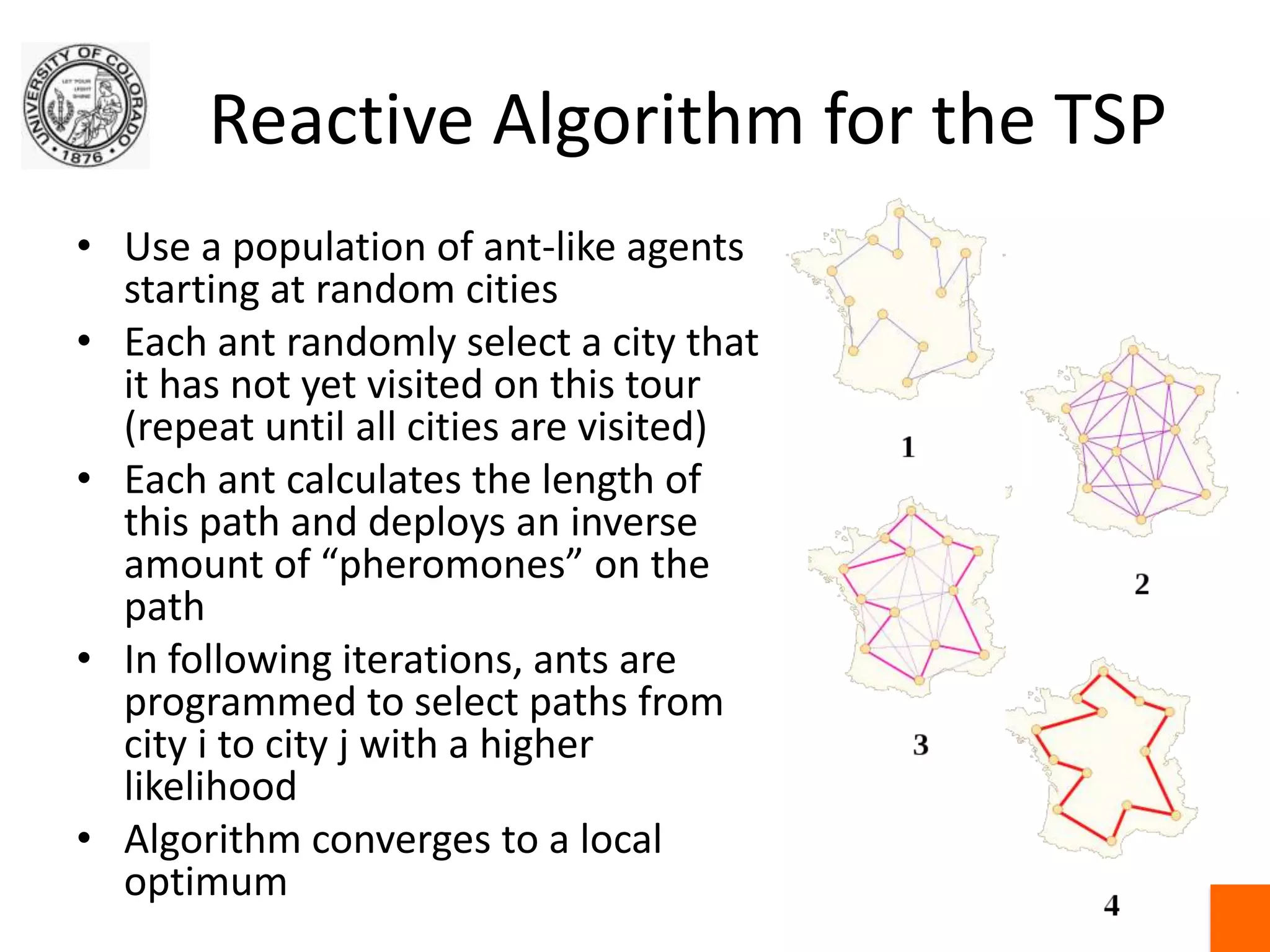
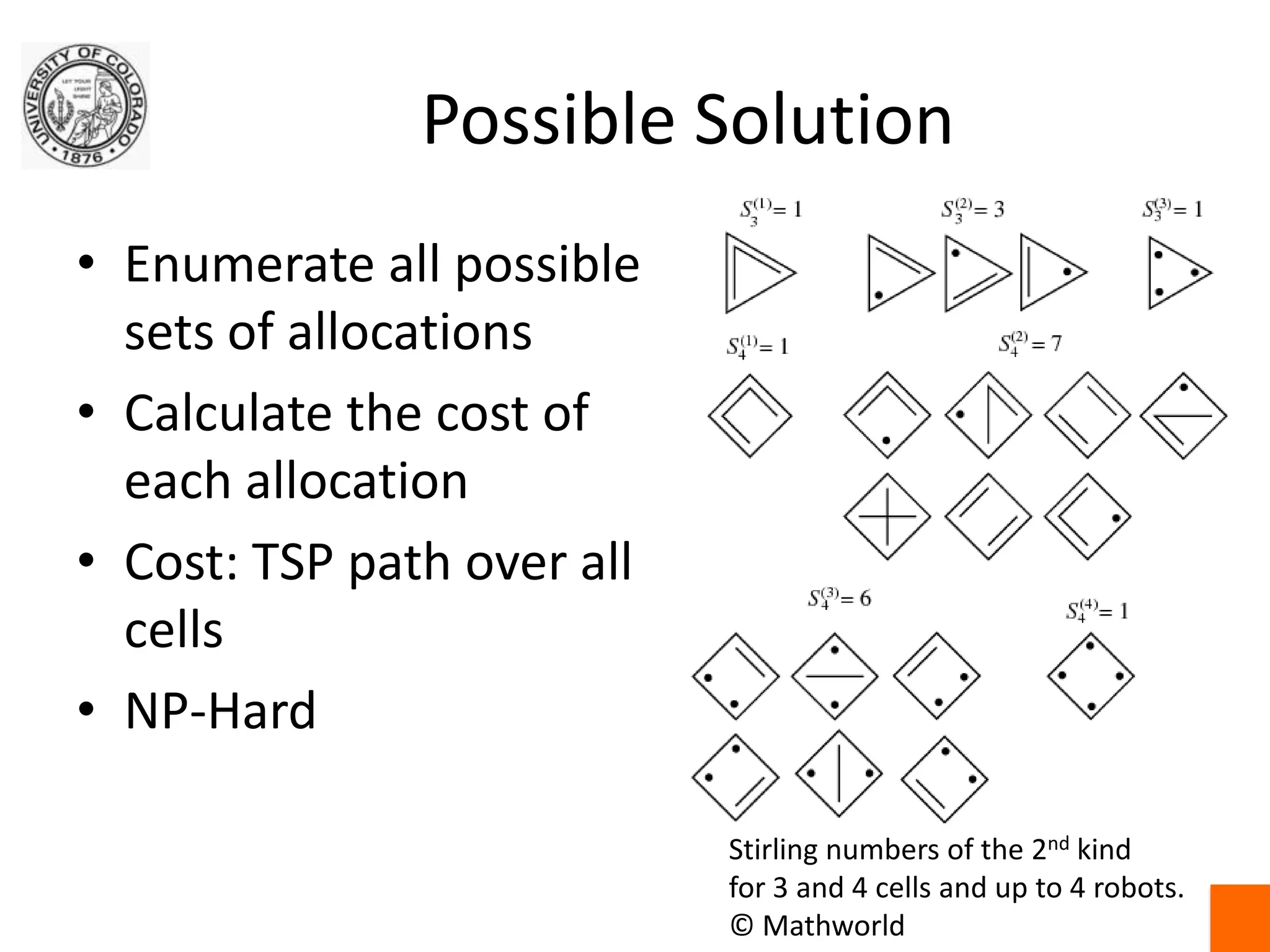
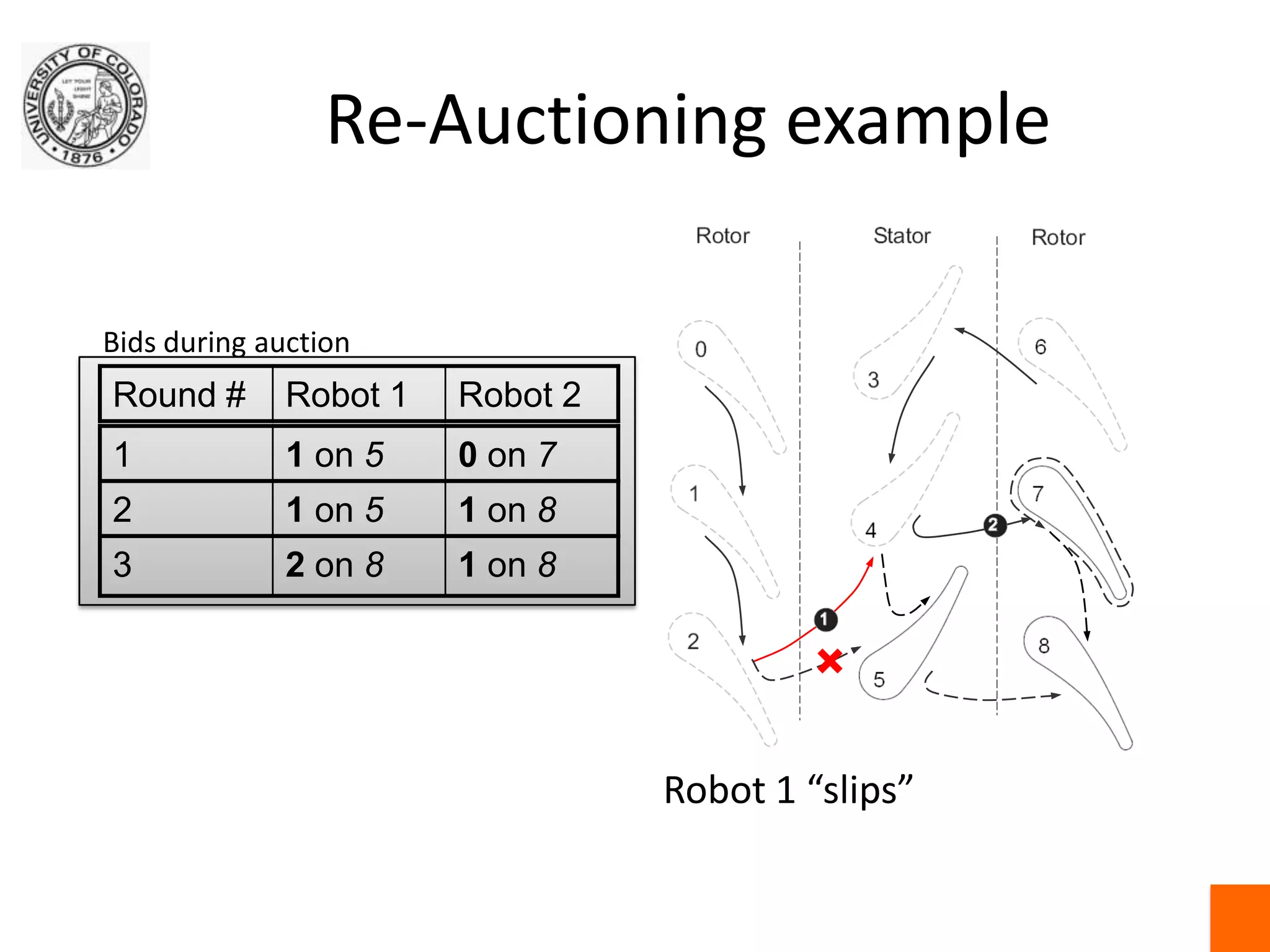
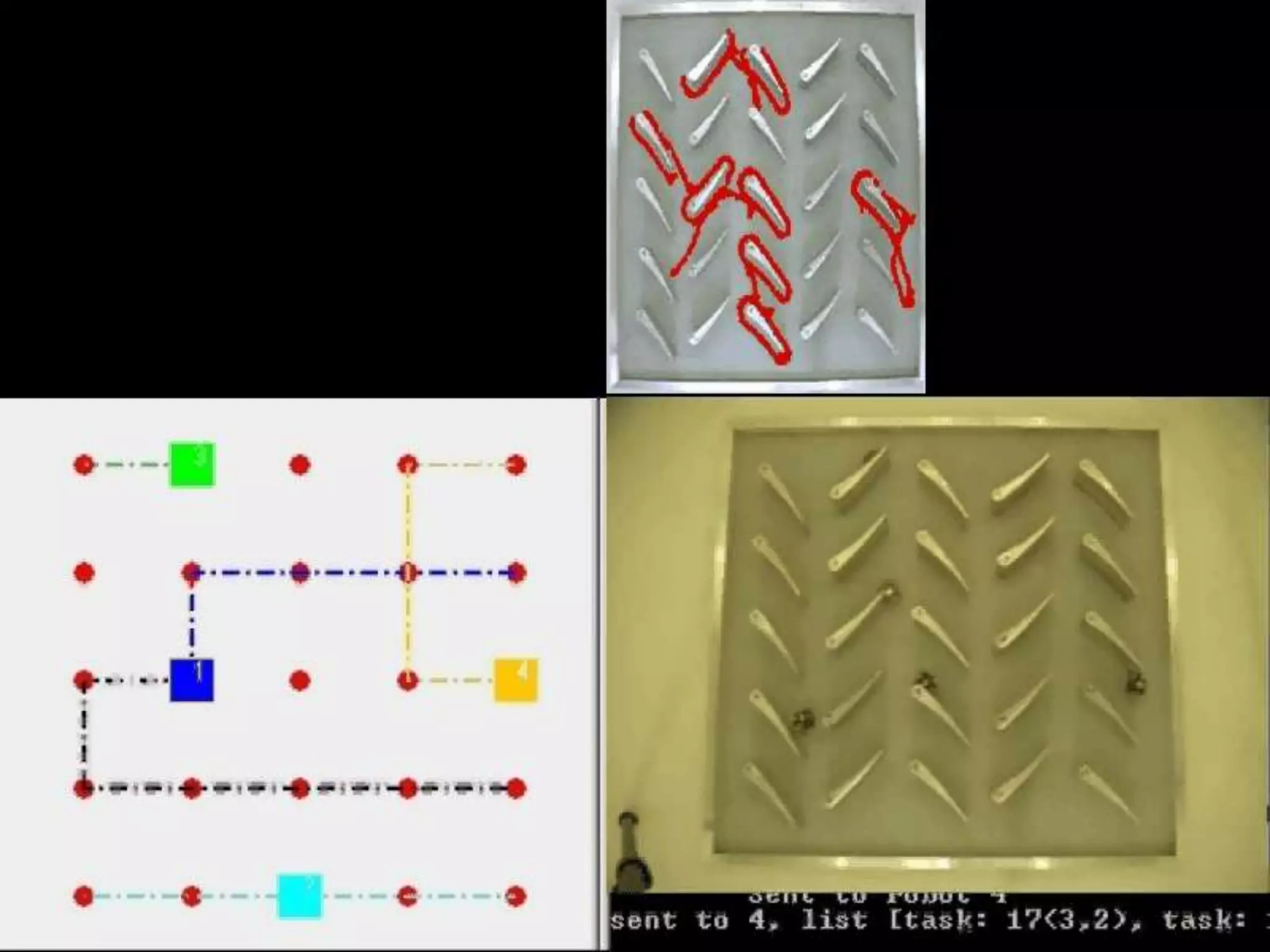
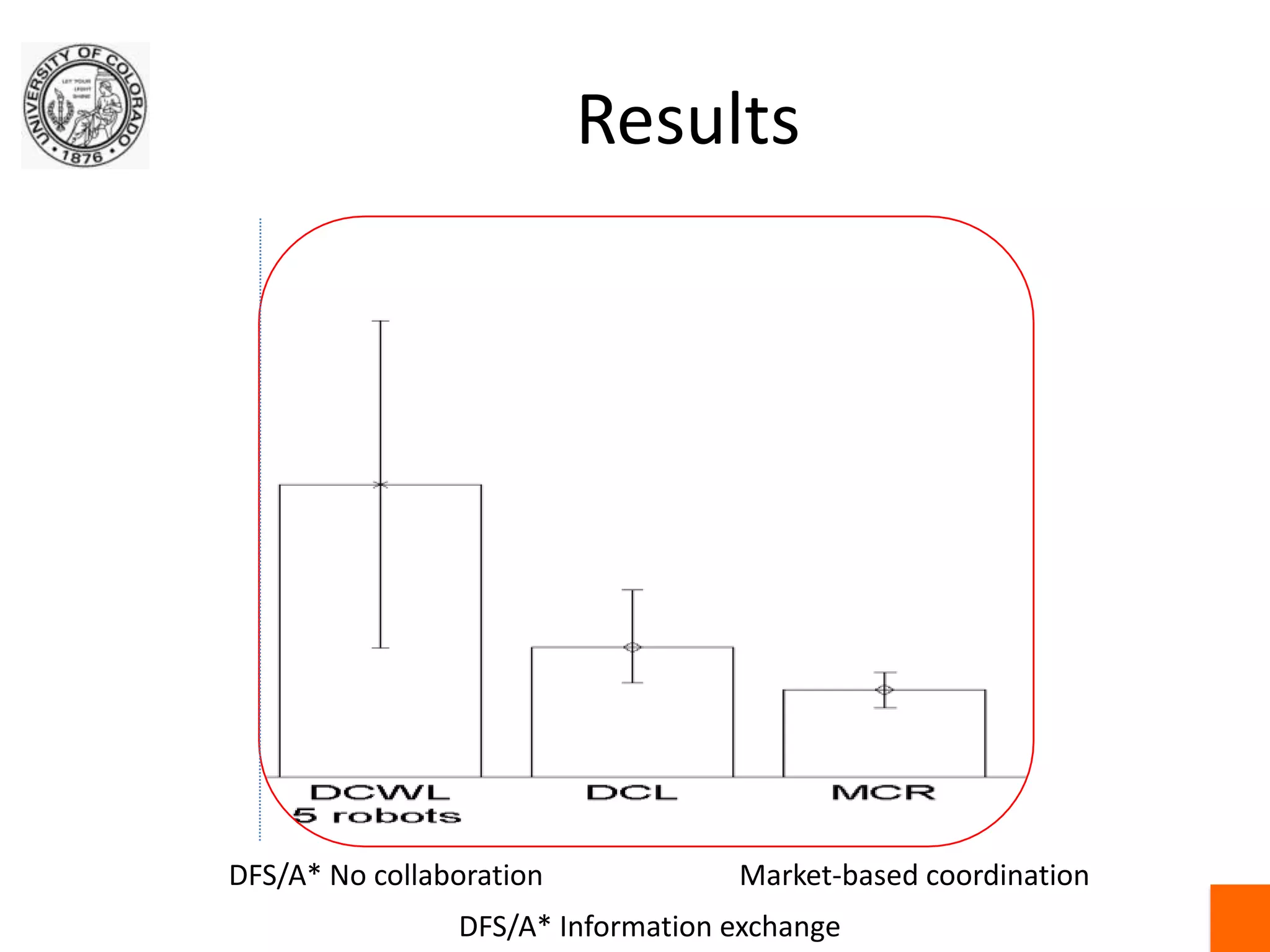
This document discusses exact and approximate algorithms for multi-robot systems. Exact algorithms always find the optimal solution but can be computationally expensive for problems like the traveling salesman problem (TSP) that are NP-hard. Approximate algorithms trade off optimality for speed. Market-based algorithms provide a distributed solution for task allocation problems where robots bid on tasks. Centralized systems require communication but have single points of failure, while distributed algorithms allow for robust self-organization but may produce ambiguous solutions.

1. Multi-Robot SystemsCSCI 7000-006Friday, September 11, 2009NikolausCorrell

2. So farReactive vs. Deliberative AlgorithmsBoth approaches are probabilistic for noisy sensors and actuatorsRobustness/Deterministic behavior can be increased byCombining different sensorsInformation exchangeActively validating hypothesisRedundancy

3. TodayExact and approximative algorithmsCentralized vs. Distributed SystemsMarket-based algorithms

4. Exact AlgorithmsFind always the best solutionSearch the entire solution spaceDetermine what “best” means (fitness function)Enumerate all solutionsPick best solutionSome problems: dynamic programmingFinding the best solution can be very time-consuming/impossible for NP-hard problems

5. Example: Traveling Salesman ProblemTraveling Salesman ProblemFind the shortest route connecting n citiesNever visit any city twiceComputational representation: sequenceBrute force algorithm: calculate length of all possible permutations60 cities -> 4.2 * 10^81 permutations NP hard, exact better than brute-force solutions exist (e.g. dynamic programming)

6. Course QuestionCome up with a reactive algorithm for solving the TSP. Hint: ants.

7. Reactive Algorithm for the TSPUse a population of ant-like agents starting at random citiesEach ant randomly select a city that it has not yet visited on this tour (repeat until all cities are visited)Each ant calculates the length of this path and deploys an inverse amount of “pheromones” on the pathIn following iterations, ants are programmed to select paths from city i to city j with a higher likelihoodAlgorithm converges to a local optimum

8. Lessons from this exampleExact problems can be very hard to solveAlso “pure” CS offers a wide range of algorithmic solutionsThe design problem trades off provable optimality with speedIn robotics algorithmic choice is constrained by sensors, actuators, computation and communication

9. Coverage example (Wednesday)Exact algorithm for single robotApproximative algorithm for multiple robotsRobots might find the optimal solutionWorst case: every robot covers everything

10. Course QuestionCome up with an exact algorithm for covering M cells with N robots as fast as possible.Hints:The problem reduces to allocate a subset of cells to each robot to minimize the maximum number of cells allocated to one robot.Identify sub-problems / algorithms

11. Possible SolutionEnumerate all possible sets of allocationsCalculate the cost of each allocationCost: TSP path over all cellsNP-Hard Stirling numbers of the 2nd kindfor 3 and 4 cells and up to 4 robots.© Mathworld

12. Centralized vs. Distributed AlgorithmsFinding the best solution requires knowing all parameters of the systemUsually requires “leader” or centralized agentCourse Question: What problems do you expect in a centralized system?

13. Centralized SystemsInformation needs to be sent to a central unitCommands need to be sent to each robotProblemsInformation get lost both waysProcess needs to be repeated when individuals failIndividual failure needs to be detected…

14. How to distribute an algorithm?Smart way: using the optimal substructure of the problem (dynamic programming)Not all problems can be efficiently distributedRobust: Every robot solves the whole problem for the entire teamProblem: ambiguous solutionsResolution: conflict resolution rules, e.g. lower id goes firstExample: Market-based task allocation

15. Market-based task allocationTasks are offered by auctioneerEvery robot bids with the cost that it would need to do the taskRobot with the lowest cost gets the jobSimplest auction: greedy, non-optimal orderingVariations: bidding on all possible permutations

16. Example: Box PushingTwo tasks: watch the box, push the boxThree robots, only one can watch the boxWatch the box requires LMSWatcher auctions off “push left” and “push right” tasks"Sold!: Auction methods for multi-robot coordination".Brian P. Gerkey and Maja J Mataric´. IEEE Transactions on Robotics and Automation, Special Issue on Multi-robot Systems, 18(5):758-768, October 2002.

17. Example: CoverageRobots calculate cost for covering a blade by solving the TSPSequential biddingapproximates near optimalDeterministic bid evaluation allows for decentralized auction-closingRe-Allocation upon errorP. Amstutz, N. Correll, and A. Martinoli. Distributed Boundary Coverage with a Team of Networked Miniature Robots using a Robust Market-Based Algorithm. Annals of Mathematics and Artifcial Intelligence. Special Issue on Coverage, Exploration, and Search, Gal Kaminka and Amir Shapiro, editors, 52(2-4):307-333, 2009.

18. Re-Auctioning exampleBids during auctionRobot 1 “slips”

19. 9/20/2007Nikolaus Correll19

20. ResultsDFS/A* No collaborationMarket-based coordinationDFS/A* Information exchange

21. SummaryThe better you plan, the better the performanceNoise requires you to re-plan all the timeFeasible algorithms determined by robot capabilities: sensors, actuators, computation and communicationAlgorithmic complexity exponential for NP hard problemsPotentially very high cost for marginal improvements!

22. OutlookControl-based approaches (in two weeks)Modeling: examining resource trade-offs on paper (in three weeks)Next week: building week