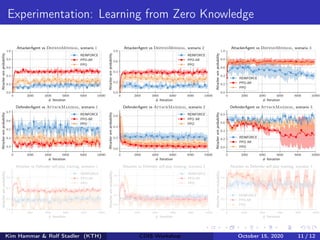
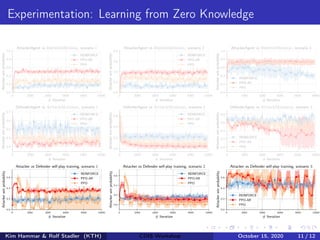
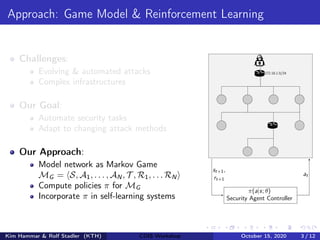
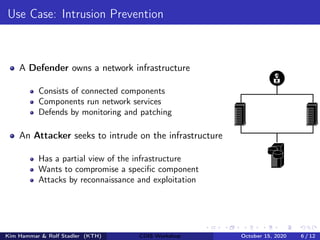
- The document describes using reinforcement learning to model network security as a Markov game and learn security strategies through self-play. - The network infrastructure is modeled as a graph and the interactions between an attacker and defender are framed as a partially observable, zero-sum Markov game. - Reinforcement learning is used to approximate optimal policies for both players by representing their policies with neural networks and optimizing rewards over many episodes of self-play without human intervention.

1. Self-learning Systems for Cyber Security1
Kim Hammar & Rolf Stadler
kimham@kth.se & stadler@kth.se
Division of Network and Systems Engineering
KTH Royal Institute of Technology
October 15, 2020
1
Kim Hammar and Rolf Stadler. “Finding Effective Security Strategies through Reinforcement Learning and
Self-Play”. In: International Conference on Network and Service Management (CNSM 2020) (CNSM 2020). Izmir,
Turkey, Nov. 2020.
Kim Hammar & Rolf Stadler (KTH) CDIS Workshop October 15, 2020 1 / 12

2. Game Learning Programs
Kim Hammar & Rolf Stadler (KTH) CDIS Workshop October 15, 2020 2 / 12

3. Challenges: Evolving and Automated Attacks
Challenges:
Evolving & automated attacks
Complex infrastructures
172.18.1.0/24
Kim Hammar & Rolf Stadler (KTH) CDIS Workshop October 15, 2020 3 / 12

4. Goal: Automation and Learning
Challenges
Evolving & automated attacks
Complex infrastructures
Our Goal:
Automate security tasks
Adapt to changing attack methods
Security Agent Controller
Observations Actions
172.18.1.0/24
Kim Hammar & Rolf Stadler (KTH) CDIS Workshop October 15, 2020 3 / 12

5. Approach: Game Model & Reinforcement Learning
Challenges:
Evolving & automated attacks
Complex infrastructures
Our Goal:
Automate security tasks
Adapt to changing attack methods
Our Approach:
Model network as Markov Game
MG = S, A1, . . . , AN , T , R1, . . . RN
Compute policies π for MG
Incorporate π in self-learning systems Security Agent Controller
st+1,
rt+1
at
π(a|s; θ)
172.18.1.0/24
Kim Hammar & Rolf Stadler (KTH) CDIS Workshop October 15, 2020 3 / 12

6. Related Work
Game-Learning Programs:
TD-Gammon2
, AlphaGo Zero3
, OpenAI Five etc.
=⇒ Impressive empirical results of RL and self-play
Network Security:
Automated threat modeling4
, automated intrusion detection etc.
=⇒ Need for automation and better security tooling
Game Theory:
Network Security: A Decision and Game-Theoretic Approach5
.
=⇒ Many security operations involves strategic decision making
2
Gerald Tesauro. “TD-Gammon, a Self-Teaching Backgammon Program, Achieves Master-Level Play”. In:
Neural Comput. 6.2 (Mar. 1994), 215–219. ISSN: 0899-7667. DOI: 10.1162/neco.1994.6.2.215. URL:
https://doi.org/10.1162/neco.1994.6.2.215.
3
David Silver et al. “Mastering the game of Go without human knowledge”. In: Nature 550 (Oct. 2017),
pp. 354–. URL: http://dx.doi.org/10.1038/nature24270.
4
Pontus Johnson, Robert Lagerström, and Mathias Ekstedt. “A Meta Language for Threat Modeling and Attack
Simulations”. In: Proceedings of the 13th International Conference on Availability, Reliability and Security. ARES
2018. Hamburg, Germany: Association for Computing Machinery, 2018. ISBN: 9781450364485. DOI:
10.1145/3230833.3232799. URL: https://doi.org/10.1145/3230833.3232799.
5
Tansu Alpcan and Tamer Basar. Network Security: A Decision and Game-Theoretic Approach. 1st. USA:
Cambridge University Press, 2010. ISBN: 0521119324.
Kim Hammar & Rolf Stadler (KTH) CDIS Workshop October 15, 2020 4 / 12

7. Outline
Use Case
Markov Game Model for Intrusion Prevention
Reinforcement Learning Problem
Method
Results
Conclusions
Kim Hammar & Rolf Stadler (KTH) CDIS Workshop October 15, 2020 5 / 12

8. Use Case: Intrusion Prevention
A Defender owns a network infrastructure
Consists of connected components
Components run network services
Defends by monitoring and patching
An Attacker seeks to intrude on the infrastructure
Has a partial view of the infrastructure
Wants to compromise a specific component
Attacks by reconnaissance and exploitation
Kim Hammar & Rolf Stadler (KTH) CDIS Workshop October 15, 2020 6 / 12

9. Markov Game Model for Intrusion Prevention
(1) Network Infrastructure
Kim Hammar & Rolf Stadler (KTH) CDIS Workshop October 15, 2020 7 / 12

10. Markov Game Model for Intrusion Prevention
(1) Network Infrastructure (2) Graph G = N, E
Ndata
Nstart
Kim Hammar & Rolf Stadler (KTH) CDIS Workshop October 15, 2020 7 / 12

11. Markov Game Model for Intrusion Prevention
(1) Network Infrastructure (2) Graph G = N, E
Ndata
Nstart
(3) State space |S| = (w + 1)|N|·m·(m+1)
SA
3 = [0, 0, 0, 0]
SD
3 = [9, 1, 5, 8, 1]
SA
0 = [0, 0, 0, 0]
SD
0 = [0, 0, 0, 0, 0]
SA
1 = [0, 0, 0, 0]
SD
1 = [1, 9, 9, 8, 1]
SA
2 = [0, 0, 0, 0]
SD
2 = [9, 9, 9, 8, 1]
Kim Hammar & Rolf Stadler (KTH) CDIS Workshop October 15, 2020 7 / 12

12. Markov Game Model for Intrusion Prevention
(1) Network Infrastructure (2) Graph G = N, E
Ndata
Nstart
(3) State space |S| = (w + 1)|N|·m·(m+1)
SA
3 = [0, 0, 0, 0]
SD
3 = [9, 1, 5, 8, 1]
SA
0 = [0, 0, 0, 0]
SD
0 = [0, 0, 0, 0, 0]
SA
1 = [0, 0, 0, 0]
SD
1 = [1, 9, 9, 8, 1]
SA
2 = [0, 0, 0, 0]
SD
2 = [9, 9, 9, 8, 1]
(4) Action space |A| = |N| · (m + 1)
?/0 ?/0 ?/0 ?/0?/0?/0
?/0 ?/0 ?/0
Kim Hammar & Rolf Stadler (KTH) CDIS Workshop October 15, 2020 7 / 12

13. Markov Game Model for Intrusion Prevention
(1) Network Infrastructure (2) Graph G = N, E
Ndata
Nstart
(3) State space |S| = (w + 1)|N|·m·(m+1)
SA
3 = [0, 0, 0, 0]
SD
3 = [9, 1, 5, 8, 1]
SA
0 = [0, 0, 0, 0]
SD
0 = [0, 0, 0, 0, 0]
SA
1 = [0, 0, 0, 0]
SD
1 = [1, 9, 9, 8, 1]
SA
2 = [0, 0, 0, 0]
SD
2 = [9, 9, 9, 8, 1]
(4) Action space |A| = |N| · (m + 1)
?/0 ?/0 ?/0 ?/0?/0?/0
?/0 ?/0 ?/0
(5) Game Dynamics T , R1, R2, ρ0
4/0 0/1 8/0 ?/0?/0?/0
0/0 9/0 8/0
Kim Hammar & Rolf Stadler (KTH) CDIS Workshop October 15, 2020 7 / 12

14. Markov Game Model for Intrusion Prevention
(1) Network Infrastructure (2) Graph G = N, E
Ndata
Nstart
(3) State space |S| = (w + 1)|N|·m·(m+1)
SA
3 = [0, 0, 0, 0]
SD
3 = [9, 1, 5, 8, 1]
SA
0 = [0, 0, 0, 0]
SD
0 = [0, 0, 0, 0, 0]
SA
1 = [0, 0, 0, 0]
SD
1 = [1, 9, 9, 8, 1]
SA
2 = [0, 0, 0, 0]
SD
2 = [9, 9, 9, 8, 1]
(4) Action space |A| = |N| · (m + 1)
?/0 ?/0 ?/0 ?/0?/0?/0
?/0 ?/0 ?/0
(5) Game Dynamics T , R1, R2, ρ0
4/0 0/1 8/0 ?/0?/0?/0
0/0 9/0 8/0
∴
- Markov game
- Zero-sum
- 2 players
- Partially observed
- Stochastic elements
- Round-based
MG = S, A1, A2, T , R1, R2, γ, ρ0
Kim Hammar & Rolf Stadler (KTH) CDIS Workshop October 15, 2020 7 / 12

15. Automatic Learning of Security Strategies
1
2 2 2
q1 = 3 q2 = 4 q3 = 6
(18,18) (15,20) (9,18)
q2 = 3
q2 = 4
q2 = 6
(20,15) (15,16) (8,12)
q2 = 3
q2 = 4
q2 = 6
(18,9) (12,8) (0,0)
q2 = 3
q2 = 4
q2 = 6
Finding strategies for the Markov game model:
Evolutionary methods
Computational game theory
Self-Play Reinforcement learning
Attacker vs Defender
Strategies evolve without human intervention
Motivation for Reinforcement Learning:
Strong empirical results in related work
Can adapt to new attack methods and threats
Can be used for complex domains that are hard to model exactly
Kim Hammar & Rolf Stadler (KTH) CDIS Workshop October 15, 2020 8 / 12

16. The Reinforcement Learning Problem
Goal:
Approximate π∗
= arg maxπ E
T
t=0 γt
rt+1
Learning Algorithm:
Represent π by πθ
Define objective J(θ) = Eo∼ρπθ ,a∼πθ
[R]
Maximize J(θ) by stochastic gradient ascent with gradient
θJ(θ) = Eo∼ρπθ ,a∼πθ
[ θ log πθ(a|o)Aπθ
(o, a)]
Domain-Specific Challenges:
Partial observability: captured in the model
Large state space |S| = (w + 1)|N|·m·(m+1)
Large action space |A| = |N| · (m + 1)
Non-stationary Environment due to presence of adversary
Agent
Environment
at
st+1
rt+1
Kim Hammar & Rolf Stadler (KTH) CDIS Workshop October 15, 2020 9 / 12

17. The Reinforcement Learning Problem
Goal:
Approximate π∗
= arg maxπ E
T
t=0 γt
rt+1
Learning Algorithm:
Represent π by πθ
Define objective J(θ) = Eo∼ρπθ ,a∼πθ
[R]
Maximize J(θ) by stochastic gradient ascent with gradient
θJ(θ) = Eo∼ρπθ ,a∼πθ
[ θ log πθ(a|o)Aπθ
(o, a)]
Domain-Specific Challenges:
Partial observability: captured in the model
Large state space |S| = (w + 1)|N|·m·(m+1)
Large action space |A| = |N| · (m + 1)
Non-stationary Environment due to presence of adversary
Agent
Environment
at
st+1
rt+1
Kim Hammar & Rolf Stadler (KTH) CDIS Workshop October 15, 2020 9 / 12

18. The Reinforcement Learning Problem
Goal:
Approximate π∗
= arg maxπ E
T
t=0 γt
rt+1
Learning Algorithm:
Represent π by πθ
Define objective J(θ) = Eo∼ρπθ ,a∼πθ
[R]
Maximize J(θ) by stochastic gradient ascent with gradient
θJ(θ) = Eo∼ρπθ ,a∼πθ
[ θ log πθ(a|o)Aπθ
(o, a)]
Domain-Specific Challenges:
Partial observability: captured in the model
Large state space |S| = (w + 1)|N|·m·(m+1)
Large action space |A| = |N| · (m + 1)
Non-stationary Environment due to presence of adversary
Agent
Environment
at
st+1
rt+1
Kim Hammar & Rolf Stadler (KTH) CDIS Workshop October 15, 2020 9 / 12

19. Our Reinforcement Learning Method
Policy Gradient & Function Approximation
To deal with large state space S
πθ parameterized by weights θ ∈ Rd
of NN.
PPO & REINFORCE (stochastic π)
Auto-Regressive Policy Representation
To deal with large action space A
To minimize interference
π(a, n|o) = π(a|n, o) · π(n|o)
Opponent Pool
To avoid overfitting
Want agent to learn a general strategy
Attacker π(a|s; θ2)
Defender π(a|s; θ1)
st+1
rt+1
a1
t , a2
t
Opponent pool
s0 s1 s2 . . .
Markov Game
Kim Hammar & Rolf Stadler (KTH) CDIS Workshop October 15, 2020 10 / 12

20. Our Reinforcement Learning Method
Policy Gradient & Function Approximation
To deal with large state space S
πθ parameterized by weights θ ∈ Rd
of NN.
PPO & REINFORCE (stochastic π)
Auto-Regressive Policy Representation
To deal with large action space A
To minimize interference
π(a, n|o) = π(a|n, o) · π(n|o)
Opponent Pool
To avoid overfitting
Want agent to learn a general strategy
Attacker π(a|s; θ2)
Defender π(a|s; θ1)
st+1
rt+1
a1
t , a2
t
Opponent pool
s0 s1 s2 . . .
Markov Game
Kim Hammar & Rolf Stadler (KTH) CDIS Workshop October 15, 2020 10 / 12

21. Our Reinforcement Learning Method
Policy Gradient & Function Approximation
To deal with large state space S
πθ parameterized by weights θ ∈ Rd
of NN.
PPO & REINFORCE (stochastic π)
Auto-Regressive Policy Representation
To deal with large action space A
To minimize interference
π(a, n|o) = π(a|n, o) · π(n|o)
Opponent Pool
To avoid overfitting
Want agent to learn a general strategy
Attacker π(a|s; θ2)
Defender π(a|s; θ1)
st+1
rt+1
a1
t , a2
t
Opponent pool
s0 s1 s2 . . .
Markov Game
Kim Hammar & Rolf Stadler (KTH) CDIS Workshop October 15, 2020 10 / 12

22. Experimentation: Learning from Zero Knowledge
0 2000 4000 6000 8000 10000
# Iteration
0.0
0.2
0.4
0.6
0.8
1.0
Attackerwinprobability
AttackerAgent vs DefendMinimal, scenario 1
REINFORCE
PPO-AR
PPO
0 2000 4000 6000 8000 10000
# Iteration
0.0
0.2
0.4
0.6
0.8
Attackerwinprobability
AttackerAgent vs DefendMinimal, scenario 2
REINFORCE
PPO-AR
PPO
0 2000 4000 6000 8000 10000
# Iteration
0.0
0.2
0.4
0.6
0.8
1.0
Attackerwinprobability
AttackerAgent vs DefendMinimal, scenario 3
REINFORCE
PPO-AR
PPO
0 2000 4000 6000 8000 10000
# Iteration
0.3
0.4
0.5
0.6
0.7
Attackerwinprobability
DefenderAgent vs AttackMaximal, scenario 1
REINFORCE
PPO-AR
PPO
0 2000 4000 6000 8000 10000
# Iteration
0.0
0.2
0.4
0.6
Attackerwinprobability
DefenderAgent vs AttackMaximal, scenario 2
REINFORCE
PPO AR
PPO
0 2000 4000 6000 8000 10000
# Iteration
0.0
0.2
0.4
0.6
0.8
Attackerwinprobability
DefenderAgent vs AttackMaximal, scenario 3
REINFORCE
PPO AR
PPO
0 2000 4000 6000 8000 10000
# Iteration
0.0
0.2
0.4
0.6
Attackerwinprobability
Attacker vs Defender self-play training, scenario 1
REINFORCE
PPO-AR
PPO
0 2000 4000 6000 8000 10000
# Iteration
0.0
0.2
0.4
0.6
Attackerwinprobability
Attacker vs Defender self-play training, scenario 2
REINFORCE
PPO-AR
PPO
0 2000 4000 6000 8000 10000
# Iteration
0.0
0.2
0.4
0.6
Attackerwinprobability
Attacker vs Defender self-play training, scenario 3
REINFORCE
PPO-AR
PPO
Kim Hammar & Rolf Stadler (KTH) CDIS Workshop October 15, 2020 11 / 12

23. Experimentation: Learning from Zero Knowledge
0 2000 4000 6000 8000 10000
# Iteration
0.0
0.2
0.4
0.6
0.8
1.0
Attackerwinprobability
AttackerAgent vs DefendMinimal, scenario 1
REINFORCE
PPO-AR
PPO
0 2000 4000 6000 8000 10000
# Iteration
0.0
0.2
0.4
0.6
0.8
Attackerwinprobability
AttackerAgent vs DefendMinimal, scenario 2
REINFORCE
PPO-AR
PPO
0 2000 4000 6000 8000 10000
# Iteration
0.0
0.2
0.4
0.6
0.8
1.0
Attackerwinprobability
AttackerAgent vs DefendMinimal, scenario 3
REINFORCE
PPO-AR
PPO
0 2000 4000 6000 8000 10000
# Iteration
0.3
0.4
0.5
0.6
0.7
Attackerwinprobability
DefenderAgent vs AttackMaximal, scenario 1
REINFORCE
PPO-AR
PPO
0 2000 4000 6000 8000 10000
# Iteration
0.0
0.2
0.4
0.6
Attackerwinprobability
DefenderAgent vs AttackMaximal, scenario 2
REINFORCE
PPO AR
PPO
0 2000 4000 6000 8000 10000
# Iteration
0.0
0.2
0.4
0.6
0.8
Attackerwinprobability
DefenderAgent vs AttackMaximal, scenario 3
REINFORCE
PPO AR
PPO
0 2000 4000 6000 8000 10000
# Iteration
0.0
0.2
0.4
0.6
Attackerwinprobability
Attacker vs Defender self-play training, scenario 1
REINFORCE
PPO-AR
PPO
0 2000 4000 6000 8000 10000
# Iteration
0.0
0.2
0.4
0.6
Attackerwinprobability
Attacker vs Defender self-play training, scenario 2
REINFORCE
PPO-AR
PPO
0 2000 4000 6000 8000 10000
# Iteration
0.0
0.2
0.4
0.6
Attackerwinprobability
Attacker vs Defender self-play training, scenario 3
REINFORCE
PPO-AR
PPO
Kim Hammar & Rolf Stadler (KTH) CDIS Workshop October 15, 2020 11 / 12

24. Conclusion & Future Work
Conclusions:
We have proposed a Method to automatically find security strategies
=⇒ Model as Markov game & evolve strategies using self-play
reinforcement learning
Addressed domain-specific challenges with Auto-regressive policy,
opponent pool, and function approximation.
Challenges of applied reinforcement learning
Stable convergence remains a challenge
Sample-efficiency is a problem
Generalization is a challenge
Current & Future Work:
Study techniques for mitigation of identified RL challenges
Learn security strategies by interacion with a cyber range
Kim Hammar & Rolf Stadler (KTH) CDIS Workshop October 15, 2020 12 / 12

25. Thank you
All code for reproducing the results is open source:
https://github.com/Limmen/gym-idsgame
Kim Hammar & Rolf Stadler (KTH) CDIS Workshop October 15, 2020 12 / 12