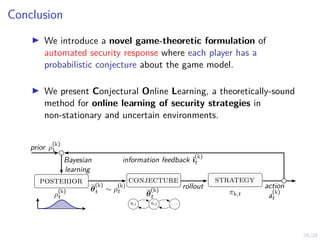
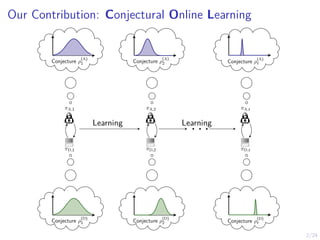
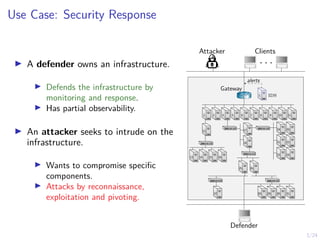
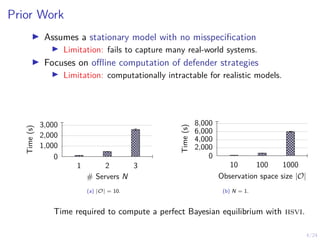
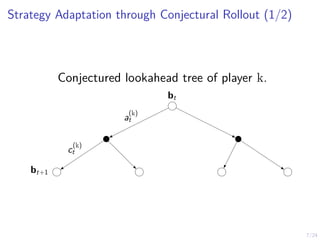
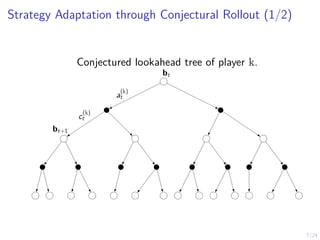
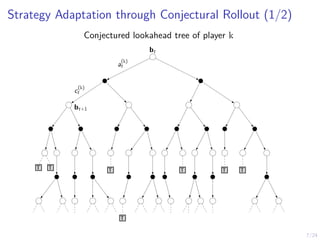
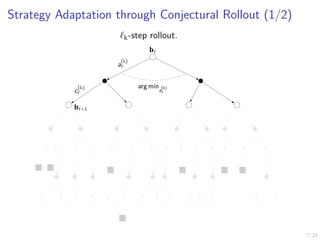
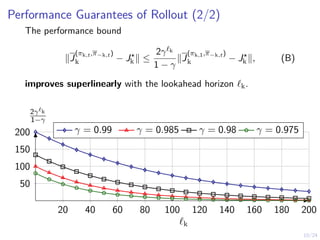
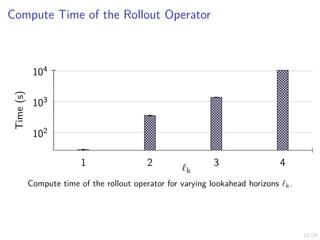
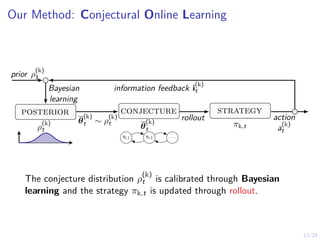
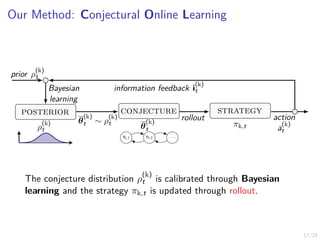
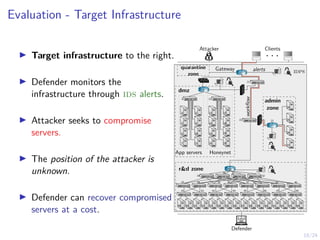
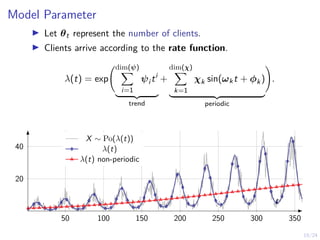
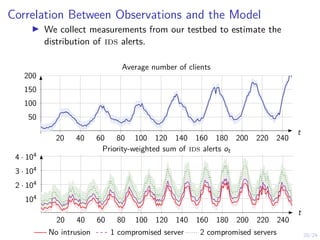
The document describes an approach called conjectural online learning for automated security response in complex IT systems. It uses Bayesian learning to continuously update conjectures about the true but unknown system model, and rollout-based strategy adaptation to update the defender's strategy based on the current conjecture. The conjectures are proven to converge asymptotically to consistent conjectures that minimize divergence from the true model. Evaluation on a target infrastructure models the evolving number of clients and correlations between observations and the true unknown model parameter.

1. 0/24
Automated Security Response through
Online Learning with Adaptive Conjectures1
Kim Hammar, Tao Li, Rolf Stadler, & Quanyan Zhu
kimham@kth.se
Division of Network and Systems Engineering
KTH Royal Institute of Technology
April 5, 2024
1
Kim Hammar, Tao Li, Rolf Stadler, and Quanyan Zhu. Automated Security Response through Online Learning
with Adaptive Conjectures. Submitted to the IEEE, https://arxiv.org/abs/2402.12499. 2024.

2. 1/24
Challenge: IT Systems are Complex
I It is not realistic that any model will capture all the details.
I =⇒ We have to work with approximate models.
I =⇒ model misspecification.
I How does misspecification affect optimality and convergence?

3. 2/24
Our Contribution: Conjectural Online Learning
πA,1
πD,1
Conjecture ρ
(A)
1
Conjecture ρ
(D)
1
πA,2
πD,2
Conjecture ρ
(A)
2
Conjecture ρ
(D)
2
. . .
πA,t
πD,t
Conjecture ρ
(A)
t
Conjecture ρ
(D)
t
Learning Learning

4. 3/24
Use Case: Security Response
I A defender owns an infrastructure.
I Defends the infrastructure by
monitoring and response.
I Has partial observability.
I An attacker seeks to intrude on the
infrastructure.
I Wants to compromise specific
components.
I Attacks by reconnaissance,
exploitation and pivoting.
Attacker Clients
. . .
Defender
1 ids
1
alerts
Gateway
7 8 9 10 11
6
5
4
3
2
12
13 14 15 16
17
18
19
21
23
20
22
24
25 26
27 28 29 30 31

5. 4/24
Prior Work
I Assumes a stationary model with no misspecification
I Limitation: fails to capture many real-world systems.
I Focuses on offline computation of defender strategies
I Limitation: computationally intractable for realistic models.
1 2 3
0
1,000
2,000
3,000
# Servers N
Time
(s)
(a) |O| = 10.
10 100 1000
0
2,000
4,000
6,000
8,000
Observation space size |O|
Time
(s)
(b) N = 1.
Time required to compute a perfect Bayesian equilibrium with hsvi.

6. 5/24
Problem
I Partially-observed stochastic game Γθt .
I Γθt is parameterized by θt, which is hidden.
I Player k has a conjecture of θt, denoted by θt ∈ Θk.
I The player is misspecified if θt 6∈ Θk.
I As θt evolves, the player adapts its conjecture.
I The player uses the conjecture to update its strategy πk,t.
I What is an effective method to update conjectures and
strategies?

7. 6/24
Our Method: Conjectural Online Learning
ρ
(k)
t
posterior
s1,1 s1,2 . . .
θ
(k)
t
conjecture
πk,t
strategy
θ
(k)
t ∼ ρ
(k)
t
rollout action
a
(k)
t
prior ρ
(k)
1
Bayesian
learning
information feedback i
(k)
t
The conjecture distribution ρ
(k)
t is calibrated through Bayesian
learning and the strategy πk,t is updated through rollout.

8. 6/24
Our Method: Conjectural Online Learning
ρ
(k)
t
posterior
s1,1 s1,2 . . .
θ
(k)
t
conjecture
πk,t
strategy
θ
(k)
t ∼ ρ
(k)
t
rollout action
a
(k)
t
prior ρ
(k)
1
Bayesian
learning
information feedback i
(k)
t
The conjecture distribution ρ
(k)
t is calibrated through Bayesian
learning and the strategy πk,t is updated through rollout.

9. 6/24
Our Method: Conjectural Online Learning
ρ
(k)
t
posterior
s1,1 s1,2 . . .
θ
(k)
t
conjecture
πk,t
strategy
θ
(k)
t ∼ ρ
(k)
t
rollout action
a
(k)
t
prior ρ
(k)
1
Bayesian
learning
information feedback i
(k)
t
The conjecture distribution ρ
(k)
t is calibrated through Bayesian
learning and the strategy πk,t is updated through rollout.

10. 6/24
Our Method: Conjectural Online Learning
ρ
(k)
t
posterior
s1,1 s1,2 . . .
θ
(k)
t
conjecture
πk,t
strategy
θ
(k)
t ∼ ρ
(k)
t
rollout action
a
(k)
t
prior ρ
(k)
1
Bayesian
learning
information feedback i
(k)
t
The conjecture distribution ρ
(k)
t is calibrated through Bayesian
learning and the strategy πk,t is updated through rollout.

11. 6/24
Our Method: Conjectural Online Learning
ρ
(k)
t
posterior
s1,1 s1,2 . . .
θ
(k)
t
conjecture
πk,t
strategy
θ
(k)
t ∼ ρ
(k)
t
rollout action
a
(k)
t
prior ρ
(k)
1
Bayesian
learning
information feedback i
(k)
t
The conjecture distribution ρ
(k)
t is calibrated through Bayesian
learning and the strategy πk,t is updated through rollout.

12. 6/24
Our Method: Conjectural Online Learning
ρ
(k)
t
posterior
s1,1 s1,2 . . .
θ
(k)
t
conjecture
πk,t
strategy
θ
(k)
t ∼ ρ
(k)
t
rollout action
a
(k)
t
prior ρ
(k)
1
Bayesian
learning
information feedback i
(k)
t
The conjecture distribution ρ
(k)
t is calibrated through Bayesian
learning and the strategy πk,t is updated through rollout.

13. 7/24
Strategy Adaptation through Conjectural Rollout (1/2)

14. 7/24
Strategy Adaptation through Conjectural Rollout (1/2)
a
(k)
t
bt
Conjectured lookahead tree of player k.

15. 7/24
Strategy Adaptation through Conjectural Rollout (1/2)
a
(k)
t
c
(k)
t
bt
bt+1
Conjectured lookahead tree of player k.

16. 7/24
Strategy Adaptation through Conjectural Rollout (1/2)
a
(k)
t
c
(k)
t
bt
bt+1
Conjectured lookahead tree of player k.

17. 7/24
Strategy Adaptation through Conjectural Rollout (1/2)
a
(k)
t
c
(k)
t
bt
bt+1
T T T
T
T
T
T
Conjectured lookahead tree of player k

18. 7/24
Strategy Adaptation through Conjectural Rollout (1/2)
a
(k)
t
c
(k)
t
bt
bt+1
arg mina
(k)
t
T T T
T
T
T
T
`k-step rollout.

19. 8/24
Strategy Adaptation through Conjectural Rollout (2/2)
`k-step rollout based on the conjectured model:
πk,t(bt) ∈ R(θ
(k)
t , bt, J
(πt )
k , `k) , arg min
a
(k)
t ,a
(k)
t+1,...,a
(k)
t+`k−1
(1)
Eπt


t+`k−1
X
j=t
γj−t
ck(Sj, A
(D)
j ) + γ`k
J
(πt )
k (Bt+`k
) | bt

 .
I θ
(k)
t is the model conjecture.
I ck is the cost function.
I J
πt
k is the conjectured cost-to-go under strategy profile πt.
I bt is the current belief state.

20. 9/24
Performance Guarantees of Rollout (1/2)
Theorem
The conjectured cost of player k’s rollout strategy πk,t satisfies
J
(πk,t ,π−k,t )
k (b) ≤ J
(πk,1,π−k,t )
k (b) ∀b ∈ B. (A)
Intuition:
I The rollout policy improves the base policy in the
conjectured model (A).

21. 9/24
Performance Guarantees of Rollout (1/2)
Theorem
The conjectured cost of player k’s rollout strategy πk,t satisfies
J
(πk,t ,π−k,t )
k (b) ≤ J
(πk,1,π−k,t )
k (b) ∀b ∈ B. (A)
Assuming (θ
(k)
t , `−k) predicts the game `k steps ahead, then
kJ
(πk,t ,π−k,t )
k − J?
k k ≤
2γ`k
1 − γ
kJ
(πk,1,π−k,t )
k − J?
k k, (B)
where J?
k is the optimal cost-to-go. k·k is the maximum norm
kJk = maxx |J(x)|.
Intuition:
I The rollout policy improves the base policy in the
conjectured model (A).
I If the conjectured model is wrong but can predict the next `k
steps, then we can bound the performance (B).

22. 10/24
Performance Guarantees of Rollout (2/2)
The performance bound
kJ
(πk,t ,π−k,t )
k − J?
k k ≤
2γ`k
1 − γ
kJ
(πk,1,π−k,t )
k − J?
k k, (B)
improves superlinearly with the lookahead horizon `k.
20 40 60 80 100 120 140 160 180 200
50
100
150
200 γ = 0.99 γ = 0.985 γ = 0.98 γ = 0.975
`k
2γ`k
1−γ

23. 11/24
Compute Time of the Rollout Operator
1 2 3 4
102
103
104
Time
(s)
`k
Compute time of the rollout operator for varying lookahead horizons `k.

24. 12/24
Our Method: Conjectural Online Learning
ρ
(k)
t
posterior
s1,1 s1,2 . . .
θ
(k)
t
conjecture
πk,t
strategy
θ
(k)
t ∼ ρ
(k)
t
rollout action
a
(k)
t
prior ρ
(k)
1
Bayesian
learning
information feedback i
(k)
t
The conjecture distribution ρ
(k)
t is calibrated through Bayesian
learning and the strategy πk,t is updated through rollout.

25. 13/24
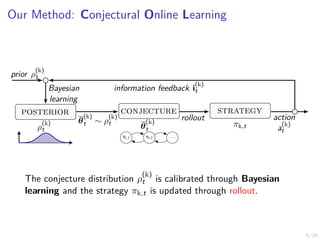
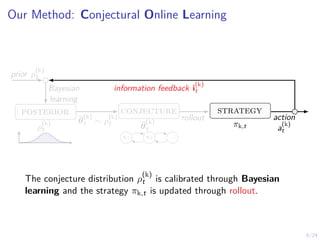
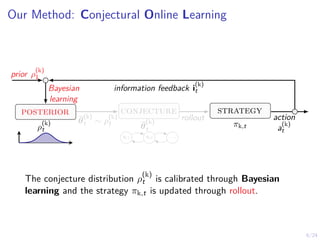
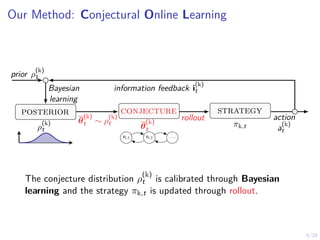
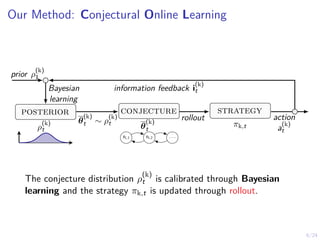
Bayesian Learning to Calibrate Conjectures
ρ
(k)
t is calibrated through Bayesian learning as
ρ
(k)
t (θ
(k)
t ) ,
P[i
(k)
t | θ
(k)
t , bt−1]ρ(k)(θ
(k)
t−1)
R
Θk
P[i
(k)
t | θ
(k)
t , bt−1]ρ
(k)
t−1(dθ
(k)
t )
,
where i
(k)
t is the information feedback at time t.
I We want to characterize limt→∞ ρ
(k)
t .
I Does the conjecture converge?
I Is the conjecture consistent asymptotically?

26. 14/24
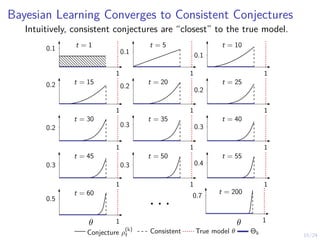
Asymptotic Analysis of Bayesian Learning
I Let ν ∈ ∆(B) be an occupancy measure over the belief space.
I We say that a conjecture θ
(k)
is consistent if it minimizes
the weighted KL-divergence:
K(θ
(k)
, ν) , Eb∼νEI(k)
"
ln
P[I(k) | θ, b]
P[I(k) | θ
(k)
, b]
!
| θ, b
#
.
I Let Θ?
k denote the set of consistent conjectures.
Remark
Due to misspecification, θ
(k)
t ∈ Θ?
k does not imply that θ
(k)
t
equals the true parameter vector θt.

27. 15/24
Bayesian Learning Converges to Consistent Conjectures
Intuitively, consistent conjectures are “closest” to the true model.
1
0.1 t = 1
1
0.1
t = 5
1
0.1
t = 10
1
0.2 t = 15
1
0.2
t = 20
1
0.2
t = 25
1
0.2
t = 30
1
0.3
t = 35
1
0.3
t = 40
1
0.3
t = 45
1
0.3
t = 50
1
0.4
t = 55
1
0.5
t = 60
1
0.7
Conjecture ρ
(k)
t
Consistent True model θ Θk
t = 200
. . .
θ θ

28. 16/24
Bayesian Learning is Consistent Asymptotically
As t → ∞, the conjecture distribution ρ
(k)
t concentrates on
the set of consistent conjectures.
Theorem
Given certain regularity conditions, the following property is
guaranteed by col.
lim
t→∞
Z
Θk
K(θ, νt) − K?
Θk
(νt)
ρ
(k)
t (dθ) = 0
a.s.-PR, where K?
Θk
denotes the minimal weighted kl-divergence.

29. 17/24
Our Method: Conjectural Online Learning
ρ
(k)
t
posterior
s1,1 s1,2 . . .
θ
(k)
t
conjecture
πk,t
strategy
θ
(k)
t ∼ ρ
(k)
t
rollout action
a
(k)
t
prior ρ
(k)
1
Bayesian
learning
information feedback i
(k)
t
The conjecture distribution ρ
(k)
t is calibrated through Bayesian
learning and the strategy πk,t is updated through rollout.

30. 18/24
Evaluation - Target Infrastructure
I Target infrastructure to the right.
I Defender monitors the
infrastructure through ids alerts.
I Attacker seeks to compromise
servers.
I The position of the attacker is
unknown.
I Defender can recover compromised
servers at a cost.
rd zone
App servers Honeynet
dmz
admin
zone
workflow
Gateway idps
quarantine
zone
alerts
Defender
. . .
Attacker Clients
2
1
3 12
4
5
6
7
8
9
10
11
13
14
15
16
17
18
19
20
21
22 23
24
25
26
27
28
29
30 31
32
33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48
49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64

31. 19/24
Model Parameter
I Let θt represent the number of clients.
I Clients arrive according to the rate function.
λ(t) = exp
dim(ψ)
X
i=1
ψi ti
| {z }
trend
+
dim(χ)
X
k=1
χk sin(ωkt + φk)
| {z }
periodic
!
.
50 100 150 200 250 300 350
20
40
X ∼ Po(λ(t))
λ(t)
λ(t) non-periodic
t

32. 20/24
Correlation Between Observations and the Model
I We collect measurements from our testbed to estimate the
distribution of ids alerts.
20 40 60 80 100 120 140 160 180 200 220 240
50
100
150
200
Average number of clients
t
20 40 60 80 100 120 140 160 180 200 220 240
104
2 · 104
3 · 104
4 · 104
No intrusion 1 compromised server 2 compromised servers
Priority-weighted sum of ids alerts ot
t

33. 21/24
Evaluation of col (1/3)
10 20 30 40 50 60 70
20
40
60
80
100
θt
t
10 20 30 40 50 60 70
5
10
E
θ
(D)
∼ρ
(D)
t
[K(θ
(D)
, νt)]
t
Remark
The conjectures do not converge if θt keep changing.

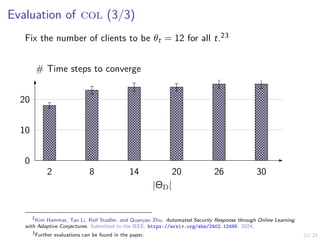
34. 22/24
Evaluation of col (2/3)
Fix the number of clients to be θt = 12 for all t.
2 4 6 8 10 12 14 16 18 20
0.5
1
ρ
(D)
t (θt = 12)
t
4 6 8 10 12 14 16 18 20
−0.05
0.05
E
θ
(D)
∼ρ
(D)
t
[K(θ
(D)
, νt)]
t

35. 23/24
Evaluation of col (3/3)
Fix the number of clients to be θt = 12 for all t.23
2 8 14 20 26 30
0
10
20
|ΘD|
# Time steps to converge
2
Kim Hammar, Tao Li, Rolf Stadler, and Quanyan Zhu. Automated Security Response through Online Learning
with Adaptive Conjectures. Submitted to the IEEE, https://arxiv.org/abs/2402.12499. 2024.
3
Further evaluations can be found in the paper.

36. 24/24
Conclusion
I We introduce a novel game-theoretic formulation of
automated security response where each player has a
probabilistic conjecture about the game model.
I We present Conjectural Online Learning, a theoretically-sound
method for online learning of security strategies in
non-stationary and uncertain environments.
ρ
(k)
t
posterior
s1,1 s1,2 . . .
θ
(k)
t
conjecture
πk,t
strategy
θ
(k)
t ∼ ρ
(k)
t
rollout action
a
(k)
t
prior ρ
(k)
1
Bayesian
learning
information feedback i
(k)
t