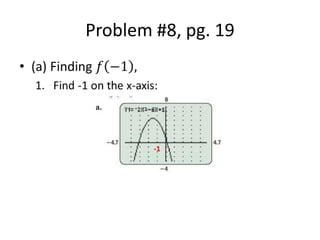
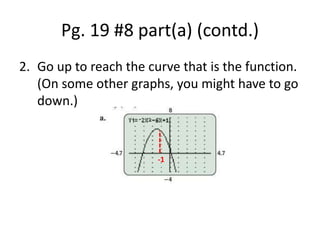
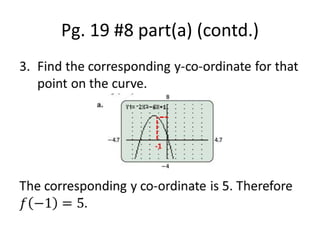
This document defines functions and discusses different ways to represent them, including ordered pairs, arrow diagrams, tables, graphs and equations. It explains how to find the domain and range of functions based on their representation. It also discusses how to recognize if a relation qualifies as a function and introduces function notation. Several examples are provided to demonstrate finding domains and ranges of functions represented by graphs and equations and evaluating functions.