The document discusses various searching algorithms like linear search and binary search. It provides details on how linear search works by sequentially checking each element of an unsorted array to find a target value. Binary search is described as more efficient for sorted arrays, as it repeatedly divides the search space in half by comparing the target to the middle element. Implementation of both iterative and recursive binary search algorithms is demonstrated through pseudocode.

1. ESIT137: Fundamentals of Data Structure
Sanjivani Rural Education Society’s
Sanjivani College of Engineering, Kopargaon-423603
(An Autonomous Institute Affiliated to Savitribai Phule Pune University, Pune)
NACC ‘A’ Grade Accredited, ISO 9001:2015 Certified
Department of Information Technology
(UG Programme - NBAAccredited)
Dr. M.A. Jawale
Professor and Head, Dept. of IT

2. Searching and Sorting
 Searching Algorithms
 Linear Search,
 Binary Search
 Comparison of linear & binary search.
 References
Unit-II: Part-I Searching and Sorting Dr. Madhuri Jawale Department of Information Technology

3. Searching Algorithms
 Searching Algorithms are designed to check for an element or retrieve an element
from any data structure where it is stored.
 Based on the type of search operation, these algorithms are generally classified
into two categories:
1. Sequential Search: In this, the list or array is traversed sequentially and every element is
checked. For example: Linear Search.
2. Interval Search: These algorithms are specifically designed for searching in sorted data-
structures. These type of searching algorithms are much more efficient than Sequential
Search as they repeatedly target the center of the search structure and divide the search space
in half. For Example: Binary Search.
Unit-II: Part-I Searching and Sorting Dr. Madhuri Jawale Department of Information Technology

4. Linear Search
 Linear Search is defined as a sequential search algorithm that starts at one end
and goes through each element of a list until the desired element is found,
otherwise the search continues till the end of the data set.
Unit-II: Part-I Searching and Sorting Dr. Madhuri Jawale Department of Information Technology

5. How Does Linear Search Algorithm Work?
 In Linear Search Algorithm,
 Every element is considered as a potential match for the key and checked for
the same.
 If any element is found equal to the key, the search is successful and the index
of that element is returned.
 If no element is found equal to the key, the search yields “No match found”.
 For example:
Consider the array arr[] = {10, 50, 30, 70, 80, 20, 90, 40} and key = 30
Unit-II: Part-I Searching and Sorting Dr. Madhuri Jawale Department of Information Technology

6. Continue…..
 Step 1: Start from the first element (index 0) and compare key with each element
(arr[i]).
 Comparing key with first element arr[0]. Since not equal, the iterator moves to the
next element as a potential match.
Unit-II: Part-I Searching and Sorting Dr. Madhuri Jawale Department of Information Technology

7. Continue…..
 Comparing key with next element arr[1]. Since not equal, the iterator moves to the
next element as a potential match.
Unit-II: Part-I Searching and Sorting Dr. Madhuri Jawale Department of Information Technology

8. Continue…..
 Step 2: Now when comparing arr[2] with key, the value matches. So the Linear
Search Algorithm will yield a successful message and return the index of the
element when key is found (here 2).
Unit-II: Part-I Searching and Sorting Dr. Madhuri Jawale Department of Information Technology

9. C code to linearly search Key in arr[].
#include <stdio.h>
main(void)
{
int arr[] = { 2, 3, 4, 10, 40 };
int key = 10;
int N = sizeof(arr) / sizeof(arr[0]);
// Function call
int result = search(arr, N, key);
if(result = = -1)
{
printf("Element is not present in array") ;
}
else
{
printf("Element is present at index %d", result);
}
}
Unit-II: Part-I Searching and Sorting Dr. Madhuri Jawale Department of Information Technology
int search(int arr[], int N, int key)
{
for (int i = 0; i < N; i++)
if (arr[i] == key)
return i;
return -1;
}

10. Complexity Analysis of Linear Search
 Time Complexity:
 Best Case: In the best case, the key might be present at the first index. So the
best case complexity is O(1)
 Worst Case: In the worst case, the key might be present at the last index i.e.,
opposite to the end from which the search has started in the list. So the worst-
case complexity is O(N) where N is the size of the list.
 Average Case: O(N)
Unit-II: Part-I Searching and Sorting Dr. Madhuri Jawale Department of Information Technology

11. Advantages of Linear Search
 Linear search can be used irrespective of whether the array is sorted or not. It can
be used on arrays of any data type.
 Does not require any additional memory.
 It is a well-suited algorithm for small datasets.
Unit-II: Part-I Searching and Sorting Dr. Madhuri Jawale Department of Information Technology

12. Drawbacks of Linear Search
 Linear search has a time complexity of O(N), which in turn makes it slow for large
datasets.
 Not suitable for large arrays.
Unit-II: Part-I Searching and Sorting Dr. Madhuri Jawale Department of Information Technology

13. When to use Linear Search?
 When we are dealing with a small dataset.
 When you are searching for a dataset stored in contiguous memory.
Unit-II: Part-I Searching and Sorting Dr. Madhuri Jawale Department of Information Technology

14. Applications of Binary Search
 It can be used for searching a database.
 Binary search can be used as a building block for more complex algorithms used in
machine learning, such as algorithms for training neural networks or finding the
optimal hyperparameters for a model.
 It can be used for searching in computer graphics such as algorithms for ray tracing
or texture mapping.
Unit-II: Part-I Searching and Sorting Dr. Madhuri Jawale Department of Information Technology

15. Binary Search
 Binary Search is defined as a searching algorithm used in a sorted array by
repeatedly dividing the search interval in half.
 The idea of binary search is to use the information that the array is sorted and
reduce the time complexity to O(log N).
Unit-II: Part-I Searching and Sorting Dr. Madhuri Jawale Department of Information Technology

16. Continue….
Unit-II: Part-I Searching and Sorting Dr. Madhuri Jawale Department of Information Technology

17. Binary Search Algorithm
 In this algorithm,
 Divide the search space into two halves by finding the middle index “mid”.
 Compare the middle element of the search space with the key.
 If the key is found at middle element, the process is terminated.
Unit-II: Part-I Searching and Sorting Dr. Madhuri Jawale Department of Information Technology

18. Continue….
 If the key is not found at middle element, choose which half will be used as the
next search space.
• If the key is smaller than the middle element, then the left side is used for
next search.
• If the key is larger than the middle element, then the right side is used for
next search.
 This process is continued until the key is found or the total search space is
exhausted.
Unit-II: Part-I Searching and Sorting Dr. Madhuri Jawale Department of Information Technology

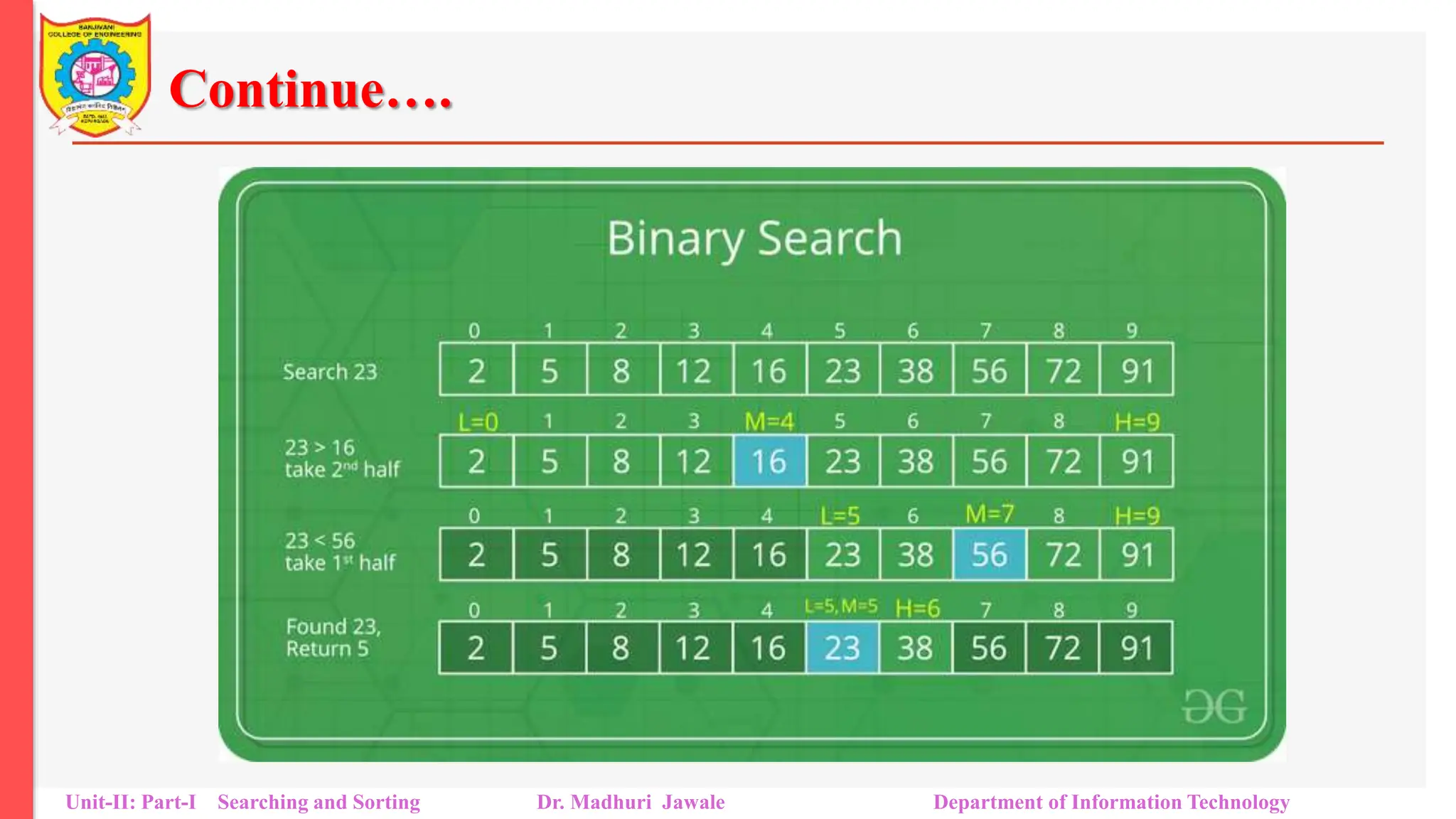
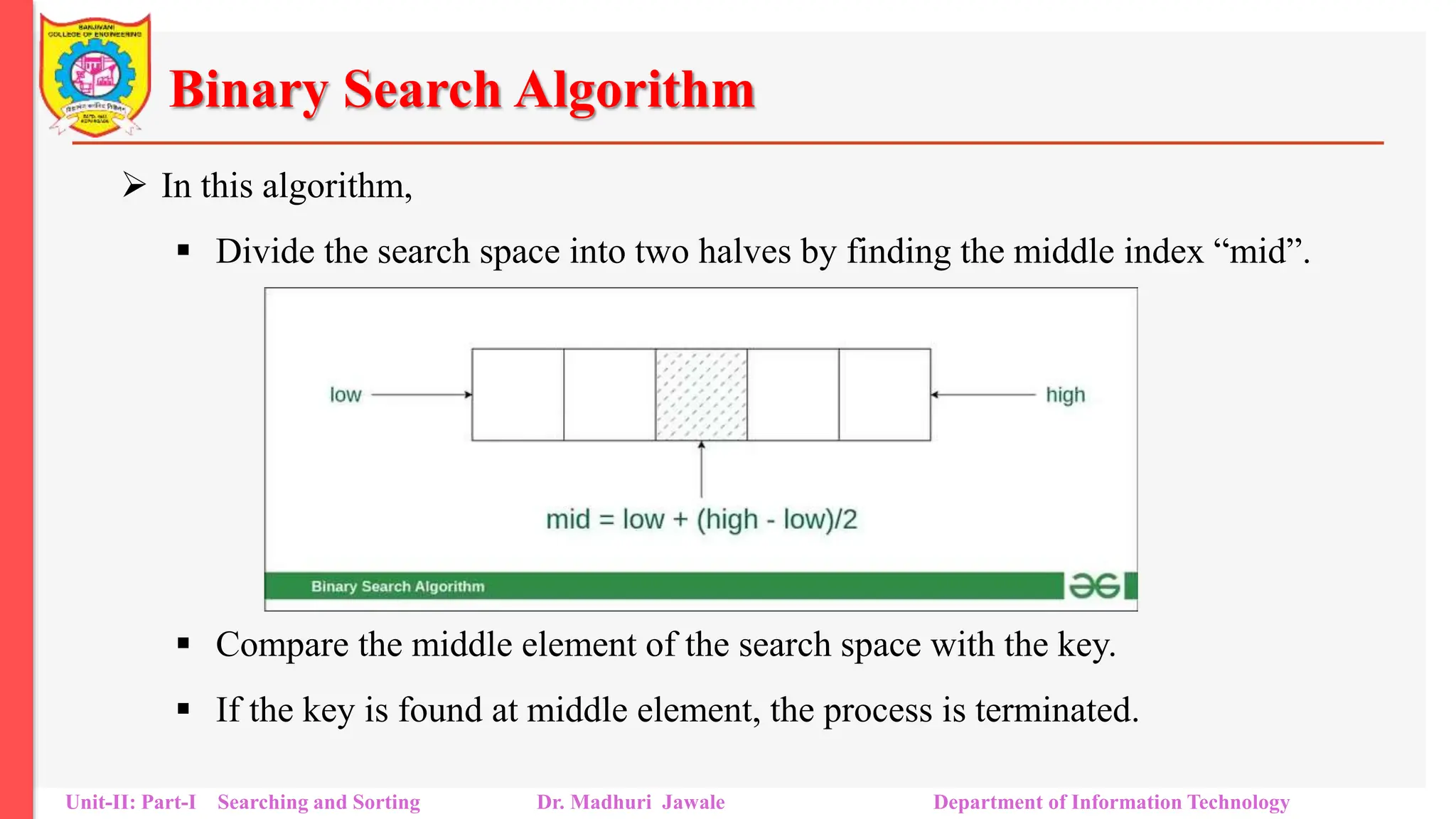
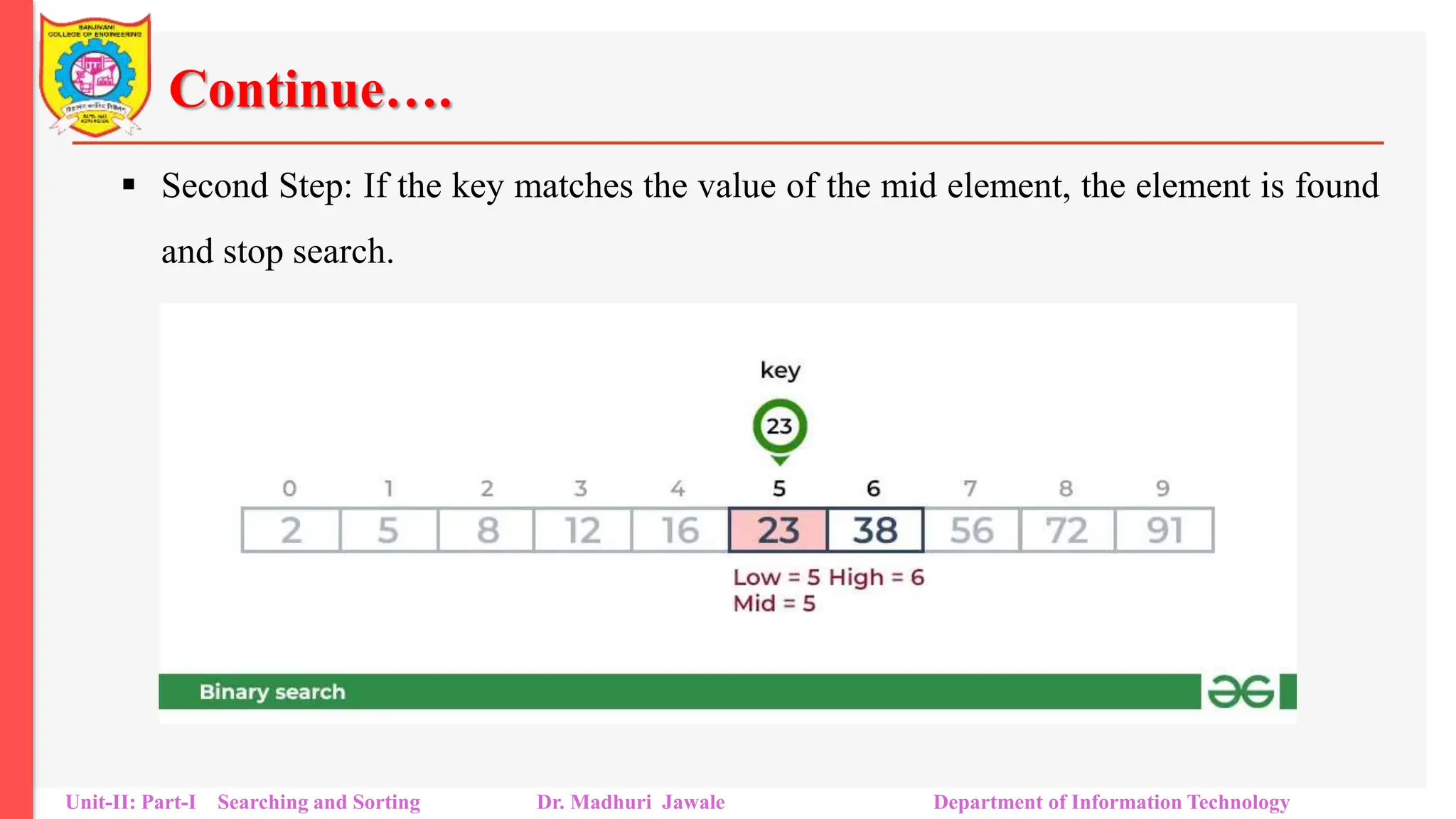
19. How does Binary Search work?
 To understand the working of binary search, consider the following illustration:
 Consider an array arr[] = {2, 5, 8, 12, 16, 23, 38, 56, 72, 91}, and
the target = 23.
 First Step: Calculate the mid and compare the mid element with the key. If the
key is less than mid element, move to left and if it is greater than the mid then
move search space to the right.
 Key (i.e., 23) is greater than current mid element (i.e., 16). The search space
moves to the right.
Unit-II: Part-I Searching and Sorting Dr. Madhuri Jawale Department of Information Technology

20. How does Binary Search work?
 Key (i.e., 23) is greater than current mid element (i.e., 16). The search space moves
to the right.
Unit-II: Part-I Searching and Sorting Dr. Madhuri Jawale Department of Information Technology

21. Continue….
 Key is less than the current mid 56. The search space moves to the left.
Unit-II: Part-I Searching and Sorting Dr. Madhuri Jawale Department of Information Technology

22. Continue….
 Second Step: If the key matches the value of the mid element, the element is found
and stop search.
Unit-II: Part-I Searching and Sorting Dr. Madhuri Jawale Department of Information Technology

23. How to Implement Binary Search?
 The Binary Search Algorithm can be implemented in the following two ways
 Iterative Binary Search Algorithm : Here we can use a while loop to continue
the process of comparing the key and splitting the search space in two halves.
 Recursive Binary Search Algorithm : Create a recursive function and
compare the mid of the search space with the key. And based on the result
either return the index where the key is found or call the recursive function for
the next search space.
Unit-II: Part-I Searching and Sorting Dr. Madhuri Jawale Department of Information Technology

24. Implementation of Iterative Binary Search Algorithm
int main(void)
{
int arr[] = { 2, 3, 4, 10, 40,34,78,56,35 };
int n = sizeof(arr);
int key = 40;
int result = binarySearch(arr, 0, n - 1, key);
if(result = = -1)
{
printf("Element is not present in array");
}
else
{
printf("Element is present at index %d", result);
}
return 0;
}
Unit-II: Part-I Searching and Sorting Dr. Madhuri Jawale Department of Information Technology
// An iterative binary search function.
int binarySearch(int arr[], int low, int high, int key)
{
while (low <= high)
{
int mid = low + (high - low) / 2;
// Check if key is present at mid
if (arr[mid] = = key)
return mid;
// If key greater, ignore left half
if (arr[mid] < key)
low = mid + 1;
// If key is smaller, ignore right half
else
high = mid - 1;
}
// If we reach here, then element was not present
return -1;
}

25. Recursive Binary Search Algorithm
int main()
{
int arr[] = { 2, 3, 4, 10, 40, 50, 35, 76, 45 };
int n = sizeof(arr) / sizeof(arr[0]);
int key = 40;
int result = binarySearch(arr, 0, n - 1, key);
if(result == -1)
{
printf("Element is not present in array");
}
else
{
printf("Element is present at index %d", result);
}
return 0;
}
Unit-II: Part-I Searching and Sorting Dr. Madhuri Jawale Department of Information Technology
int binarySearch(int arr[], int low, int high, int key)
{
if (high >= low)
{
int mid = low + (high - low) / 2;
// If the element is present at the middle itself
if (arr[mid] = = key)
return mid;
// If element is smaller than mid, then it can only be present in left subarray
if (arr[mid] > key)
return binarySearch(arr, low, mid - 1, key);
// Else the element can only be present in right subarray
return binarySearch(arr, mid + 1, high, key);
}
// We reach here when element is not present in array
return -1;
}

26. Complexity Analysis of Binary Search
 Time Complexity:
 Best Case: O(1)
 Average Case: O(log N)
 Worst Case: O(log N)
Unit-II: Part-I Searching and Sorting Dr. Madhuri Jawale Department of Information Technology

27. Advantages of Binary Search
 Binary search is faster than linear search, especially for large arrays.
 More efficient than other searching algorithms with a similar time complexity, such
as interpolation search or exponential search.
 Binary search is well-suited for searching large datasets that are stored in external
memory, such as on a hard drive or in the cloud.
Unit-II: Part-I Searching and Sorting Dr. Madhuri Jawale Department of Information Technology

28. Drawbacks of Binary Search
 The array should be sorted.
 Binary search requires that the data structure being searched be stored in
contiguous memory locations.
Unit-II: Part-I Searching and Sorting Dr. Madhuri Jawale Department of Information Technology

29. Comparison of Linear & Binary Search
Unit-II: Part-I Searching and Sorting Dr. Madhuri Jawale Department of Information Technology
Linear Search Binary Search
In linear search input data need not to be in sorted. In binary search input data need to be in sorted order.
It is also called sequential search. It is also called half-interval search.
The time complexity of linear search O(n). The time complexity of binary search O(log n).
Multidimensional array can be used. Only single dimensional array is used.
Linear search performs equality comparisons Binary search performs ordering comparisons
It is less complex. It is more complex.
It is very slow process. It is very fast process.

30. Continue….
Unit-II: Part-I Searching and Sorting Dr. Madhuri Jawale Department of Information Technology
Linear Search to find the element “J” in a given sorted list from A-X
Binary Search to find the element “J” in a given sorted list from A-X

31. Reference
1. Richard F. Gilberg & Behrouz A. Forouzan, “Data Structures: A Pseudocode
Approach with C, Second Edition”, Cengage Learning.
2. Ellis Horowitz, Sartaj Sahani, Susan Anderson-Freed “Fundamentals of Data
Structures in C”, Universities Press, 2008.
Unit-II: Part-I Searching and Sorting Dr. Madhuri Jawale Department of Information Technology