This document discusses two methods for searching in arrays: sequential search and binary search. Sequential search involves checking each element of the array sequentially until the desired value is found. Binary search works by comparing the target value to the middle element of a sorted array, then searching the upper or lower half. Binary search is faster than sequential search as it reduces the search space by half with each comparison, with an average efficiency of O(log n) comparisons versus O(n) for sequential search. The document provides pseudocode examples and compares the properties of each search method.

1. OBJECT- ORIENTED PROGRAMING
Name: Zohaib Arif
Roll no.: 6823
Semester: 2nd
Department of Information & Technology

2. SEARCHING IN ARRAY

3. Searching in array
 Sequential search
 Binary search

4. CONTENTS:
• Introduction
• Sequential search
• Binary search
• Compression
• Efficiency
• Conclusion

5. INTRODUCTION:
• Array
• Search
• Search in array
i. Sequential search
ii. Binary search

6. SEQUENTIAL SEARCH:
Algorithm involves checking all the element of array(or any structure) one
by one and in sequence until the desired result is found.

7. This algorithm follows the following steps to
search a value in array.
• Visit the first element of the array and
compare its value with required value.
• If the value of array matches with the desired
value, the search is complete.
• If the value of array doesn`t match, move to
next element and repeat same process.
Algorithm:
for(i=0; i<n; i++)
if(arr[i]==n)
return (i);
else
return (-1);

8. BINARY SEARCH:
The binary search algorithm begins by
comparing the target value to value of the
middle element of the sorted array and
then move upper or lower half. This
process repeated until the required
number is not found.

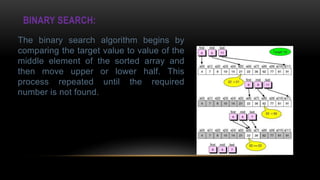
9. This algorithm follows the following steps to search a
value in array.
• It locates the middle element of array and compares
with the search number.
• If they are equal, search is successful and the index
of middle element is returned.
• If they are not equal, it reduces the search to half of
the array.
• If the search number is less than the middle
element, it searches the first half of array.
Otherwise it searches the second half of the array.
Algorithm:
low =0;
hi=n-1;
while(low<=hi)2
{ mid =(low +hi)
if (arr[mid]==n)
return(mid);
if(n<arr[mid])
hi=mid-1;
else
low=mid-1; }
return(-1);

10. Linear search
• Sorted array is not necessary.
• It is not quicker method.
• Average speed of linear search is
very slow then binary search.
• Programing code make short when
linear search is use.
Binary search
• Sorted array is necessary.
• It is quicker method.
• Average speed of binary search is
very fast then linear search.
• Programing code make big when
linear search is use.
COMPARISON:

11. EFFICIENCY:
Both search has its won benefit but each comparison in binary reduces the number of
possible candidates by a factor of 2. thus maximum number of key comparison is
approximately long with bases 2.

12. CONCLUSION:
• Searching is an important function in computer science. When data set become
larger and larger good search algorithms will become more important. Linear
search is not more efficient then binary search because we want our work do
rapidly and average comparison of linear search make more efficient then binary
search.