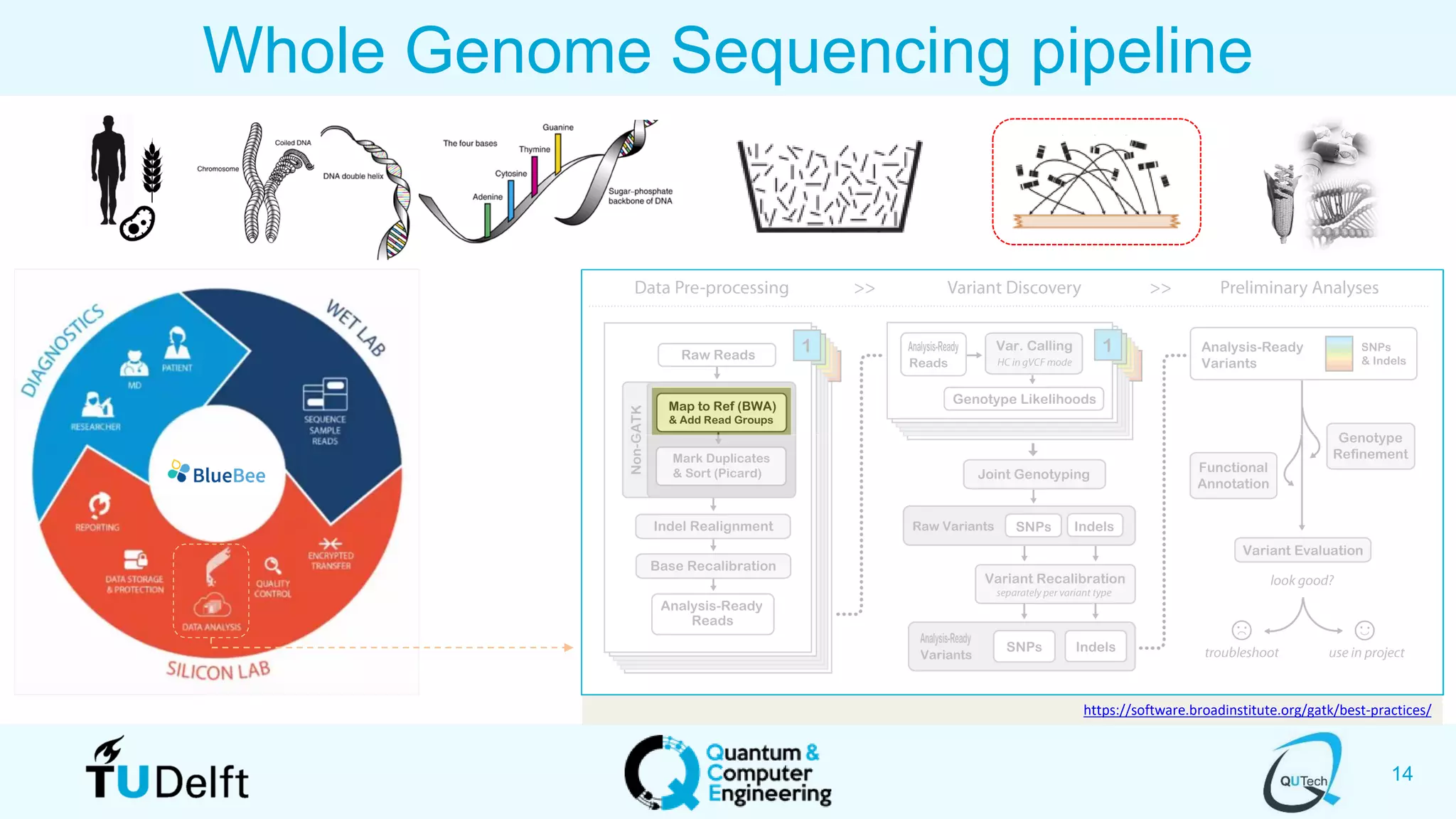
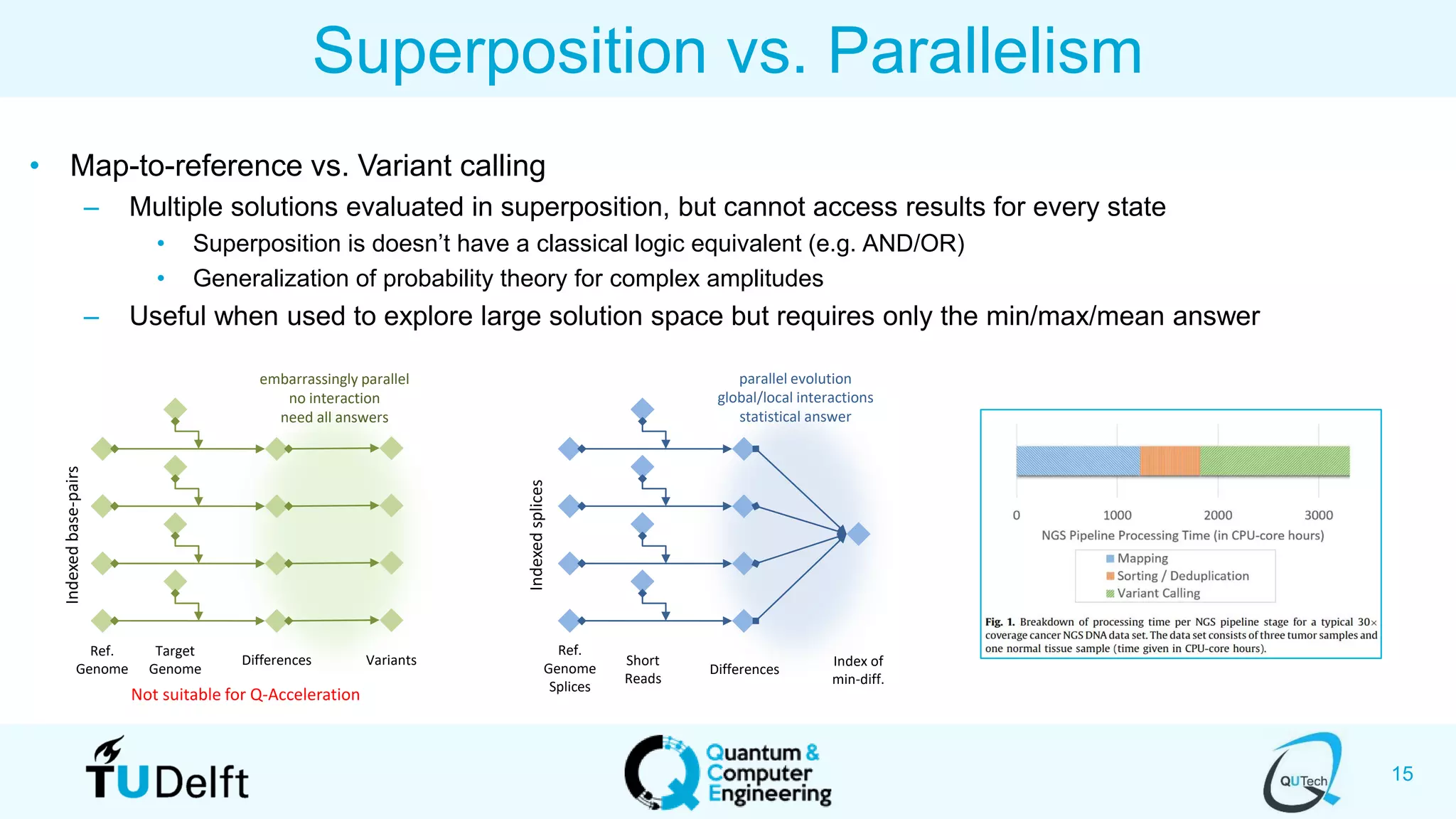
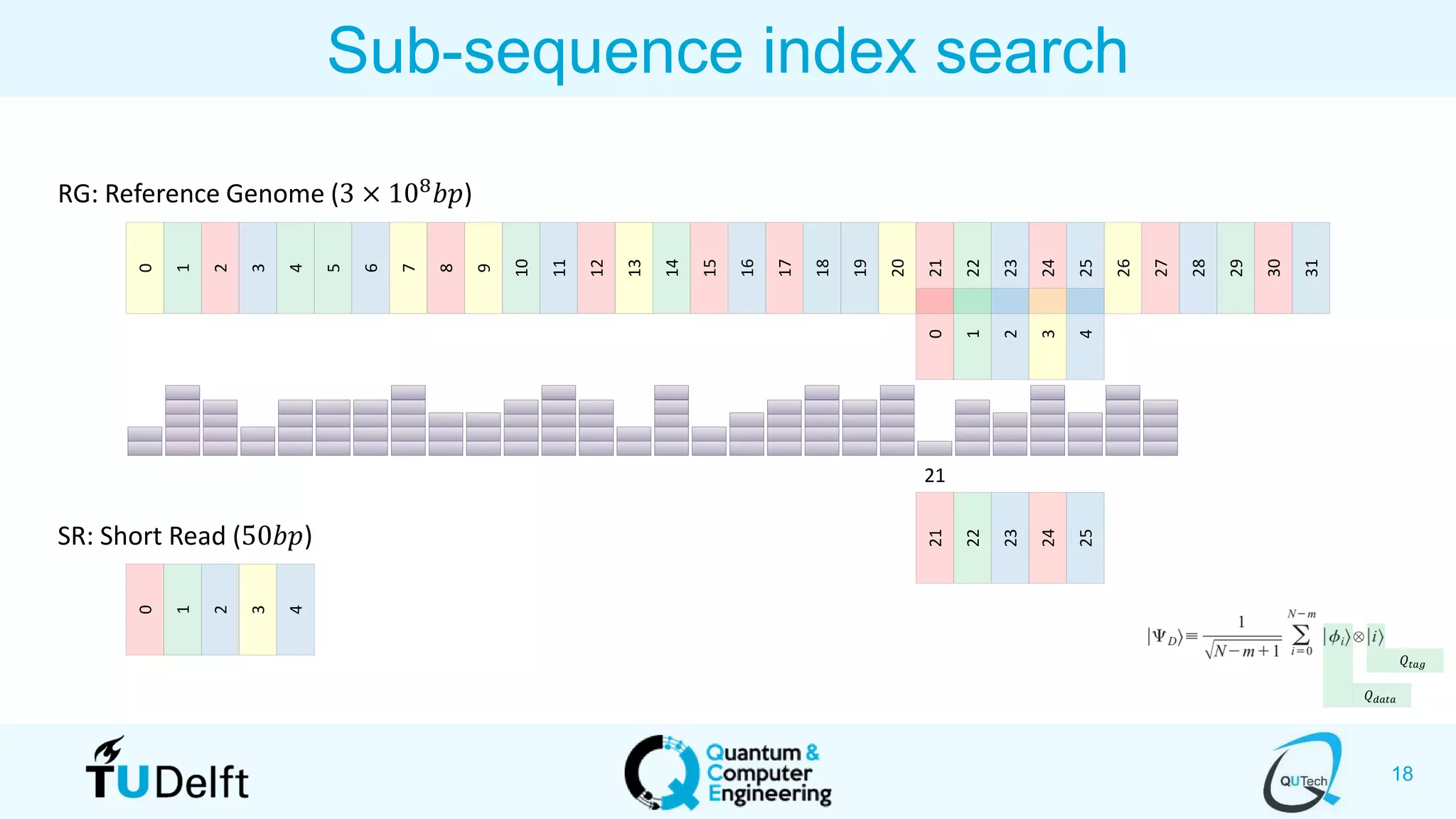
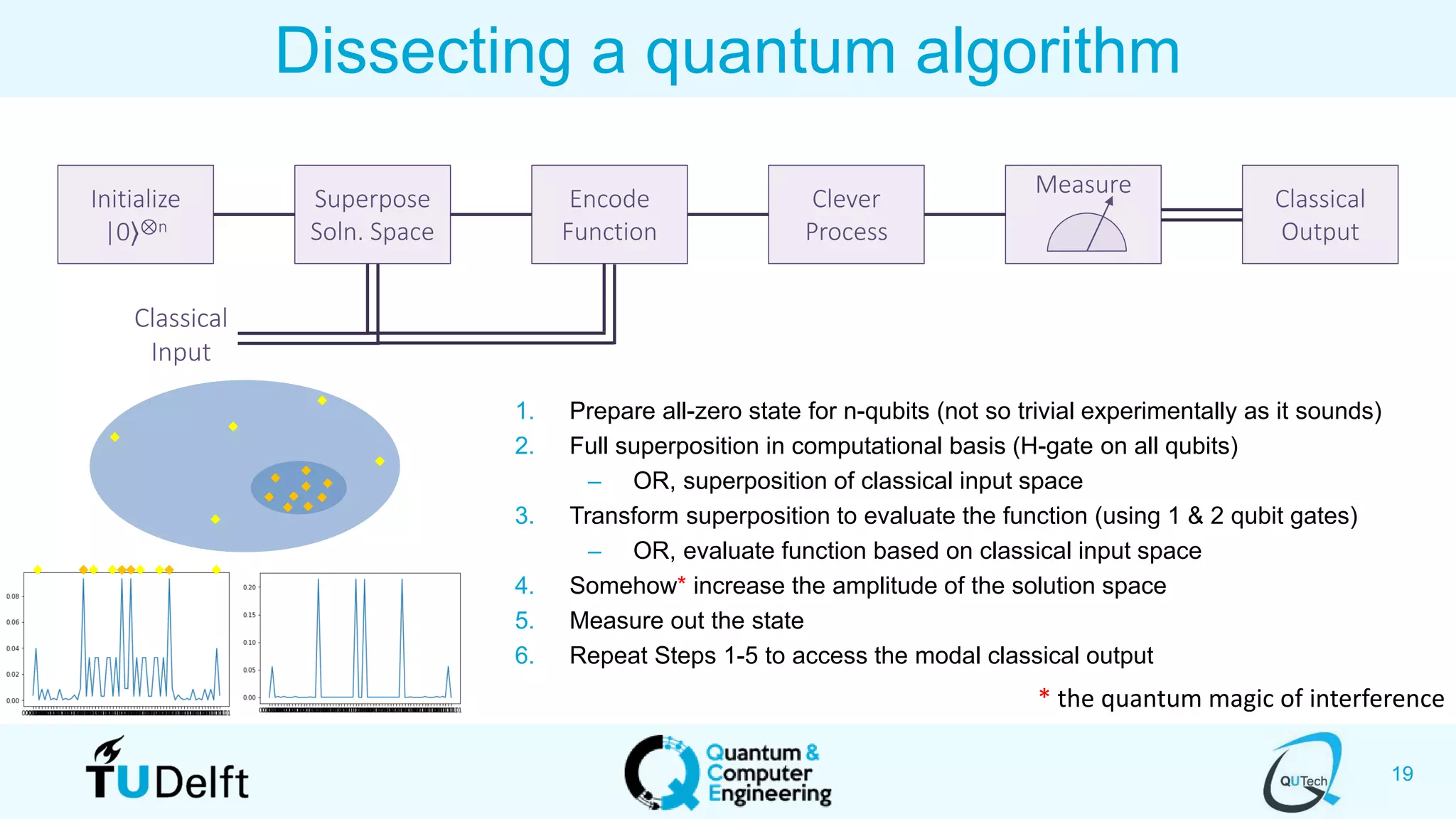
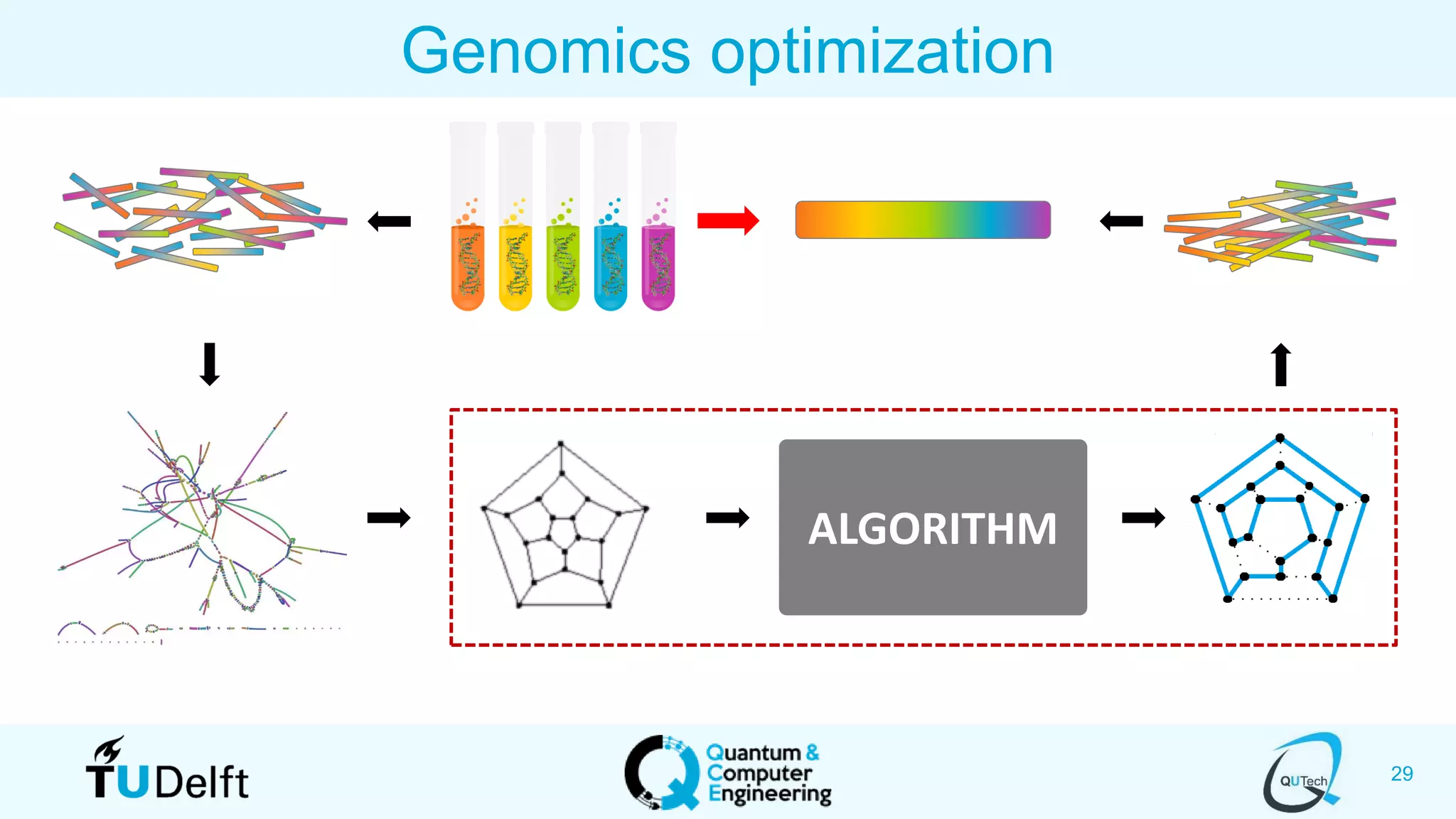
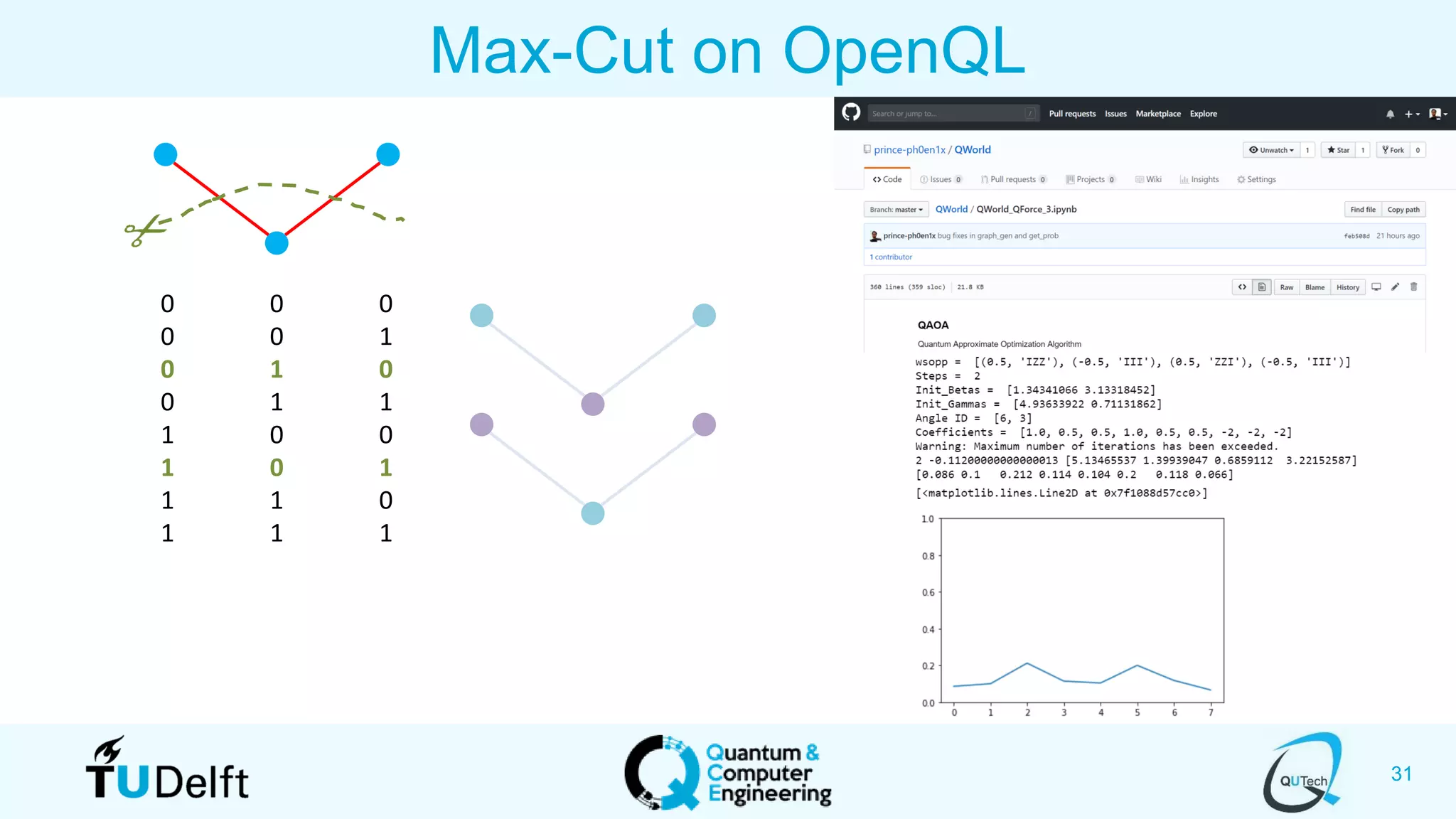
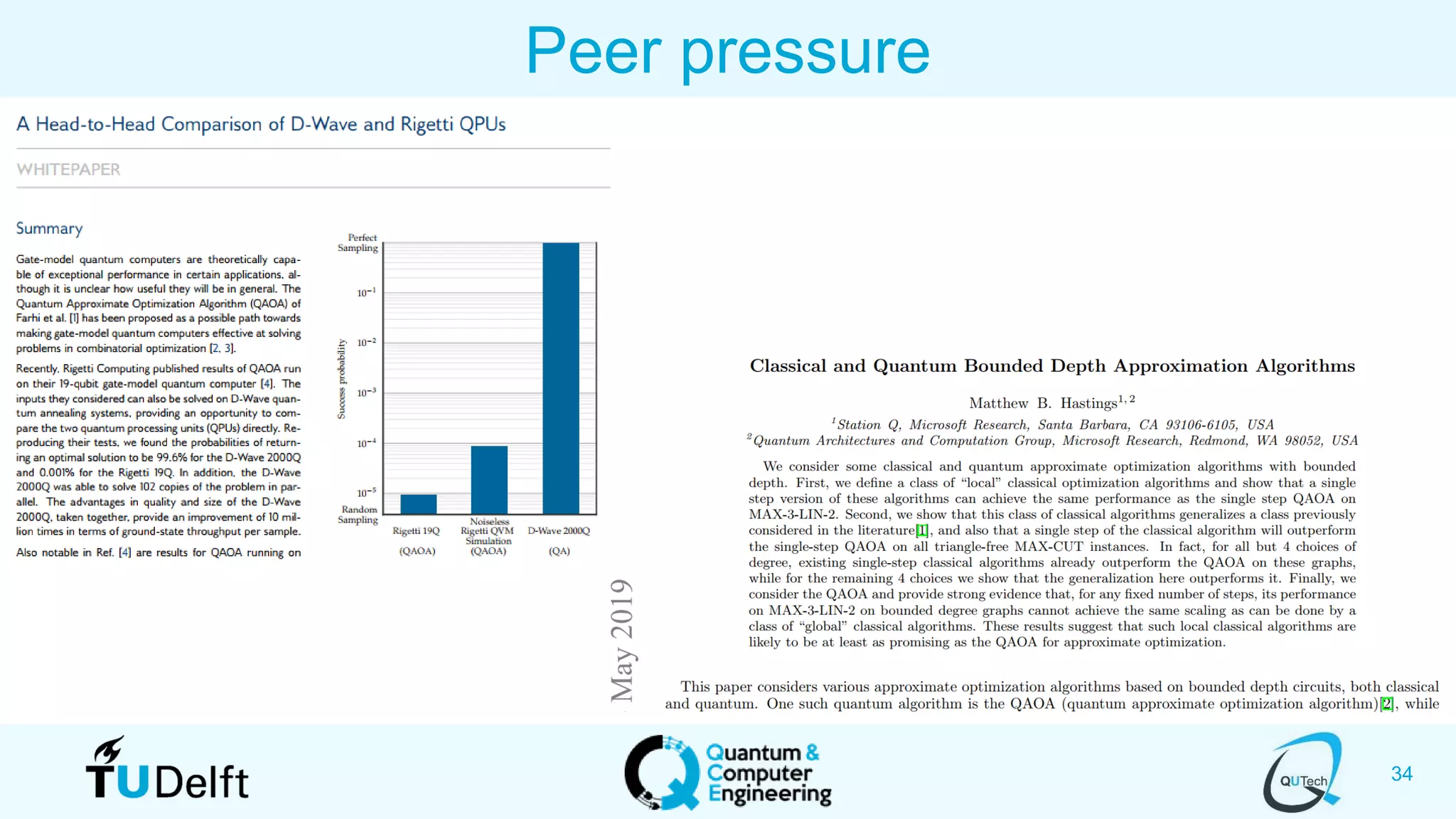
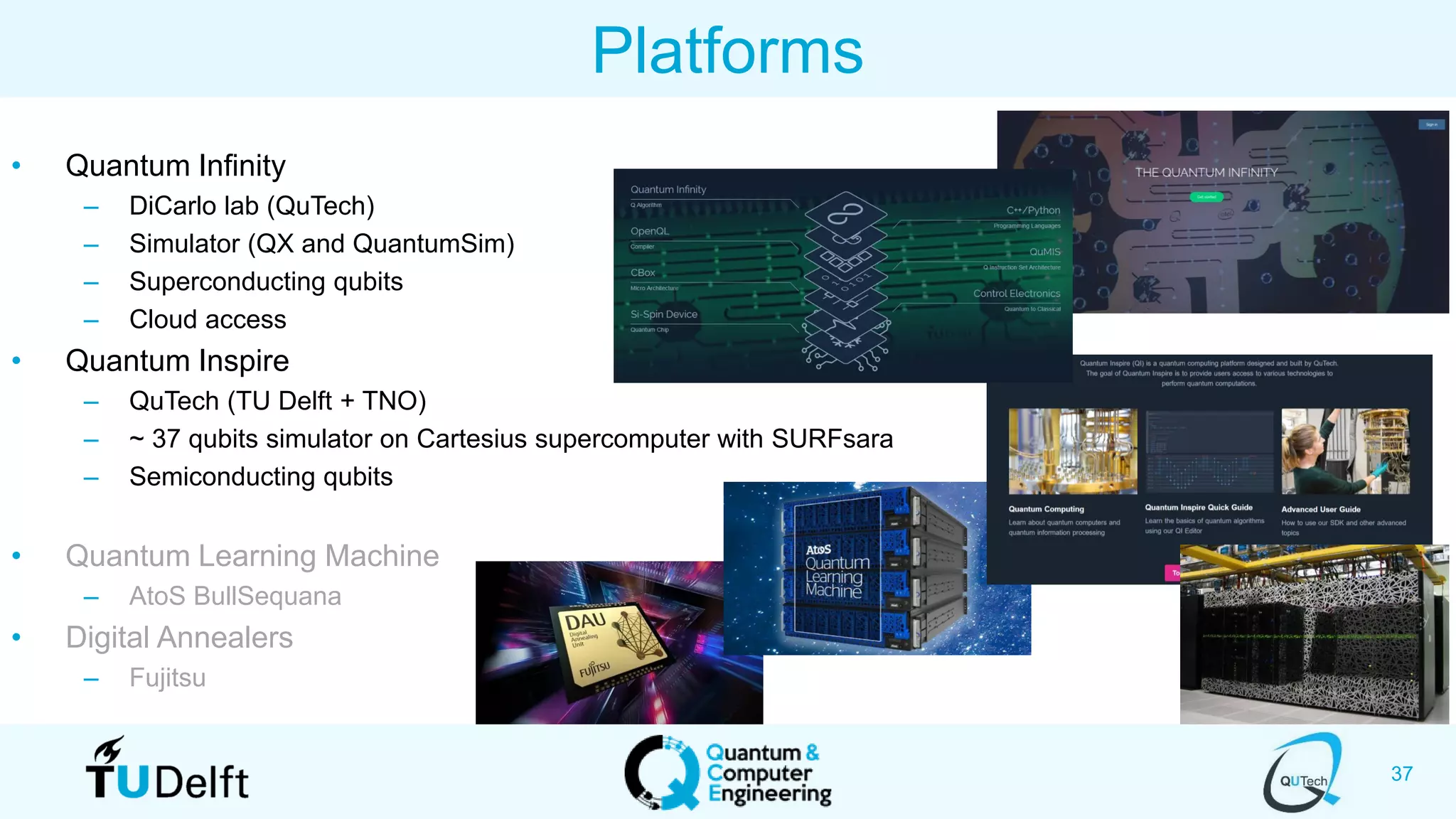
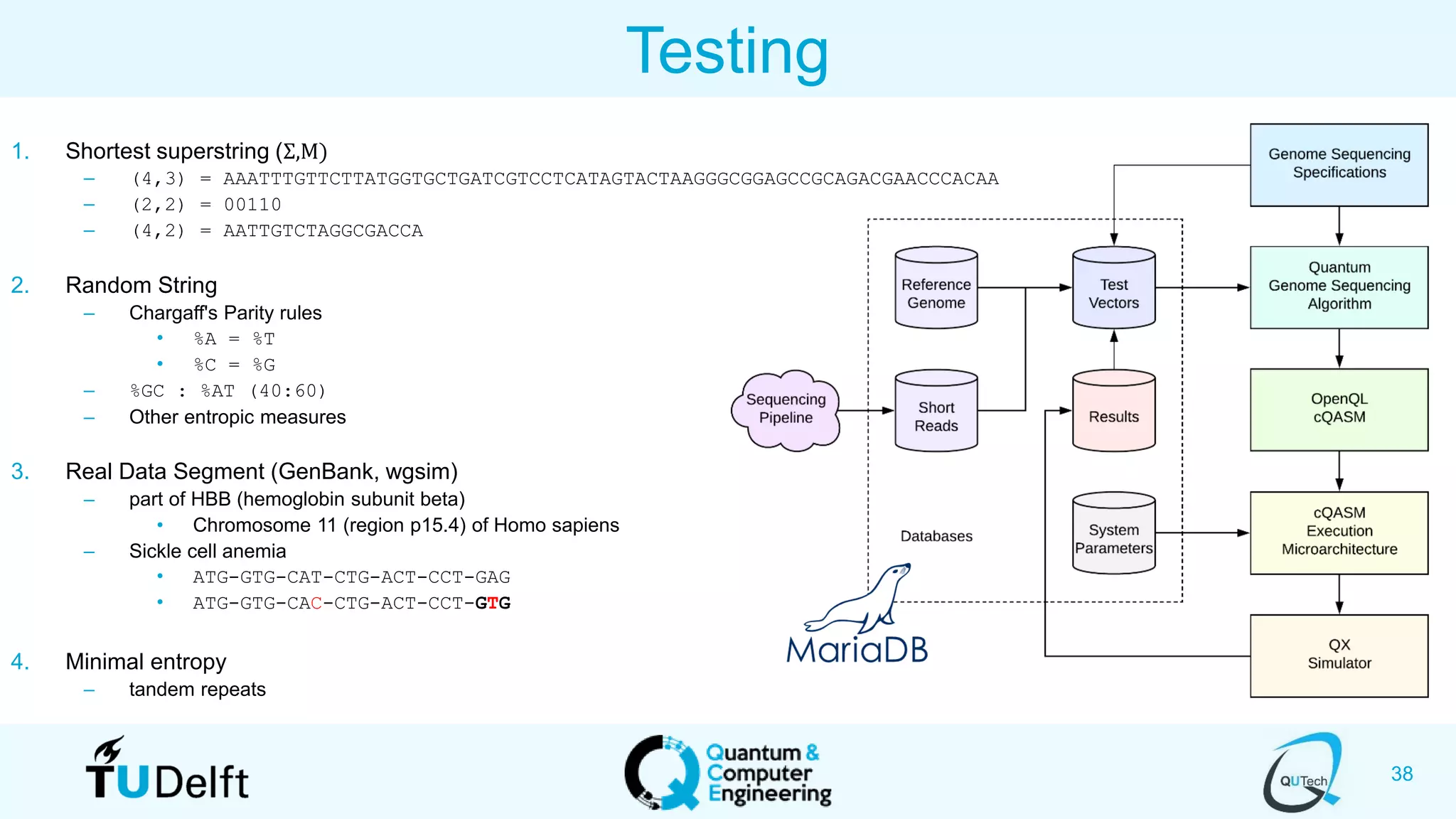
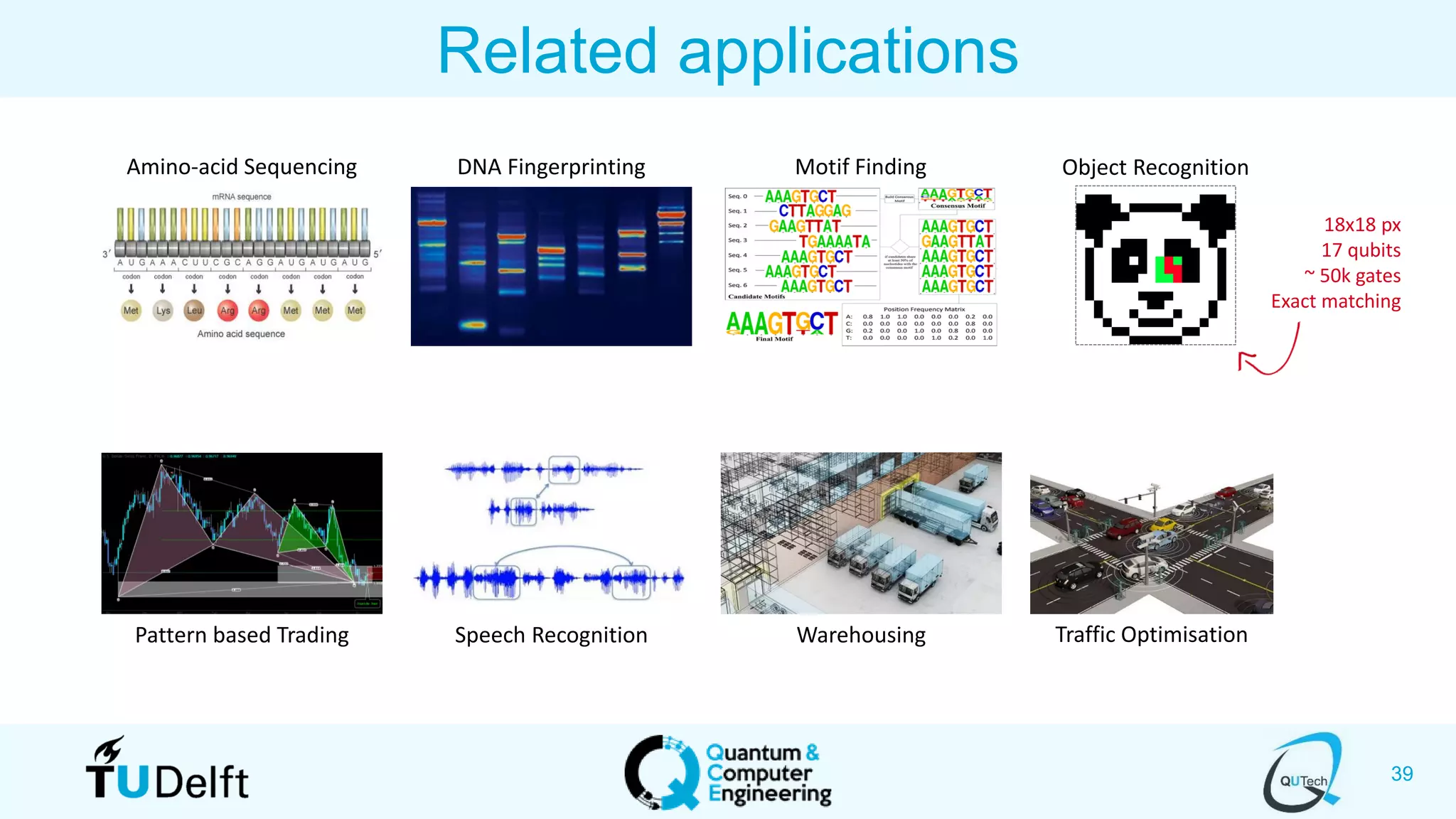
The document discusses search and optimization on quantum accelerators. It begins with an overview of the big picture of quantum search and optimization. It then discusses quantum search algorithms like Grover's algorithm and conditional oracle algorithms. It describes how these algorithms can be used for problems like sub-sequence index search. The document next discusses quantum optimization algorithms like the quantum approximate optimization algorithm (QAOA). It notes that QAOA is a hybrid quantum-classical algorithm that can be used to solve NP-hard combinatorial optimization problems. Finally, it provides an example of how QAOA could potentially be applied to problems in genomics optimization.

1. Search and optimization
on quantum accelerators
23rd May, 2019
Aritra Sarkar
PhD candidate, Quantum Computer Architecture lab
QuTech (Faculty of Applied Sciences)
Dept. of Q&CE (Faculty of Electrical Engineering, Mathematics and Computer Sciences)
Delft University of Technology
Genomics
Machine
Learning
Quantum
Computing
Application
Platform
Method
access the
presentation
here

2. 01
Big Picture
Big
Picture
Q
Search
Q
Optimise
Dev
Tools

3. 3
The 1st quantum revolution

4. 4
It from Bit

5. 5
The idea
඀ቚψ 𝑆𝑦𝑠 ඀ቚψ 𝑄𝐶
1982
Caltech
඀𝑈𝑆𝑦𝑠 𝑡 ቚψ 𝑆𝑦𝑠 ඀𝑈 𝑄𝐶 𝑡 ቚψ 𝑄𝐶
඀𝑒−𝑖 ෣𝐻 𝑆𝑦𝑠 𝑡
ቚψ 𝑆𝑦𝑠 ඀𝑒−𝑖෣𝐻 𝑄𝐶 𝑡
ቚψ 𝑄𝐶
Initialize
Evolve
Measure
besides winning a Nobel Prize for QED, inventing
Feynman diagrams, writing books and playing bongos…

6. 6
Formalizing stuffs
1985
Oxford • Quantum Turing Machines
• First (and only so far) example of violation of the
Extended Church-Turing thesis
• Universality of Gate-Model Quantum Computing
• Deutsch algorithm
• First algorithm to show exponential speedup
• Constructor Theory

7. 7
Formalizing stuffs
1996
MIT • It from Qubit
• Quantum Random Access Machine (QRAM)
• Quantum Machine Learning
• Quantum simulation for natural Hamiltonians is efficient
• k-local (each operator acts on at most k-qubits)
෣𝐻𝑆𝑦𝑠 = ෍
𝑖=1
𝑙
෡ℎ𝑖

8. 8
The 2nd quantum revolution
…and continues with us
it started with them…

9. 9
Knowing our limits
• Quantum Computers is as good as computing gets
• with our current laws of physics
• Quantum Gravity Computers?
• Sure, it’s possible once we have Interstellar tech.
• not without breaking current laws of physics (like non-
linearity in QM, Heisenberg uncertainty limit, light-speed
limit, escaping blackholes, etc.)
• Relativistic QC / Closed-Timelike-Curves
2008
MIT, UTA

10. 10
• QC vs. CC
– Given the same size QC and CC
• QC (QTM) can always simulate CC (UTM)
– Universal Gate Sets for QC: (H, Toffoli), (CX, Rx, Rz), (CX, H, T)
– Universal Gate Sets for CC: (Toffoli/CCX), (Fredkin/CSWAP), (NAND, Fanout)
» NAND: 𝐶𝐶𝑋 𝑎𝑏1 → 𝑎𝑏 𝑎. 𝑏 , FanOut: 𝐶𝐶𝑋 1𝑎0 → 1𝑎𝑎
• CC can always simulate QC (but with worst-case exponential overhead)
– QC cannot do super-Turing computation
– QC cannot solve NP-Complete problems in P time
» Factorial is in BQP (believed to not be NP-C)
» If there are no classical divide-and-conquer approach, QC can give a polynomial speedup by Grover
search
– Why not do everything in QC (since CC is proper sub-set of QC)?
• because we don’t have same size QC as CC (HPC, number of GPU cores, etc)
• because QC are still too noisy and costly
Quantum computability

11. 11
NISQ acceleration
NISQ
FTQC
QEC
ClassicalSimulationLimit
number of qubits
errorrate
https://arxiv.org/abs/1801.00862 - John Preskill, Quantum Computing in the NISQ era and beyond
 NISQ: Noisy Intermediate-Scale Quantum
map problem to quantum:
do:
run Q Algorithm
assess answer
while (result not satisfactory)
save measurement result/statistics
interpret classical answer
HostCPU
Graphics Processing Unit
Field-Programmable Gate Array
Digital Signal Processor
Neural Processing Unit
QuantumAccelerator

12. 12
Genomical exa-scale data
2-40 EB/year
Genomical Big Data

13. 13
Code of life
high sequence similarity usually implies significant functional or structural similarity
Genetic Similarity %
Other humans 99.9
Chimpanzees 98.6
Mouse 92
Cats 90
Cows 85
Dogs 84
Zebra-fish 73
Chicken 65
Banana 60
Honey bee 44
Grapes 24
Yeast 18
E. Coli 7
+ 97% Biological Dark
Matter
Expression
Replication
Metabolism
Reproduction

14. 14
Whole Genome Sequencing pipeline
https://software.broadinstitute.org/gatk/best-practices/

15. 15
• Map-to-reference vs. Variant calling
– Multiple solutions evaluated in superposition, but cannot access results for every state
• Superposition is doesn’t have a classical logic equivalent (e.g. AND/OR)
• Generalization of probability theory for complex amplitudes
– Useful when used to explore large solution space but requires only the min/max/mean answer
Superposition vs. ParallelismIndexedbase-pairs
Ref.
Genome
Target
Genome
Differences Variants
embarrassingly parallel
no interaction
need all answers
Not suitable for Q-Acceleration
Ref.
Genome
Splices
Short
Reads
Differences
Index of
min-diff.
Indexedsplices
parallel evolution
global/local interactions
statistical answer

16. 16
02
Q Search
Big
Picture
Q
Search
Q
Optimise
Dev
Tools

17. 17
NP
Searching solutions
𝑦𝑠 = 𝑓(𝑥 𝑠) 𝑦𝑠 = 𝑓(𝑥 𝑠) 𝑦𝑠 = 𝑓(𝑥 𝑠)
𝑥 𝑠 = 𝑓−1
(𝑦𝑠)
𝑦0 = 𝑓 𝑥0
𝑦1 = 𝑓 𝑥1
𝑦2 = 𝑓 𝑥2 = 𝑦𝑠
𝑦3 = 𝑓 𝑥3
⋮
Function Evaluation Inductive Logic, GP, ANN, …Function Inversion
Quantum Superposition
P
Bounded Quantum Polynomial

18. 18
Sub-sequence index search
RG: Reference Genome (3 × 108 𝑏𝑝)
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
SR: Short Read (50𝑏𝑝)
0
1
2
4
3
21
21
22
23
24
25
0
1
2
4
3
𝑄𝑡𝑎𝑔
𝑄 𝑑𝑎𝑡𝑎

19. 19
Dissecting a quantum algorithm
Superpose
Soln. Space
Encode
Function
Clever
Process
Measure
Initialize
|0⟩⊗n
Classical
Output
Classical
Input
1. Prepare all-zero state for n-qubits (not so trivial experimentally as it sounds)
2. Full superposition in computational basis (H-gate on all qubits)
– OR, superposition of classical input space
3. Transform superposition to evaluate the function (using 1 & 2 qubit gates)
– OR, evaluate function based on classical input space
4. Somehow* increase the amplitude of the solution space
5. Measure out the state
6. Repeat Steps 1-5 to access the modal classical output
* the quantum magic of interference

20. 20
Amplitude
Probability
Grover’s search
+1|000⟩
+0.3536|000⟩
+0.3536|001⟩
+0.3536|010⟩
+0.3536|011⟩
+0.3536|100⟩
+0.3536|101⟩
+0.3536|110⟩
+0.3536|111⟩
+0.3536|000⟩
+0.3536|001⟩
+0.3536|010⟩
+0.3536|011⟩
+0.3536|100⟩
-0.3536|101⟩
+0.3536|110⟩
+0.3536|111⟩
μ=+0.2652
+0.1768|000⟩
+0.1768|001⟩
+0.1768|010⟩
+0.1768|011⟩
+0.1768|100⟩
+0.8839|101⟩
+0.1768|110⟩
+0.1768|111⟩
3% |000⟩
3% |001⟩
3% |010⟩
3% |011⟩
3% |100⟩
78% |101⟩
3% |110⟩
3% |111⟩
+0.1768|000⟩
+0.1768|001⟩
+0.1768|010⟩
+0.1768|011⟩
+0.1768|100⟩
-0.8839|101⟩
+0.1768|110⟩
+0.1768|111⟩
μ=+0.0442
-0.0884|000⟩
-0.0884|001⟩
-0.0884|010⟩
-0.0884|011⟩
-0.0884|100⟩
+0.9723|101⟩
-0.0884|110⟩
-0.0884|111⟩
0.8% |000⟩
0.8% |001⟩
0.8% |010⟩
0.8% |011⟩
0.8% |100⟩
94.5% |101⟩
0.8% |110⟩
0.8% |111⟩
H⊗n Oracle
Inversion
about Mean|0⟩⊗n answer
𝑂 2 𝑛 times
• unstructured database
• assumes existence of a Black-box Oracle
• quadratic reduction in query complexity
• periodic amplification

21. 22
Conditional oracle
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
0
1
2
4
3
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
Oracle Fn. A
Oracle Fn. C
Oracle Fn. G
Oracle Fn. T
Reference
Search Pattern
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
MinimizationNP-Hard
Precomputed
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

22. 23
iBAM
• (Quantum) indexed-bidirectional associative memory
– Content Addressable Storage (CAS) + RAM
– (Q)BAM is a type of (Q) Neural Network
𝑄𝑡𝑎𝑔
𝑄 𝑑𝑎𝑡𝑎
Min.
Hamming
dist. Oracle

23. 24
QiBAM-dq: an example
• Reference: AATTGTCTAGGCGACC
• Query: CA

24. 25
QiMAM-dq
• Quantum indexed multi-associative memory (MSc thesis)
– Grover’s Search + Quantum Neural Networks + Content Addressable Storage

25. 26
03
Q Optimise
Big
Picture
Q
Search
Q
Optimise
Dev
Tools

26. 27
Purebreds
• a.k.a. Coherent Protocols
– e.g. Shor’s factorization, Shor’s discrete-log, QFT, Quantum Phase Estimation, Harrow-Hassidim-Lloyd,
Matrix inversion ...
– Most studied/popular quantum algorithms so far
• Exponential speedup
– Caveats
• Noise tolerance
– Number of qubits for FT
• Circuit depth
• Quantum I/O
– Classical Input: State preparation
– Classical Output: State tomography
– QRAM
O ( f(experimental) x g(no-cloning) x h(algorithm) )

27. 28
Workhorses
• Peter Shor estimates 2048-RSA requires ~5k qubits (times 102-103 physical qubits) & ~107 gates
• Near-term Quantum Algorithms
– low depth circuits without extensive QEC (small-codes)
– enough qubits to just store the problem (hard to do better)
– still solve useful problems with local constraints
– Adaptable optimization algorithms (easy to map to problem)
• Genetic Algorithm / Evolutionary Programs
• Deep Learning
– Quantum Approximate Optimization Algorithm
• NP-Hard combinatorial optimisation problems in Quantum Machine Learning
• Polynomial-time solution for every instance with guaranteed approximation quality bound
• Interesting because of its potential to exhibit near-term quantum supremacy
• Gate-based implementation inspired by Adiabatic QC and Q Annealing
https://www.bcg.com/en-ca/publications/2018/next-decade-quantum-computing-how-play.aspx

28. 29
Genomics optimization
ALGORITHM

29. 30
Quantum Approximate Optimization Algorithm
• Quantum/classical Hybrid algorithm
– Parameterised quantum subroutine is run within a classical optimization loop
– Prepare the quantum state | ൿ𝜓 Ԧ𝜃 , often called the ansatz
– Measure the expectation value ൻ𝜓 Ԧ𝜃 ℋ ൿ𝜓 Ԧ𝜃
• By Variational theorem, expectation value ℋ ⟩|𝑎𝑛𝑠𝑎𝑡𝑧 ≥ λ1 (smallest eigenvalue; lowest energy; ground-state)
– Find an optimal choice of real-valued parameters Ԧ𝜃 such that the expectation value is minimised via. Classical optimiser
• Challenges
– Heuristic - no general recipe of Ansatz definition works universally
– Optimiser choice
– Initial Parameter selection is arbitrary
– Convergence not always guaranteed
– High number of Iteration

30. 31
Max-Cut on OpenQL
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1

31. 32
Optimizers
• Gradient-free
– Nelder-Mead - Downhill simplex method or Amoeba method
– Powell - Powell's conjugate direction method
– multiMin - general constrained mixed-integer global optimization to find all local minima by a multi-start method
– glcCluster - hybrid algorithm for constrained mixed-integer global optimization
– LGO - global nonlinear programming
– PSO – particle swarm optimisation
• Gradient-based
– L-BGFS-B - limited-memory Broyden–Fletcher–Goldfarb–Shanno with bound/box constraints
– COBYLA - constrained optimization by linear approximation
– SPSA – simultaneous perturbation stochastic approximation
• ... and many more, e.g. in
– SciPy Python package - 22
– TOMLAB MATLAB library - 59
+ Easy to specify
- Difficulty converging for large θ space

32. 33
R-U-S for NP-C
• Convergence challenges
– Noise in expectation value measurement (estimation accuracy/precision)
– Initial parameter outside zone of attraction (non-convex landscape)
• Stuck in local minima
• Some local minima are ok for Genomics (sub-optimal solutions)
– Stuck in barren plateau
• Iteration challenges
 Optimiser stuck, rerun (a few times at max.)
 Optimisation cycles (~50)
 Estimate each Pauli group term in Hamiltonian (depends on problem size, max 4^N)
ℋ = σ 𝛼=1
𝑇
𝑐 𝛼 𝑃𝛼 𝑃𝛼 ∈ 𝑋, 𝑌, 𝑍, 𝐼 ⊗𝑁
𝐸 = ൻ𝜓 Ԧ𝜃 ℋ ൿ𝜓 Ԧ𝜃 = σ 𝛼=1
𝑇
𝑐 𝛼ൻ𝜓 Ԧ𝜃 𝑃𝛼 ൿ𝜓 Ԧ𝜃 = σ 𝛼=1
𝑇
𝑐 𝛼ൻ𝜓′ Ԧ𝜃 𝑀 𝑍
⊗𝑁
ൿ𝜓′ Ԧ𝜃 = σ 𝛼=1
𝑇
𝑐 𝛼
1
𝑆
σ𝑖=1
𝑆
𝑏𝑖𝛼 𝜓′
= 𝑅 𝛼 𝜓
 For each Pauli group, tomographic trails to estimate probability (~10000)
𝐸
Ԧ𝜃

33. 34
Peer pressure

34. 35
04
Dev Tools
Big
Picture
Q
Search
Q
Optimise
Dev
Tools

35. 36
Quantum HLL
• OpenQL
– inspired by OpenCL; Apache 2.0 license
– https://github.com/QE-Lab/OpenQL
• Programs (Kernels (Operations))
– Decompose: Toffoli, Control, Unitary, Rotation, CX-CZ
– Optimize: Cancel UU†
– Scheduling: ASAP, ALAP, Balanced
– Mapping: Surface-17 connectivity routing
– QASM: cQASM, eQASM (topology, resource constraints)
• Other features:
– Conjugate uncompute
– Classical logical/comparative operations
– Language features
• Recursion, loops, functions
• Libraries like NumPy, Matplotlib
Configure Platform
Create Program
Create Kernels
Populate each Kernel
Add Kernels to
Program
Compile Program

36. 37
Platforms
• Quantum Infinity
– DiCarlo lab (QuTech)
– Simulator (QX and QuantumSim)
– Superconducting qubits
– Cloud access
• Quantum Inspire
– QuTech (TU Delft + TNO)
– ~ 37 qubits simulator on Cartesius supercomputer with SURFsara
– Semiconducting qubits
• Quantum Learning Machine
– AtoS BullSequana
• Digital Annealers
– Fujitsu

37. 38
Testing
1. Shortest superstring (Σ,M)
– (4,3) = AAATTTGTTCTTATGGTGCTGATCGTCCTCATAGTACTAAGGGCGGAGCCGCAGACGAACCCACAA
– (2,2) = 00110
– (4,2) = AATTGTCTAGGCGACCA
2. Random String
– Chargaff's Parity rules
• %A = %T
• %C = %G
– %GC : %AT (40:60)
– Other entropic measures
3. Real Data Segment (GenBank, wgsim)
– part of HBB (hemoglobin subunit beta)
• Chromosome 11 (region p15.4) of Homo sapiens
– Sickle cell anemia
• ATG-GTG-CAT-CTG-ACT-CCT-GAG
• ATG-GTG-CAC-CTG-ACT-CCT-GTG
4. Minimal entropy
– tandem repeats

38. 39
Related applications
DNA Fingerprinting Motif FindingAmino-acid Sequencing
Pattern based Trading
Object Recognition
Speech Recognition
18x18 px
17 qubits
~ 50k gates
Exact matching
Traffic OptimisationWarehousing

39. 40
Koen
Bertels
Carmen
G. Almudever
Razvan
Nane
Imran
Ashraf
Nader
Khammassi
Hans
van Someren
Leo
DiCarlo
Jeroen
van Straten
LingLing
Lao
Savvas
Varsamopoulos
Matthijs
Brobbel
Aritra
Sarkar
Abid
Moueddene
Xiang
Fu
Leon
Riesebos
Daniel
Moreno
Miguel
Serrao
Amitabh
Yadav
Alejandro
Morais
Anneriet
Krol
Yaoling
Yang
Mengyu
Zhang
Bas
van Wee
Diogo
Valada
Zaid
Al-Ars

40. 41
Search and optimization
on quantum accelerators
23rd May, 2019
Aritra Sarkar
PhD candidate, Quantum Computer Architecture lab
QuTech (Faculty of Applied Sciences)
Dept. of Q&CE (Faculty of Electrical Engineering, Mathematics and Computer Sciences)
Delft University of Technology
Genomics
Machine
Learning
Quantum
Computing
Application
Platform
Method
access the
presentation
here