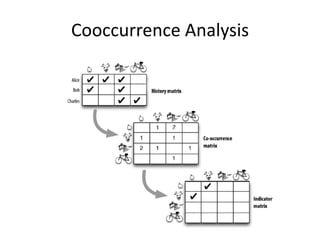
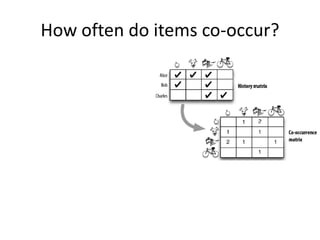
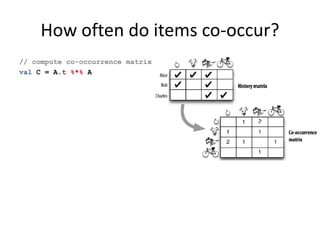
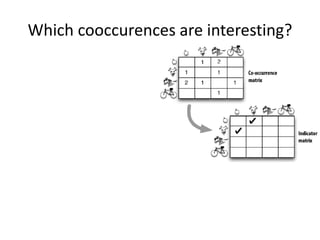
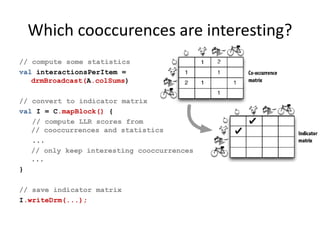
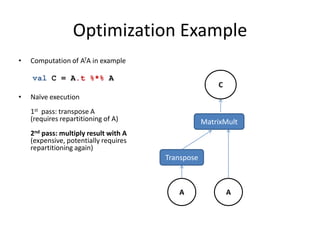
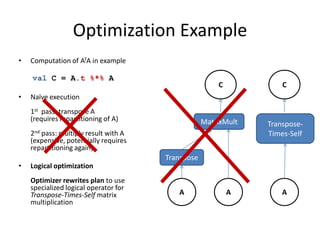
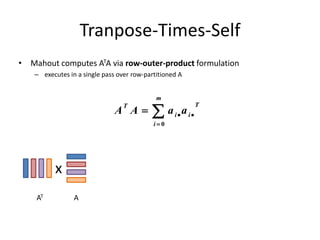
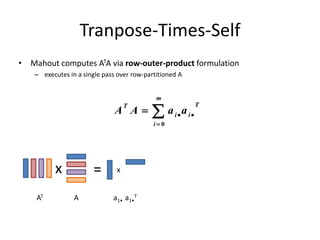
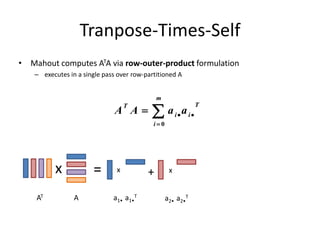
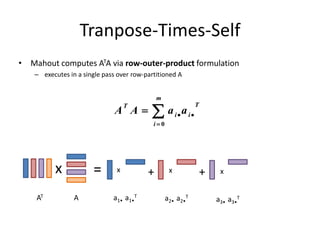
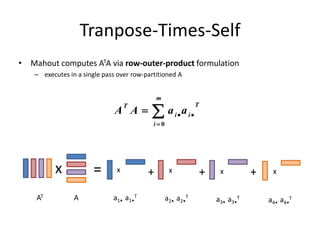
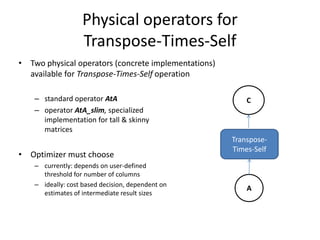
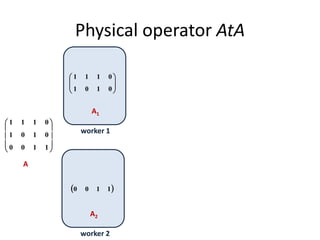
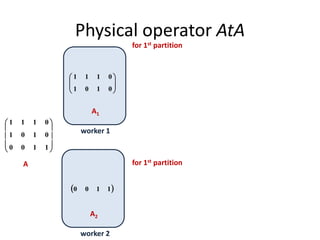
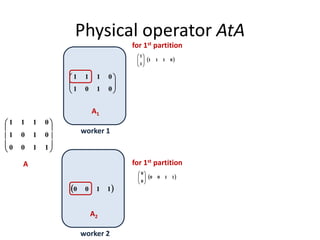
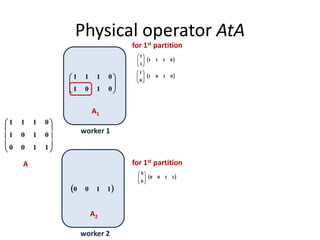
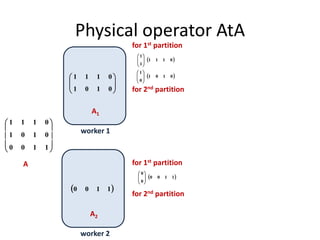
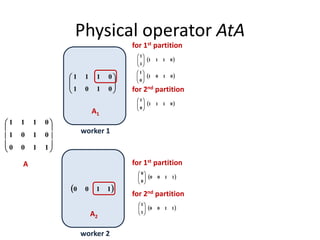
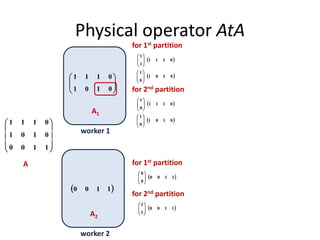
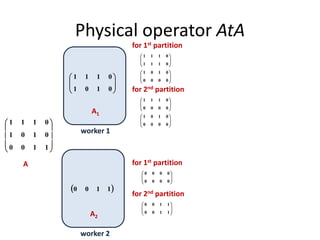
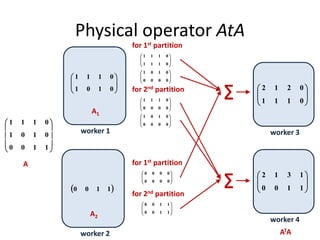
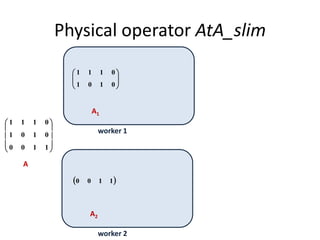
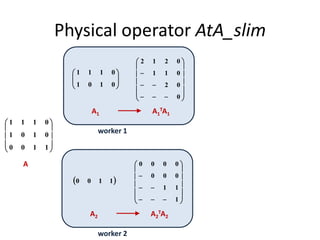
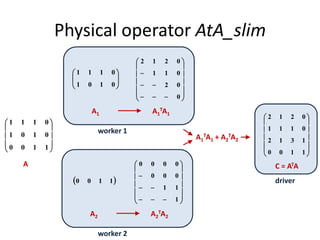
This document discusses techniques for co-occurrence-based recommendations using Apache Mahout, Scala, and Spark. It describes how Mahout computes the co-occurrence matrix ATA using a row-outer product formulation that executes in a single pass over the row-partitioned matrix A. It also explains how the computation is optimized physically by using specialized operators like Transpose-Times-Self to avoid repartitioning the matrix. Finally, it provides examples of how the distributed computation of ATA is implemented across worker nodes.

1. Co-occurrence-based recommendations
with Mahout, Scala & Spark
Sebastian Schelter
@sscdotopen
BigData Beers
05/29/2014

2. available for free at
http://www.mapr.com/practical-machine-learning

3. Cooccurrence Analysis

4. History matrix
// real usecase: load from DFS
// val A = drmFromHDFS(...)
// our toy example
val A = drmParallelize(dense(
(1, 1, 1, 0), // Alice
(1, 0, 1, 0), // Bob
(0, 0, 1, 1)), // Charles
numPartitions = 2)

5. How often do items co-occur?

6. How often do items co-occur?
// compute co-occurrence matrix
val C = A.t %*% A

7. Which cooccurences are interesting?

8. Which cooccurences are interesting?
// compute some statistics
val interactionsPerItem =
drmBroadcast(A.colSums)
// convert to indicator matrix
val I = C.mapBlock() {
// compute LLR scores from
// cooccurrences and statistics
...
// only keep interesting cooccurrences
...
}
// save indicator matrix
I.writeDrm(...);

9. Cooccurrence Analysis
prototype available
• MAHOUT-1464 provides full-fledged cooccurrence analysis protoype
– applies selective downsampling to make computation tractable
– support for cross-recommendations in datasets with multiple
interaction types, e.g.
• “people who watch this video also watch those videos”
• “people who enter this search query watch those videos”
– code to run this on the Movielens and Epinions datasets
• future plan: easy indexing of indicator matrix with Apache Solr to allow
for search-as-recommendation deployments
– prototype for MR code already existing at https://github.com/pferrel/solr-recommender
– integration is in the works

10. Under the covers

11. Underlying systems
• currently: runtime based on Apache Spark
– fast and expressive cluster
computing system
– general computation graphs,
in-memory primitives, rich API,
interactive shell
• potentially supported in the future:
• Apache Flink (formerly: “Stratosphere”)
• H20

12. Runtime & Optimization
• Execution is defered, user
composes logical operators
• Computational actions implicitly
trigger optimization (= selection
of physical plan) and execution
• Optimization factors: size of operands, orientation of operands,
partitioning, sharing of computational paths
• e. g.: matrix multiplication:
– 5 physical operators for drmA %*% drmB
– 2 operators for drmA %*% inMemA
– 1 operator for drm A %*% x
– 1 operator for x %*% drmA
val C = A.t %*% A
I.writeDrm(path);
val inMemV =(U %*% M).collect

13. Optimization Example
• Computation of ATA in example
• Naïve execution
1st pass: transpose A
(requires repartitioning of A)
2nd pass: multiply result with A
(expensive, potentially requires
repartitioning again)
• Logical optimization:
rewrite plan to use specialized
logical operator for
Transpose-Times-Self matrix
multiplication
val C = A.t %*% A

14. Optimization Example
• Computation of ATA in example
• Naïve execution
1st pass: transpose A
(requires repartitioning of A)
2nd pass: multiply result with A
(expensive, potentially requires
repartitioning again)
• Logical optimization:
rewrite plan to use specialized
logical operator for
Transpose-Times-Self matrix
multiplication
val C = A.t %*% A
Transpose
A

15. Optimization Example
• Computation of ATA in example
• Naïve execution
1st pass: transpose A
(requires repartitioning of A)
2nd pass: multiply result with A
(expensive, potentially requires
repartitioning again)
• Logical optimization:
rewrite plan to use specialized
logical operator for
Transpose-Times-Self matrix
multiplication
val C = A.t %*% A
Transpose
MatrixMult
A A
C

16. Optimization Example
• Computation of ATA in example
• Naïve execution
1st pass: transpose A
(requires repartitioning of A)
2nd pass: multiply result with A
(expensive, potentially requires
repartitioning again)
• Logical optimization
Optimizer rewrites plan to use
specialized logical operator for
Transpose-Times-Self matrix
multiplication
val C = A.t %*% A
Transpose
MatrixMult
A A
C
Transpose-
Times-Self
A
C

17. Tranpose-Times-Self
• Mahout computes ATA via row-outer-product formulation
– executes in a single pass over row-partitioned A




m
i
T
ii
T
aaAA
0

18. Tranpose-Times-Self
• Mahout computes ATA via row-outer-product formulation
– executes in a single pass over row-partitioned A




m
i
T
ii
T
aaAA
0
A

19. Tranpose-Times-Self
• Mahout computes ATA via row-outer-product formulation
– executes in a single pass over row-partitioned A




m
i
T
ii
T
aaAA
0
x
AAT

20. Tranpose-Times-Self
• Mahout computes ATA via row-outer-product formulation
– executes in a single pass over row-partitioned A




m
i
T
ii
T
aaAA
0
x = x
AAT a1• a1•
T

21. Tranpose-Times-Self
• Mahout computes ATA via row-outer-product formulation
– executes in a single pass over row-partitioned A




m
i
T
ii
T
aaAA
0
x = x + x
AAT a1• a1•
T
a2• a2•
T

22. Tranpose-Times-Self
• Mahout computes ATA via row-outer-product formulation
– executes in a single pass over row-partitioned A




m
i
T
ii
T
aaAA
0
x = x + +x x
AAT a1• a1•
T
a2• a2•
T
a3• a3•
T

23. Tranpose-Times-Self
• Mahout computes ATA via row-outer-product formulation
– executes in a single pass over row-partitioned A




m
i
T
ii
T
aaAA
0
x = x + + +x x x
AAT a1• a1•
T
a2• a2•
T
a3• a3•
T
a4• a4•
T

24. Physical operators for
Transpose-Times-Self
• Two physical operators (concrete implementations)
available for Transpose-Times-Self operation
– standard operator AtA
– operator AtA_slim, specialized
implementation for tall & skinny
matrices
• Optimizer must choose
– currently: depends on user-defined
threshold for number of columns
– ideally: cost based decision, dependent on
estimates of intermediate result sizes
Transpose-
Times-Self
A
C

25. Physical operators for the
distributed computation of ATA

26. Physical operator AtA










1100
0101
0111
A

27. A2
 1100
Physical operator AtA










1100
0101
0111
A1
A
worker 1
worker 2






0101
0111

28. A2
 1100
Physical operator AtA










1100
0101
0111
A1
A
worker 1
worker 2






0101
0111
for 1st partition
for 1st partition

29. A2
 1100
Physical operator AtA










1100
0101
0111
A1
A
worker 1
worker 2






0101
0111
 0111
1
1






 1100
0
0






for 1st partition
for 1st partition

30. A2
 1100
Physical operator AtA










1100
0101
0111
A1
A
worker 1
worker 2






0101
0111
 0111
1
1






 1100
0
0






for 1st partition
for 1st partition
 0101
0
1







31. A2
 1100
Physical operator AtA










1100
0101
0111
A1
A
worker 1
worker 2






0101
0111
 0111
1
1






 1100
0
0






for 1st partition
for 1st partition
 0101
0
1






for 2nd partition
for 2nd partition

32. A2
 1100
Physical operator AtA










1100
0101
0111
A1
A
worker 1
worker 2






0101
0111
 0111
1
1






 1100
0
0






for 1st partition
for 1st partition
 0101
0
1






 0111
0
1






for 2nd partition
 1100
1
1






for 2nd partition

33. A2
 1100
Physical operator AtA










1100
0101
0111
A1
A
worker 1
worker 2






0101
0111
 0111
1
1






 1100
0
0






for 1st partition
for 1st partition
 0101
0
1






 0111
0
1






for 2nd partition
 0101
0
1






 1100
1
1






for 2nd partition

34. A2
 1100
Physical operator AtA










1100
0101
0111
A1
A
worker 1
worker 2






0101
0111






0111
0111






0000
0000
for 1st partition
for 1st partition






0000
0101






0000
0111
for 2nd partition






0000
0101






1100
1100
for 2nd partition

35. A2
 1100
Physical operator AtA










1100
0101
0111
A1
A
worker 1
worker 2






0101
0111






0111
0111






0000
0000
for 1st partition
for 1st partition






0000
0101






0000
0111
for 2nd partition






0000
0101






1100
1100
for 2nd partition






0111
0212
worker 3






1100
1312
worker 4
∑
∑
ATA

36. Physical operator AtA_slim










1100
0101
0111
A

37. A2
 1100
Physical operator AtA_slim










1100
0101
0111
A1
A
worker 1
worker 2






0101
0111

38. A2
TA2A2
 1100

















1
11
000
0000
Physical operator AtA_slim










1100
0101
0111
A1
TA1A1
A
worker 1
worker 2






0101
0111

















0
02
011
0212

39. A2
TA2A2
 1100

















1
11
000
0000
Physical operator AtA_slim










1100
0101
0111
A1
TA1A1
A C = ATA
worker 1
worker 2
A1
TA1 + A2
TA2
driver






0101
0111

















0
02
011
0212














1100
1312
0111
0212

40. Thank you. Questions?
Overview of Mahout‘s Scala & Spark Bindings:
http://s.apache.org/mahout-spark
Tutorial on playing with Mahout‘s Spark shell
http://s.apache.org/mahout-spark-shell