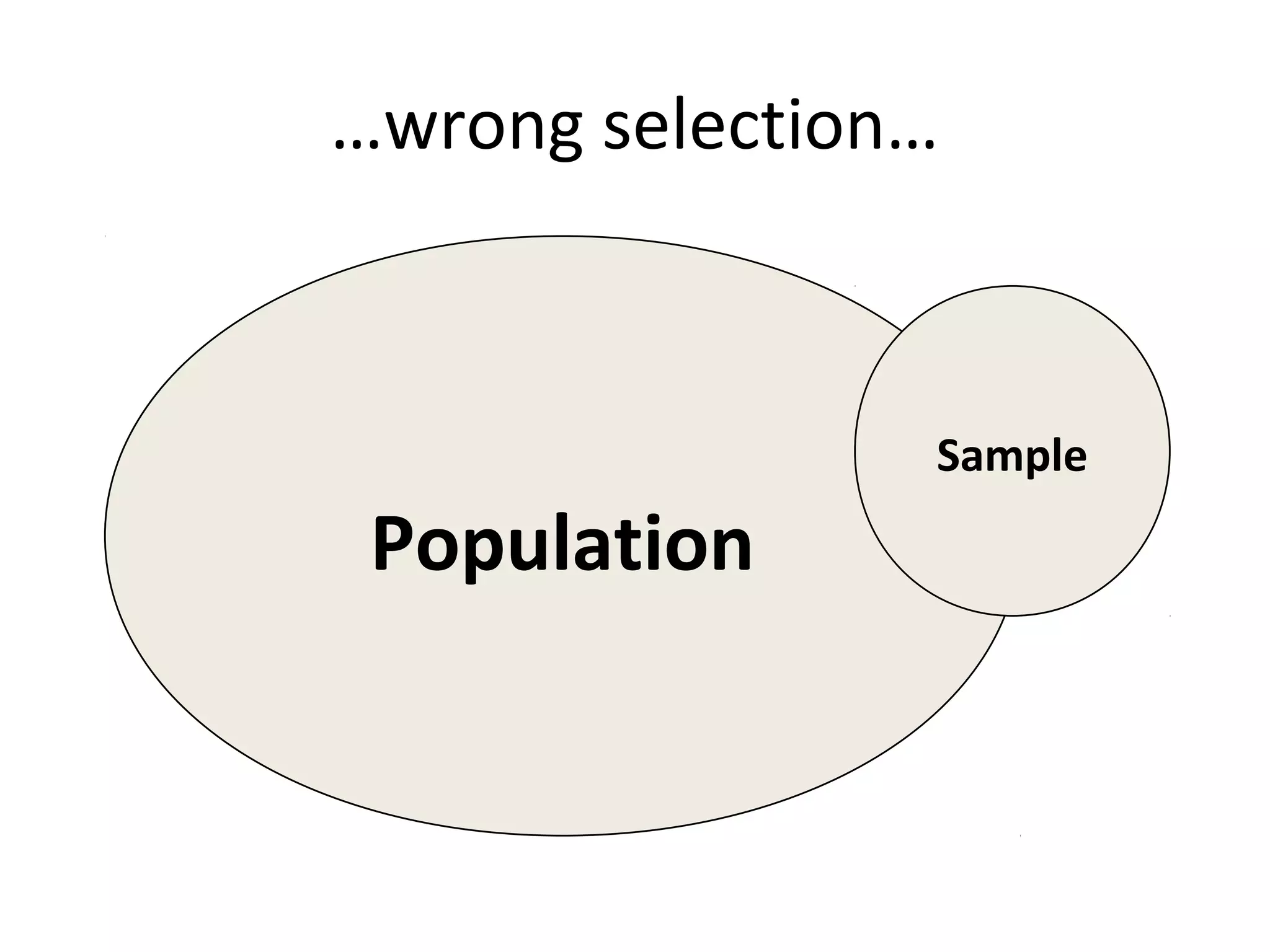
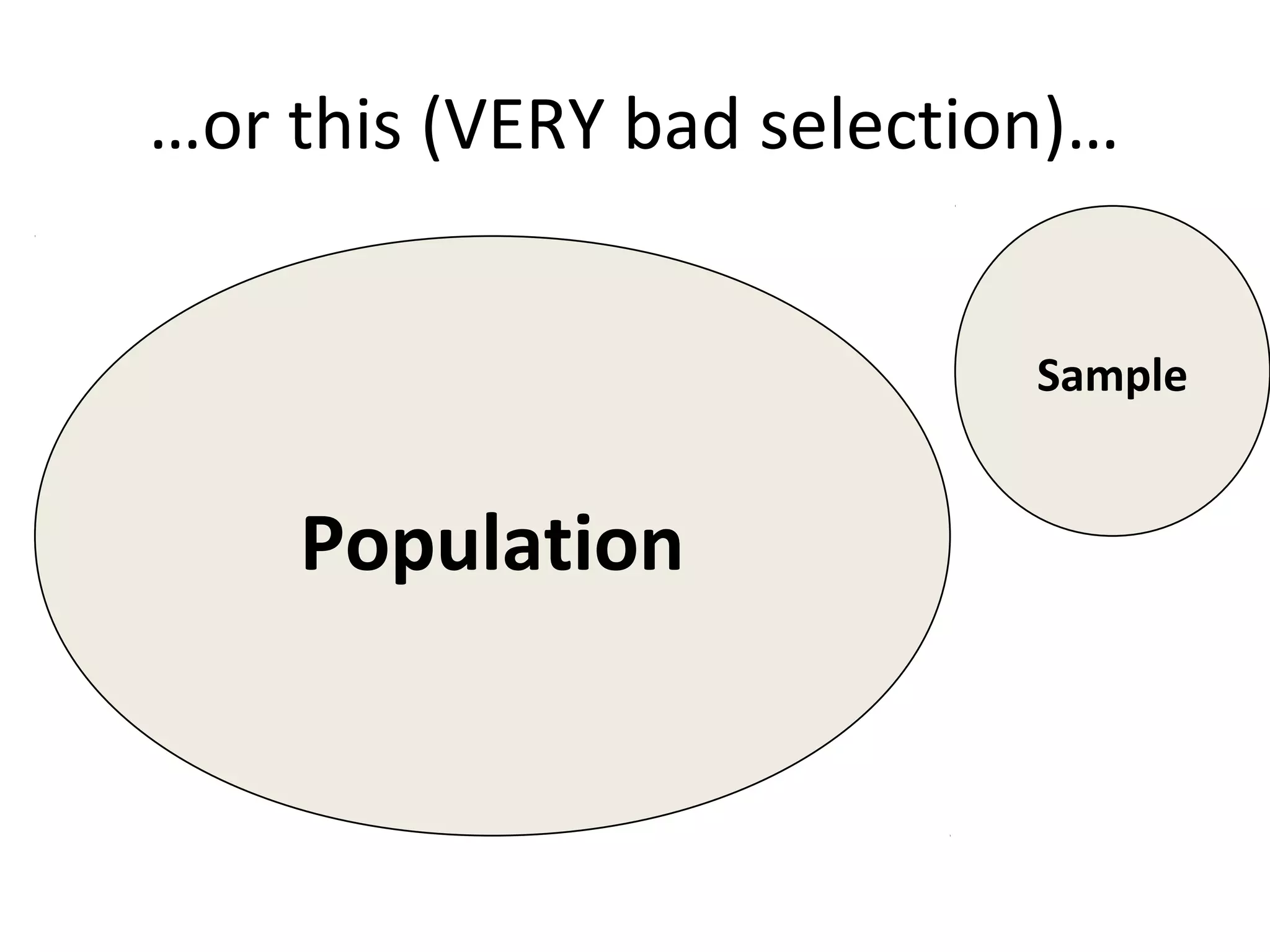
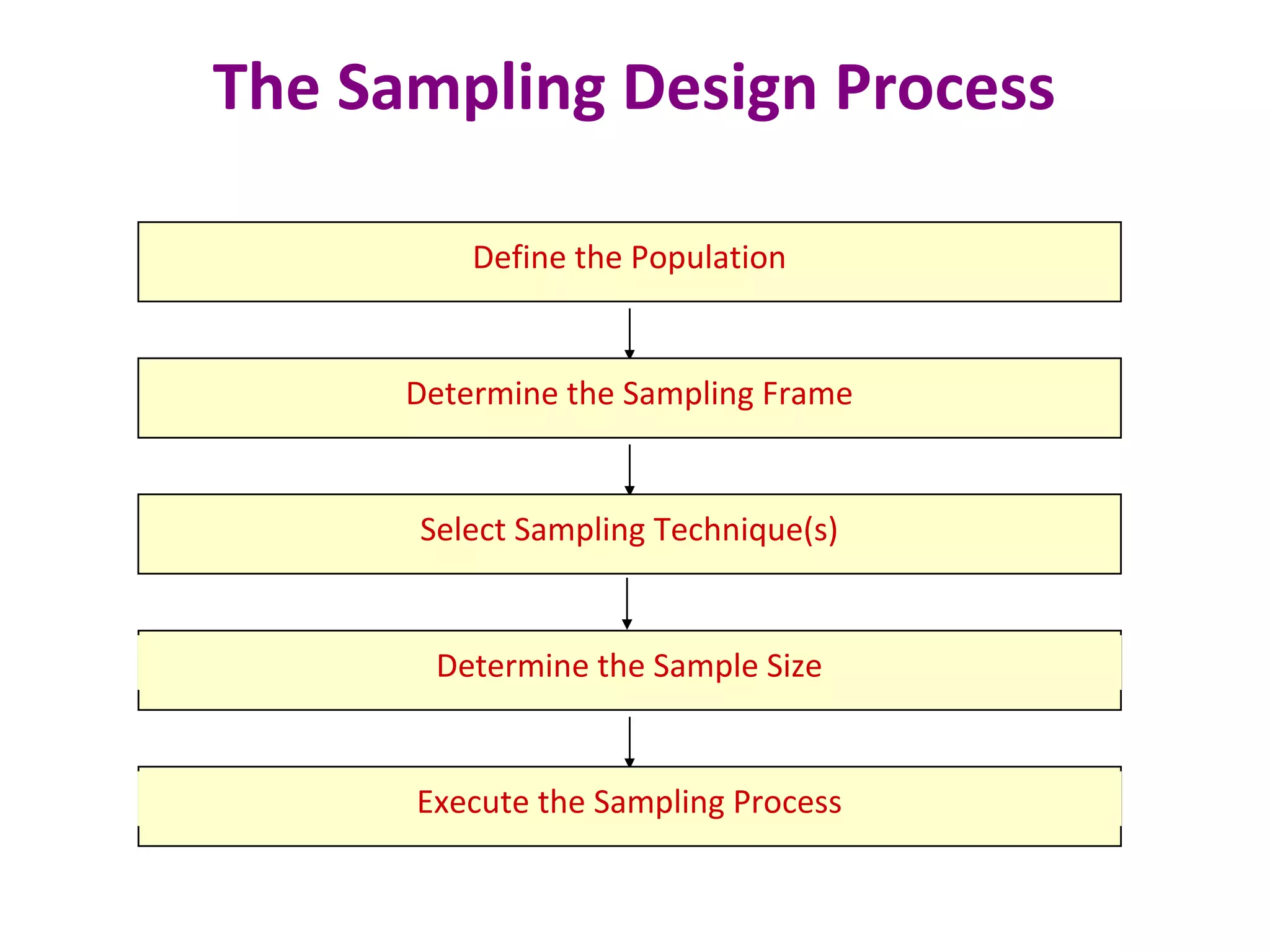
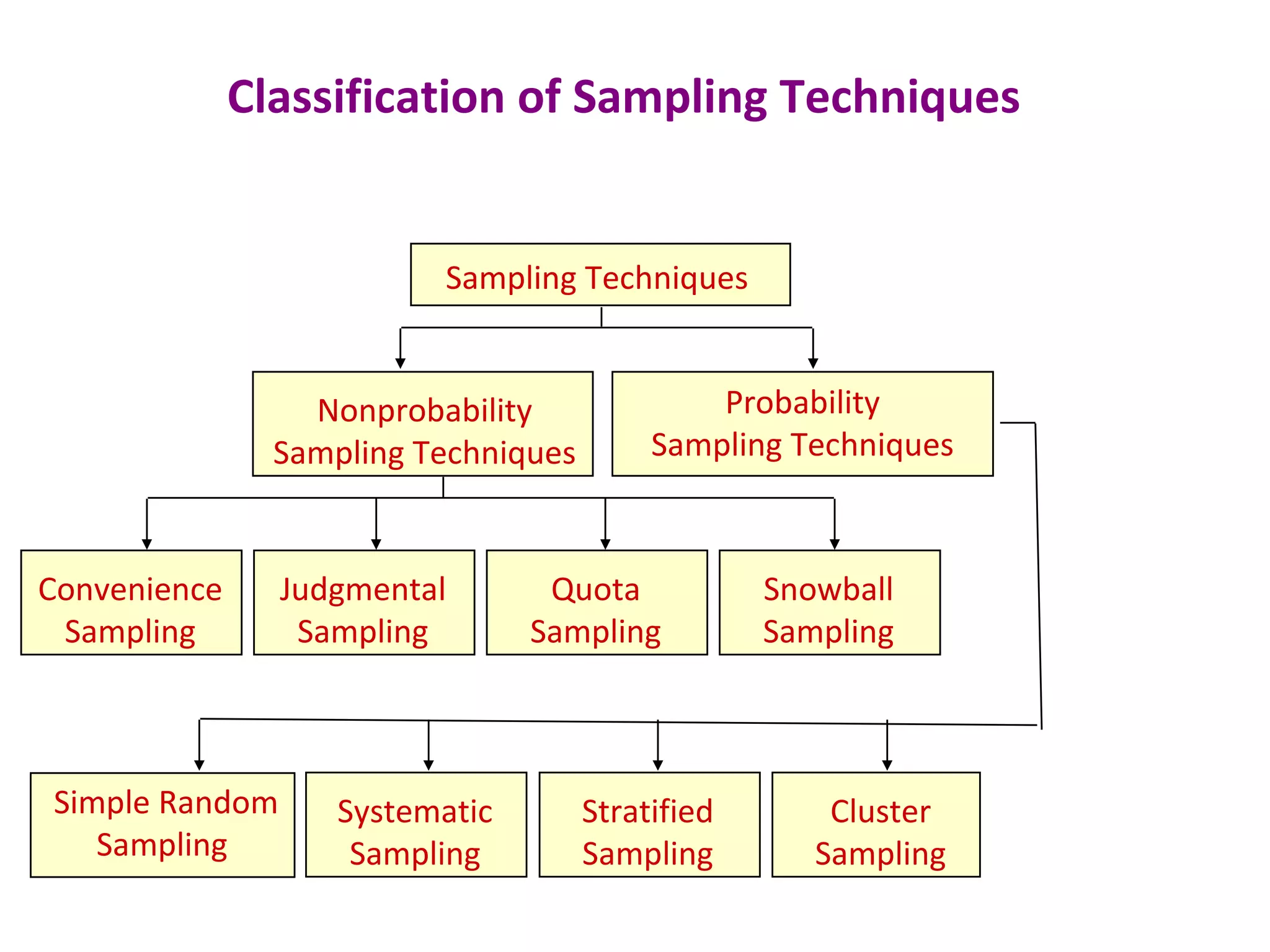
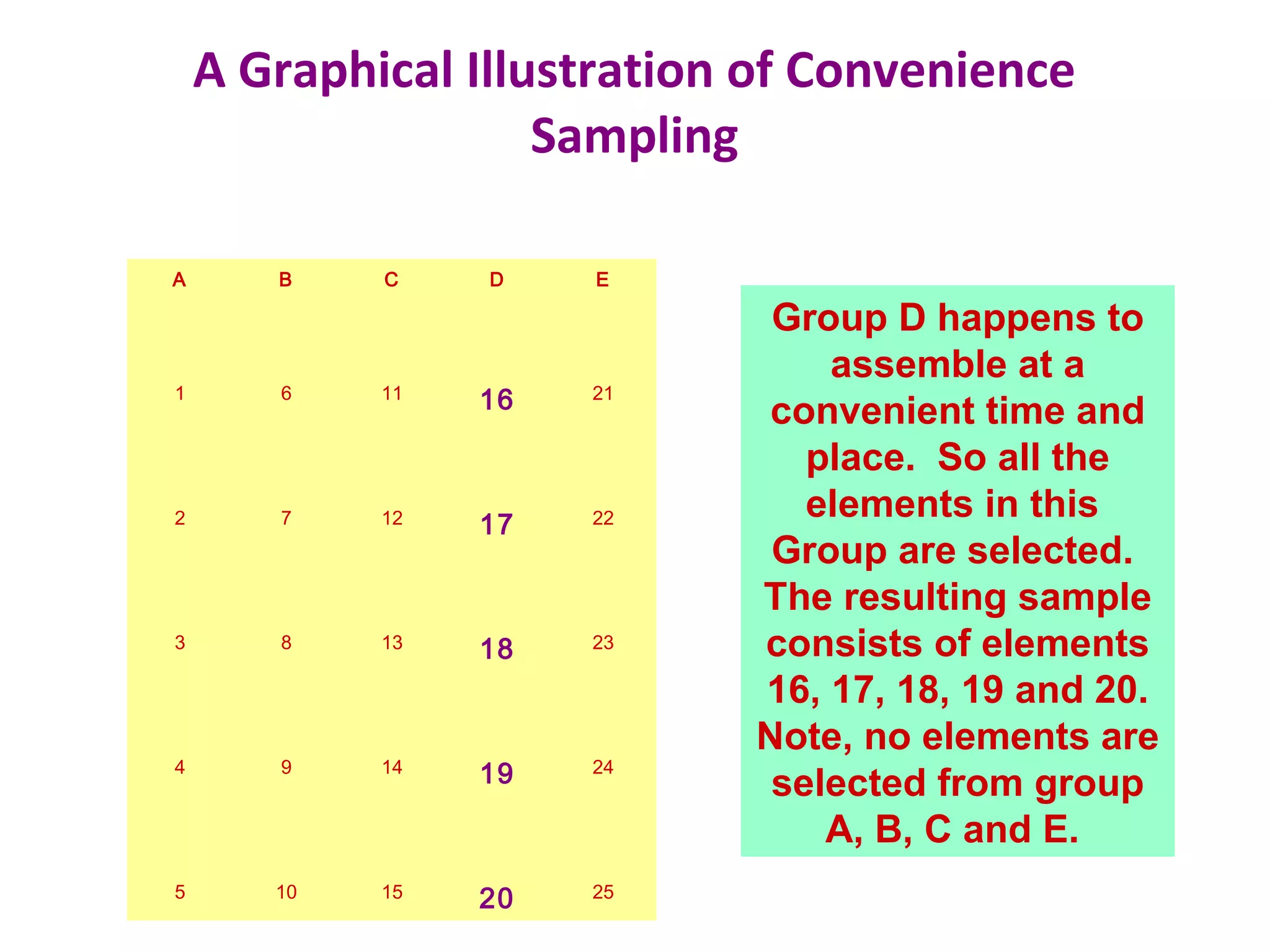
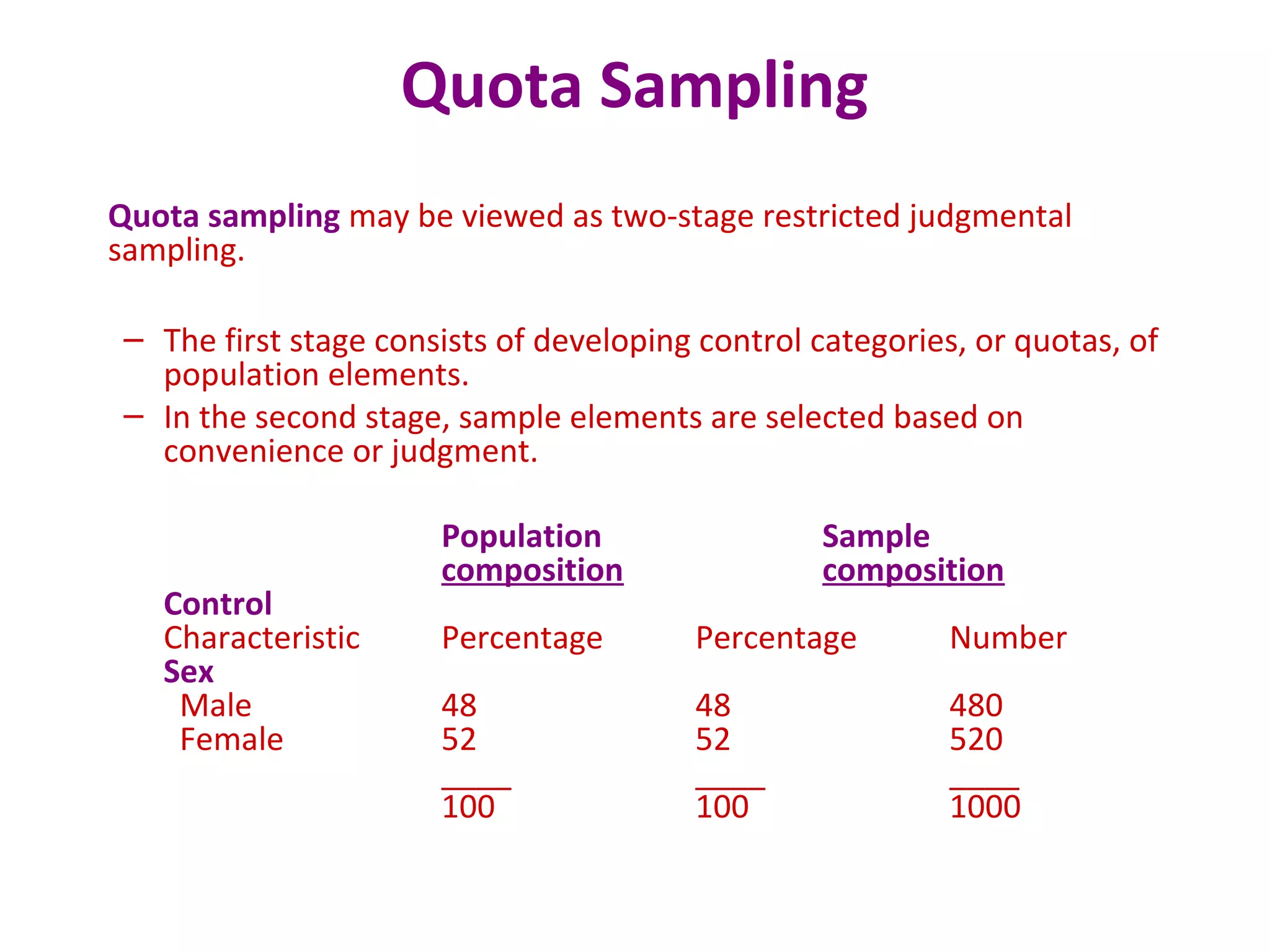
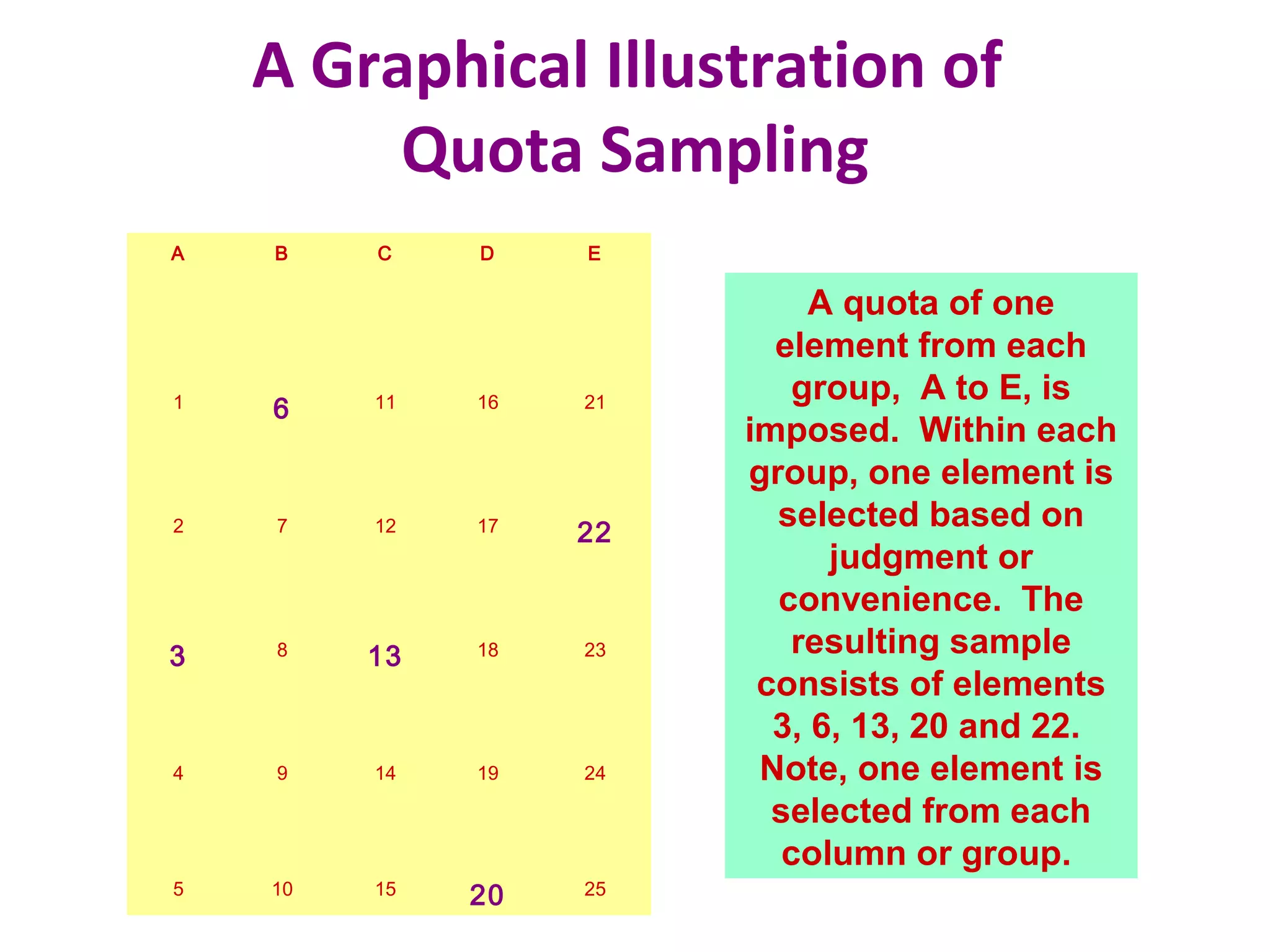
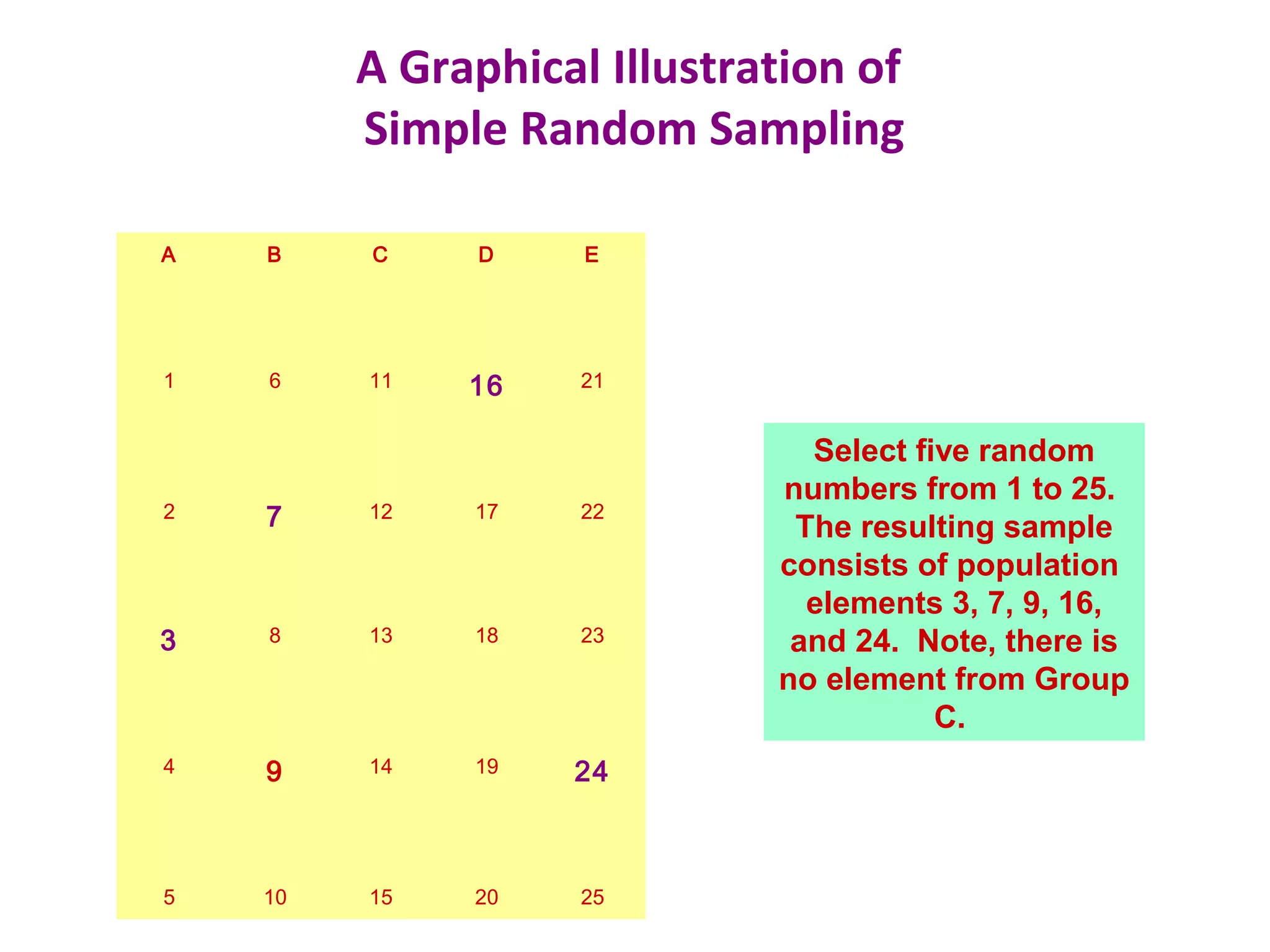
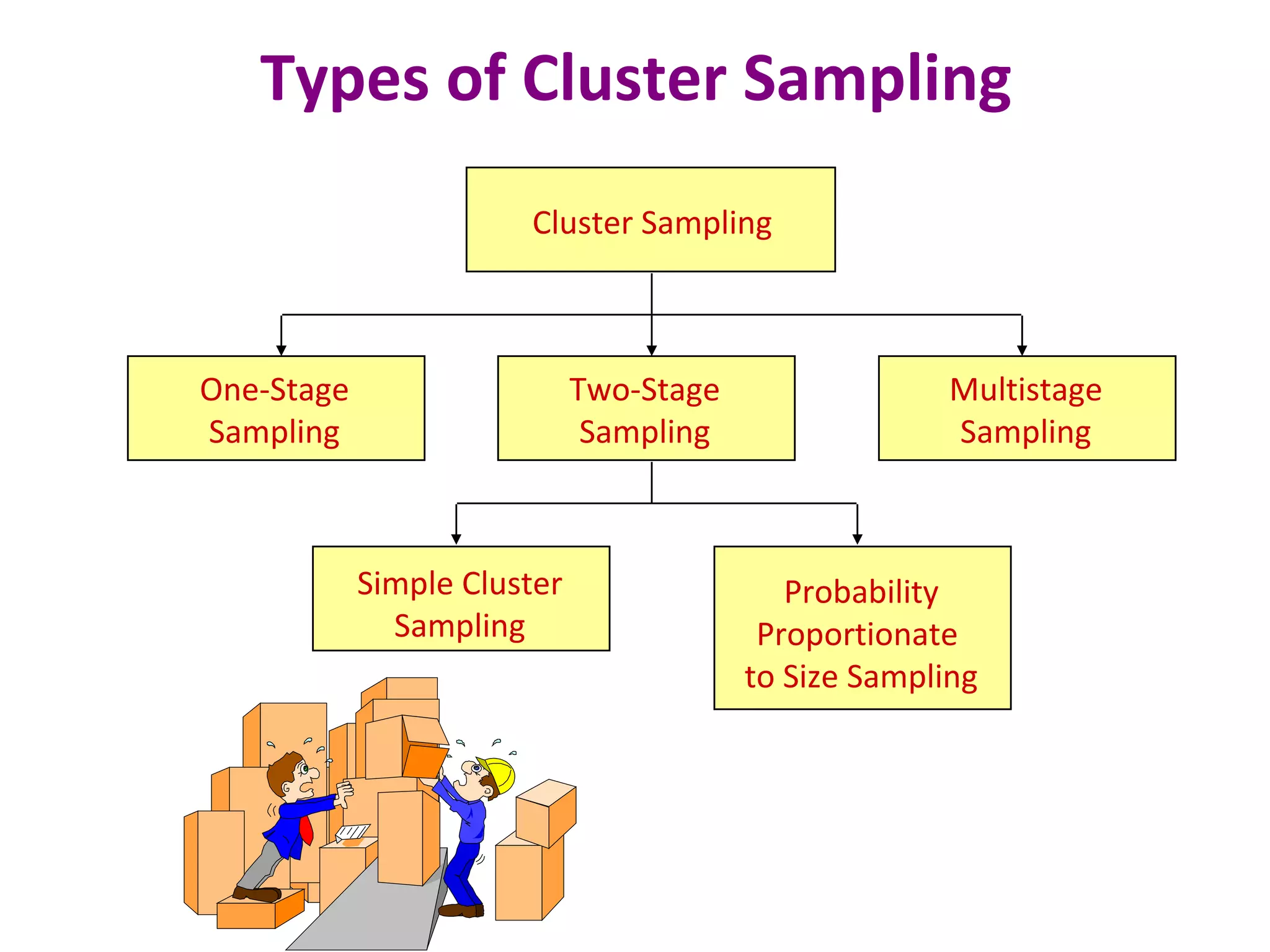
This document discusses various sampling techniques used in research. It defines key terms like population, sample, and sampling frame. It then describes and provides examples of different probability and non-probability sampling methods like simple random sampling, systematic sampling, stratified sampling, cluster sampling, convenience sampling, judgmental sampling, and quota sampling. The techniques are compared in terms of their strengths, weaknesses, and suitability for different research situations.

1. UNIT-II
Sample
&
Sample Design

2. Some basic terms
• Population
• Census
• Sample
• Sampling Unit
• Sampling Frame

3. …wrong selection…
Population
Sample

4. …or this (VERY bad selection)…
Population
Sample

5. Population Vs. Sample
Population of Interest
Sample
We measure the sample using statistics in order to draw
inferences about the population and its parameters.

6.  The process of obtaining information from a
subset (sample) of a larger group (population)
 The results for the sample are then used to
make estimates of the larger group
 Faster and cheaper than asking the entire
population…..
Sampling

7. Advantages of Sampling
• Economy
• Speed
• Accuracy
• Reliability
• Detailed Study
• Scientific Base
• Greater Suitability in most Situations
In cases, when the universe is very large, then the
sampling method is the only practical method for
collecting the data.

8. Limitations of Sampling
• Less Accuracy
• Changeability of Units
• Misleading Conclusion
• Need for specialized knowledge
• When sampling is not possible

9. The Sampling Design Process
Define the Population
Determine the Sampling Frame
Select Sampling Technique(s)
Determine the Sample Size
Execute the Sampling Process

10. Classification of Sampling Techniques
Sampling Techniques
Nonprobability
Sampling Techniques
Probability
Sampling Techniques
Convenience
Sampling
Judgmental
Sampling
Quota
Sampling
Snowball
Sampling
Systematic
Sampling
Stratified
Sampling
Cluster
Sampling
Simple Random
Sampling

11. Convenience Sampling
Convenience sampling attempts to obtain a sample of
convenient elements. Often, respondents are selected
because they happen to be in the right place at the right
time.

12. A Graphical Illustration of Convenience
Sampling
A B C D E
1 6 11 16 21
2 7 12 17 22
3 8 13 18 23
4 9 14 19 24
5 10 15 20 25
Group D happens to
assemble at a
convenient time and
place. So all the
elements in this
Group are selected.
The resulting sample
consists of elements
16, 17, 18, 19 and 20.
Note, no elements are
selected from group
A, B, C and E.

13. Judgmental Sampling
Judgmental sampling is a form of convenience
sampling in which the population elements are
selected based on the judgment of the researcher.

14. Graphical Illustration of Judgmental
Sampling
A B C D E
1 6 11 16 21
2 7 12 17 22
3 8 13 18 23
4 9 14 19 24
5 10 15 20 25
The researcher
considers groups B, C
and E to be typical and
convenient. Within each
of these groups one or
two elements are
selected based on
typicality and
convenience. The
resulting sample
consists of elements 8,
10, 11, 13, and 24. Note,
no elements are selected
from groups A and D.

15. Quota Sampling
Quota sampling may be viewed as two-stage restricted judgmental
sampling.
– The first stage consists of developing control categories, or quotas, of
population elements.
– In the second stage, sample elements are selected based on
convenience or judgment.
Population Sample
composition composition
Control
Characteristic Percentage Percentage Number
Sex
Male 48 48 480
Female 52 52 520
____ ____ ____
100 100 1000

16. A Graphical Illustration of
Quota Sampling
A B C D E
1 6 11 16 21
2 7 12 17 22
3 8 13 18 23
4 9 14 19 24
5 10 15 20 25
A quota of one
element from each
group, A to E, is
imposed. Within each
group, one element is
selected based on
judgment or
convenience. The
resulting sample
consists of elements
3, 6, 13, 20 and 22.
Note, one element is
selected from each
column or group.

17. Snowball Sampling
In snowball sampling, an initial group of respondents is
selected, usually at random.
– After being interviewed, these respondents are asked
to identify others who belong to the target population
of interest.
– Subsequent respondents are selected based on the
referrals.

18. A Graphical Illustration of
Snowball Sampling
A B C D E
1 6 11 16 21
2 7 12 17 22
3 8 13 18 23
4 9 14 19 24
5 10 15 20 25
Elements 2 and 9 are selected
randomly from groups A and
B. Element 2 refers elements
12 and 13. Element 9 refers
element 18. The resulting
sample consists of elements
2, 9, 12, 13, and 18. Note,
there are no element from
group E.
Random Selection
Referrals

19. Simple Random Sampling
• Each element in the population has a known and
equal probability of selection.
• Each possible sample of a given size (n) has a known
and equal probability of being the sample actually
selected.
• This implies that every element is selected
independently of every other element.

20. A Graphical Illustration of
Simple Random Sampling
A B C D E
1 6 11 16 21
2 7 12 17 22
3 8 13 18 23
4 9 14 19 24
5 10 15 20 25
Select five random
numbers from 1 to 25.
The resulting sample
consists of population
elements 3, 7, 9, 16,
and 24. Note, there is
no element from Group
C.

21. Systematic Sampling
• The sample is chosen by selecting a random starting point
and then picking every ith element in succession from the
sampling frame.
• The sampling interval, i, is determined by dividing the
population size N by the sample size n and rounding to the
nearest integer.
• When the ordering of the elements is related to the
characteristic of interest, systematic sampling increases
the representativeness of the sample.

22. Systematic Sampling
• If the ordering of the elements produces a cyclical
pattern, systematic sampling may decrease the
representativeness of the sample.
For example, there are 100,000 elements in the
population and a sample of 1,000 is desired. In this case
the sampling interval, i, is 100. A random number
between 1 and 100 is selected. If, for example, this
number is 23, the sample consists of elements 23, 123,
223, 323, 423, 523, and so on.

23. A Graphical Illustration of
Systematic Sampling
A B C D E
1 6 11 16 21
2 7 12 17 22
3 8 13 18 23
4 9 14 19 24
5 10 15 20 25
Select a random number
between 1 to 5, say 2.
The resulting sample
consists of population 2,
(2+5=) 7, (2+5x2=) 12,
(2+5x3=)17, and (2+5x4=) 22.
Note, all the elements are
selected from a single row.

24. Stratified Sampling
• A two-step process in which the population is partitioned
into subpopulations, or strata.
• The strata should be mutually exclusive and collectively
exhaustive in that every population element should be
assigned to one and only one stratum and no population
elements should be omitted.
• Next, elements are selected from each stratum by a random
procedure, usually SRS.
• A major objective of stratified sampling is to increase
precision without increasing cost.

25. Stratified Sampling
• The elements within a stratum should be as
homogeneous as possible, but the elements in different
strata should be as heterogeneous as possible.
• The stratification variables should also be closely
related to the characteristic of interest.
• Finally, the variables should decrease the cost of the
stratification process by being easy to measure and
apply.

26. Stratified Sampling
• In proportionate stratified sampling, the size of the
sample drawn from each stratum is proportionate to the
relative size of that stratum in the total population.
• In disproportionate stratified sampling, the size of the
sample from each stratum is proportionate to the relative
size of that stratum and to the standard deviation of the
distribution of the characteristic of interest among all the
elements in that stratum.

27. A Graphical Illustration of
Stratified Sampling
A B C D E
1 6 11 16 21
2 7 12 17 22
3 8 13 18 23
4 9 14 19 24
5 10 15 20 25
Randomly select a number
from 1 to 5
for each stratum, A to E. The
resulting
sample consists of
population elements
4, 7, 13, 19 and 21. Note, one
element
is selected from each
column.

28. Cluster Sampling
• The target population is first divided into mutually
exclusive and collectively exhaustive subpopulations, or
clusters.
• Then a random sample of clusters is selected, based on a
probability sampling technique such as SRS.
• For each selected cluster, either all the elements are
included in the sample (one-stage) or a sample of
elements is drawn probabilistically (two-stage).

29. Cluster Sampling
• Elements within a cluster should be as heterogeneous
as possible, but clusters themselves should be as
homogeneous as possible. Ideally, each cluster should
be a small-scale representation of the population.
• In probability proportionate to size sampling, the
clusters are sampled with probability proportional to
size. In the second stage, the probability of selecting a
sampling unit in a selected cluster varies inversely with
the size of the cluster.

30. A Graphical Illustration of
Cluster Sampling (2-Stage)
A B C D E
1 6 11 16 21
2 7 12 17 22
3 8 13 18 23
4 9 14 19 24
5 10 15 20 25
Randomly select 3 clusters,
B, D and E.
Within each cluster,
randomly select one
or two elements. The
resulting sample
consists of population
elements 7, 18, 20, 21, and
23. Note, no elements are
selected from clusters A and
C.

31. Types of Cluster Sampling
Cluster Sampling
One-Stage
Sampling
Multistage
Sampling
Two-Stage
Sampling
Simple Cluster
Sampling
Probability
Proportionate
to Size Sampling

32. Technique Strengths Weaknesses
Nonprobability Sampling
Convenience sampling
Least expensive, least
time-consuming, most
convenient
Selection bias, sample not
representative, not recommended for
descriptive or causal research
Judgmental sampling Low cost, convenient,
not time-consuming
Does not allow generalization,
subjective
Quota sampling Sample can be controlled
for certain characteristics
Selection bias, no assurance of
representativeness
Snowball sampling Can estimate rare
characteristics
Time-consuming
Probability sampling
Simple random sampling
(SRS)
Easily understood,
results projectable
Difficult to construct sampling
frame, expensive, lower precision,
no assurance of representativeness.
Systematic sampling Can increase
representativeness,
easier to implement than
SRS, sampling frame not
necessary
Can decrease representativeness
Stratified sampling Include all important
subpopulations,
precision
Difficult to select relevant
stratification variables, not feasible to
stratify on many variables, expensive
Cluster sampling Easy to implement, cost
effective
Imprecise, difficult to compute and
interpret results
Strengths and Weaknesses of
Basic Sampling Techniques