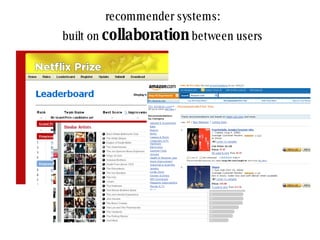
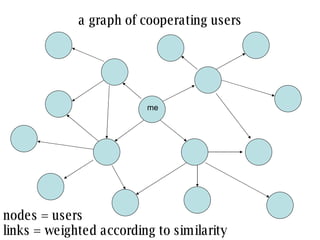
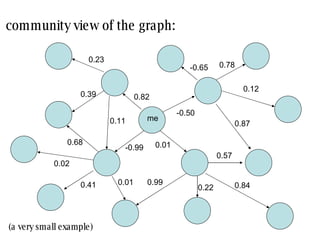
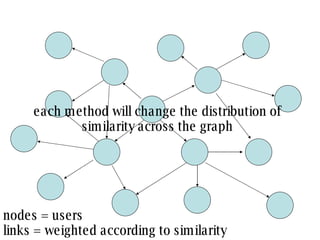
The document discusses collaborative filtering recommender systems which are built on collaboration between users. It focuses on k-nearest neighbors collaborative filtering, which can be modeled as a graph of cooperating users. The document examines different similarity measures that can be used to weight the links between users in the graph, and evaluates their impact on recommendation accuracy and coverage using a movie rating dataset. It also considers how the graph properties and communities of recommenders may evolve over time.

1. the effect of correlation coefficients on communities of recommenders neal lathia, stephen hailes, licia capra department of computer science university college london [email_address] ACM SAC TRECK, Fortaleza, Brazil: March 2008 Trust, Recommendations, Evidence and other Collaboration Know-how

2. recommender systems: built on collaboration between users

3. collaborative filtering research  design methods to solve problems accuracy, coverage data sparsity, cold-start incorporating tag knowledge for example,

4. … a method to classify content correctly data   predicted ratings intelligent process our focus: k-nearest neighbours (kNN)

5. how do we model kNN collaborative filtering?

6. a graph of cooperating users me nodes = users links = weighted according to similarity

7. accuracy, coverage to answer this question, we need to find the optimal weighting: the best similarity measure for the dataset, from the many available: and there are more still…

8. concordance: proportion of agreement +0.5 +3.0 -1.5 +1.5 +1.5 +/-? concordant discordant tied Somers’ d }

9. community view of the graph: -0.43 0.57 (a very small example) me -0.50 -0.65 0.12 0.87 0.01 0.57 0.84 0.22 0.99 0.82 0.23 0.39 0.11 0.68 0.02 0.41 0.01 -0.99 0.78

10. or, put another way: -0.43 0.57 (a very small example) me good bad none good good good good none none good bad bad good good good good none good good

11. what is the best way of generating the graph?

12. like this? -0.43 0.57 (a very small example) me good bad none none good bad bad good good good good good bad none none good none bad bad

13. or like this? -0.43 0.57 (a very small example) me good bad none good good good good none none bad bad bad good good good good none good good

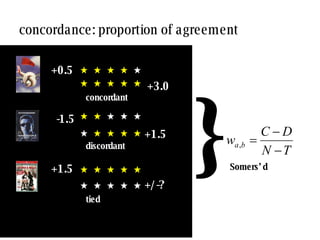
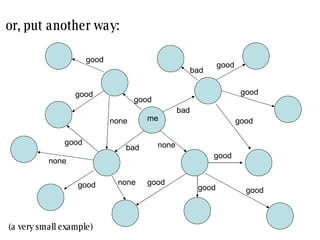
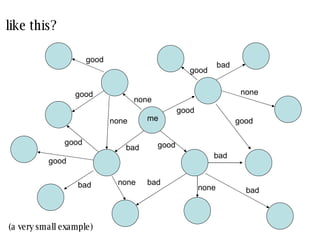
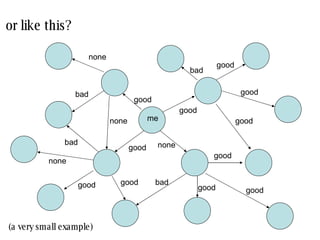
14. similarity values depend on the method used: there is no agreement between measures [2] [3] [1] [5] [3] [4] [1] [3] [2] [3]  my profile neighbour profile  pearson -0.50 weighted- pearson -0.05 cosine angle 0.76 co-rated proportion 1.00 concordance -0.06 bad near zero good very good near zero

15. each method will change the distribution of similarity across the graph nodes = users links = weighted according to similarity

16. … the pearson distribution  intelligent process

17. … the modified pearson distributions weighted-PCC, constrained-PCC

18. … and other measures  intelligent process somers’ d, co-rated, cosine angle

19. an experiment with random numbers

20. what happens if we do this? me java.util.Random r = new java.util.Random() for all neighbours i { similarity(i) = (r.nextDouble()*2.0)-1.0); }

21. accuracy  … cross-validation results in paper movielens u1 subset… 0.7811 0.7769 0.7773 0.8025 0.8073 0.7992 0.7718 459 0.8058 0.7992 0.7919 0.7679 0.7716 0.7771 0.7717 229 0.8024 0.8243 0.8053 0.7638 0.7817 0.7727 0.7726 153 0.8153 0.8511 0.8222 0.7647 0.8136 0.7728 0.7759 100 0.8498 0.8922 0.8584 0.7733 0.9007 0.7817 0.7852 50 0.8848 0.9108 0.8903 0.7847 0.9464 0.7931 0.7979 30 0.9689 0.9495 0.9595 0.8277 1.0455 0.8355 0.8498 10 1.0341 1.0406 1.0665 0.9596 1.1150 0.9492 0.9449 1 R(-1.0, 1.0) Constant(1.0) R(0.5, 1.0) wPCC PCC Somers’ d Co Rated Neighborhood

22. coverage  … cross-validation results in paper movielens u1 subset… (best coverage when all of community used) 0.00495 0.00495 0.00495 0.0054 0.00495 459 0.00495 0.00915 0.01165 0.00965 0.00715 229 0.00495 0.01135 0.0273 0.0122 0.00945 153 0.00495 0.01485 0.08345 0.01645 0.01515 100 0.00495 0.0251 0.3641 0.0266 0.03065 50 0.00495 0.04135 0.57225 0.0407 0.0512 30 0.00495 0.1114 0.80515 0.0999 0.15455 10 0.00495 0.61375 0.96725 0.57165 0.67795 1 Oracle wPCC PCC Somers’ d Co Rated Neighborhood

23. why do we get these results?

24. a) our error measures are not good enough? J. Herlocker, J. Konstan, L. Terveen, and J. Riedl. Evaluating collaborative filtering recommender systems. In ACM Transactions on Information Systems, volume 22, pages 5–53. ACM Press, 2004. S.M. McNee, J. Riedl, and J.A. Konstan. Being accurate is not enough: How accuracy metrics have hurt recommender systems . In Extended Abstracts of the 2006 ACM Conference on Human Factors in Computing Systems. ACM Press, 2006.

25. b) is there something wrong with the dataset?

26. c) is user-similarity not strong enough to capture the best recommender relationships in the graph?

27. one proposal… N. Lathia, S. Hailes, L. Capra. Trust-Based Collaborative Filtering. To appear In IFIPTM 2008: Joint iTrust and PST Conferences on Privacy, Trust management and Security. Trondheim, Norway. June 2008. is modelling filtering as a trust-management problem a potential solution? once we do that, more questions arise…

28. current work what other graph properties emerge from kNN collaborative filtering? how does the graph evolve over time? N. Lathia, S. Hailes, L. Capra. Evolving Communities of Recommenders: A Temporal Evaluation. Research Note RN/08/01, Department of Computer Science, University College London. Under Submission. N. Lathia, S. Hailes, L. Capra. kNN User Filtering: A Temporal Implicit Social Network. Current Work.

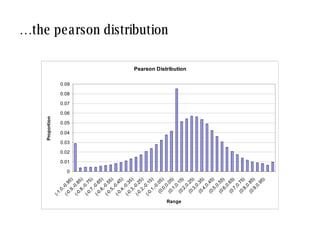
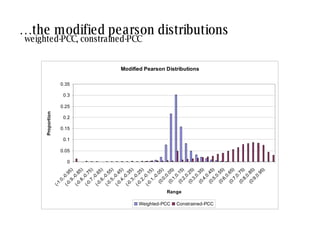
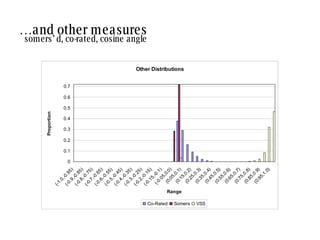
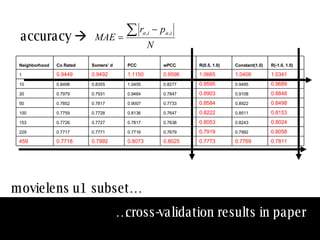
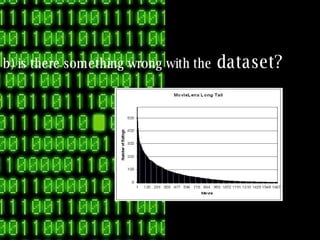
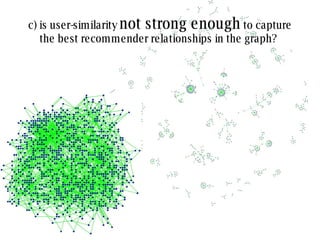
29. questions? read more: http://mobblog.cs.ucl.ac.uk trust, recommendations, … neal lathia, stephen hailes, licia capra department of computer science university college london [email_address] ACM SAC TRECK, Fortaleza, Brazil: March 2008 Trust, Recommendations, Evidence and other Collaboration Know-how